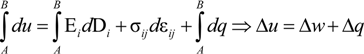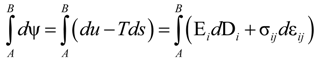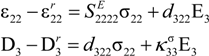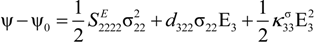1. Introduction
Ternary lead indium niobate-lead magnesium niobate-lead titanate,
xPb(In
1/2Nb
1/2)O
3-(1−
x−
y)Pb(Mg
1/3Nb
2/3)O
3-
yPbTiO
3 (PIN-PMN-PT) single crystals have been developed with the goal of expanding the thermal, mechanical, and electrical operating ranges of relaxor ferroelectrics while reducing the temperature dependence of the material coefficients. Compared to binary lead magnesium niobate-lead titanate, (1−
x)Pb(Mg
1/3Nb
2/3)O
3-
xPbTiO
3 (PMN-
xPT,
x = 0.28–0.33), which has a limited operating range, PIN-PMN-PT exhibits an increased coercive field (
EC: PIN-PMN-PT up to 0.7 MV/m, PMN-PT~0.25 MV/m), depoling temperature (
TR/T: PIN-PMN-PT up to 137 °C, PMN-PT < 97 °C) and Curie temperature (
TC: PIN-PMN-PT up to 200 °C, PMN-PT ~ 150 °C) [
1,
2,
3,
4,
5,
6,
7] while maintaining similar extraordinary piezoelectric and electromechanical properties [
8,
9,
10]. The high
TR/T, increased thermal operating range, increased coercive field, and large piezoelectric and electromechanical properties of PIN-PMN-PT with compositions near the morphotropic phase boundary (MPB) make this relaxor single crystal useful in transducer applications such as sonar and medical ultrasound [
11,
12,
13,
14]. Recently, [011]
C relaxor ferroelectric single crystals have also been used as a platform for studying magnetoelectric heterostructures due to the anisotropic transverse piezoelectric strain response of the domain engineered crystal cut [
15,
16]. Miller indices are used and the notation [
hkl]
C is used to indicate the directions are relative to a cubic phase.
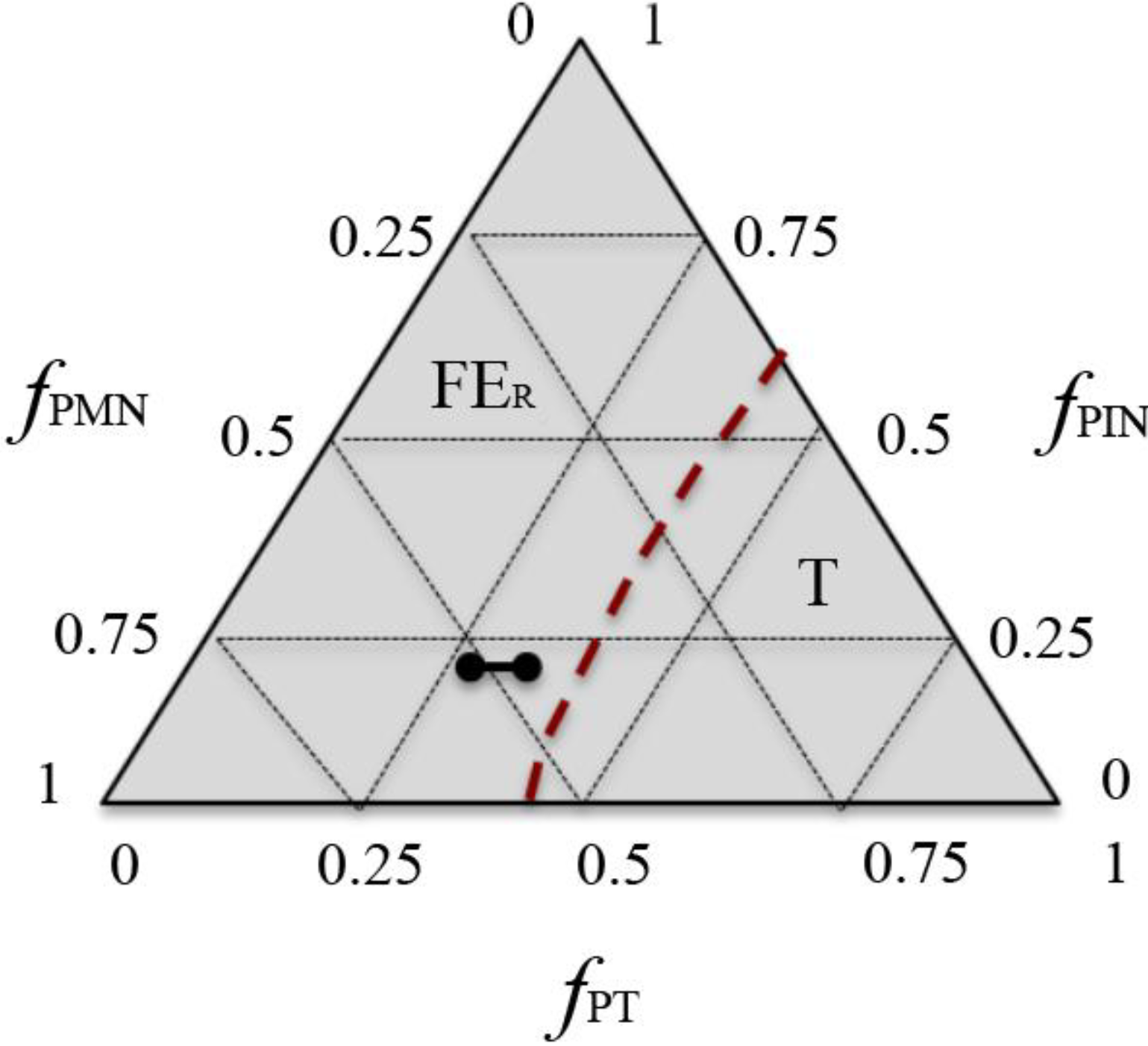
The material properties depend on composition, orientation, domain structure, and crystallographic phase [
17,
18]. The compositional dependence of the stable phases at room temperature and under no applied loading for the ternary PIN-PMN-PT system is shown in
Figure 1. As seen in the phase diagram
fPIN,
fPMN, and
fPT correspond to the concentration of each component and low PT concentration stabilizes the rhombohedral phase (FE
R) by reducing its Helmholtz energy density relative to other phases. The dashed line denotes the morphotropic phase boundary (MPB) that separates the rhombohedral from the tetragonal phase. The tetragonal phase is stable for higher concentrations of PT. Application of external loads above a certain threshold and in certain orientations relative to the crystal structure induces a phase transformation to a non-equilibrium phase [
19,
20,
21,
22]. Compositions of [011]
C cut and poled PMN-PT (
d32 mode) in the ferroelectric rhombohedral phase (FE
R) can be driven to the ferroelectric orthorhombic phase (FE
O) by an applied uniaxial compressive stress in the [100]
C direction or by an applied electric field in the [011]
C direction [
19,
21,
22]. Similar results were reported recently for PIN-PMN-PT [
23]. The polarization reorientation is shown schematically in
Figure 2. The mechanical and electrical loads shown work cooperatively to induce the transformations,
i.e., each provides a positive driving force for the transformation because the applied stress and electric field components shown do positive work on the strain and electric displacement change associated with the transformation. The FE
R-FE
O transformation is associated with a large non-linear and hysteretic jump in strain and electric displacement and the transformation from FE
R to FE
O results in large reductions in compliance, piezoelectric, and dielectric constants [
21,
22]. In this work experiments were run on [011]
C cut and poled
d32-mode PIN-PMN-PT single crystals in the FE
R phase to characterize their large field behavior under thermal and electromechanical loading. The effects of composition and temperature on the phase transition in two PT concentrations and at two different temperatures was compared. Non-linear material behavior was observed in the electric displacement-electric field, strain-electric field and stress-strain diagrams. The hysteretic jump is analyzed and discussed in some detail.
Figure 1.
Room temperature phase diagram for PIN-PMN-PT [
24]. The morphotropic phase boundary (MPB) between the ferroelectric rhombohedral (FE
R) and ferroelectric tetragonal (T) phases is depicted by the dashed red line. The black dots show the approximate compositions used in this work.
Figure 1.
Room temperature phase diagram for PIN-PMN-PT [
24]. The morphotropic phase boundary (MPB) between the ferroelectric rhombohedral (FE
R) and ferroelectric tetragonal (T) phases is depicted by the dashed red line. The black dots show the approximate compositions used in this work.
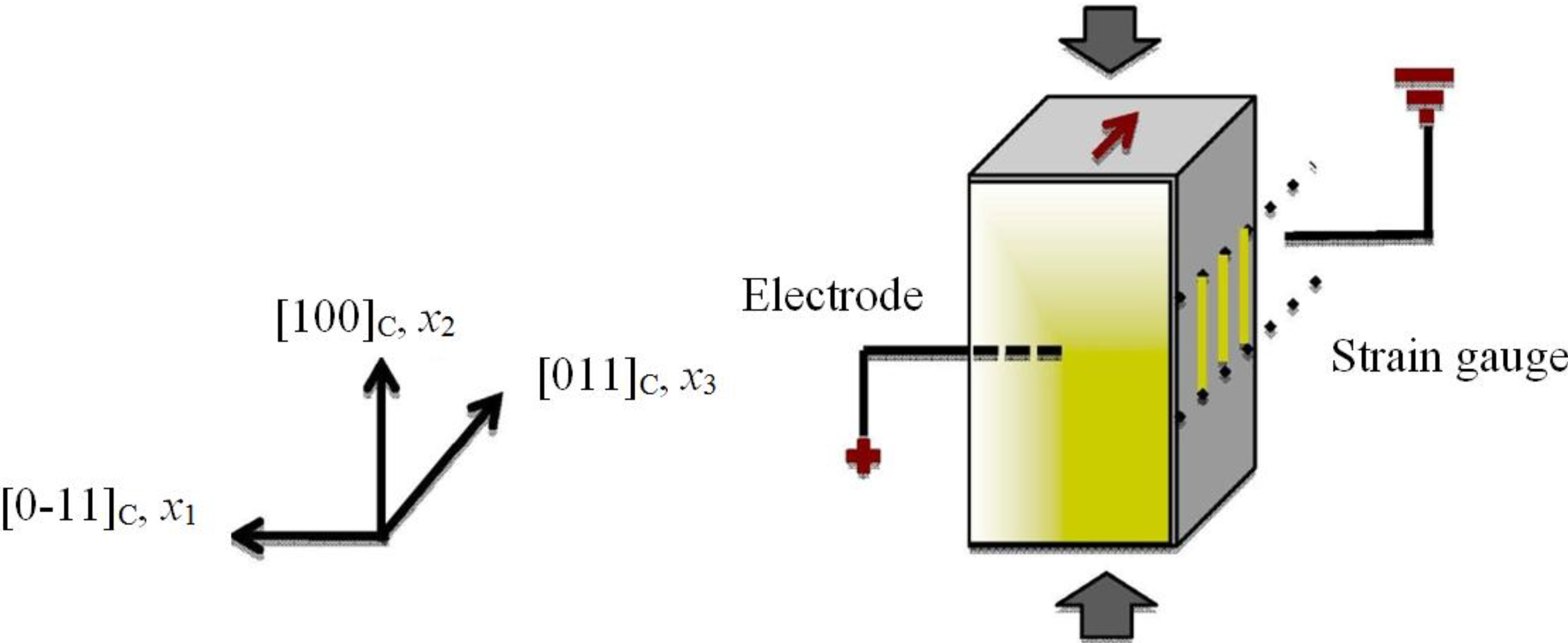
Figure 2.
Domain states and field driven phase transformations for [011]C cut and poled ferroelectric single crystals. (a) [011]C cut and poled single crystals made by cutting the single crystal at a 45 degree rotation about [100]C. Two of the <111> FER variants are populated with the volume average remanent polarization in the [011]C direction; (b) Compressive stress (σ22) in the [100]C direction induces a FER to FEO phase transformation where only the [011]C variant is populated; (c) Application of electric field (E3) in the [011]C direction induces the same FER-FEO transformation.
Figure 2.
Domain states and field driven phase transformations for [011]C cut and poled ferroelectric single crystals. (a) [011]C cut and poled single crystals made by cutting the single crystal at a 45 degree rotation about [100]C. Two of the <111> FER variants are populated with the volume average remanent polarization in the [011]C direction; (b) Compressive stress (σ22) in the [100]C direction induces a FER to FEO phase transformation where only the [011]C variant is populated; (c) Application of electric field (E3) in the [011]C direction induces the same FER-FEO transformation.
Non-linear behavior of ferroelectric materials can be described using a thermodynamics based approach outlined by Devonshire [
25]. This approach was extended in the phenomenological Landau-Devonshire theory that has been used to explain a range of phase transformations and nonlinearities in the material behavior [
26]. These phase transformations display jumps in the Helmholtz free energy and discontinuities in the derivatives of the Gibbs free energy and can be described using higher-order Devonshire theory. In this work, path integrals of experimental electric field—electric displacement and stress—strain curves were used to calculate the Helmholtz energy. Such an approach has previously been used to describe the multi-field transformation behavior of PMN-0.32PT and PZN-0.045PT [
27].
The thermodynamics based analysis was used to determine the effect of PT concentration on the energy associated with the transformation. Path integrals were used to determine the external work done by electrical and mechanical loading at two temperatures to induce the FER-FEO phase transformation. The heat generated during the loading cycle was removed from the external work by assuming equal parts of heat are generated by irreversible strain and electric displacement increments during the forward and reverse transformation. Although the phase transformation displays asymmetry, the assumption that half of the dissipation occurs on the forward transformation and half on the reverse transformation does not affect the results appreciably. The relative Helmholtz energy density levels of the phases was determined by fitting the linear behavior of the material on the rhombohedral and orthorhombic phases. The results are discussed in terms of the Landau-Devonshire theory for phase transformations.
3. Experimental Results
The measured nonlinear electromechanical response at 35 °C and 65 °C of 0.24PIN-PMN-
xPT for
x = 0.30 and
x = 0.32 PT is shown in
Figure 5. The electric displacement
vs. electric field and strain
vs. electric field response at zero applied stress are plotted in
Figure 5a,b respectively. The stress
vs. strain response at zero electric field is plotted in
Figure 5c. In both the electrical and mechanical loading, as the loading is increased past a certain threshold the specimen undergoes a phase transformation. It is assumed that due to the crystal cut of the specimens and the loading direction, the secondary phase has orthorhombic symmetry resulting from the polarization rotation of the <111> variants to the <011> direction, an FE
R to FE
O phase transformation. The phase transformation occurs with a well-defined hysteresis in the D
3-E
3, ε
22-E
3 and ε
22-σ
22 diagrams, enclosed by the forward (FE
R-FE
O) reverse (FE
O-FE
R) transformation paths.
Figure 5.
(a) D3-E3 (b) ε22-E and (c) ε22-σ22 loops for 0.24PIN-PMN-xPT for two different temperatures. The black lines correspond to x = 0.30 PT and the red lines to x = 0.32 PT with increasing PT percentage pointing towards the MPB. The solid and dashed lines correspond to low (35 °C) and high (65 °C) bath temperature respectively.
Figure 5.
(a) D3-E3 (b) ε22-E and (c) ε22-σ22 loops for 0.24PIN-PMN-xPT for two different temperatures. The black lines correspond to x = 0.30 PT and the red lines to x = 0.32 PT with increasing PT percentage pointing towards the MPB. The solid and dashed lines correspond to low (35 °C) and high (65 °C) bath temperature respectively.
The effect of increasing PT is evident in the electromechanical response and the phase transformation behavior as seen in
Figure 5a–c. In the D
3-E
3 plotted data for 0.30 PT and 0.32 PT concentration at 35 °C a small offset was detected in the electric displacement upon unloading to zero electric field. It was assumed that the offset was a result of a small leakage current in the system and the data were corrected by assuming a linear resistor in parallel with the specimen with resistance equal to the offset. The phase transformation for the 0.32 PT composition occurred with a sharp jump in the strain and electric displacement and a well-defined hysteresis width. On the other hand, the 0.30 PT composition exhibited a more distributed (FE
R-FE
O) and (FE
O-FE
R) transition and a distinct transformation threshold was not as clearly deduced. For both compositions the transformation pattern persisted at higher temperatures. The 0.32 concentration of PT, closer to the MPB, shows a lower threshold for transformation under electric field and stress. The polarization and strain changes associated with the transformation are larger for the composition closer to the MPB. As the temperature is increased, the transformation threshold is reduced for both compositions. The effect of temperature on the strain and polarization jumps is similar, both decrease with increasing temperature.
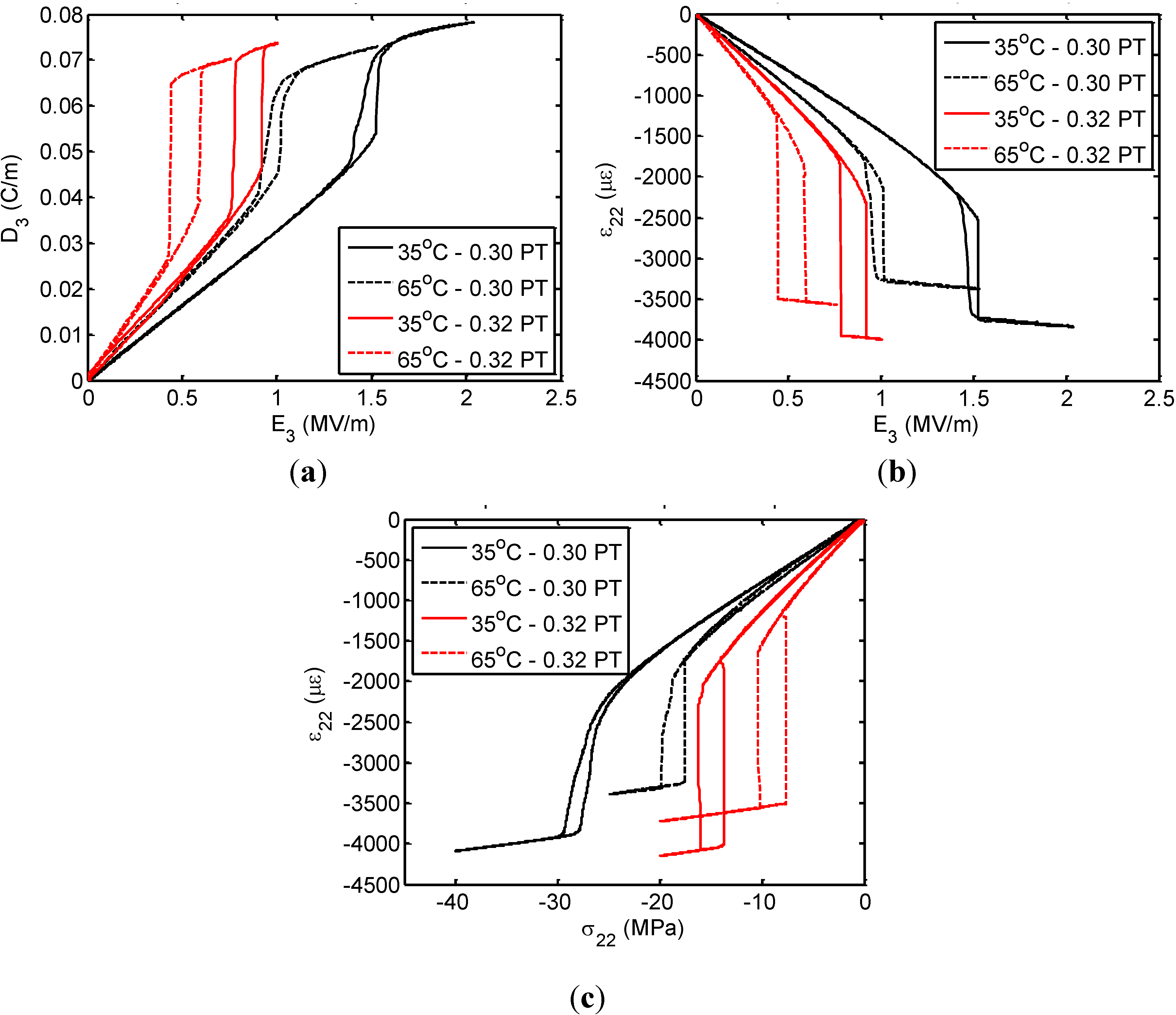
The decrease in the transformation threshold with increasing PT concentration and temperature is accompanied by a change in the corresponding material properties. As it can be seen from the D
3-E
3 loop, the
![Crystals 04 00377 i001]()
dielectric permittivity is larger in the composition closer to the MPB. There is a similar effect on the piezoelectric coefficient, leading to an increase of the
d32 parameter of ε
22-E and of the compliance
![Crystals 04 00377 i002]()
of ε
22-σ
22. Increasing the temperature led to a further increase of the dielectric and piezoelectric and compliance constants for both compositions, however the temperature dependence of the material properties is not the same for the two compositions.
The composition further from the MPB was more sensitive to the thermal loading,
i.e., there are larger slope changes with temperature in the FE
R phase and a larger reduction in the phase transformation threshold than in the composition closer to the MPB. The material constants were deduced by fitting the corresponding measured data in the linear regimes corresponding to the rhombohedral and orthorhombic phase when saturation was achieved are presented in
Table 1, together with error estimates. The phase transformation leads to a large decrease in the material dielectric, piezoelectric, and compliance constants, with the orthorhombic material constants being an order of magnitude less than the corresponding material constants of the rhombohedral phase.
Table 1.
Fitted material properties. κ0 = 8.855 × 10−12 F/m is the permittivity of free space.
Table 1.
Fitted material properties. κ0 = 8.855 × 10−12 F/m is the permittivity of free space.
| Fitted properties | x = 0.30 PT | x = 0.32 PT |
|---|
| 35 °C | 65 °C | 35 °C | 65 °C |
|---|
![Crystals 04 00377 i001]() /κ0 /κ0 |
| FER | 3260 ± 30 | 4573 ± 30 | 4320 ± 30 | 6381 ± 30 |
| FEO | 880 ± 30 | 960 ± 30 | 1290 ± 30 | 883 ± 30 |
| d32 (pC/N) |
| FER | −1436 ± 30 | −2022 ± 30 | −2052 ± 30 | −2708 ± 30 |
| FEO | −212 ± 30 | −259 ± 30 | −200 ± 30 | −277 ± 30 |
![Crystals 04 00377 i002]() (10−12 1/Pa) (10−12 1/Pa) |
| FER | 79 ± 3 | 94 ± 3 | 113 ± 3 | 183 ± 3 |
| FEO | 17 ± 3 | 26 ± 3 | 16 ± 3 | 18 ± 3 |
4. Thermodynamic Analysis
A thermodynamic based analysis of the data is presented in this section. It follows the analysis applied by Liu
et al. [
27] of field induced phase transformations in relaxor ferroelectric single crystals. The main points of the theory are given herein. The rate of change of internal energy in a stationary ferroelectric crystal in the absence of body forces and charges can be written in the local form as:
where
![Crystals 04 00377 i004]()
the change in internal energy density,
![Crystals 04 00377 i005]()
the rate of heat added by external sources and
ẇ =
ẇm +
ẇe the rate of work done on the body which, in the case of ferroelectric crystals, can be separated in a mechanical and an electrical part. Assuming that the elastic and electric behavior of the ferroelectric is fully described by the components of electric field E
i electric displacement D
i the components of the Cauchy stress tensor, σ
ij and the small deformation strain, ε
ij the incremental form of the above equation can be written as:
For the material under consideration the electric displacement and mechanical strain can be represented by a summation of a reversible (elastic) part,
![Crystals 04 00377 i006]()
and
![Crystals 04 00377 i007]()
, and an irreversible (dissipative) part,
![Crystals 04 00377 i008]()
and
![Crystals 04 00377 i009]()
associated with the dissipation that arises during to domain wall motion and phase transformation in the material upon loading and unloading. Substitution of the additive decomposition of the strain and electric displacement increments in Equation (2) gives:
where
T is the temperature and s the entropy density. Equation (3) implies that the work done by the irreversible parts of the strain and electric displacement increments contributes to the total dissipation resulting in an increase of the thermal energy in the body according to the second law of thermodynamics. Integrating Equation (2) along a loading path we have:
Note that ∆q = 0 under adiabatic loading conditions where there is no heat transfer between the body and the surroundings, which will result in a temperature increase in the body due to dissipation. If the loading process is isothermal and under a full cycle of loading where the electric and mechanical loads return to the same point, and the loading rate is sufficiently slow that temperature gradients in the specimen can be neglected, the ∆q term in the second part of Equation (4) represents the heat generated due to the dissipation in the material since ∆u= 0 and ∆q = −∆w Although the phase transformation itself may be adiabatic due to the transformation rate, the dissipation associated with the forward/reverse phase transformation does not change the temperature enough to affect the transformation. The specific heat is around 0.5 kJ/kg-K, the density is around 7800 kg/m3 and the dissipation is around 5 kJ/m3. The temperature change in a single cycle associated with this dissipation is on the order of 0.002 degrees.
Therefore during a closed loading cycle under quasi-isothermal conditions we have:
Equation (5) is applied directly to integrate measured experimental data for the mechanical and electrical loading cycles and any offset represents the heat generated due to dissipation in the material. This offset is equal to the area within the hysteresis loops. The results are shown in
Figure 6.
Figure 6a shows the numerical integration results for the electric field cycle data reported in
Figure 5a. Note that in this case only the electric term of the first part of Equation (5) contributes to the work done on the material.
Figure 6b, represents the integrated work done on the material during the stress cycle data that was presented in
Figure 5c. The inserts in
Figure 6a,b are a close up of the offset of the integrated electrical and mechanical work that, as stated above, represent the heat generated due to the dissipative part of the loading. A first observation of the integrated work is that the amount of heat generated during the loading cycles is approximately 5.6 kJ/m
3 for the 0.32 PT, and approximately 2 kJ/m
3 for the 0.30 PT concentrations. The effect of temperature on the dissipation is very small, within the margin of error of the experimental data. The effect of PT concentration on the dissipation is in accordance with the area of the hysteresis loops in D
3-E
3 and ε
22-σ
22 of
Figure 5a,c respectively. The material with PT concentration closer to the MPB dissipates approximately twice as much energy as the material with PT concentration away from the boundary. The dissipation in the material during the phase transformation under mechanical or electrical loading is almost equal for a given composition.
Figure 6.
Integrated work done during the (a) electric field and (b) stress loading. The insert is a close up to the amount of heat generated by the irreversible electric displacement and strain increments for the x = 0.30 PT and x = 0.32 PT at 35 °C and 65 °C.
Figure 6.
Integrated work done during the (a) electric field and (b) stress loading. The insert is a close up to the amount of heat generated by the irreversible electric displacement and strain increments for the x = 0.30 PT and x = 0.32 PT at 35 °C and 65 °C.
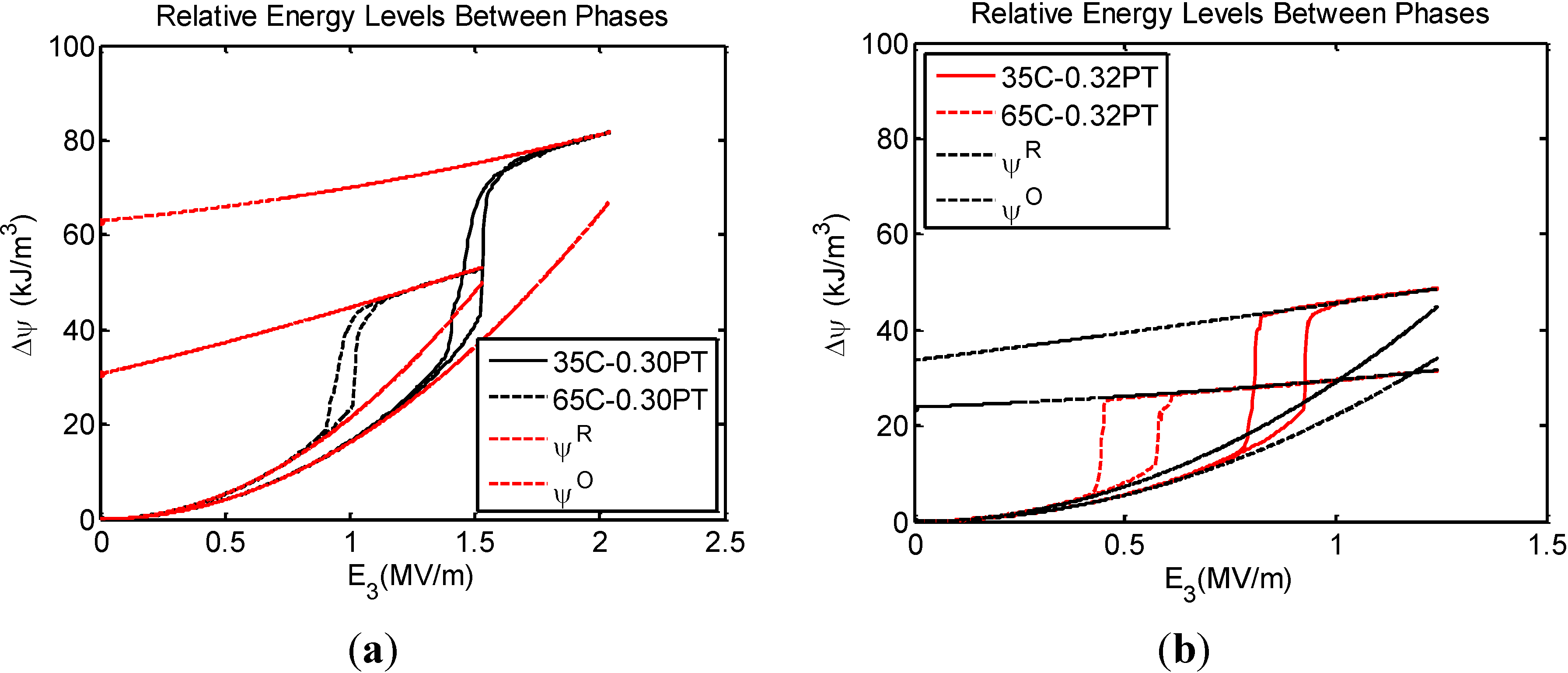
Relative changes in the Helmholtz energy levels of the rhombohedral and orthorhombic phases were determined using the results of
Figure 6, obtained by applying Equation (5) to the measured experimental data. The effect of the heat generated during the loading cycles was removed by assuming that the energy dissipated during the full loading cycle can be divided into equal parts during the loading and unloading. This assumption is supported to great extent by the hysteretic paths during the loading and unloading cycles retaining similar symmetry for a given PT concentration at both temperatures. For the full loading cycle after correction for the offset associated with the dissipation, the Helmholtz free energy is given by Equation (6):
Figure 7 shows the Helmholtz free energy after subtracting the heat generated from the work done during the electric loading cycle for the two concentrations at 35 °C. As shown and discussed in
Section 3 the PT concentration has an effect on phase transformation behavior of the material. For the PT concentration closer to the MPB boundary the transformation is abrupt and the transformation threshold and polarization jump are clearly associated with a distinct field value. In this case it is assumed that the dissipation is constant with respect to the electric displacement increment and half of the dissipation takes place during the forward transformation and the other half during the reverse transformation. For the PT concentration away from the MPB, the transformation is distributed and the threshold not as clearly associated with a single distinct field value. Here it was assumed that dissipation was distributed equally between the forward and reverse transformation paths but in this case the dissipation was taken to be linear with respect to the electric displacement increment. Applying these assumptions gives the plots shown in
Figure 7, with no offset in the Helmholtz free energy upon unloading and a slight change in slope on the part corresponding to the loading and unloading of the orthorhombic phase.
Figure 7.
Helmholtz free energy obtained by subtracting the dissipation from the external work done during the loading cycle.
Figure 7.
Helmholtz free energy obtained by subtracting the dissipation from the external work done during the loading cycle.
Since the material behavior is linear for the parts corresponding to the FE
R phase before the forward transformation and the FE
O phase after the forward and before the reverse transformation they can be represented by the linear piezoelectric Equation (7):
The quadratic form of the Helmholtz free energy corresponding to the above constitutive equations is then written as:
Here ψ
0 is a reference free energy level at zero electric field and zero stress. Using the fitted data reported in
Table 1 the quadratic forms of the free energy corresponding to the linear regime in the FE
R or FE
O phases are superimposed on the Helmholtz energy plots. This enables extrapolation of the energy of the FE
O phase to zero load, giving the energy difference between the phases.
Figure 8 shows the relative free energy levels of the FE
R and FE
O phases for the PT concentration closer to the MPB at two different temperatures. The relative change of free energy between the phases is overall smaller for the PT concentration closer to the MPB, which implies a lower energy barrier to the transformation.
Figure 8.
Relative free energy levels the FER and FEO phases for the PT concentration closer to the MPB boundary at 35 °C and 65 °C.
Figure 8.
Relative free energy levels the FER and FEO phases for the PT concentration closer to the MPB boundary at 35 °C and 65 °C.

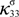 dielectric permittivity is larger in the composition closer to the MPB. There is a similar effect on the piezoelectric coefficient, leading to an increase of the d32 parameter of ε22-E and of the compliance
dielectric permittivity is larger in the composition closer to the MPB. There is a similar effect on the piezoelectric coefficient, leading to an increase of the d32 parameter of ε22-E and of the compliance  of ε22-σ22. Increasing the temperature led to a further increase of the dielectric and piezoelectric and compliance constants for both compositions, however the temperature dependence of the material properties is not the same for the two compositions.
of ε22-σ22. Increasing the temperature led to a further increase of the dielectric and piezoelectric and compliance constants for both compositions, however the temperature dependence of the material properties is not the same for the two compositions.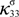 /κ0
/κ0 (10−12 1/Pa)
(10−12 1/Pa)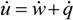
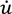 the change in internal energy density,
the change in internal energy density, 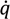 the rate of heat added by external sources and ẇ = ẇm + ẇe the rate of work done on the body which, in the case of ferroelectric crystals, can be separated in a mechanical and an electrical part. Assuming that the elastic and electric behavior of the ferroelectric is fully described by the components of electric field Ei electric displacement Di the components of the Cauchy stress tensor, σij and the small deformation strain, εij the incremental form of the above equation can be written as:
the rate of heat added by external sources and ẇ = ẇm + ẇe the rate of work done on the body which, in the case of ferroelectric crystals, can be separated in a mechanical and an electrical part. Assuming that the elastic and electric behavior of the ferroelectric is fully described by the components of electric field Ei electric displacement Di the components of the Cauchy stress tensor, σij and the small deformation strain, εij the incremental form of the above equation can be written as:
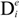 and
and 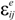 , and an irreversible (dissipative) part,
, and an irreversible (dissipative) part, 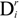 and
and 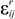 associated with the dissipation that arises during to domain wall motion and phase transformation in the material upon loading and unloading. Substitution of the additive decomposition of the strain and electric displacement increments in Equation (2) gives:
associated with the dissipation that arises during to domain wall motion and phase transformation in the material upon loading and unloading. Substitution of the additive decomposition of the strain and electric displacement increments in Equation (2) gives: