High-Q Defect-Free 2D Photonic Crystal Cavity from Random Localised Disorder
Abstract
:1. Introduction
2. Theory and Method



3. Results and Discussion
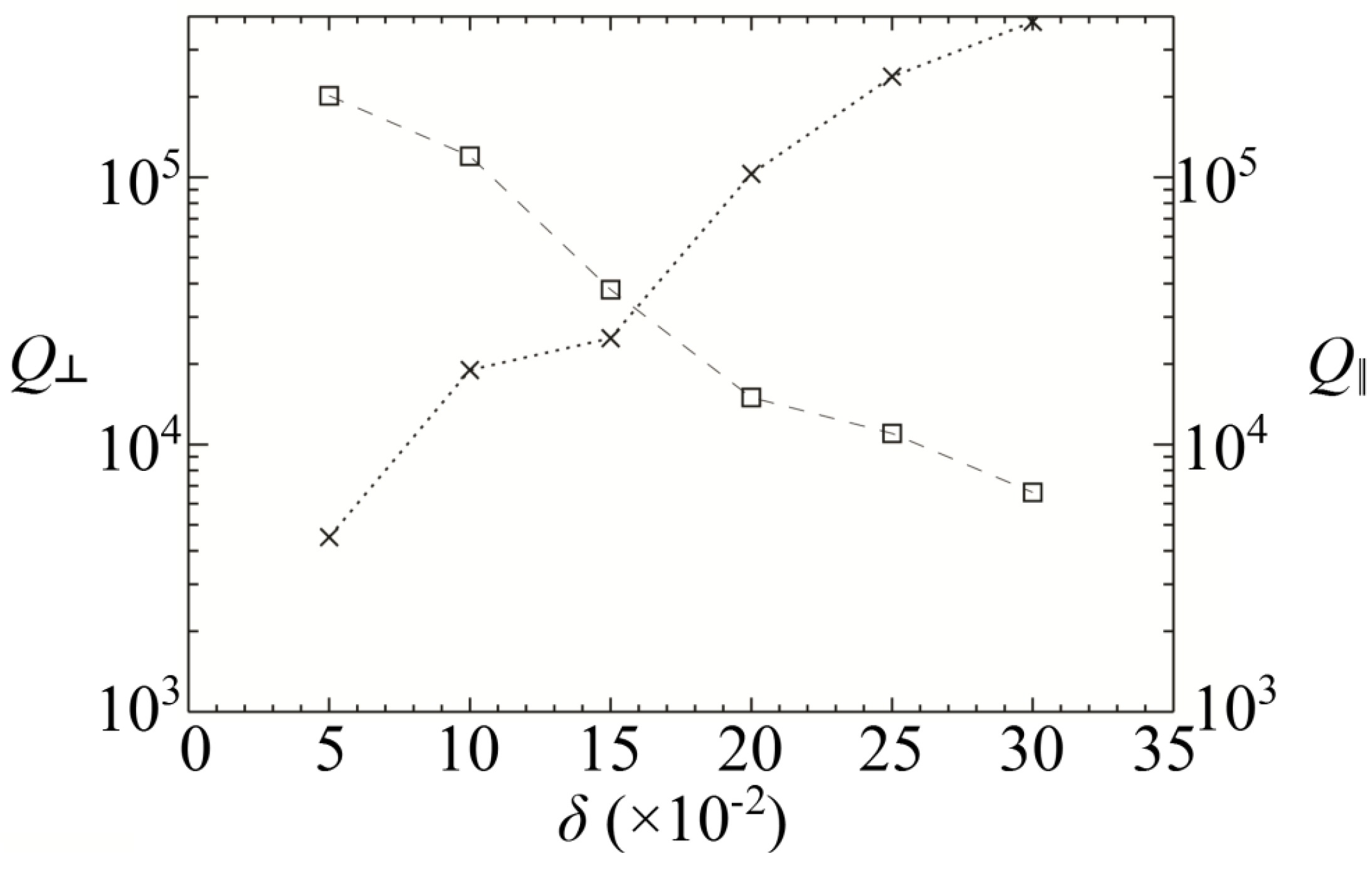
3.1. Total, Partial Qs and Purcell Effect
| δ | Q⊥ (×104) | Q|| (×104) | Q (×104) | V (λ/n)3 | F |
|---|---|---|---|---|---|
| 0.05 | 20.2 | 0.45 | 0.44 | – | – |
| 0.1 | 12 | 1.9 | 1.65 | 2.03 | 618 |
| 0.15 | 3.77 | 2.5 | 1.5 | 1.6 | 712 |
| 0.2 | 1.5 | 10.3 | 1.21 | 1.20 | 766 |
| 0.25 | 1.1 | 23.8 | 1.1 | 1.02 | 820 |
| 0.3 | 0.66 | 38.2 | 0.65 | 0.93 | 531 |
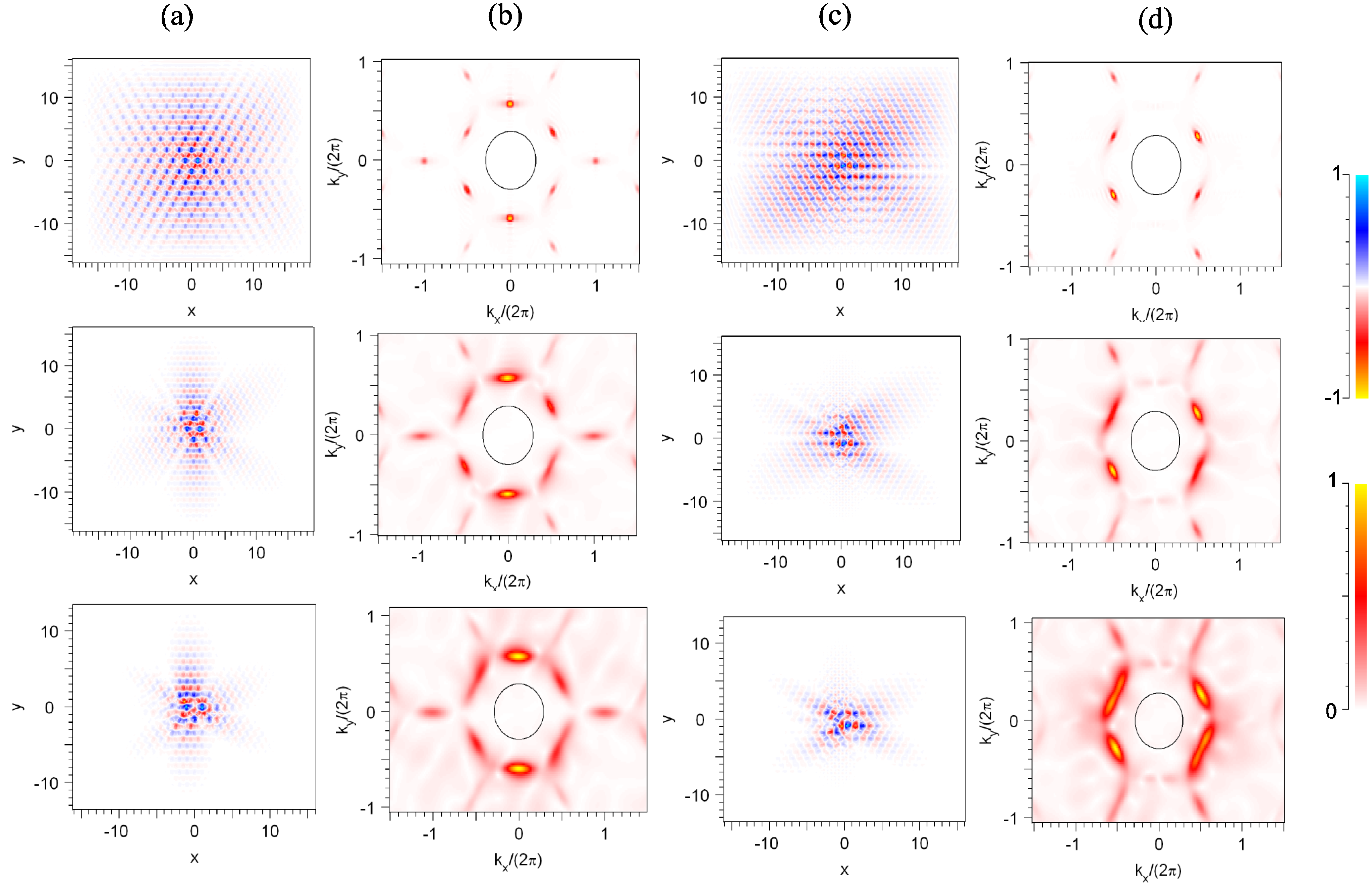
3.2. Mode Profiles
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Krauss, T.F.; Rue, R.M.D.L.; Brand, S. Two-dimensional photonic-bandgap structures operating at near-infrared wavelengths. Nature 1996, 383, 699–702. [Google Scholar] [CrossRef]
- Noda, S.; Chutinan, A.; Imada, M. Trapping and emission of photons by a single defect in a photonic bandgap structure. Nature 2000, 407, 608–610. [Google Scholar] [CrossRef]
- Intonti, F.; Vignolini, S.; Turck, V.; Colocci, M.; Bettotti, P.; Pavesi, L.; Schweizer, S.L.; Wehrspohn, R.; Wiersma, D. Rewritable photonic circuits. Appl. Phys. Lett. 2006, 89, 211117:1–211117:3. [Google Scholar]
- Painter, O.; Lee, R.; Scherer, A.; Yariv, A.; O’Brien, J.; Dapkus, P.; Kim, I. Two-dimensional photonic band-gap defect mode laser. Science 1999, 284, 1819–1821. [Google Scholar] [CrossRef]
- Akahane, Y.; Asano, T.; Song, B.-S.; Noda, S. High-Q photonic nanocavity in a two-dimensional photonic crystal. Nature 2003, 425, 944–947. [Google Scholar] [CrossRef]
- Vučković, J.; Lončar, M.; Mabuchi, H.; Scherer, A. Design of photonic crystal microcavities for cavity QED. Phys. Rev. E 2001, 65, 016608:1–016608:11. [Google Scholar]
- Kiraz, A.; Reese, C.; Gayral, B.; Zhang, L.; Schoenfeld, W.; Gerardot, B.; Petroff, P.; Hu, E.; Imamoglu, A. Cavity-quantum electrodynamics with quantum dots. J. Opt. B Quantum Semiclass. Opt. 2003, 5. [Google Scholar] [CrossRef]
- Aharonovich, I.; Greentree, A.D.; Prawer, S. Diamond photonics. Nat. Photon. 2011, 5, 397–405. [Google Scholar] [CrossRef]
- Yoshie, T.; Scherer, A.; Hendrickson, J.; Khitrova, G.; Gibbs, H.; Rupper, G.; Ell, C.; Shchekin, O.; Deppe, D. Vacuum rabi splitting with a single quantum dot in a photonic crystal nanocavity. Nature 2004, 432, 200–203. [Google Scholar] [CrossRef]
- Englund, D.; Faraon, A.; Fushman, I.; Stoltz, N.; Petroff, P.; Vučković, J. Controlling cavity reflectivity with a single quantum dot. Nature 2007, 450, 857–861. [Google Scholar] [CrossRef]
- Hennessy, K.; Badolato, A.; Winger, M.; Gerace, D.; Atatüre, M.; Gulde, S.; Fält, S.; Hu, E.L.; Imamoğlu, A. Quantum nature of a strongly coupled single quantum dot-cavity system. Nature 2007, 445, 896–899. [Google Scholar] [CrossRef]
- Yang, J.; Heo, J.; Zhu, T.; Xu, J.; Topolancik, J.; Vollmer, F.; Ilic, R.; Bhattacharya, P. Enhanced photoluminescence from embedded pbse colloidal quantum dots in silicon-based random photonic crystal microcavities. Appl. Phys. Lett. 2008, 92, 261110:1–261110:3. [Google Scholar]
- Faraon, A.; Santori, C.; Huang, Z.; Acosta, V.M.; Beausoleil, R.G. Coupling of nitrogen-vacancy centers to photonic crystal cavities in monocrystalline diamond. Phys. Rev. Lett. 2012, 109. [Google Scholar] [CrossRef]
- Englund, D.; Shields, B.; Rivoire, K.; Hatami, F.; Vučković, J.; Park, H.; Lukin, M.D. Deterministic coupling of a single nitrogen vacancy center to a photonic crystal cavity. Nano Lett. 2010, 10, 3922–3926. [Google Scholar] [CrossRef]
- Wolters, J.; Schell, A.W.; Kewes, G.; Nüsse, N.; Schoengen, M.; Döscher, H.; Hannappel, T.; Löchel, B.; Barth, M.; Benson, O. Enhancement of the zero phonon line emission from a single nitrogen vacancy center in a nanodiamond via coupling to a photonic crystal cavity. Appl. Phys. Lett. 2010, 97, 141108:1–141108:3. [Google Scholar]
- Srinivasan, K.; Barclay, P.; Painter, O. Fabrication-tolerant high quality factor photonic crystal microcavities. Opt. Express 2004, 12, 1458–1463. [Google Scholar] [CrossRef]
- Moon, S.-K.; Yang, J.-K. Numerical study of the photonic-bandgap effect in two-dimensional slab photonic structures with long-range order. J. Opt. 2013, 15, 075704:1–075704:7. [Google Scholar]
- Molinari, D.; Fratalocchi, A. Route to strong localization of light: The role of disorder. Opt. Express 2012, 20, 18156–18164. [Google Scholar] [CrossRef]
- Li, Z.-Y.; Zhang, X.; Zhang, Z.-Q. Disordered photonic crystals understood by a perturbation formalism. Phys. Rev. B 2000, 61. [Google Scholar] [CrossRef]
- Tomljenovic-Hanic, S.; de Sterke, C.M. Design of ultrahigh-Q photoinduced cavities in defect-free photonic crystal slabs. Opt. Express 2010, 18, 21397–21403. [Google Scholar] [CrossRef]
- Tomljenovic-Hanic, S.; Greentree, A.D.; Gibson, B.C.; Karle, T.J.; Prawer, S. Nanodiamond induced high-Q resonances in defect-free photonic crystal slabs. Opt. Express 2011, 19, 22219–22226. [Google Scholar]
- Srinivasan, K.; Barclay, P.E.; Painter, O.; Chen, J.; Cho, A.Y.; Gmachl, C. Experimental demonstration of a high quality factor photonic crystal microcavity. Appl. Phys. Lett. 2003, 83, 1915–1917. [Google Scholar] [CrossRef]
- Feiertag, G.; Ehrfeld, W.; Freimuth, H.; Kolle, H.; Lehr, H.; Schmidt, M.; Sigalas, M.; Soukoulis, C.; Kiriakidis, G.; Pedersen, T. Fabrication of photonic crystals by deep X-ray lithography. Appl. Phys. Lett. 1997, 71, 1441–1443. [Google Scholar] [CrossRef]
- Awazu, K.; Wang, X.; Fujimaki, M.; Kuriyama, T.; Sai, A.; Ohki, Y.; Imai, H. Fabrication of two- and three-dimensional photonic crystals of titania with submicrometer resolution by deep X-ray lithography. J. Vac. Sci. Technol. B 2005, 23, 934–939. [Google Scholar] [CrossRef]
- Khankhoje, U.; Kim, S.-H.; Richards, B.; Hendrickson, J.; Sweet, J.; Olitzky, J.; Khitrova, G.; Gibbs, H.; Scherer, A. Modelling and fabrication of GaAs photonic-crystal cavities for cavity quantum electrodynamics. Nanotechnology 2010, 21, 065202:1–065202:7. [Google Scholar]
- Fan, S.; Villeneuve, P.R.; Joannopoulos, J. Theoretical investigation of fabrication—Related disorder on the properties of photonic crystals. J. Appl. Phys. 1995, 78, 1415–1418. [Google Scholar] [CrossRef]
- Chutinan, A.; Noda, S. Effects of structural fluctuations on the photonic bandgap during fabrication of a photonic crystal. J. Opt. Soc. Am. B 1999, 16, 240–244. [Google Scholar] [CrossRef]
- Zhu, Z.; Ye, W.; Ji, J.; Yuan, X.; Zen, C. Influence of random errors on the characteristics of typical 2D photonic crystal microcavity. Appl. Phys. B 2007, 88, 231–236. [Google Scholar]
- Vahala, K. Optical Microcavities; World Scientific: Hackensack, NJ, USA, 2004. [Google Scholar]
- Englund, D.; Fushman, I.; Vučković, J. General recipe for designing photonic crystal cavities. Opt. Express 2005, 13, 5961–5975. [Google Scholar] [CrossRef]
- Sapienza, L.; Thyrrestrup, H.; Stobbe, S.; Garcia, P.D.; Smolka, S.; Lodahl, P. Cavity quantum electrodynamics with Anderson-localized modes. Science 2010, 327, 1352–1355. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Chung, K.; Karle, T.J.; Rajasekharan, R.; De Sterke, C.M.; Tomljenovic-Hanic, S. High-Q Defect-Free 2D Photonic Crystal Cavity from Random Localised Disorder. Crystals 2014, 4, 342-350. https://doi.org/10.3390/cryst4030342
Chung K, Karle TJ, Rajasekharan R, De Sterke CM, Tomljenovic-Hanic S. High-Q Defect-Free 2D Photonic Crystal Cavity from Random Localised Disorder. Crystals. 2014; 4(3):342-350. https://doi.org/10.3390/cryst4030342
Chicago/Turabian StyleChung, Kelvin, Timothy J. Karle, Ranjith Rajasekharan, C. Martijn De Sterke, and Snjezana Tomljenovic-Hanic. 2014. "High-Q Defect-Free 2D Photonic Crystal Cavity from Random Localised Disorder" Crystals 4, no. 3: 342-350. https://doi.org/10.3390/cryst4030342
APA StyleChung, K., Karle, T. J., Rajasekharan, R., De Sterke, C. M., & Tomljenovic-Hanic, S. (2014). High-Q Defect-Free 2D Photonic Crystal Cavity from Random Localised Disorder. Crystals, 4(3), 342-350. https://doi.org/10.3390/cryst4030342




