Abstract
Rational electrolyte design stands as a frontier in the research and development of Li-ion batteries. Nevertheless, detailed investigations about the influence of the dielectric continuum solvation model on molecular interactions are still limited. Herein, we systematically study the impacts of the dielectric constant (ε) on isolated molecules (i.e., ions and solvent molecules), isolated ion pairs, and solvation complexes via density functional theory calculations. The energy shift due to solvation cavity creation is the largest, and charged species always have larger energy shifts than neutral species. For charged species, the energy shifts gradually decrease with a decreasing proportion of Li ions and an increasing proportion of anions, while for neutral species, larger dipole moments lead to higher energy shifts. As predicted by the relative method, the energetic order of ion pairs and solvation complexes in vacuum can be dramatically changed in various dielectric continuums. Furthermore, electrochemical stability windows of charged species change dramatically with ε, while those of neutral species stay almost constant. By clarifying the impacts of dielectric continuum solvation on molecular interactions, we hope to set a benchmark for the molecular interaction calculation, which is critical for the rational design of electrolytes in Li-ion batteries.
1. Introduction
Rational electrolyte design stands as a frontier in the research and development of Li-ion batteries, especially given the increasingly higher demands on battery performance [1,2,3]. During the past decade, many innovative concepts related to electrolytes have emerged. The “water in salt” electrolyte initially developed by Suo expanded the narrow electrochemical stability window of aqueous electrolytes from 1.23 V to 3 V, laying the foundation for high-voltage and high-safety aqueous Li-ion chemistry [4]. Inspired by this remarkable concept, a series of electrolytes is proposed to optimize the key electrolyte properties of ionic conductivity, electrochemical stability window, and operating conditions, from the perspective of the salt concentration [5,6,7,8]. Typical examples include highly concentrated electrolytes, locally highly concentrated electrolytes, and water in polymer electrolytes. With the recent rapid development of computational materials science, high-throughput screening technology, and artificial intelligence tools, research and development of electrolytes in Li-ion batteries is entering a new era [9,10,11]. Unique concepts (i.e., molecular-docking electrolytes, ligand–channel Li-ion conduction, compressed solvation structure, and asymmetrical anions in Li salts), design strategies driven by data and application, and platforms built on artificial intelligence are all making contributions to the acceleration of battery electrolytes [12,13,14,15,16,17,18,19,20].
Solvation structure regulation plays a major role in the rational electrolyte design by tuning the Li-ion transport mechanism and electrochemical stability window [21]. Solvation structures are the comprehensive result of interactions among all molecular species involved and the corresponding steric effects. As experimental characterization, such as Fourier transform infrared spectroscopy and linear sweep voltammetry, may still be subjected to ambiguity from peak fitting and variability in test conditions, computational predictions of binding energies and solvation structures become a feasible approach for fair comparison and design guidelines [22,23]. Due to the much alleviated computational cost compared to explicit solvation models, implicit continuum solvation models are widely used, including VASPsol, the conductor-like screening model (COSMO), and a universal solvation model based on solute electron density (SMD) [24,25,26,27]. Nevertheless, the influence of the dielectric continuum solvation model has received limited research attention. For example, when designing solvation-based low-temperature electrolytes, C. Yang [28] and J. Yang [29] directly characterized the binding energies in vacuum without a dielectric solvation model. Implicit solvation models with ε values of pure solvents were also utilized for a series of publications [30,31,32,33]. In the solvent screening framework by Lu, the solvation energies were compared at the same ε level, regardless of the variation in different solutions [13]. Regarding geometry optimization, it is also unclear whether this process should be performed once the dielectric continuum is changed or whether the optimized configuration in the vacuum should be kept fixed. With continuously improved understanding, it was revealed that the unique electrochemical double layer could also cause great variation in the solvation structure at the electrolyte–electrode interface, as compared to that in the bulk structure [34,35]. Yao’s classical molecular dynamics simulation revealed that ε values of electrolytes could change dramatically with both temperature and salt concentration [36]. Given this condition, a detailed investigation of molecular interactions in electrolytes from the perspective of the dielectric continuum is of great significance.
Herein, we systematically study the impacts of the dielectric continuum on isolated ions, solvent molecules, ion pairs, and solvation complexes via density functional theory (DFT) calculations. The total energy shift can be attributed to three aspects (i.e., solvation cavity creation, geometry reconstruction, and electronic rearrangement). The solvation cavity creation has the largest contribution, and charged species always have larger energy shifts than neutral species. For charged species, the energy shifts gradually decrease with the decreasing proportion of Li ions and the increasing proportion of anions, while for neutral species, larger dipole moments lead to higher energy shifts. As predicted by the relative method, the energetic order of ion pairs and solvation complexes in vacuum can be dramatically changed by the dielectric continuum. Regarding the electrochemical stability window, the highest occupied and lowest unoccupied molecular orbital (HOMO and LUMO) energy levels of charged species change dramatically with ε values, while those of neutral species stay almost constant. By clarifying the impacts of dielectric continuum solvation on molecular interactions, we hope to set a benchmark for the molecular interaction calculation, which is critical for rational electrolyte design for Li-ion batteries.
2. Methods
2.1. Model Development
The Li ion is chosen together with 2 types of anions and 4 types of solvent molecules. These include the bis(trifluoromethylsulfonyl)imide anion (TFSI−), hexafluorophosphate (PF6−), ethylene carbonate (EC), dimethyl carbonate (DMC), 1,2−dimethoxyethane (DME), and 1,3−dioxolane (DOL). The corresponding configurations after geometry optimization in vacuum are summarized in Figure 1.
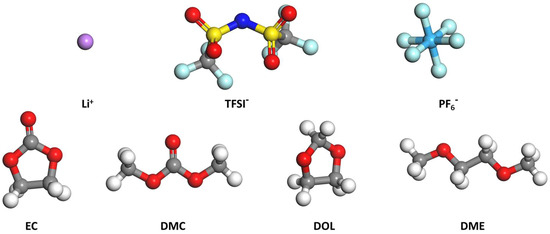
Figure 1.
Configuration of isolated Li ions, anions, and solvents after geometry optimization. Color code: red (O), gray (C), white (H), green (F), yellow (S), dark blue (N), light blue (P), purple (Li).
Taking EC as a typical example, Figure 2 represents the schematic energy landscape when it is moved from the vacuum to the continuum with a dielectric constant of ε. The corresponding energy change can be classified into three steps. The solute molecule first forms a cavity within the dielectric continuum, leading to the generation of screening charges on the cavity surface. To describe different dielectric continuums, the screening charges are scaled by a factor of f(ε), shown in Equation (1) [26]. The corresponding energy shift due to the solvation surface creation is then labeled as Ecos.
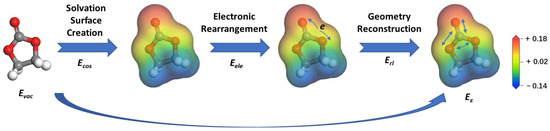
Figure 2.
The schematic energy landscape when one isolated molecule in the vacuum is moved into the continuum with an ε value. The arrows in the third and last panels indicate the electronic rearrangement and geometry reconstruction caused by the dielectric continuum, as compared to the optimized configuration in vacuum. The screening charge values on the solvation surface are illustrated by the contour bar, with red and blue colors representing positive and negative charge, respectively.
Besides Ecos, the dielectric continuum also causes changes in two other aspects of the solute molecule. On the one hand, even with the same optimized configuration in vacuum, the screening charge can also cause electronic rearrangement, with the corresponding energy shift of Eele. Since all bond lengths, angles, and dihedrals are still maintained, the sum of Ecos and Eele is also called the direct energy shift (Ed). On the other hand, the screening charge can also lead to geometry reconstruction in the dielectric continuum compared to the optimized geometry in vacuum, contributing to the term of Erl. Denoting the total energies of the molecule in the vacuum and the dielectric continuum as Evac and Eε, the energy shifts in this process can be summarized by the following equations.
Eε − Evac = Ecos + Eele + Erl
Regarding the solvation energy, two methods are used with different treatments of the reference state. Suppose that A and S represent an anion with −1 valence charge and a neutral solvent molecule; a Li-ion solvation complex consisting of n anions and m solvents can then be represented as (Li·nA·mS)1−n, with the superscript 1 − n denoting the valence charge. In the relative method, the isolated molecules in the corresponding dielectric continuum serve as the reference state, and the solvation energy is determined by Equation (3).
Ed(ε) = Eε(Li·nA·mS)1−n − Eε(Li+) − nEε(A−) − mEε(S)
In the absolute method, the isolated molecules in the vacuum are always set as the reference state, regardless of ε. Thus, the solvation energy as a function of ε can be calculated according to Equation (4).
Ed(ε) = Eε(Li·nA·mS)1−n − Evac(Li+) − nEvac(A−) − mEvac(S)
When the sum of n and m equals 1, the solvation complexes can be simplified to isolated Li–solvent ion pairs of (Li·S)+ and Li–anion ion pairs of LiA, and the above two equations become the binding energy calculations. Nevertheless, we still use the same symbol of Ed to represent both the binding and solvation energies.
2.2. Computational Details
All DFT calculations were performed in the Dmol3 module implemented in Materials Studio and within the local basis set of Double Numerical plus Polarization (DNP) [37,38]. The meta-generalized gradient approximation (mGGA) M06−L functional was used for the exchange–correlation, and all electrons were included [39]. All ion positions were relaxed during geometry optimization, and the convergence criteria were 3 × 10−4 eV/system, 0.05 eV/Å, and 0.005 Å for energy change, force, and displacement, respectively. The conductor-like screening model (COSMO) was used to characterize the effect of the dielectric continuum [26].
In a typical process, the isolated molecules, ion pairs, and solvation complexes are first subject to geometry optimization in vacuum. After that, the optimized molecules are put into the continuum with the given ε value for energy calculation without further geometry optimization. These facilitate the calculation of Ecos and Eele. A final round of geometry optimization is then performed for the molecules and solvation complexes in the dielectric continuum, enabling the quantification of the energy and molecular orbital shifts due to geometry reconstruction, namely, Erl.
3. Results and Discussion
As a validation case, we first calculate the Ed values of (Li·EC)+ using different combinations of functionals and basis sets. Tables S1 and S2 illustrate that the corresponding variations are within 0.21 eV, which is acceptable for the molecular interaction calculation. Furthermore, the energy calculated by DFT is actually the total electronic energy at 0 K without consideration of finite temperatures. To determine a thermodynamic property (such as Gibbs free energy), the corresponding correction term of Gcor needs to be added. In such a case, we also record the Gcor value at 300K for EC, (Li·EC)+, and (Li·5EC)+. A maximum Gcor difference of 0.1 eV in the vacuum and the dielectric continuum with an ε of 80 is observed. With these validations, we can confirm that different functionals and basis sets, together with the Gibbs free energy correction term, can only introduce limited variation. Thus, the main flow to investigate the impacts of the dielectric continuum on the energy shifts of the solvation structure will not be affected.
A brief discussion should also be made for the two typical types of DFT. The first type is plane-wave DFT based on periodic boundary conditions, which is generally performed in the Vienna Ab initio Simulation Package (VASP [40,41]) or Castep [42]. Specifically, the corresponding implicit solvation effects in VASP are considered in VASPsol [25]. It is efficient and accurate for periodic systems (e.g., crystalline materials, 2D materials, surfaces, and interfaces) and related properties (e.g., bulk properties, adsorption energies, density of states, and band structures). The relatively low computational cost also guarantees its compatibility with Ab Initio Molecular Dynamics (AIMD) simulation. However, it may be subject to certain deviations when dealing with charged or non-periodic systems. The second type is the basis-set DFT, which is generally performed in Dmol3 [37] or Gaussian [43]. It is based on atomic orbitals rather than periodic boundary conditions, with implicit solvation effects treated in COSMO [26] or SMD [27]. It offers high accuracy for isolated or molecular systems, regardless of charge neutrality. But it may require considerable computational resources when dealing with large and periodic systems. Certain errors may also be caused by the artificial confinement of the electrons.
In most publications, plane-wave DFT and AIMD are mainly used to reveal the evolution of solvation structures in bulk electrolytes and on the electrode surface [6,7,9], while basis-set DFT is used for charged and neutral solvation structures and related properties (binding energies and HOMO/LUMO energy levels) [28,29,30,31,32,33]. Obviously, the calculations here fall in the range of basis-set DFT. We also compare the two types of DFT in VASP and DMol3 using the ionization energy from an isolated neutral Li atom to a positive Li ion in vacuum as a test case. While the Dmol3 result only shows 0.4 eV deviation from the standard value in the NIST database [44], a large deviation of 2 eV is illustrated according to VASP. Given all the above results, we validate that the selection of Dmol3 should be appropriate in the calculation here.
3.1. Energy Shift of Isolated Ions and Solvent Molecules
Figure 3a,c,d show the energy shift components Ecos, Eele, and Erl of the Li ion, TFSI−, and PF6−. It is not surprising to see that the total energies become more negative with increasing ε values, since a higher ε value indicates stronger interaction with the dielectric continuum. The linear trend observed in Figure 3b further reveals that the screening charge scale of f(ε) plays an even more important role than the ε value in the determination of Ecos. For instance, even with a dramatic increase in ε from 20 to 80, f(ε) only changes slightly from 0.93 to 0.98, leading to a tiny drop of 0.12 eV in Ecos of the TFSI− anion.
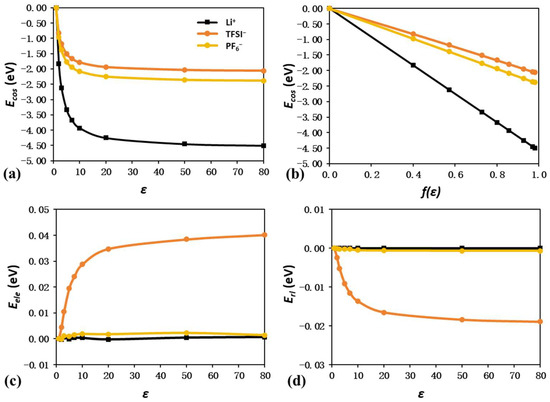
Figure 3.
Energy shift quantification of Li+, PF6−, and TFSI− due to solvation effect. Plot of Ecos as a function of ε (a) and f(ε) (b). Plot of Eele (c) and Erl (d) as a function of ε.
Furthermore, detailed analysis also reveals that the Ecos value dominates the total energy shift, while Eele and Erl become almost negligible. For the Li ion and PF6− anion with high symmetry, Eele and Erl are well maintained near 0, as shown in Figure 3c,d. For the less symmetrical TFSI− anion, Eele and Erl reach 0.04 and −0.02 eV at an ε of 80, but the contributions of these values are still small enough compared to the Ecos of −2.38 eV. The following ranking can also be made by sorting the Ecos contributions in descending order: Li ion > PF6− > TFSI−. This coincides with their molecular size ranking and indicates a possible descriptor for Ecos contribution.
Figure 4a,c,d show the energy shift components Ecos, Eele, and Erl of four solvent molecules as a function of ε. The Ecos values are also plotted against f(ε) in Figure 4b. Although all these molecules are charge-neutral, the linear trend between f(ε) and Ecos values is still illustrated, indicating that Ecos is universally determined by f(ε) charge for both neutral and charged molecules. Nevertheless, several different trends can still be concluded by comparing the energy shift components of charged ions and neutral solvent molecules. Firstly, neutral solvent molecules generally have less negative Ecos values than charged ions. At the ε value of 80, EC has the most negative Ecos value of −0.54 eV among all four solvents, which only accounts for about one-fourth of that of the TFSI− anion. The weakened Ecos also indicate that the contributions from Eele and Erl can no longer be neglected. For EC, Eele reaches 0.10 at an ε of 80, which is already one-fifth of the corresponding Ecos. In addition, while all four solvents have similar molecular size, EC has the largest values of Ecos, Eele, and Erl. As EC has an ultrahigh ε value of 78 compared to the value of ~3 for DMC and ~7 for DOL and DME [45,46], this indicates that, other than the molecular size, the dipole moment also serves as a key descriptor for the energy shift components, especially for neutral solvent molecules.
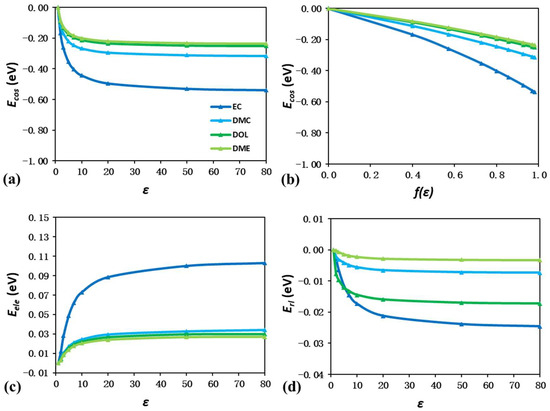
Figure 4.
Energy shift quantification of isolated EC, DMC, DOL, and DME molecules due to solvation effect. Plot of Ecos as a function of ε (a) and screening charge (b). Plot of Eele (c) and Erl (d) as a function of ε.
3.2. Energy Shift of Isolated Ion Pairs
Figure 5 lists all isolated ion pairs considered in this section. The Li–anion type includes LiTFSI and LiPF6, while the Li–solvent type includes (Li·EC)+, (Li·DMC)+, (Li·DOL)+, and (Li·DMC)+. Among them, LiTFSI, LiPF6, and (Li·EC)+ have two configurations. For LiTFSI, two Li−O bonds and one Li−N bond are formed in the first configuration, while only the two Li−O bonds are maintained in the second configuration. For LiPF6, the Li ion is bonded with two and three F atoms in the two configurations, respectively. Regarding (Li·EC)+, the Li−O and C=O bonds are almost collinear in the first configuration but form an angle of ~40° in the second configuration.
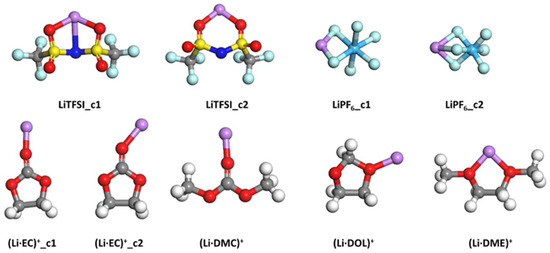
Figure 5.
Configuration of all ion pairs after geometry optimization. There is more than one configuration for certain compositions, which are differentiated by the number after the underline symbol. The atomic color code is the same as that used in Figure 1.
Figure 6 and Figure 7 show the energy shift components of Li–anion and Li–solvent ion pairs as a function of ε, respectively. For all nine ion pairs, Ecos still has larger contributions to the energy shift than Eele and Erl. Figure 6b and Figure 7b also reveal the linear trend between Ecos and f(ε). These results are consistent with those observed in isolated ions and solvent molecules.
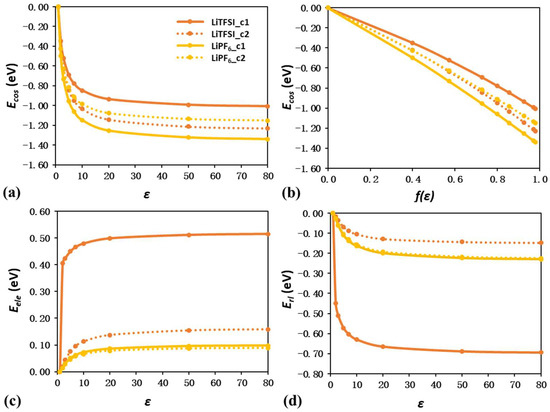
Figure 6.
Energy shift quantification of LiPF6 and LiTFSI ion pairs due to solvation effect. Plot of Ecos as a function of ε (a) and f(ε) (b). Plot of Eele (c) and Erl (d) as a function of ε.
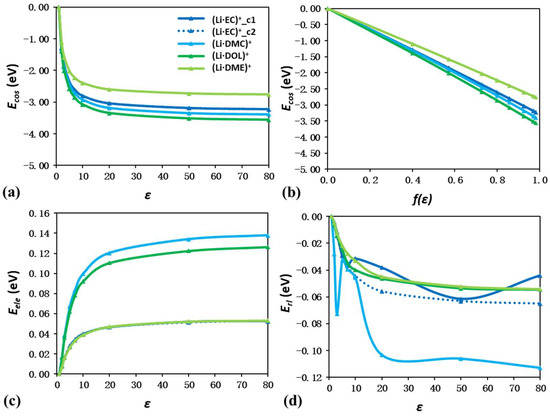
Figure 7.
Energy shift quantification of (Li·EC)+, (Li·DMC)+, (Li·DOL)+, and (Li·DME)+ ion pairs due to solvation effect. Plot of Ecos as a function of ε (a) and f(ε) (b). Plot of Eele (c) and Erl (d) as a function of ε.
Nevertheless, further analysis illustrates the difference between isolated species and ion pairs. For TFSI− and PF6− anions with −1 valence charge, the corresponding Li–anion pair becomes charge-neutral, leading to a far less negative Ecos value. Among all four Li–anion ion pairs, the first configuration of LiPF6 has the most negative Ecos value of −1.34 eV at the ε value of 80, which only accounts for 55% the Ecos value of the corresponding PF6− anion. Detailed analysis can be further performed through the investigation of the ion pair configuration. The average Ecos value between two LiTFSI configurations is higher than that between two LiPF6 configurations, indicating that smaller molecular sizes can generally result in larger Ecos contributions. For LiTFSI, the first configuration has a shorter Li−N distance than the second configuration, leading to a less negative Ecos value, while for LiPF6, the Li−P distance in the first configuration is longer than that in the second configuration, resulting in a more negative Ecos value. Since the Li−N and Li−P distance is closely related to the dipole moment in the isolated ion pairs, the results not only confirm but also extend the previous proposal in Section 3.1; namely, the dipole moment also serves as a key descriptor for the energy shift components in charge-neutral species, including both solvent molecules and Li–anion ion pairs.
In addition, the second configuration of LiTFSI and both configurations of LiPF6 all demonstrate a small positive Eele ~0.10 eV and a small negative Erl ~−0.15 eV, suggesting limited electronic rearrangement and geometry reconstruction. In contrast, the first configuration of LiTFSI has Eele and Erl values as large as 0.51 and −0.69 eV, indicating the large contribution from electronic rearrangement and geometry reconstruction.
For charge-neutral solvent molecules, the corresponding Li–solvent ion pairs become positively charged. This leads to large Ecos drops compared to the corresponding solvent molecules. At an ε of 80, the Ecos values of (Li·EC)+, (Li·DMC)+, (Li·DOL)+, and (Li·DME)+ are −3.22, −3.38, −3.55, and −2.75 eV, which are far more negative than the corresponding values of −0.53, −0.31, −0.25, and −0.23 eV for isolated EC, DMC, DOL, and DME molecules. The Ecos curves of both (Li·EC)+ configurations almost overlap, as the rotation of the Li−O bond only causes a negligible change in the molecular size and dipole moment of EC molecules. Regarding Eele and Erl, their maximum contributions are only 0.13 and −0.11 eV at an ε of 80. Although an irregular curve trend in the Erl curves of (Li·EC)+ and (Li·DMC)+ is observed due to the Li−O bond rotation caused by different ε values, the negligible contributions of both Eele and Erl can still be concluded.
Figure 8 further represents the binding energy (Ed) change as a function of both ε and f(ε). It should be noted that the Ed values from both relative and absolute methods are exactly the same in vacuum due to the identical reference state. The Li ion can only form one Li−O bond with EC, DMC, and DOL, and the strongest Li−O bond in (Li·EC)+ is reported [47,48]. Although the single Li−O bond in (Li·DME)+ is not strong enough, the chelating structure with two Li−O bonds contributes an even more negative binding energy than (Li·EC)+ [49]. These results are well reproduced by the Ed calculation in vacuum here. With the increasing value of ε, the relative Ed values approach 0, while the absolute Ed values become more negative, regardless of the specific type of ion pairs. The linear trends in Figure 8b,d,f also validate the critical role of screening charge in the determination of Ed values.
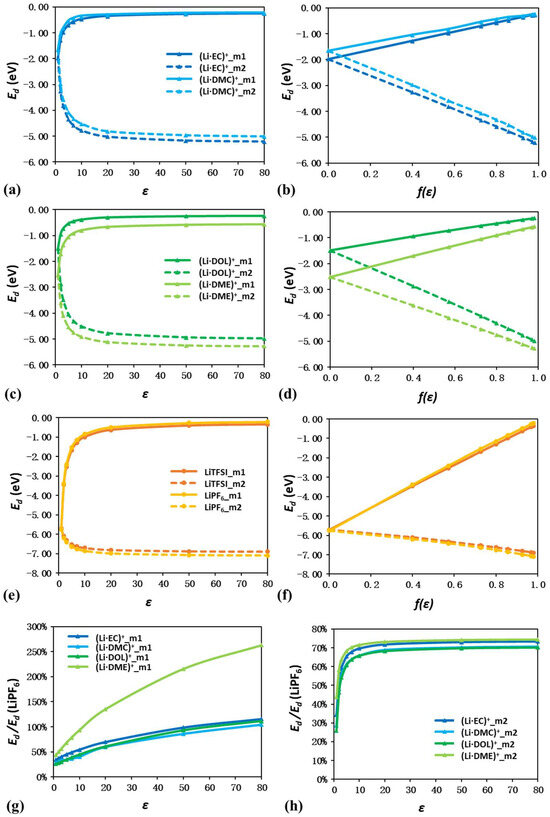
Figure 8.
Plots of binding energies of ion pairs as a function of ε (a,c,e) and f(ε) (b,d,f). The ratio between the binding energy of LiPF6 and Li–solvent ion pairs as a function of ε (g,h). The two calculation methods according to Equations (3) and (4) are indicated as (m1) and (m2). For ion pairs with multiple configurations, only the ones with the lowest energy are used for binding energy calculations.
Despite these general observations, detailed quantification of the Ed value changes for different ion pairs can offer more insights. Figure 8g,h further compare the ratio between the binding energy of LiPF6 and Li–solvent ion pairs as a function of ε. In vacuum, the Ed values of all four Li–solvent ion pairs fall into the range of −1.50 to −2.50 eV, which only accounts for 25–50% of LiPF6. In such a condition, the Li ion shows a strong binding preference for the anions over the solvent molecules. LiTFSI and LiPF6 both show an absolute Ed reduction of ~1.2 eV when ε increases to 80, which is dramatically smaller than the ~3 eV reduction of the Li–solvent ion pair. As a result, the absolute Ed values of Li–solvent ion pairs fall into the range from −4.97 to −5.28 eV and become comparable to those of Li–anion ion pairs, as shown in Figure 8h.
Considering that the isolated ions and solvent molecules are still subject to the dielectric continuum in the solution, we also add the influence of ε on the reference state in the relative calculation method. As shown in Figure 8g, (Li·EC)+, (Li·DMC)+, and (Li·DOL)+ all share relative Ed values ~−0.5 eV at a medium ε of 7, which accounts for 30–40% of LiPF6. Surprisingly, the relative Ed of (Li·DME)+ is as high as −0.91 eV, which becomes comparable to that of LiPF6. At a high ε of 80, this phenomenon becomes even more obvious. The relative Ed of (Li·EC)+, (Li·DMC)+, and (Li·DOL)+ almost converged to −0.24 eV, comparable to the −0.22 and −0.35 eV of LiPF6 and LiTFSI. Furthermore, (Li·DME)+ maintains a highly negative value of −0.57 eV, which is almost 2.5 times that of LiTFSI. The increasingly preferential formation of the chelation solvation structure of (Li·DME)+ with increasing ε values may indicate a possible alternative approach to the electrolyte design.
3.3. Energy Shift of Solvation Complex
While the Li–solvent and Li–anion ion pairs provide significant insights into the Li ion’s interactions with the Li ion and solvent, these ion pairs are unlikely to exist in the real electrolyte. Instead, the Li-ion solvation complex in the form of (Li·nA·mS)1−n is widely reported and analyzed in multiple publications. Based on the literature and our previous experiences, the Li−O coordination in EC, DMC, and DOL is usually around 5 [50,51]. Due to the unique chelating structure of DME (i.e., each DME contributes two coordinating O atoms), a Li−O coordination of six is preferred [52]. These are our bases for using five EC molecules, five DMC molecules, five DOL molecules, and three DME molecules for typical SSIP configurations. Considering the size of PF6− and TFSI−, we determine that each anion can replace two coordinating O atoms. For a typical Li-ion coordination number of 5 with EC as the solvent, all Li-ion solvation complexes are listed in Figure 9. These include the solvent-separated ion pair (SSIP) of (Li·5EC)+, contact ion pairs (CIPs) of LiPF6·3EC and LiTFSI·3EC, and aggregates (AGGs) of (Li·2PF6·EC)− and (Li·2TFSI·EC)−. Specifically, (Li·2TFSI·EC)− has two configurations, which can be differentiated by the formation and breaking of Li−N bonds.
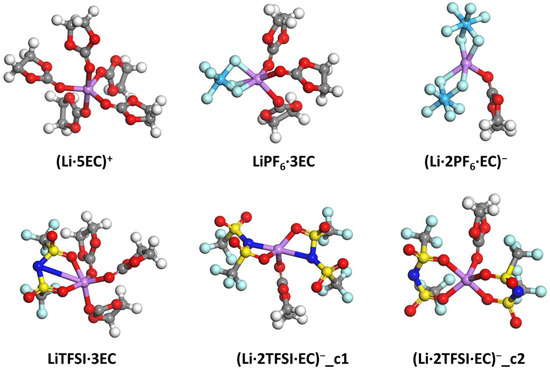
Figure 9.
Configurations of all Li-ion solvation complexes related to EC after geometry optimization. The atomic color code is the same as that used in Figure 1.
The energy shift components of all solvation complexes are plotted as a function of ε in Figures S1 and S2. The major contribution of Ecos and the linear relationship between ε and Ecos are still maintained. Furthermore, CIPs also have less negative Ecos values compared to SSIP and AGG solvation complexes. Thus, it can be concluded that the Ecos contributions of charged species are always larger than those of neutral species, regardless of isolated ions, solvation molecules, ion pairs, and solvation complexes. Furthermore, while the other contribution of Eele and Erl can almost be negligible for charged species, it should be carefully considered for neutral species (i.e., solvent molecules, Li–anion ion pairs, and CIPs) due to their weaker interactions with the dielectric continuum. Taking LiPF6·3EC as an example, the Erl of −0.27 eV at an ε of 80 already accounts for 15% of the Ecos.
Certain insightful results can also be obtained regarding the specific Ecos values. The Ecos values of charged species can be ranked from most to least negative in the following order: Li ion, Li–solvent ion pair, SSIP, AGG, and anions. Since anions are smaller than SSIP and AGG, the order here definitely conflicts with the relationship between molecular size and Ecos value. Except for the molecular size, we can also notice that the order is in agreement with the decreasing percentage of Li ions and the increasing percentage of anions in the molecular species. Since the valence charge is more localized in Li ions but becomes diverged in PF6 and TFSI anions, the Ecos order suggests that the localization of valence charge may be even more critical than the molecular size in quantifying and ranking the interaction with the dielectric continuum across different types of solvation structures.
For neutral species, the Ecos order can also be summarized as CIP, Li–anion ion pair, solvent molecule with high ε (i.e., EC), and solvent molecule with low ε (i.e., DMC, DOL, and DME). The CIP and Li–anion ion pair both consist of the positively charged Li-ion part and negatively charged anion part, contributing to a larger dipole moment than the solvent molecules. Furthermore, the introduction of solvent molecules into the Li–anion ion pair will not buffer the dipole moment. Instead, the interaction between the Li ion and solvent can weaken the competing Li–anion interaction and elongate the corresponding Li−O and Li−N bonds formed in LiPF6·3EC and LiTFSI·3EC, resulting in an even larger dipole moment in CIP. Thus, the Ecos determination method via dipole moment proposed for solvent molecules in Section 3.1 can be successfully extended for the coverage of different molecular species.
The Ed values of solvation complexes related to EC and PF6− are plotted as a function of f(ε) in Figure 10a,b. Similar to the trends observed in Figure 8, the relative Ed values of all solvation complexes linearly approach 0 with increasing f(ε), while the absolute Ed values show linear reduction. The Ed values in vacuum are −5.64, −7.75, and −8.12 eV for (Li·5EC)+, LiPF6·3EC, and (Li·2PF6·EC)−, demonstrating a gradual declining tendency as more solvent molecules are replaced by anions. According to the absolute method, these Ed values further drop to −7.09, −9.52, and −10.53 eV at an ε of 80, with enlargements of 1.25, 1.23, and 1.30. The similar increasing proportion illustrates the well-maintained energetic order of AGG, CIP, and SSIP regardless of the dielectric continuum, which is completely different from the results for ion pairs. In sharp contrast, the second method predicts totally opposite behaviors. At a medium ε of 7, the three values become −2.26, −2.45, and −2.13 eV, which are almost identical. At an even higher ε of 80, the corresponding values further change to −1.45, −1.26, and −0.81 eV. Thus, the energetic order is converted to SSIP, CIP, and AGG, which is opposite to the order in vacuum and that predicted by the absolute method.
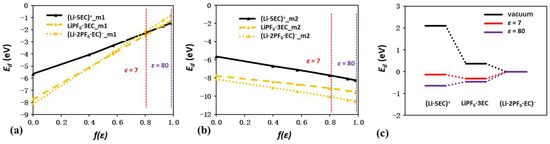
Figure 10.
Plots of binding energies in EC- and PF6−-related solvation complexes as a function of f(ε), as calculated from both methods (a,b). The energy barrier during the transition among SSIP, CIP, and AGG in EC- and PF6−-related solvation complexes (c).
Despite only serving as a reference state for Ed calculation, the isolated ions and solvent molecules are still influenced by the dielectric continuum. In such a case, the relative Ed value changes of solvation complexes related to the combination of EC and TFSI−, DMC and PF6−, DOL and PF6−, and DME and PF6− are shown in Figure S3, with the corresponding optimized configurations shown in Figure S4. While the Ed values of SSIP, CIP, and AGG all increase linearly with increasing f(ε), the slopes of CIP and AGG are always higher than that of SSIP. As a result, the corresponding energetic order may change with the ε value. To further quantify the energetic order change, the energy barriers during the transition among SSIP, CIP, and AGG in vacuum and with ε values of 7 and 80 are also plotted in Figure 10c and Figure S5. For EC and PF6−, the energy shifts from SSIP to CIP and from CIP to AGG in vacuum are −1.43 and −1.01 eV, respectively. The highly negative shift indicates the favorable formation of AGG. Taking the high ε of 80 into consideration, the two energy shifts change to 0.19 and 0.45 eV. The predicted favorable formation of SSIP is consistent with the high solvation ability of EC. Similar trends can also be concluded for EC and TFSI− in Figure S5a. Regarding DMC and PF6−, Figure S5b illustrates an even higher solvating ability of DMC than EC at an ε of 80. Nevertheless, due to the low ε value of DMC solvents, the CIP of LiPF6·3DMC becomes more stable at low ε values. Thus, the inclusion of ε values successfully explains the lower solvating ability of DMC compared to that of EC. Regarding DOL and DME, with similar ε values around 7, Figure S5c,d also illustrate their similar energy shifts during the transition among SSIP, CIP, and AGG. However, the unique chelating solvation structure formed by DME indicates that DME can provide more coordination sites for Li than DOL under a similar Li salt concentration, which can be claimed as the main reason for the strong solvating ability of DME.
Combined with previous publications, the findings here can also provide insights for electrolyte design. According to MD simulation [36], ε values of electrolytes drop with increasing temperature. The high ε values of low-temperature electrolytes are beneficial for the Li–anion interaction and AGG/CIP formation. Exactly because of this, achieving high ionic conductivity within the CIP/AGG solvation structure [13,32] has recently emerged as a more efficient approach to the design of low-temperature electrolytes, compared to traditional solvation regulation strategies, to realize a higher SSIP proportion. Furthermore, ε values also decrease with salt concentration in the range above the standard concentration of 1 mol/L [36]. In electrolytes based on high salt concentration, the ε drop also leads to a slight energy barrier among SSIP, CIP, and AGG. This indicates that the Li ion may hop among different solvation structures, instead of being trapped within SSIP and CIP. Thus, the influence of the dielectric continuum should not be neglected, especially at low temperatures or high salt concentrations.
3.4. Shift of HOMO/LUMO Levels
Figure 11a,b show the HOMO and LUMO changes of isolated anions and solvent molecules as a function of f(ε). The HOMO and LUMO levels of neutral solvent molecules remain almost constant, regardless of ε. As reported by many publications, carbonate-based electrolytes of EC and DMC share lower LUMO levels, making it easy for them to undergo reduction reactions and form solid–electrolyte interphases (SEIs) on the anodic surface. But their low HOMO levels make them less likely to undergo oxidation on the cathodic surface, which is appropriate for the high-voltage cathode [53]. In sharp contrast, ether-based electrolytes of DOL and DME are less likely to be reduced and become compatible with the Li metal anode, mainly due to higher LUMO levels [54]. These experimental observations are well reproduced by Figure 11a,b.
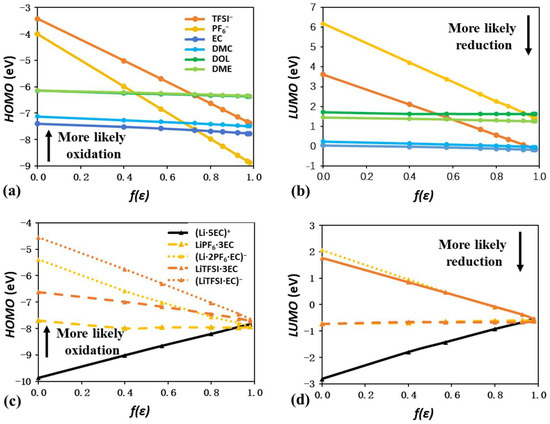
Figure 11.
Plots of HOMO and LUMO energy levels of isolated anions and solvent molecules (a,b), and solvation complexes related to the combination of EC and PF6− and TFSI− (c,d).
The HOMO and LUMO levels of both isolated anions show a negative linear shift with the increase in f(ε). The LUMO levels of isolated PF6− are always higher than those of isolated solvents, suggesting the rare reduction possibility. Similarly, isolated TFSI− will not be reduced in EC and DMC. In the specific combination of TFSI− and ether-based electrolytes, solvent reduction will occur with a low ε value but will be prevented by a high ε value. Regarding HOMO levels, the only exception is that the oxidation of TFSI− is always preferred in carbonate-based electrolytes. For all other combinations, low ε favors anion oxidation, while high ε values favor solvent oxidation.
Figure 11c,d and Figure S6 further represent the HOMO and LUMO levels of solvation complexes with various combinations of anions and solvents. Due to the low probability of Li–anion and Li–solvent ion pairs, their HOMO and LUMO levels are not discussed. With the increase in f(ε), HOMO and LUMO levels of positively charged SSIP demonstrate a linear increase, while those of negatively charged AGG show a linear decrease. The HOMO and LUMO levels of the neutral CIP remain almost constant. Also, the HOMO and LUMO levels of SSIP, CIP, and AGG will finally converge at a high ε of 80, regardless of the anion and solvent type. The reduction priority for CIP and AGG over the isolated anion is also worth noting. As the reduction of F-containing species is beneficial for the LiF-rich SEI and battery cycling performance, this result validates the widely used CIP and AGG regulation strategy. Nevertheless, an increase in ε can be proposed as a potential strategy to promote CIP/AGG reduction and better design of SEI.
The specific types of anions and solvents also have distinct impacts. As shown in Figure 11c, LiPF6·3EC and (Li·2PF6·EC)− have lower HOMO levels than their counterparts LiTFSI·3EC and (Li·2TFSI·EC)−, which is consistent with the trends of PF6− and TFSI− in Figure 11a. However, the distinct LUMO levels of PF6− and TFSI− do not cause a dramatic difference in the LUMO levels of LiPF6·3EC and LiTFSI·3EC or (Li·2PF6·EC)− and (Li·2TFSI·EC)−. This indicates that the anion plays a more important role in the determination of HOMO levels. Furthermore, solvation complexes with PF6− and ether-based electrolytes always have higher HOMO and LUMO levels than their counterparts with PF6− and ether-based electrolytes. For instance, the LUMO levels of (Li·2PF6·DOL)− and (Li·2 PF6·DME)− are around 3.7 eV in vacuum, which is higher than the 2.06 and 1.55 eV of (Li·2PF6·EC)− and (Li·2PF6·DMC)−. This is also consistent with the higher HOMO and LUMO levels of isolated DOL and DME compared to EC and DMC.
4. Conclusions
In this paper, we systematically study the impacts of ε on isolated ions, solvent molecules, ion pairs, and solvation complexes via density functional theory calculations. By attributing the total energy shift to three aspects (i.e., solvation surface creation, geometry reconstruction, and electronic rearrangement), different trends are illustrated. The results reveal that the energy shift due to dielectric solvation, which changes linearly with f(ε), is larger than those caused by the other two contributions. Furthermore, the total energy shifts of charged species are larger than those of neutral species, indicating the need to consider geometry reconstruction and electronic rearrangement for the latter types. More importantly, the determining factor in the energy shift is also different for charged and neutral species. For charged species, the energy shift gradually changes from large to small with a decreasing proportion of Li ions and an increasing proportion of anions, leading to the ranking of Li ion, Li−solvent ion pair, SSIP, AGG, and anions. This is because the charge is more localized in Li ions and divergent in anions. For neutral species, larger dipole moments lead to higher energy shifts, and the rank is CIP, Li–anion ion pair, and solvent molecules with high and low ε values.
Regarding Ed values, their linear relationship with f(ε) is also revealed. However, the reference states serve major roles in the specific trend. Using the ions and solvent molecules in vacuum as the reference states, the absolute method predicts that Ed becomes more negative at high ε values. In contrast, Ed obtained from the relative method gradually approaches 0 with increasing ε values, as the ions and molecules in the corresponding dielectric continuum are used as references. As more negative Ed values indicate higher thermodynamic stability, the energetic order for solvation complexes in vacuum can be summarized as AGG > CIP > SSIP. According to the relative method, this order changes to AGG ~ CIP ~ SSIP at a medium ε of 7 and finally becomes inverted to SSIP > CIP > AGG at a high ε of 80, suggesting an alternative way to tune the molecular interactions in electrolytes from the perspective of the dielectric continuum. The HOMO and LUMO energy levels of charged species change dramatically with the ε value, while those of neutral species stay almost constant. The HOMO and LUMO levels of SSIP, CIP, and AGG will finally converge at a high ε of 80, regardless of the anion and solvent type. As the reduction of CIP and AGG is beneficial for the LiF-rich SEI and also the battery cycling performance, increasing the ε value can be proposed as a potential strategy to promote better design of SEI. By clarifying the impacts of the dielectric continuum solvation model on molecular interactions, we hope to accelerate the rational design process of electrolytes in Li-ion batteries.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/cryst15090796/s1. Table S1: Binding energy of (Li·EC)+ and LiPF6 calculated from the combination of the DNP basis set and different functionals [39,55,56,57,58,59]. Table S2: Binding energy of (Li·EC)+ calculated from the combination of mGGA M06L functional and different basis sets [38]. Table S3: Gibbs free energy correction term of EC, (Li·EC)+, and (Li·5EC)+ at 300K, which are calculated from the vibrational analysis [60]. Table S4: Energy shift quantification of isolated EC molecule. Table S5: Energy shift quantification of isolated DMC molecule. Table S6: Energy shift quantification of isolated DOL molecule. Table S7: Energy shift quantification of isolated DME molecule. Figure S1: Energy shift quantification of (Li·5EC)+, LiPF6·3EC, and (Li·2PF6·EC)− solvation complex due to solvation effect. Plot of Ecos as a function of ε (a) and screening charge (b). Plot of Eele (c) and Erl (d) as a function of ε. Figure S2: Energy shift quantification of LiTFSI·3EC and (Li·2TFSI·EC)− solvation complex due to solvation effect. Plot of Ecos as a function of ε (a) and screening charge (b). Plot of Eele (c) and Erl (d) as a function of ε. Figure S3: Plot of binding energy in solvation complexes related to EC and TFSI− (a), DMC and PF6− (b), DOL and PF6− (c), and DME and PF6− (d). Figure S4: Configuration of all Li-ion solvation complexes related to DMC and PF6−, DOL, and PF6−, and DME and PF6− after geometry optimization. The atomic color code is the same as that used in Figure 1. Figure S5: Energy barrier during transition among SSIP, CIP, and AGG in relation to EC and TFSI− (a), DMC and PF6− (b), DOL and PF6− (c), and DME and PF6− (d). Figure S6: Plot of HOMO and LUMO energy levels of isolated solvation complexes related to the combination of DMC and PF6− (a, b), DOL and PF6− (c,d), and DME and PF6− (e,f).
Author Contributions
Conceptualization, Y.Z., X.Z. and Y.L. (Yuxiao Lin); methodology, Y.Z., R.L. and Y.L. (Yuxiao Lin); formal analysis, Y.Z., X.Z. and Y.L. (Yuxiao Lin); investigation, Y.Z., R.L. and Y.L. (Yuxiao Lin); data curation, Y.Z., R.L. and Y.L. (Yuxiao Lin); writing—original draft preparation, Y.Z., R.L. and Y.L. (Yuxiao Lin); writing—review and editing, all authors; supervision, X.L., X.Z., Y.L. (Yunsong Li) and Y.L. (Yuxiao Lin); funding acquisition, Y.L. (Yunsong Li) and Y.L. (Yuxiao Lin). All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (No. 52202245), a previous research project of the New Materials Computing Research Center (No. 3700-32601), and the Jiangsu Special Term Professor Program.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding authors.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Meng, Y.S.; Srinivasan, V.; Xu, K. Designing better electrolytes. Science 2022, 378, 3750. [Google Scholar] [CrossRef] [PubMed]
- Xiao, J.; Shi, F.; Glossmann, T.; Burnett, C.; Liu, Z. From laboratory innovations to materials manufacturing for lithium-based batteries. Nat. Energy 2023, 8, 329–339. [Google Scholar] [CrossRef]
- Xin, S.; Zhang, X.; Wang, L.; Yu, H.; Chang, X.; Zhao, Y.M.; Meng, Q.; Xu, P.; Zhao, C.Z.; Chen, J.; et al. Roadmap for rechargeable batteries: Present and beyond. Sci. China Chem. 2024, 67, 13–42. [Google Scholar] [CrossRef]
- Suo, L.; Borodin, O.; Gao, T.; Olguin, M.; Ho, J.; Fan, X.; Luo, C.; Wang, C.; Xu, K. “Water-in-salt” electrolyte enables high-voltage aqueous lithium-ion chemistries. Science 2015, 350, 938–943. [Google Scholar] [CrossRef]
- Lai, J.; Guo, Y.; Lai, H.E.; Ospina-Acevedo, F.A.; Tian, W.; Kuai, D.; Chen, D.; Balbuena, P.B.; Shi, F. Linking Solvation Equilibrium Thermodynamics to Electrolyte Transport Kinetics for Lithium Batteries. J. Am. Chem. Soc. 2025, 147, 14348–14358. [Google Scholar] [CrossRef]
- Fan, X.; Wang, C. High-voltage liquid electrolytes for Li batteries: Progress and perspectives. Chem. Soc. Rev. 2021, 50, 10486–10566. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, J.; Pollard, T.P.; Li, Q.; Tan, S.; Hou, S.; Wang, C. Electrolyte design for Li-ion batteries under extreme operating conditions. Nature 2023, 614, 694–700. [Google Scholar] [CrossRef]
- Zhang, Y.; Lu, Y.; Jin, J.; Wu, M.; Yuan, H.; Zhang, S.; Davey, K.; Guo, Z.; Wen, Z. Electrolyte design for lithium-ion batteries for extreme temperature applications. Adv. Mater. 2024, 36, 2308484. [Google Scholar] [CrossRef]
- Chen, Y.; Li, M.; Liu, Y.; Jie, Y.; Li, W.; Huang, F.; Li, X.; He, Z.; Ren, X.; Chen, Y.; et al. Origin of dendrite-free lithium deposition in concentrated electrolytes. Nat. Commun. 2023, 14, 2655. [Google Scholar] [CrossRef]
- Wu, Z.; Li, R.; Zhang, S.; Deng, T.; Zhang, H.; Zhang, R.; Liu, J.; Ding, S.; Fan, L.; Chen, L.; et al. Deciphering and modulating energetics of solvation structure enables aggressive high-voltage chemistry of Li metal batteries. Chem 2023, 9, 650–664. [Google Scholar] [CrossRef]
- Efaw, C.M.; Wu, Q.; Gao, N.; Zhang, Y.; Zhu, H.; Gering, K.; Hurley, M.F.; Xiong, H.; Hu, E.; Cao, X.; et al. Localized high-concentration electrolytes get more localized through micelle-like structures. Nat. Mater. 2023, 22, 1531–1539. [Google Scholar] [CrossRef]
- Ma, B.; Zhang, H.; Li, R.; Zhang, S.; Chen, L.; Zhou, T.; Wang, J.; Zhang, R.; Ding, S.; Xiao, X.; et al. Molecular-docking electrolytes enable high-voltage lithium battery chemistries. Nat. Chem. 2024, 16, 1427–1435. [Google Scholar] [CrossRef]
- Lu, D.; Li, R.; Rahman, M.M.; Yu, P.; Lv, L.; Yang, S.; Huang, Y.; Sun, C.; Zhang, S.; Zhang, H.; et al. Ligand-channel-enabled ultrafast Li-ion conduction. Nature 2024, 627, 101–107. [Google Scholar] [CrossRef] [PubMed]
- Yang, W.; Chen, A.; He, P.; Zhou, H. Advancing lithium metal electrode beyond 99.9% coulombic efficiency via super-saturated electrolyte with compressed solvation structure. Nat. Commun. 2025, 16, 4229. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.; Cao, Q.; Zhang, W.; Zeng, T.; Ou, Y.; Yan, S.; Liu, H.; Song, X.; Zhou, H.; Hou, W.; et al. Breaking the molecular symmetricity of sulfonimide anions for high-performance lithium metal batteries under extreme cycling conditions. Nat. Energy 2025, 10, 191–204. [Google Scholar] [CrossRef]
- Xia, Y.; Zhou, P.; Kong, X.; Tian, J.; Zhang, W.; Yan, S.; Hou, W.H.; Zhou, H.Y.; Dong, H.; Chen, X.; et al. Designing an asymmetric ether-like lithium salt to enable fast-cycling high-energy lithium metal batteries. Nat. Energy 2023, 8, 934–945. [Google Scholar] [CrossRef]
- Wang, B.; Doan, H.A.; Son, S.B.; Abraham, D.P.; Trask, S.E.; Jansen, A.; Xu, K.; Liao, C. Data-driven design of electrolyte additives supporting high-performance 5 V LiNi0.5Mn1.5O4 positive electrodes. Nat. Commun. 2025, 16, 3413. [Google Scholar] [CrossRef]
- Wang, H.; Yan, X.; Zhang, R.; Sun, J.; Feng, F.; Li, H.; Liang, J.; Wang, Y.; Ye, G.; Luo, X.; et al. Application-driven design of non-aqueous electrolyte solutions through quantification of interfacial reactions in lithium metal batteries. Nat. Nanotechnol. 2025, 20, 1034–1052. [Google Scholar] [CrossRef]
- Yang, Y.; Yao, N.; Gao, Y.C.; Chen, X.; Huang, Y.X.; Zhang, S.; Zhu, H.B.; Xu, L.; Yao, Y.X.; Yang, S.J.; et al. Data–Knowledge-Dual-Driven Electrolyte Design for Fast-Charging Lithium Ion Batteries. Angew. Chem. 2025, 64, e202505212. [Google Scholar] [CrossRef]
- Chen, X.; Liu, M.; Yin, S.; Gao, Y.C.; Yao, N.; Zhang, Q. Uni-Electrolyte: An Artificial Intelligence Platform for Designing Electrolyte Molecules for Rechargeable Batteries. Angew. Chem. 2025, 137, e202503105. [Google Scholar] [CrossRef]
- Xiao, P.; Yun, X.; Chen, Y.; Guo, X.; Gao, P.; Zhou, G.; Zheng, C. Insights into the solvation chemistry in liquid electrolytes for lithium-based rechargeable batteries. Chem. Soc. Rev. 2023, 52, 5255–5316. [Google Scholar] [CrossRef]
- Wu, L.; Hu, J.; Chen, S.; Yang, X.; Liu, L.; Foord, J.S.; Pobedinskas, P.; Haenen, K.; Hou, H.; Yang, J. Lithium nitrate mediated dynamic formation of solid electrolyte interphase revealed by in situ Fourier transform infrared spectroscopy. Electrochim. Acta 2023, 466, 142973. [Google Scholar] [CrossRef]
- Uchida, Y.; Kätelhön, E.; Compton, R.G. Linear sweep voltammetry with non-triangular waveforms: New opportunities in electroanalysis. J. Electroanal. Chem. 2018, 818, 140–148. [Google Scholar] [CrossRef]
- Tomasi, J.; Persico, M. Molecular Interactions in Solution: An Overview of Methods Based on Continuous Distributions of the Solvent. Chem. Rev. 1994, 94, 2027–2094. [Google Scholar] [CrossRef]
- Mathew, K.; Sundararaman, R.; Letchworth-Weaver, K.; Arias, T.A.; Hennig, R.G. Implicit solvation model for density-functional study of nanocrystal surfaces and reaction pathways. J. Chem. Phys. 2014, 140, 084106. [Google Scholar] [CrossRef]
- Klamt, A.; Schüürmann, G. COSMO: A new approach to dielectric screening in solvents with explicit expressions for the screening energy and its gradient. J. Chem. Soc. 1993, 2, 799–805. [Google Scholar] [CrossRef]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef]
- Yang, C.; Liu, X.; Lin, Y.; Yin, L.; Lu, J.; You, Y. Entropy-Driven Solvation toward Low-Temperature Sodium-Ion Batteries with Temperature-Adaptive Feature. Adv. Mater. 2023, 35, 2301817. [Google Scholar] [CrossRef]
- Yang, J.; Ruan, J.; Li, Q.; Fang, F.; Song, Y.; Sun, D.; Wang, F. Improved Low-Temperature Performance of Rocking-Chair Sodium-Ion Hybrid Capacitor by Mitigating the De-Solvation Energy and Interphase Resistance. Adv. Funct. Mater. 2022, 32, 2200566. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, D.; Zhu, L.; Liu, M.; Zheng, T.; Xu, J.; Li, J.; Wang, F.; Wang, Y.; Dong, X.; et al. Hybridizing carbonate and ether at molecular scales for high-energy and high-safety lithium metal batteries. Nat. Commun. 2024, 15, 3217. [Google Scholar] [CrossRef]
- Sheng, L.; Wang, Q.; Liu, X.; Cui, H.; Wang, X.; Xu, Y.; Li, Z.; Wang, L.; Chen, Z.; Xu, G.; et al. Suppressing electrolyte-lithium metal reactivity via Li+-desolvation in uniform nano-porous separator. Nat. Commun. 2022, 13, 172. [Google Scholar] [CrossRef]
- Ge, B.; Deng, J.; Wang, Z.; Liang, Q.; Hu, L.; Ren, X.; Li, R.; Lin, Y.; Li, Y.; Wang, Q.; et al. Aggregate-Dominated Dilute Electrolytes with Low-Temperature-Resistant Ion-Conducting Channels for Highly Reversible Na Plating/Stripping. Adv. Mater. 2024, 36, 2408161. [Google Scholar] [CrossRef] [PubMed]
- Hu, L.; Deng, J.; Lin, Y.; Liang, Q.; Ge, B.; Weng, Q.; Li, Y.; Deng, Y.; Chen, G.; Yu, X. Restructuring Electrolyte Solvation by a Versatile Diluent Toward Beyond 99.9% Coulombic Efficiency of Sodium Plating/Stripping at Ultralow Temperatures. Adv. Mater. 2024, 36, 2312161. [Google Scholar] [CrossRef] [PubMed]
- Azemtsop, M.T.; Mehra, R.M.; Kumar, Y.; Gupta, M. Physical Characterization of Ionic Liquid-Modified Polyvinyl Alcohol and Sodium Thiocyanate Polymer Electrolytes for Electrochemical Double-Layer Capacitor Application. J. Shanghai Jiaotong Univ. 2023, 28, 161–171. [Google Scholar] [CrossRef]
- Wu, Q.; Qi, Y. Revealing heterogeneous electric double layer (EDL) structures of localized high-concentration electrolytes (LHCEs) and their impact on solid–electrolyte interphase (SEI) formation in lithium batteries. Energy Environ. Sci. 2025, 18, 3036–3046. [Google Scholar] [CrossRef]
- Yao, N.; Chen, X.; Shen, X.; Zhang, R.; Fu, Z.; Ma, X.; Zhang, X.; Li, B.; Zhang, Q. An Atomic Insight into the Chemical Origin and Variation of the Dielectric Constant in Liquid Electrolytes. Angew. Chem. 2021, 60, 21473–21478. [Google Scholar] [CrossRef]
- Delley, B. From molecules to solids with the DMol3 approach. J. Phys. Chem. 2000, 113, 7756–7764. [Google Scholar] [CrossRef]
- Delley, B. An all-electron numerical method for solving the local density functional for polyatomic molecules. J. Phys. Chem. 1990, 92, 508–517. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D. A new local density functional for main-group thermochemistry, transition metal bonding, thermochemical kinetics, and noncovalent interactions. J. Phys. Chem. 2000, 125, 194101. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for open-shell transition metals. Phys. Rev. B 1993, 48, 13115–13118. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmuller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–508. [Google Scholar] [CrossRef]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.J.; Refson, K.; Payne, M.C. First principles methods using CASTEP. Z. Fuer Krist. 2005, 220, 567–570. [Google Scholar] [CrossRef]
- Reed, A.E.; Curtiss, L.A.; Weinhold, F. Intermolecular interactions from a natural bond orbital, donor-acceptor viewpoint. Chem. Rev. 1988, 88, 899–926. [Google Scholar] [CrossRef]
- Available online: https://physics.nist.gov/PhysRefData/ASD/ionEnergy.html (accessed on 19 August 2025).
- Daniels, I.N.; Wang, Z.; Laird, B. Dielectric Properties of Organic Solvents in an Electric Field. J. Phys. Chem. C 2017, 121, 1025–1031. [Google Scholar] [CrossRef]
- Park, C.; Kanduč, M.; Chudoba, R.; Ronneburg, A.; Risse, S.; Ballauff, M.; Dzubiella, J. Molecular simulations of electrolyte structure and dynamics in lithium–sulfur battery solvents. J. Power Sources 2018, 373, 70–78. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, Y. Electrolyte solvation structure as a stabilization mechanism for electrodes. Energy Mater. 2021, 373, 100004. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, H.; Qi, S.; Wu, D.; Huang, J.; Li, X.; Wang, C.; Ma, J. Structural regulation chemistry of lithium ion solvation for lithium batteries. Ecomat 2022, 4, e12200. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, X.; Li, H.; Zhang, Q. Cation−Solvent, Cation−Anion, and Solvent−Solvent Interactions with Electrolyte Solvation in Lithium Batteries. Batter. Supercaps 2019, 2, 128–131. [Google Scholar] [CrossRef]
- Han, S. Structure and dynamics in the lithium solvation shell of nonaqueous electrolytes. Sci. Rep. 2019, 9, 5555. [Google Scholar] [CrossRef]
- Hou, T.; Fong, K.; Wang, J.; Persson, K. The solvation structure, transport properties and reduction behavior of carbonate-based electrolytes of lithium-ion batteries. Chem. Sci. 2021, 12, 14740. [Google Scholar] [CrossRef]
- Xia, M.; Jiao, T.; Liu, G.; Chen, Y.; Gao, J.; Cheng, Y.; Yang, Y.; Wang, M.; Zheng, J. Rational design of electrolyte solvation structure for stable cycling and fast charging lithium metal batteries. J. Power Sources 2022, 548, 232106. [Google Scholar] [CrossRef]
- Yeddala, M.; Rynearson, L.; Lucht, B. Modification of Carbonate Electrolytes for Lithium Metal Electrodes. ACS Energy Lett. 2023, 8, 4782–4793. [Google Scholar] [CrossRef]
- Kang, H.; Kang, H.; Lyu, M.; Cho, E. A review of recent developments in the design of electrolytes and solid electrolyte interphase for lithium metal batteries. EcoMat 2022, 6, e12498. [Google Scholar] [CrossRef]
- Perdew, J.P.; Wang, Y. Accurate and simple analytic representation of the electron−gas correlation energy. Phys. Rev. B 1992, 45, 23, 13244−13249. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 18, 3865−3868. [Google Scholar] [CrossRef]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab initio calculation of vibrational absorption and circular dichroism spectra using density functional force fields. J. Phys. Chem. 1994, 98, 45, 11623−11627. [Google Scholar] [CrossRef]
- Ortmann, F.; Bechstedt, F.; Schmidt, W.G. Semiempirical van der Waals correction to the density functional description of solids and molecular structures. Phys. Rev. B 2006, 73, 205201. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical GGA−type density functional constructed with a long−range dispersion correction. J. Comput. Chem. 2006, 27, 15, 1787−1799. [Google Scholar] [CrossRef]
- Hirano, T. MOPAC Manual, 7th ed.; Stewart, J.J.P., Ed.; US Air Force Academy: Colorado Springs, CO, USA, 1993. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).