Surface-Mounted PMN-PT Piezoelectric Sensor with Time-Reversal Signal Processing for High-Strength Bolt Loosening Detection

Abstract

High-strength bolts play an essential role in connecting steel structural components across bridges, buildings, and machinery, thanks to their low cost and broad adaptability. However, prolonged exposure to complex loading and harsh environments can cause loosening, which increases the risk of structural distortion or catastrophic collapse. Conventional monitoring tools, such as strain gauges or fiber-optic sensors, often suffer from high expense, short service life, and poor early-warning performance. To overcome these challenges, this study presents a novel surface-mounted piezoelectric sensor built on lead magnesium niobate–lead titanate (PMN-PT) single crystals, selected for their superior piezoelectric constants, energy density, and low-frequency sensitivity. The sensor integrates a PMN-PT wafer, monolithic washer, epoxy resin encapsulation, and shielded cabling. It was experimentally validated through waterproofing and electrical tests across five working conditions, maintaining capacitance stability within 3.25% and infinite insulation resistance. Preload monitoring experiments were conducted using a time-reversal method, and a tightening index based on focused signal amplitude was proposed to quantify bolt-loosening conditions. Results confirmed a strong linear association (R² = 0.986) between the focused signal amplitude and preload torque (0–120 N·m), with a maximum error of only 5.7% in validation trials under unknown torque. Overall, this PMN-PT-based sensor offers a cost-efficient, sensitive, and durable solution for early detection of bolt loosening in steel structures.

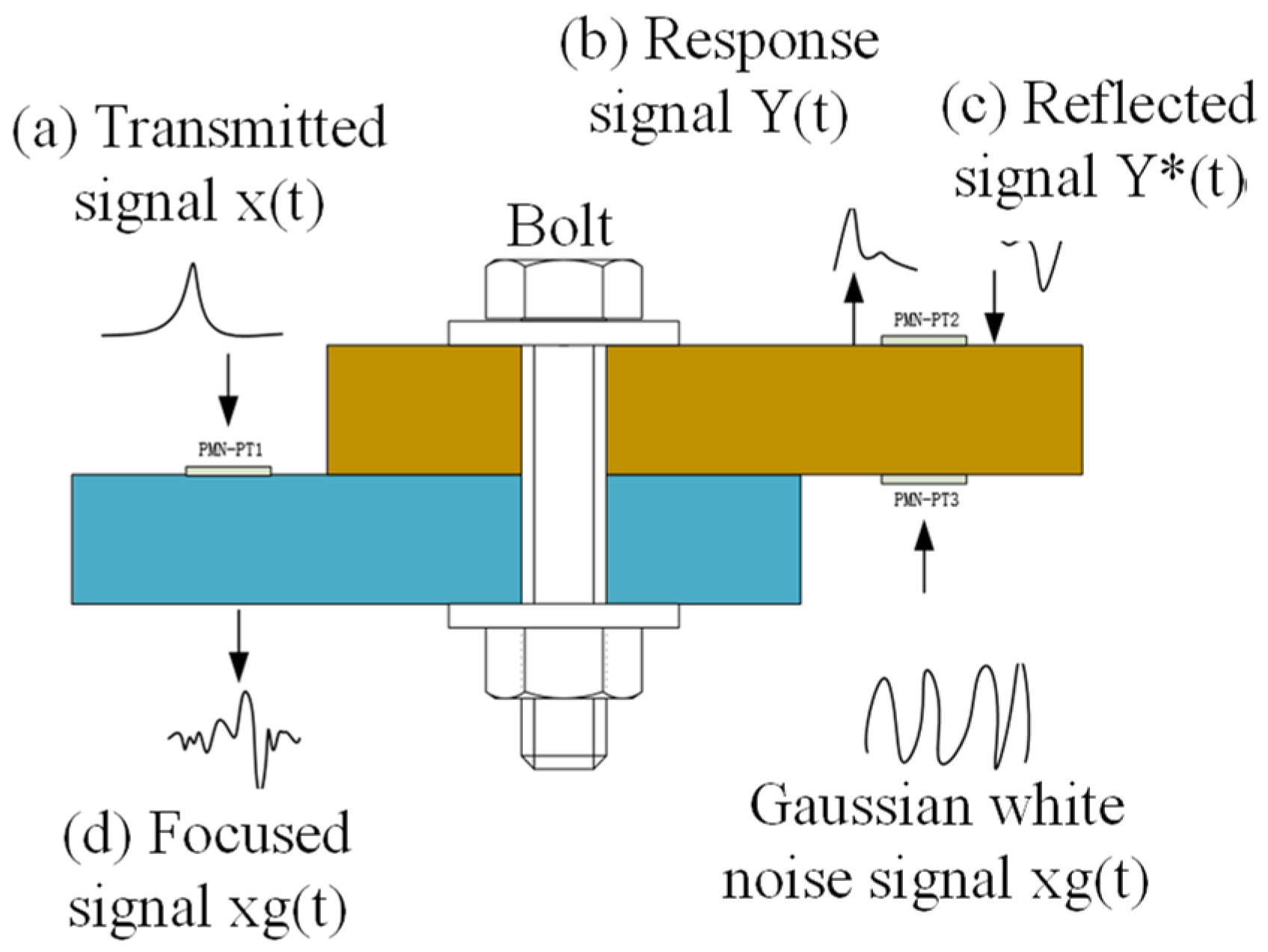
1. Introduction

As critical connecting elements, high-strength bolts are widely used in large-scale steel structures such as bridges, buildings, and mechanical systems. However, under the combined effects of structural vibrations [1,2] and extreme weather conditions, bolts can loosen, causing component misalignment or global instability, and potentially triggering severe safety incidents [3,4]. Consequently, developing highly sensitive bolt-loosening monitoring technologies capable of early warning is of urgent engineering significance to safeguard critical infrastructure.

Current mainstream monitoring approaches include visual inspection [5] and vibration-based methods [6,7,8]. Visual inspection, a conventional technique, relies heavily on operator expertise and lacks both quantitative loosening assessment and real-time monitoring capabilities. Vibration-based methods primarily focus on identifying structural damage at the global level and typically detect anomalies only after significant deterioration has occurred [9,10]. These methods have inherent limitations, especially in achieving reliable early-stage monitoring of severely degraded bolts. In order to address micro-damage detection and timely warning needs, recent research has focused on strain-gauge-based direct preload measurement [11]. This approach quantifies preload variations through stress–strain monitoring at bolt connections. Most existing methods determine the degree of bolt loosening by directly or indirectly observing preload levels. Common monitoring methods can be broadly categorized into direct methods and indirect methods, as summarized in

Table 1. Comparison of direct and indirect bolt monitoring methods.

Monitoring Method	Monitoring Content	Advantages	Disadvantages
Direct Method	Stress, strain	Simple principle, low cost	Low accuracy, not suitable for field monitoring
Indirect Method	Impedance, time–frequency domain, acceleration, etc.	High accuracy, suitable for field monitoring	Theoretical complexity, relatively high cost

. The direct measurement method involves monitoring the stress and strain generated at bolt locations. For example, Nelson et al. [11] summarized and proposed a direct preload measurement technique based on strain gauges. Jia et al. [12] proposed an indirect stress evaluation method using axial stress distribution analysis at nut locations. Nevertheless, strain gauges are susceptible to installation damage and environmental instability, limiting their application to bolts under ambient-temperature tensile loads within the elastic range.

With the advancement of smart materials, increasing attention has been given to their unique sensing-response capabilities. Ren et al. [13] developed an intelligent bolt that employs embedded fiber Bragg grating (FBG) sensors to simultaneously measure axial and shear forces. Li et al. [14] established a thermo-sensitive model of dual-metal-layer metal-coated FBG (MFBG) and analyzed the thermal sensitivity parameters of single-metal-layer MFBG and Ni/Ni-coated MFBG. Yang et al. [15] developed an embedded FBG sensor for bolt torque monitoring, demonstrating high reliability with an R² > 0.98 between applied torque and wavelength shifts. However, high implementation costs and fiber fragility restrict their deployment in extreme environments or under dynamic loading scenarios. Sidorov et al. [16] proposed an IoT sensor node named Ten Sense M30, capable of accurately monitoring bolt joint preload. It offers secure non-line-of-sight communication over a distance of 800 m and has an expected service life of over five years. Liu et al. [7] proposed a bolt-loosening monitoring method based on APGDF and prototype networks, which achieves optimal detection by tapping near the loosened bolt position. This method is particularly effective in scenarios with insufficient samples and noise interference, such as single-bolt and multi-bolt loosening in complex tower structures. Li et al. [17] evaluated bolt connection faults in ring structures caused by nonlinear defects in terms of load and transfer functions. By applying harmonic excitation three times with appropriate amplitudes, they defined evaluation features based on nonlinear fault-induced load and transfer functions, ultimately establishing an effective evaluation method with sensitive local indicators for complex ring-like structures. Zhao et al. [18] proposed a digital image correlation (DIC)-based method for bolt preload monitoring by analyzing the strain field of the bolt head surface. Artificial speckles were sprayed onto the bolt head, and images before and after deformation were captured with a camera. Using DIC, the strain field of the bolt head surface was calculated, and the linear relationship between surface strain and bolt preload was used for monitoring.

Direct measurement methods generally suffer from constraints such as limited sensor placement and low monitoring accuracy. To overcome these challenges, indirect measurement methods have been proposed by researchers worldwide. For instance, line-marking methods were among the earliest indirect techniques for bolt-loosening monitoring. Huang et al. [19] conducted multi-mode loosening detection of threaded fasteners using both active sensing and impact methods, proposing a multimodal loosening detection approach that leverages the complementarity of ultrasonic and acoustic response signals. They introduced the concept of multi-scale cross-fuzzy entropy to map multimodal information into a unified feature space, thereby constructing more representative and effective loosening features. Redundant features were removed using linear discriminant analysis (LDA). Fu et al. [20] proposed a method using acoustic emission (AE) sensors and deep learning, which also reduces noise by filtering corresponding frequency components. After continuous wavelet transform (CWT), one-dimensional signal data were converted into two-dimensional image data. Convolutional neural networks (CNNs) were then employed to learn these image features and classify different degrees of bolt loosening. Li et al. [21] applied principal component and probability density analysis for diagnostic signal evaluation, successfully identifying bolt loosening levels. Coelho et al. [22] introduced regression algorithms to quantify torque loosening levels, aimed at pattern recognition, detection, and quantification of bolt joint torque loosening.

Even when the bolt system state was unknown, this machine learning classification method effectively identified and categorized torque loss by analyzing indirect vibration measurements. The challenge of recognizing and monitoring torque loosening stems from variability and nonlinear effects present in bolt joints. Chen et al. [23] was the first to attempt combining impact-based methods with both deep and shallow learning approaches to address the problem of underwater bolt flange loosening detection. Liang et al. [24] proposed a one-dimensional coupled model using electromechanical impedance (EMI) techniques, exciting structures with high-frequency sweeping signals (>20 kHz). Structural damage was then evaluated by detecting changes in coupled electromechanical parameters using resistive or conductive admittance through surface-mounted sensor–actuators. Shao et al. [25] applied the frequency shift method of piezoelectric impedance features to monitor bolt axial force, finding that sensitive high-frequency resonances mainly originated from the piezoelectric patch itself. As axial load increased, both resonance and anti-resonance frequencies showed a linear downward trend. Liao et al. [26] proposed a novel damage index (DI) by integrating piezoelectric impedance and ultrasonic-guided waves. By combining the two sensing technologies, they eliminated disadvantages of single-sensor approaches in signal interpretation, stability, and structural adaptability, enabling identification of early bolt loosening and crack damage. Sun and Zhang [27] developed a quantitative EMI (Q-EMI) method for measuring structural damping in bolt-loosening monitoring. This approach employed distributed thickness-shear mode piezoelectric transducers for selective excitation of vibration modes. Nguyen et al. [28] proposed a predictive simulation strategy to comprehensively study EMI response characteristics of smart interfaces subjected to typical functional degradation. Chen et al. [29] introduced a multi-resolution full-range bolt-tightening monitoring method using time shifts of direct and trailing waves. Based on the acoustoelastic effect and wave path summation, a theoretical model was established and a monitoring principle proposed. Tong et al. [30] presented a bolt condition identification method based on Lamb wave propagation models and imaging techniques. Han et al. [31] proposed an energy attenuation calibration formula for bolt preload length, addressing cylindrical guided-wave problems through ultrasonic energy attenuation. Xu et al. [32] and Na et al. [33] combined piezoelectric impedance techniques with neural networks to achieve effective damage identification, localization, and severity assessment, providing important references for health monitoring of bolt-sphere joints in large-span space structures. Fan et al. [34] proposed a signal-processing method to extract modulation information from complex response signals obtained under frequency sweep excitation. A nonlinear modulation index was defined to quantify the degree of bolt loosening. Finally, Razi et al. [35] employed an impact hammer to consistently excite systems. By striking pipelines and receiving vibrations with Piezoelectric (PZT) sensors attached to flange bolts, the signals were normalized and filtered, and empirical mode decomposition was applied to establish an effective energy-based damage index.

Perceptive materials possess the capability to sense physical or chemical changes in the external environment and are primarily used for the fabrication of sensors. Actuating materials, on the other hand, refer to those that respond to physical or chemical changes in the external environment, often being manufactured into actuators to control adverse structural responses. The characteristics of commonly used smart materials are summarized in

Table 2. Characteristics of common smart materials.

Material Type	Advantages	Disadvantages	Primary Functions
Optical Fiber	Strong resistance to electromagnetic interference, low energy consumption, small size, wide transmission bandwidth, low density	High elastic modulus, easily brittle and fractured, high testing system cost	Monitoring structural health, temperature, pressure, and other parameters
Carbon Fiber	Lightweight and high strength, low thermal expansion coefficient, good electrical conductivity	Easily brittle and fractured, high recycling cost, complex processing	Monitoring structural cracks, fatigue, vibration, stress–strain, etc.
Shape Memory Alloy (SMA)	Good elasticity, high plasticity, corrosion resistance, wear resistance, biocompatibility	Temperature-dependent, difficult to process, expensive	Fabricated into thermal-driven sensors for monitoring configuration changes, displacement, and damage
Piezoelectric Materials	High energy conversion efficiency, fast response, high sensitivity	Easily brittle, highly temperature-sensitive	Monitoring dynamic stress and strain, structural damage and localization, fatigue monitoring
Magnetorheological/Electrorheological Fluids	Fast response, wide adjustment range, high durability, low energy consumption	High cost, encapsulation required, need for periodic stirring or vibration	Fabricated into controllers for semi-active and active structural control
Magnetostrictive/Electrostrictive Materials	High-temperature resistance, fast response, wide operating frequency, good durability	Require external magnetic field, prone to stress concentration, high energy consumption	Used as drivers in high-power ultrasonic testing, sonar systems, and actuators

.

In contrast, piezoelectric materials have emerged as promising alternatives due to their high sensitivity, rapid response, cost-effectiveness, and environmental stability [36]. In structural health monitoring (SHM), piezoelectric ceramics such as polyvinylidene fluoride (PVDF) [37] and lead zirconate titanate (PZT) [38] are typically fabricated into sensors or actuators for surface mounting or structural embedding [39,40,41,42]. Yang et al. [43] divided the concrete surface into multiple regions, where PZT patches were arranged in arrays. Each array was equipped with both a driver and a sensor, and frequency sweep excitation along with various pulse signals was applied, enabling stress monitoring of concrete in different regions. Ai et al. [44] employed raw admittance features measured from three embedded PZT sensors to extract effective structural mechanical impedance (ESMI) and structural mechanical impedance (SMI) features, which were then used for detecting impact damage in reinforced concrete structures. Pedro et al. [45] investigated the interplay between self-sensing capabilities and the piezoelectric properties of PZT and barium titanate (BT) in aluminum components. Their study demonstrated how BT and PZT particles were incorporated into AA2017-T451 aluminum to create self-sensing materials (SSMs) that respond to external stimuli. Under cyclic loading, these SSMs exhibited a linear correlation between load and electrical response, with sensitivity increasing at lower frequencies. Pedro et al. [46] further examined the sensorial properties of heat-treated AA7075-T651 aluminum plates embedded with PZT and BT particles via friction stir processing (FSP). The results showed that the sensitivity of AA7075-PZT was significantly higher than that of AA7075-BT, with AA7075-PZT achieving a maximum sensitivity of 15.27 × 10⁻⁴ μV/MPa, whereas AA7075-BT exhibited only 7.28 × 10⁻⁴ μV/MPa—52% lower. Ryan et al. [47] focused on developing ultrasonic additive manufacturing (UAM) composites with aluminum matrices embedded with shape memory NiTi, magnetostrictive Galfenol, and electroactive PVDF phases. Their research addressed (i) electrical insulation between NiTi and Al phases for strain sensing, modeling NiTi–Al composites as tunable stiffness materials and thermally invariant structures via the shape memory effect; (ii) process development and testing of Galfenol–Al composites; and (iii) creation of PVDF–Al composites for embedded sensing applications, including the development of a PVDF–Al composite sensor. Philipp et al. [48] evaluated the feasibility of embedding eddy current (EC) sensors for non-destructive testing (NDT) into selective laser melting (SLM) components for SHM. A robust embedding process for EC sensors was developed, ensuring sensor survivability during the harsh conditions of laser powder bed fusion (LPBF). Shao et al. [49] developed a piezoelectric impedance frequency-shift method to estimate bolt preload, designing and manufacturing an experimental device capable of precisely controlling the axial preload of bolts for bolt-loosening detection in engineering structures. Jiang et al. [41] quantified multi-bolt loosening by extracting nonlinear features from stress wave signals, using recurrence plots (RP), phase trajectories, and recurrence quantification analysis (RQA). Garrett et al. [50] introduced an artificial intelligence approach employing acoustic-emission-based SHM to estimate fatigue crack length in thin metal plates. Sun and Wang [51] applied lead magnesium niobate–lead titanate (PMN-PT) material onto the surface of concrete, subjecting specimens to both linear and impact loads. By monitoring the time-domain signal variations of the piezoelectric material, dynamic stress monitoring of concrete was achieved. Results indicated that PMN-PT exhibited superior sensing characteristics under impact loading. Duddi et al. [42] monitored concrete Young’s modulus and crack development through passive sensing technologies, including vibration and acoustic emission (AE). Sha et al. [52] developed an embedded intelligent piezoelectric sensor specifically for SHM of concrete structures.

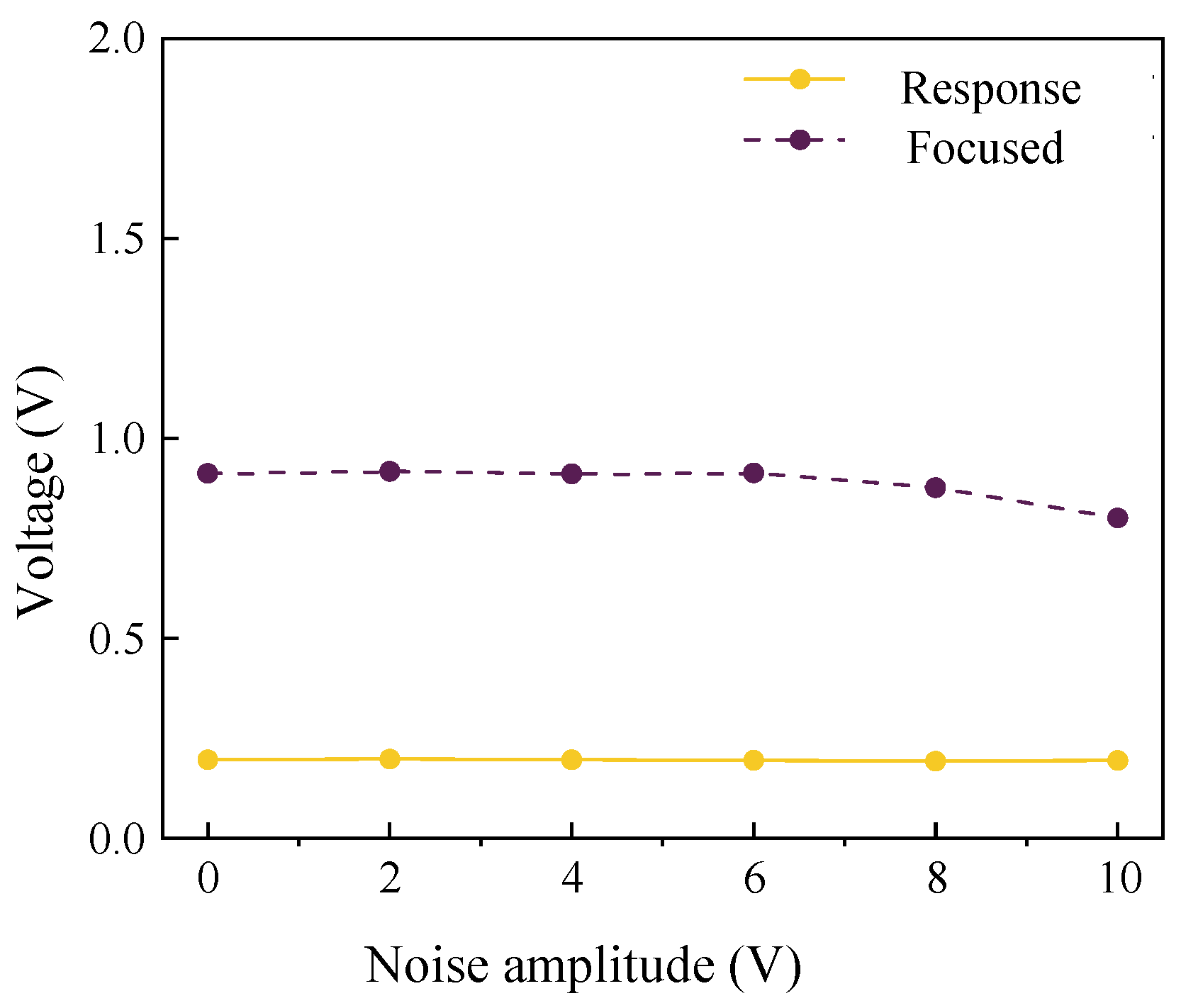
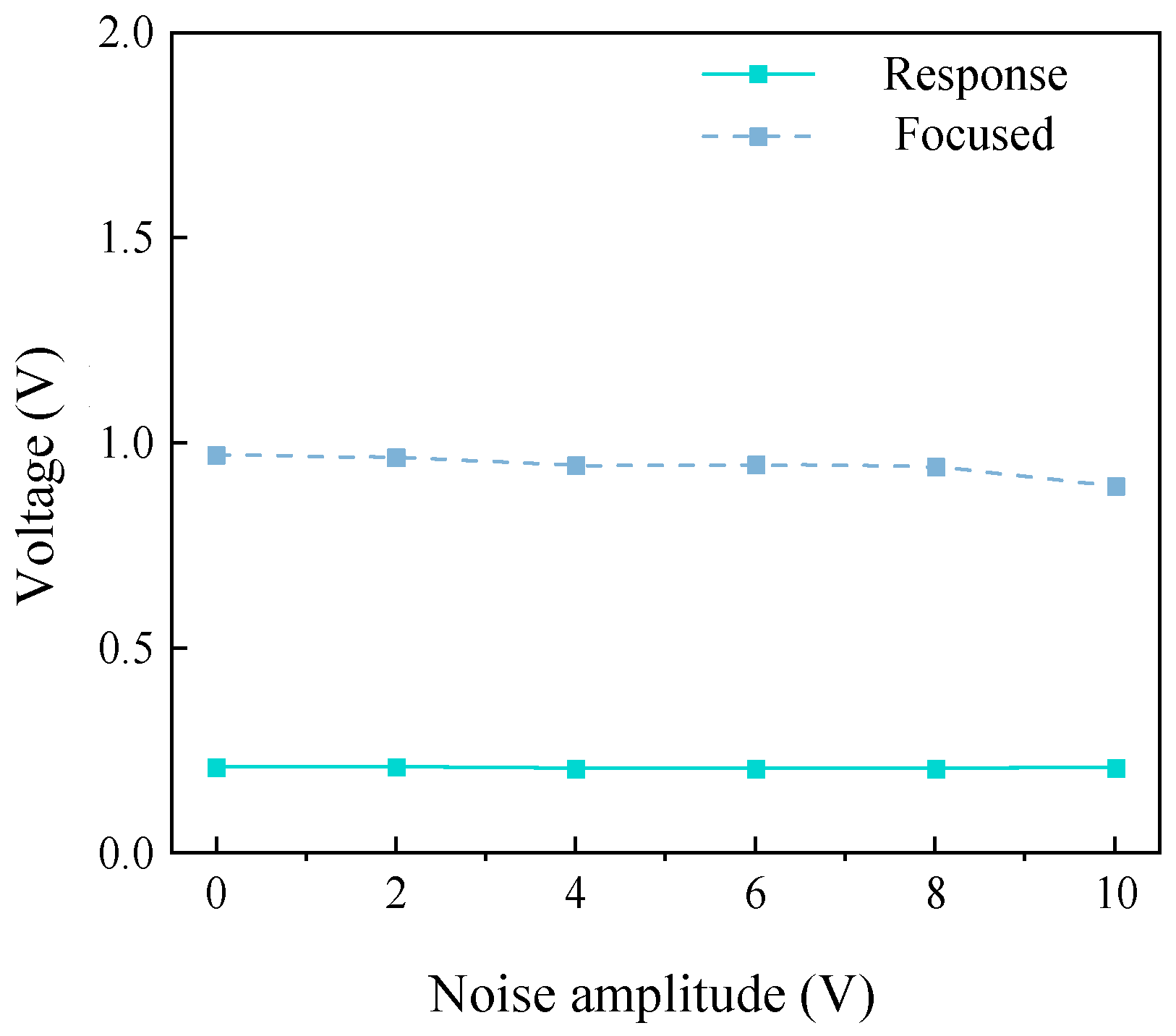
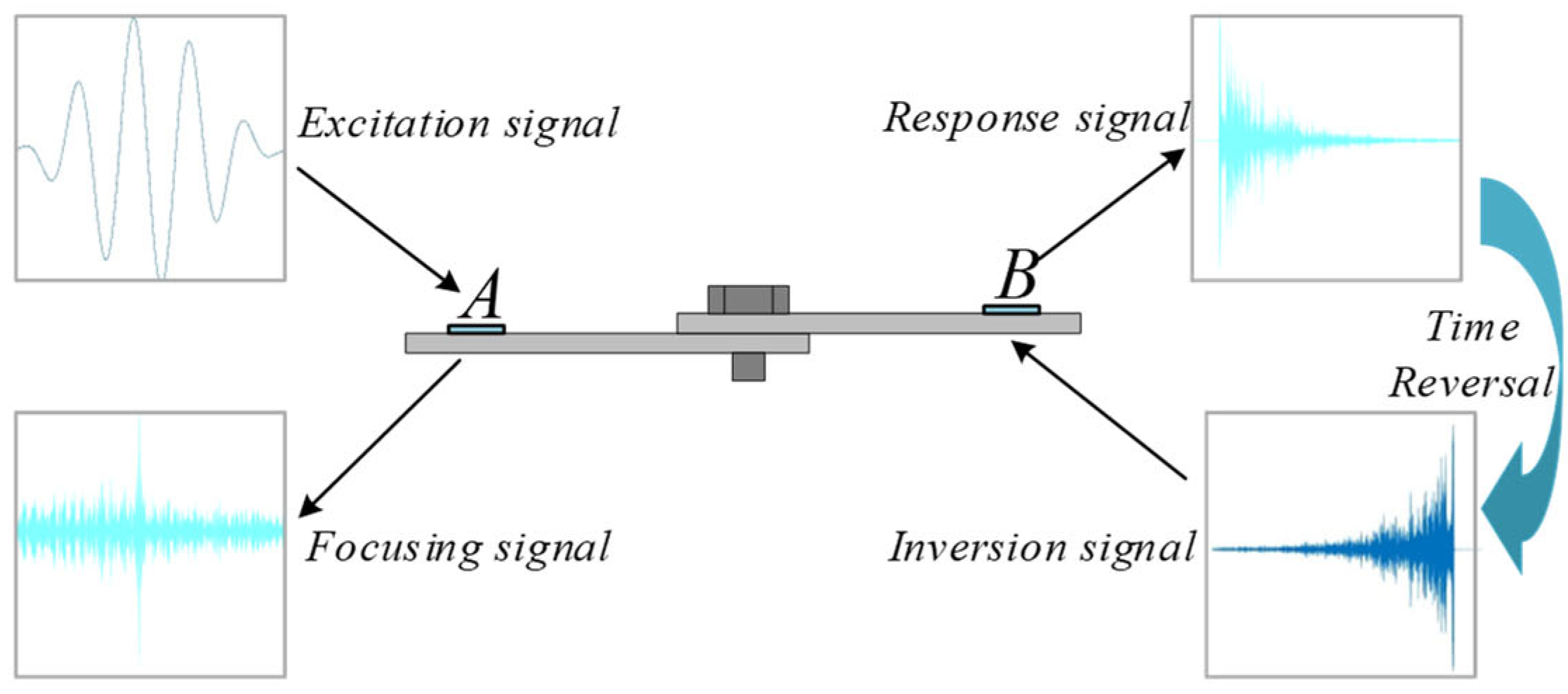
Linear ultrasonic energy dissipation and time-of-flight delay effects derived from piezoelectric ceramic sensors have been widely applied for bolt-loosening detection [53]. Wang et al. [54,55] identified limitations in early-stage detection using ultrasonic propagation across bolted interfaces, noting that energy dissipation stabilizes once preload surpasses critical thresholds. However, environmental interference significantly undermines ultrasonic-based methods, as external noise disrupts wave propagation and hinders practical implementation. To address this, Fink’s time-reversal technique (1998) [56,57] enables phase compensation and signal-energy focusing, yielding noise-immune signal reconstruction. While extensively applied for enhancing structural damage detection [58,59], its application to high-strength bolt-loosening monitoring remains underexplored. From the research outcomes, it can be observed that ultrasonic techniques possess advantages such as a wide frequency response range, low energy consumption, and broad propagation distance, making them widely used in metal and composite material detection [60]. However, they also suffer from shortcomings, including frequency sensitivity, susceptibility to noise interference, and severe scattering in concrete structures. The impedance method has been widely applied for real-time monitoring of localized damage and enables effective damage localization. Nonetheless, its strict frequency requirements limit it to local and surface monitoring, and its accuracy for detecting internal structural damage still requires improvement. Passive monitoring methods that leverage the direct piezoelectric effect can effectively reduce monitoring costs and are commonly employed for overall structural damage detection. However, for localized monitoring, passive approaches still demand further research.

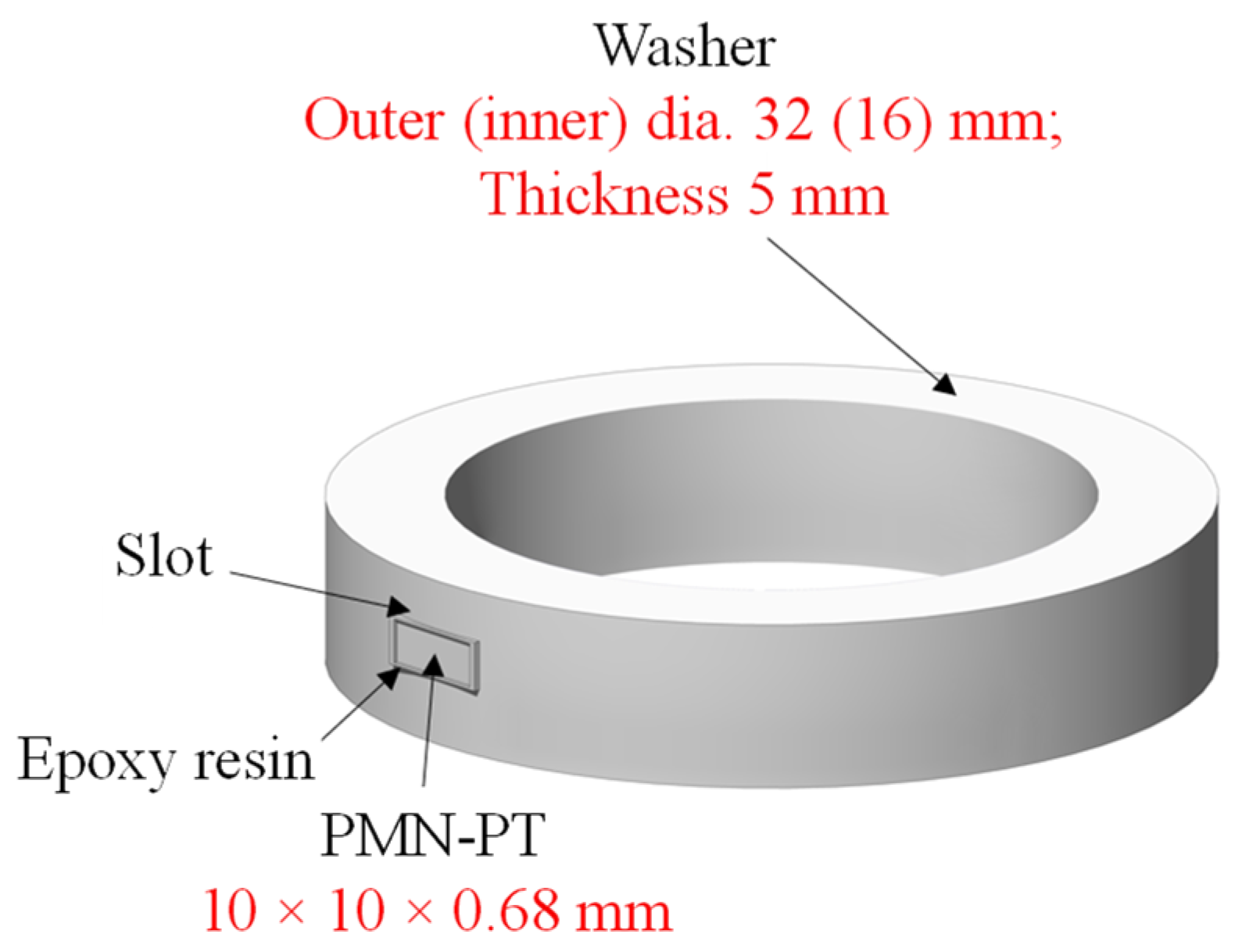
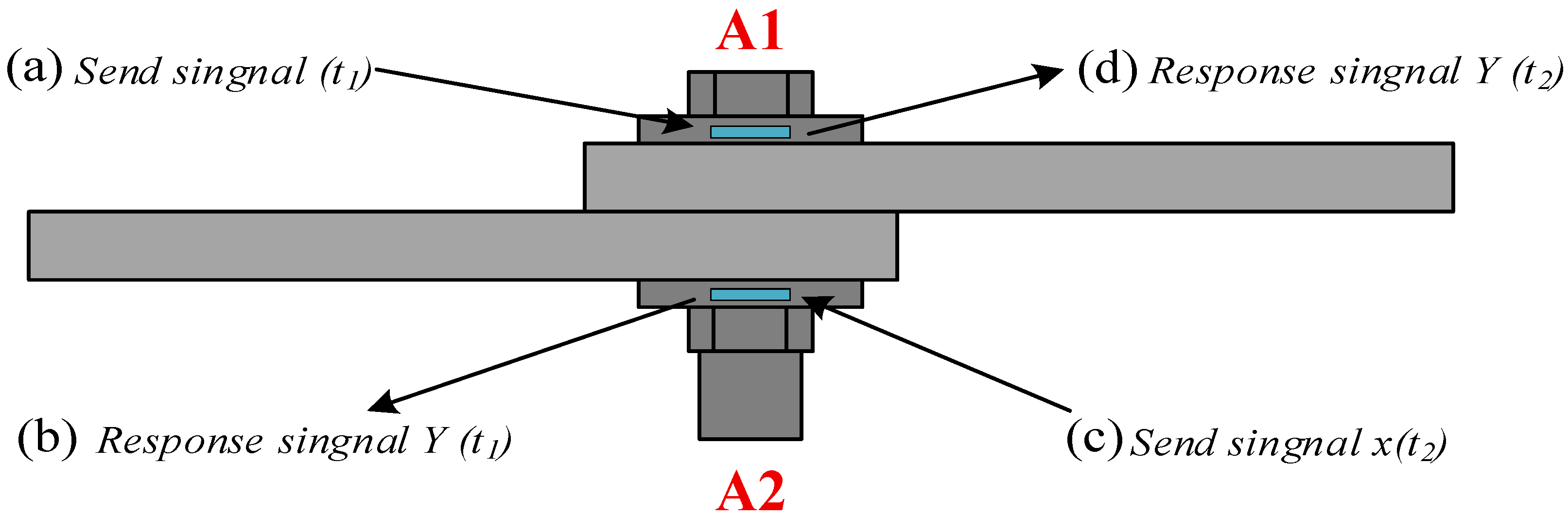
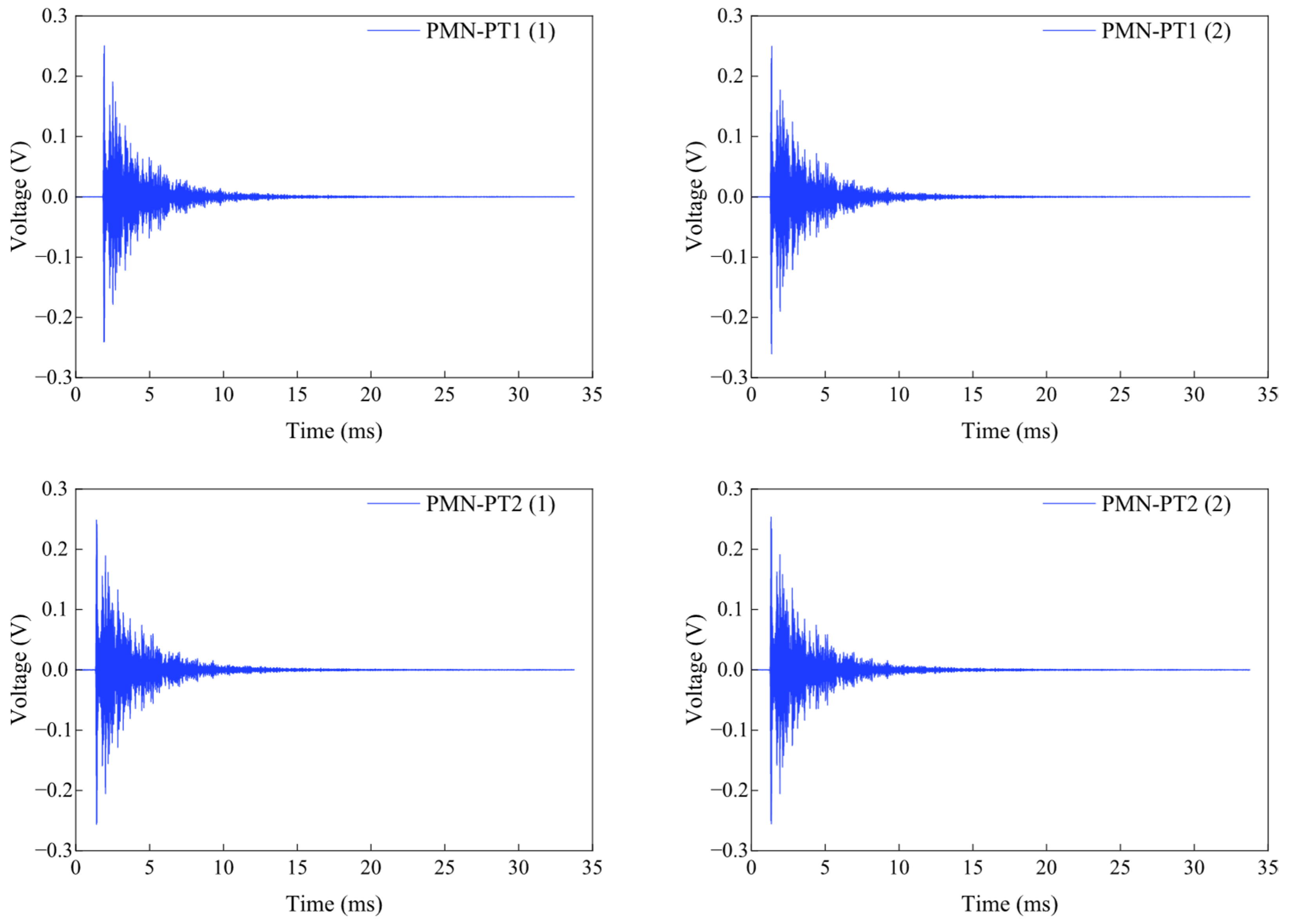
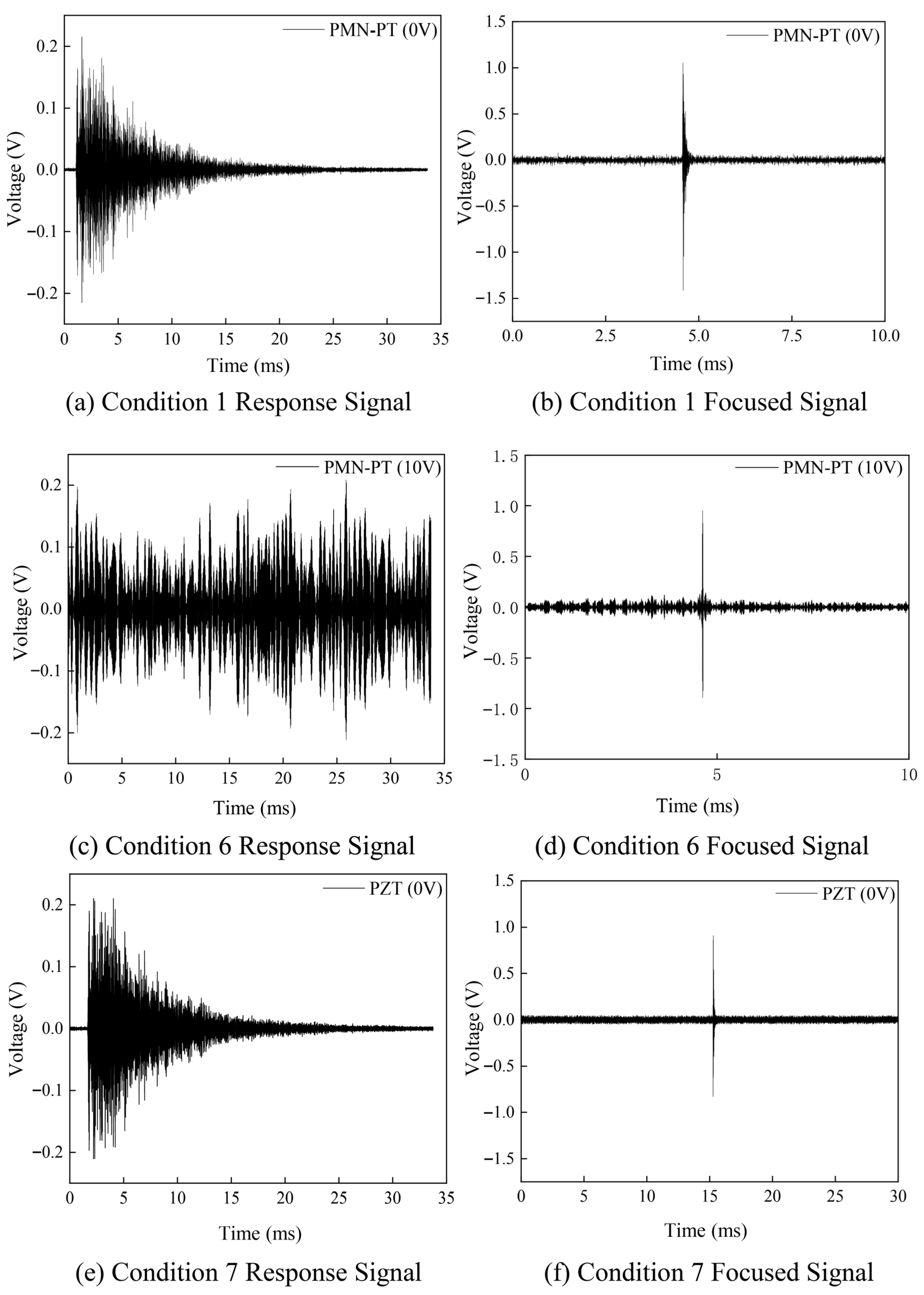
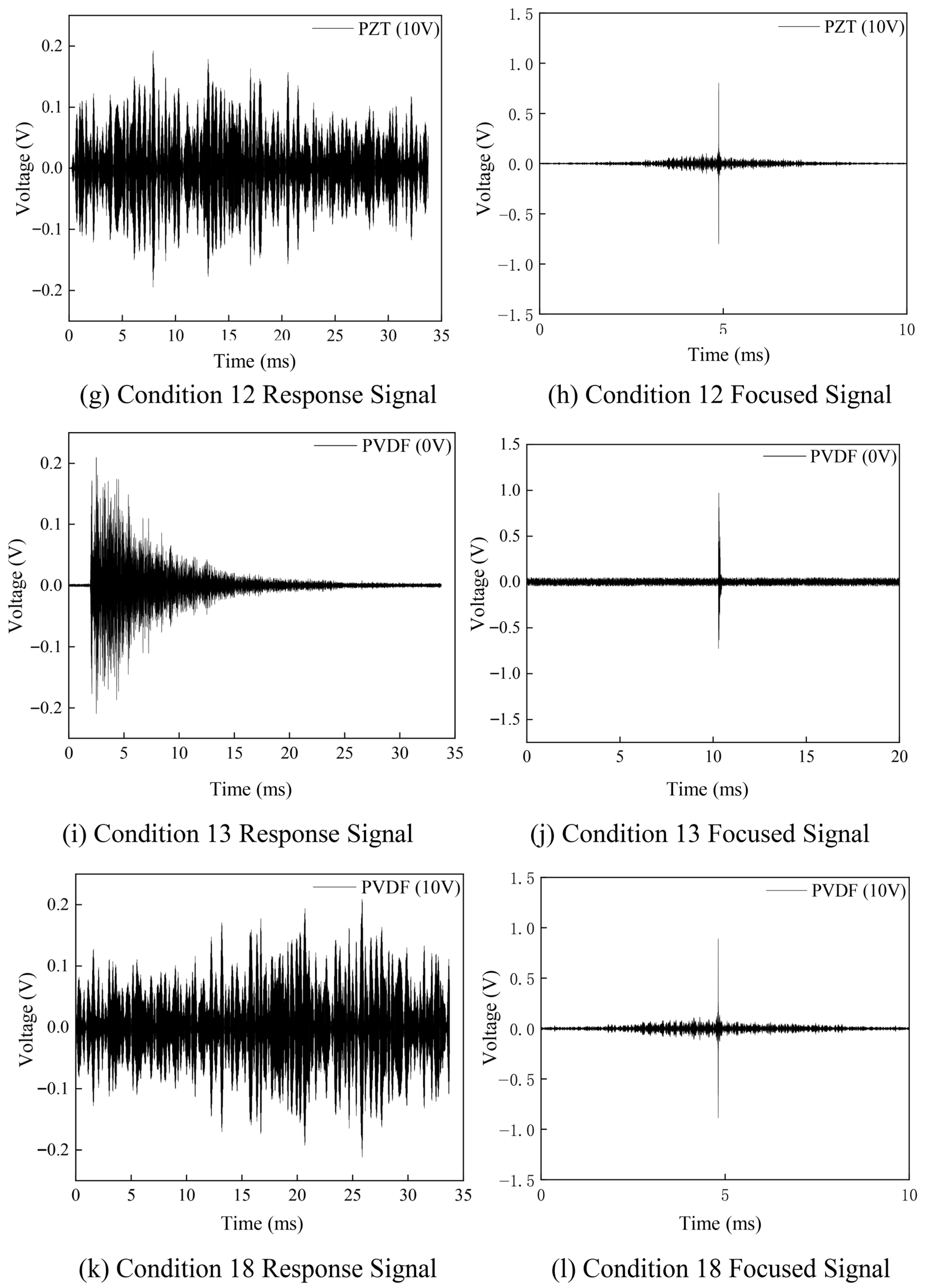
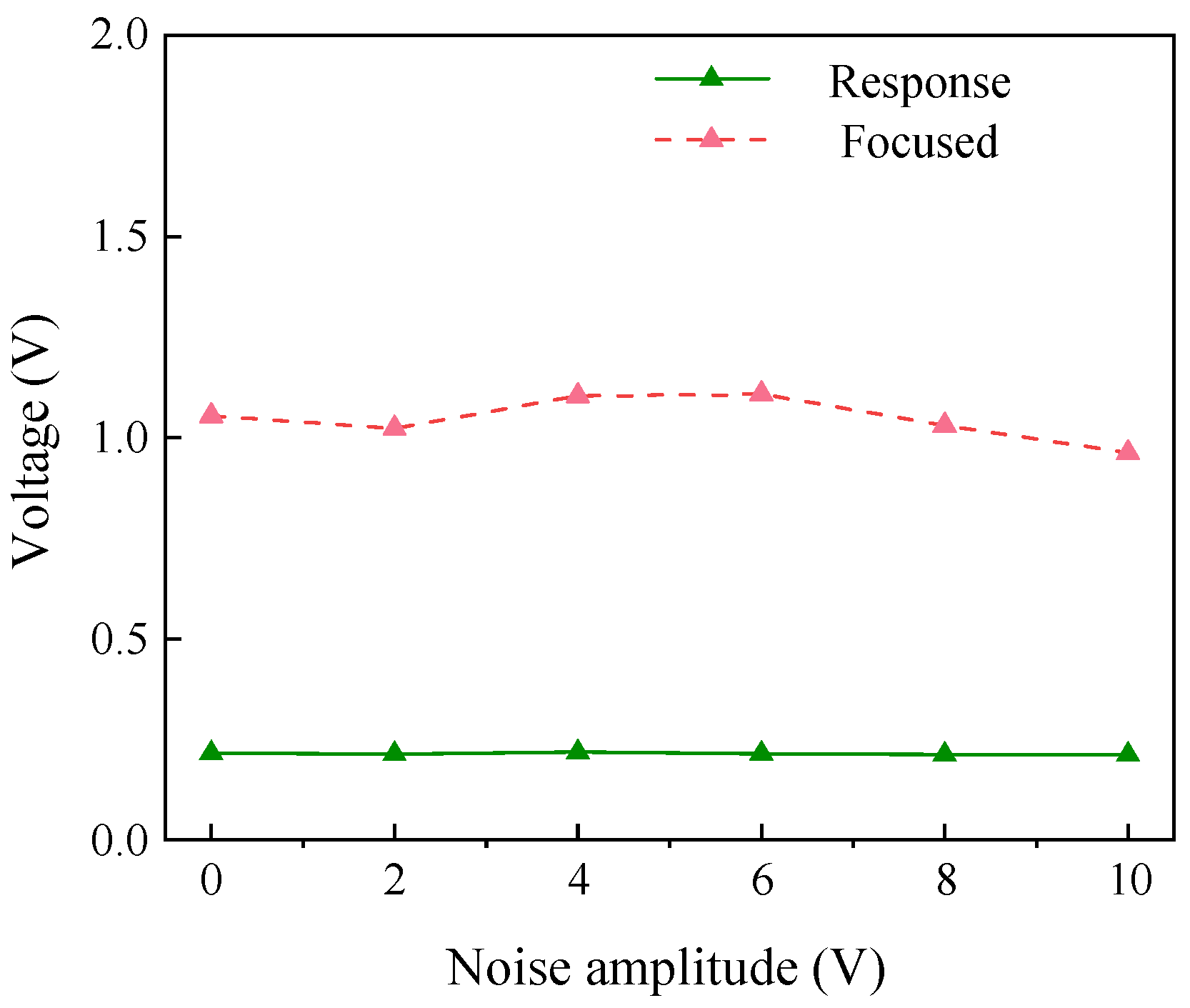
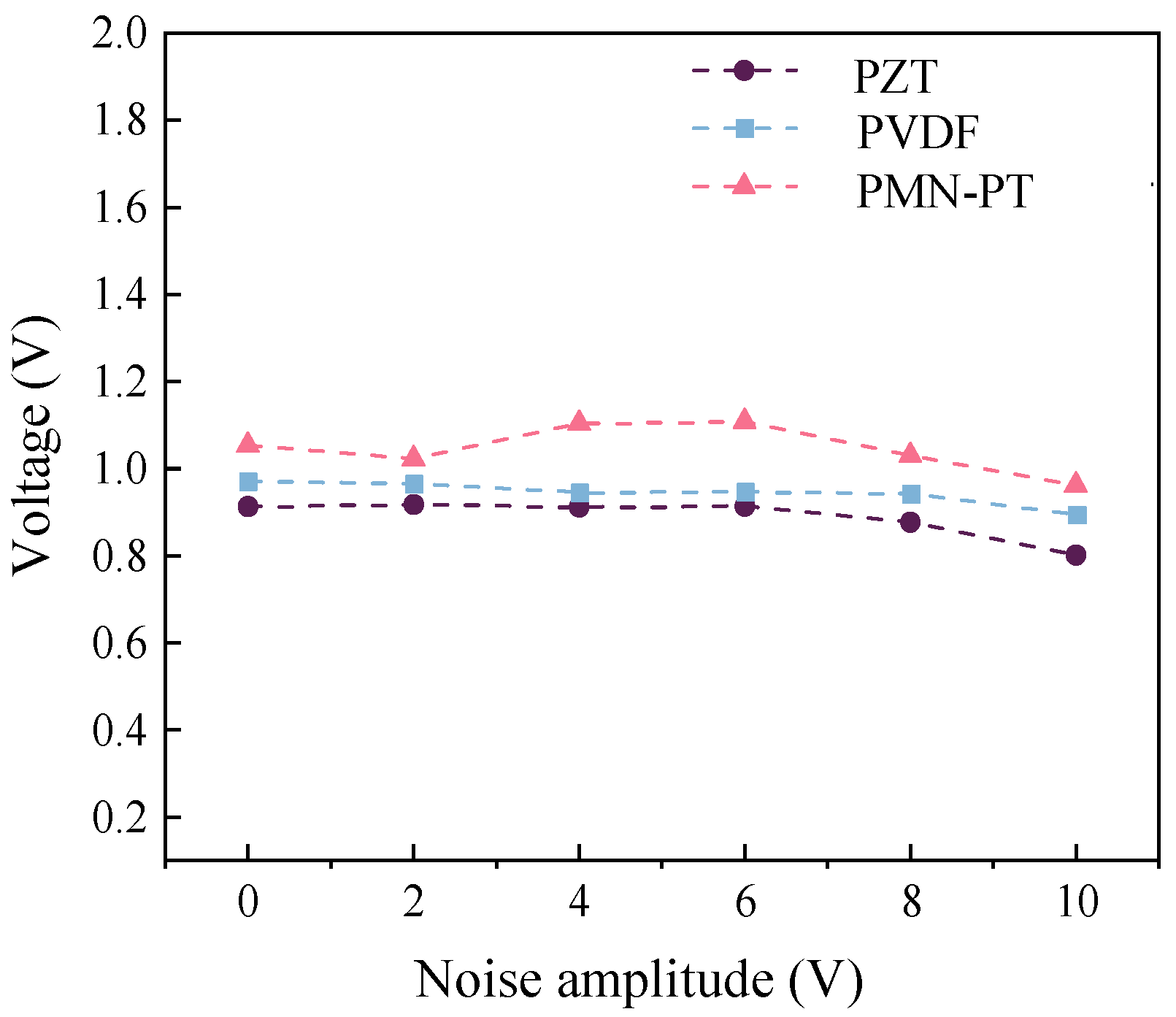
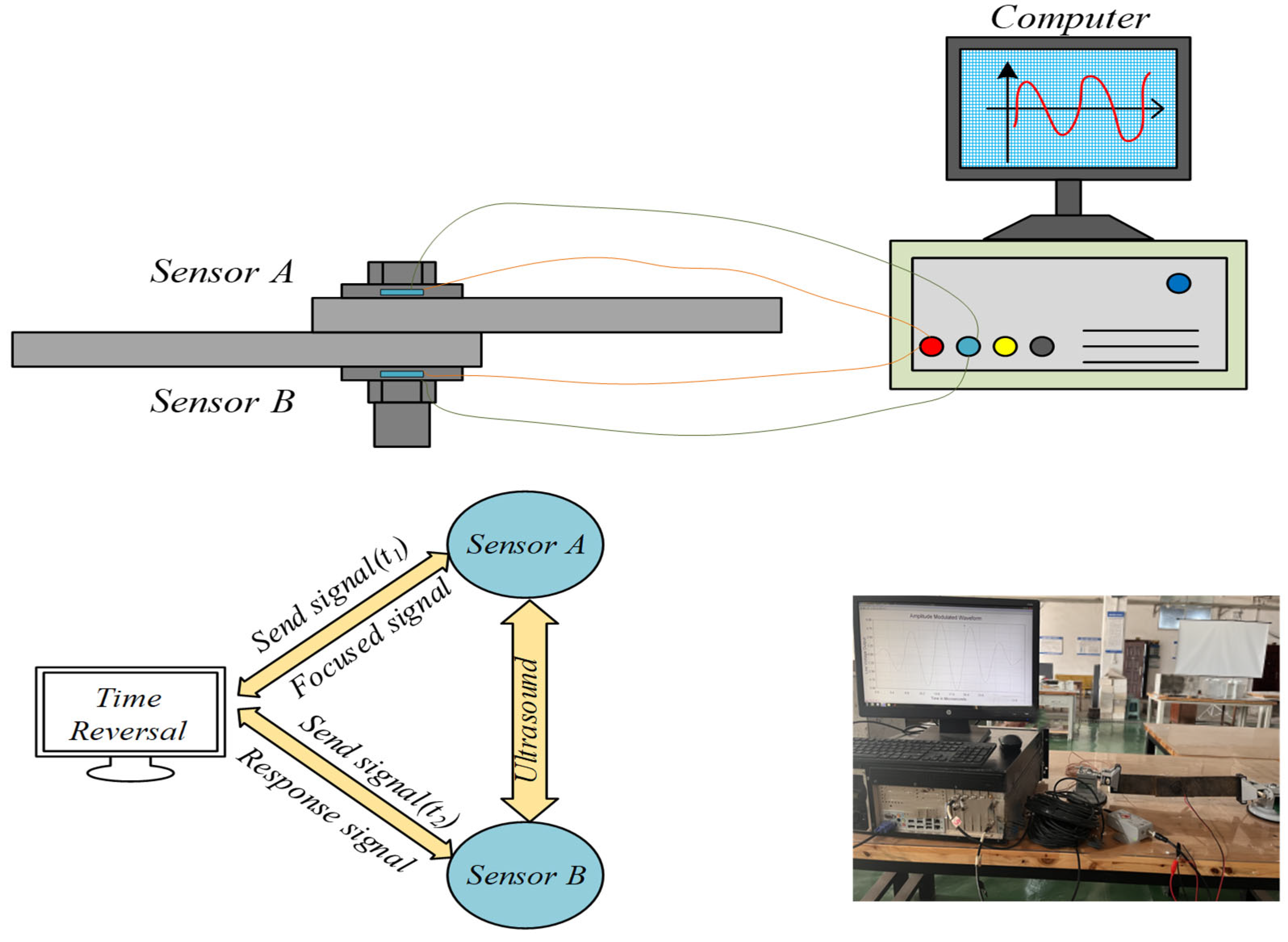
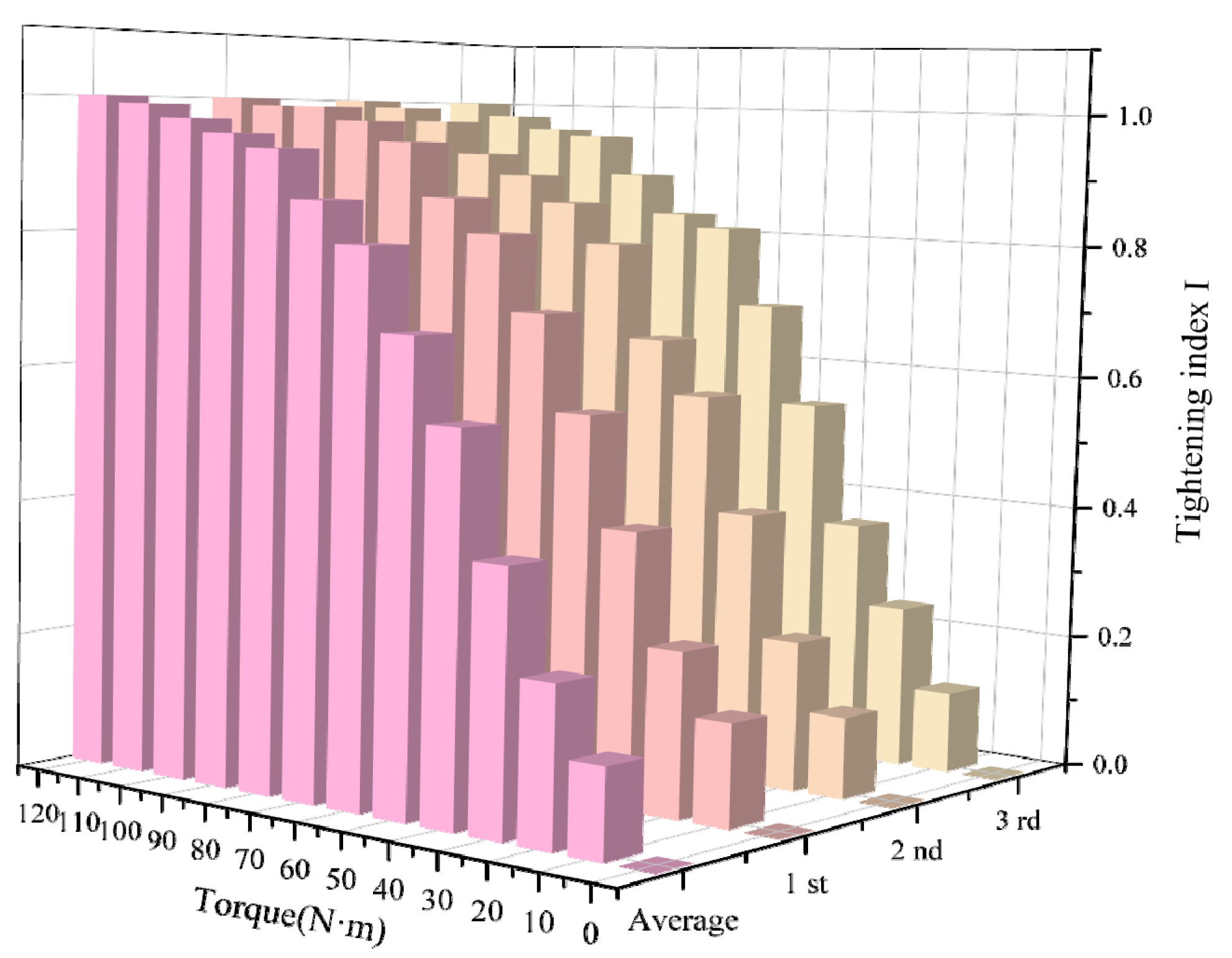
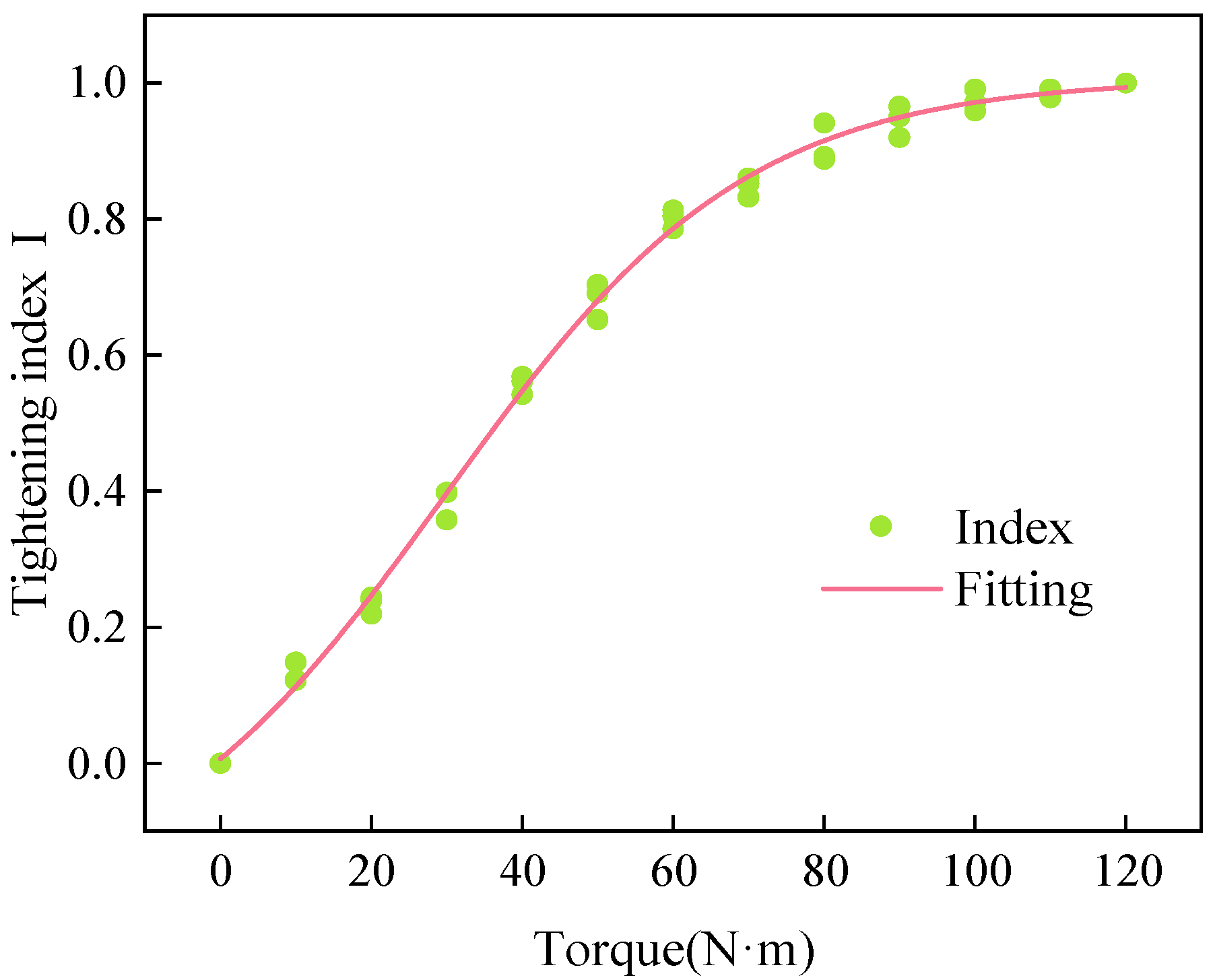
From the perspective of prior research and the characteristics of PMN-PT single-crystal materials, most existing studies have employed traditional PZT ceramics (d₃₃~600 pC/N) or resistive strain gauges as sensing elements. This study is pioneering in its use of PMN-PT single-crystal material (d₃₃ > 2000 pC/N), whose piezoelectric constant is more than four times higher than that of PZT. Benefiting from the ultra-high piezoelectric performance of PMN-PT, sensors fabricated with this material achieve superior sensitivity and signal-to-noise ratio. This work presents a novel surface-mounted piezoelectric sensor based on PMN-PT single-crystal material, composed of a PMN-PT sheet, an integral washer, an epoxy encapsulation layer, and shielded wiring. 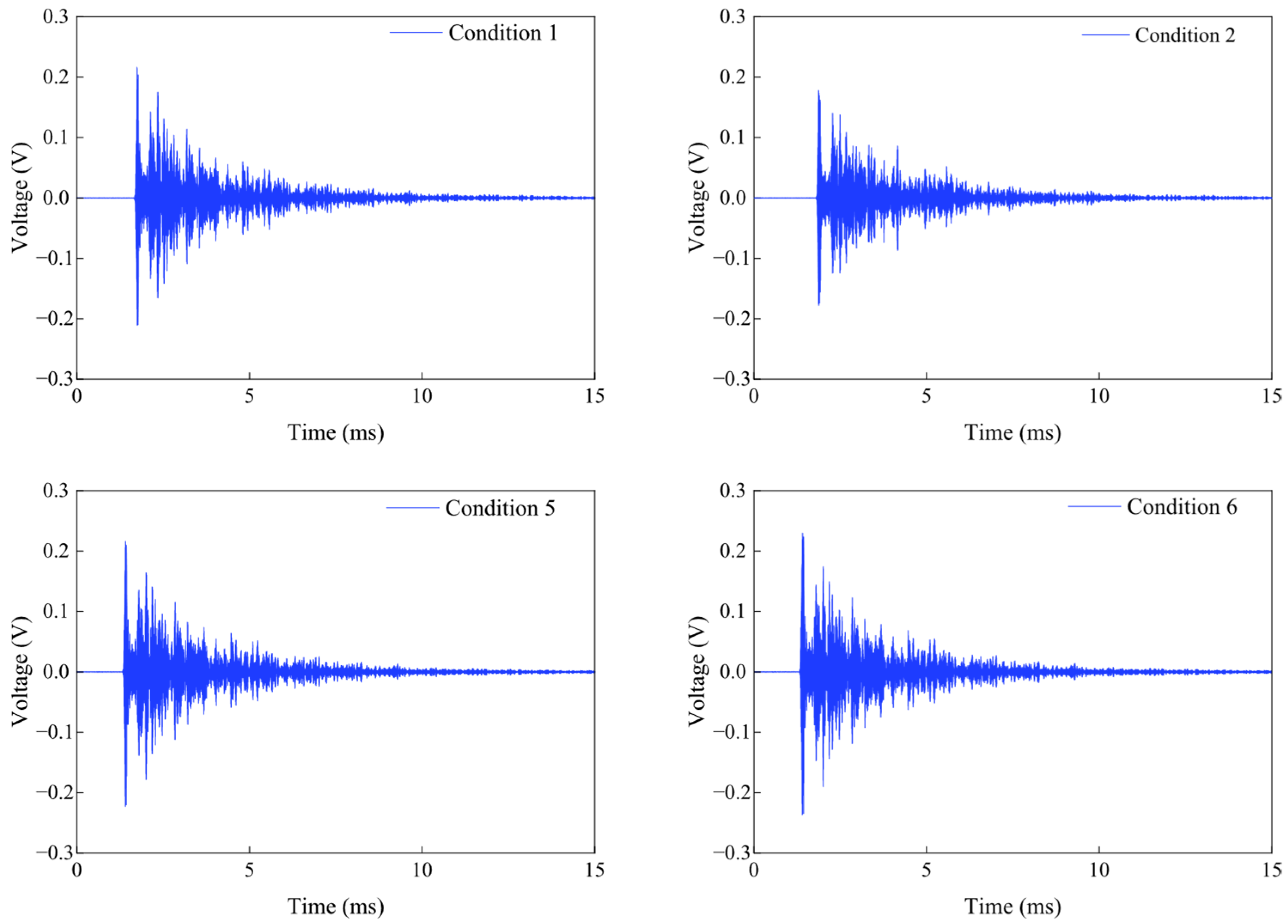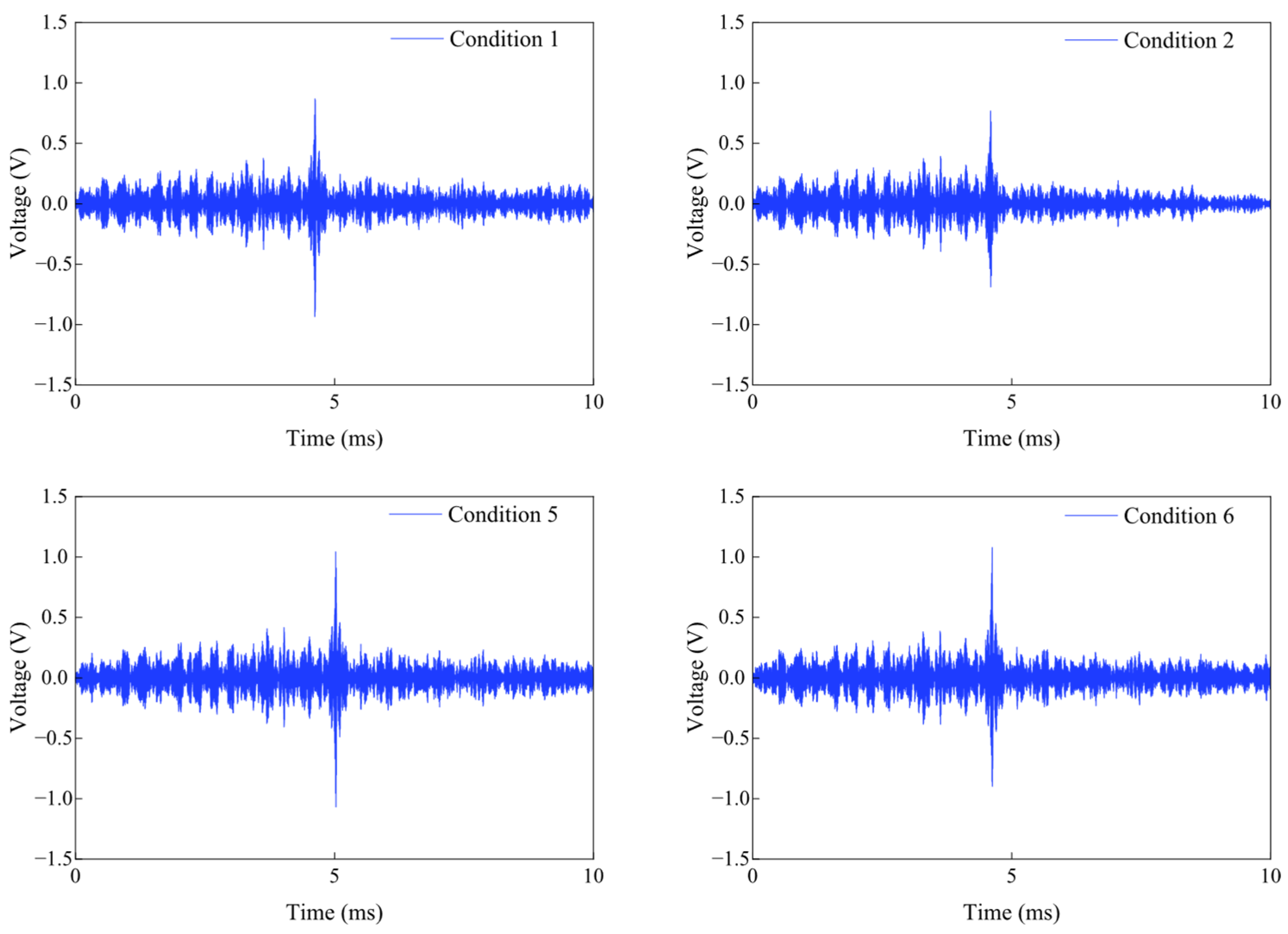Compared with conventional piezoelectric sensors, PMN-PT single crystals offer outstanding advantages in piezoelectric coefficients, energy density, and low-frequency sensitivity [61]. A series of fundamental performance tests and actuation experiments collectively verify the feasibility of the sensor for bolt preload monitoring. Furthermore, preload experiments incorporating the time-reversal (TR) algorithm demonstrate effective suppression of environmental noise through signal-energy focusing. Finally, a fastening index derived from the focused signal is proposed, enabling high-precision evaluation of bolt-loosening states. The application of the new PMN-PT material to bolt-loosening monitoring, owing to its excellent sensitivity and signal-to-noise performance, holds critical significance for enabling early warning and predictive maintenance of bolted connections.

2. Methodology

The TR algorithm is a mathematical technique that was first proposed in 1965 [62]. Later, Fink [56,57] and other scholars introduced the concepts of the time-reversal mirror and the time-reversal cavity. In simple terms, time-reversal technology refers to the process of performing a temporal inversion of the received signal, that is, reversing the order of the signal in time. In the frequency domain, this operation is equivalent to performing a phase conjugation. The time-reversal algorithm has been widely applied in the field of structural health monitoring. In this study, the same method is employed, with its fundamental principle outlined as follows: when dealing with complex propagation paths and environmental noise interference in practical engineering applications, the time-reversal method can effectively achieve adaptive signal-energy focusing and significantly improve the signal-to-noise ratio (SNR). Based on these advantages, this work utilizes the time-reversal algorithm to design the monitoring experiments.

Time-Reversal (TR) Algorithm

As shown in Figure 1, based on the positive and negative piezoelectric effects of piezoelectric materials [63], the Gaussian sinusoidal wave excited by Sensor A as a driver is denoted as $x(t)$, and the signal received by Sensor B is denoted as $y(t)$.

$$y(t)=x(t)\otimes h(t)$$

(1)

where $\otimes$ denotes the convolution operation, and $h(t)$ represents the transfer function between the driver and the sensor. Applying the Fourier transform to Equation (1) yields Equation (2):

$$Y(\omega )=X(\omega )H(\omega )$$

(2)

where $Y(\omega )$, $X(\omega )$, and $H(\omega )$ represent the frequency-domain results of $y(t)$, $x(t)$, and $h(t)$, respectively. The signal $y(t)$ received by the PMN-PT2 sensor is then processed by time reversal, resulting in the time-domain signal $y(-t)$. Time reversal in the time domain corresponds to a phase-conjugate operation in the frequency domain.

$$Y(\omega )=Y^{\ast }(\omega )$$

(3)

where $\ast$ denotes the complex conjugate operation, leading to Equation (4):

$$Y^{\ast }(\omega )=X^{\ast }(\omega )H^{\ast }(\omega )$$

(4)

According to the fundamental principle of the time-reversal algorithm, the propagation process from the source to the receiver and its return during stress-wave propagation are theoretically equivalent. Therefore, the time-reversed response signal $Y^{\ast }(\omega )$ from PMN-PT2, upon secondary excitation, is received by PMN-PT1 as the focused signal $Y^{TR}(\omega )$, defined by Equation (5):

$$Y^{TR}(\omega )=Y^{\ast }(\omega )H(\omega )=X^{\ast }(\omega )H^{\ast }(\omega )H(\omega )$$

(5)

For sine-wave, square-wave, and other symmetric signals, $x(t)=x(-t)$ holds, implying that in the frequency domain, $X^{\ast }(\omega )=X(\omega )$. Therefore, Equation (6) follows from Equation (5):

$$Y^{TR}(\omega )=X(\omega )H^{\ast }(\omega )H(\omega )=X(\omega )H{(\omega )}^2$$

(6)

Applying the inverse Fourier transform to Equation (6) yields Equation (7):

$$y^{TR}(t)={\displaystyle \frac{1}{2\pi }}{\int }_{-\infty }^{\infty }X(\omega )|H(\omega ){|}^2{e}^{i\omega t}d(\omega )$$

(7)

To ensure that the time-reversal process focuses exclusively on phase adjustment of propagating waves without introducing additional coupling between the excitation signal and the medium’s transfer characteristics, maintaining independence between $X(\omega )$ and $|H(\omega )|$ is critical. Assuming parameter $|H(\omega ){|}^2$ is independent of angular frequency $\omega$, Equation (7) can be reformulated as Equation (8):

$$y^{TR}(t)=C_{0}x(t)$$

(8)

where $C_0=|H(\omega ){|}^2$. According to Equation (8), the excitation signal has similar mathematical properties to the focused signal. For example, the excitation signal $x(n)=a\delta (n)$, where $\delta (n)$ is the unit pulse function and $a$ its amplitude, leads to $x(0)=a$. Consequently, $y^{TR}(0)=a{C}_0$, showing that once the excitation amplitude is determined, the focused signal amplitude depends only on the transfer function between the two sensors. In addition, noise interference in the time-reversal algorithm has less impact when the excitation signal amplitude is low. Even when the transfer function is large, the time-reversal algorithm can still achieve effective signal monitoring.

3. Sensor Preparation and Performance Verification

This section describes the use of a self-developed Type-001 cut PMN-PT material to fabricate a novel surface-mounted piezoelectric sensor for bolt preload monitoring. To assess the feasibility of bolt preload monitoring, a series of performance evaluations were carried out, including waterproof capability tests, electrical performance tests, and capacitance characterization.

3.1. Sensor Preparation

The sensor (smart washer) consists of a PMN-PT wafer, a monolithic washer, an epoxy resin layer, and shielded wiring. As shown in Figure 2, the monolithic washer, manufactured by Dongguan Endun, has an outer diameter of 32 mm, an inner diameter of 16 mm, and a thickness (height) of 5 mm. The core sensing element is a PMN-PT wafer measuring 10 mm × 10 mm × 0.68 mm, poled along its thickness direction. Silver electrodes were deposited on both surfaces using spray coating to ensure optimal sensing performance. For embedding, the wafer is inserted horizontally into a machined tangential slot on the washer’s circumference. In this arrangement, the 0.68 mm thickness spans the washer’s 5 mm thickness, while the wafer’s embedded radial extent (≤8 mm) fits within the washer’s ring width (32 − 16 = 16 mm, i.e., 8 mm per side). Slight edge trimming and epoxy encapsulation provide clearance and protection against brittle fracture under torque. Silver electrodes were deposited on both wafer surfaces via spray coating, with electrical leads bonded to the top and bottom. The wafer was then precisely placed into the washer slot, and interfacial gaps were filled with K-9741 epoxy resin (Guangdong Hengda New Materials Co., Ltd., Zhuhai, China). Controlled preloading was applied prior to a 24 h curing process in a dry, ventilated environment to ensure uniform epoxy encapsulation. Key material properties of the washer and epoxy are provided in

Table 3. Mechanical performance parameters of the monolithic washer material.

Material Name	Elastic Modulus (GPa)	Poisson’s Ratio (v)	Density ρ (kg/m3)
Washer	90	0.35	8400

and

Table 4. Key performance parameters of Ergo-1309 epoxy resin material.

$\mathbf{Dielectric} \mathbf{Constant} \left(\mathit{\epsilon }\right)$	$\mathbf{Dielectric} \mathbf{Loss} \left(\mathit{t}\mathit{a}\mathit{n}\mathit{\delta }\right)$	$\mathbf{Poisson}’\mathbf{s} \mathbf{Ratio} \left(\mathit{v}\right)$	Density ρ (kg/m3)
2.84	0.082	0.38	1.2

, respectively. Figure 2 shows the schematic geometry, while Figure 3 illustrates the complete assembly process with a real-view photograph.

3.2. Basic Performance Test

In bolt preload monitoring, sensors must maintain operational stability under diverse environmental conditions, necessitating stringent requirements for consistent fundamental performance. Two PMN-PT wafers (designated A1 and A2) with dimensions 10 mm × 10 mm × 0.68 mm were selected for standardized evaluation through waterproof capability and electrical performance testing. These assessments primarily involved systematic measurements of resistance and capacitance parameters.

Water Resistance and Electrical Performance Test

Elvin et al. [64] reported that the capacitance value of piezoelectric elements changes significantly when embedded in a substrate after welding. To evaluate the waterproofness and electrical performance of the sensor, different working conditions were established, and the resistance and capacitance of the PMN-PT sheet were measured for the first time, recorded as condition G1. Epoxy resin was evenly applied around the welded PMN-PT material, then left for one hour to cure, recorded as condition G2. The sensor was immersed in a glass of water and stirred with a glass rod for 15 min, recorded as condition G3. The finished sensor was pre-pressurized for 24 h and marked as condition G4. The assembled smart washer sensor was then recorded as condition G5. The resistance and capacitance values are shown in Figure 4, with measurements summarized in

Table 5. PMN-PT sheet resistance test results.

Condition	G1	G2	G3	G4	G5
A1	infinite
A2	infinite
Averages	infinite

and

Table 6. PMN-PT sheet capacitance test results.

Condition	G1	G2	Magnitude of Change (%)	G3	Magnitude of Change (%)	G4	Magnitude of Change (%)	G5	Magnitude of Change (%)
A1	4.11	3.99	−3.007%	3.95	−1.012%	3.94	−0.253%	3.91	−0.767%
A2	4.13	4.00	−3.250%	3.96	−1.010%	3.95	−0.253%	3.91	−1.023%
Averages	4.12	3.995	−3.129%	3.955	−1.011%	3.945	−0.253%	3.91	−0.895%

.

As shown in Table 5 and Table 6, PMN-PT wafers A1 and A2 exhibited infinite resistance across all test conditions. According to the first category of piezoelectric constitutive equations (stress-charge form), the PMN-PT sensor operates under mechanically free and electrically short-circuited boundary conditions. The relationship between external circuit resistance $R_1$ and internal piezoelectric material resistance $R_2$ theoretically satisfies $R_1\ll R_2$, resulting in infinite interelectrode resistance, confirming the stable electrical performance of the PMN-PT wafers under the tested conditions. During the transition from G1 to G2, a slight capacitance reduction was observed, primarily due to partial delamination of the silver electrode layer during lead welding, which altered the capacitive characteristics. Under G3 conditions, further minor capacitance decrease occurred due to increased interelectrode distance caused by epoxy resin thickness variations. Comparative analysis between G3 and G4 revealed stabilized capacitance values, demonstrating effective waterproof encapsulation. The final capacitance reduction in G5 originated from microstructural deformations induced by assembly preloading and epoxy curing shrinkage. These results collectively confirm that the PMN-PT wafers maintain robust waterproof integrity (<0.01% moisture penetration) and stable electrical performance (capacitance fluctuation rate ≤ 3.25%) throughout fabrication and operation.

3.3. Sensor Drive Performance Test

The operational principle for monitoring bolt preload using the time-reversal algorithm involves deploying two smart washers: one functioning as an actuator and the other as a sensor. By comparing the time-domain response signals from both devices, piezoelectric performance deviations can be detected, thereby validating functional symmetry between the actuator and sensor modes. The experimental implementation included (1) installing the sensors using a torque wrench; (2) connecting the actuator, charge amplifier, and computer sequentially for signal excitation and acquisition; and (3) validating signal consistency through bidirectional testing in actuator-to-sensor and sensor-to-actuator configurations. The 3D experimental setup (Figure 5) illustrates the integrated system topology, showing the bolted joint assembly and spatial positioning of the smart washers.

The excitation signal was set as a sine wave with a center frequency of 150 kHz and processed using a window function. The voltage amplitude was 5 V, with a loading duration of 3.5 ms. Smart washer A1 excited the signal while smart washer A2 received it, with the excitation repeated twice. Then, smart washer A2 was used to excite the signal while smart washer A1 received it, again repeating the excitation twice. The voltage output curve is shown in Figure 6. The time-history voltage curves from repeated experiments with smart washers A1 and A2 were similar, indicating that the performance of different smart washers as sensors or actuators was very consistent, confirming good stability.

3.4. Comparison with Other Piezoelectric Sensors

This study conducted an environmental noise comparison experiment to evaluate the SNR of sensors fabricated from PZT, PVDF, and PMN-PT materials under varying noise levels, comparing direct signal reception with signals obtained after time-reversal processing (see

Table 7. Piezoelectric sensor material parameters.

Model	Thickness (mm)	Flexibility Coefficient S11 (Nm2)	Piezoelectric Coefficient d33 (pC/N)	Dielectric Constant ε33 (FM−1)	Young’s Modulus Ep (GPa)
PZT-5H	0.6	1.65 × 10−11	450	3.01 × 10−8	60
LDT0-028K	0.2	3.0 × 10−10	520	1.2 × 10−10	3
PMNT67/33	0.7	1.64 × 10−11	860	5.0 × 10−10	18

). In this experiment, three different types of piezoelectric sensors were studied in detail: piezoelectric ceramic (PZT) sensors, piezoelectric film (PVDF) sensors, and (001) cut relaxor ferroelectric single-crystal (0.67PMN-0.33PT) sensors, as shown in Figure 7a. PZT sensors are primarily used for converting force into electrical signals. Their high sensitivity, simple force-to-electricity conversion mechanism, customizable shape, and low cost make them the most commonly used sensors in structural health monitoring. Although PVDF sensors are slightly inferior to PZT in piezoelectric performance, they offer higher elasticity and tensile strength, fast response, and strong stability, making them suitable for long-term operation in complex environments. As shown in Figure 7b, for structures undergoing large deformations, PVDF sensors, due to their high flexibility, are less prone to damage or detachment. They can deform synchronously with the base structure and capture signals throughout the deformation process. The piezoelectric sensing element is made from cut lead magnesium niobate–lead titanate (PMN-PT) material, as shown in Figure 7c. Compared to PZT materials, PMN-PT sensors exhibit significant improvements in piezoelectric and electromechanical coupling coefficients, with maximum strain reaching up to 1.7%—ten times that of traditional piezoelectric materials—and a very fast response speed [65,66].

PMN-PT piezoelectric single crystals exhibit a higher SNR compared to traditional PZT and PVDF materials [66]. Furthermore, the time-reversal algorithm is robust in handling environmental noise. To evaluate the specific SNR capabilities under different noise levels, a comparison of different piezoelectric materials in various noise environments is essential. This further explores the extent to which the time-reversal algorithm enhances SNR in practical engineering applications. The study examines the compatibility of three piezoelectric materials with the time-reversal algorithm, designing an environmental noise comparison experiment based on time-reversal with different piezoelectric materials. The dimensions of the piezoelectric materials used are provided, with the experimental process shown in Figure 8.

The required hardware and software for the experiment include a data acquisition system with a MATLAB version R2023a-integrated PCI-2 card, charge amplifier, torque wrench, two steel plates, and high-strength bolts (Model M14). The maximum applied torque is 120 N·m, assuming the bolt is fully tightened at 120 N·m. The charge amplifier amplifies the signal by a factor of 40. A sine wave with a central frequency of 150 kHz is excited by PMN-PT1, modulated by a Hanning window, with a maximum amplitude of 5 V. Additionally, PMN-PT3 excites a Gaussian white noise signal to simulate environmental noise. The on-site experimental setup is shown in Figure 9.

It is important to note that preparation before the experiment aimed to minimize potential sources of error. Specific measures included the following: To ensure consistent propagation of ultrasonic signals, the contact surfaces of the specimens were finely processed. The connection points of the two steel plates and the areas where the piezoelectric materials were attached were polished with sandpaper to remove surface irregularities and impurities. After polishing, the surfaces of the connection points were thoroughly cleaned with ethanol. This step ensured the removal of dust and oil generated during polishing, and the rapid evaporation of ethanol ensured cleaning efficiency while avoiding potential impacts of moisture on the experimental results.

By adjusting the Gaussian white noise signal amplitude to represent different conditions, the signal received by PMN-PT2 at Condition 1 was considered the response signal. The response signal was processed using MATLAB’s time-reversal method, then re-excited by PMN-PT2 and received by PMN-PT1 to obtain the focused signal. The same procedure was repeated for PZT and PVDF materials. The summarized results for the conditions are shown in

Table 8. Summary of different conditions.

Condition	Material	Noise Amplitude (V)	Condition	Material	Noise Amplitude (V)	Condition	Material	Noise Amplitude (V)
1	PMN-PT	0	7	PZT	0	13	PVDF	0
2	PMN-PT	2	8	PZT	2	14	PVDF	2
3	PMN-PT	4	9	PZT	4	15	PVDF	4
4	PMN-PT	6	10	PZT	6	16	PVDF	6
5	PMN-PT	8	11	PZT	8	17	PVDF	8
6	PMN-PT	10	12	PZT	10	18	PVDF	10

. The experimental results are presented in Figure 10a–l.

From Figure 10a–l, it is evident that the time-domain plots for both response and focused signals from the three piezoelectric materials are generally similar, with peak signal values varying due to differences in piezoelectric coefficients. During the experiment, variations in the coupling between the piezoelectric materials and the steel plates, due to manual attachment, may have influenced the results. Moreover, as the amplitude of the white noise increases (from Conditions 1, 7, 13 to Conditions 6, 12, 18), the peak values of the response signals become less noticeable. However, the focused signal peak values after time-reversal processing are less affected. To further analyze the superior noise performance of the three piezoelectric materials, the response signal and focused signal amplitudes for different conditions were compared, as shown in Figure 11, Figure 12 and Figure 13.

According to the results shown in Figure 11, Figure 12 and Figure 13, it can be observed that as the noise amplitude increases, the response signals for all three piezoelectric materials slightly decrease, but the change is not significant. This is because the noise primarily affects the overall peak value of the signal. Overall, the peak value of the PMN-PT response signal is consistently greater than that of the focused signal, directly attributable to its good SNR and high piezoelectric coefficient. The peak values of the focused signals for all three materials show a decreasing trend as environmental noise increases, with PMN-PT still outperforming the other two materials. The focused signal for PMN-PT increases by an average of approximately 4.89 times compared to the response signal. The focused signal for PZT increases by an average of approximately 4.58 times compared to the response signal. The focused signal for PVDF increases by an average of 4.51 times compared to the response signal. This difference in response and focused signal peaks can be attributed to the fact that the initial response signal peak for PMN-PT is higher than that of the other two materials. During the second excitation, when the ultrasonic signal is received, the higher piezoelectric coefficient of PMN-PT leads to a significantly larger peak value for the focused signal. This sequence reflects the materials’ piezoelectric coefficients, from high to low.

A comparison of the focused signal amplitudes for the three materials is shown in Figure 14. The data clearly show that PMN-PT yields better results compared to the other two materials. Through time-reversal processing, the results for all three materials significantly improved, with noticeable increases in voltage amplitude, demonstrating the time- and space-focusing capability of the time-reversal algorithm. In the experimental results, the difference between the response and focused signals for the three piezoelectric materials is relatively small, but their piezoelectric coefficients vary greatly. Theoretically, there should be a significant distinction between the peak values of the response and focused signals for the three materials. The reasons for this discrepancy may include the following: (1) PZT and PVDF are commercial sensors, and differences in wire soldering and silver polarization compared to the homemade sensors could account for significant variations. (2) The coupling between the piezoelectric materials and the steel plate during sensor attachment could also cause noticeable differences. However, the ranking of signal amplitudes aligns with the sequence of piezoelectric coefficients. In summary, PMN-PT piezoelectric composite materials exhibit superior noise reduction performance compared to PZT ceramics and PVDF films. Time-reversal technology significantly optimizes the received voltage amplitude, especially in noisy environments, demonstrating its effectiveness in improving signal quality. However, the effectiveness of the time-reversal algorithm in enhancing voltage amplitude decreases as the level of environmental noise increases.

4. Bolt Preload Monitoring Test

4.1. Experimental Design

To validate the effectiveness of the time-reversal method in monitoring high-strength bolt preload, the experimental setup comprised two steel plates, high-strength bolts, and two PMN-PT sensors. The specifications of these components are detailed in

Table 9. Specifications of experimental components for high-strength bolt testing.

Component	Plate	Bolt	Sensor
Model/Specification	Q345	M14	PMN-PT
Dimensions (mm)	400 × 100 × 10	14 × 1.25 × 60	5 × 5 × 0.68 32 × 16 × 5

.

This section reports bolt preload experiments using the developed sensor system. The procedure involved adjusting bolt torque with a torque wrench, analyzing the relationship between preload variations and signal characteristics through received response signals and focused signal processing, deriving a fastening index via normalized data processing, and validating its accuracy through tests with unknown preload levels. Bolt preload refers to the axial force exerted between connected plates by the bolt-nut assembly. If the friction coefficient remains constant during torque application, the axial force shows a linear relationship with applied torque—higher torque corresponds to greater preload, thus enabling indirect preload assessment through torque measurements. The experimental workflow incrementally increased bolt torque while using ultrasonic techniques to monitor preload variations, thereby establishing correlations between preload levels and ultrasonic signal features. Material specifications and schematic diagrams are presented in Figure 15a–f and Figure 16.

4.2. Analysis of Test Results

4.2.1. Response Signal Analysis

This section investigates the variation trends of received response signals under different operating conditions, with a focus on establishing the correlation between signal characteristics and bolt preload changes. In the first experimental group, Figure 16 and Figure 17 present the voltage time-domain plots of ultrasonic waves transmitted from Actuator A through the high-strength bolted connection to Receiver B. Three sets of peak signals corresponding to different torque levels were subsequently fitted to quantify the relationship between directly received response signals and applied bolt torque, as shown in Figure 18.

The results shown in Figure 17 and Figure 18 demonstrate a linear correlation between the response signal amplitude and bolt preload. As the applied torque increases, the peak amplitude of the response signals correspondingly rises. Notably, within the 80–120 N·m torque range, signal variations diminish significantly, indicating stable bolt fastening with minimal changes in the actual contact area between connected components. Under this condition, ultrasonic wave propagation experiences reduced energy reflection and dissipation. Conversely, within the 0–50 N·m torque range, substantial signal amplitude fluctuations are observed due to pronounced energy reflection and loss caused by bolt loosening. The transitional 60–80 N·m torque range exhibits intermediate signal behavior, reflecting partial stabilization of the interfacial contact during the tightening process.

4.2.2. Focused Signal Analysis

The bolt preload experiments based on the time-reversal method maintained fixed actuator–sensor positions. Temporal discrepancies in the initial ultrasonic excitation received by Sensor B were corrected by adjusting the transmission sequence of the secondary excitation signals, ensuring that energy from variably timed wavefronts reconverged at the source to achieve focused energy amplification. Since all signals propagated through identical paths, their coherent superposition at Sensor A generated a localized energy peak with a significantly amplified amplitude compared to adjacent temporal regions. Figure 19 presents representative focused signal time-domain diagrams from the first experimental group, while Figure 20 illustrates the fitted relationship between the time-reversed focused signal peaks and applied bolt torque across three preload levels.

Figure 19 and Figure 20 demonstrate that the peak amplitude of the focused signal decreases linearly with reduced bolt preload. During the initial tightening phase (0–50 N·m), the voltage amplitude exhibits rapid growth, reflecting significant ultrasonic energy dissipation caused by substantial variations in the actual contact area of loose bolted connections. As the preload increases to 60–90 N·m, the amplitude growth rate slows, indicating stabilized contact conditions and reduced energy loss. When the preload further reaches 100–120 N·m, the amplitude stabilizes around 1.212 V with minimal variation, demonstrating that additional mechanical tightening has negligible effects on ultrasonic signal characteristics due to saturated interfacial contact.

4.2.3. Comparative Analysis of Response Signal and Focused Signal

Figure 21 compares the voltage amplitudes of time-reversed focused signals and directly received response signals under varying bolt preload levels. Both signal types exhibit increasing amplitudes with applied torque, showing significant variations during initial tightening stages (0–50 N·m) and progressively stabilizing as the bolt approaches full fastening. In low preload conditions, both signals serve as viable indicators for preload assessment. However, when the torque reaches 50 N·m, the response signal demonstrates diminished sensitivity to further preload changes, while the focused signal maintains pronounced amplitude variations, establishing its reliability as the primary evaluation metric for medium-to-high preload monitoring.

4.3. Evaluation of Bolt Preload Condition

4.3.1. Fastening Index

To further investigate the distribution characteristics of focused signal amplitudes under varying bolt preload conditions and enable accurate assessment of bolt loosening, a fastening index metric defined by Equation (9) was developed based on focused signal analysis. The derived relationship between the loosening index I and bolt preload levels is graphically presented in Figure 22.

$$I={\displaystyle \frac{U-U_{min}}{U_{max}-U_{min}}}$$

(9)

where $U$ represents the value in each set of focused signals, $U_{min}$ denotes the minimum value within each set, and $U_{max}$ corresponds to the maximum value. As shown in Figure 22, when the bolt preload reaches 80 N·m, the third experimental group exhibits the largest deviation (≈0.05 loosening index difference) from the normalized mean value, with a relative error of approximately 2% compared to the original focused signal average. These results confirm the measurement accuracy. Nonlinear curve fitting of the fastening indices from all three experimental groups is presented in Figure 23.

Figure 23 demonstrates a well-fitted curve (R² = 0.986) that aligns closely with experimental measurements. The fastening index exhibits minimal variation (consistently > 0.8) as the bolt preload decreases from 120 N·m to 70 N·m, followed by a pronounced reduction when the preload drops from 50 N·m to 0, ultimately reaching zero. These results validate the operational state classifications: the bolt remains fastened (index > 0.8) when the preload exceeds 70 N·m, transitions to a loosened state (index approaching 0) below 50 N·m, and resides in a partially stabilized transitional state between 50 and 70 N·m. The index effectively correlates with bolt tightening conditions, confirming its reliability for preload monitoring across all operational phases.

4.3.2. Verification of Unknown Bolt Preload

To validate the accuracy of the fastening index, experimental tests were conducted under six unknown preload conditions spanning the full operational range from fully loosened to fully tightened states. The validation process involved calculating the loosening index to estimate preload ranges, applying the differential method for preload quantification, and incrementally increasing torque using a calibrated torque wrench to obtain ground-truth measurements. Comparative analysis between calculated and measured preload values (

Table 10. Comparison of calculated and measured bolt preload values under various test conditions.

Condition	Focus Signal (V)	Fastening Index	Calculated Value of Preload Force (N·m)	Measured Preload Force (N·m)	Inaccuracies
Condition 1	0.9347	0.709	52.37	54	3.1%
Condition 2	0.7492	0.515	37.83	40	5.7%
Condition 3	0.6353	0.395	30.64	32	4.4%
Condition 4	0.8253	0.594	43.36	44	3.8%
Condition 5	1.0695	0.850	67.98	69	1.5%
Condition 6	1.0785	0.860	69.42	71	3.7%

) confirmed the method’s reliability, with representative response and focused signals illustrated in Figure 24 and Figure 25.

According to Table 10, the calculated and measured bolt preload results show that the overall error is small, with the smallest error in working condition five (about 1.5%) and the largest error in working condition two (about 5.7%). The possible reasons for these errors include (1) measurement error in the peak value of the coalescence signal; (2) the assumption that the maximum bolt preload corresponds to 120 N·m, while the actual preload may be slightly higher, causing the calculated tightening index to be overestimated; (3) the torque wrench measuring only integer values; and (4) the method of loosening the bolt using the torque wrench introducing slight overestimation of the applied torque. Nevertheless, the overall error of the test is negligible. Overall, the small test errors indicate that the bolt tightening index can reliably serve as a preload evaluation metric.

5. Conclusions

This study designed and fabricated a novel surface-mounted piezoelectric sensor based on PMN-PT material, systematically evaluating its waterproof capability, electrical properties, and capacitance characteristics through experiments. Subsequently, bolt preload monitoring experiments employing the time-reversal method were conducted, leading to the development of a fastening index based on comparative analysis of response and focused signals. Key conclusions are as follows:

(1) The developed PMN-PT piezoelectric sensor demonstrates exceptional insulation performance (infinite resistance) and operational stability (capacitance fluctuation rate ≤ 3.25%) under five operating conditions, with significantly higher energy density and piezoelectric properties compared to conventional PZT and PVDF sensors.

(2) Comparative signal analysis shows that both response and focused signals serve as reliable indicators for preload monitoring at low torque levels (<50 N·m). However, beyond 50 N·m, response signals exhibit diminished sensitivity, while focused signals maintain significant amplitude change, enabling precise loosening detection.

(3) The proposed fastening index enables three-state classification: fastened (I > 0.8), partially fastened (0.5 < I ≤ 0.8), and loosened (I ≤ 0.5). Validation tests under unknown preload conditions demonstrated measurement errors ranging from 1.5% (Condition 5) to 5.7% (Condition 2), with performance surpassing conventional strain-gauge and FBG sensor methods in both sensitivity and operational range.