Temperature- and Emission Wavelength-Dependent Time Responses of Strontium Aluminates
Abstract
1. Introduction
2. Materials and Experimental Setup
2.1. Materials Under Study
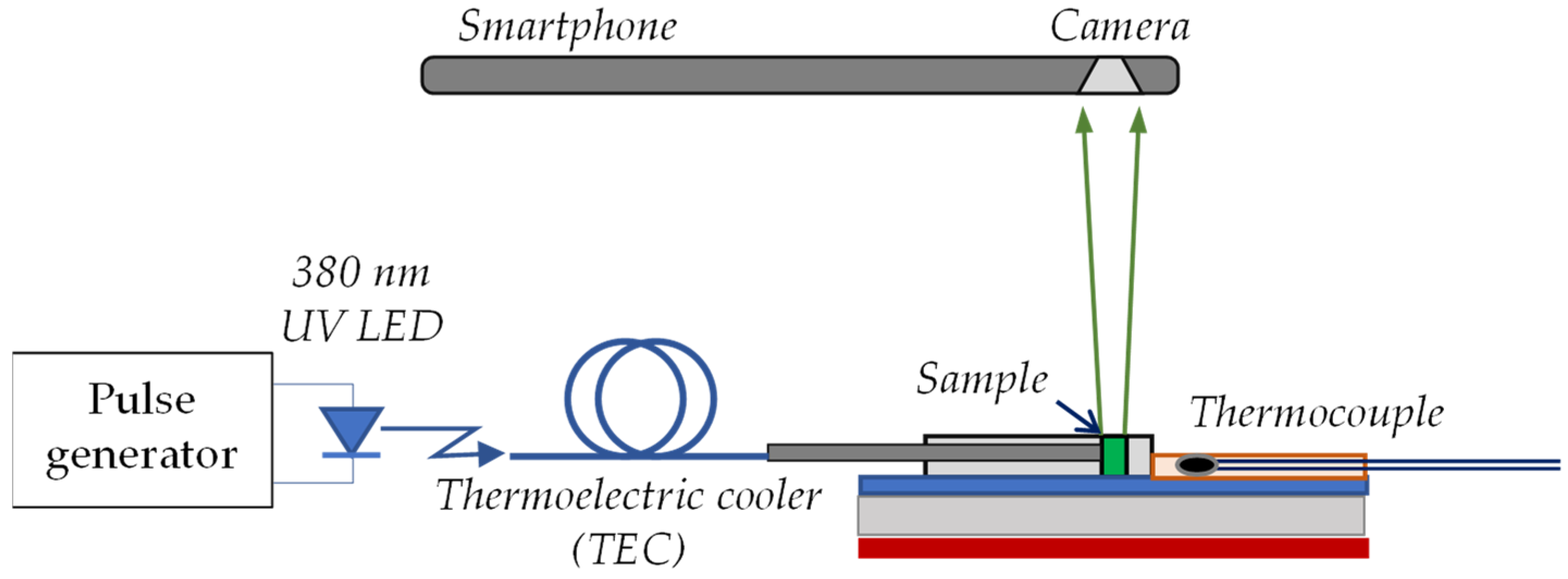
2.2. Experimental Arrangement
3. Results and Analysis
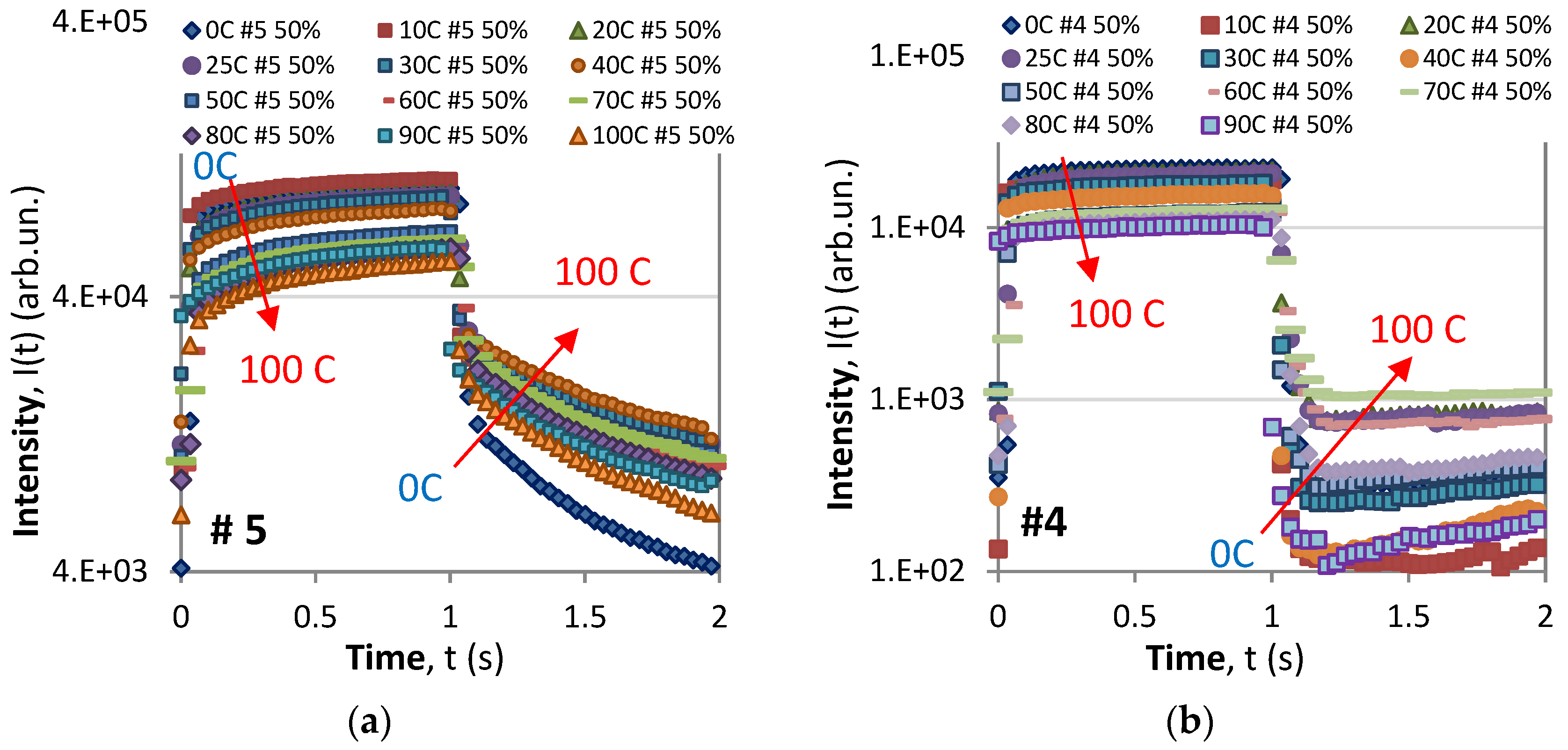
3.1. Rise and Decay Time Responses
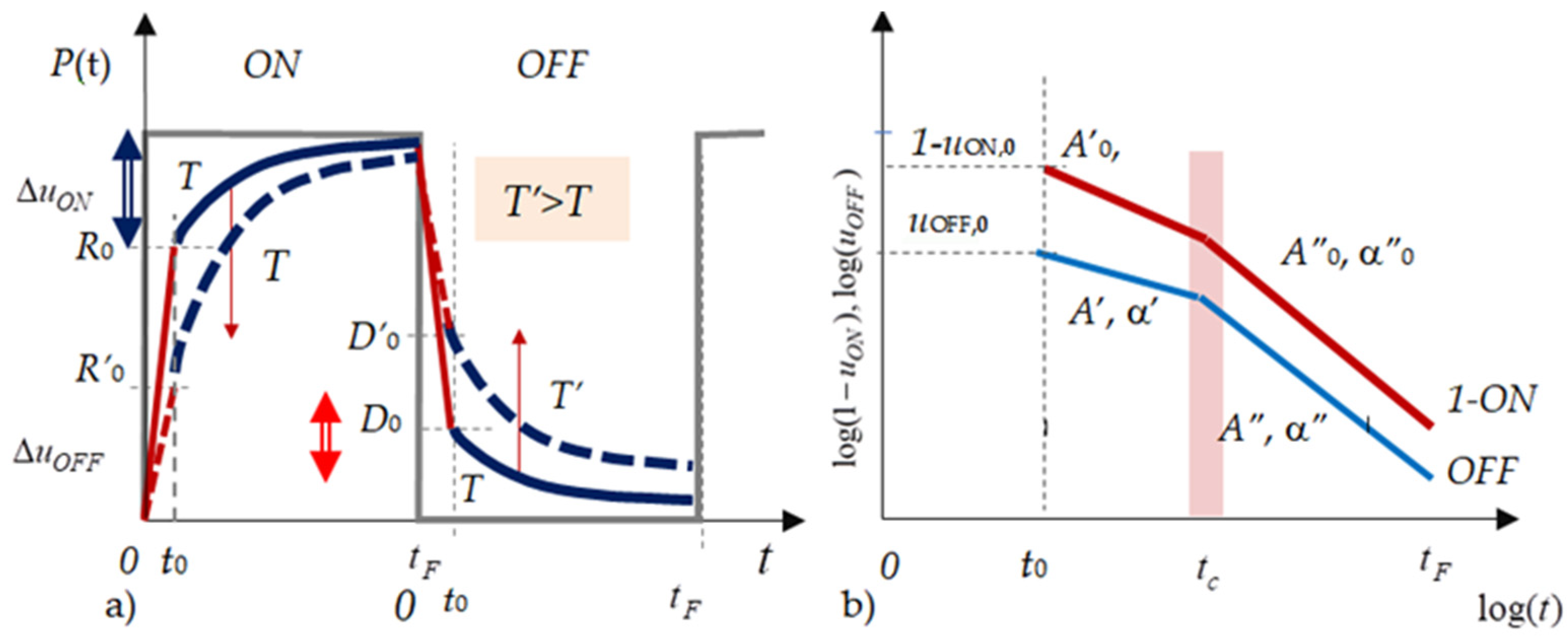
3.1.1. Two Types of Time Responses
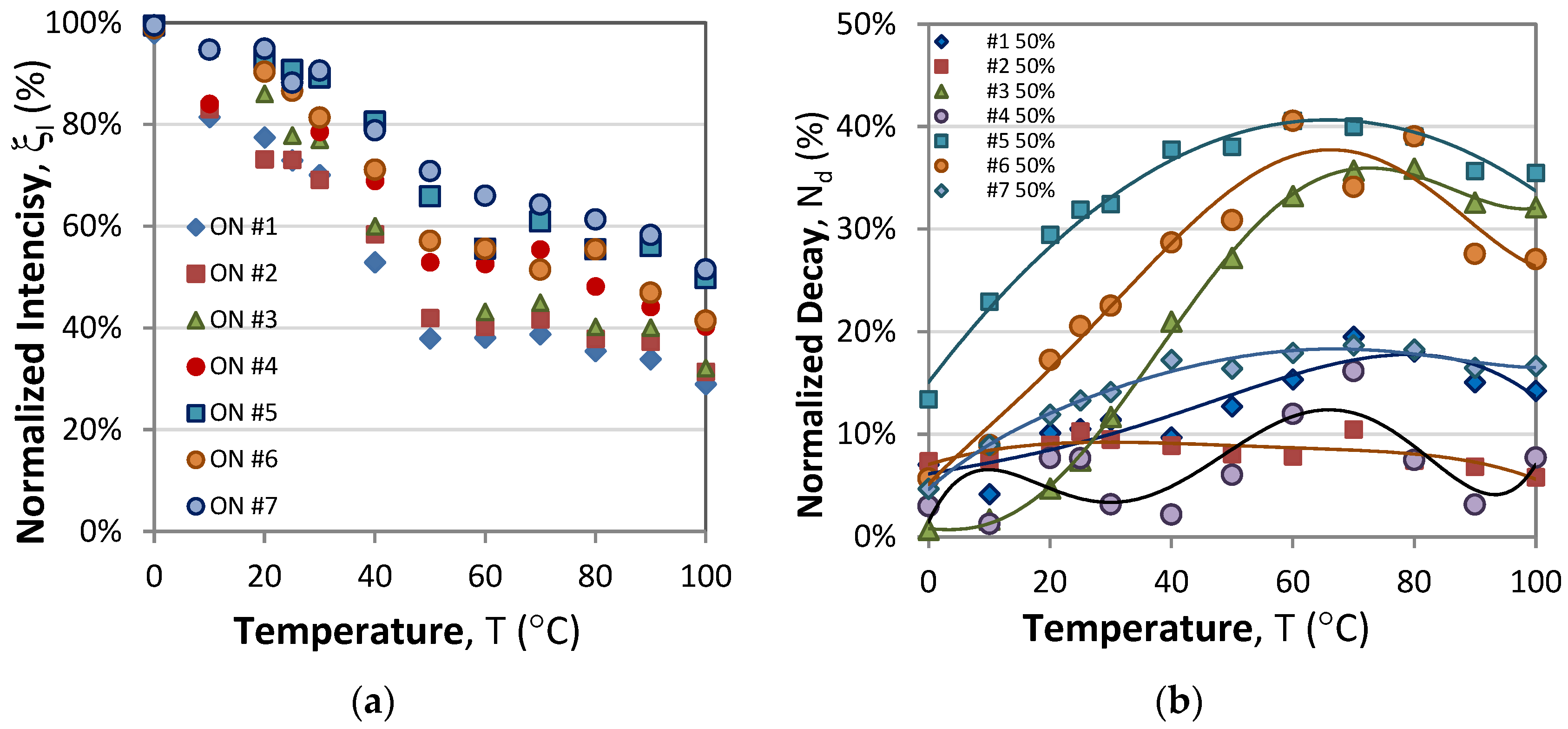
3.1.2. Normalized Responses
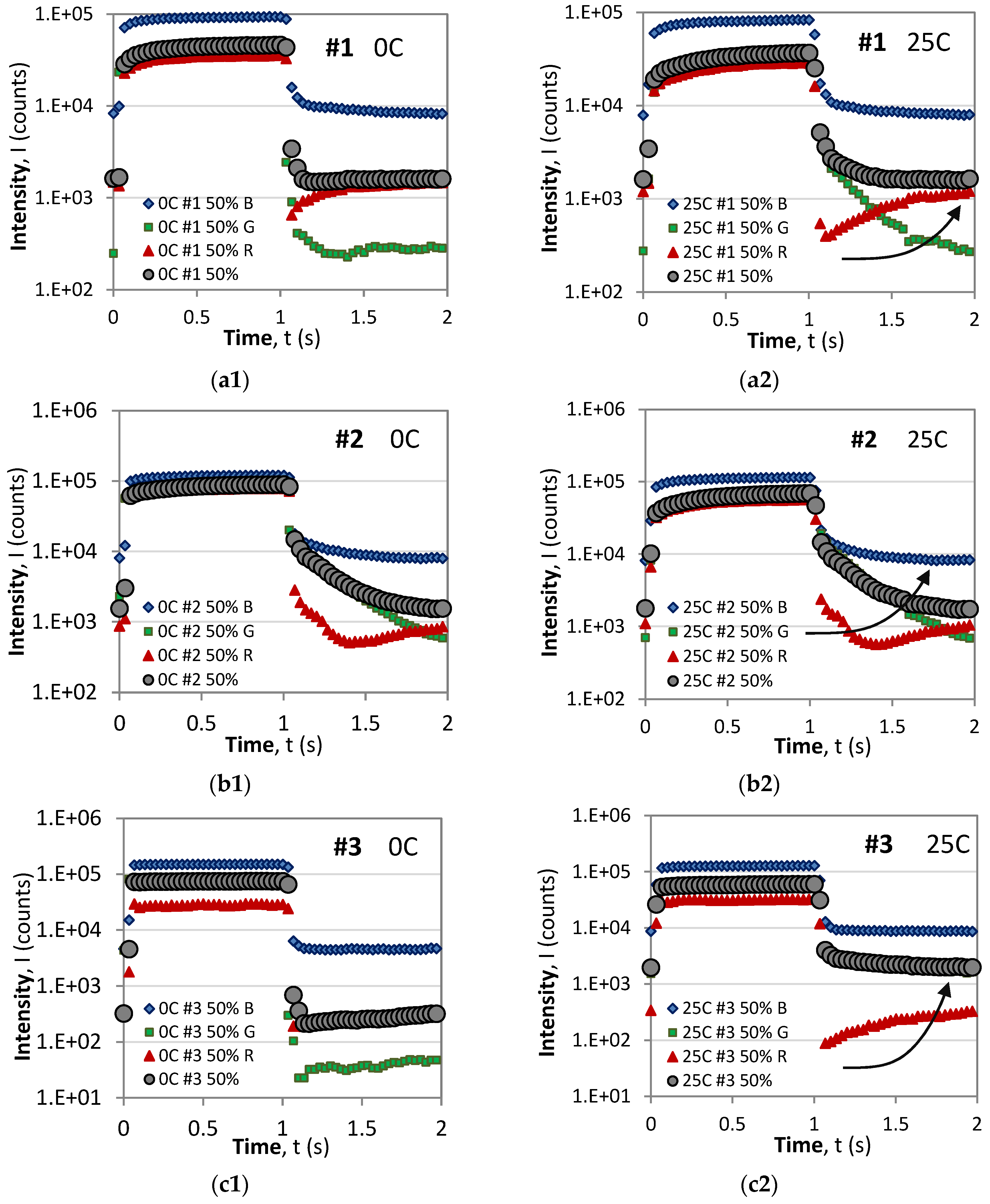
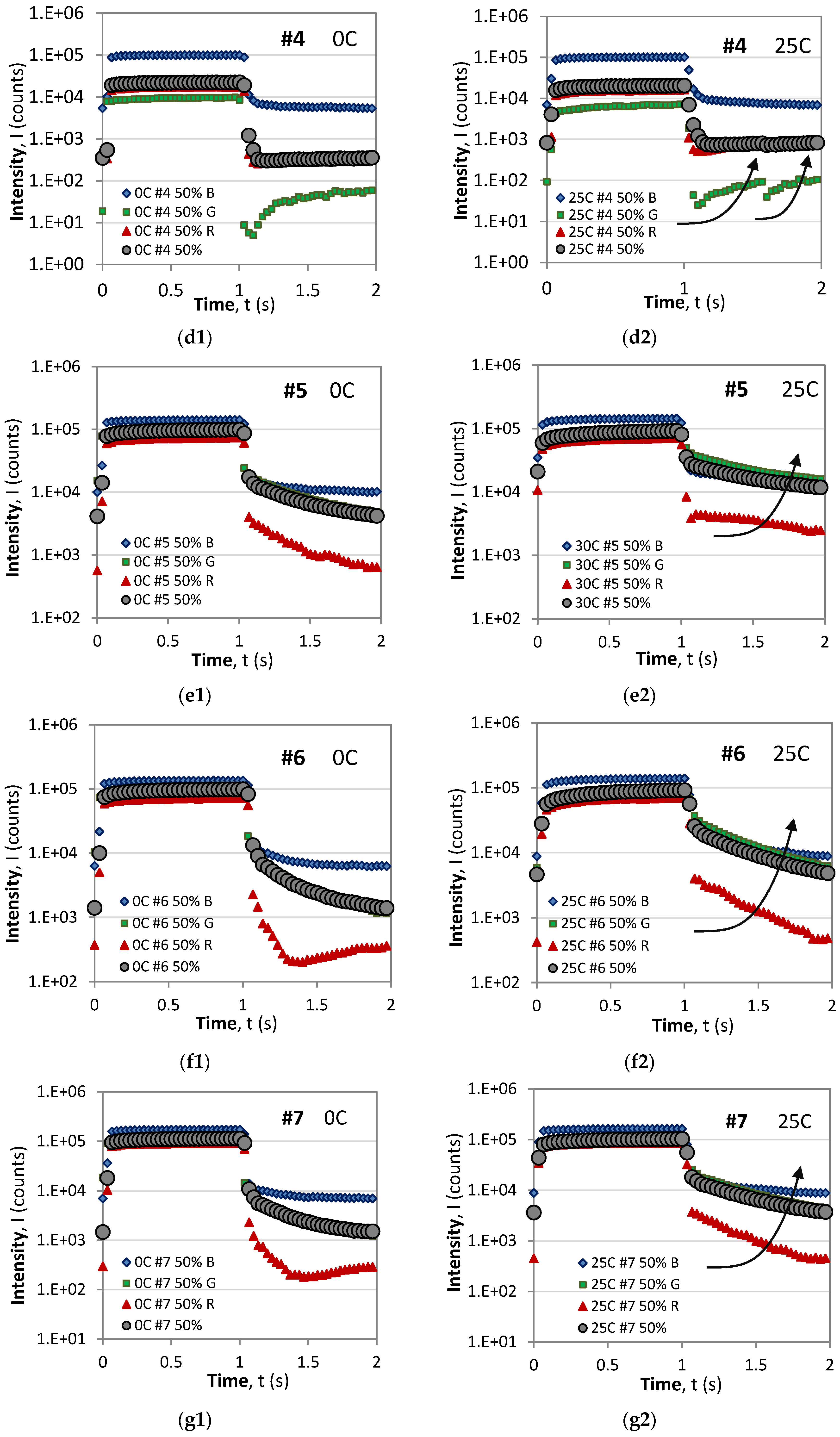
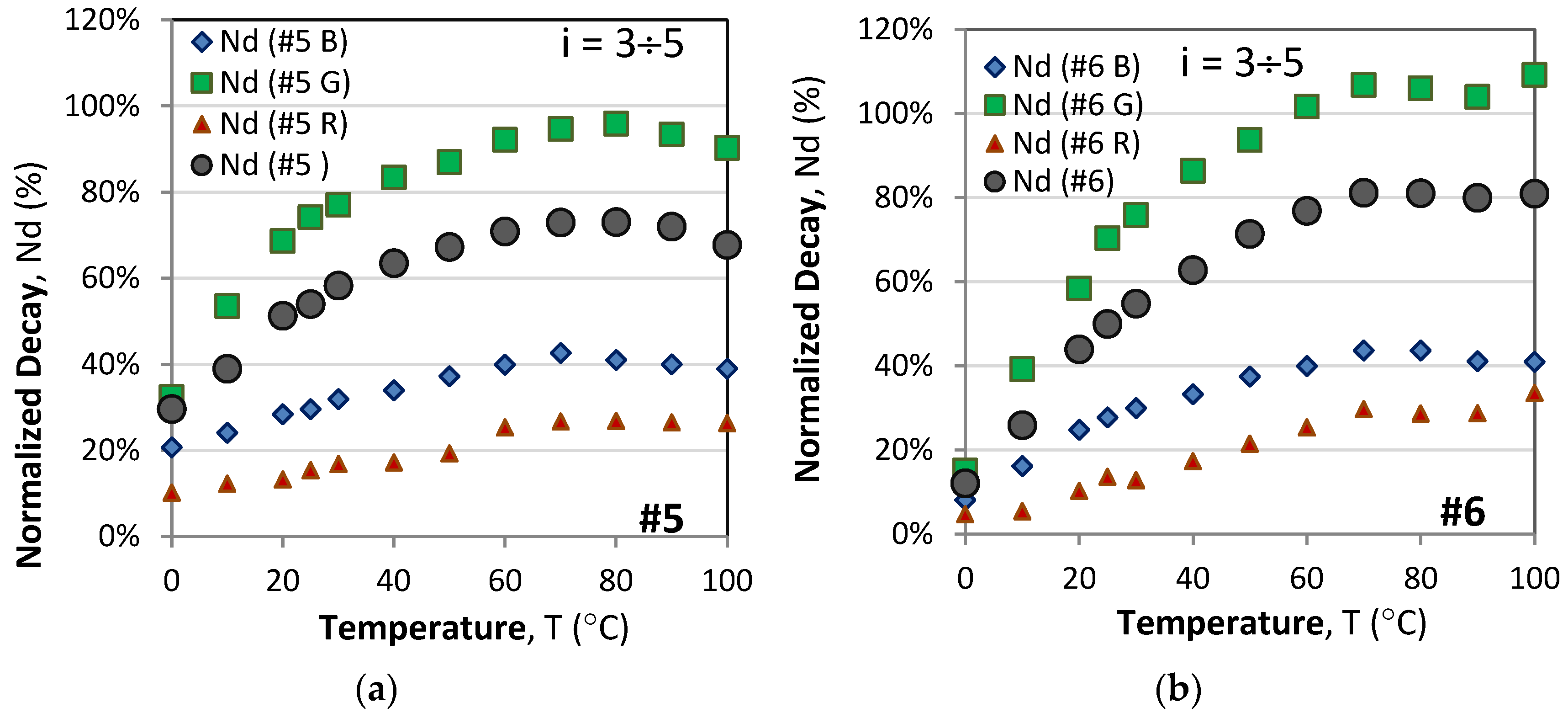
3.2. RGB Color Dependence of the Rise/Decay Time Responses
3.2.1. RGB Time Responses at Different Temperatures
- (i)
- For all samples and all color pixels (R, G, and B), the saturation level during the ON phase decreases with temperature, which is in agreement with Equation (A1) [28].
- (ii)
- In all of the cases, the dominant component during the ON (excitation) phase are the blue (B) pixels followed by the green (G), and the weakest, except for sample #4, are the red (R) pixels.
- (iii)
- For all samples, the B component exhibits the standard behavior of monotonic rise and decay responses.
- (iv)
- During the OFF (decay) phase, with the exception of #5, the R components of the time responses exhibit the anomalous behavior manifested as a fast drop to a minimum value followed by a slow rise in luminescence. Though not observed in these graphs in the case of a larger period, the slow rise in the R component reaches a local maximum and is followed by a slow decay. A similar behavior is observed for the G component at 0C for samples #1, #3, and #4.
- (v)
- As a result of the behavior of the R and G components, the resultant overall response in grey of samples #1, #3, and #4 also exhibits anomalous behavior at 0C, of which only #4 is anomalous at 25C.
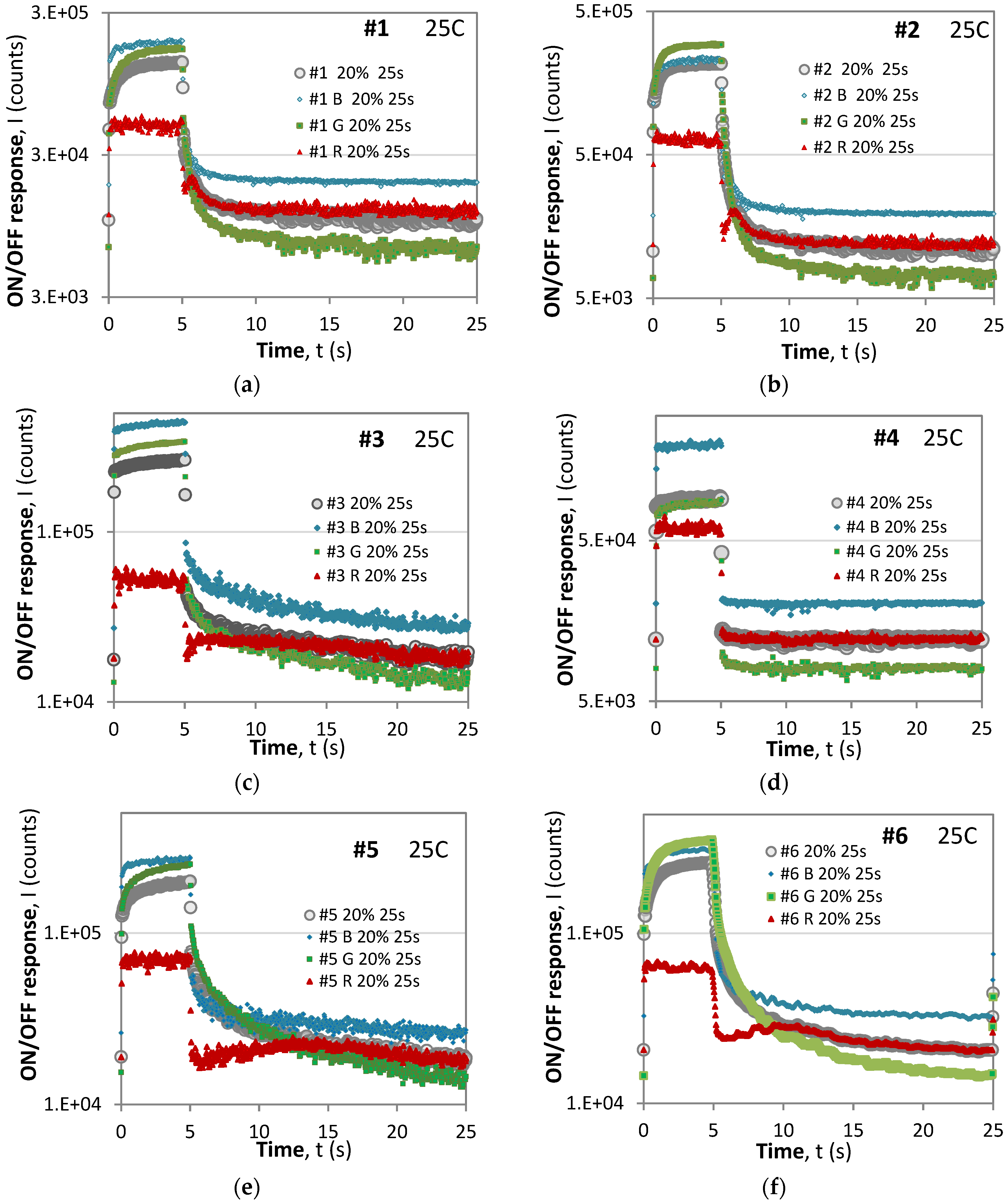
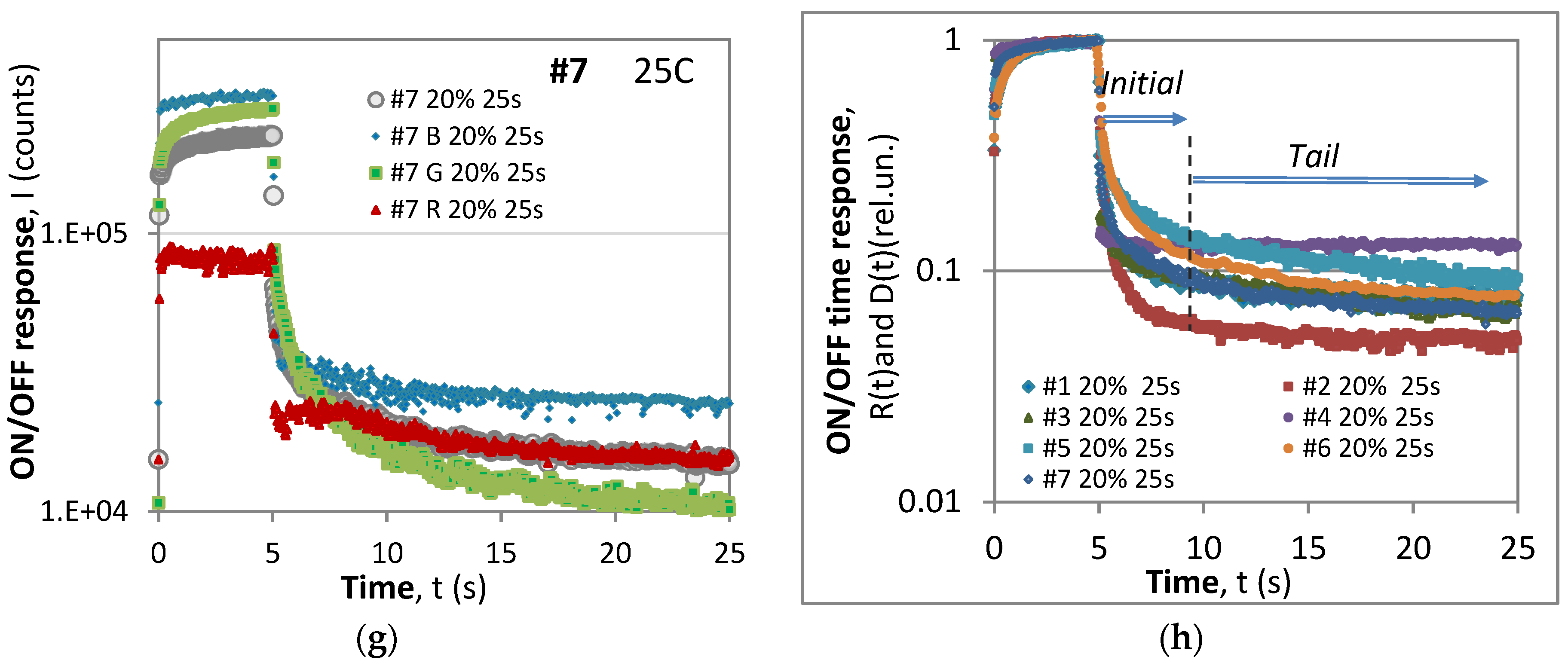
- (i)
- With the exception of #4, all of the samples exhibit anomalous behavior of the R component.
- (ii)
- Unlike the B and G components, both the rise and the decay responses of the R components exhibit an initial surge in the intensity followed by a slower decay in both the ON and OFF phases.
- (iii)
- For short time excitation (τ = 1 s) (Figure 4), the dominant component during excitation was the blue (B) component, while for longer excitation (τ = 5 s), the G component gained dominance for samples #2 and #6 and was close for samples #5 and #7. This signifies that the overall color of the phosphorescent sample changes and depends on the excitation conditions.
- (iv)
- A comparison of the maximum levels during short-period excitations (T = 2 s) from Figure 3 and those from long-period excitations (T = 25 s) from Figure 5 reveals that in the former case, the samples would reach saturation during the ON phase, while the latter saturation would not be reached, though the excitation duration was longer, i.e., 5 s at η = 20% vs. 1 s at η = 50%. This observation suggests that the saturation level depends on the period of modulation as well as on the duty cycle.
- (v)
- The particular shape of the rise and decay responses depend on the excitation duration.
3.2.2. RGB Time Responses at Different Duty Cycles
3.3. Analysis of the Obtained Results
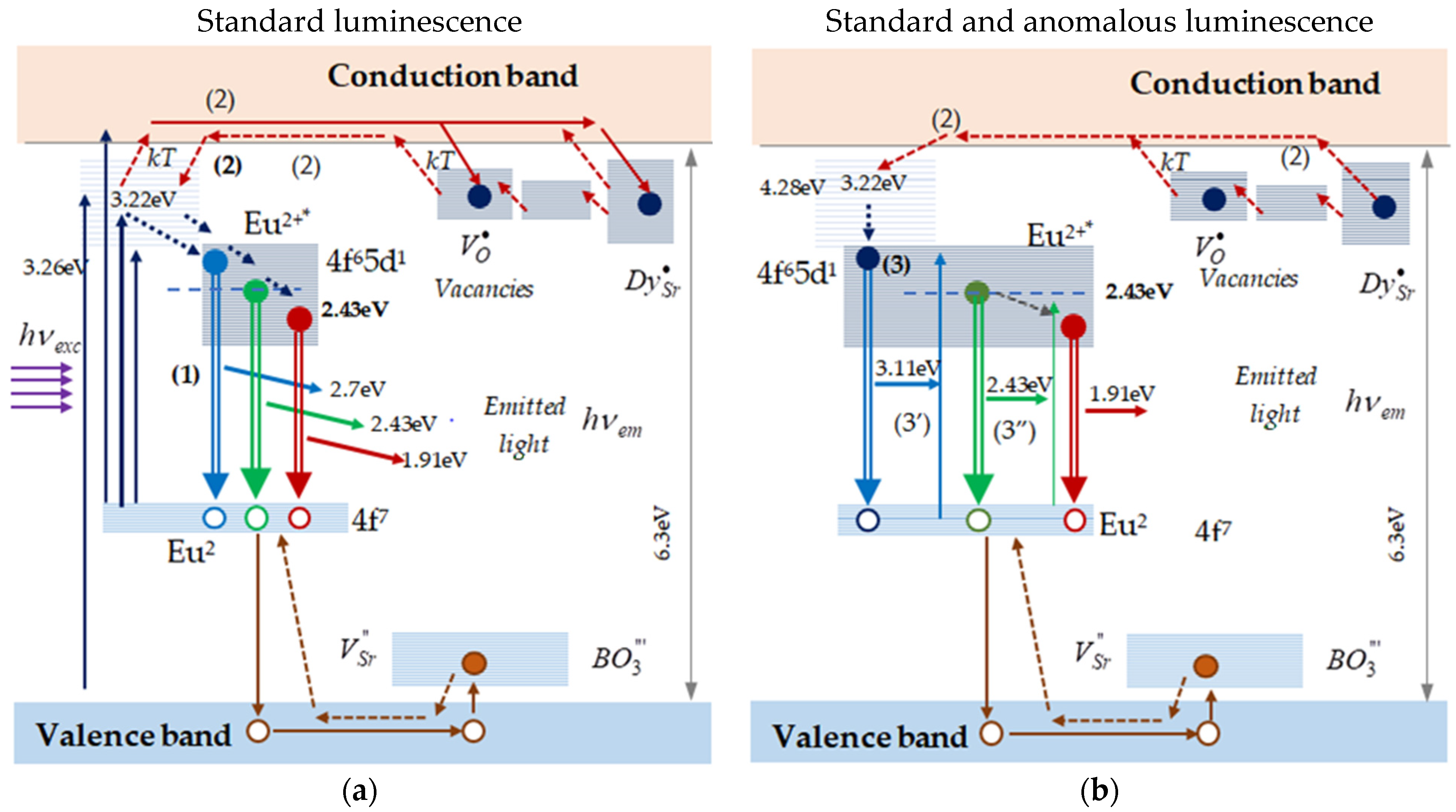
3.3.1. The Standard and the Anomalous Time Responses
- Standard luminescence response
- B.
- Anomalous time responses
3.3.2. Description of the Anomalous Time Responses
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Power Law and Exponential Approximations for the Time Responses
The Power Law Approximations
| Time Response | Type of Approximation | Power Law (A) | Exponential Law (B) | ||
|---|---|---|---|---|---|
| Rise time response (ON phase) | Absolute | (A2a) | (A2b) | ||
| Normalized | (A3a) | (A3b) | |||
| (A3c) | |||||
| Decay time response (OFF phase) | Absolute (A4) | (A4a) | (A4b) | ||
| Normalized (A5) | (A5a) | (A5b) | |||
| (A5c) | |||||
References
- Mushtaq, U.; Ayoub, I.; Kumar, V.; Sharma, V.; Swart, H.C.; Chamanehpour, E.; Rubahn, H.-G.; Mishra, Y.K. Persistent luminescent nanophosphors for applications in cancer theranostics, biomedical, imaging and security. Mater. Today Bio 2023, 23, 100860. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Z.; Huo, X.; Meng, X.; Wang, Y.; Suo, H.; Li, P. Anti-Counterfeiting Application of Persistent Luminescence Materials and Its Research Progress. Laser Photon. Rev. 2024, 18, 2300751. [Google Scholar] [CrossRef]
- Brito, H.F.; Hölsä, J.; Laamanen, T.; Lastusaari, M.; Malkamäki, M.; Rodrigues, L.C.V. Persistent luminescence mechanisms: Human imagination at work. Opt. Mater. Express 2012, 2, 371. [Google Scholar] [CrossRef]
- Vitola, V.; Millers, D.; Bite, I.; Smits, K.; Spustaka, A. Recent progress in understanding the persistent luminescence in SrAl2O4:Eu,Dy. Mater. Sci. Technol. 2019, 35, 1661–1677. [Google Scholar] [CrossRef]
- Einbergs, E.; Zolotarjovs, A.; Bite, I.; Vītola, V.; Spustaka, A.; Tunēns, G.; Arnautov, A. A mechanoluminescence based approach to spatial mechanical stress visualisation of additively manufactured (3D printed) parts. Materialia 2022, 24, 101516. [Google Scholar] [CrossRef]
- Vitola, V.; Dile, M.; Krizmane, K.; Einbergs, E.; Eftimov, T.; Nikolov, K.; Fouzar, S. Tailoring the luminescence properties of strontium aluminate phosphors for unique smartphone detectable optical tags. Crystals 2025, 15, 474. [Google Scholar] [CrossRef]
- Fouzar, S.; Kostova, I.; Eftimov, T.; Benmounah, A.; Ouchabane, M.; Lakhssassi, A. Excitation and spectral dependence of the rise and decay time responses of Eu2+ and Dy3+ doped strontium aluminates. J. Mater. Sci. Mater. Electron. 2022, 33, 20962–20980. [Google Scholar] [CrossRef]
- Eftimov, T.; Kostova, I.; Arapova, A.; Patronov, G. Rise and decay time responses of Sr aluminate phosphorescent materials. J. Lumin. 2021, 235, 117985. [Google Scholar] [CrossRef]
- Fouzar, S.; Eftimov, T.; Kostova, I.; Benmounah, A.; Lakhssassi, A. Effects of temperature on the time responses of strontium aluminates. Opt. Mater. 2021, 122, 111619. [Google Scholar] [CrossRef]
- Van der Heggen, D.; Joos, J.J.; Feng, A.; Fritz, V.; Delgado, T.; Gartmann, N.; Walfort, B.; Rytz, D.; Hagemann, H.; Poelman, D.; et al. Persistent Luminescence in Strontium Aluminate: A Roadmap to a Brighter Future. Adv. Funct. Mater. 2022, 32, 2208809. [Google Scholar] [CrossRef]
- Leimane, M.; Krizmane, K.; Bite, I.; Grube, J.; Vitola, V. Sol–Gel Synthesis of Translucent and Persistent Luminescent SiO2@ SrAl2O4 Eu, Dy, B Materials. Materials 2023, 16, 4416. [Google Scholar] [CrossRef] [PubMed]
- Van den Eeckhout, K.; Smet, P.F.; Poelman, D. Persistent Luminescence in Eu2+-Doped Compounds: A Review. Materials 2010, 3, 2536–2566. [Google Scholar] [CrossRef]
- Aitasalo, T.; Hölsä, J.; Jungner, H.Ö.; Lastusaari, M.; Niittykoski, J. Sol-gel processed Eu2+-doped alkaline earth aluminates. J. Alloys Compd. 2002, 341, 76–78. [Google Scholar] [CrossRef]
- Yang, L.; Liu, Q.; Zheng, H.; Zhou, S.; Zhang, W. The decay model of Eu2+ and Eu2+, Dy3+ substituted SrAl2O4 prepared by high temperature solid phase method. J. Phys. Chem. Solids 2019, 124, 151–156. [Google Scholar] [CrossRef]
- Li, Q.; Zhao, J.; Sun, F. Energy transfer mechanism of Sr4Al14O25:Eu2+ phosphor. J. Rare Earths 2010, 28, 26–29. [Google Scholar] [CrossRef]
- Aitasalo, T.; Holsa, J.; Lastusaari, M.; Niittykoski, J. Mechanisms of persistent luminescence in Eu2+, RE3+ doped alkaline earth aluminates. J. Lumin. 2001, 94–95, 59–63. [Google Scholar] [CrossRef]
- Clabau, F.; Rocquefelte, X.; Jobic, S.; Deniard, P.; Whangbo, M.-H.; Garcia, A.; Le Mercier, T. On the phosphorescence mechanism in SrAl2O4:Eu2+ and its codoped derivatives. Solid State Sci. 2007, 9, 608–612. [Google Scholar] [CrossRef]
- Dorenbos, P. Mechanism of Persistent Luminescence in Eu2+ and Dy3+ Codoped Aluminate and Silicate Compounds. J. Electrochem. Soc. 2005, 152, H107. [Google Scholar] [CrossRef]
- Clabau, F.; Rocquefelte, X.; Jobic, S.; Deniard, P.; Whangbo, M.-H.; Garcia, A.; Le Mercier, T. Mechanism of Phosphorescence Appropriate for the Long-Lasting Phosphors Eu2+-Doped SrAl2O4 with Codopants Dy3+ and B3+. Chem. Mater. 2005, 17, 3904–3912. [Google Scholar] [CrossRef]
- Randall, J.T.; Wilkins, M.H.F. Phosphorescence and electron traps—I. The study of trap distributions. Proc. R. Soc. Lond. 1945, 184, 365–389. [Google Scholar]
- Randall, J.T.; Frederick, W.M.H. Phosphorescence and electron traps—II. The interpretation of long-period phosphorescence. Proc. R. Soc. Lond. 1945, 184, 390–407. [Google Scholar]
- Huntley, D.J. An explanation of the power-law decay of luminescence. J. Phys. Condens. Matter 2006, 18, 1359. [Google Scholar] [CrossRef]
- Sahai, M.K.; Bakshi, A.K.; Datta, D. Revisit to power law decay of luminescence. J. Lumin. 2017, 195, 240–246. [Google Scholar] [CrossRef]
- Romero, M.; Castaing, V.; Lozano, G.; Miguez, H. Trap Depth Distribution Determines Afterglow Kinetics: A Local Model Applied to ZnGa2O4:Cr3+. J. Phys. Chem. Lett. 2024, 15, 9129–9135. [Google Scholar] [CrossRef]
- Fouzar, S.; Eftimov, T.; Kostova, I.; Dimitrova, T.L.; Benmounah, A.; Lakhssassi, A. A Simple Fiber Optic Temperature Sensor For Fire Detection In Hazardous Environment Based On Differential Time Rise/Decay Phosphorescence Response. IEEE Trans. Instrum. Meas. 2022, 71, 1–8. [Google Scholar] [CrossRef]
- Eftimov, T.A.; Kostova, I.; Peltekov, A.; Hristova, K.; Brabant, D.; Fouzar, S.; Nikolov, K. A study of strontium aluminates for all optical contactless sensing applications using smartphone interrogation. Opt. Laser Technol. 2024, 176, 110965. [Google Scholar] [CrossRef]
- Nikolova, K.; Nikolov, K.; Eftimov, T.; Panova, N.; Vitola, V. The Smartphone as an Affordable 2D Spectrometer for Parallel Spectral and Time-dependent Measurements. In Proceedings of the 8th International Conference on Optics, Photonics and Lasers (OPAL’ 2025), Rhodes, Greece, 14–16 May 2025; pp. 143–146. [Google Scholar]
- Wang, L.; Wang, W.; Shang, Z.; Cao, P.; Shi, M.; Yang, B.; Zou, J. Optical and reliability properties studies of Sr4Al14O25:Eu2+ film for high-CRI white LEDs. J. Mater. Sci. Mater. Electron. 2020, 31, 13561–13569. [Google Scholar] [CrossRef]
- Katumo, N.; Gao, G.; Laufer, F.; Richards, B.S.; Howard, I.A. Smartphone-Based Luminescent Thermometry via Temperature-Sensitive Delayed Fluorescence from Gd2O2S:Eu3+. Adv. Opt. Mater. 2020, 8, 2000507. [Google Scholar] [CrossRef]
- Eftimov, T.; Kostova, I.; Fouzar, S.; Brabant, D.; Nikolov, K.; Vladev, V. Smartphone-Readable Optical-Fiber Quasi-Distributed Phosphorescent Temperature Sensor. Photonics 2024, 11, 694. [Google Scholar] [CrossRef]

| ID | Precursor (Anion) | Main Crystal Phase(s) | Particle Morphology | Trap Depth (eV) | Sr: Al (wt) |
|---|---|---|---|---|---|
| #1 | HMTA | Mostly Sr3Al2O6 + trace Sr4Al14O25 | Compact spheres | 0.05/0.17 | 4.1 |
| #2 | LiOH | ~60% monoclinic SrAl2O4 + cubic Sr3Al2O6 | Fused platelets | 0.103 | 1.4 |
| #3 | KOH | Monoclinic SrAl2O4 rich | Ragged plates | 0.055 | 1.2 |
| #4 | NaOH | Monoclinic SrAl2O4 with ≈18% cubic phase | Plate-like | 0.161/0.112 | 2.0 |
| #5 | K2CO3 | >90% cubic Sr3Al2O6 | Smooth quasi spheres | 0.117/0.186 | 2.7 |
| #6 | Na2CO3 | Nearly pure Sr3Al2O6 | Dense spheres | 0.148 | 3.2 |
| #7 | (NH4)2CO3 | ~1:1 monoclinic SrAl2O4/cubic Sr3Al2O6 mix | Compact, partly sintered | 0.150 | 1.6 |
| Sample # | Rise Time Response Approximation | Decay Time Response Approximation | ||||
|---|---|---|---|---|---|---|
| Decay Initial | Decay Tail | |||||
| Sample #1 | Exponential | 1 − 0.3801 × e−0.752t | Power law | 0.1324 × t−0.3 | Exponential | 0.0897 × e−0.009t |
| Sample #2 | Power | 1 − 0.0808 × t−1.252 | Power law | 0.1025 × t−0.494 | Exponential | 0.0583 × e−0.009t |
| Sample #3 | Exponential | 1 − 0.1597 × e−0.537t | Power law | 0.1016 × t−0.516 | Exponential | 0.0591 × e−0.01t |
| Sample #4 | Exponential | 1 − 0.0927 × e−0.334x | Power law | 0.1338 × t−0.034 | Exponential | 0.1271 × e−0.0014t |
| Sample #5 | Exponential | 1 − 0.2854 × e−0.586t | Power law | 0.2137 × t−1.285 | ||
| Sample #6 | Exponential | 1 − 0.4495 × e−0.869t | Power law | 0.2008 × t−0.341 | ||
| Sample #7 | Exponential | 1 − 0.205 × e−0.752t | Power law | 0.137 × t−0.253 | ||
| # | Rise | Decay | |||
|---|---|---|---|---|---|
| R1(t) | R2(t) | D1(t) | D2(t) | D2(t) | |
| #1 | 1 − 0.5732 − e−2.545t | 1 − 0.3732 − e−1.596t | 0.0107 − t−0.92 | 0.0289 − t−0.422 | 0.0399 − t−0.022 |
| #1 B | 1 − 0.0216 − t−1.025 | 1 − 1.4439 − e−5.648t | 0.0348 − t−0.656 | 0.0933 − t−0.151 | |
| #1 G | 1 − 0.0348 − t−0.656 | 1 − 0.0348 − t−0.656 | 0.0048 − t−1.253 | 0.0064 − t−1.257 | 0.0246 − e−1.239t |
| #1 R | 1 − 0.1863 − t−0.393 | 1 − 0.0904 − t−0.914 | 0.0022 − t−0.761 | 0.0308 − e−1.665t | 0.038 − (1 − 0.0563 − e−3.509t) |
| #4 | 1 − 0.0278 − t−0.851 | 0.0018 − t−1.528 | 0.044 − (1 − 0.0123 − e−1.282t) | 0.044 − (1 − 0.0107 − e−0.75t) | |
| #4 B | 1 − 0.0028 − t−1.57 | 0.0084 − t−1.168 | 0.0677 − t−0.176 | ||
| #4 G | 1 − 0.1897 − t−0.39 | 2 − 10−09 − t−5.454 | 0.014 − (1 − 0.0156 − e−2.581t) | 0.014 − (1 − 0.1211 − e−4.257t) | |
| #4 R | 1 − 0.0665 − t−0.58 | 0.0054 − t−0.715 | 0.045 − (1 − 0.0264 − e−3.81t) | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vitola, V.; Eftimov, T.; Nikolov, K.; Fouzar, S.; Krizmane, K. Temperature- and Emission Wavelength-Dependent Time Responses of Strontium Aluminates. Crystals 2025, 15, 744. https://doi.org/10.3390/cryst15080744
Vitola V, Eftimov T, Nikolov K, Fouzar S, Krizmane K. Temperature- and Emission Wavelength-Dependent Time Responses of Strontium Aluminates. Crystals. 2025; 15(8):744. https://doi.org/10.3390/cryst15080744
Chicago/Turabian StyleVitola, Virginija, Tinko Eftimov, Kristian Nikolov, Samia Fouzar, and Katrina Krizmane. 2025. "Temperature- and Emission Wavelength-Dependent Time Responses of Strontium Aluminates" Crystals 15, no. 8: 744. https://doi.org/10.3390/cryst15080744
APA StyleVitola, V., Eftimov, T., Nikolov, K., Fouzar, S., & Krizmane, K. (2025). Temperature- and Emission Wavelength-Dependent Time Responses of Strontium Aluminates. Crystals, 15(8), 744. https://doi.org/10.3390/cryst15080744







