Structure and Nonlinear Optical Characterization of a New Acentric Crystal of a 4-Hydroxybenzohydrazide Derivative
Abstract
1. Introduction
2. Materials and Methods
2.1. General
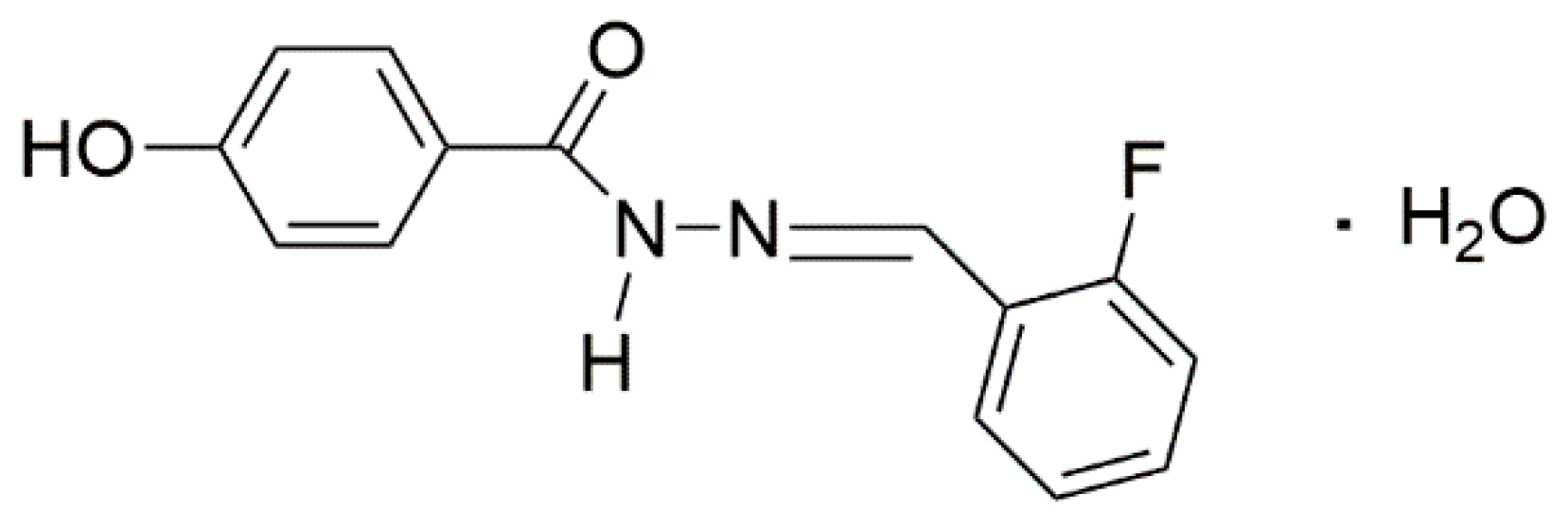
2.2. Synthesis
2.3. Crystal Growth
2.4. Crystal Structure Determination
2.5. Differential Scanning Calorimetry
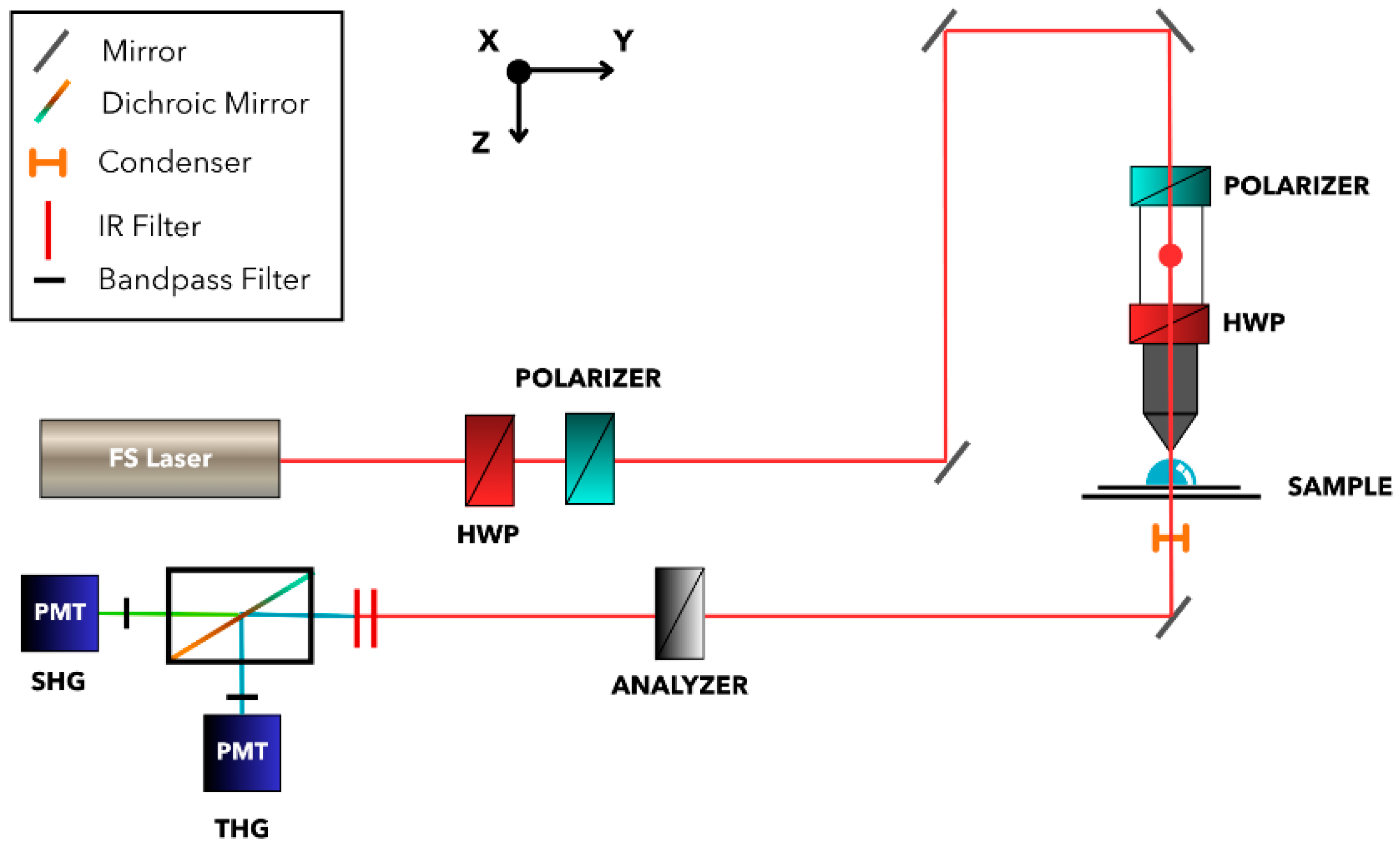
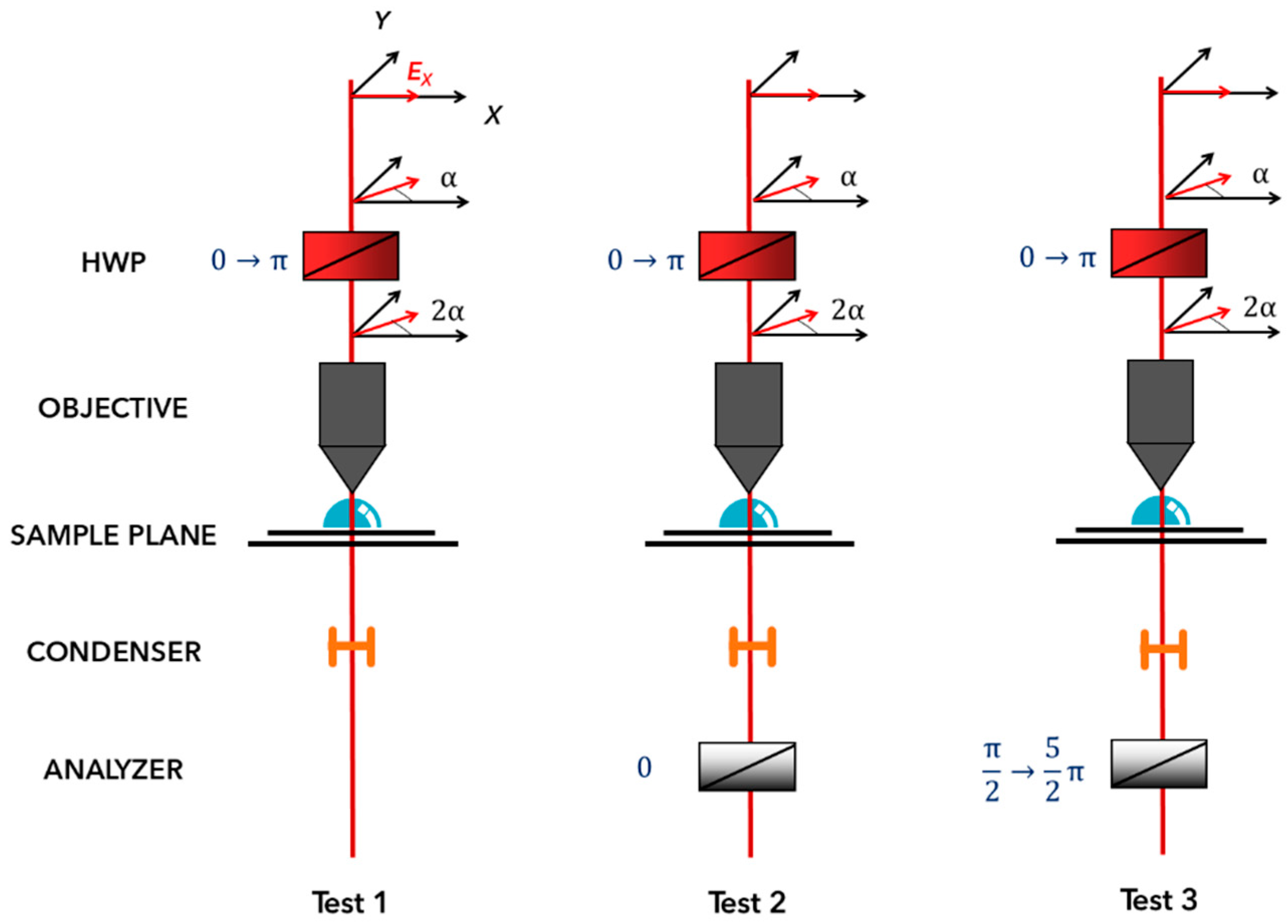
2.6. NLO Microscopy Methodology
3. Results
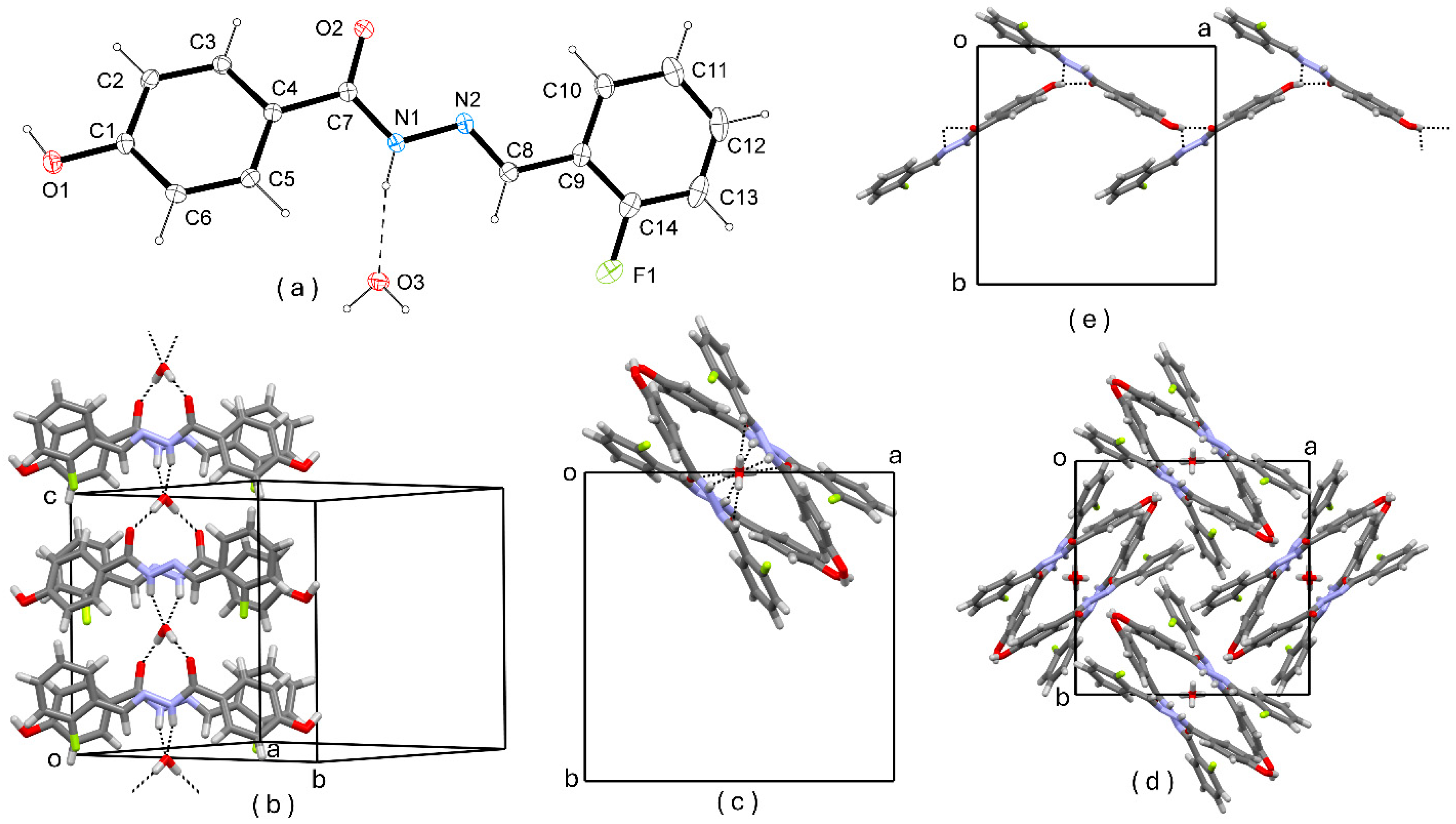
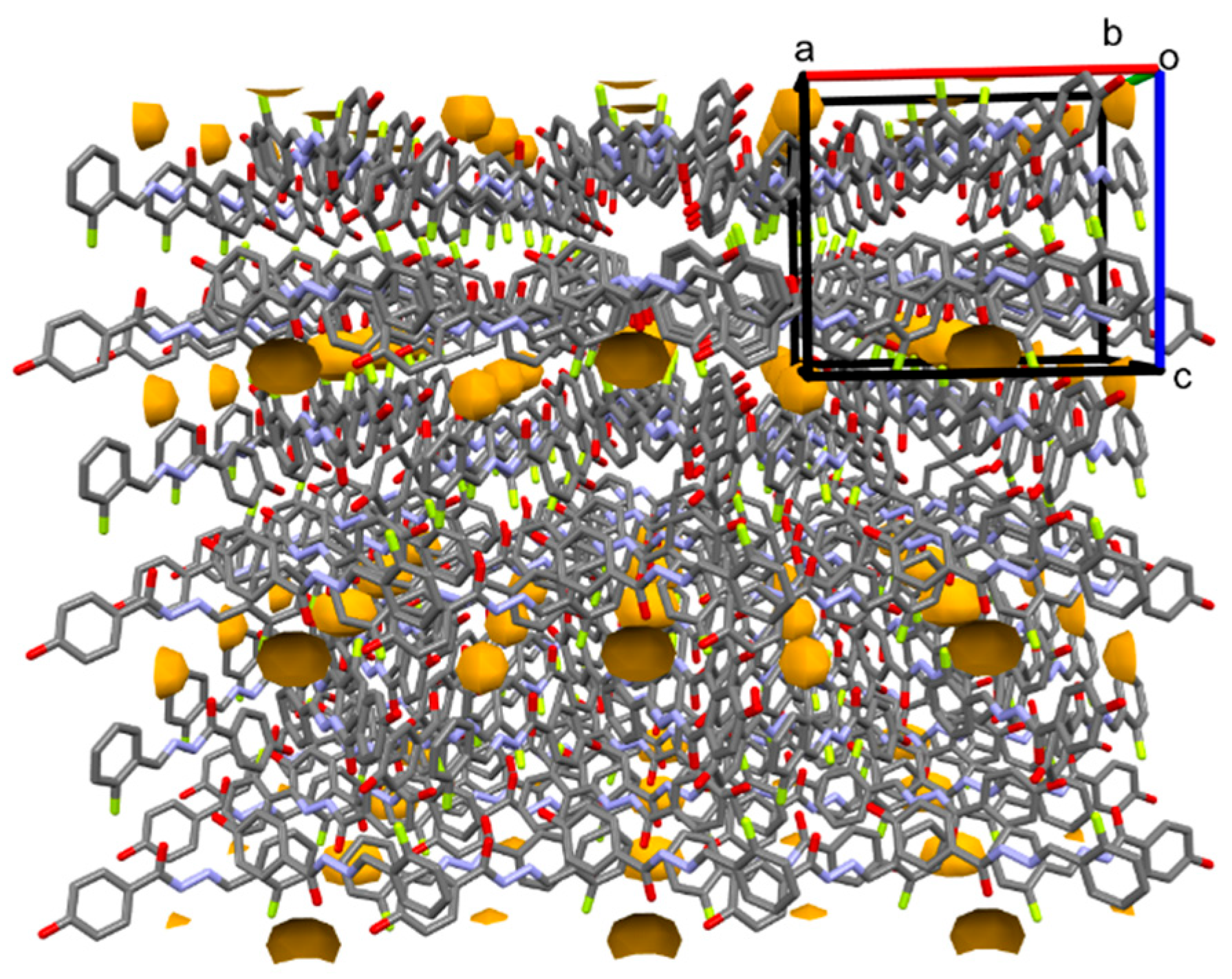
3.1. Crystal Structure Description
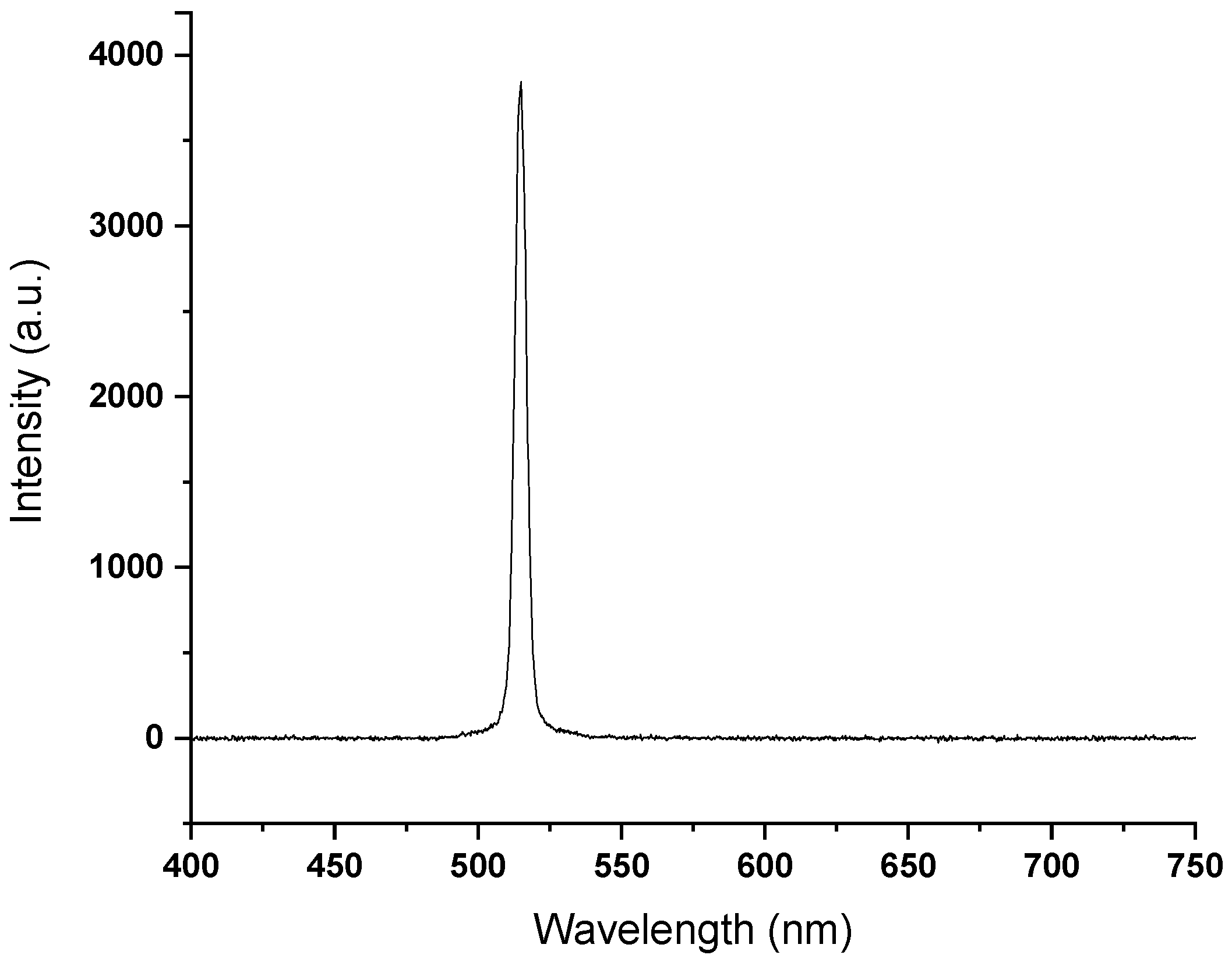
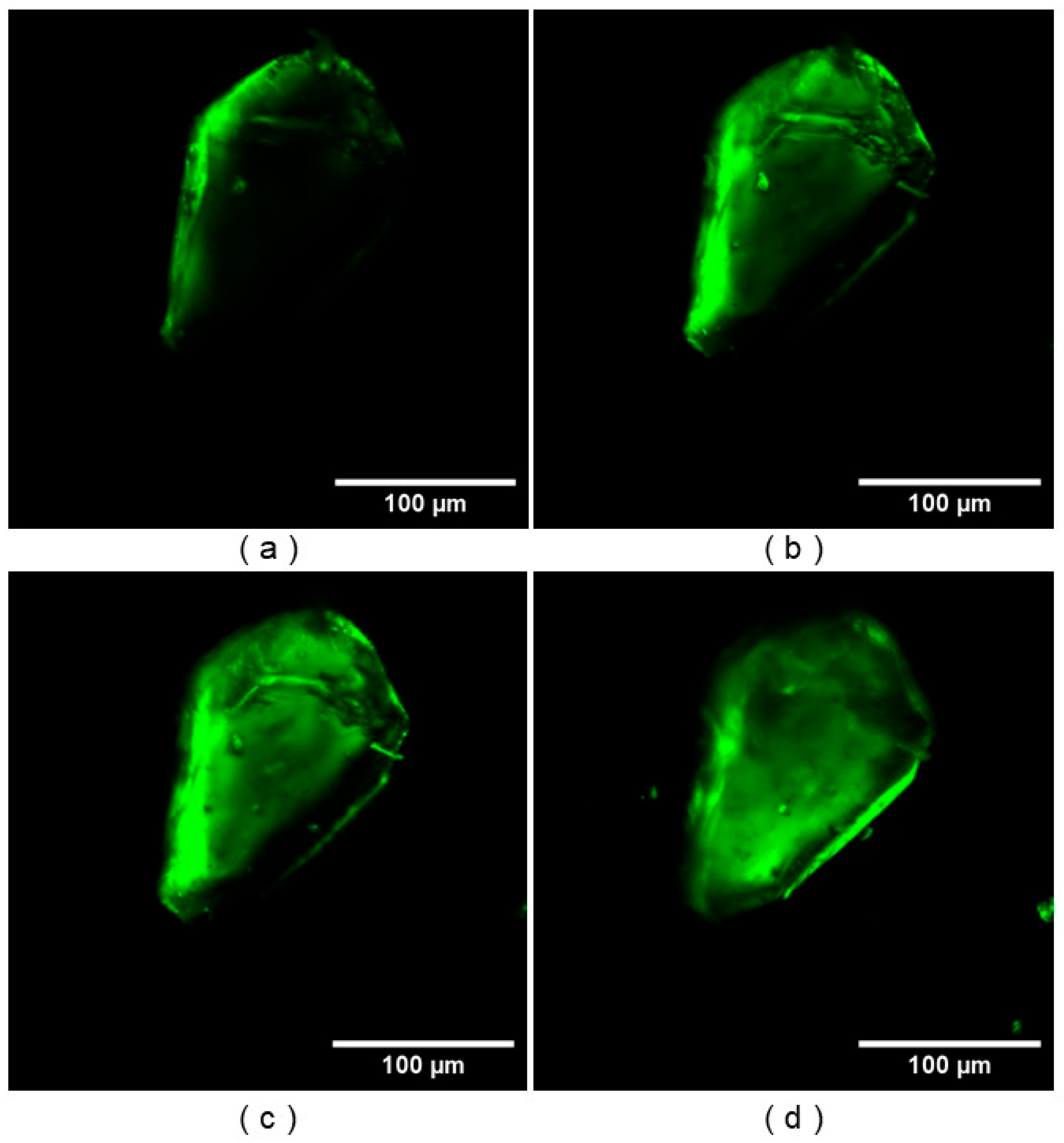
3.2. NLO Microscopy
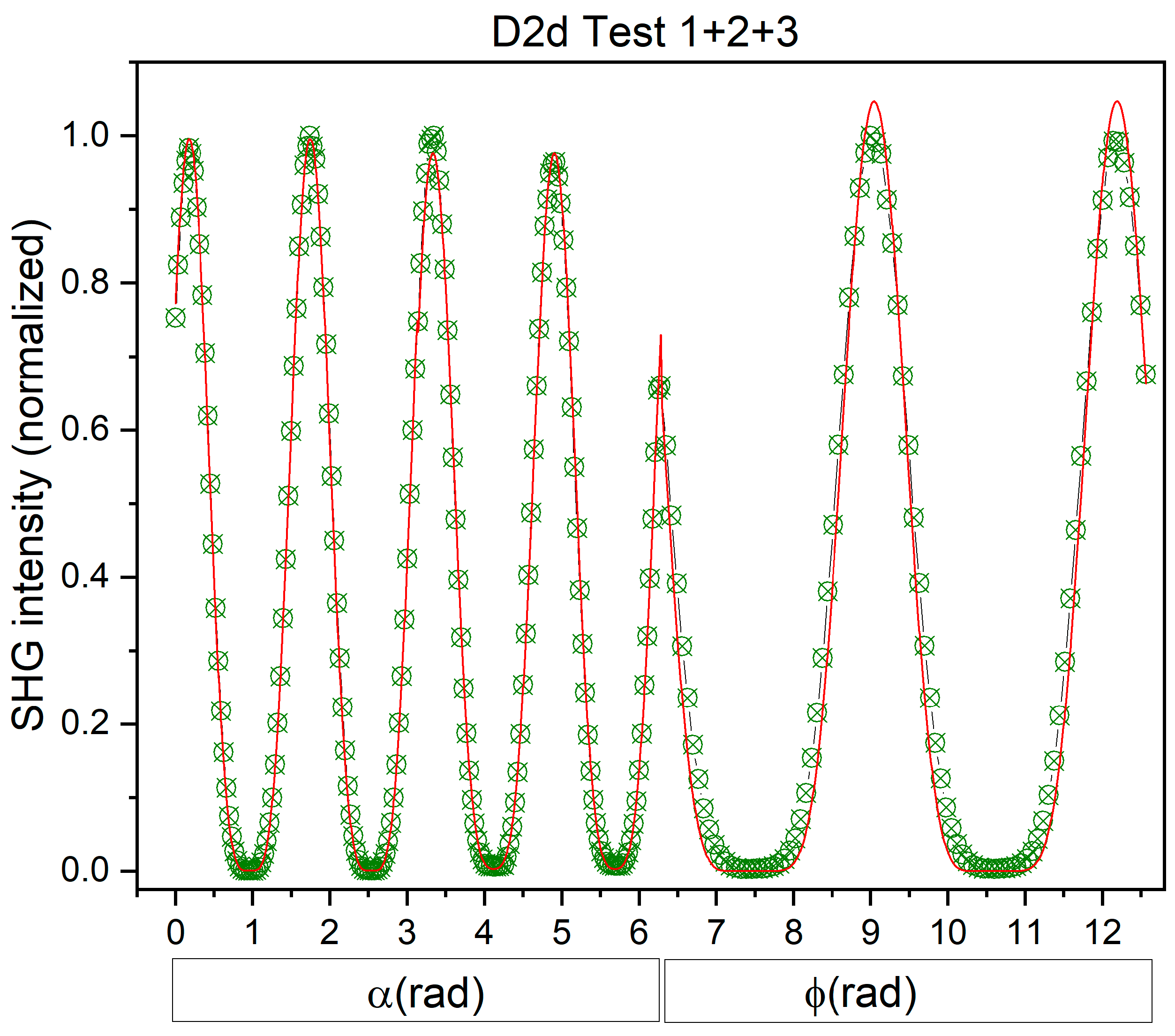
3.3. Symmetry Determination with NLO Polarimetry
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Shkuratov, S.I.; Lynch, C.S. A review of ferroelectric materials for high power devices. J. Mater. 2022, 8, 739–752. [Google Scholar] [CrossRef]
- Gradauskaite, E.; Goossens, A.S.; Li, X.; Iglesias, L.; Gloter, A.; Meier, Q.N.; Bibes, M. Polarization Boost and Ferroelectricity Down to One Unit Cell in Layered Carpy-Galy La2Ti2O7 Thin Films. Adv. Mater. 2025, 37, 2416963. [Google Scholar] [CrossRef] [PubMed]
- Sekhar, M.C.; Veena, E.; Kumar, N.S.; Naidu, K.C.B.; Mallikarjuna, A.; Basha, D.B. A Review on Piezoelectric Materials and Their Applications. Cryst. Res. Technol. 2022, 58, 2200130. [Google Scholar] [CrossRef]
- Dishon Ben Ami, S.; Ehre, D.; Ushakov, A.; Mehlman, T.; Brandis, A.; Alikin, D.; Shur, V.; Kholkin, A.; Lahav, M.; Lubomirsky, I. Engineering of Pyroelectric Crystals Decoupled from Piezoelectricityas Illustrated by Doped α-Glycine. Angew. Chem. Int. Ed. 2022, 61, e202213955. [Google Scholar] [CrossRef]
- Venkataramudu, U.; Sahoo, C.; Leelashree, S.; Venkatesh, M.; Ganesh, D.; Naraharisetty, S.R.G.; Caudhary, A.K.; Srinath, S.; Chandrasekar, R. Terahertz radiation and second-harmonic generation from a single-component polar organic ferroelectric crystal. J. Mater. Chem. 2018, 6, 9330. [Google Scholar] [CrossRef]
- Das, K.; Ghosh, I.; Chakraborty, S.; Nambiar, A.G.; Maji, S.; Karan, S.K.; Kumar, D.; Bansal, A.K.; Reddy, C.M. Structural origin of fracture-induced surface charges in piezoelectric pharmaceutical crystals for engineering bulk properties. Nat. Commun. 2025, 16, 6858. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.-J.; Kang, B.J.; Puc, U.; Kim, W.T.; Jazbinsek, M.; Rotermund, F.; Kwon, O.-P. Highly Nonlinear Optical Organic Crystals for Efficient Terahertz Wave Generation, Detection, and Applications. Adv. Opt. Mater. 2021, 9, 2101019. [Google Scholar] [CrossRef]
- Fang, Y.; Hao, J.; Sang, J.; Gao, J.; Song, L.; Tian, Y.; Li, R. Coherent manipulation of second-harmonic generation via terahertz-field mediated phonon-polariton in zinc oxide. Nat. Commun. 2025, 16, 5598. [Google Scholar] [CrossRef]
- Chelladurai, D.; Kohli, M.; Winiger, J.; Moor, D.; Messner, A.; Fedoryshyn, Y.; Eleraky, M.; Liu, Y.; Wang, H.; Leuthold, J. Barium titanate and lithium niobate permittivity and Pockels coefficients from megahertz to sub-terahertz frequencies. Nat. Mater. 2025, 24, 868. [Google Scholar] [CrossRef]
- Sun, M.-J.; Zheng, C.; Gao, Y.; Johnston, A.; Najarian, A.M.; Wang, P.-X.; Voznyy, O.; Hoogland, S.; Sargent, E.H. Linear Electro-Optic Modulation in Highly Polarizable Organic Perovskites. Adv. Mater. 2021, 33, 2006368. [Google Scholar] [CrossRef] [PubMed]
- Centore, R.; Roviello, A. Macromolecular Systems with Second Order Nonlinear Optical Properties. In Advances in Macromolecules: Perspectives and Applications, 1st ed.; Russo, M.V., Ed.; Springer: Dordrecht, The Netherlands, 2010; pp. 79–117. [Google Scholar]
- Groom, C.R.; Bruno, I.J.; Lightfoot, M.P.; Ward, S.C. The Cambridge Structural Database. Acta Crystallogr. Sect. B Struct. Sci. Cryst. Eng. Mater. 2016, 72, 171−179. [Google Scholar] [CrossRef]
- Brock, C.P.; Dunitz, J.D. Towards a Grammar of Crystal Packing. Chem. Mater. 1994, 6, 1118−1127. [Google Scholar] [CrossRef]
- Holland, K.M.; Aldair, A.; Ludlow, D.J.H.; Petersen, P.K.; Wright, M.A.; Chartrand, C.C.; Michaelis, S.J.; Johnson, J.A.; Patterson, J.E. Characterization of organic crystals for second-harmonic generation. Opt. Lett. 2023, 48, 5855–5858. [Google Scholar] [CrossRef]
- Debrus, S.; Ratajczak, H.; Venturini, J.; Pincon, N.; Baran, J.; Barycki, J.; Glowiak, T.; Pietraszko, A. Novel nonlinear optical crystals of noncentrosymmetric structure based on hydrogen bonds interactions between organic and inorganic molecules. Synth. Met. 2002, 127, 99–104. [Google Scholar] [CrossRef]
- Frazão, N.F.; Carvalho, P.J.; Leitão, M.M.; Lima, C.F.R.A.C. Organic–Inorganic Hybrid Materials with Enhanced Nonlinear Optical Response: Crystal Engineering Perspectives. J. Mater. Chem. C 2024, 12, 11215–11231. [Google Scholar]
- Radhakrishnan, T.P. Molecular structure, symmetry, and shape as design elements in the fabrication of molecular crystals for second harmonic generation and the role of molecules-in-materials. Acc. Chem. Res. 2008, 41, 367–376. [Google Scholar] [CrossRef]
- Chen, J.; Hu, C.L.; Kong, F.; Mao, J.G. High-performance second-harmonic-generation (SHG) materials: New developments and new strategies. Acc. Chem. Res. 2021, 54, 2775–2783. [Google Scholar] [CrossRef] [PubMed]
- Barhum, H.; McDonnell, C.; Alon, T.; Hammad, R.; Attrash, M.; Ellenbogen, T.; Ginzburg, P. Organic kainate single crystals for second-harmonic and broadband THz generation. ACS Appl. Mater. Interfaces 2023, 15, 8590–8600. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Zhang, X.; Hu, Z.; Wu, Y. Organic Nonlinear Optical Crystals for Highly Efficient Terahertz-Wave Generation. Crystals 2023, 13, 144. [Google Scholar] [CrossRef]
- Zhang, W.; Yao, J.; Yu, L. Organic Nonlinear Optical Crystals: Design Principles and Growth Techniques for High-Efficiency Frequency Conversion. Adv. Mater. 2020, 32, 1904083. [Google Scholar]
- Halfpenny, P.J.; Morrison, H.; Ristic, R.I.; Shepherd, E.E.A.; Sherwood, J.N.; Simpson, G.S.; Yoon, C.S. The growth of large single crystals of the organic nonlinear optical material 2-(α-methylbenzylamino)-5-nitropyridine. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1993, 440, 683–699. [Google Scholar]
- Parisi, E.; Borbone, F.; Carella, A.; Lettieri, S.; Capobianco, A.; Peluso, A.; Centore, R. Winning Strategy toward Acentric Crystals: Transverse Dipole Moment Molecules. Cryst. Growth Des. 2023, 23.6, 4538–4544. [Google Scholar] [CrossRef]
- Parisi, E.; Santagata, E.; Simone, E.; Borbone, F.; Centore, R. Frustration of H-Bonding and Frustrated Packings in a Hexamorphic Crystal System with Reversible Crystal–Crystal Transitions. J. Am. Chem. Soc. 2024, 146.28, 19405–19413. [Google Scholar] [CrossRef]
- Bruker-Nonius. SADABS; Bruker-Nonius: Delft, The Netherlands, 2002. [Google Scholar]
- Altomare, A.; Burla, M.C.; Camalli, M.; Cascarano, G.L.; Giacovazzo, C.; Guagliardi, A.; Moliterni, G.G.; Polidori, G.; Spagna, R. SIR97: A new tool for crystal structure determination and refinement. J. Appl. Crystallogr. 1999, 32, 115–119. [Google Scholar] [CrossRef]
- Sheldrick, G.M. Crystal structure refinement with SHELXL. Acta Crystallogr. Sect. C Struct. Chem. 2015, 71, 3–8. [Google Scholar] [CrossRef]
- Farrugia, L.J. WinGX and Ortep for Windows: An update. J. Appl. Crystallogr. 2012, 45, 849–854. [Google Scholar] [CrossRef]
- Macrae, C.F.; Bruno, I.J.; Chisholm, J.A.; Edgington, P.R.; McCabe, P.; Pidcock, E.; Rodriguez-Monge, L.; Taylor, R.; van de Streek, J.; Wood, P.A. Mercury CSD 2.0—New features for the visualization and investigation of crystal structures. J. Appl. Crystallogr. 2008, 41, 466–470. [Google Scholar] [CrossRef]
- Nicolas, P.; Minon, C.; Abdallah, S.; Chen, D.; Rizzi, G.; de Coene, Y.; Liu, W.; Jeannin, O.; Clays, K.; Bellec, N.; et al. Multiphoton-And SHG-Active Pyrimidine-Based Liquid Crystalline Thin Films Toward 3D Optical Data Storage. Adv. Opt. Mater. 2025, 13.2, 2402083. [Google Scholar] [CrossRef]
- de Coene, Y.; Jooken, S.; Deschaume, O.; Van Steenbergen, V.; Vanden Berghe, P.; Van den Haute, C.; Boon, V.; Callewaert, G.; Van Cleuvenbergen, S.; Verbiest, T.; et al. Label-Free Imaging of Membrane Potentials by Intramembrane Field Modulation, Assessed by Second Harmonic Generation Microscopy. Small 2022, 18.18, 2200205. [Google Scholar] [CrossRef]
- van der Veen, M.A.; Vermoortele, F.; De Vos, D.E.; Verbiest, T. Point-Group Symmetry Determination via Observables Revealed by Polarized Second-Harmonic Generation Microscopy: (1) Theory. Anal. Chem. 2012, 84, 6378. [Google Scholar] [CrossRef]
- Legat, T.; Grachev, V.; Kabus, D.; Lettinga, M.P.; Clays, K.; Verbiest, T.; de Coene, Y.; Thielemans, W.; Van Cleuvenbergen, S. Imaging with a Twist: Three-Dimensional Insights of the Chiral Nematic Phase of Cellulose Nanocrystals via SHG Microscopy. Sci. Adv. 2024, 10, eadp2384. [Google Scholar] [CrossRef]
- Dow, X.Y.; DeWalt, E.L.; Newman, J.A.; Dettmar, C.M.; Simpson, G.J. Unified Theory for Polarization Analysis in Second Harmonic and Sum Frequency Microscopy. Biophys. J. 2016, 111.7, 1553–1568. [Google Scholar] [CrossRef]
- Fusco, S.; Parisi, E.; Borbone, F.; Carella, A.; Capobianco, A.; Peluso, A.; Centore, R. Solid State Selection between Nearly Isoenergetic Tautomeric Forms Driven by Right Hydrogen-Bonding Pairing. Cryst. Growth Des. 2018, 18.10, 6293–6301. [Google Scholar] [CrossRef]
- Goswami, M.; Mukhopadhyay, S.; Kar, T. Role of Solvent Molecules in Directing Crystal Packing toward Noncentrosymmetric Structures: Insights from Hydrated Organic Crystals. CrystEngComm 2019, 21, 6731–6740. [Google Scholar]
- Verbiest, T.; Clays, K.; Rodriguez, V. General aspects of second-order nonlinear optics. In Second-Order Nonlinear Optical Characterization Techniques: An Introduction, 1st ed.; Taylor & Francis Group, CRC Press: Boca Raton, FL, USA, 2009; pp. 1–26. [Google Scholar]
- Kleinman, D.A. Nonlinear Dielectric Polarization in Optical Media. Phys. Rev. 1962, 126, 1977–1979. [Google Scholar] [CrossRef]
- Dailey, C.A.; Burke, B.J.; Simpson, G.J. The General Failure of Kleinman Symmetry in Practical Nonlinear Optical Applications. Chem. Phys. Lett. 2004, 390, 8–13. [Google Scholar] [CrossRef]

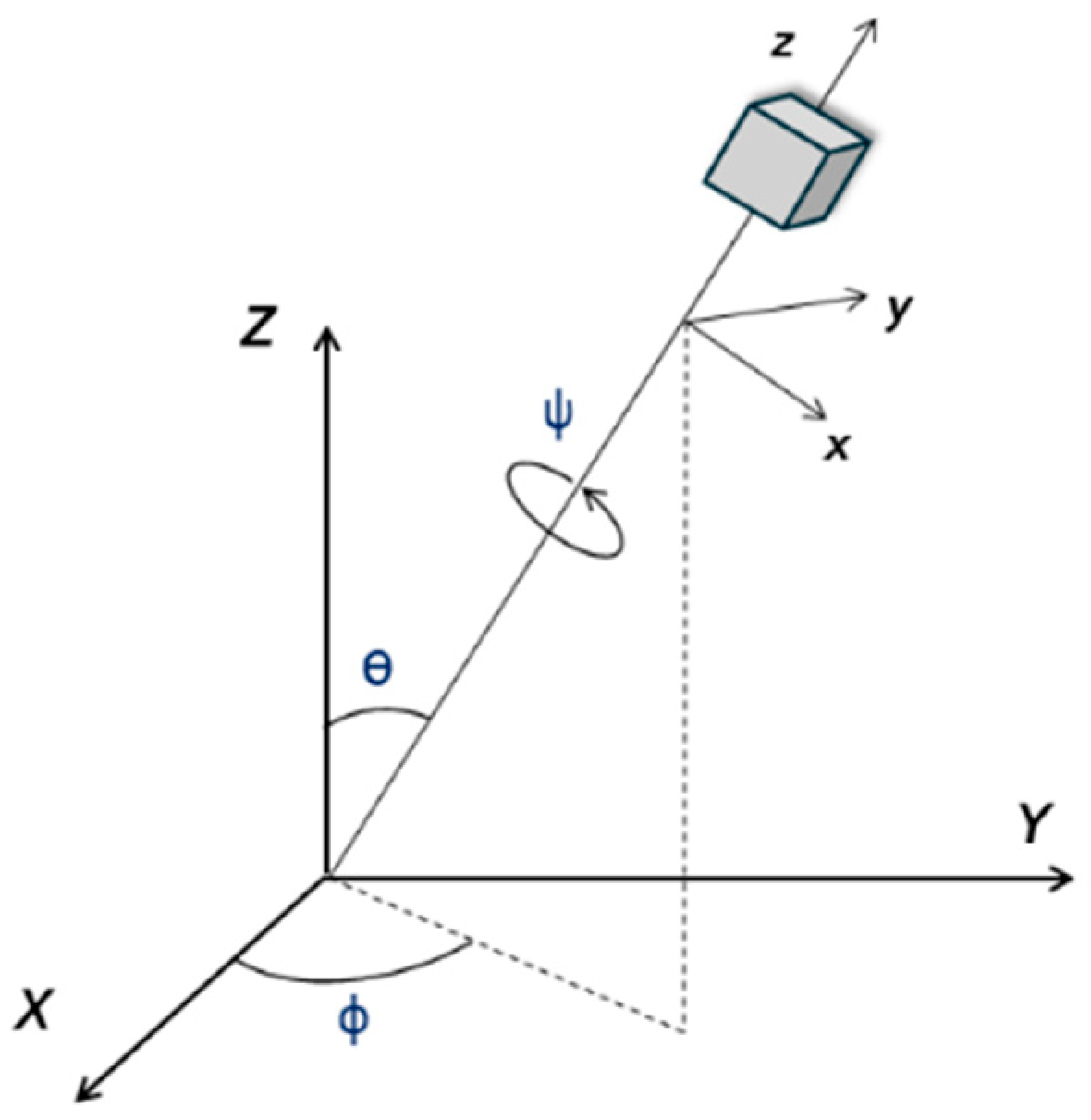

| Φ | θ | ψ | |
|---|---|---|---|
| −0.97 ± 0.02 | 0.332 ± 0.002 | 0.36 ± 0.01 | 1.589 ± 0.002 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santagata, E.; de Coene, Y.; Van Cleuvenbergen, S.; Clays, K.; Parisi, E.; Borbone, F.; Centore, R. Structure and Nonlinear Optical Characterization of a New Acentric Crystal of a 4-Hydroxybenzohydrazide Derivative. Crystals 2025, 15, 739. https://doi.org/10.3390/cryst15080739
Santagata E, de Coene Y, Van Cleuvenbergen S, Clays K, Parisi E, Borbone F, Centore R. Structure and Nonlinear Optical Characterization of a New Acentric Crystal of a 4-Hydroxybenzohydrazide Derivative. Crystals. 2025; 15(8):739. https://doi.org/10.3390/cryst15080739
Chicago/Turabian StyleSantagata, Emanuela, Yovan de Coene, Stijn Van Cleuvenbergen, Koen Clays, Emmanuele Parisi, Fabio Borbone, and Roberto Centore. 2025. "Structure and Nonlinear Optical Characterization of a New Acentric Crystal of a 4-Hydroxybenzohydrazide Derivative" Crystals 15, no. 8: 739. https://doi.org/10.3390/cryst15080739
APA StyleSantagata, E., de Coene, Y., Van Cleuvenbergen, S., Clays, K., Parisi, E., Borbone, F., & Centore, R. (2025). Structure and Nonlinear Optical Characterization of a New Acentric Crystal of a 4-Hydroxybenzohydrazide Derivative. Crystals, 15(8), 739. https://doi.org/10.3390/cryst15080739









