First-Principles Study of Structural, Elastic, and Optical Properties of Trigonal CaCO3 Under Pressure
Abstract
1. Introduction
2. Method
3. Results and Discussion
3.1. Structural Properties
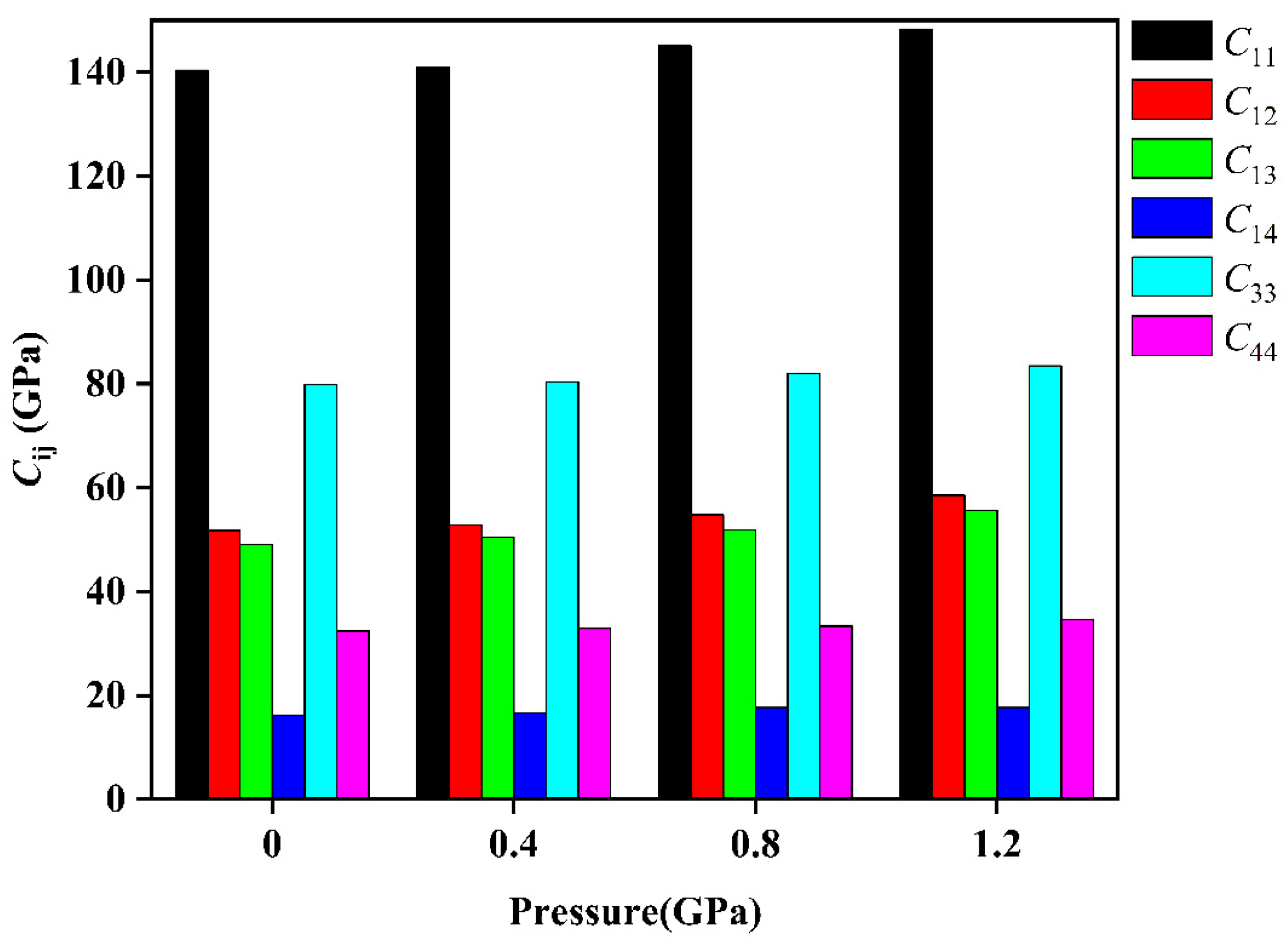
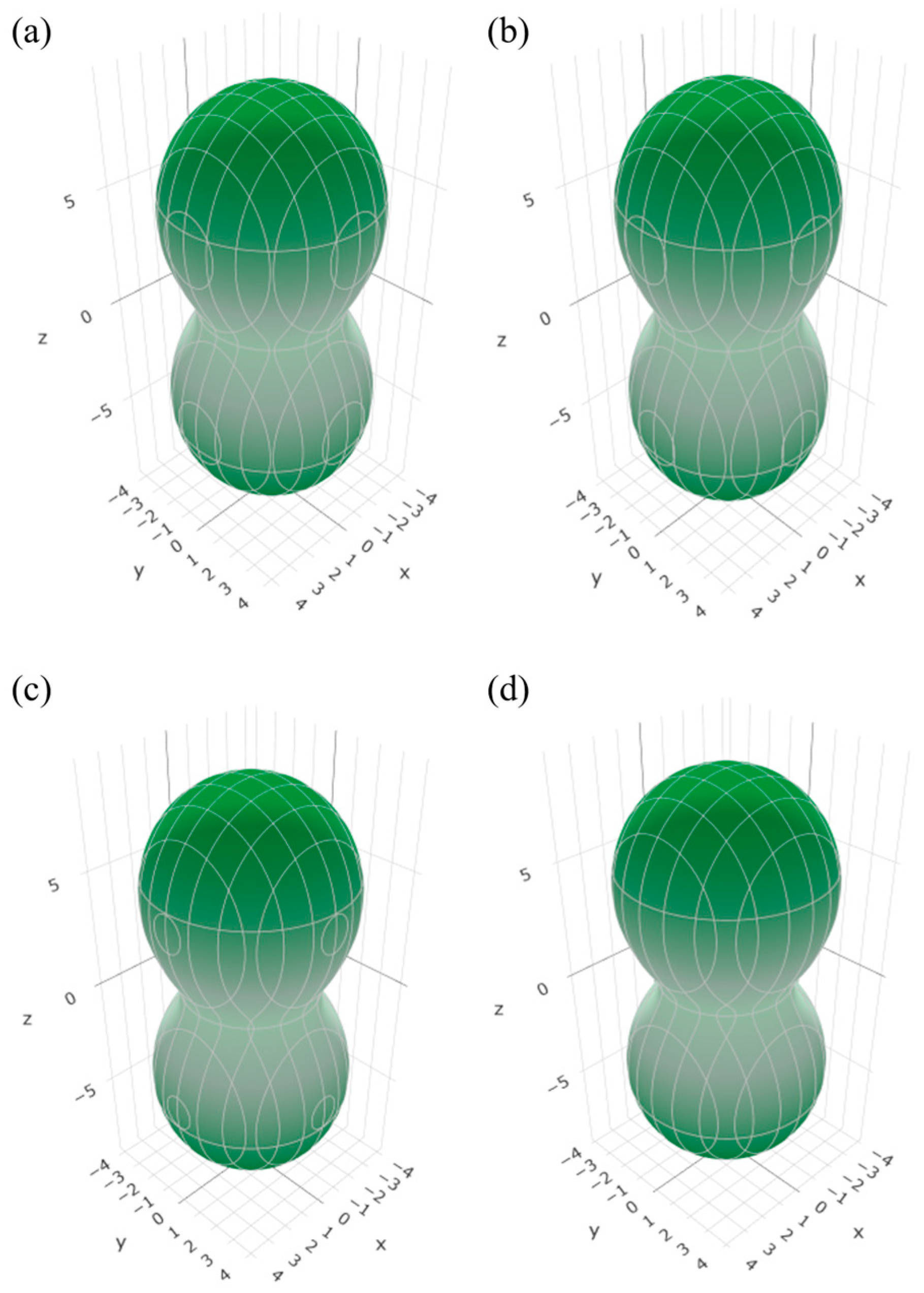
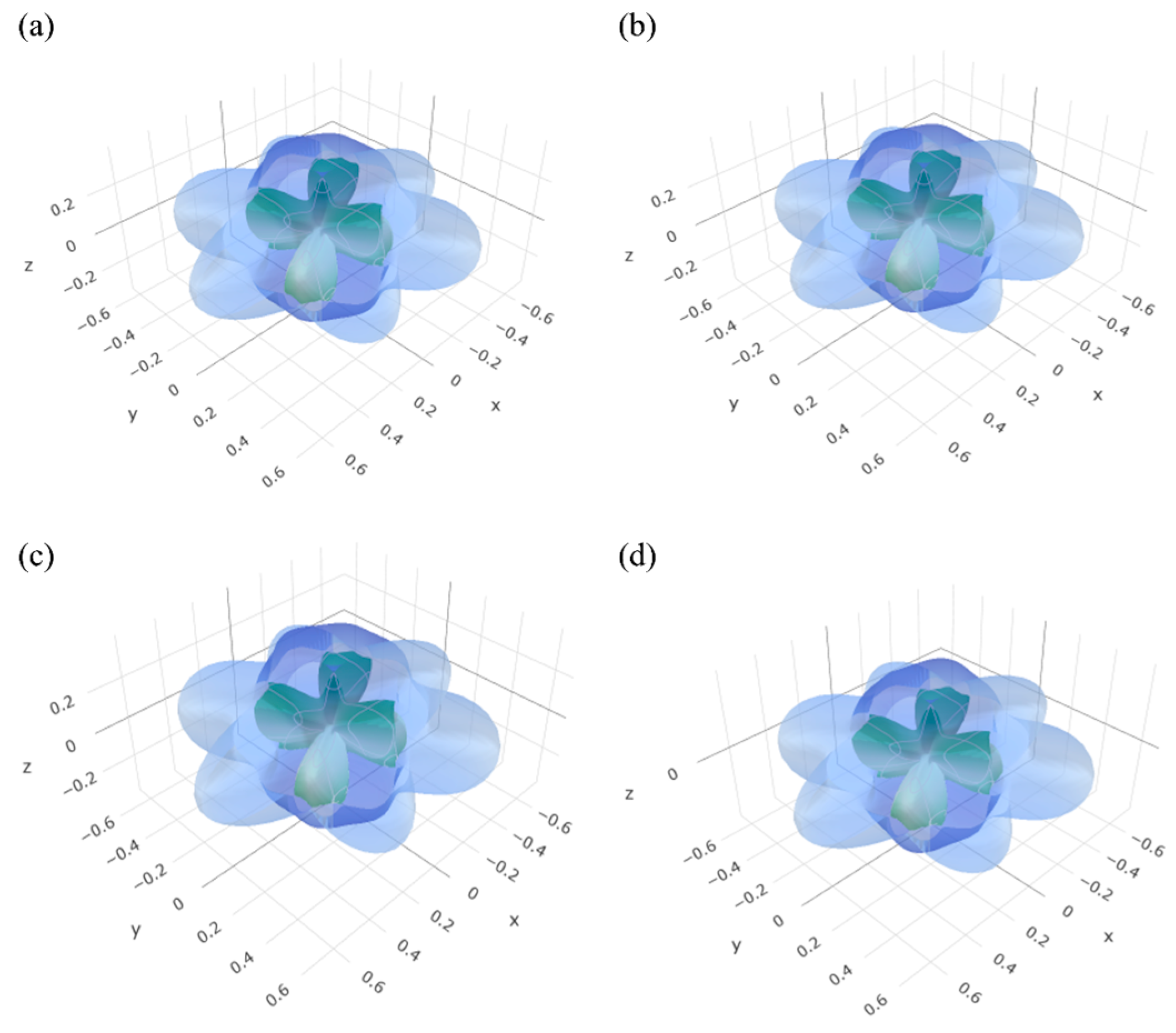
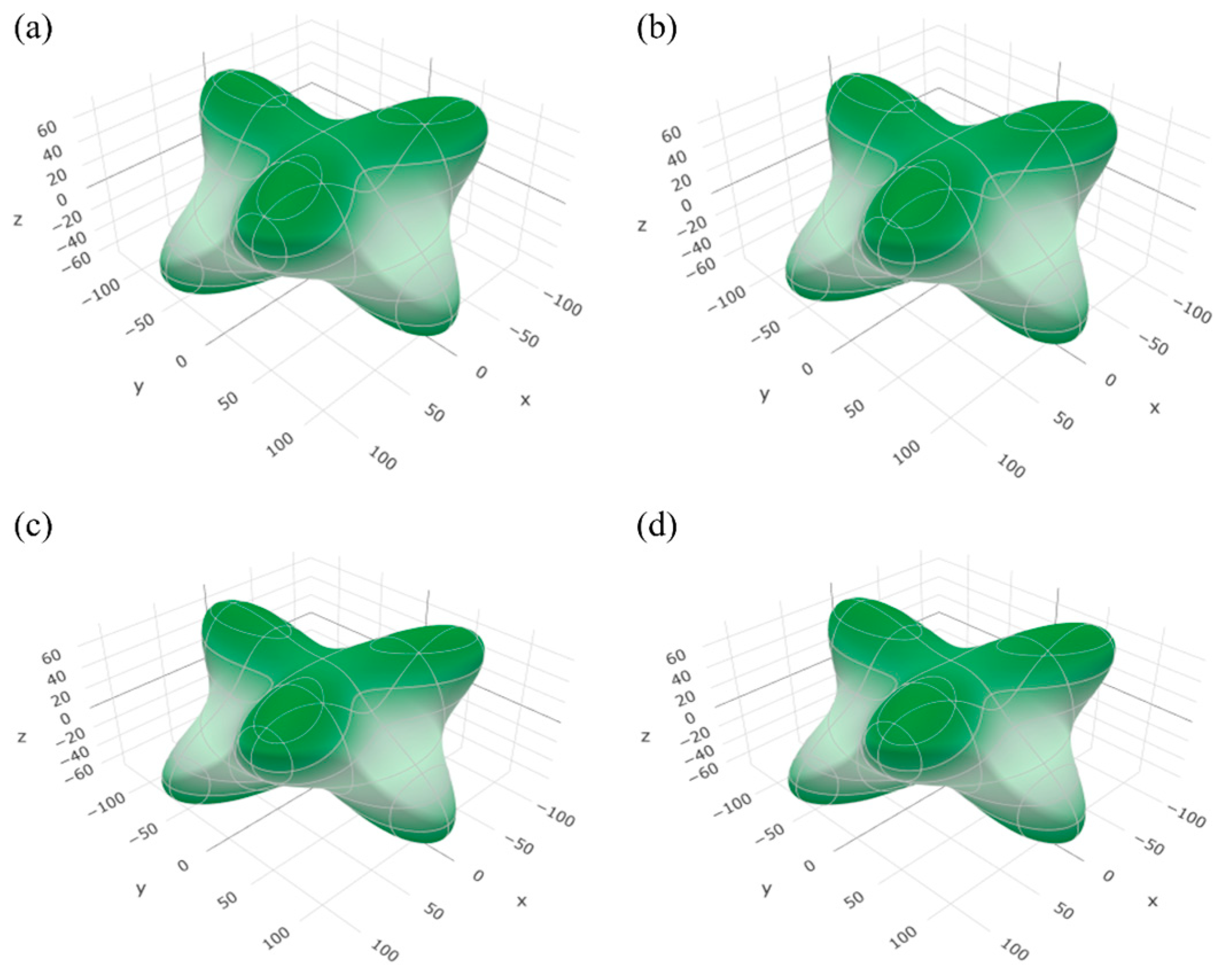
3.2. Elastic Properties
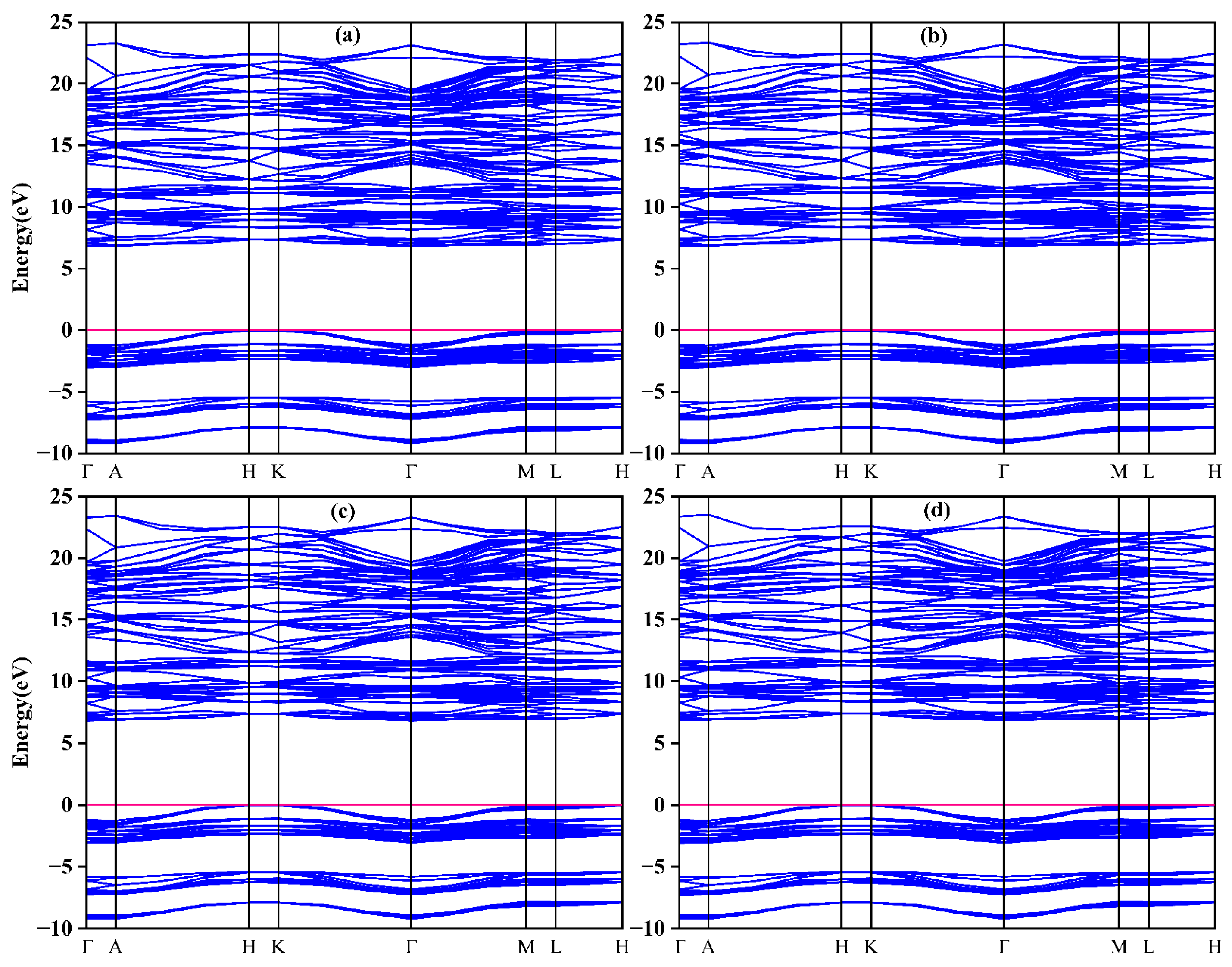
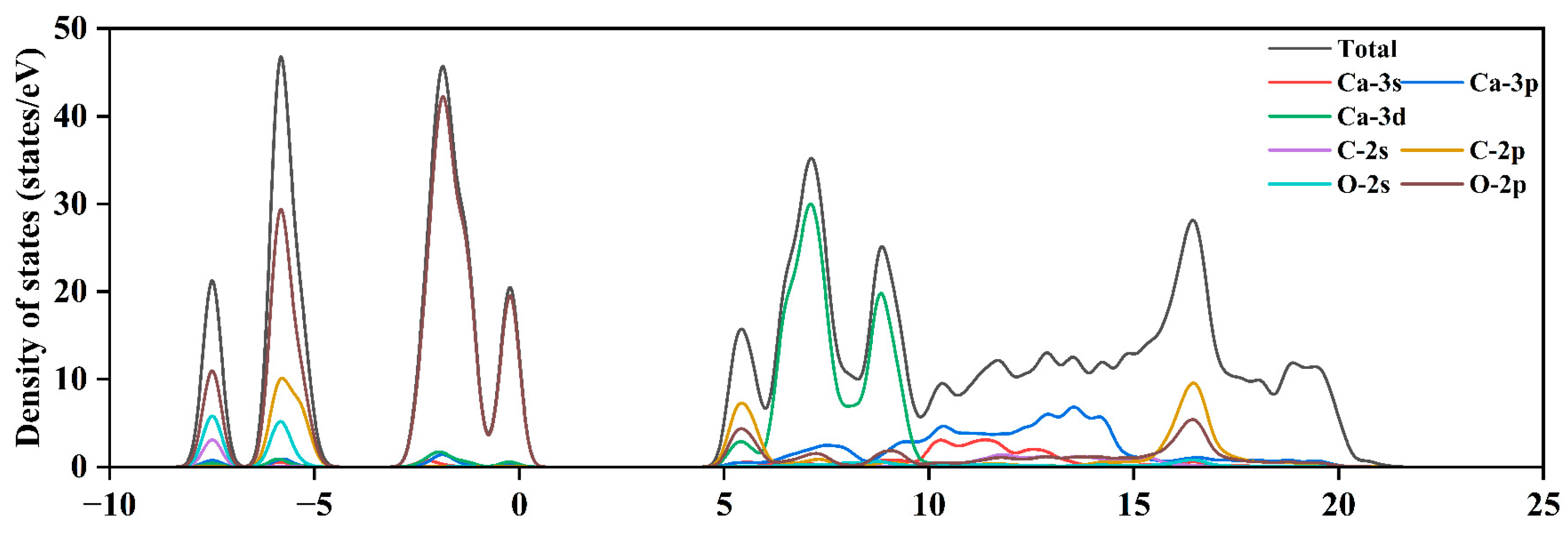
3.3. Electronic Properties
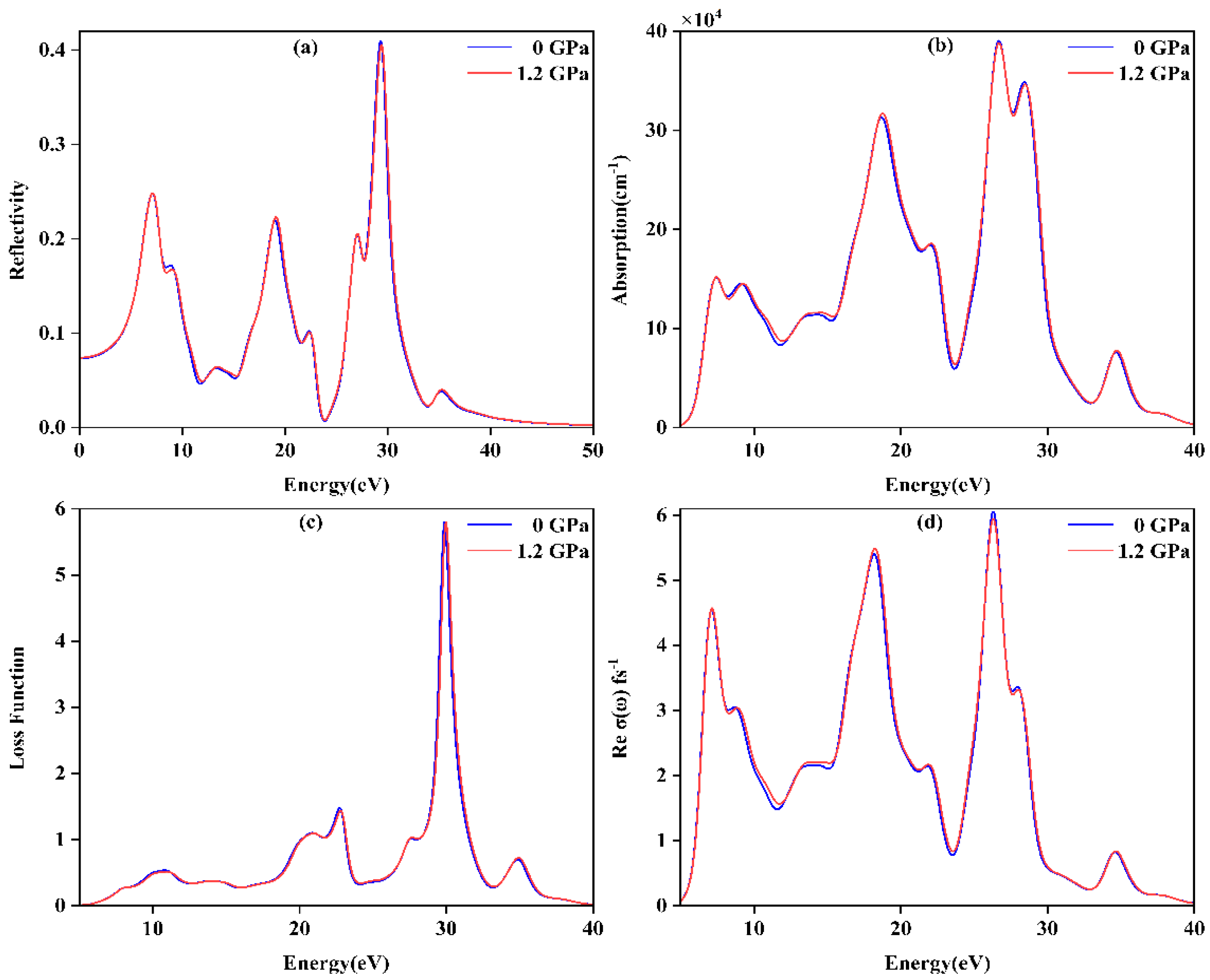
3.4. Optical Properties
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yao, X.; Xie, C.; Dong, X.; Oganov, A.R.; Zeng, Q. Novel high-pressure calcium carbonates. Phys. Rev. B 2018, 98, 014108. [Google Scholar] [CrossRef]
- Schmidt, C.A.; Tambutté, E.; Venn, A.A.; Zou, Z.; Alvarez, C.C.; Devriendt, L.S.; Bechtel, H.A.; Stifler, C.A.; Anglemyer, S.; Breit, C.P.; et al. Myriad Mapping of nanoscale minerals reveals calcium carbonate hemihydrate in forming nacre and coral biominerals. Nat. Commun. 2024, 15, 1812. [Google Scholar] [CrossRef]
- Zhou, J.; Chen, H.; Guo, Y.; Chen, Q.; Ren, H.; Tao, Y. Changes in metal adsorption ability of microplastics upon loss of calcium carbonate filler masterbatch through natural aging. Sci. Total Environ. 2022, 832, 155142. [Google Scholar] [CrossRef]
- Mishra, S.; Shimpi, N.G.; Mali, A.D. Influence of stearic acid treated nano-CaCO3 on the properties of silicone nanocomposites. J. Polym. Res. 2011, 18, 1715–1724. [Google Scholar] [CrossRef]
- Zhu, C.; Fang, Y.; Wei, H. Carbonation-cementation of recycled hardened cement paste powder. Constr. Build. Mater. 2018, 192, 224–232. [Google Scholar] [CrossRef]
- Rada, R.; Manea, D.L.; Nowakowski, A.; Rada, S. Nanocomposites Derived from Construction and Demolition Waste for Cement: X-ray Diffraction, Spectroscopic and Mechanical Investigations. Nanomaterials 2024, 14, 890. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Du, J.; Meng, W. Achieving low-carbon cementitious materials with high mechanical properties using CaCO3 suspension produced by CO2 sequestration. J. Clean. Prod. 2022, 373, 133546. [Google Scholar] [CrossRef]
- Fu, J.; Leo, C.P.; Show, P.L. Recent advances in the synthesis and applications of pH-responsive CaCO3. Biochem. Eng. J. 2022, 187, 108446. [Google Scholar] [CrossRef]
- Remy, M.T.; Ding, Q.; Krongbaramee, T.; Hu, J.; Mora Mata, A.V.; Haes, A.J.; Amendt, B.A.; Sun, H.; Buchakjian, M.R.; Hong, L. Plasmid Encoding miRNA-200C Delivered by CaCO3-Based Nanoparticles Enhances Rat Alveolar Bone Formation. Nanomedicine 2022, 17, 1339–1354. [Google Scholar] [CrossRef] [PubMed]
- Tao, T.; Zhu, Z.; Jia, S.; Tang, W.; Gong, J. Bioinspired transparent ultratough birefringent photonic films with engineerable interference colors derived from in-situ synthesis of CaCO3. Chem. Eng. J. 2024, 498, 155148. [Google Scholar] [CrossRef]
- Available online: https://oqmd.org/materials/entry/3547 (accessed on 4 March 2025).
- Available online: https://materialsproject.org/materials/mp-3953/ (accessed on 4 March 2025).
- Singh, A.K.; Kennedy, G.C. Compression of Calcite to 40 kbar. J. Geophys. Res. 1974, 79, 2615–2622. [Google Scholar] [CrossRef]
- Thanh, D.V.; Lacam, A. Experimental study of the elasticity of single crystalline calcite under high pressure (the calcite I–calcite II transition at 14.6 kbar). Phys. Earth Planet. Inter. 1984, 34, 195–203. [Google Scholar] [CrossRef]
- Merrill, L.; Bassett, W.A. The Crystal Structure of CaCO3(II), a High-Pressure Metastable Phase of Calcium Carbonate. Acta Cryst. B 1975, 31, 343–349. [Google Scholar] [CrossRef]
- Brik, M.G. First-principles calculations of structural, electronic, optical and elastic properties of magnesite MgCO3 and calcite CaCO3. Phys. B 2011, 406, 1004–1012. [Google Scholar] [CrossRef]
- Prencipe, M.; Pascale, F.; Zicovich-Wilson, C.M.; Saunders, V.R.; Orlando, R.; Dovesi, R. The vibrational spectrum of calcite (CaCO3): An ab initio quantum-mechanical calculation. Phys. Chem. Miner. 2004, 31, 559–564. [Google Scholar] [CrossRef]
- Chessin, H.; Hamilton, W.C.; Post, B. Position and thermal parameters of oxygen atoms in calcite. Acta Cryst. 1965, 18, 689–693. [Google Scholar] [CrossRef]
- Pilati, T.; Demartin, F.; Gramaccioli, C.M. Lattice-Dynamical Estimation of Atomic Displacement Parameters in Carbonates: Calcite and Aragonite CaCO3, Dolomite CaMg(CO3)2 and Magnesite MgCO3. Acta Cryst. B 1998, 54, 515–523. [Google Scholar] [CrossRef]
- Maslen, E.N.; Streltsov, V.A.; Streltsova, N.R.; Ishizawa, N. Electron density and optical anisotropy in rhombohedral carbonates. III. Synchrotron X-ray studies of CaCO3, MgCO3 and MnCO3. Acta Cryst. B 1995, 51, 929–939. [Google Scholar] [CrossRef]
- Payne, M.C.; Teter, M.P.; Allan, D.C.; Arias, T.A.; Joannopoulos, A.J. Iterative minimization techniques for ab initio total-energy calculations: Molecular dynamics and conjugate gradients. Rev. Mod. Phys. 1992, 64, 1045–1097. [Google Scholar] [CrossRef]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.I.; Refson, K.; Payne, M.C. First principles methods using CASTEP. Z. Kristallogr. 2005, 220, 567–570. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Lin, J.S.; Qteish, A.; Payne, M.C.; Heine, V. Optimized and transferable nonlocal separable ab initio pseudopotentials. Phys. Rev. B 1993, 47, 4174–4180. [Google Scholar] [CrossRef]
- Catti, M.; Pavese, A.; Apra, E.; Roetti, C. Quantum-mechanical Hartree-Fock study of calcite (CaCO3) at variable pressure, and comparison with magnesite (MgCO3). Phys. Chem. Miner. 1993, 20, 104–110. [Google Scholar] [CrossRef]
- Markgraf, S.A.; Reeder, R.J. High-temperature structure refinements of calcite and magnesite. Am. Mineral. 1985, 70, 590–600. [Google Scholar]
- Golosova, N.O.; Kozlenko, D.P.; Kichanov, S.E.; Lukin, E.V.; Dubrovinsky, L.S.; Mammadov, A.I.; Mehdiyeva, R.Z.; Jabarov, S.H.; Liermann, H.P.; Glazyrin, K.V.; et al. Structural, magnetic and vibrational properties of multiferroic GaFeO3 at high pressure. J. Alloys Compd. 2016, 684, 352–358. [Google Scholar] [CrossRef]
- Birch, F.J. Equation of State and Thermodynamic Parameters of NaC1 to 300 kbar in the High-Temperature Domain. J. Geophys. Res. 1986, 91, 4949–4954. [Google Scholar] [CrossRef]
- Gao, J.; Liu, Q.J.; Tang, B. Elastic stability criteria of seven crystal systems and their application under pressure: Taking carbon as an example. J. Appl. Phys. 2023, 133, 135901. [Google Scholar] [CrossRef]
- Pavese, A.; Catti, M.; Parker, S.C.; Wall, A. Modelling of the thermal dependence of structural and elastic properties of calcite, CaCO3. Phys. Chem. Miner. 1996, 23, 89–93. [Google Scholar] [CrossRef]
- Dandekar, D.P. Pressure Dependence of the Elastic Constants of Calcite. Phys. Rev. 1968, 172, 873–877. [Google Scholar] [CrossRef]
- Voigt, W. Lehrbuch der Kristallphysik (mit Ausschluss der Kristalloptik); Vieweg+Teubner Verlag: Wiesbaden, Germany, 1928; Volume XXVI, p. 979. [Google Scholar] [CrossRef]
- Reuss, A. Berechnung der Fließgrenze von Mischkristallen auf Grund der Plastizitätsbedingung für Einkristalle. Z. Angew. Math. Mech. 1929, 9, 49–58. [Google Scholar] [CrossRef]
- Hill, R. The Elastic Behaviour of a Crystalline Aggregate. Proc. Phys. Soc. A 1952, 65, 349–354. [Google Scholar] [CrossRef]
- Liu, Z.J.; Sun, X.W.; Zhang, C.R.; Zhang, S.J.; Zhang, Z.R.; Jin, N.Z. First-principles calculations of high-pressure physical properties anisotropy for magnesite. Sci. Rep. 2022, 12, 3691. [Google Scholar] [CrossRef] [PubMed]
- Tian, Y.; Xu, B.; Zhao, Z. Microscopic theory of hardness and design of novel superhard crystals. Int. J. Refract. Met. Hard Mater. 2012, 33, 93–106. [Google Scholar] [CrossRef]
- Pugh, S.F. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Philos. Mag. 1954, 45, 823–843. [Google Scholar] [CrossRef]
- Yang, J.; Shahid, M.; Wan, C.; Jing, F.; Pan, W. Anisotropy in elasticity, sound velocities and minimum thermal conductivity of zirconia from first-principles calculations. J. Eur. Ceram. Soc. 2017, 37, 689–699. [Google Scholar] [CrossRef]
- Panda, K.B.; Chandran, K.S.R. Determination of elastic constants of titanium diboride (TiB2) from first principles using FLAPW implementation of the density functional theory. Comput. Mater. Sci. 2006, 35, 134–150. [Google Scholar] [CrossRef]
- Ranganathan, S.I.; Ostoja-Starzewski, M. Universal elastic anisotropy index. Phys. Rev. Lett. 2008, 101, 055504. [Google Scholar] [CrossRef]
- Vahldiek, F.W.; Mersol, S.A. Anisotropy in Single-Crystal Refractory Compounds; Springer: Berlin/Heidelberg, Germany, 1968. [Google Scholar] [CrossRef]
- Gaillac, R.; Pullumbi, P.; Coudert, F.X. ELATE: An open-source online application for analysis and visualization of elastic tensors. J. Phys. Condens. Matter 2016, 28, 275201. [Google Scholar] [CrossRef]
- Baer, D.R.; Blanchard, D.L., Jr. Studies of the calcite cleavage surface for comparison with calculation. Appl. Surf. Sci. 1993, 72, 295–300. [Google Scholar] [CrossRef]
- Sun, H.G.; Zhou, Z.X.; Yuan, C.X.; Yang, X.N. Research with KNbO3 Bulk and Surface Properties Based on Density Functional Theory. Chin. Phys. Lett. 2013, 30, 027302. [Google Scholar] [CrossRef]
- Kittel, C.; Masi, J.F. Introduction to Solid State Physics. Phys. Today 1953, 7, 18–19. [Google Scholar] [CrossRef]



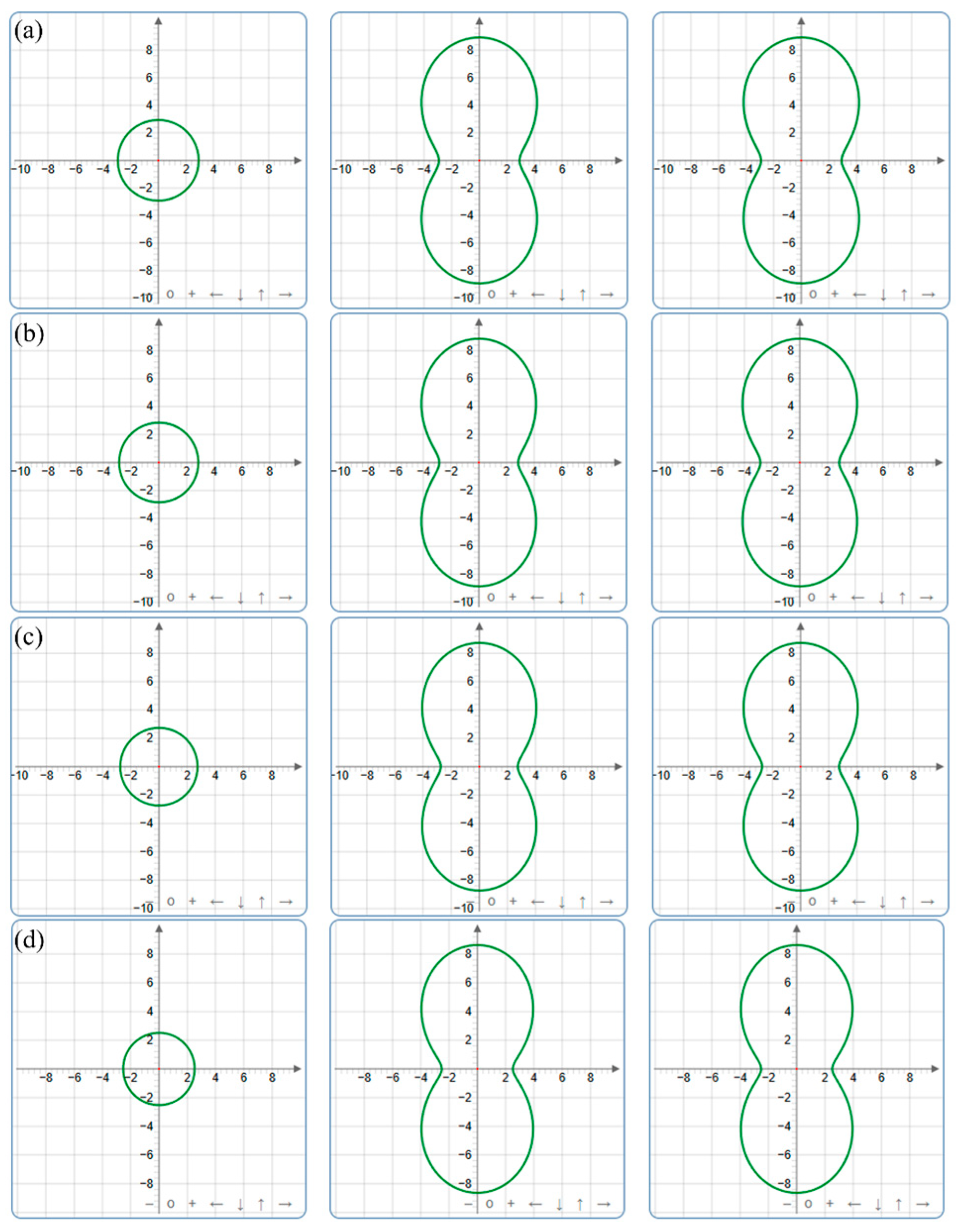
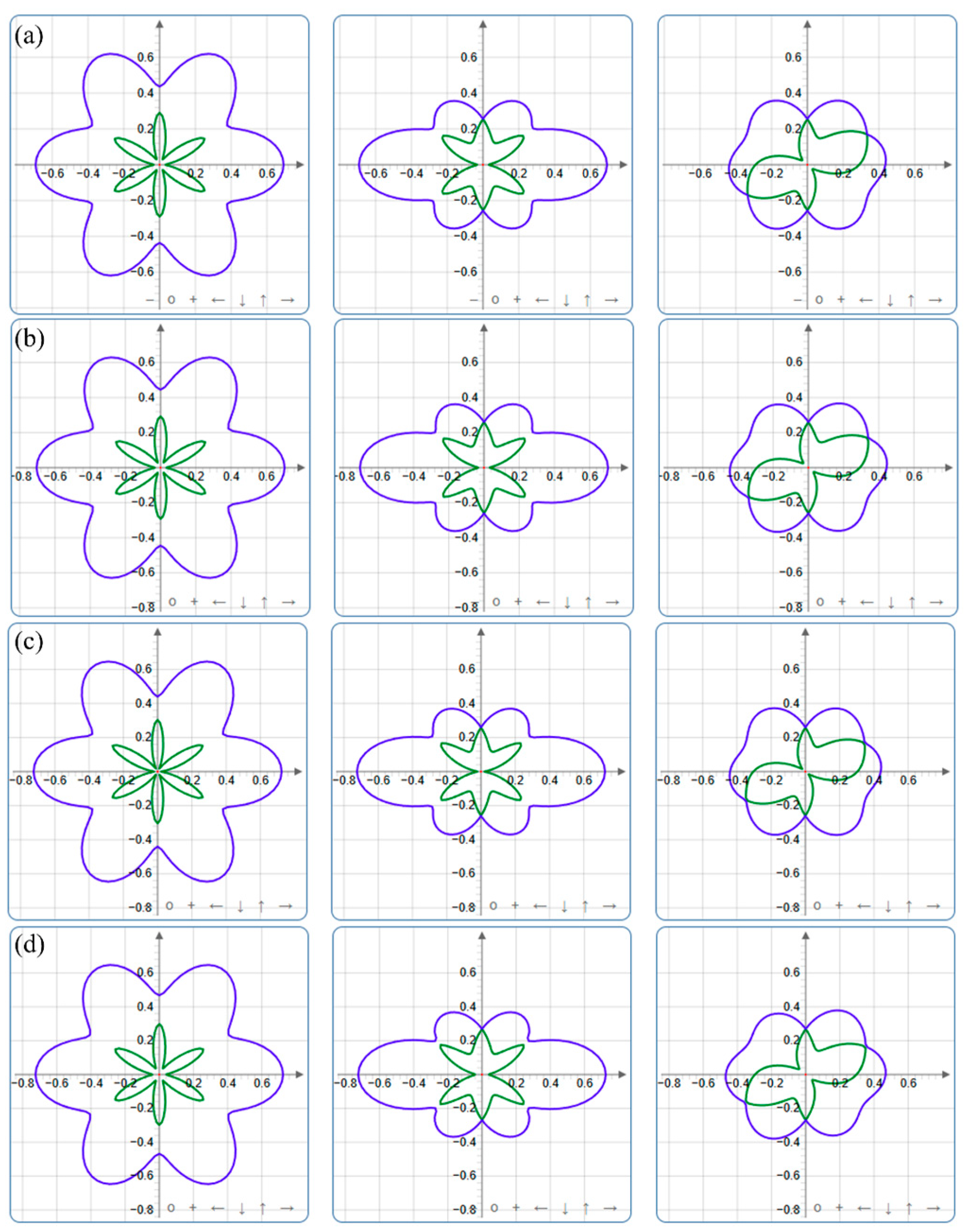

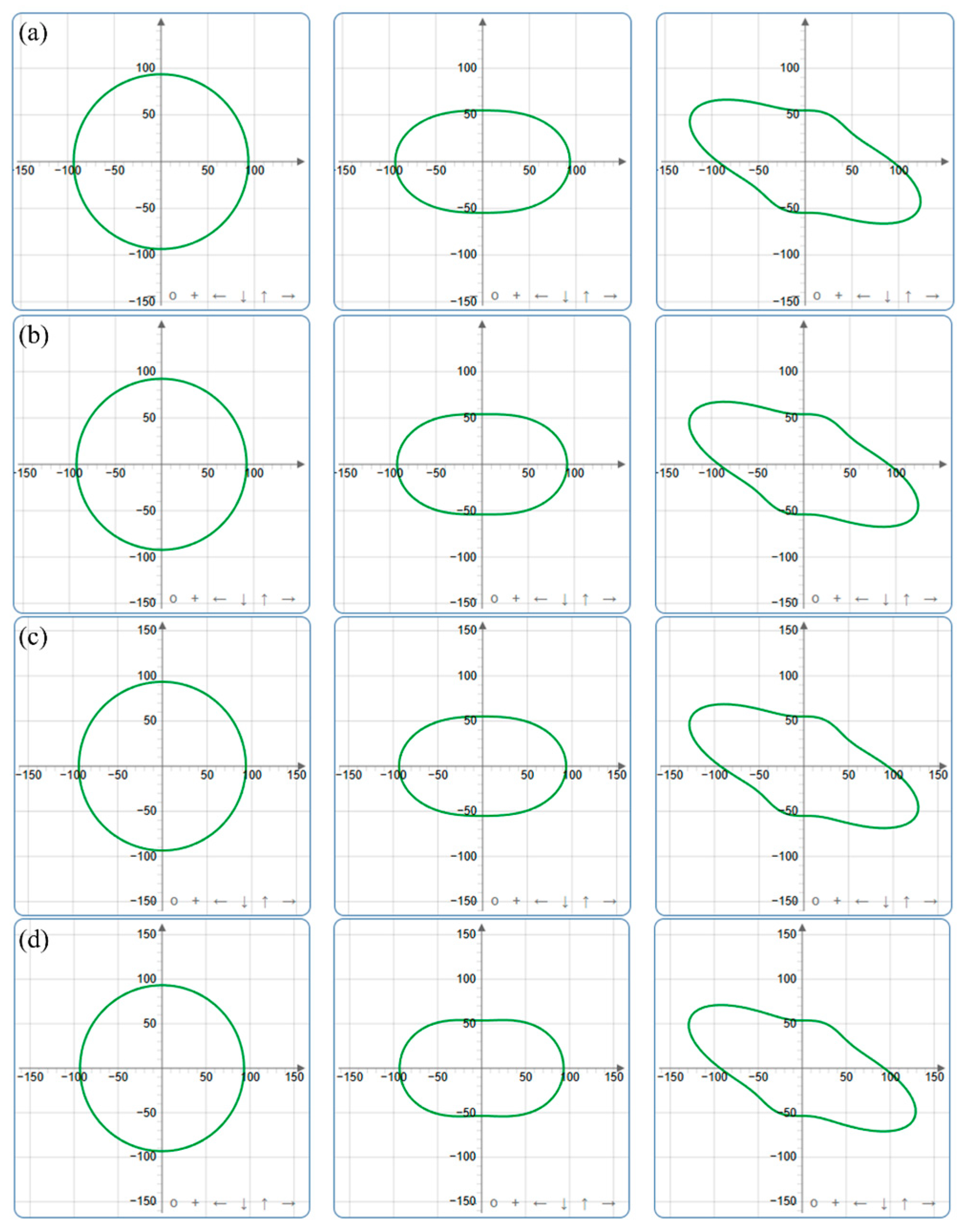

| Pressure (GPa) | a (Å) | c (Å) | ρ (g/cm3) | V (Å3) | |
|---|---|---|---|---|---|
| 0 | Present | 5.0473 | 17.2499 | 2.62032 | 380.564 |
| Ref. [16] | 5.0533 | 17.3260 | - | 383.2 | |
| Ref. [17] | 5.0492 | 17.3430 | - | 382.9 | |
| Ref. [25] | 5.045 | 17.504 | - | 385.9 | |
| Ref. [18] | 4.993 | 16.9169 | - | 365.24 | |
| Ref. [19] | 4.991 | 17.062 | - | 368.07 | |
| Ref. [20] | 4.988 | 17.068 | - | 367.76 | |
| Ref. [26] | 4.984 | 17.121 | - | 368.31 | |
| 0.4 | Present | 5.0392 | 17.2127 | 2.63441 | 378.530 |
| 0.8 | Present | 5.0361 | 17.1373 | 2.64919 | 376.418 |
| 1.2 | Present | 5.0302 | 17.0881 | 2.66313 | 374.447 |
| Pressure (GPa) | (GPa) | (GPa) | (GPa) | (GPa) | (GPa) | (GPa) | |
|---|---|---|---|---|---|---|---|
| 0 | Present | 140.38 | 51.76 | 49.12 | 16.17 | 79.89 | 32.41 |
| Ref. [30] | 153 | 55 | 50 | 13 | 82 | 37 | |
| Ref. [31] | 146.26 | 59.70 | 50.76 | −20.76 | 85.31 | 34.05 | |
| 0.4 | Present | 141.01 | 52.80 | 50.52 | 16.66 | 80.36 | 32.93 |
| 0.8 | Present | 145.09 | 54.77 | 51.86 | 17.63 | 82.01 | 33.31 |
| 1.2 | Present | 148.29 | 58.48 | 55.59 | 17.66 | 83.45 | 34.64 |
| Pressure | (GPa) | (GPa) | (GPa) | (GPa) | (GPa) | (GPa) | (GPa) | |||
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 73.404 | 67.705 | 70.555 | 35.869 | 28.789 | 32.329 | 84.361 | 0.3007 | 2.1757 | 4.4382 |
| 0.4 | 74.450 | 68.679 | 71.564 | 35.896 | 28.766 | 32.331 | 84.298 | 0.3037 | 2.2135 | 4.3676 |
| 0.8 | 76.573 | 70.386 | 73.479 | 36.605 | 28.866 | 32.735 | 85.508 | 0.3061 | 2.2447 | 4.3367 |
| 1.2 | 79.931 | 73.195 | 76.563 | 36.860 | 29.201 | 33.031 | 86.634 | 0.3114 | 2.3179 | 4.2079 |
| Pressure | ) | ) | ) |
|---|---|---|---|
| 0 | 3.9241 | 6.5861 | 3.5125 |
| 0.4 | 3.9149 | 6.5976 | 3.5032 |
| 0.8 | 3.9294 | 6.6492 | 3.5152 |
| 1.2 | 3.9395 | 6.7295 | 3.5218 |
| Pressure | ||||
|---|---|---|---|---|
| 0 | 0.0403 | 0.1095 | 0.0974 | 1.3138 |
| 0.4 | 0.0404 | 0.1103 | 0.1012 | 1.3233 |
| 0.8 | 0.0421 | 0.1159 | 0.1069 | 1.4035 |
| 1.2 | 0.0439 | 0.1182 | 0.1085 | 1.4284 |
| Pressure (GPa) | (TPa−1) | (TPa−1) | (GPa) | (GPa) | (GPa) | (GPa) | ||
|---|---|---|---|---|---|---|---|---|
| 0 | 2.9235 | 8.9229 | 0.0369 | 0.6934 | 21.129 | 55.591 | 54.773 | 131.99 |
| 0.4 | 2.8502 | 8.8602 | 0.0378 | 0.7044 | 20.943 | 56.093 | 54.023 | 133.27 |
| 0.8 | 2.7378 | 8.7317 | 0.0232 | 0.7238 | 20.638 | 57.839 | 55.090 | 137.37 |
| 1.2 | 2.5155 | 8.6311 | 0.0413 | 0.7243 | 21.385 | 58.160 | 53.551 | 139.26 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, S.; Zhang, X.; Hou, H.; Liu, Q.; Guo, H. First-Principles Study of Structural, Elastic, and Optical Properties of Trigonal CaCO3 Under Pressure. Crystals 2025, 15, 712. https://doi.org/10.3390/cryst15080712
Fan S, Zhang X, Hou H, Liu Q, Guo H. First-Principles Study of Structural, Elastic, and Optical Properties of Trigonal CaCO3 Under Pressure. Crystals. 2025; 15(8):712. https://doi.org/10.3390/cryst15080712
Chicago/Turabian StyleFan, Shenghai, Xuelin Zhang, Haijun Hou, Qingyuan Liu, and Hongli Guo. 2025. "First-Principles Study of Structural, Elastic, and Optical Properties of Trigonal CaCO3 Under Pressure" Crystals 15, no. 8: 712. https://doi.org/10.3390/cryst15080712
APA StyleFan, S., Zhang, X., Hou, H., Liu, Q., & Guo, H. (2025). First-Principles Study of Structural, Elastic, and Optical Properties of Trigonal CaCO3 Under Pressure. Crystals, 15(8), 712. https://doi.org/10.3390/cryst15080712






