Pressure Response of Crystalline Fluoranthene Probed by Raman Spectroscopy
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
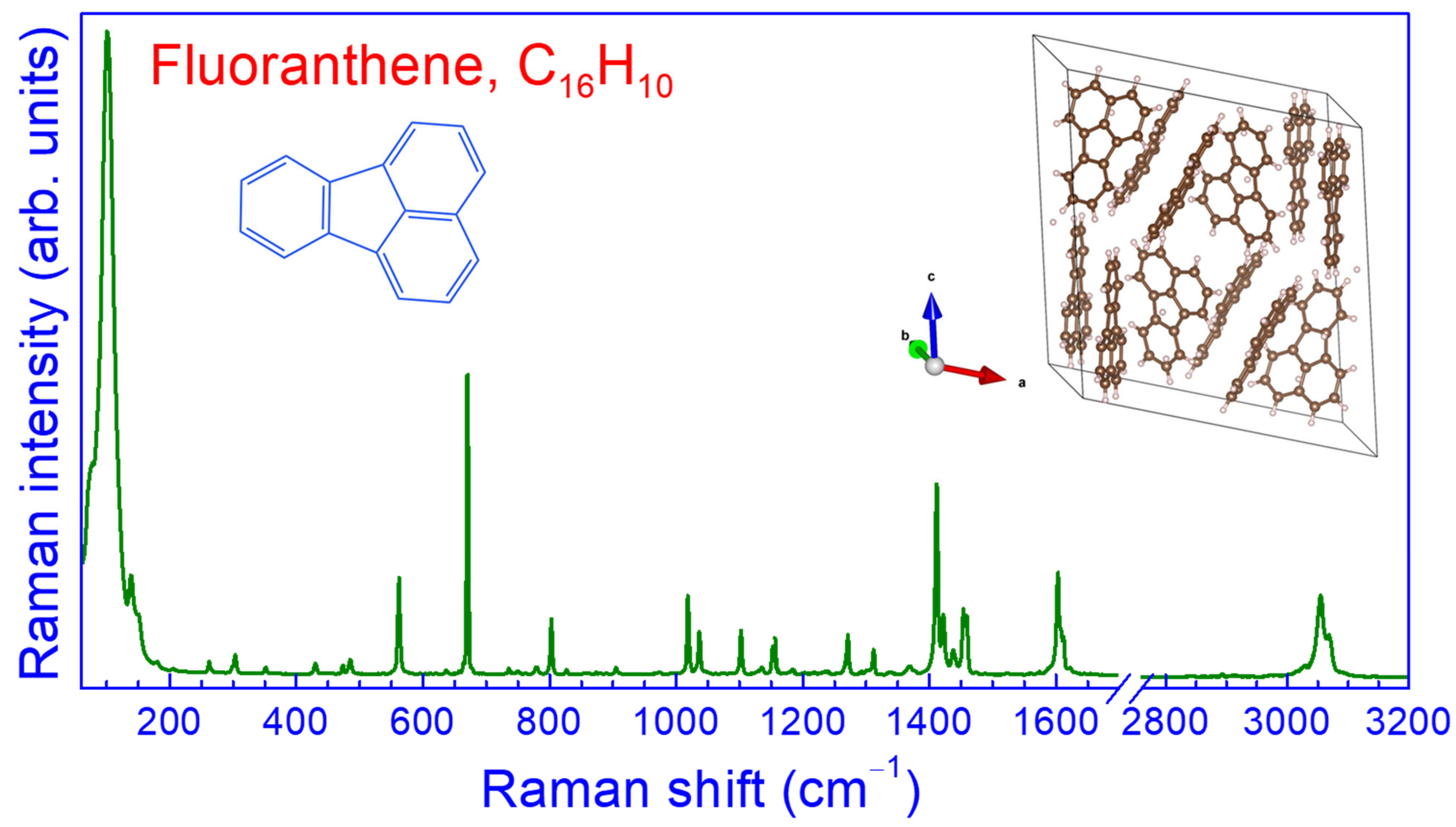
3.1. Crystal Structure and Raman Spectrum of Fluoranthene
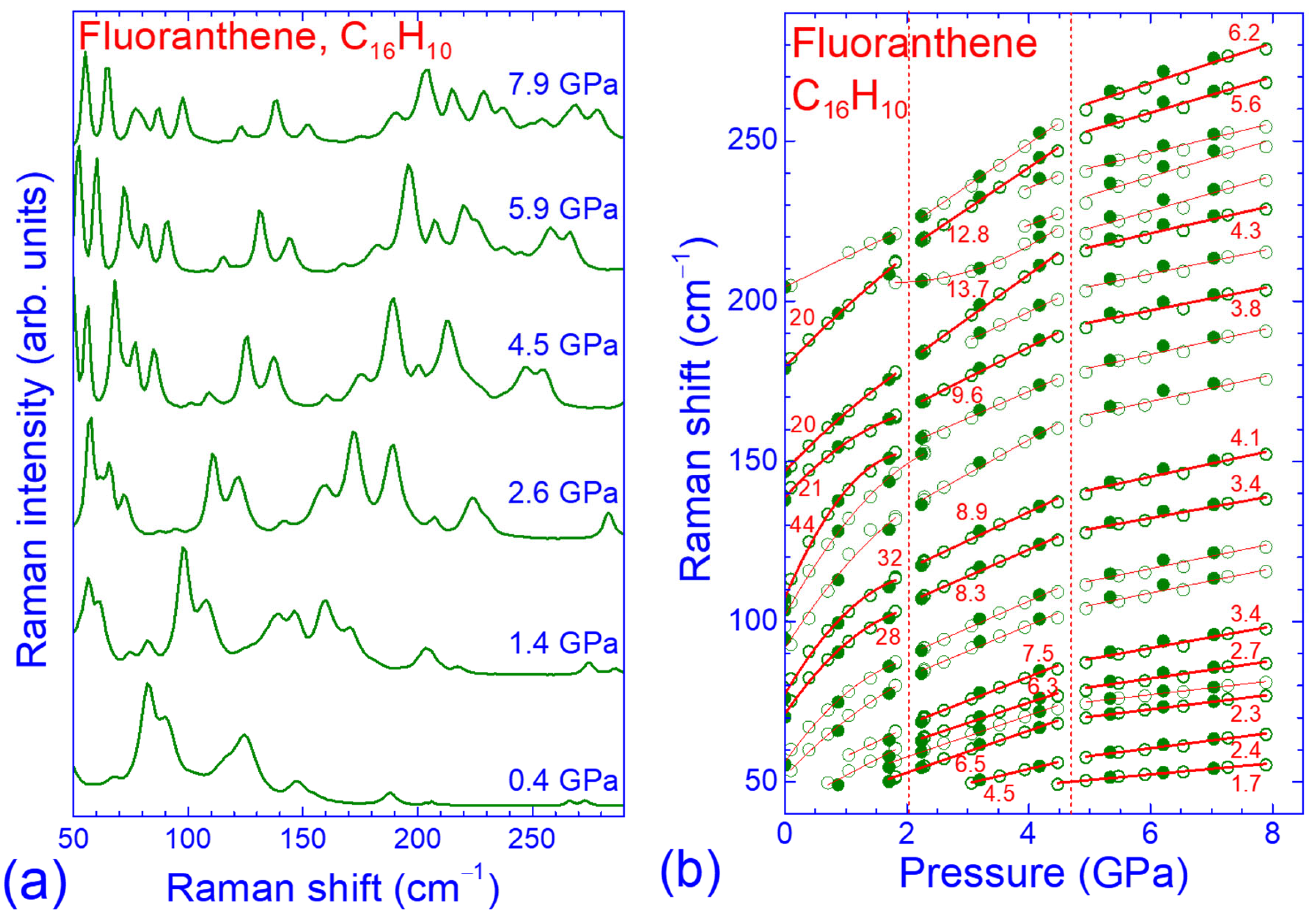
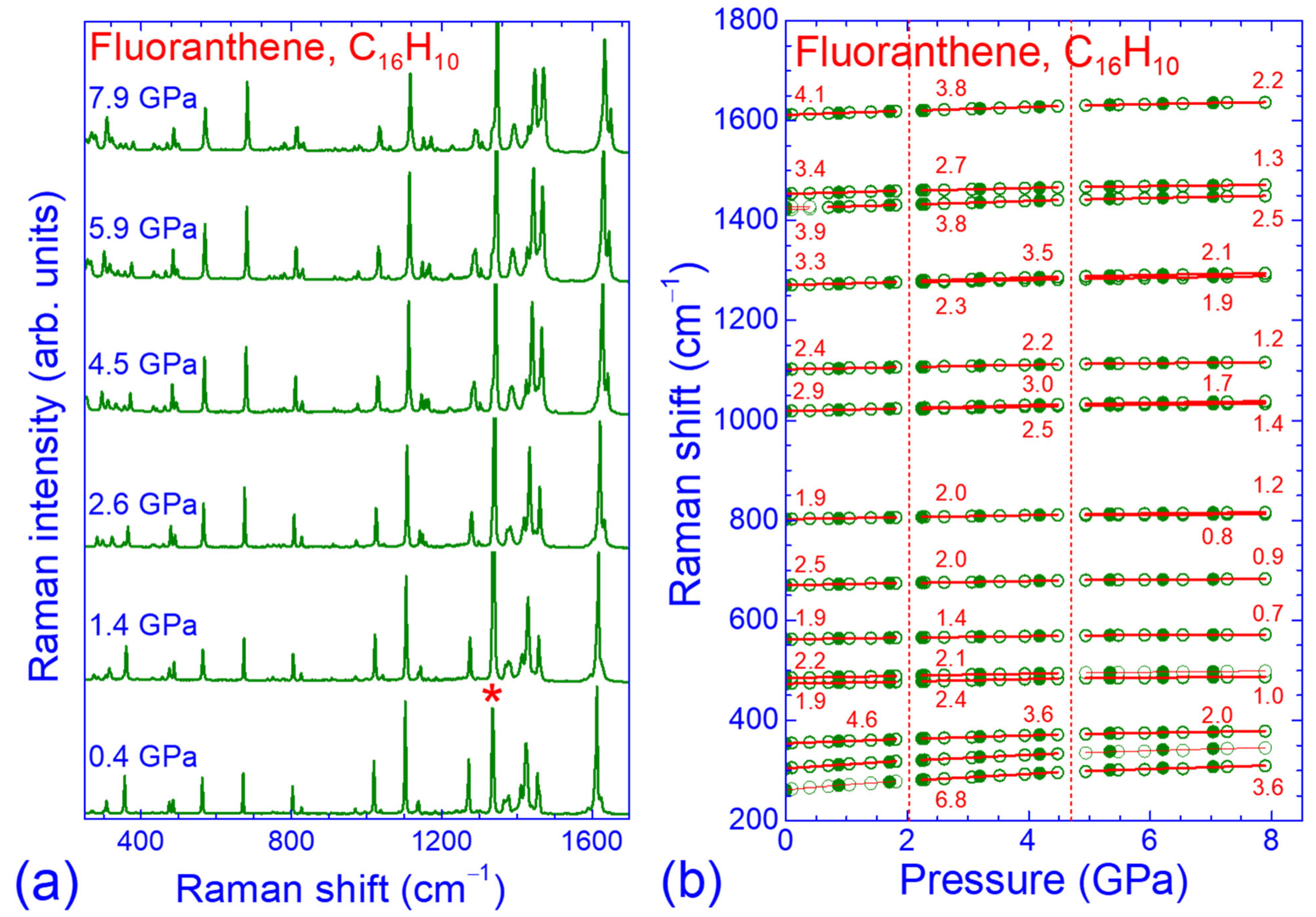
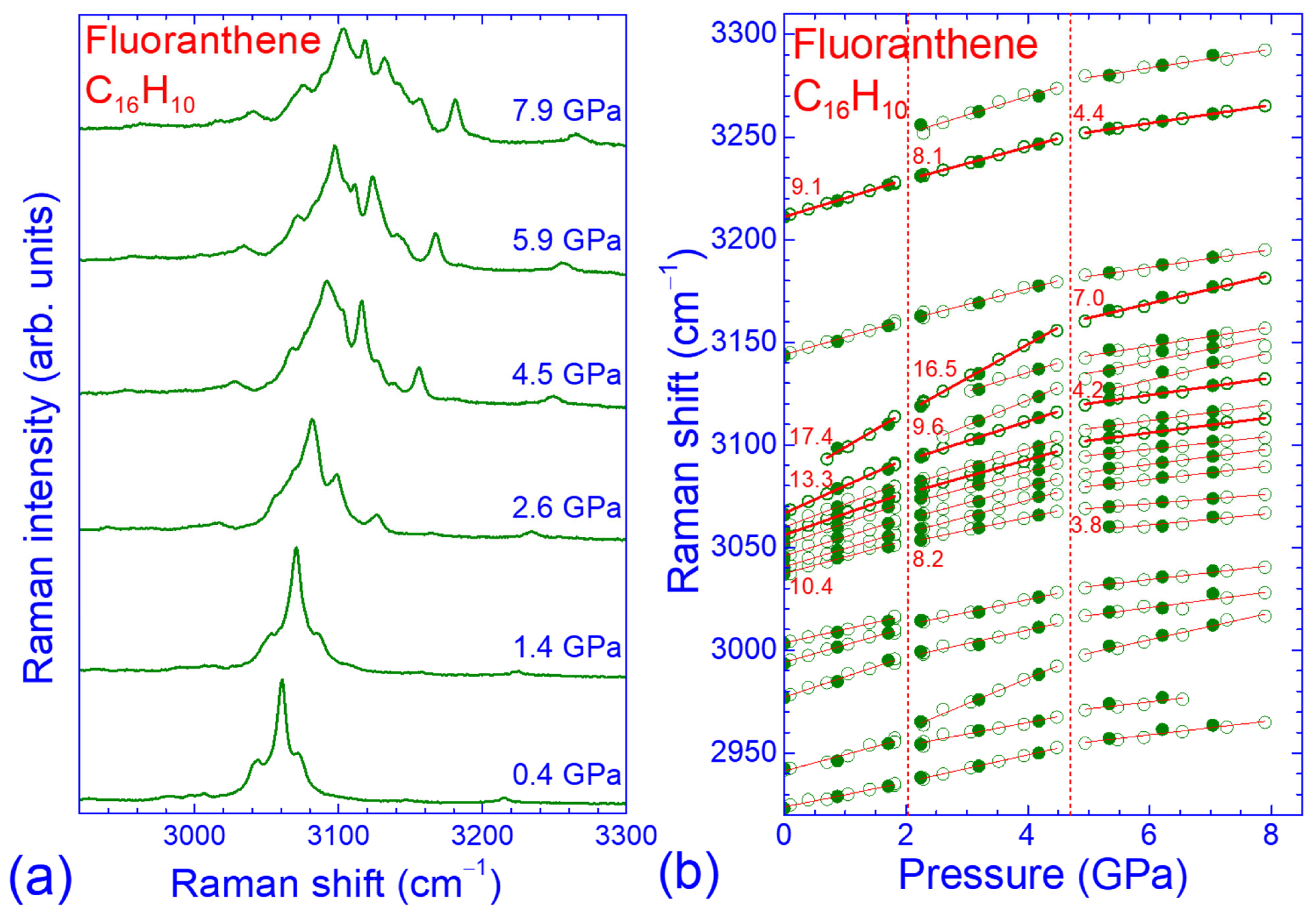
3.2. Pressure Dependence of the Raman Spectrum of Fluoranthene
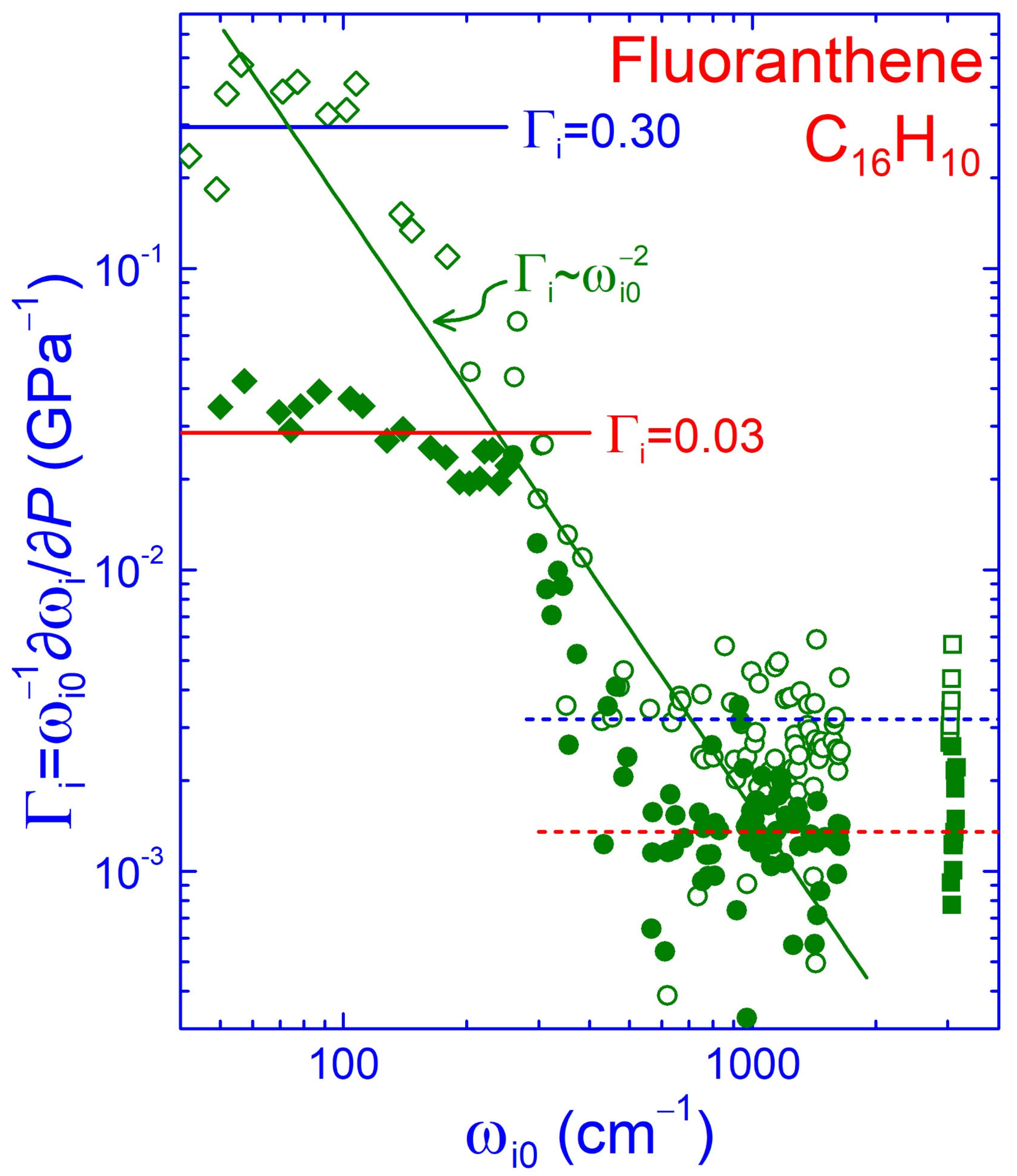
3.3. Force Constant Hierarchy and Stifness of Fluoranthene
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PAH | Polycyclic aromatic hydrocarbon |
| LMW | Low-molecular-weight |
| HMW | High-molecular-weight |
| XRD | X-ray diffraction |
| DFT | Density functional theory |
| B3LYP | Becke 3-Lee-Yang-Parr |
| DAC | Diamond anvil cell |
| PTM | Pressure transmitting medium |
| IR | Infrared |
| SBF | 9,9′-spirobifluorene |
References
- Desiraju, G.R. Crystal Engineering: The Design of Organic Solids; Elsevier Scientific Publishers: New York, NY, USA, 1989. [Google Scholar]
- Mirza Alizadeh, A.; Mohammadi, M.; Hashempour-baltork, F.; Hosseini, H.; Shahidi, F. Process-induced toxicants in food: An overview on structures, formation pathways, sensory properties, safety and health implications. Food Prod. Process. Nutr. 2025, 7, 7. [Google Scholar] [CrossRef]
- Vaz-Ramos, J.; Le Calvé, S.; Begin, S. Polycyclic aromatic hydrocarbons in water environments: Impact, legislation, depollution processes and challenges, and magnetic iron oxide/graphene-based nanocomposites as promising adsorbent solutions. J. Hazard. Mater. 2025, 490, 137726. [Google Scholar] [CrossRef] [PubMed]
- Hu, W.; Zhang, J.; Li, D.; Yuan, Y.; Tang, Y.; Hui, K.; Jiang, Y.; Tan, W. Study on factors influencing the transport and transformation of polycyclic aromatic hydrocarbons in soil-groundwater systems. Emerg. Contam. 2025, 11, 100472. [Google Scholar] [CrossRef]
- Wu, S.; Mou, B.; Liu, G.; Liu, R.; Wang, X. Contamination, risk assessment, and reduction strategies for hazardous polycyclic aromatic hydrocarbons in food. Curr. Opin. Food Sci. 2025, 62, 101270. [Google Scholar] [CrossRef]
- Zhang, Z.-F.; Chen, J.-C.; Zhao, Y.-X.; Wang, L.; Teng, Y.-Q.; Cai, M.-H.; Zhao, Y.-H.; Nikolaev, A.; Li, Y.-F. Determination of 123 polycyclic aromatic hydrocarbons and their derivatives in atmospheric samples. Chemosphere 2022, 296, 134025. [Google Scholar] [CrossRef]
- Harvey, R.G. Polycyclic Aromatic Hydrocarbons; Wiley-VCH: New York, NY, USA, 1997. [Google Scholar]
- Neilson, A.H. (Ed.) PAHs and Related Compounds, Chemistry; Springer: New York, NY, USA, 1998. [Google Scholar]
- Bandeira, G.C.; Meneses, H.E. (Eds.) Handbook of Polycyclic Aromatic Hydrocarbons: Chemistry, Occurrence and Health Issues; Nova Science Publishers: Hauppauge, NY, USA, 2012. [Google Scholar]
- Lawal, A.T. Polycyclic aromatic hydrocarbons. A review. Cogent Environ. Sci. 2017, 3, 1339841. [Google Scholar] [CrossRef]
- Ifegwu, O.C.; Anyakora, C. Chapter six—Polycyclic aromatic hydrocarbons: Part I. Exposure. Adv. Clin. Chem. 2015, 72, 277–304. [Google Scholar]
- Keyte, I.J.; Harrison, R.M.; Lammel, G. Chemical reactivity and long-range transport potential of polycyclic aromatic hydrocarbons—A review. Chem. Soc. Rev. 2013, 42, 9333–9391. [Google Scholar] [CrossRef]
- Gachanja, A.N. Polycyclic aromatic hydrocarbons, Environmental Applications. In Encyclopedia of Analytical Science, 2nd ed.; Worsfold, P.J., Poole, C.F., Eds.; Elsevier Ltd.: Waltham, MA, USA, 2005. [Google Scholar]
- Anthony, J.E. Functionalized acenes and heteroacenes for organic electronics. Chem. Rev. 2006, 106, 5028–5048. [Google Scholar] [CrossRef]
- Ye, Q.; Chi, C. Recent highlights and perspectives on acene based molecules and materials. Chem. Mater. 2014, 26, 4046–4056. [Google Scholar] [CrossRef]
- Delouche, T.; Hissler, M.; Bouit, P.-A. Polycyclic aromatic hydrocarbons containing heavy group 14 elements: From synthetic challenges to optoelectronic devices. Coord. Chem. Rev. 2022, 464, 214553. [Google Scholar] [CrossRef]
- Ma, L.; Han, Y.; Shi, O.; Huang, H. The design, synthesis and application of rubicene based polycyclic aromatic hydrocarbons (PAHs). J. Mater. Chem. C 2023, 11, 16429–16438. [Google Scholar] [CrossRef]
- Mathur, C.; Gupta, R.; Bansal, R.K. Organic donor-acceptor complexes as potential semiconducting materials. Chem. Eur. J. 2024, 30, e202304139. [Google Scholar] [CrossRef]
- Ahn, T.K.; Kim, K.S.; Kim, D.Y.; Noh, S.B.; Aratani, N.; Ikeda, C.; Osuka, A.; Kim, D. Relationship between two-photon absorption and the π-conjugation pathway in porphyrin arrays through dihedral angle control. J. Am. Chem. Soc. 2006, 128, 1700–1704. [Google Scholar] [CrossRef]
- Yadav, B.; Ravikanth, M. Porphyrinoid framework embedded with polycyclic aromatic hydrocarbons: New synthetic marvels. Org. Biomol. Chem. 2024, 22, 1932–1960. [Google Scholar] [CrossRef] [PubMed]
- Monte, M.J.S.; Notario, R.; Pinto, S.P.; Lobo Ferreira, A.I.M.C.; Ribeiro da Silva, M.D.M.C. Thermodynamic properties of fluoranthene: An experimental and computational study. J. Chem. Thermodyn. 2012, 49, 159–164. [Google Scholar] [CrossRef]
- Kanaly, R.A.; Harayama, S. Biodegradation of high-molecular-weight polycyclic aromatic hydrocarbons by bacteria. J. Bacteriol. 2000, 182, 2059–2067. [Google Scholar] [CrossRef] [PubMed]
- Gundlapalli, M.; Sivagami, K.; Gopalakrishnan, M.; Harshini, P.; Janjaroen, D.; Ganesan, S. Biodegradation of low molecular weight polycyclic aromatic hydrocarbons in soil: Insights into bacterial activities and bioremediation techniques. Sustain. Chem. Environ. 2024, 7, 100146. [Google Scholar] [CrossRef]
- Klaeboe, P.; Cyvin, S.J.; Phongsatha Asbjørnsen, A.; Cyvin, B.N. Condensed aromatics—XIV. Fluoranthene. Spectrochim. Acta A 1981, 37, 655–661. [Google Scholar] [CrossRef]
- Bark, K.-M.; Force, R.K. Fluorescence properties of fluoranthene as a function of temperature and environment. Spectrochim. Acta A 1993, 49, 1605–1611. [Google Scholar] [CrossRef]
- Slodek, A.; Maron, A.; Pajak, M.; Matussek, M.; Grudzka-Flak, I.; Malecki, J.G.; Switlicka, A.; Krompiec, S.; Danikiewicz, W.; Grela, M.; et al. Luminescent-substituted fluoranthenes—Synthesis, structure, electrochemistry, and optical properties. Chem. Eur. J. 2018, 24, 9622–9631. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, D.; Patil, Y.; Patil, S. Fluoranthene derivatives as blue fluorescent materials for non-doped organic light-emitting diodes. J. Mater. Chem. C 2016, 4, 193–200. [Google Scholar] [CrossRef]
- Jia, C.; Wang, L.; Ma, Y.-N.; Duan, Z. Synthesis and electronic properties of arene-fused o-carborane. Organometallics 2025, 44, 938–943. [Google Scholar] [CrossRef]
- Debnath, S.; Mohanty, A.; Naik, P.; Salzner, U.; Dasgupta, J.; Patil, S. Deciphering intramolecular charge transfer in fluoranthene derivatives. J. Mater. Chem. C 2024, 12, 9200–9209. [Google Scholar] [CrossRef]
- Liang, Y. Core-modified of fluoranthene with “propeller” structure for highly sensitive detection of nitroaromatic compounds. Spectrochim. Acta A 2019, 206, 474–483. [Google Scholar] [CrossRef]
- Hino, Y.; Matsuo, T.; Hayashi, S. Unique 2D face topologies in naphthyl-appended naphtho[k] fluoranthene-based 3D crystals for optical waveguide. Adv. Opt. Mater. 2023, 11, 2201810. [Google Scholar] [CrossRef]
- Hazell, A.C.; Jones, D.W.; Sowden, J.M. The crystal structure of fluoranthene, Cl6H10: A Study by X-ray and neutron diffraction. Acta Cryst. B 1977, 33, 1516–1522. [Google Scholar] [CrossRef]
- Jones, D.W.; Matthews, R.S. 4 Carcinogenicity and structure in polycyclic hydrocarbons. Progr. Med. Chem. 1974, 10, 159–203. [Google Scholar] [CrossRef]
- Orgzall, I.; Emmerling, F.; Schulz, B.; Franco, O. High-pressure studies on molecular crystals—Relations between structure and high-pressure behavior. J. Phys. Condens. Matter 2008, 20, 295206. [Google Scholar] [CrossRef]
- Meyer, B.; Barthel, S.; Mace, A.; Vannay, L.; Guillot, B.; Smit, B.; Corminboeuf, C. DORI reveals the influence of noncovalent interactions on covalent bonding patterns in molecular crystals under pressure. J. Phys. Chem. Lett. 2019, 10, 1482–1488. [Google Scholar] [CrossRef]
- Guan, J.; Zhang, C.; Gao, D.; Tang, X.; Dong, X.; Lin, X.; Wang, Y.; Wang, X.; Wang, L.; Lee, H.H.; et al. Drastic photoluminescence modulation of an organic molecular crystal with high pressure. Mater. Chem. Front. 2019, 3, 1510–1517. [Google Scholar] [CrossRef]
- Zallen, R. Pressure-Raman effects and vibrational scaling laws in molecular crystals: S8 and As2S3. Phys. Rev. B 1974, 9, 4485–4496. [Google Scholar] [CrossRef]
- Zallen, R.; Slade, M.L. Influence of pressure and temperature on phonons in molecular chalcogenides: Crystalline As4S4 and S4N4. Phys. Rev. B 1978, 18, 5775–5798. [Google Scholar] [CrossRef]
- Marinopoulou, A.; Christopoulou, V.; Karabinaki, O.; Christofilos, D.; Arvanitidis, J. The high-pressure response of trans-cinnamic acid crystals studied by Raman spectroscopy. Appl. Res. 2024, 3, e202300129. [Google Scholar] [CrossRef]
- Zallen, R.; Griffiths, C.H.; Slade, M.L.; Hayek, M.; Brafman, O. The solid state transition in pyrene. Chem. Phys. Lett. 1976, 39, 85–89. [Google Scholar] [CrossRef]
- Zhao, L.; Baer, B.J.; Chronister, E.L. High-pressure Raman study of anthracene. J. Phys. Chem. A 1999, 103, 1728–1733. [Google Scholar] [CrossRef]
- Venuti, E.; Guido Della Valle, R.; Farina, L.; Brillante, A.; Masino, M.; Girlando, A. Phonons and structures of tetracene polymorphs at low temperature and high pressure. Phys. Rev. B 2004, 70, 104106. [Google Scholar] [CrossRef]
- Sun, B.; Dreger, Z.A.; Gupta, Y.M. High-pressure effects in pyrene crystals: Vibrational spectroscopy. J. Phys. Chem. A 2008, 112, 10546–10551. [Google Scholar] [CrossRef]
- Zhou, M.; Wang, K.; Mena, Z.; Gao, S.; Li, Z.; Sun, C. Study of high-pressure Raman intensity behavior of aromatic hydrocarbons: Benzene, biphenyl and naphthalene. Spectrochim. Acta A 2012, 97, 526–531. [Google Scholar] [CrossRef]
- Meletov, K.P. Phonon spectrum of a naphthalene crystal at a high pressure: Influence of shortened distances on the lattice and intramolecular vibrations. Phys. Solid State 2013, 55, 581–588. [Google Scholar] [CrossRef]
- O’Bannon, E., III; Williams, Q. Vibrational spectra of four polycyclic aromatic hydrocarbons under high pressure: Implications for stabilities of PAHs during accretion. Phys. Chem. Miner. 2016, 43, 181–208. [Google Scholar] [CrossRef]
- Zhao, X.-M.; Zhong, G.-H.; Zhang, J.; Huang, Q.-W.; Goncharov, A.F.; Lin, H.Q.; Chen, X.-J. Combined experimental and computational study of high-pressure behavior of triphenylene. Sci. Rep. 2016, 6, 25600. [Google Scholar] [CrossRef]
- Capitani, F.; Höppner, M.; Malavasi, L.; Marini, C.; Dore, P.; Boeri, L.; Postorino, P. The effect of high pressure on the lattice structure and dynamics of phenacenes. J. Phys. Conf. Ser. 2017, 950, 042017. [Google Scholar] [CrossRef]
- Du, M.; Dong, J.; Zhang, Y.; Yang, X.; Li, Z.; Wang, M.; Liu, R.; Liu, B.; Zhou, Q.; Wei, T.; et al. Vibrational properties and polymerization of corannulene under pressure, probed by Raman and infrared spectroscopies. J. Phys. Chem. C 2019, 123, 23674–23681. [Google Scholar] [CrossRef]
- Terzidou, A.G.V.; Sorogas, N.; Pinakidou, F.; Paloura, E.C.; Arvanitidis, J. The pressure-induced structural phase transition of fluorene studied by Raman spectroscopy. Vib. Spectrosc. 2021, 115, 103272. [Google Scholar] [CrossRef]
- Zhao, X.; Suo, T.; Mao, Q.; Zhao, Z.; Wang, S.; Wan, B.; Liu, J.; Zhang, L.; Liang, X.; Xu, A.; et al. Structure and piezochromism of chrysene at high pressures. Dyes Pigm. 2024, 227, 112161. [Google Scholar] [CrossRef]
- Siavou, M.-T.; Siapaka, K.; Karabinaki, O.; Christofilos, D.; Arvanitidis, J. The high-pressure response of 9,9′-spirobifluorene studied by Raman spectroscopy. Molecules 2025, 30, 638. [Google Scholar] [CrossRef]
- Bruker Analytical X-ray Systems, Inc. Apex2, Version 2 User Manual; M86-E01078; Bruker: Madison, WI, USA, 2006. [Google Scholar]
- Siemens Industrial Automation Inc. SADABS: Area-Detector Absorption Correction; Siemens Industrial Automation, Inc.: Madison, WI, USA, 1996. [Google Scholar]
- Palatinus, L.; Chapuis, G. SUPERFLIP—A computer program for the solution of crystal structures by charge flipping in arbitrary dimensions. J. Appl. Crystallogr. 2007, 40, 786–790. [Google Scholar] [CrossRef]
- Betteridge, P.W.; Carruthers, J.R.; Cooper, R.I.; Prout, K.; Watkin, D.J. CRYSTALS version 12: Software for guided crystal structure analysis. J. Appl. Crystallogr. 2003, 36, 1487. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision C.02; Gaussian, Inc.: Wallingford, CT, USA, 2019. [Google Scholar]
- Hariharan, P.C.; Pople, J.A. The influence of polarization functions on molecular orbital hydrogenation energies. Theor. Chim. Acta 1973, 28, 213–222. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D. A new mixing of Hartree-Fock and local density-functional theories. J. Chem. Phys. 1993, 98, 1372–1377. [Google Scholar] [CrossRef]
- Onchoke, K.K.; Parks, M. Experimental and theoretical study of vibrational spectra of 3-nitrofluoranthene. J. Mol. Struct. 2011, 999, 22–28. [Google Scholar] [CrossRef]
- Onchoke, K.K.; Ojeda, J.J. A DFT study of vibrational spectra and mutagenicity predictions of mononitrated fluoranthenes. J. Mol. Struct. 2013, 33, 473–500. [Google Scholar] [CrossRef]
- Jayaraman, A. Ultrahigh pressures. Rev. Sci. Instrum. 1986, 57, 1013–1031. [Google Scholar] [CrossRef]
- Dunstan, D.J. Theory of the gasket in diamond anvil high-pressure cells. Rev. Sci. Instrum. 1989, 60, 3789–3795. [Google Scholar] [CrossRef]
- Mao, H.K.; Xu, J.; Bell, P.M. Calibration of the ruby pressure gauge to 800 kbar under quasi-hydrostatic conditions. J. Geophys. Res. 1986, 91, 4673–4676. [Google Scholar] [CrossRef]
- Syassen, K. Ruby under pressure. High Press. Res. 2008, 28, 75–126. [Google Scholar] [CrossRef]
- Osakabe, T.; Kakurai, K. Feasibility tests on pressure-transmitting media for single-crystal magnetic neutron diffraction under high pressure. Jpn. J. Appl. Phys. 2008, 47, 6544–6547. [Google Scholar] [CrossRef]
- Klotz, S.; Takemura, K.; Strassle, T.; Hansen, T. Freezing of glycerol-water mixtures under pressure. J. Phys. Condens. Matter 2012, 24, 325103. [Google Scholar] [CrossRef]
- Śmiszek-Lindert, W.; Michta, A.; Tyl, A.; Małecki, G.; Chełmecka, E.; Maślanka, S. X-ray, Hirshfeld surface analysis, spectroscopic and DFT studies of polycyclic aromatic hydrocarbons: Fluoranthene and acenaphthene. J. Serb. Chem. Soc. 2015, 80, 1489–1504. [Google Scholar] [CrossRef]
- Li, L.; Wang, H.; Wang, W.; Jin, W.J. Interactions between haloperfluorobenzenes and fluoranthene in luminescent cocrystals from π-hole⋯π to σ-hole⋯π bonds. CrystEngComm 2017, 19, 5058–5067. [Google Scholar] [CrossRef]
- Hu, R.; Lin, S.; Huang, H.; Xie, W.; Wang, M.; Li, R.; Tian, M.; Shuai, Z.; Wei, Y. A family of planar luminogens with active photoluminescence in both dispersion and aggregation states. ChemPhotoChem 2022, 6, e202200079. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Bauschlicher, C.W., Jr.; Ricca, A.; Boersma, C.; Allamandola, L.J. The NASA Ames PAH IR spectroscopic database: Computational version 3.00 with updated content and the introduction of multiple scaling factors. Astrophys. J. Suppl. Ser. 2018, 234, 32. [Google Scholar] [CrossRef]
- Rousseau, D.L.; Bauman, R.P.; Porto, S.P.S. Normal mode determination in crystals. J. Raman Spectrosc. 1981, 10, 253–290. [Google Scholar] [CrossRef]
- Likhacheva, A.Y.; Rashchenkoa, S.V.; Litasov, K.D. High-pressure structural properties of naphthalene. J. Appl. Crystallogr. 2014, 47, 984–991. [Google Scholar] [CrossRef]
- Heimel, G.; Hummer, K.; Ambrosh-Draxl, C.; Chunwachirasiri, W.; Winokur, M.J.; Hanfland, M.; Oehzelt, M.; Aichholzer, A.; Resel, R. Phase transition and electronic properties of fluorene: A joint experimental and theoretical high-pressure study. Phys. Rev. B 2006, 73, 024109. [Google Scholar] [CrossRef]
- Grüneisen, E. Handbuch der Physik; Springer: Berlin, Germany, 1926; Volume 10. [Google Scholar]
- Bridgman, P.W. Further rough compressions to 40,000 Kg/cm2, especially certain liquids. Proc. Am. Acad. Arts Sci. 1949, 77, 129–146. [Google Scholar] [CrossRef]
- Murnaghan, F.D. Finite deformations of an elastic solid. Am. J. Math. 1937, 59, 235–260. [Google Scholar] [CrossRef]
- Murnaghan, F.D. The compressibility of media under extreme pressures. Proc. Natl. Acad. Sci. USA 1944, 30, 244–247. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karabinaki, O.; Papastylianos, S.; Padrón, N.M.; Hatzidimitriou, A.; Christofilos, D.; Arvanitidis, J. Pressure Response of Crystalline Fluoranthene Probed by Raman Spectroscopy. Crystals 2025, 15, 697. https://doi.org/10.3390/cryst15080697
Karabinaki O, Papastylianos S, Padrón NM, Hatzidimitriou A, Christofilos D, Arvanitidis J. Pressure Response of Crystalline Fluoranthene Probed by Raman Spectroscopy. Crystals. 2025; 15(8):697. https://doi.org/10.3390/cryst15080697
Chicago/Turabian StyleKarabinaki, Olga, Stylianos Papastylianos, Nayra Machín Padrón, Antonios Hatzidimitriou, Dimitrios Christofilos, and John Arvanitidis. 2025. "Pressure Response of Crystalline Fluoranthene Probed by Raman Spectroscopy" Crystals 15, no. 8: 697. https://doi.org/10.3390/cryst15080697
APA StyleKarabinaki, O., Papastylianos, S., Padrón, N. M., Hatzidimitriou, A., Christofilos, D., & Arvanitidis, J. (2025). Pressure Response of Crystalline Fluoranthene Probed by Raman Spectroscopy. Crystals, 15(8), 697. https://doi.org/10.3390/cryst15080697






