Abstract
We simulate the dispersoid distribution within the Al matrix grains of an aluminum 6082 alloy by combining finite difference cell modeling with mean-field precipitation simulations. The results demonstrate that the initial as-cast microstructure and the heating rate during the ramp-up to the isothermal homogenization temperature are the most important factors governing the dispersoid particle distribution. The simulation results are validated by Electron Probe Microanalysis (EPMA) and Optical Microscopy on experimental run products. The results indicate that dispersoids can only achieve uniform distribution throughout the grain when the heating rate to the homogenization temperature is sufficiently slow.
1. Introduction
During the fabrication process of a wide variety of aluminum products, a fine and homogeneous distribution of small precipitates, referred to as dispersoids, is desired. The fine distribution of dispersoids has a significant, positive effect on the mechanical properties of the material, such as their role in preventing recrystallization during cold rolling and extrusion at elevated temperatures [1,2,3,4]. During the different stages of the processing of the 6xxx series Al alloys containing Mn, cubic α-Al15(Fe,Mn)3Si2 dispersoids act as preferential nucleation sites for both metastable (β′-Mg3Si1.67, B′-Al4Mg8Si7) and stable (β-Mg2Si) phases, involved in the hardening response of the material [5,6,7].
Dispersoids typically precipitate during the heating ramp to the homogenization temperature. The 6xxx series Al alloys usually contain small amounts of dispersoid-forming elements, such as Mn, Fe, and Cr. The supersaturation of these elements in the matrix after the casting leads to the formation of highly stable intermetallic phases inside the grains. The crystal structures of the dispersoids depend on the nominal alloy composition [8] and particularly on the Mn:Fe ratio [9]. In the Al 6082 alloy, which is relatively high-alloyed by Mn, cubic α-Al15(Fe,Mn)3Si2 dispersoids are predominantly stabilized [10,11,12].
A detailed analysis of the microstructure [13] revealed that dispersoids do not nucleate evenly throughout the grain. Two distinctive zones depleted of dispersoids are observed. One is located near the grain boundaries, which is known as the Dispersoid Free Zone (DFZ). A second area can be found in the center of the grains, sometimes referred to as the Coarse Dispersoid Zone (CDZ). In the CDZ, dispersoids are typically larger than in other domains of the grains and occur with a significantly lower number density. Both the CDZ and the DFZ depend on the heat treatment applied. Different heating rates or temperature profiles lead to different dispersoid distributions, as reported by the addition of a holding step to the heating process [13,14]. This paper aims to explain the thermodynamic reasons for the observed formation of the CDZ in the center of the grains, including experimental results and a computational analysis of the problem.
2. Experimental
EN-AW 6082 ingots with the nominal composition shown in Table 1 were prepared by the company partner, Neuman Aluminium, via direct chill casting. The samples were cut from the central region of the as-cast material. Using a Bähr 805 A/D dilatometer (TA Instruments, New Castle, DE , USA), four different heating rates from room temperature to 560 °C, which is a typical homogenization temperature for the processing of Al 6082 alloys, were applied: 0.01 K/s, 0.1 K/s, 1 K/s, and 10 K/s, with a holding time of 1 h at 560 °C, followed by rapid quenching. The heat treatments were performed under vacuum. To observe the intermetallic phases and their distribution across the grains, samples were polished and etched with a solution of 10% NaOH and 90% distilled water. The etching was performed for 75 s.

Table 1.
Chemical composition of the Al 6082 alloy in mass percent.
Electron probe microanalysis (EPMA) was performed on samples in their as-cast state and after reaching 300, 400, and 560 °C when heated at 0.01 K/s. These measurements were performed using a CAMECA SX Five Field Emission Gun Electron Microprobe (CAMECA, Gennevilliers, France) at the EPMA laboratory of the Core Facility Electron Beam Microanalysis, Faculty of Earth Sciences, Geography and Astronomy at the University of Vienna (AT). The instrument was operated at an acceleration voltage of 18 keV, a beam current of 62 nA, and a working distance of 10 mm.
3. Modeling
To perform a computational study with high predictive capacity on the dispersoid nucleation and their heterogeneous distribution inside the Al matrix grains, the underlying modeling of the simulation must take into account the relevant physical mechanisms at all stages of the process, from the initial as-cast condition, where microsegregation is of the utmost importance, to the fundamental laws for nucleation (Classical Nucleation Theory) and diffusion-mediated precipitate growth, including the thermodynamic CALPHAD description of all relevant phases present in the material [15].
Section 3.1 explains the definition of the simulation domain and how it is discretized to account for the initial chemical heterogeneity, with elements being unevenly distributed within the grains. Section 3.2, Section 3.3 and Section 3.4 discuss the thermodynamic essence of the nucleation process, starting with the Classical Nucleation Theory (CNT), followed by the treatment of the nucleation sites and the particular nucleation sequence in these alloys. The chapter concludes with the treatment of chemical gradients inside the grain. It is shown how CNT can provide a reasonable explanation on why α-Al15(Fe,Mn)3Si2 dispersoids can only distribute evenly throughout the grain when the heating rate to the homogenization temperature is sufficiently slow.
3.1. Domain Discretization
The typical microstructure after solidification is characterized by the relatively large primary phases located near the grain or dendrite boundaries of the Al matrix, and a non-uniform distribution of solute elements in the Al matrix grains, commonly known as microsegregation [16]. Microsegregation results from thermodynamically controlled minor element partitioning between the liquid and the Al-fcc matrix phase and its temperature dependence during the solidification stage.
The segregated as-cast state of an alloy can be approximated by the Scheil–Gulliver hypothesis [17,18,19], according to which the solidification of the material is treated as a sequential concatenation of concentric layers (or shells) of newly formed solid. Each layer has the equilibrium concentration of solute elements given by the phase diagrams, with no diffusion allowed between the successive solid shells. This results in the widely described layered nature of the as-cast material [20]. Contrary to the solid portion, the Scheil–Gulliver hypothesis considers diffusion-mediated elemental redistribution to be fast enough in the liquid to assume instantaneous chemical homogenization and uniform composition of the liquid, which includes the solidification front. The Scheil–Gulliver hypothesis has been extensively employed to describe the inhomogeneous compositional nature of a wide variety of materials in their as-cast state [21,22,23,24,25].
The Scheil–Gulliver calculation can be used to obtain the theoretical element distribution in mass % in the Al-fcc matrix grains as a function of the liquid fraction, Fliquid. It is possible to estimate the element distribution within the grains by relating the amount of liquid remaining (Fliquid) in mol. % and the measured mean grain diameter once solidification is completed, as shown in Equation (1). The x coordinate has its origin at the hypothetical center of the Al matrix grain and its maximum (when the phase fraction of liquid approaches 0) at half of the average grain diameter , where the grain boundary is located. For the case under study, the mean grain diameter after solidification is approximately 120 μm.
Using the MatCalc software, version 6.05 [26], along with its thermodynamic and diffusion databases, mc_al.tdb [27] and mc_al.ddb [28] respectively, the primary phases formed during casting and their relative amounts are calculated with the Scheil–Gulliver module for the composition presented in Table 1. Results are shown in Figure 1a. The main primary intermetallic phase is the α-Al15(Fe,Mn)3Si2 phase. In lower amounts, the presence of silicon in its diamond crystal structure, Mg2Si, and β-Al4.5FeSi is also predicted in the as-cast microstructure. Similar results were obtained by [11,29].
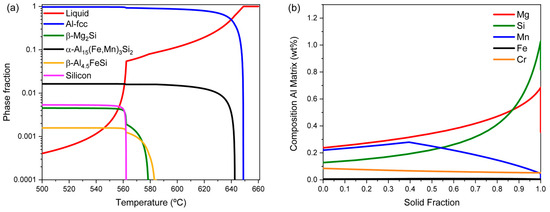
Figure 1.
Phase fraction as a function of temperature resulting from the Scheil–Gulliver calculation (a). Element distribution in the Al-fcc matrix as a function of fraction solidified (b).
As can be interpreted from the element distribution calculation shown in Figure 1b, there are significant Mg and Si concentration differences between the center of the grain or dendrite arm, representing the location of the first Al-fcc crystallization from the liquid, and the regions located closer to the boundary, which correspond to the stage when the solid fraction approaches 1, i.e., where the latest portion of the solid is formed. As explained in the following paragraphs, the concentration gradients of the solute elements within the Al-fcc matrix grains (microsegregation) are responsible for the heterogeneous distribution of precipitates formed during homogenization.
To establish a reasonable computational study for the highly heterogeneous element distribution present within the microstructure, the simulation domain is treated as a linear 1D geometrical setup, divided into 10 regions (“cells”). The simulation cells cover all domains from the center to the border of the grain, as schematized in Figure 2a. To account for the initial as-cast state, Mg and Si concentrations are assigned to each simulation cell following the Scheil–Gulliver calculation, shown as continuous dashed lines in Figure 2b. This simulation is carried out using the “Cell Simulation” module available in the MatCalc software, which has been introduced in [30]. A finite differences formulation solving Fick′s second law of diffusion is used to couple the transient multi-element diffusion between the discretized subdomains. The formulation is shown for one element in Equation (2).
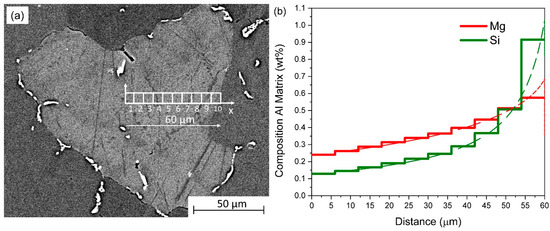
Figure 2.
As-cast state of the material. (a) Discretization of a grain into subdomains along the horizontal x-axis, extending from the hypothetical grain center (left) to its boundary (right). (b) Initial Mg and Si concentrations of the discretized cells are shown as solid lines, while the calculated Scheil–Gulliver concentration profiles are depicted with dashed lines. The horizontal x-axis represents the distance from the grain center to its boundary.
With cit being the element content of cell i at time t, and cit+ the concentration of the element at t + ∆t. Di,i+1 and Di,i-1 are the mean diffusion coefficients of cell i + 1 and cell i − 1, respectively. ∆x represents the width of one cell. A system containing n cells and j elements results in j linear equation systems, each with n equations and n variables.
3.2. Classical Nucleation Theory
The nucleation of a new crystalline phase within a solid can be addressed by means of the CNT [31]. In CNT, the exact location and time at which an individual particle forms cannot be determined, as the process is of stochastic nature. However, the rate of new stable nuclei in a volume under a given temperature and chemical condition can be calculated, giving rise to the fundamental parameter in precipitation kinetics, the nucleation rate, J (nuclei/s·m3) [31]. The equation describing the nucleation rate reads as follows:
The pre-exponential terms N0, Z, and β* represent the number of available nucleation sites, the Zeldovich factor, and the atomic attachment rate, respectively. Gc*, in J/atom, is the Gibbs energy of a cluster with critical size, which may be understood as the transition point between stable and unstable nuclei, kB is the Boltzmann constant, T is the absolute temperature, τ is the incubation time, and t is the time of the precipitation event. The effect of Gc* is particularly relevant for the nucleation rate, as a small variation in Gc* strongly affects the probability of nucleation events. To obtain an expression for Gc*, the energy required to form a nucleus, ∆Gnucl (J), can be split into a negative contribution, stemming from the driving force for the formation of a favorable phase, ∆Gvol, and a positive contribution, resulting from the creation of a new interface between the nucleating and parent phase, ∆Gsurf. For a spherical nucleus of radius ρ, ∆Gnucl is then given by the following:
where γ (J/m2) represents the interfacial energy, ∆Gelas (J/m3) is the elastic energy related to the misfit in crystal structure between precipitate and matrix, is the molar volume of the matrix phase (m3/mol), and dchem is the chemical driving force for nucleation (J/mol). This value can be directly calculated from the thermodynamic database.
In CNT, the Gibbs energy of the critical cluster, Gc*, is calculated as the maximum of ∆Gnucl in the ∆Gnucl vs. ρ curve by the following:
which results in the expression of the Gibbs energy of the critical cluster:
This states that the larger the chemical driving force for the nucleation of a phase, the lower the energy barrier required to form a stable nucleus.
3.3. Nucleation Sequence and Nucleation Sites
To perform a computational analysis with predictive capacity on the spatial distribution of α-Al15(Fe,Mn)3Si2 dispersoids, the simulation scheme must include the microsegregation and the sequence of the nucleation events. The complete sequence of precipitates forming in the Al-Mg-Si system has been extensively studied [32,33,34,35]. For the current analysis, metastable phases, such as Guinier–Preston zones and β″-Mg5Si6, nucleating and dissolving at temperatures lower than the appearance of dispersoids, are not considered, as they do not appear to contribute to their nucleation. Within the alloy composition range considered in this study, and based on Transmission Electron Microscopy images, the metastable β′-Mg3Si1.67 and B′-Al4Mg8Si7 phases are reported to nucleate during the heating stage of the homogenization treatment at a temperature of ~250 °C [5,6,10]. These precipitates play an essential role in the microstructure evolution since they act as preferential nucleation sites for dispersoids at temperatures of ~300–350 °C [5,8,36,37,38]. It should be noted that for a similar composition range, Lodgard et al. [10] reported the presence of a second intermediate phase nucleating in between β′-Mg3Si1.67 and the dispersoids, the “u-phase”. Due to the lack of unambiguous evidence, this additional transformation is not included in the present simulation, and β′ will be the term used to group and address the metastable phases leading to dispersoid nucleation.
A simplified schematic illustration of the dispersoid nucleation sequence, as inferred from previous microanalytical findings [5,8,10], is shown in Figure 3. Initially, as the temperature rises to T1, metastable β′ particles nucleate within the Al matrix grains. As the temperature increases further to the range at which dispersoids nucleate (T2), the dispersoids precipitate preferentially at the interfaces between the β′ and the Al matrix. Once the solvus of the metastable β′ particles is exceeded (T3), they dissolve while the dispersoids remain.
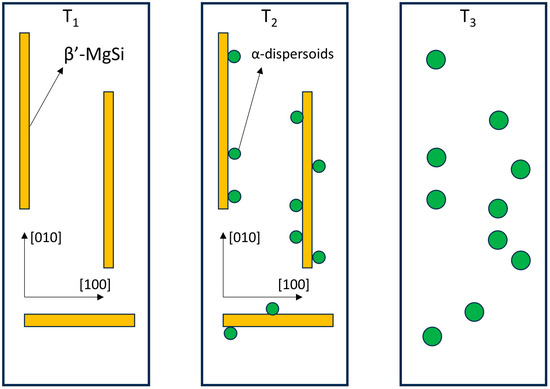
Figure 3.
Schematic illustration of the sequence leading to the heterogeneous nucleation of α-Al15(Fe,Mn)3Si2 dispersoids in 6xxx series Al alloys. T1 < T2 < T3. The indicated crystallographic directions refer to the lattice of the Al matrix phase.
The metastable MgSi-rich phases nucleating during the heating to homogenization temperature have a platelet morphology, as schematized in Figure 3, and are of a semi-coherent nature with the Al matrix, yielding crystallographic coherency in the <100> direction [33]. The nucleation of these phases occurs inside the grain, probably at dislocation cores or other defects in the matrix phase.
The simulation aims to link the nucleation events of metastable MgSi-rich phases and favored dispersoid formation via the “excess” availability of nucleation sites due to MgSi pre-nuclei. To achieve such a scenario in a physically sound simulation setup, the β′ phase nucleation in the bulk is initially computed, following CNT. Since these metastable precipitates are known to distribute evenly within the grain [8,10], the number of their possible nucleation sites, N, can be considered to be constant throughout the volume of the grain. To simplify the nucleation nature of β′, a homogeneous nucleation is assumed. Therefore, spatial variations in the nucleation rate of the β′ phase can only be explained by the value of Gc*, which depends on the chemical driving force (Gc* ∝ 1/dchem2); see Equation (6).
Subsequently, in the simulation, α-Al15(Fe,Mn)3Si2 dispersoids are set to nucleate on the surface of the metastable β′ phase. A mean-field model connecting the available nucleation sites for a precipitating phase to the presence of a precursor phase—a pre-nucleus—is included in MatCalc in the section of “nucleation on precipitate surface”, obtaining the parameter N = Nα in the formula of the nucleation rate (Equation (7)) as the number of atoms at the surface of the parent precipitate. The calculation of Nα in MatCalc has been addressed in our research group [39] as the ratio between the interfacial area of precursor phase Aint/β′ and the mean area of a single atom Aat.
It should be noted that Nα depends on time and temperature, but also on the spatial coordinate Nα = Nα(x), as the precursor phase will populate the inner and outer regions of the grain differently due to the differences in the respective chemical driving forces. At temperatures above the solvus of β′, and as it dissolves, dispersoid nucleation will stop, even at large driving forces, due to the absence of available nucleation sites (Nα → 0).
3.4. Analysis of the Interrelation Between Chemical Gradients and Precipitation
The impact of microsegregation on the nucleation of precipitates can be understood by examining the differences in the evaluated chemical driving forces between solute-enriched and solute-depleted zones within the grain (see Figure 4a,b). After solidification, areas of the microstructure closer to the grain boundaries contain Mg and Si atoms at higher concentrations than the more internal regions of the grains. The associated higher solute supersaturation translates into larger driving forces for the nucleation of metastable phases. The calculated gradient in the chemical driving force for the precipitation of α-Al15(Fe,Mn)3Si2 dispersoids and β′ at 200 and 300 °C is shown in Figure 4a and Figure 4b, respectively.
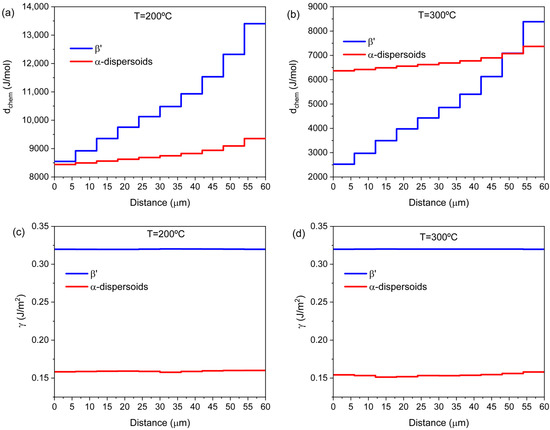
Figure 4.
Calculated chemical driving forces for precipitation of β′-MgSi and α-Al15(Fe,Mn)3Si2 dispersoids in the discretized domain at T = 200 °C (a) and T = 300 °C (b). Calculated interfacial energies with the Al-fcc matrix of β′-MgSi and α-Al15(Fe,Mn)3Si2 dispersoids at T = 200 °C (c) and T = 300 °C (d). The x-axis has its origin in the theoretical center of the grain and extends to its boundary.
The elastic strain energy (∆Gelas) always acts against the nucleation event [31]. For nucleation to occur, the driving force for the nuclei formation must be larger than the elastic strain energy (dchem/ʋα > ∆Gela). As a simplification, ∆Gelas is ignored in the analysis. Furthermore, it can be assumed that interfacial energies are largely independent of element distribution in the grain, as shown in Figure 4c,d, where interfacial energies for β′-MgSi and α-dispersoids are calculated at 200 and 300 °C. As a consequence, the ratio of critical nucleation energy between areas closer to the boundary, Gc*bound, and the center of the grain, Gc*center, can be approximated from Equation (6) as follows:
As shown in Figure 4a,b, upon temperature evolution, differences in Mg and Si concentration between the outer and inner regions of the grain translate into differences in β′ nucleation driving forces between and . Following Equation (8), the ratios in critical nucleation energy can be calculated as a first approximation by the following: .
Recalling the nucleation rate expression (Equation (5)) and assuming all factors multiplying the exponential term (N0, Z, and β*) remain constant throughout the grain, the ratio between the nucleation rate in the region close to the grain boundary and at the central area of the grain can be expressed as follows:
With a characteristic value of Gc* = 5 · 10−20 at 200 °C, the previous ratio in nucleation probability of metastable β′ between the internal and external domains of a grain can be estimated as approximately 4–5 orders of magnitude higher in the outer regions of the grain as compared to the inner zone, where the CDZ typically appears.
Mn is the slowest diffusing element of the microstructure. Therefore, its availability is the limiting factor for the nucleation and growth of α-dispersoids. Mn microsegregation resulting from the solidification of the material does not produce such sharp concentration gradients within the grain as in the case of Mg and Si, as seen in Figure 5. EPMA results indicate that Mn is evenly distributed in the dendrite arms, having a pronounced peak at the boundaries, where the large primary Mn-rich intermetallic particles are located. For simplicity, the Mn concentration is subsequently treated as a constant averaged value from the Scheil–Gulliver calculation.
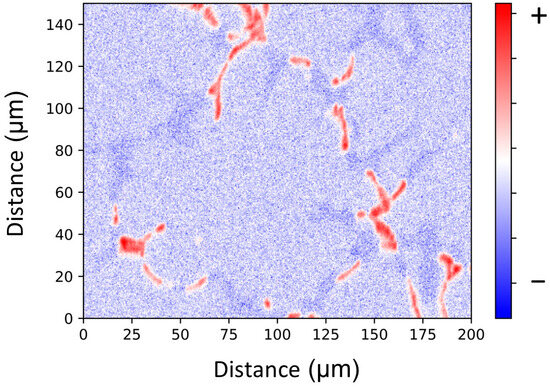
Figure 5.
EPMA analysis of the Mn distribution in the as-cast state.
Compared to metastable MgSi phases, the differences in driving force for the precipitation of dispersoids between the different regions within the grain are insignificant (Mn is not strongly segregated). Consequently, their associated nucleation barrier is similar between the central and outer areas of the grain. Added to the nucleation site availability, the ratio of dispersoid nucleation rate can be expressed as follows:
This results in a linear dependence of the nucleation rate ratio on the available nucleation sites.
4. Results and Discussion
4.1. Formation of Coarse Dispersoid Zones
The prediction of the effect of the heating rate on dispersoid nucleation is demonstrated in Figure 6, where etched samples are shown after heating to 560 °C at four different rates (0.01, 0.1, 1, and 10 K/s) and held at 560 °C for 1 h. For the slowest heating rate, 0.01 K/s, small regions of DFZ appear near the grain boundaries, where primary phases are prominent. At the same time, α-Al15(Fe,Mn)3Si2 dispersoids distribute evenly throughout the grain, and the CDZ is absent (Figure 6a,b). On the contrary, CDZ develops at faster heating rates and becomes more prominent at higher rates. In Figure 6c,d, at a heating rate of 0.1 K/s, the heterogeneous distribution of dispersoids is seen. Marked in red, a CDZ appears in the inner section of the grains. At 1 K/s, shown in Figure 6e,f, the area of the CDZ within the grain significantly increases, where there is an even more prominent effect at the highest heating rate (10 K/s), displayed in Figure 6g,h. The optical microscopy results suggest that a larger CDZ results from faster ramps to homogenization temperatures.


Figure 6.
Optical microscopy images showing the dispersoid distribution in samples that were heated with four different heating rates. No CDZ is observed at a heating rate of 0.01 K/s (a,b). CDZ appears at the grain centers after heating at 0.1 K/s (c,d), 1 K/s (e,f), and 10 K/s (g,h) heating rates and keeping the samples at 560 °C for 1 h.
4.2. Concentration Gradients
We hypothesize that the heterogeneous dispersoid distribution within the grain is directly related to the initial microsegregation. The variation in dispersoid distribution at different heating rates could be linked to changes in the extent of element diffusion under the various heating conditions. By this reasoning, concentration gradients would be effectively removed by diffusion at sufficiently low heating rates. A more even element distribution would then translate into a uniform nucleation of the initial β′ precursor phase and, subsequently, of the α-Al15(Fe,Mn)3Si2 dispersoids, hindering the formation of CDZs.
To test this conjecture, the current discretized setup is used to simulate the diffusion effect on concentration gradients. Initially, a diffusion calculation is performed in MatCalc from room temperature until the homogenization temperature of 560 °C at the slowest heating rate of 0.01 K/s. The results of element distribution at selected temperatures are shown in Figure 7.
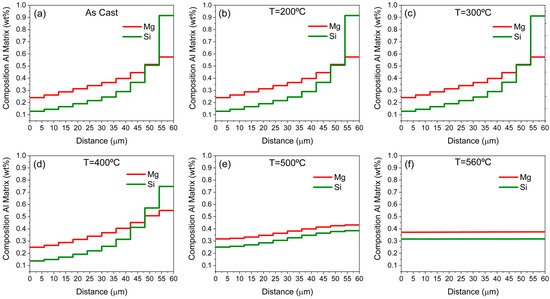
Figure 7.
Diffusion calculation on the discretized domain at different states during heating to the homogenization temperature at a rate of 0.01 K/s, (a) at the as-cast state, (b) at 200 °C, (c) at 300 °C, (d) at 400 °C, (e) at 500 °C, (f) at 560 °C.
As shown in Figure 7, only at temperatures higher than 400 °C, even for the slowest heating rate studied, is the diffusion of Mg and Si atoms from the more concentrated areas to the less concentrated ones appreciable. Diffusion results at higher heating rates are not included, as faster heating only results in lower overall element redistribution. It should be noted that the Mn evolution can be neglected due to its low segregation tendency and its slow diffusion. An estimation of the average distance an atom can travel at a given temperature is given by the relation:
where D is the diffusivity of the given element in the matrix, and t is the time. The diffusivity can be calculated as follows:
where D0 is the frequency factor, with unit m2/s, and QR is the activation energy, expressed in J/mol. Accepted values of D0 and QR for both Mg and Si can be retrieved from published diffusion databases. In MatCalc [28], these values are D0-Mg = 7.5 × 10−6 m2/s, QR-Mg = 115,000 J/mol, D0-Si = 3 × 10−5 m2/s, and QR-Si = 123,900 J/mol.
By heating the material at 350 °C for 1 h, the average length that Mg and Si atoms can move within the grain, according to Equation 11, is around 2.7 μm and 3.2 μm, respectively, a distance more than an order of magnitude lower than the mean grain radius of ~60 μm. This suggests that during the heating stage of the homogenization treatment, at temperatures where metastable phases nucleate and regardless of the heating rate, the atomic mobility is insufficient to level out the concentration gradients present in the grain. This can only happen at the prolonged holding stages at elevated temperatures: the average distance Mg and Si atoms can move, calculated after 1 h at 560 °C, results in values of 49.8 μm and 64.5 μm, respectively, in the same order of magnitude as the average grain radius.
EPMA results confirm that segregation of Mg and Si is still present at 300 and 400 °C during the heating stage of the homogenization treatment, as shown in Figure 8c–f, and it is only at higher temperatures that elements distribute evenly in the grain, as seen in Figure 8g,h. Due to its low mobility in the Al matrix, changes in Mn distribution from its initial state, shown in Figure 5, are not observed.
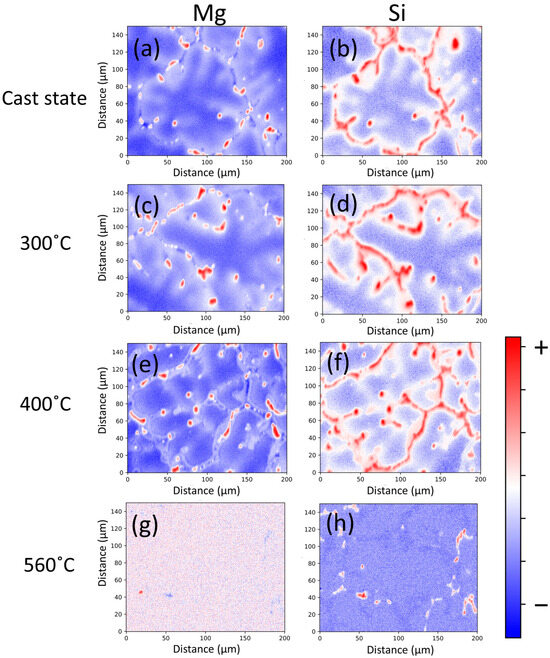
Figure 8.
EPMA results showing the distribution of Mg and Si atoms within the grain at various stages of the homogenization heating ramp. (a,b) correspond to the as-cast state. (c,d) associate with the grain at 300 °C; (e,f) at 400 °C; and (g,h) at 560 °C.
Chemical gradients translate into driving force gradients for the precipitation inside the grain. Due to the sparse mobility at temperatures where metastable phases nucleate, it has already been shown that the original compositional gradients are largely retained despite the large chemical potential gradients acting against them, and therefore, the evolution of the microstructure follows, regardless of the heating rate, the kinetic environment established by the initial element segregation.
The formation of the large areas of depleted and coarse dispersoid zones within the grain cannot be understood as a diffusion effect but rather as a situation where differences in the chemical driving forces for the nucleation of precursor β′ phase, and therefore in critical nucleation energy Gc*, scale exponentially in the nucleation rate formula that describes the probability of a single nucleation event. This results in several orders of magnitude of difference in probable nucleation events between areas near the boundary and the center of the grain, linearly determining the available nucleation sites for subsequent dispersoid nucleation.
Lower heating rates or isothermal steps at sufficiently high temperatures allow more time for nucleation, leveling out the effect of nucleation rate differences between zones depleted in Mg and Si, where the nucleation of metastable β′ is less likely, and zones with higher Mg and Si concentrations, which are more prone to the nucleation of metastable β′. At sufficiently low heating rates, metastable β′ particles may thus nucleate even in larger numbers and also in the less favorable zones for nucleation. At the same time, initial β′ nuclei formed near the boundaries of the grain grow (and later dissolve) upon heating. Assuming a temperature range for preferred β′ nucleation, ∆T, alloys heated at 0.01 K/s would have 103 more seconds to undergo particle generation compared to a material heated at 10 K/s, which would be enough time to compensate for the calculated differences in nucleation rates within the grain.
4.3. Simulation
The simulation results are shown in Figure 9. After one hour at 560 °C, differences in dispersoid precipitation for the four heating rates studied can be expressed in terms of the Mn content of the Al matrix, predicted phase fraction, calculated number densities, and remaining driving force for α-Al15(Fe,Mn)3Si2 nucleation. The evolution of Mn concentration in the Al matrix depends indirectly on the heating rate and the associated dispersoid evolution. Supersaturated Mn from the casting process is consumed by the formation but mainly by the growth of dispersoids, as their growth potential will be higher at lower heating rates. Mn supersaturation is entirely eliminated throughout the entire grain at 0.01 K/s heating rate, while Mn remains supersaturated in the inner regions of the grain for the faster heating rates, as shown in Figure 9a, the latter being associated with incomplete dispersoid nucleation.
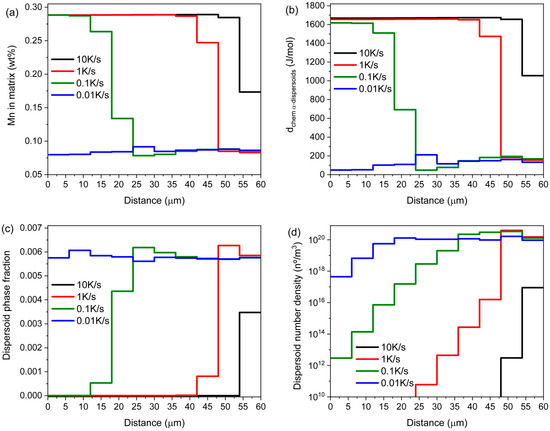
Figure 9.
Simulation results showing (a) Mn dissolved in the Al matrix as solid solution, (b) driving force for α-Al15(Fe,Mn)3Si2 nucleation, (c) α-Al15(Fe,Mn)3Si2 dispersoids phase fraction, (d) and α-Al15(Fe,Mn)3Si2 number densities as function of the spatial coordinate of the grain for four different heating rates.
The nucleation of dispersoids is expected to be completed when, after the heat treatment, the remaining driving force for their formation is close to zero, i.e., it is too low to enable any further nucleation event in all grain regions. It is seen in Figure 9b that this is only achieved at the lowest heating rate, while large driving forces for the nucleation of dispersoid remain present in the inner regions of the grain, reaching broader areas at higher heating rates, as exemplified in the 10 K/s heating instance.
Figure 9c,d show the calculated dispersoid phase fraction and number density after the heat treatments. For the lowest heating rate, the variation in the dispersoid fraction is small throughout the grain, which is supported by the experimental evidence shown in Figure 6a,b. Number densities calculated for a heating rate of 0.01 K/s vary from 1018 n°/m3 in the central domain to 1020 n°/m3 in the outer regions. Compared to published data by [40], for an Al 6082 alloy, density values after a homogenization treatment at a slightly higher temperature of 570 °C and 2 h were approximately 1012 n°/m2. Assuming the characteristic dimension of dispersoids to be lc ≈ 100 nm, the measured number densities were in the range of 1019 n°/m3. At higher heating rates, the dispersoid number density and phase fraction in the inner regions of the grains tend to zero, demonstrating the formation of the experimentally observed CDZ (Figure 6c–h).
5. Summary
The heating rate effect on the evolution of the spatial distribution of α-Al15(Fe,Mn)3Si2 dispersoid precipitation during the heating of an Al 6082 alloy from the as-cast state at room temperature to the homogenization temperature was studied, combining experiments and thermokinetic modeling. The experiments show that after relatively rapid heating at heating rates of 0.1 K/s to 10 K/s, dispersoid particles are unevenly distributed within the Al matrix grains, typically showing a Coarse Dispersoid Zone (CDZ) in the internal regions of the grains. Only after comparatively slow heating at 0.01 K/s is a nearly uniform distribution of dispersoid particles is obtained. Both experimental and computational results point to the initial concentration gradients of solute Mg and Si within the Al matrix grains (microsegregation) attained during the casting as the main cause for the heterogeneous dispersoid distribution after rapid heating. Element diffusion is insufficient to eliminate the initial solute concentration differences during heating to the temperatures where dispersoid nucleation occurs. The resulting differences in the driving forces for the nucleation of the intermediate β′ phase between the inner and outer areas of the grain lead to the observed heterogeneous dispersoid distribution. Only at the low heating rate of 0.01 K/s is there enough time available in the relevant temperature range to allow for the sufficient nucleation of the intermediate β′ phase, which largely compensates for the chemically induced nucleation rate differences and results in a more homogeneous dispersoid distribution throughout the Al matrix grains.
Author Contributions
Conceptualization, N.G.A.; methodology, N.G.A., R.S., R.A. and E.P.-K.; software, N.G.A.; investigation, N.G.A., R.S., R.A. and E.P.-K.; writing—original draft preparation, N.G.A.; writing—review and editing, N.G.A., R.S., R.A. and E.P.-K.; visualization, N.G.A.; supervision, E.P.-K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Christian Doppler Forschungsgesellschaft in the framework of the CD-Laboratory of Interfaces and Precipitation Engineering (CDL-IPE).
Data Availability Statement
Data will be made available on request.
Acknowledgments
The financial support from the Austrian Federal Ministry for Digital and Economic Affairs and the National Foundation for Research, Technology, and Development is gratefully acknowledged. The authors acknowledge TU Wien Bibliothek for financial support through its Open Access Funding Programme. The authors gratefully acknowledge the provision of sample material by Neuman Aluminium.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study, in the collection, analysis, or interpretation of data, in the writing of the manuscript, or in the decision to publish the results.
References
- Zhang, G.W.; Nagaumi, H.; Han, Y.; Xu, Y.; Parish, C.M.; Zhai, T.G. Effects of Mn and Cr additions on the recrystallization behavior of Al-Mg-Si-Cu alloys. Mater. Sci. Forum 2017, 877, 172–179. [Google Scholar] [CrossRef]
- Dorward, R.C.; Bouvier, C. A rationalization of factors affecting strength, ductility and toughness of AA6061-type Al-Mg-Si-(Cu) alloys. Mater. Sci. Eng. A 1998, 254, 33–44. [Google Scholar] [CrossRef]
- Arnoldt, A.R.; Schiffl, A.; Höppel, H.W.; Österreicher, J.A. Influence of different homogenization heat treatments on the microstructure and hot flow stress of the aluminum alloy AA6082. Mater. Charact. 2022, 191, 112129. [Google Scholar] [CrossRef]
- Polmear, I.; St. John, D.; Nie, J.F.; Qian, M. Light Alloys: Metallurgy of the Light Metals, 5th ed.; Butterworth-Heinemann: Oxford, UK, 2017; pp. 1–525. [Google Scholar]
- García Arango, N.; Kahlenberg, R.; Schuster, R.; Miesenberger, B.; Maawad, E.; Wojcik, T.; Povoden-Karadeniz, E. In-situ Analysis of EN-AW 6082 during Homogenization. Soc. Sci. Res. Netw. 2025. [Google Scholar] [CrossRef]
- Milkereit, B.; Starink, M.J.; Rometsch, P.A.; Schick, C.; Kessler, O. Review of the quench sensitivity of aluminium alloys: Analysis of the kinetics and nature of quench-induced precipitation. Materials 2019, 12, 4083. [Google Scholar] [CrossRef] [PubMed]
- Kahlenberg, R.; Wojcik, T.; Falkinger, G.; Krejci, A.L.; Milkereit, B.; Kozeschnik, E. On the precipitation mechanisms of β-Mg2Si during continuous heating of AA6061. Acta Mater. 2023, 261, 119345. [Google Scholar] [CrossRef]
- Farh, H.; Djemmal, K.; Guemini, R.; Serradj, F. Nucleation of dispersoids study in some Al-Mg-Si alloys. Ann. Chim. Sci. Matér. 2010, 35, 283–289. [Google Scholar] [CrossRef]
- Becker, H.; Bergh, T.; Vullum, P.E.; Leineweber, A.; Li, Y. Effect of Mn and cooling rates on α-, β- and δ-Al–Fe–Si intermetallic phase formation in a secondary Al–Si alloy. Materialia 2019, 5, 100198. [Google Scholar] [CrossRef]
- Lodgaard, L.; Ryum, N. Precipitation of dispersoids containing Mn and/or Cr in Al-Mg-Si alloys. Mater. Sci. Eng. A 2000, 283, 144–152. [Google Scholar] [CrossRef]
- Mrówka-Nowotnik, G.; Sieniawski, J.; Wierzbinska, M. Intermetallic phase particles in 6082 aluminium alloy. Arch. Mater. Sci. Eng. 2007, 28, 69–76. [Google Scholar]
- Davignon, G.; Serneels, A.; Verlinden, B.; Delaey, L. An isothermal section at 550 °C in the Al-rich corner of the Al-Fe-Mn-Si system. Metall. Mater. Trans. A 1996, 27, 3357–3361. [Google Scholar] [CrossRef]
- Lodgaard, L.; Ryum, N. Distribution of Mn- and Cr-containing dispersoids in Al-Mg-Si-alloys. Mater. Sci. Forum 2000, 331–337, 945–950. [Google Scholar] [CrossRef]
- Li, Z.; Qin, J.; Zhang, H.; Wang, X.; Zhang, B.; Nagaumi, H. Improved distribution and uniformity of α-Al(Mn,Cr)Si dispersoids in Al-Mg-Si-Cu-Mn (6xxx) alloys by two-step homogenization. Metall. Mater. Trans. A 2021, 52, 3204–3220. [Google Scholar] [CrossRef]
- Kozeschnik, E. Modeling Solid-State Precipitation; Momentum Press: New York, NY, USA, 2013. [Google Scholar]
- Ohno, M.; Yamashita, M.; Matsuura, K. Importance of microstructural evolution on prediction accuracy of microsegregation in Al-Cu and Fe-Mn alloys. Int. J. Heat Mass Transf. 2019, 133, 1120–1128. [Google Scholar] [CrossRef]
- Scheil, E. Bemerkungen zur Schichtkristallbildung. Int. J. Mater. Res. 1942, 34, 70–72. [Google Scholar] [CrossRef]
- Gulliver, G.H. The quantitative effect of rapid cooling upon the constitution of binary alloys. J. Inst. Met. 1913, 9, 120–157. [Google Scholar]
- Glicksman, M.E. Principles of Solidification: An Introduction to Modern Casting and Crystal Growth Concepts; Springer: New York, NY, USA, 2011. [Google Scholar]
- Schaffnit, P.; Stallybrass, C.; Konrad, J.; Stein, F.; Weinberg, M. A Scheil-Gulliver model dedicated to the solidification of steel. Calphad 2015, 48, 184–188. [Google Scholar] [CrossRef]
- Samaras, S.N.; Haidemenopoulos, G.N. Modelling of microsegregation and homogenization of 6061 extrudable Al-alloy. J. Mater. Process. Technol. 2007, 194, 63–73. [Google Scholar] [CrossRef]
- Basak, C.B.; Krishnan, M. Applicability of Scheil-Gulliver solidification model in real alloy: A case study with Cu-9wt%Ni-6wt%Sn alloy. Philos. Mag. Lett. 2015, 95, 376–383. [Google Scholar] [CrossRef]
- Sarafoglou, P.I.; Serafeim, A.; Fanikos, I.A.; Aristeidakis, J.S.; Haidemenopoulos, G.N. Modeling of microsegregation and homogenization of 6xxx Al-alloys including precipitation and strengthening during homogenization cooling. Materials 2019, 12, 1421. [Google Scholar] [CrossRef]
- Cai, M.; Robson, J.D.; Lorimer, G.W. Simulation and control of dispersoids and dispersoid-free zones during homogenizing an AlMgSi alloy. Scr. Mater. 2007, 57, 603–606. [Google Scholar] [CrossRef]
- Malakhov, D.V.; Panahi, D.; Gallerneault, M. On the formation of intermetallics in rapidly solidifying Al-Fe-Si alloys. Calphad 2010, 34, 159–166. [Google Scholar] [CrossRef]
- Kozeschnik, E.; MatCalc. Solid State and Precipitation Kinetics Simulation Software. Available online: http://www.matcalc.at (accessed on 10 June 2025).
- Institute of Materials Science and Technology, TU Wien. Open-License Multi-Component MatCalc Thermodynamic Database mc_al Version 2.036. Vienna. Available online: https://www.matcalc.at/index.php/databases/open-databases (accessed on 10 June 2025).
- Institute of Materials Science and Technology, TU Wien. Open-License Multi-Component MatCalc Diffusion Mobilities Database mc_al Version 2.008. Vienna. Available online: https://www.matcalc.at/index.php/databases/open-databases (accessed on 10 June 2025).
- Sarafoglou, P.I.; Haidemenopoulos, G.N. Phase fraction mapping in the ascast microstructure of extrudable 6xxx aluminum alloys. Int. J. Mater. Res. 2014, 105, 1202–1209. [Google Scholar] [CrossRef]
- Retzl, P.; Zamberger, S.; Kozeschnik, E. Computational analysis of austenite film thickness and C-redistribution in carbide-free bainite. Mater. Res. Express 2021, 8, 7. [Google Scholar] [CrossRef]
- Christian, J.W. The Classical Theory of Nucleation. In The Theory of Transformations in Metals and Alloys; Springer: Pergamon, Turkey, 2002; Chapter 10; pp. 422–479. [Google Scholar]
- Feufel, H.; Gödecke, T.; Lukas, H.L.; Sommer, F. Investigation of the Al-Mg-Si system by experiments and thermodynamic calculations. J. Alloys Compd. 1997, 247, 31–42. [Google Scholar] [CrossRef]
- Matsuda, K.; Sakaguchi, Y.; Miyata, Y.; Sato, T.; Kamio, A.; Ikeno, S. Precipitation sequence of various kinds of metastable phases in Al-1.0mass% Mg2Si-0.4mass% Si alloy. J. Mater. Sci. 2000, 35, 179–189. [Google Scholar] [CrossRef]
- Marioara, C.D.; Andersen, S.J.; Zandbergen, H.W.; Holmestad, R. The Influence of Alloy Composition on Precipitates of the Al-Mg-Si System. Metall. Mater. Trans. A 2005, 36, 691–702. [Google Scholar]
- Povoden-Karadeniz, E.; Lang, P.; Warczok, P.; Falahati, A.; Jun, W.; Kozeschnik, E. CALPHAD modeling of metastable phases in the Al-Mg-Si system. CALPHAD 2013, 43, 94–104. [Google Scholar] [CrossRef]
- Hu, R.; Ogura, T.; Tezuka, H.; Sato, T.; Liu, Q. Dispersoid formation and recrystallization behavior in an Al-Mg-Si-Mn alloy. J. Mater. Sci. Technol. 2010, 26, 237–243. [Google Scholar] [CrossRef]
- Li, Y.J.; Arnberg, L. Quantitative study on the precipitation behavior of dispersoids in DC-cast AA3003 alloy during heating and homogenization. Acta Mater. 2003, 51, 3415–3428. [Google Scholar] [CrossRef]
- Kemsies, R.H.; Milkereit, B.; Wenner, S.; Holmestad, R.; Kessler, O. In situ DSC investigation into the kinetics and microstructure of dispersoid formation in Al-Mn-Fe-Si(-Mg) alloys. Mater. Des. 2018, 146, 96–107. [Google Scholar] [CrossRef]
- Sobotka, E.; Kreyca, J.; Fuchs, N.; Wojcik, T.; Kozeschnik, E.; Povoden-Karadeniz, E. The Role of MX Carbonitrides for the Particle-Stimulated Nucleation of Ferrite in Microalloyed Steel. Metall. Mater. Trans. A 2023, 54, 2903–2923. [Google Scholar] [CrossRef]
- Strobel, K.; Easton, M.A.; Sweet, L.; Couper, M.J.; Nie, J.F. Relating quench sensitivity to microstructure in 6000 series aluminium alloys. Mater. Trans. 2011, 52, 914–919. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).