Multiple-Q States in Bilayer Triangular-Lattice Systems with Bond-Dependent Anisotropic Interaction
Abstract
1. Introduction
2. Model and Method
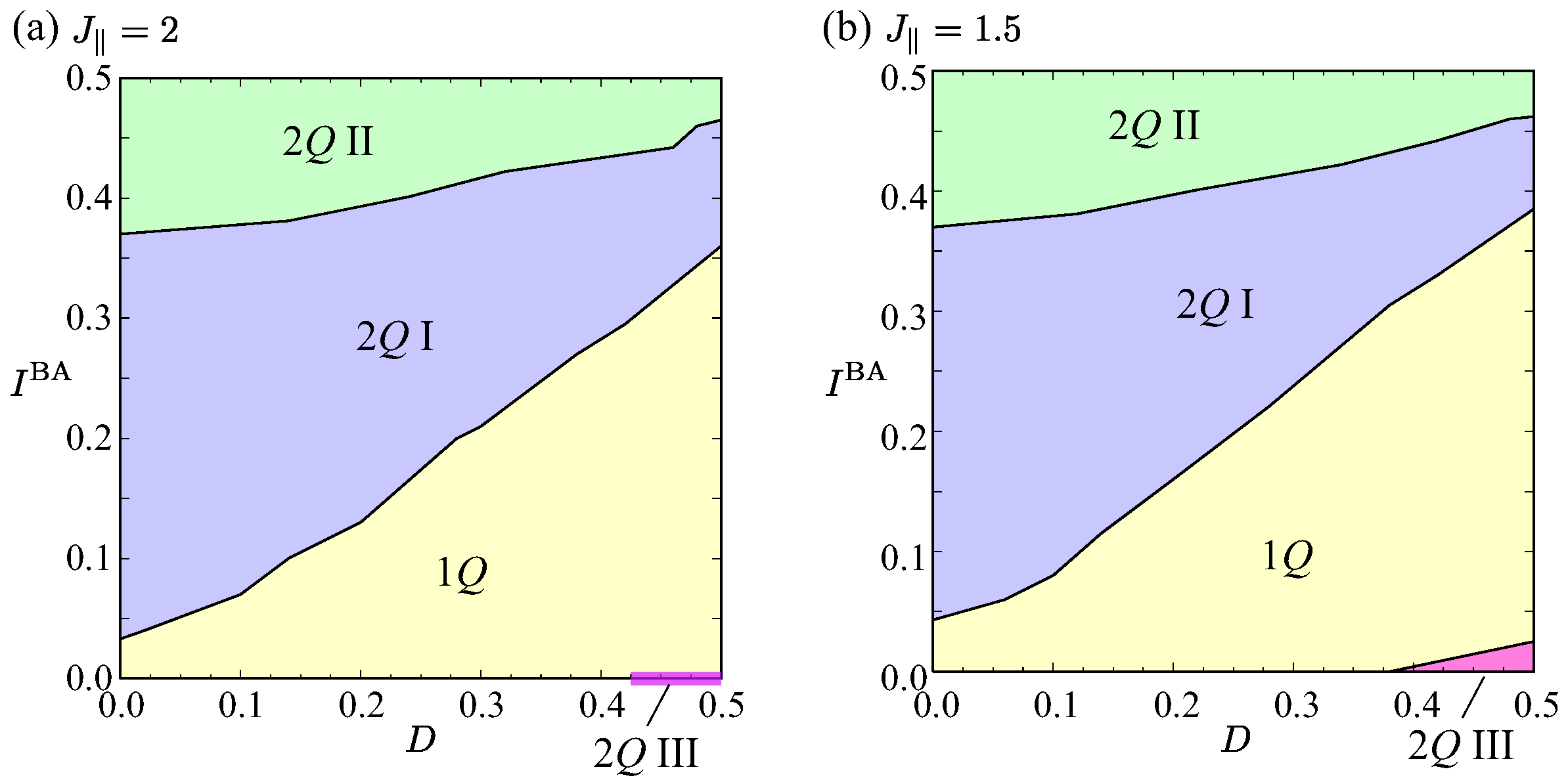
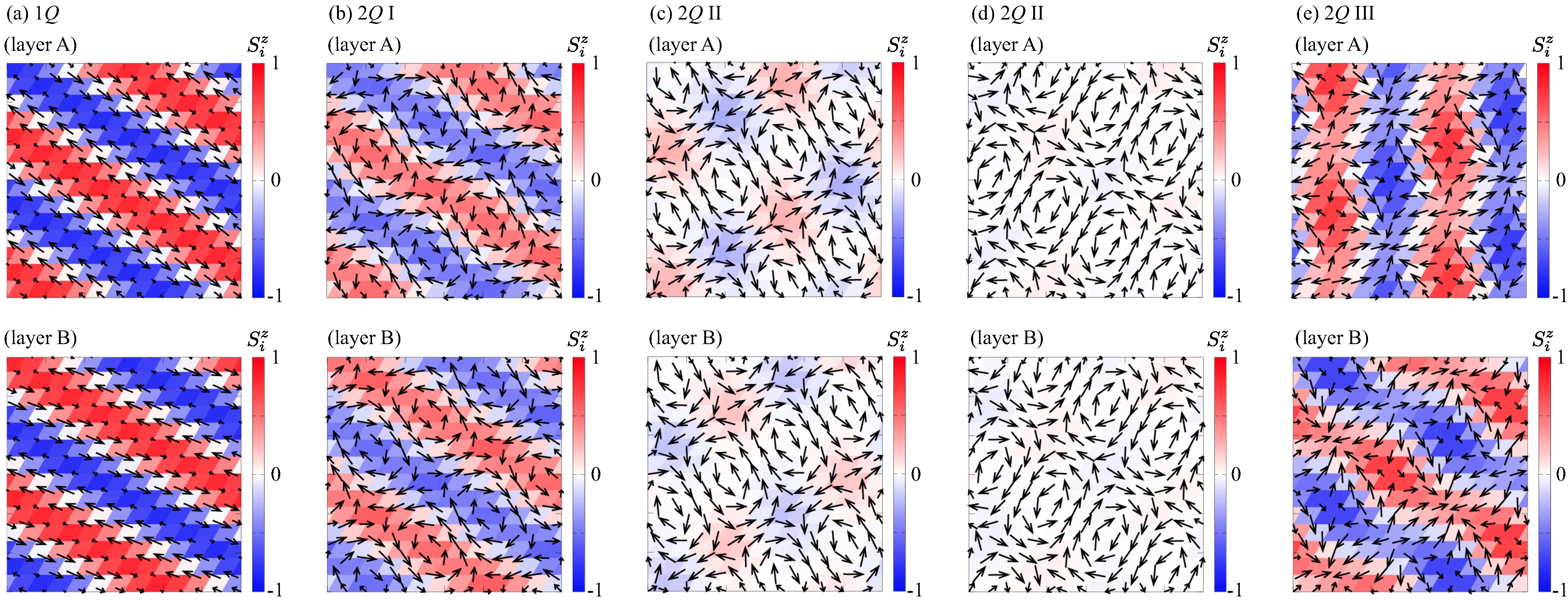
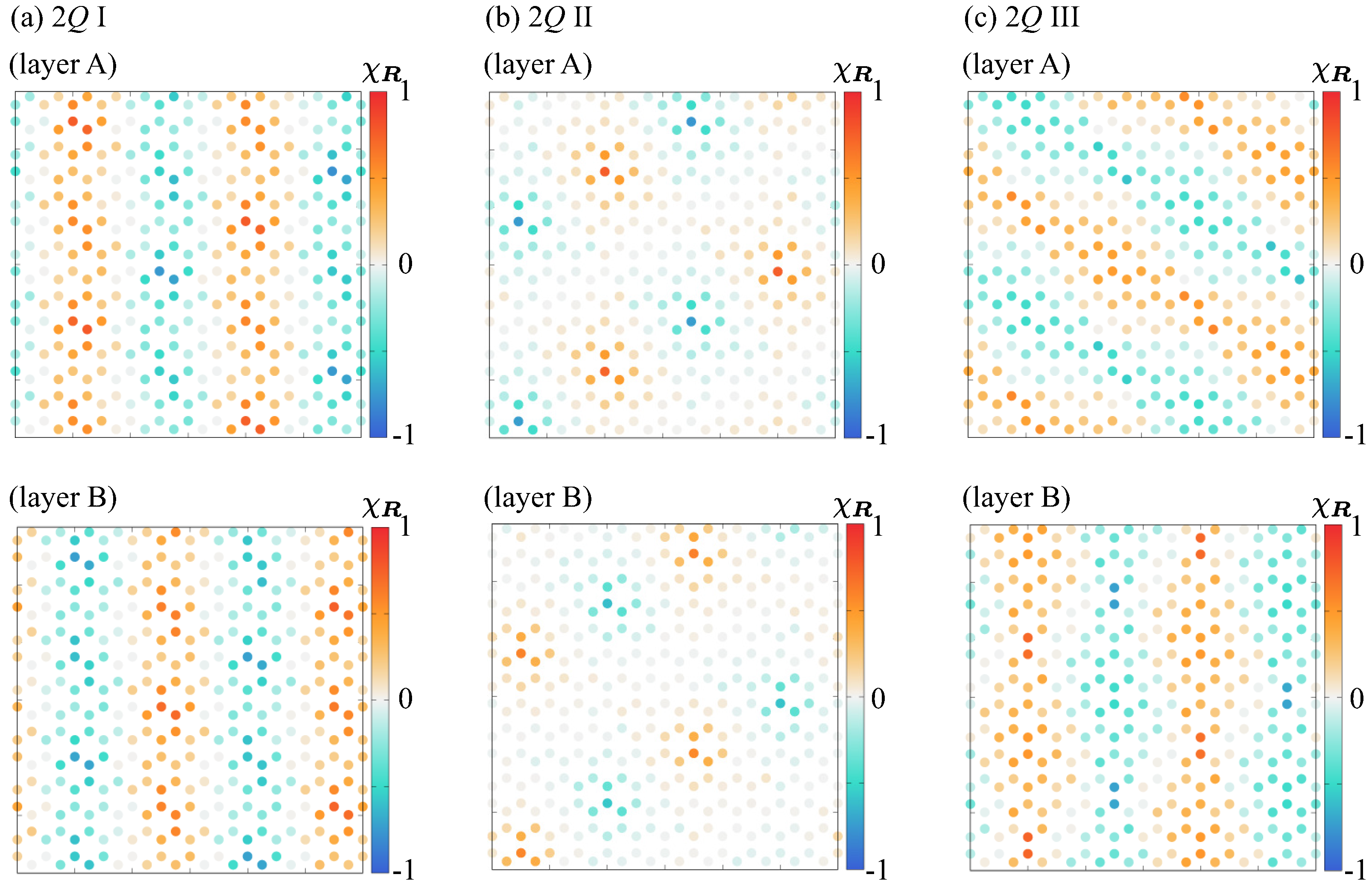
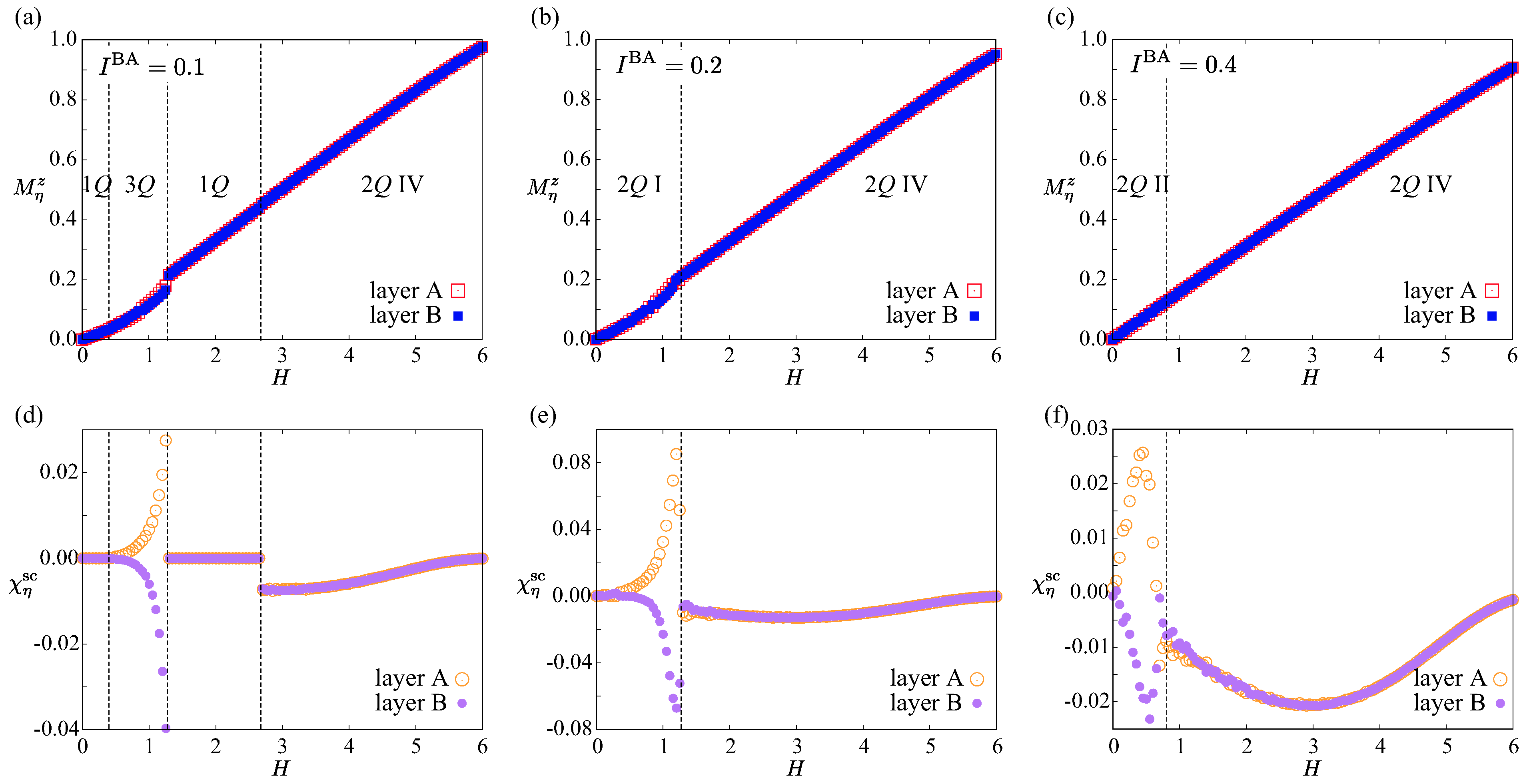
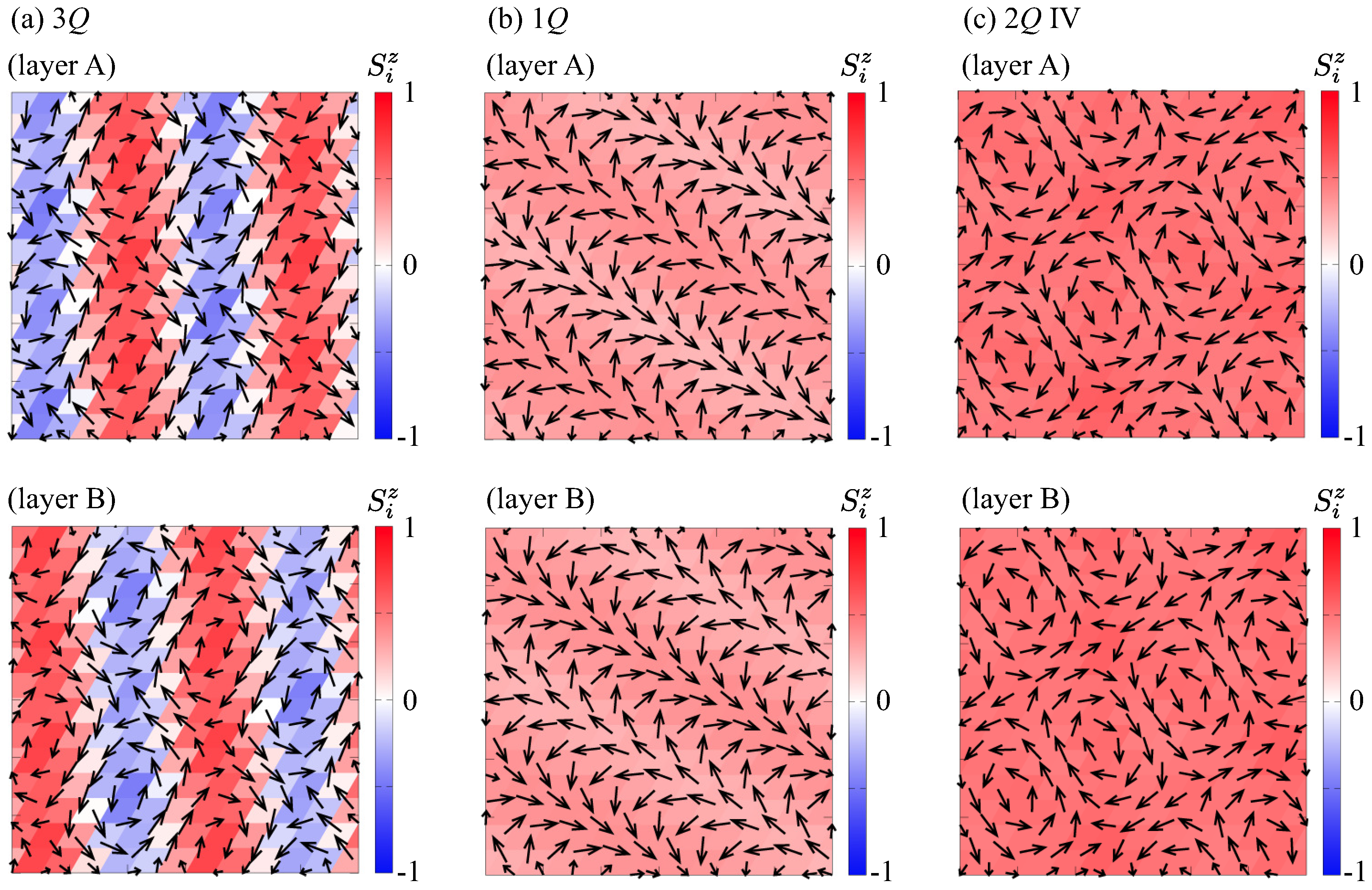
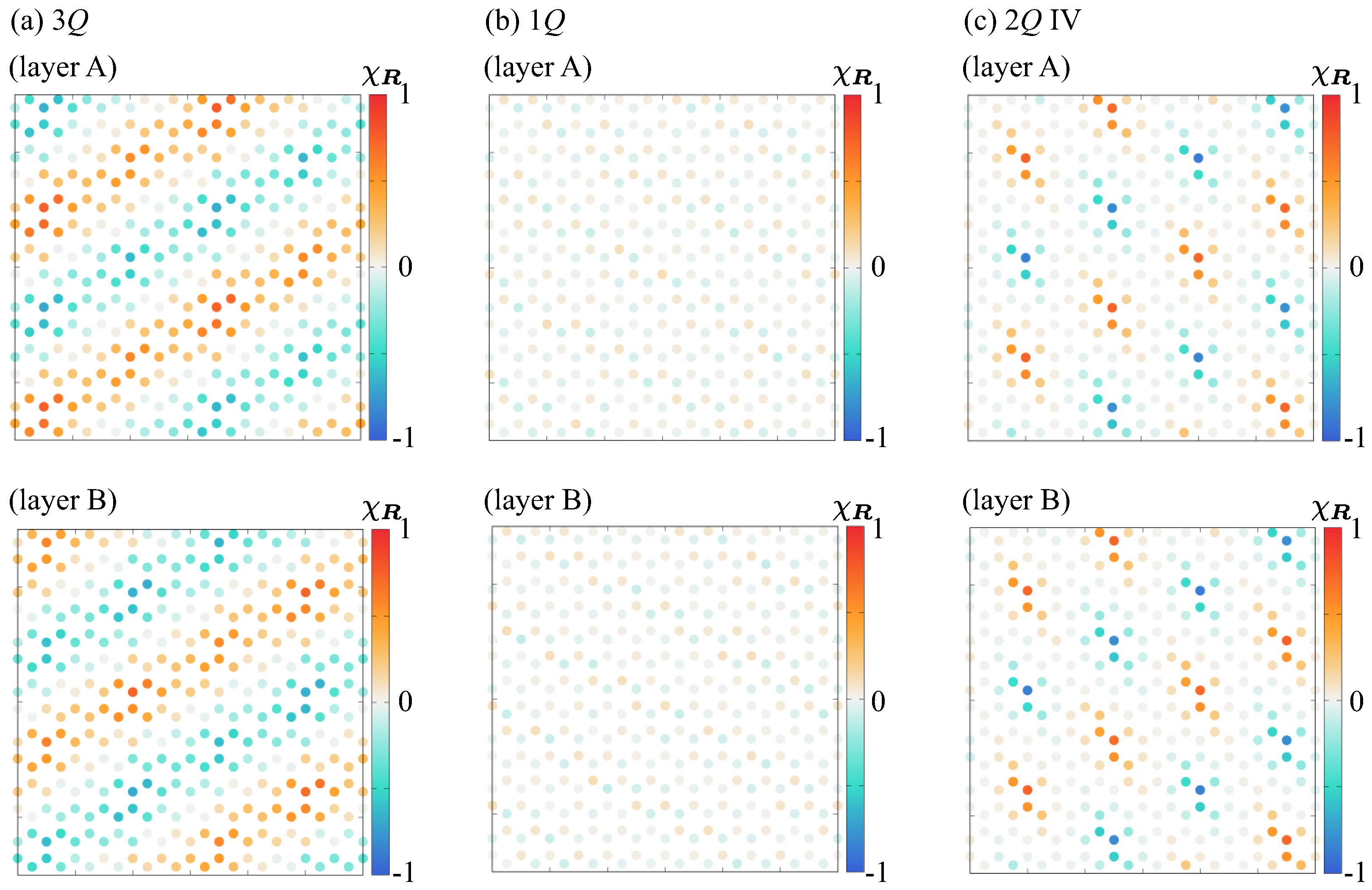
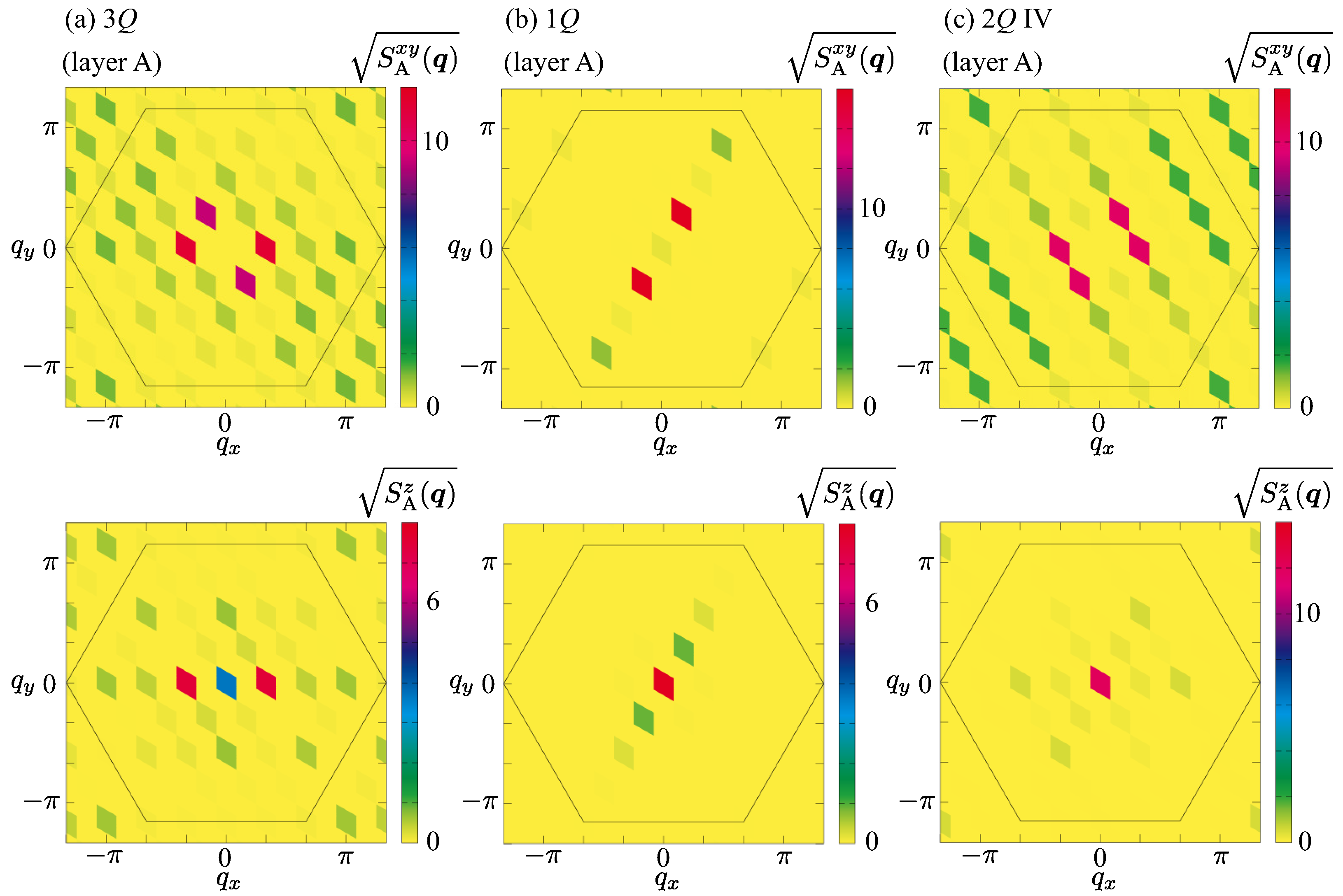
3. Results
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bak, P.; Lebech, B. “Triple-q” Modulated Magnetic Structure and Critical Behavior of Neodymium. Phys. Rev. Lett. 1978, 40, 800–803. [Google Scholar] [CrossRef]
- McEwen, K.A.; Walker, M.B. Free-energy analysis of the single-q and double-q magnetic structures of neodymium. Phys. Rev. B 1986, 34, 1781–1783. [Google Scholar] [CrossRef] [PubMed]
- Zochowski, S.; McEwen, K. Thermal expansion study of the magnetic phase diagram of neodymium. J. Magn. Magn. Mater. 1986, 54, 515–516. [Google Scholar] [CrossRef]
- Forgan, E.; Rainford, B.; Lee, S.; Abell, J.; Bi, Y. The magnetic structure of CeAl2 is a non-chiral spiral. J. Phys. Condens. Matter 1990, 2, 10211. [Google Scholar] [CrossRef]
- Longfield, M.J.; Paixão, J.A.; Bernhoeft, N.; Lander, G.H. Resonant x-ray scattering from multi-k magnetic structures. Phys. Rev. B 2002, 66, 054417. [Google Scholar] [CrossRef]
- Bernhoeft, N.; Paixão, J.A.; Detlefs, C.; Wilkins, S.B.; Javorský, P.; Blackburn, E.; Lander, G.H. Resonant x-ray scattering from UAs0.8Se0.2: Multi-k configurations. Phys. Rev. B 2004, 69, 174415. [Google Scholar] [CrossRef]
- Stewart, J.; Ehlers, G.; Wills, A.; Bramwell, S.T.; Gardner, J. Phase transitions, partial disorder and multi-k structures in Gd2Ti2O7. J. Phys. Condens. Matter 2004, 16, L321. [Google Scholar] [CrossRef]
- Watson, D.; Forgan, E.M.; Nuttall, W.J.; Stirling, W.G.; Fort, D. High-resolution magnetic x-ray diffraction from neodymium. Phys. Rev. B 1996, 53, 726–730. [Google Scholar] [CrossRef] [PubMed]
- Harris, A.B.; Schweizer, J. Theoretical analysis of the double-q magnetic structure of CeAl2. Phys. Rev. B 2006, 74, 134411. [Google Scholar] [CrossRef]
- Martin, I.; Batista, C.D. Itinerant Electron-Driven Chiral Magnetic Ordering and Spontaneous Quantum Hall Effect in Triangular Lattice Models. Phys. Rev. Lett. 2008, 101, 156402. [Google Scholar] [CrossRef] [PubMed]
- Chern, G.W. Noncoplanar Magnetic Ordering Driven by Itinerant Electrons on the Pyrochlore Lattice. Phys. Rev. Lett. 2010, 105, 226403. [Google Scholar] [CrossRef] [PubMed]
- Venderbos, J.W.F.; Daghofer, M.; van den Brink, J.; Kumar, S. Switchable Quantum Anomalous Hall State in a Strongly Frustrated Lattice Magnet. Phys. Rev. Lett. 2012, 109, 166405. [Google Scholar] [CrossRef] [PubMed]
- Barros, K.; Venderbos, J.W.F.; Chern, G.W.; Batista, C.D. Exotic magnetic orderings in the kagome Kondo-lattice model. Phys. Rev. B 2014, 90, 245119. [Google Scholar] [CrossRef]
- Ghosh, S.; O’Brien, P.; Henley, C.L.; Lawler, M.J. Phase diagram of the Kondo lattice model on the kagome lattice. Phys. Rev. B 2016, 93, 024401. [Google Scholar] [CrossRef]
- Balla, P.; Iqbal, Y.; Penc, K. Degenerate manifolds, helimagnets, and multi-Q chiral phases in the classical Heisenberg antiferromagnet on the face-centered-cubic lattice. Phys. Rev. Res. 2020, 2, 043278. [Google Scholar] [CrossRef]
- Amano Patino, M.; Denis Romero, F.; Goto, M.; Saito, T.; Orlandi, F.; Manuel, P.; Szabó, A.; Kayser, P.; Hong, K.H.; Alharbi, K.N.; et al. Multi-k spin ordering in CaFe3Ti4O12 stabilized by spin-orbit coupling and further-neighbor exchange. Phys. Rev. Res. 2021, 3, 043208. [Google Scholar] [CrossRef]
- Szabó, A.; Orlandi, F.; Manuel, P. Fragmented Spin Ice and Multi-k Ordering in Rare-Earth Antiperovskites. Phys. Rev. Lett. 2022, 129, 247201. [Google Scholar] [CrossRef] [PubMed]
- Georgiou, M.; Rousochatzakis, I.; Betouras, J.J. Multi-Q magnetic phases from frustration and chiral interactions. Phys. Rev. B 2023, 108, 024412. [Google Scholar] [CrossRef]
- Hayami, S.; Yambe, R. Stabilization mechanisms of magnetic skyrmion crystal and multiple-Q states based on momentum-resolved spin interactions. Mater. Today Quantum 2024, 3, 100010. [Google Scholar] [CrossRef]
- Dzyaloshinsky, I. A thermodynamic theory of “weak” ferromagnetism of antiferromagnetics. J. Phys. Chem. Solids 1958, 4, 241–255. [Google Scholar] [CrossRef]
- Moriya, T. Anisotropic superexchange interaction and weak ferromagnetism. Phys. Rev. 1960, 120, 91. [Google Scholar] [CrossRef]
- Bogdanov, A.N.; Yablonskii, D.A. Thermodynamically stable “vortices” in magnetically ordered crystals: The mixed state of magnets. Sov. Phys. JETP 1989, 68, 101. [Google Scholar]
- Bogdanov, A.; Hubert, A. Thermodynamically stable magnetic vortex states in magnetic crystals. J. Magn. Magn. Mater. 1994, 138, 255–269. [Google Scholar] [CrossRef]
- Rößler, U.K.; Bogdanov, A.N.; Pfleiderer, C. Spontaneous skyrmion ground states in magnetic metals. Nature 2006, 442, 797–801. [Google Scholar] [CrossRef] [PubMed]
- Binz, B.; Vishwanath, A.; Aji, V. Theory of the Helical Spin Crystal: A Candidate for the Partially Ordered State of MnSi. Phys. Rev. Lett. 2006, 96, 207202. [Google Scholar] [CrossRef] [PubMed]
- Binz, B.; Vishwanath, A. Theory of helical spin crystals: Phases, textures, and properties. Phys. Rev. B 2006, 74, 214408. [Google Scholar] [CrossRef]
- Binz, B.; Vishwanath, A. Chirality induced anomalous-Hall effect in helical spin crystals. Phys. B 2008, 403, 1336. [Google Scholar] [CrossRef]
- Yi, S.D.; Onoda, S.; Nagaosa, N.; Han, J.H. Skyrmions and anomalous Hall effect in a Dzyaloshinskii-Moriya spiral magnet. Phys. Rev. B 2009, 80, 054416. [Google Scholar] [CrossRef]
- Nagaosa, N.; Tokura, Y. Topological properties and dynamics of magnetic skyrmions. Nat. Nanotechnol. 2013, 8, 899–911. [Google Scholar] [CrossRef] [PubMed]
- Tokura, Y.; Kanazawa, N. Magnetic Skyrmion Materials. Chem. Rev. 2021, 121, 2857. [Google Scholar] [CrossRef] [PubMed]
- Ishikawa, Y.; Tajima, K.; Bloch, D.; Roth, M. Helical spin structure in manganese silicide MnSi. Solid State Commun. 1976, 19, 525–528. [Google Scholar] [CrossRef]
- Mühlbauer, S.; Binz, B.; Jonietz, F.; Pfleiderer, C.; Rosch, A.; Neubauer, A.; Georgii, R.; Böni, P. Skyrmion lattice in a chiral magnet. Science 2009, 323, 915–919. [Google Scholar] [CrossRef] [PubMed]
- Neubauer, A.; Pfleiderer, C.; Binz, B.; Rosch, A.; Ritz, R.; Niklowitz, P.G.; Böni, P. Topological Hall Effect in the A Phase of MnSi. Phys. Rev. Lett. 2009, 102, 186602. [Google Scholar] [CrossRef] [PubMed]
- Jonietz, F.; Mu¨hlbauer, S.; Pfleiderer, C.; Neubauer, A.; Mu¨nzer, W.; Bauer, A.; Adams, T.; Georgii, R.; Bo ¨ni, P.; Duine, R.A.; et al. Spin Transfer Torques in MnSi at Ultralow Current Densities. Science 2010, 330, 1648. [Google Scholar] [CrossRef] [PubMed]
- Adams, T.; Mühlbauer, S.; Pfleiderer, C.; Jonietz, F.; Bauer, A.; Neubauer, A.; Georgii, R.; Böni, P.; Keiderling, U.; Everschor, K.; et al. Long-Range Crystalline Nature of the Skyrmion Lattice in MnSi. Phys. Rev. Lett. 2011, 107, 217206. [Google Scholar] [CrossRef] [PubMed]
- Bauer, A.; Pfleiderer, C. Magnetic phase diagram of MnSi inferred from magnetization and ac susceptibility. Phys. Rev. B 2012, 85, 214418. [Google Scholar] [CrossRef]
- Bauer, A.; Garst, M.; Pfleiderer, C. Specific Heat of the Skyrmion Lattice Phase and Field-Induced Tricritical Point in MnSi. Phys. Rev. Lett. 2013, 110, 177207. [Google Scholar] [CrossRef] [PubMed]
- Chacon, A.; Bauer, A.; Adams, T.; Rucker, F.; Brandl, G.; Georgii, R.; Garst, M.; Pfleiderer, C. Uniaxial Pressure Dependence of Magnetic Order in MnSi. Phys. Rev. Lett. 2015, 115, 267202. [Google Scholar] [CrossRef] [PubMed]
- Mühlbauer, S.; Kindervater, J.; Adams, T.; Bauer, A.; Keiderling, U.; Pfleiderer, C. Kinetic small angle neutron scattering of the skyrmion lattice in MnSi. New J. Phys. 2016, 18, 075017. [Google Scholar] [CrossRef]
- Reiner, M.; Bauer, A.; Leitner, M.; Gigl, T.; Anwand, W.; Butterling, M.; Wagner, A.; Kudejova, P.; Pfleiderer, C.; Hugenschmidt, C. Positron spectroscopy of point defects in the skyrmion-lattice compound MnSi. Sci. Rep. 2016, 6, 29109. [Google Scholar] [CrossRef] [PubMed]
- Beille, J.; Voiron, J.; Roth, M. Long period helimagnetism in the cubic B20 FexCo1-xSi and CoxMn1-x Si alloys. Solid State Commun. 1983, 47, 399–402. [Google Scholar] [CrossRef]
- Yu, X.Z.; Onose, Y.; Kanazawa, N.; Park, J.H.; Han, J.H.; Matsui, Y.; Nagaosa, N.; Tokura, Y. Real-space observation of a two-dimensional skyrmion crystal. Nature 2010, 465, 901–904. [Google Scholar] [CrossRef] [PubMed]
- Münzer, W.; Neubauer, A.; Adams, T.; Mühlbauer, S.; Franz, C.; Jonietz, F.; Georgii, R.; Böni, P.; Pedersen, B.; Schmidt, M.; et al. Skyrmion lattice in the doped semiconductor Fe1-xCoxSi. Phys. Rev. B 2010, 81, 041203. [Google Scholar] [CrossRef]
- Adams, T.; Mühlbauer, S.; Neubauer, A.; Münzer, W.; Jonietz, F.; Georgii, R.; Pedersen, B.; Böni, P.; Rosch, A.; Pfleiderer, C. Skyrmion lattice domains in Fe1-xCoxSi. J. Phys. Conf. Ser. 2010, 200, 032001. [Google Scholar] [CrossRef]
- Yu, X.Z.; Kanazawa, N.; Onose, Y.; Kimoto, K.; Zhang, W.; Ishiwata, S.; Matsui, Y.; Tokura, Y. Near room-temperature formation of a skyrmion crystal in thin-films of the helimagnet FeGe. Nat. Mater. 2011, 10, 106–109. [Google Scholar] [CrossRef] [PubMed]
- Lebech, B.; Bernhard, J.; Freltoft, T. Magnetic structures of cubic FeGe studied by small-angle neutron scattering. J. Phys. Condens. Matter 1989, 1, 6105. [Google Scholar] [CrossRef]
- Seki, S.; Yu, X.Z.; Ishiwata, S.; Tokura, Y. Observation of skyrmions in a multiferroic material. Science 2012, 336, 198–201. [Google Scholar] [CrossRef] [PubMed]
- Adams, T.; Chacon, A.; Wagner, M.; Bauer, A.; Brandl, G.; Pedersen, B.; Berger, H.; Lemmens, P.; Pfleiderer, C. Long-Wavelength Helimagnetic Order and Skyrmion Lattice Phase in Cu2OSeO3. Phys. Rev. Lett. 2012, 108, 237204. [Google Scholar] [CrossRef] [PubMed]
- Seki, S.; Kim, J.H.; Inosov, D.S.; Georgii, R.; Keimer, B.; Ishiwata, S.; Tokura, Y. Formation and rotation of skyrmion crystal in the chiral-lattice insulator Cu2OSeO3. Phys. Rev. B 2012, 85, 220406. [Google Scholar] [CrossRef]
- Langner, M.C.; Roy, S.; Mishra, S.K.; Lee, J.C.T.; Shi, X.W.; Hossain, M.A.; Chuang, Y.D.; Seki, S.; Tokura, Y.; Kevan, S.D.; et al. Coupled Skyrmion Sublattices in Cu2OSeO3. Phys. Rev. Lett. 2014, 112, 167202. [Google Scholar] [CrossRef] [PubMed]
- White, J.S.; Prša, K.; Huang, P.; Omrani, A.A.; Živković, I.; Bartkowiak, M.; Berger, H.; Magrez, A.; Gavilano, J.L.; Nagy, G.; et al. Electric-Field-Induced Skyrmion Distortion and Giant Lattice Rotation in the Magnetoelectric Insulator Cu2OSeO3. Phys. Rev. Lett. 2014, 113, 107203. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.L.; Bauer, A.; Berger, H.; Pfleiderer, C.; van der Laan, G.; Hesjedal, T. Resonant elastic x-ray scattering from the skyrmion lattice in Cu2OSeO3. Phys. Rev. B 2016, 93, 214420. [Google Scholar] [CrossRef]
- Kakihana, M.; Aoki, D.; Nakamura, A.; Honda, F.; Nakashima, M.; Amako, Y.; Nakamura, S.; Sakakibara, T.; Hedo, M.; Nakama, T.; et al. Giant Hall resistivity and magnetoresistance in cubic chiral antiferromagnet EuPtSi. J. Phys. Soc. Jpn. 2018, 87, 023701. [Google Scholar] [CrossRef]
- Kaneko, K.; Frontzek, M.D.; Matsuda, M.; Nakao, A.; Munakata, K.; Ohhara, T.; Kakihana, M.; Haga, Y.; Hedo, M.; Nakama, T.; et al. Unique Helical Magnetic Order and Field-Induced Phase in Trillium Lattice Antiferromagnet EuPtSi. J. Phys. Soc. Jpn. 2019, 88, 013702. [Google Scholar] [CrossRef]
- Tabata, C.; Matsumura, T.; Nakao, H.; Michimura, S.; Kakihana, M.; Inami, T.; Kaneko, K.; Hedo, M.; Nakama, T.; Ōnuki, Y. Magnetic Field Induced Triple-q Magnetic Order in Trillium Lattice Antiferromagnet EuPtSi Studied by Resonant X-ray Scattering. J. Phys. Soc. Jpn. 2019, 88, 093704. [Google Scholar] [CrossRef]
- Kakihana, M.; Aoki, D.; Nakamura, A.; Honda, F.; Nakashima, M.; Amako, Y.; Takeuchi, T.; Harima, H.; Hedo, M.; Nakama, T.; et al. Unique Magnetic Phases in the Skyrmion Lattice and Fermi Surface Properties in Cubic Chiral Antiferromagnet EuPtSi. J. Phys. Soc. Jpn. 2019, 88, 094705. [Google Scholar] [CrossRef]
- Hayami, S.; Yambe, R. Field-Direction Sensitive Skyrmion Crystals in Cubic Chiral Systems: Implication to 4f-Electron Compound EuPtSi. J. Phys. Soc. Jpn. 2021, 90, 073705. [Google Scholar] [CrossRef]
- Matsumura, T.; Tabata, C.; Kaneko, K.; Nakao, H.; Kakihana, M.; Hedo, M.; Nakama, T.; Ōnuki, Y. Single helicity of the triple-q triangular skyrmion lattice state in the cubic chiral helimagnet EuPtSi. Phys. Rev. B 2024, 109, 174437. [Google Scholar] [CrossRef]
- Kézsmárki, I.; Bordács, S.; Milde, P.; Neuber, E.; Eng, L.M.; White, J.S.; Rønnow, H.M.; Dewhurst, C.D.; Mochizuki, M.; Yanai, K.; et al. Neel-type skyrmion lattice with confined orientation in the polar magnetic semiconductor GaV4S8. Nat. Mater. 2015, 14, 1116–1122. [Google Scholar] [CrossRef] [PubMed]
- Hicken, T.J.; Wilson, M.N.; Holt, S.J.R.; Khassanov, R.; Lees, M.R.; Gupta, R.; Das, D.; Balakrishnan, G.; Lancaster, T. Magnetism in the Néel-skyrmion host GaV4S8 under pressure. Phys. Rev. B 2022, 105, 134414. [Google Scholar] [CrossRef]
- Borisov, V.; Salehi, N.; Pereiro, M.; Delin, A.; Eriksson, O. Dzyaloshinskii-Moriya interactions, Néel skyrmions and V4 magnetic clusters in multiferroic lacunar spinel GaV4S8. npj Comput. Mater. 2024, 10, 53. [Google Scholar] [CrossRef]
- Bordács, S.; Butykai, A.; Szigeti, B.G.; White, J.S.; Cubitt, R.; Leonov, A.O.; Widmann, S.; Ehlers, D.; von Nidda, H.A.K.; Tsurkan, V.; et al. Equilibrium skyrmion lattice ground state in a polar easy-plane magnet. Sci. Rep. 2017, 7, 7584. [Google Scholar] [CrossRef] [PubMed]
- Fujima, Y.; Abe, N.; Tokunaga, Y.; Arima, T. Thermodynamically stable skyrmion lattice at low temperatures in a bulk crystal of lacunar spinel GaV4Se8. Phys. Rev. B 2017, 95, 180410. [Google Scholar] [CrossRef]
- Liu, Z.; Ide, R.; Arima, T.H.; Itoh, S.; Asai, S.; Masuda, T. Inelastic Neutron Scattering Study on Skyrmion Host Compound GaV4Se8. J. Phys. Soc. Jpn. 2024, 93, 124707. [Google Scholar] [CrossRef]
- Takeda, H.; Ishikawa, M.; Takigawa, M.; Yamashita, M.; Fujima, Y.; Arima, T.H. Magnetic structure of polar magnet GaV4Se8 with Néel-type skyrmion lattice probed by 51V NMR. Phys. Rev. B 2024, 110, 224430. [Google Scholar] [CrossRef]
- Kurumaji, T.; Nakajima, T.; Ukleev, V.; Feoktystov, A.; Arima, T.H.; Kakurai, K.; Tokura, Y. Néel-Type Skyrmion Lattice in the Tetragonal Polar Magnet VOSe2O5. Phys. Rev. Lett. 2017, 119, 237201. [Google Scholar] [CrossRef] [PubMed]
- Kurumaji, T.; Nakajima, T.; Feoktystov, A.; Babcock, E.; Salhi, Z.; Ukleev, V.; Arima, T.H.; Kakurai, K.; Tokura, Y. Direct observation of cycloidal spin modulation and field-induced transition in Néel-type skyrmion-hosting VOSe2O5. J. Phys. Soc. Jpn. 2021, 90, 024705. [Google Scholar] [CrossRef]
- Nayak, A.K.; Kumar, V.; Ma, T.; Werner, P.; Pippel, E.; Sahoo, R.; Damay, F.; Rößler, U.K.; Felser, C.; Parkin, S.S. Magnetic Antiskyrmions Above Room Temperature in Tetragonal Heusler Materials. Nature 2017, 548, 561–566. [Google Scholar] [CrossRef] [PubMed]
- Peng, L.; Takagi, R.; Koshibae, W.; Shibata, K.; Nakajima, K.; Arima, T.H.; Nagaosa, N.; Seki, S.; Yu, X.; Tokura, Y. Controlled transformation of skyrmions and antiskyrmions in a non-centrosymmetric magnet. Nat. Nanotechnol. 2020, 15, 181–186. [Google Scholar] [CrossRef] [PubMed]
- Zuniga Cespedes, B.E.; Vir, P.; Milde, P.; Felser, C.; Eng, L.M. Critical sample aspect ratio and magnetic field dependence for antiskyrmion formation in Mn1.4PtSn single crystals. Phys. Rev. B 2021, 103, 184411. [Google Scholar] [CrossRef]
- Karube, K.; Peng, L.; Masell, J.; Yu, X.; Kagawa, F.; Tokura, Y.; Taguchi, Y. Room-temperature antiskyrmions and sawtooth surface textures in a non-centrosymmetric magnet with S4 symmetry. Nat. Mater. 2021, 20, 335–340. [Google Scholar] [CrossRef] [PubMed]
- Dzyaloshinskii, I. Theory of helicoidal structures in antiferromagnets. I. Nonmetals. Sov. Phys. JETP 1964, 19, 960–971. [Google Scholar]
- Kataoka, M.; Nakanishi, O. Helical spin density wave due to antisymmetric exchange interaction. J. Phys. Soc. Jpn. 1981, 50, 3888–3896. [Google Scholar] [CrossRef]
- Okubo, T.; Chung, S.; Kawamura, H. Multiple-q States and the Skyrmion Lattice of the Triangular-Lattice Heisenberg Antiferromagnet under Magnetic Fields. Phys. Rev. Lett. 2012, 108, 017206. [Google Scholar] [CrossRef] [PubMed]
- Leonov, A.O.; Mostovoy, M. Multiply periodic states and isolated skyrmions in an anisotropic frustrated magnet. Nat. Commun. 2015, 6, 8275. [Google Scholar] [CrossRef] [PubMed]
- Utesov, O.I. Thermodynamically stable skyrmion lattice in a tetragonal frustrated antiferromagnet with dipolar interaction. Phys. Rev. B 2021, 103, 064414. [Google Scholar] [CrossRef]
- Utesov, O.I. Mean-field description of skyrmion lattice in hexagonal frustrated antiferromagnets. Phys. Rev. B 2022, 105, 054435. [Google Scholar] [CrossRef]
- Amoroso, D.; Barone, P.; Picozzi, S. Spontaneous skyrmionic lattice from anisotropic symmetric exchange in a Ni-halide monolayer. Nat. Commun. 2020, 11, 5784. [Google Scholar] [CrossRef] [PubMed]
- Hayami, S.; Motome, Y. Noncoplanar multiple-Q spin textures by itinerant frustration: Effects of single-ion anisotropy and bond-dependent anisotropy. Phys. Rev. B 2021, 103, 054422. [Google Scholar] [CrossRef]
- Yambe, R.; Hayami, S. Skyrmion crystals in centrosymmetric itinerant magnets without horizontal mirror plane. Sci. Rep. 2021, 11, 11184. [Google Scholar] [CrossRef] [PubMed]
- Amoroso, D.; Barone, P.; Picozzi, S. Interplay between Single-Ion and Two-Ion Anisotropies in Frustrated 2D Semiconductors and Tuning of Magnetic Structures Topology. Nanomaterials 2021, 11, 1873. [Google Scholar] [CrossRef] [PubMed]
- Hayami, S. Multiple skyrmion crystal phases by itinerant frustration in centrosymmetric tetragonal magnets. J. Phys. Soc. Jpn. 2022, 91, 023705. [Google Scholar] [CrossRef]
- Kurumaji, T.; Nakajima, T.; Hirschberger, M.; Kikkawa, A.; Yamasaki, Y.; Sagayama, H.; Nakao, H.; Taguchi, Y.; Arima, T.H.; Tokura, Y. Skyrmion lattice with a giant topological Hall effect in a frustrated triangular-lattice magnet. Science 2019, 365, 914–918. [Google Scholar] [CrossRef] [PubMed]
- Kumar, R.; Iyer, K.K.; Paulose, P.L.; Sampathkumaran, E.V. Magnetic and transport anomalies in R2RhSi3 (R = Gd, Tb, and Dy) resembling those of the exotic magnetic material Gd2PdSi3. Phys. Rev. B 2020, 101, 144440. [Google Scholar] [CrossRef]
- Spachmann, S.; Elghandour, A.; Frontzek, M.; Löser, W.; Klingeler, R. Magnetoelastic coupling and phases in the skyrmion lattice magnet Gd2PdSi3 discovered by high-resolution dilatometry. Phys. Rev. B 2021, 103, 184424. [Google Scholar] [CrossRef]
- Hirschberger, M.; Nakajima, T.; Gao, S.; Peng, L.; Kikkawa, A.; Kurumaji, T.; Kriener, M.; Yamasaki, Y.; Sagayama, H.; Nakao, H.; et al. Skyrmion phase and competing magnetic orders on a breathing kagome lattice. Nat. Commun. 2019, 10, 5831. [Google Scholar] [CrossRef] [PubMed]
- Hirschberger, M.; Hayami, S.; Tokura, Y. Nanometric skyrmion lattice from anisotropic exchange interactions in a centrosymmetric host. New J. Phys. 2021, 23, 023039. [Google Scholar] [CrossRef]
- Nakamura, S. Magnetic anisotropies and skyrmion lattice related to magnetic quadrupole interactions of the RKKY mechanism in the frustrated spin-trimer system Gd3Ru4Al12 with a breathing kagome structure. Phys. Rev. B 2025, 111, 184433. [Google Scholar] [CrossRef]
- Khanh, N.D.; Nakajima, T.; Yu, X.; Gao, S.; Shibata, K.; Hirschberger, M.; Yamasaki, Y.; Sagayama, H.; Nakao, H.; Peng, L.; et al. Nanometric square skyrmion lattice in a centrosymmetric tetragonal magnet. Nat. Nanotechnol. 2020, 15, 444. [Google Scholar] [CrossRef] [PubMed]
- Khanh, N.D.; Nakajima, T.; Hayami, S.; Gao, S.; Yamasaki, Y.; Sagayama, H.; Nakao, H.; Takagi, R.; Motome, Y.; Tokura, Y.; et al. Zoology of Multiple-Q Spin Textures in a Centrosymmetric Tetragonal Magnet with Itinerant Electrons. Adv. Sci. 2022, 9, 2105452. [Google Scholar] [CrossRef] [PubMed]
- Matsuyama, N.; Nomura, T.; Imajo, S.; Nomoto, T.; Arita, R.; Sudo, K.; Kimata, M.; Khanh, N.D.; Takagi, R.; Tokura, Y.; et al. Quantum oscillations in the centrosymmetric skyrmion-hosting magnet GdRu2Si2. Phys. Rev. B 2023, 107, 104421. [Google Scholar] [CrossRef]
- Wood, G.D.A.; Khalyavin, D.D.; Mayoh, D.A.; Bouaziz, J.; Hall, A.E.; Holt, S.J.R.; Orlandi, F.; Manuel, P.; Blügel, S.; Staunton, J.B.; et al. Double-Q ground state with topological charge stripes in the centrosymmetric skyrmion candidate GdRu2Si2. Phys. Rev. B 2023, 107, L180402. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, Q.; Luo, J.W.; Freeman, A.J.; Zunger, A. Hidden spin polarization in inversion-symmetric bulk crystals. Nat. Phys. 2014, 10, 387–393. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H.; Motome, Y. Spontaneous parity breaking in spin-orbital coupled systems. Phys. Rev. B 2014, 90, 081115. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H.; Motome, Y. Emergent spin-valley-orbital physics by spontaneous parity breaking. J. Phys. Condens. Matter 2016, 28, 395601. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Yartsev, A.; Guan, S.; Zhu, L.; Zhao, Q.; Yao, Z.; He, C.; Zhang, L.; Bai, J.; Luo, J.W.; et al. Hidden spin polarization in the centrosymmetric MoS2 crystal revealed via elliptically polarized terahertz emission. Phys. Rev. B 2020, 102, 085205. [Google Scholar] [CrossRef]
- Hayami, S. Skyrmion crystal and spiral phases in centrosymmetric bilayer magnets with staggered Dzyaloshinskii-Moriya interaction. Phys. Rev. B 2022, 105, 014408. [Google Scholar] [CrossRef]
- Lin, S.Z. Skyrmion lattice in centrosymmetric magnets with local Dzyaloshinsky-Moriya interaction. Mater. Today Quantum 2024, 2, 100006. [Google Scholar] [CrossRef]
- Kaplan, T. Single-band Hubbard model with spin-orbit coupling. Zeitschrift für Physik B Condensed Matter 1983, 49, 313–317. [Google Scholar] [CrossRef]
- Yanase, Y. Magneto-Electric Effect in Three-Dimensional Coupled Zigzag Chains. J. Phys. Soc. Jpn. 2014, 83, 014703. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H.; Motome, Y. Spontaneous Multipole Ordering by Local Parity Mixing. J. Phys. Soc. Jpn. 2015, 84, 064717. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H.; Motome, Y. Asymmetric Magnon Excitation by Spontaneous Toroidal Ordering. J. Phys. Soc. Jpn. 2016, 85, 053705. [Google Scholar] [CrossRef]
- Sumita, S.; Yanase, Y. Superconductivity in magnetic multipole states. Phys. Rev. B 2016, 93, 224507. [Google Scholar] [CrossRef]
- Cysne, T.P.; Guimarães, F.S.M.; Canonico, L.M.; Rappoport, T.G.; Muniz, R.B. Orbital magnetoelectric effect in zigzag nanoribbons of p-band systems. Phys. Rev. B 2021, 104, 165403. [Google Scholar] [CrossRef]
- Yatsushiro, M.; Oiwa, R.; Kusunose, H.; Hayami, S. Analysis of model-parameter dependences on the second-order nonlinear conductivity in PT-symmetric collinear antiferromagnetic metals with magnetic toroidal moment on zigzag chains. Phys. Rev. B 2022, 105, 155157. [Google Scholar] [CrossRef]
- Suzuki, Y. Tunneling spin current in systems with spin degeneracy. Phys. Rev. B 2022, 105, 075201. [Google Scholar] [CrossRef]
- Kane, C.L.; Mele, E.J. Quantum Spin Hall Effect in Graphene. Phys. Rev. Lett. 2005, 95, 226801. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Cao, T.; Niu, Q.; Shi, J.; Feng, J. Coupling the valley degree of freedom to antiferromagnetic order. Proc. Natl. Acad. Sci. USA 2013, 110, 3738–3742. [Google Scholar] [CrossRef] [PubMed]
- Yanagi, Y.; Kusunose, H. Optical Selection Rules in Spin–Orbit Coupled Systems on Honeycomb Lattice. J. Phys. Soc. Jpn. 2017, 86, 083703. [Google Scholar] [CrossRef]
- Yanagi, Y.; Hayami, S.; Kusunose, H. Manipulating the magnetoelectric effect: Essence learned from Co4Nb2O9. Phys. Rev. B 2018, 97, 020404. [Google Scholar] [CrossRef]
- Matsumoto, T.; Hayami, S. Nonreciprocal magnons due to symmetric anisotropic exchange interaction in honeycomb antiferromagnets. Phys. Rev. B 2020, 101, 224419. [Google Scholar] [CrossRef]
- Fu, L.; Kane, C.L.; Mele, E.J. Topological Insulators in Three Dimensions. Phys. Rev. Lett. 2007, 98, 106803. [Google Scholar] [CrossRef] [PubMed]
- Hayami, S.; Kusunose, H.; Motome, Y. Emergent odd-parity multipoles and magnetoelectric effects on a diamond structure: Implication for the 5d transition metal oxides AOsO4 (A = K, Rb, and Cs). Phys. Rev. B 2018, 97, 024414. [Google Scholar] [CrossRef]
- Ishitobi, T.; Hattori, K. Magnetoelectric Effects and Charge-Imbalanced Solenoids: Antiferro Quadrupole Orders in a Diamond Structure. J. Phys. Soc. Jpn. 2019, 88, 063708. [Google Scholar] [CrossRef]
- Paramekanti, A.; Maharaj, D.D.; Gaulin, B.D. Octupolar order in d-orbital Mott insulators. Phys. Rev. B 2020, 101, 054439. [Google Scholar] [CrossRef]
- Maharaj, D.D.; Sala, G.; Stone, M.B.; Kermarrec, E.; Ritter, C.; Fauth, F.; Marjerrison, C.A.; Greedan, J.E.; Paramekanti, A.; Gaulin, B.D. Octupolar versus Néel Order in Cubic 5d2 Double Perovskites. Phys. Rev. Lett. 2020, 124, 087206. [Google Scholar] [CrossRef] [PubMed]
- Winkler, R.; Zülicke, U. Theory of electric, magnetic, and toroidal polarizations in crystalline solids with applications to hexagonal lonsdaleite and cubic diamond. Phys. Rev. B 2023, 107, 155201. [Google Scholar] [CrossRef]
- Yambe, R.; Hayami, S. Effective spin model in momentum space: Toward a systematic understanding of multiple-Q instability by momentum-resolved anisotropic exchange interactions. Phys. Rev. B 2022, 106, 174437. [Google Scholar] [CrossRef]
- Loss, D.; Goldbart, P.M. Persistent currents from Berry’s phase in mesoscopic systems. Phys. Rev. B 1992, 45, 13544–13561. [Google Scholar] [CrossRef] [PubMed]
- Ye, J.; Kim, Y.B.; Millis, A.J.; Shraiman, B.I.; Majumdar, P.; Tešanović, Z. Berry Phase Theory of the Anomalous Hall Effect: Application to Colossal Magnetoresistance Manganites. Phys. Rev. Lett. 1999, 83, 3737–3740. [Google Scholar] [CrossRef]
- Ohgushi, K.; Murakami, S.; Nagaosa, N. Spin anisotropy and quantum Hall effect in the kagomé lattice: Chiral spin state based on a ferromagnet. Phys. Rev. B 2000, 62, R6065–R6068. [Google Scholar] [CrossRef]
- Solenov, D.; Mozyrsky, D.; Martin, I. Chirality Waves in Two-Dimensional Magnets. Phys. Rev. Lett. 2012, 108, 096403. [Google Scholar] [CrossRef] [PubMed]
- Brey, L.; Fertig, H.; Côté, R.; MacDonald, A. Skyrme and meron crystals in quantum Hall ferromagnets. Phys. Scr. 1996, 1996, 154. [Google Scholar] [CrossRef]
- Ezawa, M. Compact merons and skyrmions in thin chiral magnetic films. Phys. Rev. B 2011, 83, 100408. [Google Scholar] [CrossRef]
- Lin, S.Z.; Saxena, A.; Batista, C.D. Skyrmion fractionalization and merons in chiral magnets with easy-plane anisotropy. Phys. Rev. B 2015, 91, 224407. [Google Scholar] [CrossRef]
- Tan, A.; Li, J.; Scholl, A.; Arenholz, E.; Young, A.T.; Li, Q.; Hwang, C.; Qiu, Z.Q. Topology of spin meron pairs in coupled Ni/Fe/Co/Cu(001) disks. Phys. Rev. B 2016, 94, 014433. [Google Scholar] [CrossRef]
- Bera, S.; Mandal, S.S. Theory of the skyrmion, meron, antiskyrmion, and antimeron in chiral magnets. Phys. Rev. Res. 2019, 1, 033109. [Google Scholar] [CrossRef]
- Yu, X.Z.; Koshibae, W.; Tokunaga, Y.; Shibata, K.; Taguchi, Y.; Nagaosa, N.; Tokura, Y. Transformation between meron and skyrmion topological spin textures in a chiral magnet. Nature 2018, 564, 95–98. [Google Scholar] [CrossRef] [PubMed]
- Gao, N.; Je, S.G.; Im, M.Y.; Choi, J.W.; Yang, M.; Li, Q.C.; Wang, T.; Lee, S.; Han, H.S.; Lee, K.S.; et al. Creation and annihilation of topological meron pairs in in-plane magnetized films. Nat. Commun. 2019, 10, 5603. [Google Scholar] [CrossRef] [PubMed]
- Hayami, S.; Okubo, T.; Motome, Y. Phase shift in skyrmion crystals. Nat. Commun. 2021, 12, 6927. [Google Scholar] [CrossRef] [PubMed]
- Chen, K.; Luo, Q.; Zhou, Z.; He, S.; Xi, B.; Jia, C.; Luo, H.G.; Zhao, J. Triple-meron crystal in high-spin Kitaev magnets. New J. Phys. 2023, 25, 023006. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hayami, S. Multiple-Q States in Bilayer Triangular-Lattice Systems with Bond-Dependent Anisotropic Interaction. Crystals 2025, 15, 663. https://doi.org/10.3390/cryst15070663
Hayami S. Multiple-Q States in Bilayer Triangular-Lattice Systems with Bond-Dependent Anisotropic Interaction. Crystals. 2025; 15(7):663. https://doi.org/10.3390/cryst15070663
Chicago/Turabian StyleHayami, Satoru. 2025. "Multiple-Q States in Bilayer Triangular-Lattice Systems with Bond-Dependent Anisotropic Interaction" Crystals 15, no. 7: 663. https://doi.org/10.3390/cryst15070663
APA StyleHayami, S. (2025). Multiple-Q States in Bilayer Triangular-Lattice Systems with Bond-Dependent Anisotropic Interaction. Crystals, 15(7), 663. https://doi.org/10.3390/cryst15070663





