Research on Fatigue Strength Evaluation Method of Welded Joints in Steel Box Girders with Open Longitudinal Ribs
Abstract
1. Introduction
2. Methodology
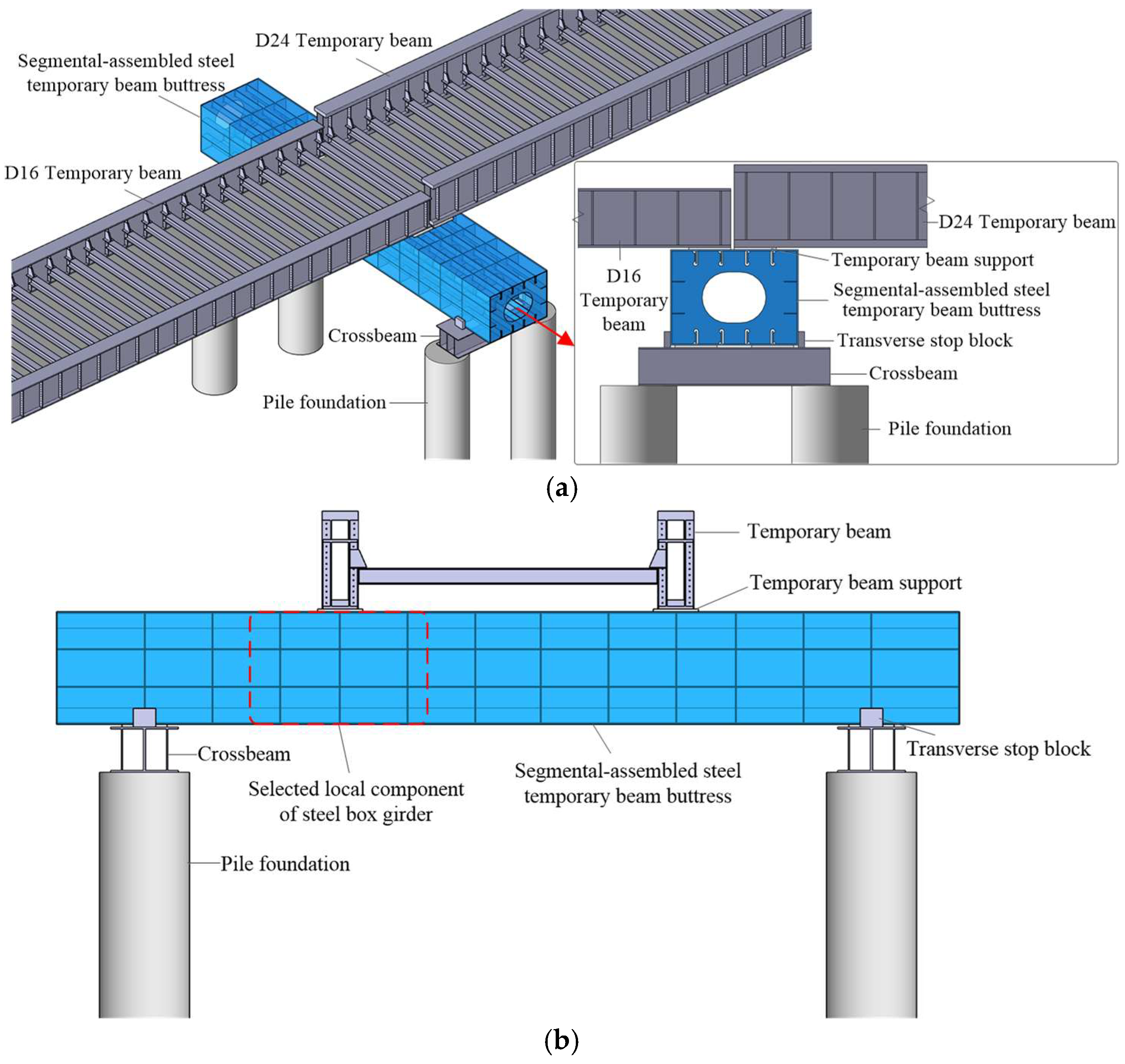
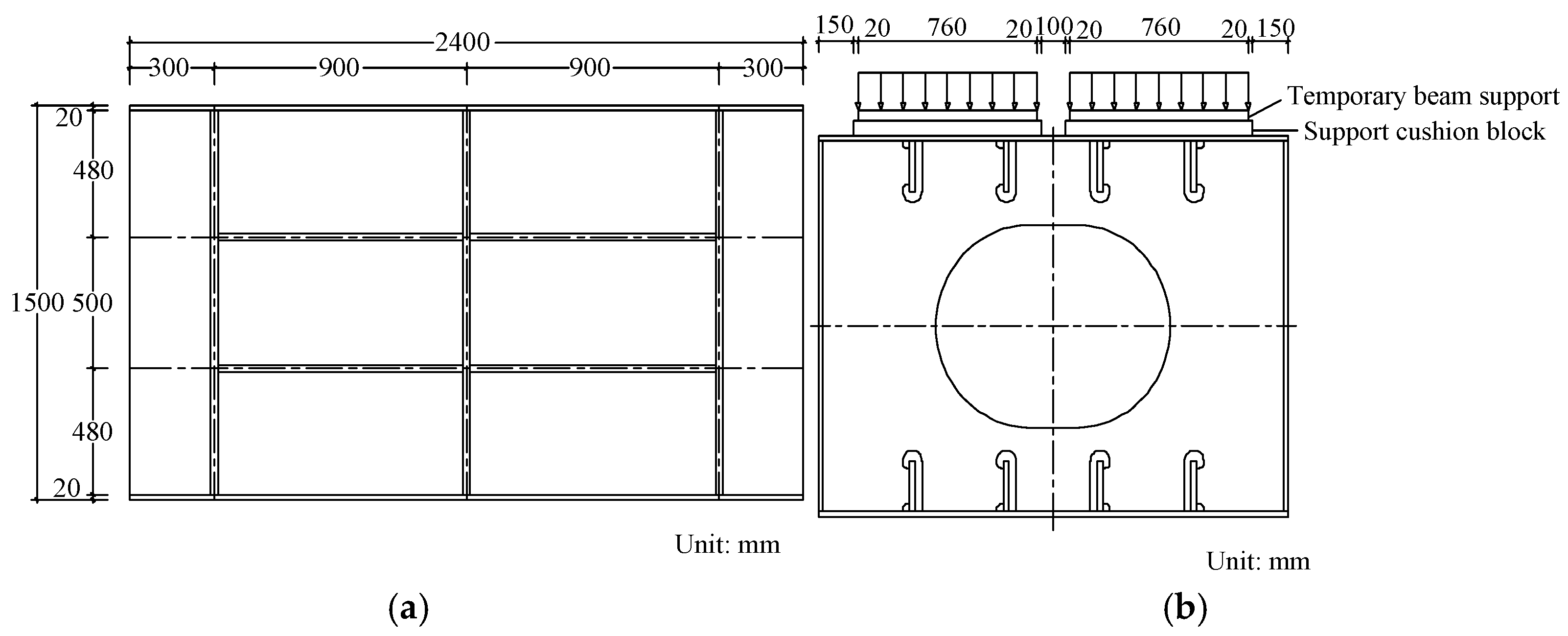
2.1. Overview of Steel Box Girder Local Component
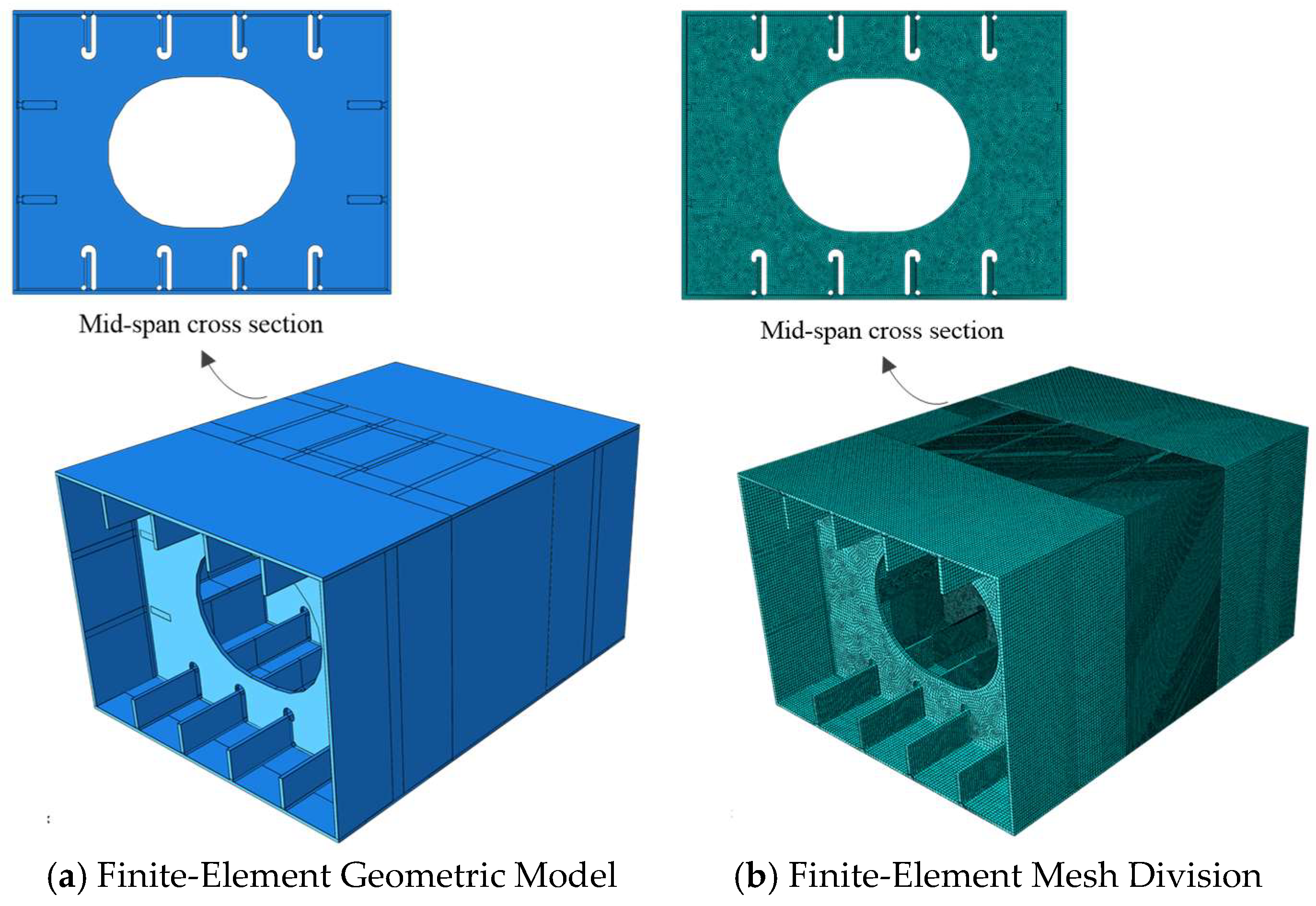
2.2. Numerical Simulation
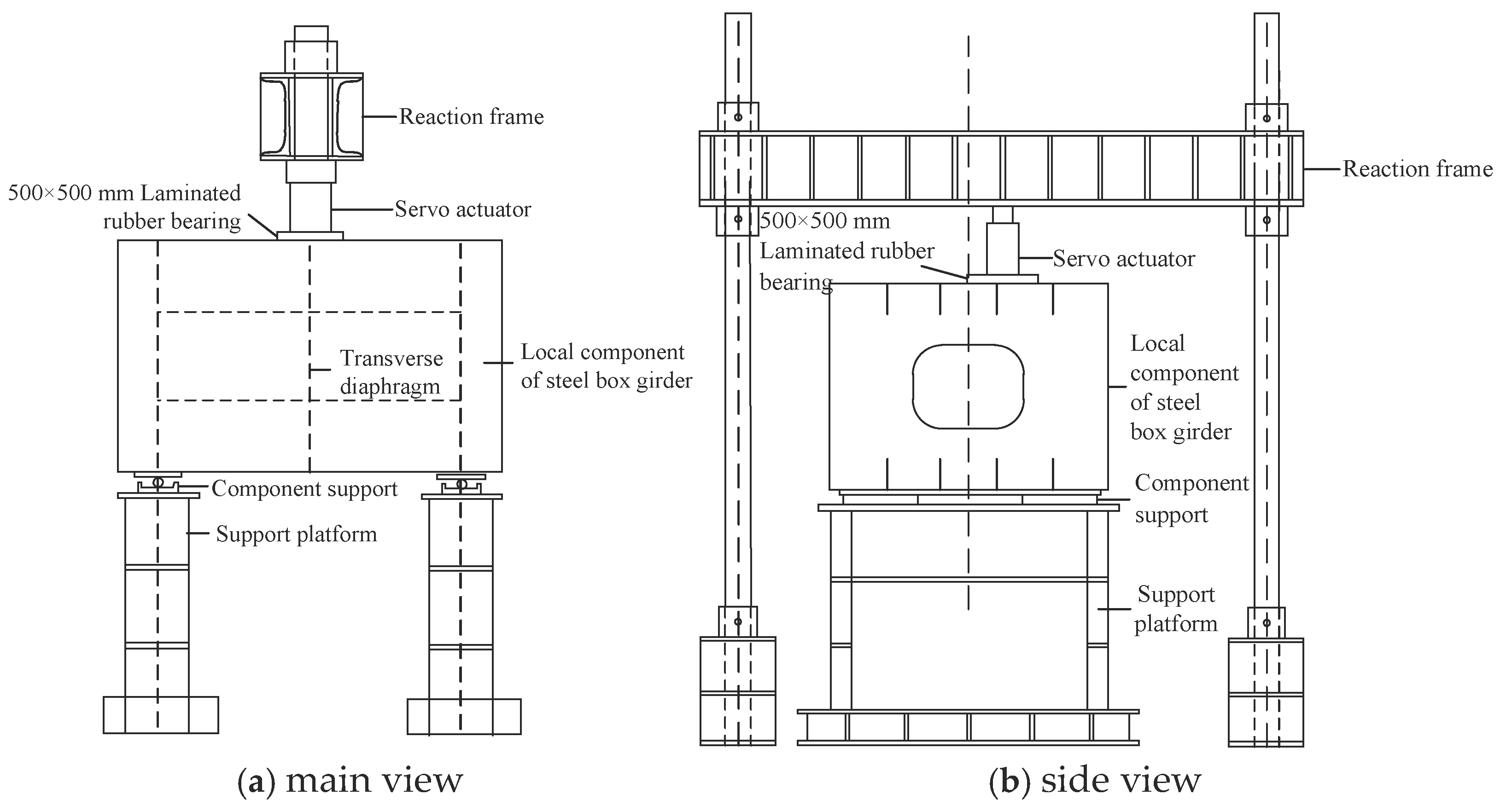
2.3. Fatigue Loading Test
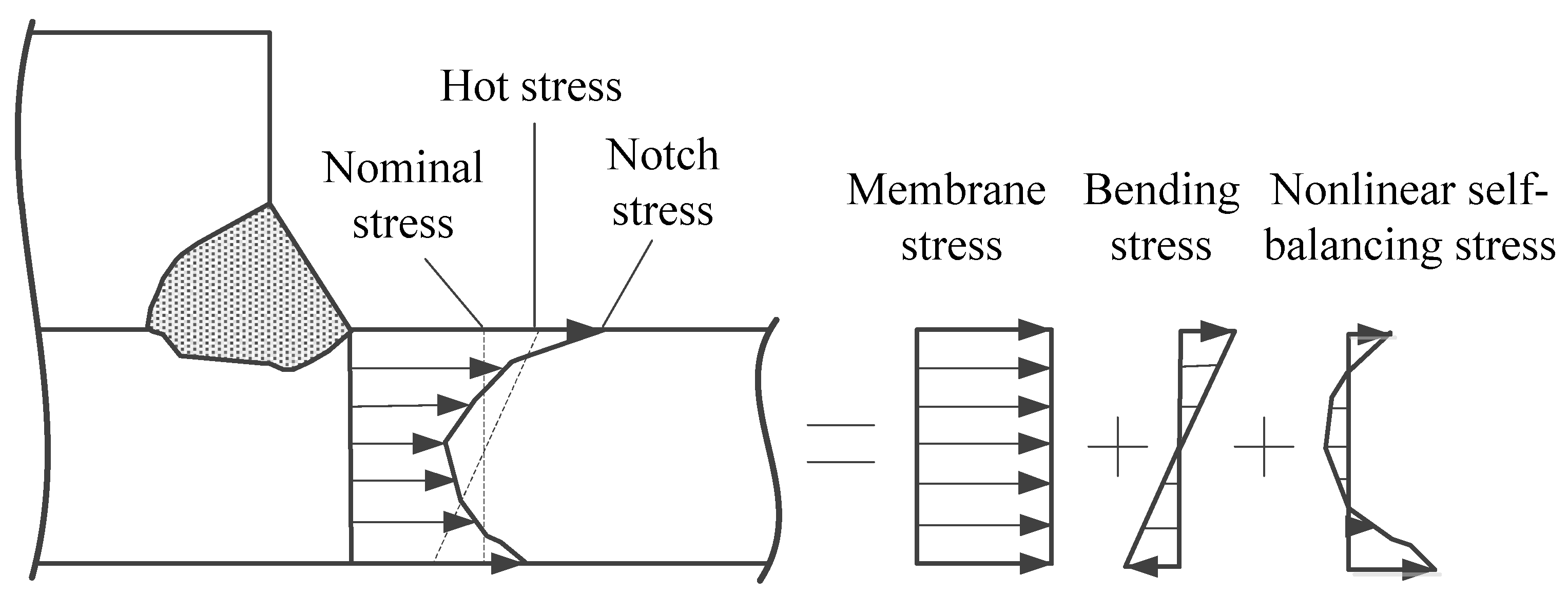
2.4. Fatigue Strength Evaluation Method
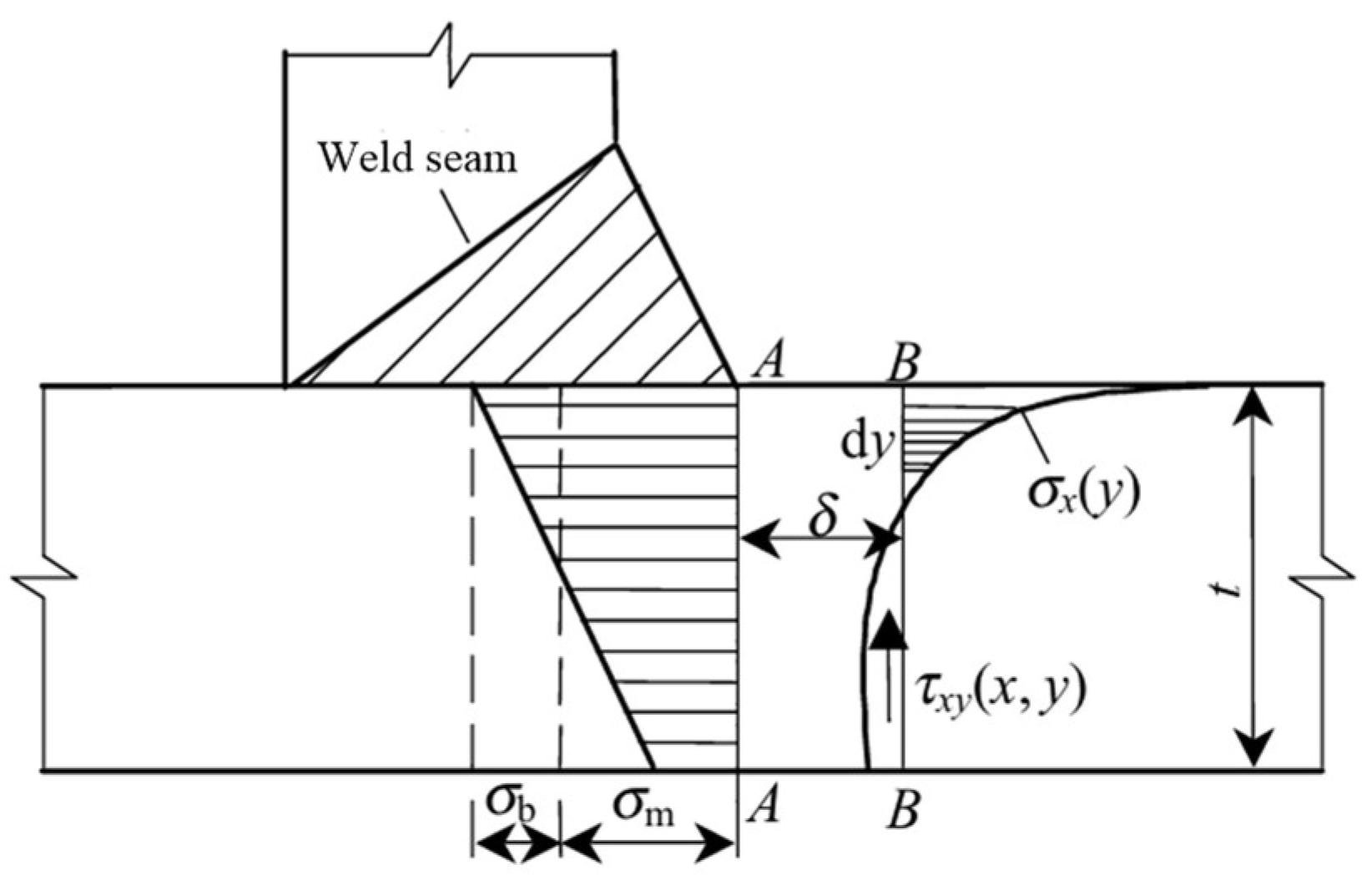
2.4.1. Nominal Stress Method
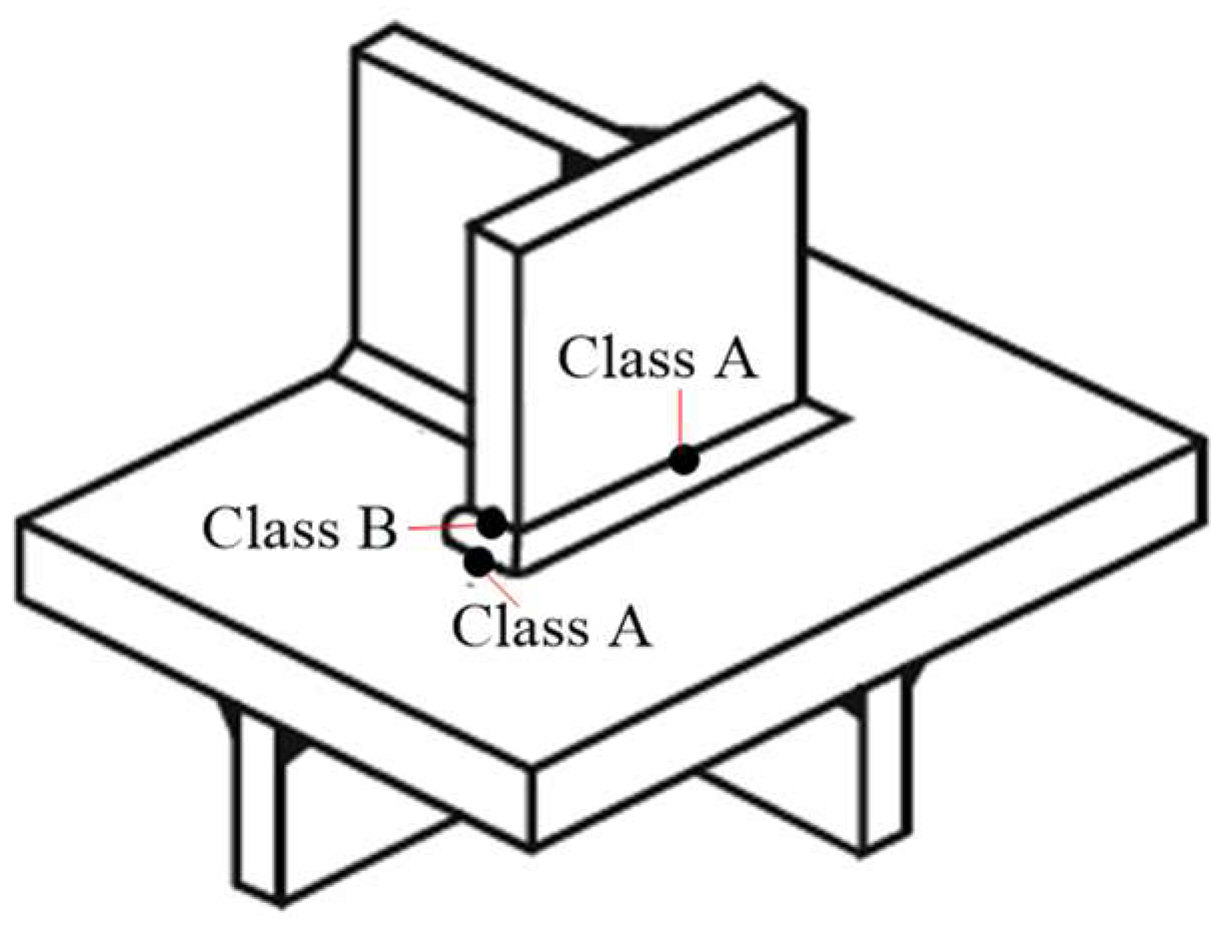
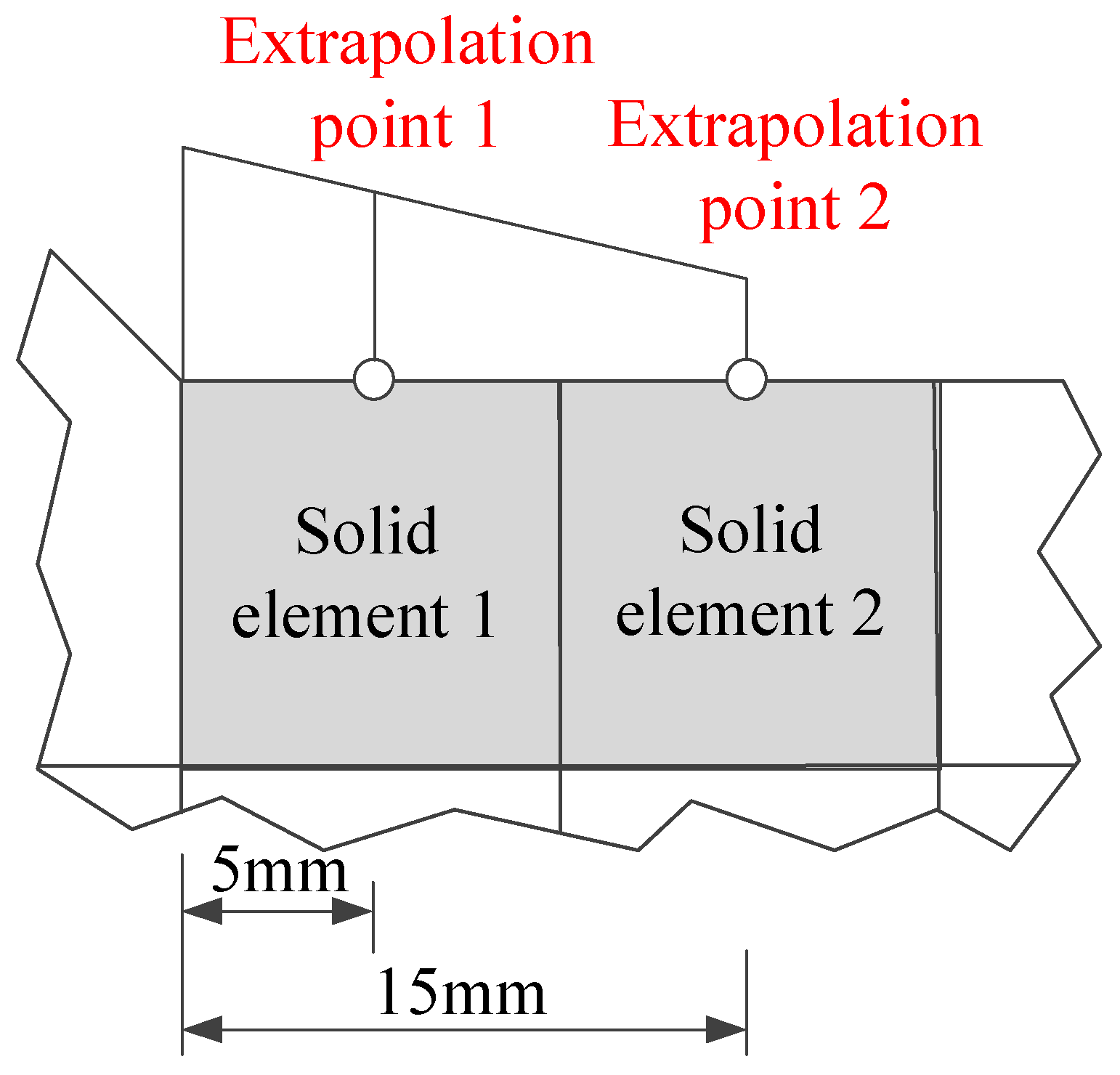
2.4.2. Hot-Spot Stress Method
2.4.3. Equivalent Structural Stress Method
3. Results and Discussion
3.1. Finite-Element Analysis Results
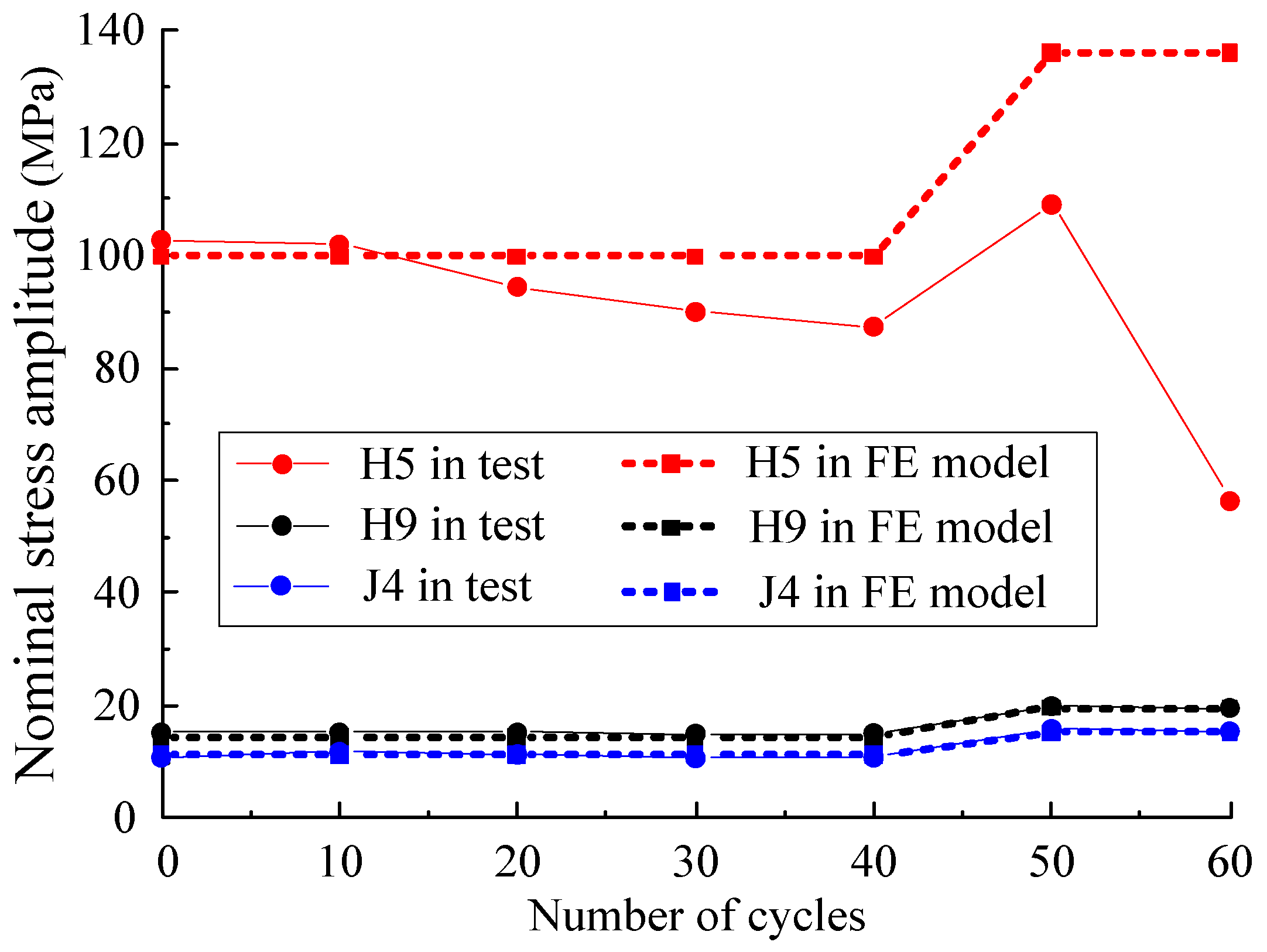
3.2. Fatigue Performance in Test
3.3. Fatigue Strength Evaluation
4. Conclusions
- (1)
- According to the results of the FE analysis, eccentric loading was determined as the unfavorable fatigue condition of the welded joints of the steel box girder with open longitudinal ribs after fatigue optimization design. In the experiment, the eccentric load condition was selected for fatigue loading.
- (2)
- The maximum nominal stress occurs at the edge of the weld toe between the transverse diaphragm and the top plate at the support edge of the load area, which is the fatigue-vulnerable position of the component. The nominal stresses of the weld between the transverse diaphragm and the longitudinal ribs, as well as the weld between the top plate and the longitudinal ribs, are very low.
- (3)
- The fatigue strengths corresponding to 2 million cycles of the nominal stress method and the hot-spot stress method, calculated based on the finite-element model and the number of experimental fatigue failure cycles, are 72.1 MPa and 93.8 MPa, respectively. It is reasonable to use the nominal stress S-N curve with a fatigue life of 2 million cycles at 70 MPa and the hot-spot stress S-N curve with a fatigue life of 2 million cycles at 90 MPa (FAT90) for the fatigue evaluation of welded joints in the fatigue design of steel box girders with open longitudinal ribs.
- (4)
- The initial stress of each measuring point is in good agreement with the finite-element calculation results. The static load measured stress of the fatigue-vulnerable position measuring point shows a certain decrease, while the stress of the other measuring points remains basically unchanged. Fatigue cracks penetrating the weld seam appeared at the fatigue-vulnerable position, and the number of fatigue failure cycles of the test component was 600,000.
- (5)
- Based on the slope of the main S-N curve in the equivalent structural stress method, the fatigue strength corresponding to 2 million cycles calculated by the finite-element model is 94.1 MPa, which is close to the results of the hot-spot stress method. This result is slightly lower than the corresponding result of the main S-N curve but within the range of two standard deviations of the curve. The equivalent structural stress method is applicable for evaluating the fatigue performance of steel box girders with open longitudinal ribs.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, Q.H.; Li, J.; Guo, Y.W.; Yuan, D.Y.; Bu, Y.Z. Fatigue Failure Modes and Resistance Evaluation of Orthotropic Steel Bridge Deck Structural System. China Civ. Eng. J. 2019, 52, 71–81. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, Q.H.; Cui, C.; Bu, Y.Z.; Li, Q. Study on Fatigue Features of Orthotropic Decks in Steel Box Girder of Hong Kong-Zhuhai-Macao Bridge. China Civ. Eng. J. 2014, 47, 110–119. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, Q.H.; Zhang, P.; Liu, Y.; Yu, J.; Ye, Z.T. Study on Fatigue Performance of Orthotropic Composite Bridge Deck with Large Longitudinal Ribs. China J. Highw. Transp. 2017, 30, 226–235. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, Q.H.; Li, J.; Yuan, D.; Zhu, J.Z.; Cui, C. Fatigue Model Tests of Orthotropic Steel Bridge Deck of Shenzhen-Zhongshan Link. China Civ. Eng. J. 2020, 53, 102–115. (In Chinese) [Google Scholar] [CrossRef]
- Ju, X.C. Experimental Study on Fatigue Performance of Full Penetration Welded Joints of U-shaped Rib-plate. China J. Highw. Transp. 2019, 32, 176–183. (In Chinese) [Google Scholar] [CrossRef]
- Heng, J.; Zheng, K.; Gou, C.; Zhang, Y.; Bao, Y. Fatigue Performance of Rib-to-deck Joints in Orthotropic Steel Decks with Thickened Edge U-ribs. J. Bridge Eng. 2017, 22, 04017059. [Google Scholar] [CrossRef]
- Zhang, S.; Shao, X.; Cao, J.; Cui, J.; Hu, J.; Deng, L. Fatigue Performance of a Lightweight Composite Bridge Deck with Open Ribs. J. Bridge Eng. 2016, 21, 04016039. [Google Scholar] [CrossRef]
- Ma, G.M.; Jin, X.N.; Li, W.X.; Zhao, Y.W. Research on Propagation Characteristics of Fatigue Crack for steel Bridge Decks with Open-Shaped Longitudinal Ribs. Ind. Constr. 2021, 51, 100–105. (In Chinese) [Google Scholar] [CrossRef]
- Xu, X.L.; Qian, S.B.; Li, H.T.; Wu, C.; Wang, R.G.; Li, Q.; Ding, X.G.; Li, Z.J.; Li, X.H. Comparative Test Study on Fatigue Performance of New Orthotropic Steel Bridge Decks with Open-Shaped Longitudinal Ribs. China Civ. Eng. J. 2025, 58, 50–67. (In Chinese) [Google Scholar] [CrossRef]
- Ministry of Transport, PRC. JTG D64-2015; Specifications for Design of Highway Steel Bridge. China Communications Press: Beijing, China, 2015. (In Chinese)
- National Railway Administration of the People's Republic of China. TB 10091-2017; Code for Design on Steel Structure of Railway Bridge. China Railway Publishing House: Beijing, China, 2017. (In Chinese)
- EN 1993-1-9; Eurocode 3: Design of Steel Structures, Part1-9: Fatigue Strength of Steel Structures. CEN: Brussels, Belgium, 2005.
- Intemational Institute of Welding. Recommendations for Fatigue Design of Welded Joints and Components; IIW document IIW-2259-15ex XIII-2460-13/XV-1440-13; Springer International Publishing: Cham, Switzerland, 2014. [Google Scholar]
- Dong, P. A structural stress definition and numerical implementation for fatigue analysis of welded joints. Int. J. Fatigue 2001, 23, 865–876. [Google Scholar] [CrossRef]
- American Society of Mechanical Engineers. Boiler and Pressure Vessel Code, Section III, Rules for Construction of Nuclear Power Plant Components, NB, Class 1 Components and Section VIII, Rules for Construction of Pressure Vessels; Division 2—Alternate Rules, American Society of Mechanical Engineers: New York, NY, USA, 1997. [Google Scholar]
- Zhang, Q.H.; Wei, C.; Xu, Z.; Yang, C.; Zhang, C.Q.; Cui, C. Experimental Study on Fatigue Performance of Integral Welded Joints in Steel Truss Bridges. China J. Highw. Transp. 2022, 35, 77–90. (In Chinese) [Google Scholar]
- Cui, C.; Liu, Y.M.; Liao, G.X. Fatigue Evaluation Approaches of Welded Joints on Orthotropic Steel Bridge Deck. J. Southwest Jiaotong Univ. 2015, 50, 1011–1017. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, Q.H.; Da, L.T.; Li, J.; Wang, K.; Yuan, D.; Cui, C.; Bu, Y. Fatigue Resistance of an Innovative Rib-to-deck Both-sides Welded Joint in Orthotropic Steel Bridge Deck. China Civ. Eng. J. 2022, 35, 162–174. (In Chinese) [Google Scholar] [CrossRef]
- National Railway Administration of the People’s Republic of China. TB 10002-2017; Code for Design on Railway Bridge and Culvert. China Railway Publishing House: Beijing, China, 2017. (In Chinese)
- National Railway Administration of the People’s Republic of China. TB 10092-2017; Code for Design of Concrete Structures of Railway Bridge and Culvert. China Railway Publishing House: Beijing, China, 2017. (In Chinese)
- Wang, Z.H.; Fang, Y.W.; Zhu, Z.B.; Huang, M.Q.; Wang, Y. Mechanical Performance Analysis of Bolted Steel Joints for New Prefabricated Railway Beam Steel Support Piers. Bull. Sci. Technol. 2024, 40, 89–96. (In Chinese) [Google Scholar]
- Huang, M.Q.; Wang, Y.; Shen, B.; Jia, Y.Q.; Wang, Z.H. Research on Ultimate Bearing Capacity and Mechanical Properties of New Steel Piers for Railway. J. Heilongjiang Inst. Technol. 2024, 38, 16–23. (In Chinese) [Google Scholar] [CrossRef]
- Dong, P.; Hong, J.K. The master S-N curve approach to fatigue of vessel and piping welds. Weld. World 2004, 48, 28–36. [Google Scholar] [CrossRef]
- Coletti, D.A.; Ream, A.P.; Chavel, B.W. Evaluation of Steel Bridge Details for Susceptibility to Constraint-Induced Fracture. Transp. Res. Rec. J. Transp. Res. Board 2022, 2679, 93–103. [Google Scholar] [CrossRef]
- Dong, P.; Prager, M.; Osage, D. The design master S-N curve in Asme Div 2 rewrite and its validations. Weld. World 2007, 51, 53–63. [Google Scholar] [CrossRef]






| Fatigue Assessment Method | Corresponding Stress Obtained by FE Analysis (MPa) | Theoretical Fatigue Life |
|---|---|---|
| Nominal stress method | 99.83 | 689,500 |
| Hot-spot stress method | 130.05 | 663,600 |
| Equivalent structural stress method | 128.02 | 918,600 |
| Fatigue Assessment Method | Fatigue Strength Obtained from Test (MPa) | Fatigue Strength Obtained from FE Model (MPa) |
|---|---|---|
| Nominal stress method | 65.7 | 72.1 |
| Hot-spot stress method | 82.5 | 93.8 |
| Equivalent structural stress method | / | 94.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, B.; Liu, M.; Wang, Y.; Zhuge, H. Research on Fatigue Strength Evaluation Method of Welded Joints in Steel Box Girders with Open Longitudinal Ribs. Crystals 2025, 15, 646. https://doi.org/10.3390/cryst15070646
Shen B, Liu M, Wang Y, Zhuge H. Research on Fatigue Strength Evaluation Method of Welded Joints in Steel Box Girders with Open Longitudinal Ribs. Crystals. 2025; 15(7):646. https://doi.org/10.3390/cryst15070646
Chicago/Turabian StyleShen, Bo, Ming Liu, Yan Wang, and Hanqing Zhuge. 2025. "Research on Fatigue Strength Evaluation Method of Welded Joints in Steel Box Girders with Open Longitudinal Ribs" Crystals 15, no. 7: 646. https://doi.org/10.3390/cryst15070646
APA StyleShen, B., Liu, M., Wang, Y., & Zhuge, H. (2025). Research on Fatigue Strength Evaluation Method of Welded Joints in Steel Box Girders with Open Longitudinal Ribs. Crystals, 15(7), 646. https://doi.org/10.3390/cryst15070646






