Abstract
This study investigates the coupling mechanism between a parabolic notch and dislocations in one-dimensional (1D) hexagonal piezoelectric quasicrystals (PQCs) based on the theory of complex variable functions. By applying perturbation techniques and the Cauchy integral, analytical solutions for complex potentials are derived, yielding closed-form expressions for the phonon–phason stress field and electric displacement field. Numerical examples reveal several key findings: significant stress concentration occurs at the notch root, accompanied by suppression of electric displacement; interference patterns between dislocation cores and notch-induced stress singularities are identified; the J-integral quantifies distance-dependent forces, size effects, and angular force distributions reflecting notch symmetry; and the energy-driven dislocation slip toward free surfaces leads to the formation of dislocation-free zones. These results provide new insights into electromechanical fracture mechanisms in quasicrystals.
1. Introduction
Quasicrystals (QCs) have demonstrated tremendous potential in aerospace, micro-electromechanical systems (MEMS), and flexible electronic devices since their discovery in rapidly quenched Al-Mn alloys by Shechtman in 1982 [1]. These materials exhibit unique quasiperiodic structures (possessing long-range order without translational symmetry) and exceptional physical properties (such as low thermal conductivity, high hardness, and negative temperature coefficient). As an important subclass of quasicrystals, 1D hexagonal PQCs display sixfold rotational symmetry in the plane perpendicular to the quasiperiodic direction while maintaining a periodic arrangement along the quasiperiodic direction. Their mechanical behavior requires a coupled description through both the phonon field (describing atomic displacements) and phason field (characterizing the phase ordering of quasiperiodic structures). When piezoelectric effects are incorporated, these materials further exhibit mechano-electrical coupling characteristics: mechanical loading induces electrical polarization (direct piezoelectric effect) while applied electric fields generate mechanical strain (converse piezoelectric effect). Notably, the coupling between the phason field and electric field produces nonzero piezoelectric constants distinct from conventional piezoelectric crystals, significantly increasing the complexity of constitutive relations [2]. Recent studies on fracture mechanics in 1D hexagonal PQCs have achieved remarkable progress across multiple domains, including elastoplastic fracture mechanics, dynamic response, nanoscale defects, and multi-crack interactions. Notably, Zhang et al. [3] derived the inhibitory effect of electric field saturation zones on the J-integral using Fourier transforms and singular integral equations, establishing a theoretical framework for anti-fatigue design in quasicrystalline devices. In investigations of dynamic fracture behavior, Ma et al. [4,5] solved Cauchy singular integral equations to obtain dynamic stress intensity factors for interfacial cracks in coating–substrate systems subjected to plane waves and Love waves. For nanoscale defect characterization, Su et al. [6,7] and Xin et al. [8] applied Gurtin–Murdoch (G-M) elasticity theory to elucidate Mode III fracture mechanisms. Additionally, studies on complex crack configurations have addressed anti-plane problems of double cracks at rhombic holes (Liu et al. [9]), secondary quadruple cracks near lip-shaped apertures (Wang et al. [10]), and asymmetric crack propagation at elliptical hole boundaries (Zhang et al. [11]).
Quasicrystals exhibit exceptional hardness properties, yet this characteristic also renders them susceptible to crack initiation and dislocation generation under external mechanical loading. Dislocations, as critical defects within crystalline structures, play a pivotal role in mediating plastic deformation and stress redistribution. The formation and propagation of these defects significantly influence the mechanical performance and fatigue resistance of quasicrystal materials. This line of investigation traces its origins to foundational studies by Volterra, Weingarten, and Somigliana in the early 20th century [12], who pioneered the theoretical framework for analyzing stress fields around dislocations in conventional crystals. Subsequent advancements were achieved through systematic reviews by Yang Shunhua and Ding Dihua [13,14], who established the theoretical foundations of linear elasticity and dislocation mechanics specifically tailored to quasicrystalline systems. Subsequent research has extensively explored dislocation–defect interactions. Pi et al. [15] employed conformal mapping to investigate the interaction between screw dislocations and two unequal interfacial cracks in 1D hexagonal PQC bimaterials, deriving analytical expressions for interfacial stresses, electric displacements, and field intensity factors. Similarly, Zhang et al. [16] applied complex variable methods to analyze the interference between elliptical inclusions and screw dislocations. Jiang et al. [17] introduced the wedge-shaped crack model from classical elasticity into piezoelectric quasicrystals using conformal mapping and perturbation techniques, obtaining analytical solutions for stress intensity factors and dislocation forces. Pi et al. [18] discovered distinctive singularities in phonon and phason stress components near the core of moving screw dislocations. Through analytical continuation techniques, Li and Cui [19,20,21] successively solved three fundamental problems (i) screw dislocation–crack interactions in semi-infinite quasicrystals, (ii) fracture problems in finite wedge-shaped specimens containing dislocations, and (iii) interactions between screw dislocations and elliptical holes with asymmetric cracks—all yielding explicit complex potentials and general solutions for generalized stress fields, intensity factors, and image forces. Parallel work by Li and Zhao [22,23,24] examined dislocation behaviors in quasicrystal bimaterials, specifically addressing screw dislocation–interface interactions and their coupling with interfacial wedge cracks. Contemporary research focuses not only on dislocation–defect (cracks, voids, inclusions) interactions but also on defect interplay and their collective impact on material performance. The unique quasiperiodic structure and multifield coupling properties of 1D hexagonal PQCs present both advantages for applications and challenges for fundamental understanding. These studies substantially advance the knowledge of PQCs while providing theoretical foundations for their applications in energy harvesting, sensing technologies, and nanoelectromechanical systems.
Notches represent a category of geometric defects present on material surfaces or within bulk structures, exhibiting distinct stress concentration effects that have garnered significant attention in materials science and engineering fields. When the root of a notch is sharply tapered, it manifests as a V-shaped notch or wedge-shaped crack, while smooth root geometries correspond to parabolic notches. Doitrand and Leguillon [25] established a plasticity-incorporated coupled criterion for evaluating brittle crack initiation, which was experimentally validated through bending tests on V-notched steel specimens. Complementary studies by Bahrami et al. [26] on crack deflection in marble, Gou and Mallikarjunaiah [27] on three-dimensional nonlinear strain-limited elastic fields near V-crack tips, and Iizuka and Tanaka [28] on grain size effects on wedge crack initiation under high-temperature low-cycle fatigue conditions have collectively enriched our understanding of V-notch mechanics through combined experimental and theoretical approaches.
The stress concentration characteristics of parabolic notches were systematically investigated by Kazberuk et al. [29], who employed boundary transformation methods to analyze stress distributions around both elliptical holes and parabolic notches in quasi-orthotropic planes. This work was extended by Savruk [30] through a detailed examination of stress concentration phenomena at curved holes and non-smooth notches, with particular emphasis on quantitative evaluation using stress concentration factors. Ma et al. [31,32] conducted a detailed investigation into the interaction between parabolic notches and edge dislocations, deriving the dislocation driving force induced by notch configurations based on the vector J-integral. Subsequently, they developed an analytical solution for the interaction between a semi-infinite wedge and generalized singularities, obtaining the dislocation driving force caused by the wedge geometry when the singularity was treated as a dislocation. These studies not only deepen our understanding of the fracture behavior of parabolic notches but also provide a critical theoretical foundation for material design and failure prediction in practical engineering applications.
The analysis of how complex defects and screw dislocations influence the properties of piezoelectric quasicrystals represents a key research focus at the intersection of materials science and solid-state physics. Compared to classical materials, fracture mechanics in 1D hexagonal PQCs involves more intricate constitutive relations due to their unique quasiperiodic structure and coupled phonon–phason–electrical fields. A screw dislocation, characterized by a spiral atomic displacement along the dislocation line, is a fundamental line defect in crystalline materials. While the interaction between dislocations and various defects (e.g., cracks, inclusions) has been extensively studied, parabolic notches—a special type of geometric defect—remain unexplored in piezoelectric quasicrystals. Both defects, as non-ideal microstructures, significantly affect the mechanical and electromechanical properties of these materials. In this study, we employ the complex variable method to systematically investigate the interference effect between a parabolic notch and a screw dislocation in 1D hexagonal PQCs. The paper is organized as follows: Section 2 presents the physical model and governing equations. Section 3 details the derivation of the complex potentials for the dislocation and the perturbed field. Numerical case studies are conducted in Section 4 to analyze the defect interaction mechanisms. Section 5 derives the driving force acting on the dislocation and examines the parametric dependencies. Finally, Section 6 summarizes the key findings and implications.
2. Physical Model and Fundamental Equations
2.1. Physical Model of the Problem
This investigation examines an infinite 1D hexagonal PQC containing a parabolic notch. Let region denote the matrix material and region represent the notch domain. A screw dislocation parallel to the quasiperiodic -direction exists in the matrix material, characterized by the Burgers vector , where is the displacement jump in the phonon field, is the displacement jump in the phason field, is the electric potential jump, as illustrated in Figure 1.
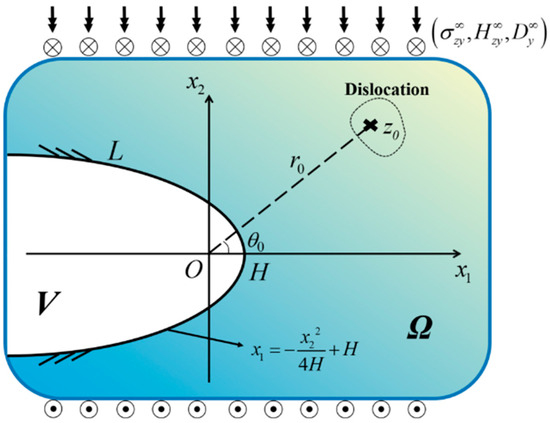
Figure 1.
Interaction between a parabolic notch and a screw dislocation in 1D hexagonal PQCs.
The parabola has its focus at the origin , and its mathematical representations in polar and Cartesian coordinate systems are respectively given by [31]:
2.2. Fundamental Equations of the Problem
The constitutive equations for 1D hexagonal PQCs are given as follows [33]:
The geometric equations are:
The equilibrium equations are:
where , represent the strain, stress, and displacement in the phonon field, respectively; denote the strain, stress, and displacement in the phason field, respectively; indicate the electric field, electric displacement, and electric potential, respectively; are the independent elastic constants of the phonon and phason fields; represent the piezoelectric constants of the phonon and phason fields, respectively; are the dielectric constant and the coupling elastic constant between phonon and phason fields, respectively.
The equations satisfy the following symmetry relations:
When considering defects penetrating along both the quasiperiodic atomic arrangement direction and the electric polarization direction, both along the positive -axis, the deformation becomes independent of variable , meaning all variables satisfy:
For anti-plane deformation in 1D hexagonal PQCs, the fundamental Equations (2)–(4) can be simplified as:
where i = 1,2. The material coefficient matrix and generalized displacement function vector are defined as:
The matrix is non-singular. Substituting Equations (5) and (6) into Equation (7) yields the following governing equation:
According to the properties of analytic functions, the general solution of the harmonic Equation (11) can be expressed by an analytic function vector as follows:
From Equations (7) and (12), we obtain the complex representations of the phonon field stress, phason field stress, and electric displacement:
Equation (13) leads to:
Considering the boundary conditions shown in Figure 2, where represents the resultant normal traction, curve denotes an arbitrary boundary segment , and is the arc length measured from point to point along the boundary, the geometric relationship gives:
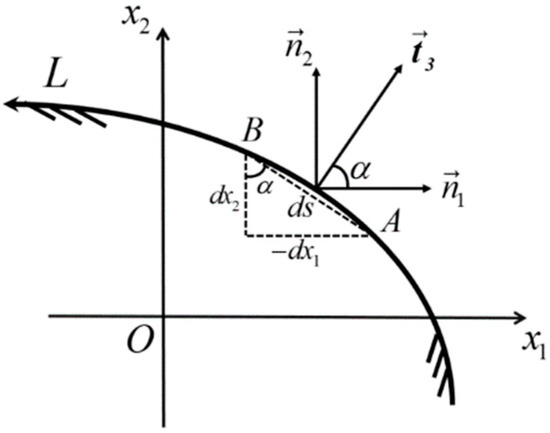
Figure 2.
The geometric relationships of boundary conditions for 1D hexagonal PQCs.
The complex representation of the resultant traction acting on any arc is then:
Based on the above analysis, once the analytic function vector is established under the specified boundary conditions, the corresponding solutions for mechanical fields (stress, strain, displacement) in both phonon and phason components, as well as electrical quantities including displacement, field, and potential, can be derived analytically.
3. Problem Solution
Based on the physical model, the analytic function vector can be expressed in the following form:
where represents the complex potential of the screw dislocation in the complex plane undisturbed by the parabolic notch, and denotes the complex potential of the part perturbed by the parabolic notch, which is determined by the curved boundary conditions.
3.1. Solution for the Dislocation Complex Potential
The force condition at the dislocation core is given by:
Here, the integral curve represents the Burgers circuit around the dislocation . From Equation (19), can be expressed as:
3.2. Complex Potential of the Perturbation Field
To simplify the physical modeling, the original domain in the physical -plane (see Figure 3a) is conformally mapped onto a mathematical domain in the -plane, where the base material region corresponds to the upper half-plane , and the notch region maps to the lower half-plane (see Figure 3b). Through this transformation, the parabolic boundary becomes a straight line, enabling easier analysis. The mapping yields the coordinate correspondences , , and , as illustrated in Figure 4.
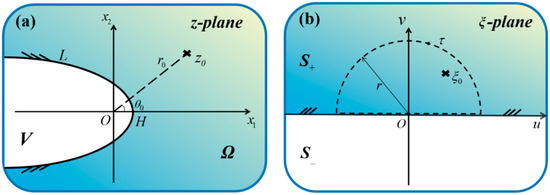
Figure 3.
(a) Physical plane and (b) mathematical plane.
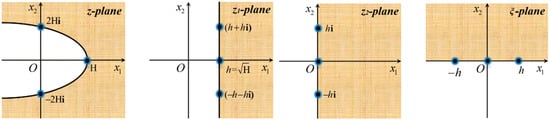
Figure 4.
The conformal mapping transformation process.
The transformation process is as follows:
The composite conformal mapping is given by [31]:
Based on the mapping relationship, let denote the function of after mapping. Equation (18) can then be rewritten as:
Thus,
Using the conformal mapping, Equation (15) can be transformed into:
Since the free boundary is traction-free, the boundary condition is:
Substituting Equation (23) into Equation (25) yields:
Further substituting Equation (24) into Equation (27) gives:
According to Liourille’s theorem, assuming is holomorphic in and singular in , then is holomorphic in and singular in . By applying the Cauchy integral, which connects the function values in the analytic region with the integral values on the boundary, we multiply both sides of Equation (28) by and integrate along the curve , where is any point inside the curve:
Rearranging Equation (28) gives:
This demonstrates that is holomorphic in region , confirming the earlier assumption.
Substituting into Equation (30) yields:
By substituting Equations (20) and (31) into Equation (18), the analytic function vector can be expressed as:
Omitting the constant , which does not affect the results, and noting that is real, we obtain , simplifying the above expression to:
The analytic function vector for this problem has now been solved. Substituting it into Equations (10) and (11) provides the analytical solutions for the stress field, strain field, and generalized displacement.
4. Case Study
We select the material constants for 1D hexagonal PQCs [34] and values of Burgers vectors for a screw dislocation [22]. The specific data are listed in Table 1.

Table 1.
Material constants of 1D hexagonal PQCs and values of Burgers vectors for a screw dislocation.
By differentiating Equation (33), we obtain:
Substituting into Equation (11) yields:
The phonon stress field, phason stress field, and electric displacement field exhibit distinct characteristics, governed primarily by material parameters , , and , respectively. If normalized using a uniform scaling factor, certain physical quantities may be excessively compressed in numerical range, leading to blurred contour plots that fail to reflect their true distributions. To address this, each field should be normalized by its respective characteristic stress, ensuring comparable dimensionless magnitudes across all stress components. This approach enhances both scientific rigor and visual clarity in comparative analyses. The dimensionless scaling factors are defined as follows:
The parabolic notch under investigation exhibits symmetry about the -axis. To clearly visualize the distribution patterns of the stress and electric displacement fields, we simplify the analysis by positioning the dislocation core along the -axis. By substituting the relevant parameters into Equation (35) and incorporating the normalization factors from Equation (36), with the dislocation core located at point and the parabolic notch size set as , we obtain the dimensionless contour plots for the phonon stress field, phason stress field, and electric displacement field (Figure 5, Figure 6 and Figure 7).
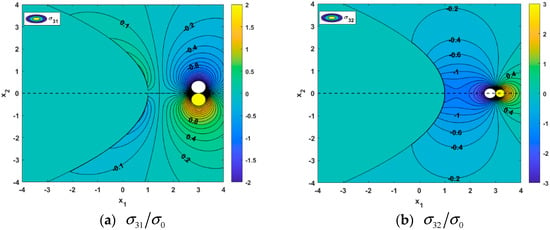
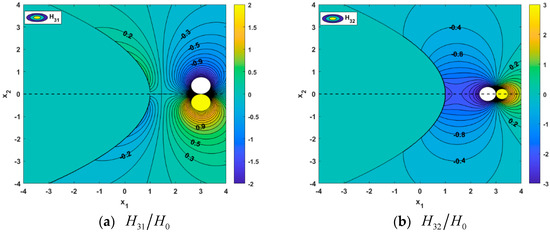
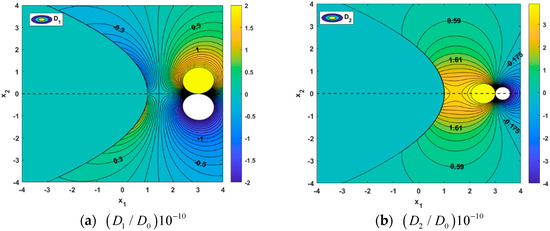

Figure 5.
Contour of phonon stress with dislocation at (3, 0) (a) ; (b).

Figure 6.
Contour of phason stress with dislocation at (3,0) (a) ; (b) .

Figure 7.
Contour of electric displacement with dislocation at (3,0) (a); (b) .
Analysis of the contour distributions in Figure 5, Figure 6 and Figure 7 reveals two key findings: (1) The phonon and phason stress fields display comparable patterns, in contrast to the opposing behavior observed in the electric displacement field. Although phonon stresses originate from lattice vibrations (long-range elastic response) and phason stresses arise from polar distortions (short-range or local elastic response)—suggesting distinct distributions—their combined action in the fracture behavior of piezoelectric quasicrystals creates a superimposed field near defects. The normalization process brings their magnitudes to comparable levels, resulting in locally similar contour patterns near the notch and dislocation. Notably, as the stress field intensifies near defects, the piezoelectric effect suppresses the local concentration of electric displacement through charge redistribution, leading to weakened electric displacement in stress concentration zones and demonstrating a complementary “see-saw” distribution pattern. (2) The contour plots of components , , and exhibit antisymmetric variations about the origin, while those of , , and show symmetric variations. All fields display singularities at the dislocation core . The dislocation-induced lattice distortion alters atomic bonding states around the dislocation line, generating localized stress fields. For screw dislocations specifically, the surrounding atoms experience tangential stresses, with these atomic-scale distortions manifesting macroscopically as stress singularities near the dislocation core. Furthermore, the influence of the dislocation stress field introduces an “image dislocation” on the opposite side of the notch’s free surface, creating a corresponding “image stress field” that produces similar symmetric and antisymmetric gradient distributions. Consequently, near the notch root, the magnitudes of the phonon and phason stresses, along with the electric displacement, increase substantially and demonstrate sharper gradients.
5. Driving Force on the Dislocation
In elastic media, dislocations can be characterized as singular stress sources that induce characteristic stress fields in their vicinity. When a dislocation approaches a stress-free surface of a defect, the boundary condition requiring zero traction at the free surface necessitates the introduction of a virtual “image dislocation” symmetrically positioned on the opposite side of the boundary.
The elastic strain energy in the system is affected by the position of the dislocation, which experiences a driving force due to the free surface in the material. This force can be evaluated using the J-integral, originally introduced by Eshelby [35] and later by Cherepanov [36] and Rice [37] in fracture mechanics. The components and are given by:
Here, refers to the closed contour enclosing the dislocation, denotes the outward normal to the path, is the total force along this contour, represents the out-of-plane displacement, and is the strain energy density. The quantities and are contour-independent and correspond to the driving force components in the and directions at the dislocation site. Therefore, the resulting combined driving force can be formulated as [38]:
where . Setting and substituting into Equation (38), we obtain:
The normalized components are:
According to Equation (40), Figure 8 presents the variation of the normalized driving force component as angular parameter for different values of . To maintain generality in our analysis, we assume and set . Taking into account both the periodic nature of the system and the geometric configuration of the notch, the results are specifically shown for the angular range .
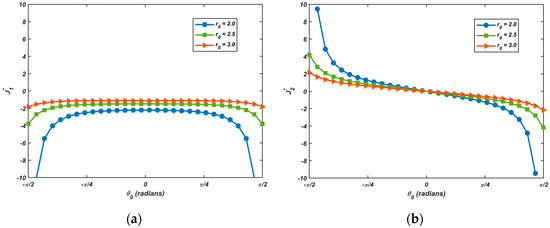
Figure 8.
Relationship of normalized
with for varying (a) Normalized ; (b) Normalized .
As shown in Figure 8a, the curve exhibits symmetry about with all values being negative (). At , this indicates an attractive force component along the -direction from the free surface to the dislocation. Within , decreases monotonically with increasing , demonstrating weakened attraction as the dislocation core moves away from the free surface. Due to the -axis symmetry of the parabolic notch, the attraction intensifies again when as the dislocation core approaches the surface. Notably, this trend becomes more pronounced at smaller values. These results confirm that the -component attractive force strengthens with decreasing dislocation–surface distance.
As shown in Figure 8b, the curve exhibits antisymmetry about . Within the angular range , the driving force component increases monotonically with increasing . Since the force direction opposes the predefined positive orientation, this behavior can be physically interpreted as a repulsive interaction, where the repulsive force gradually weakens as the dislocation core moves away from the free surface. Notably, within the narrower angular range , the inherent -axis symmetry of the parabolic notch causes the dislocation core to approach the free surface again with increasing , resulting in a progressively stronger attractive force aligned with the positive direction. This trend becomes more pronounced for smaller values of . These observations collectively demonstrate that the -component of the driving force (whether attractive or repulsive) exhibits significant enhancement when the dislocation is in close proximity to the notch surface.
Figure 9 presents the variation in the normalized driving force component as parameter under different values, with general conditions assumed as and . Consistent with previous analyses, when , both and exhibit negative values, indicating attractive forces whose characteristics become more distinctly resolved through systematic variations. At , denotes the absence of force interaction, while demonstrates a gradual decrease with increasing . This inverse relationship confirms that the attractive force from the free surface intensifies as the dislocation core approaches the boundary. Notably, under the condition , the attractive force abruptly “vanishes” at (extreme proximity of dislocation core to free surface), resulting in dislocation-free zone formation. This phenomenon persists under specific parametric conditions: at and , the attractive force abruptly “vanishes” when and , respectively. For the case , geometric constraints imposed by the parabolic boundary (vertex at ) lead to dislocation-free zone generation precisely at . These collective results demonstrate that when dislocations approach critical proximity to notch-free surfaces, the attractive force generated by the surface image force balances the short-range repulsive force, resulting in a net driving force of zero. This leads to the formation of a dislocation-free zone. This mechanical response represents a fundamental shielding effect whereby crystal defects modulate dislocation interactions through localized stress field cancellation. The parametric sensitivity revealed in this analysis provides quantitative criteria for predicting dislocation-free zone formation in piezoelectric quasicrystalline materials.
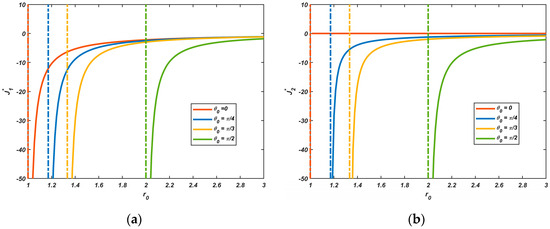

Figure 9.
Relationship of normalized with for varying (a) Normalized ; (b) Normalized .
Figure 10 presents the variation in the normalized driving force component as parameter for different values of , with . Here, represents the geometric parameter of the parabolic notch, which determines both the size and position of the notch. When , indicates no force interaction, consistent with the analysis in Figure 8 and Figure 9. The increases progressively with increasing . As parameter increases, corresponding to an enlargement of the parabolic notch, the free surface of the notch approaches closer to the dislocation core, resulting in stronger attractive forces. This finding agrees well with the previous numerical analysis results. The figure further demonstrates that when (corresponding to ), at , the attractive force vanishes, creating a dislocation-free zone. Similarly, under conditions of and , dislocation-free zones emerge at and , respectively. These results collectively indicate that larger angle values require smaller critical values to form dislocation-free zones near the boundary. This shielding effect arises from the combined influence of notch size and dislocation position.
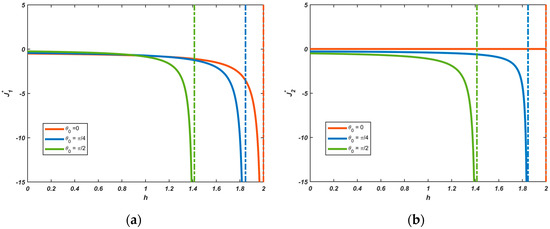

Figure 10.
Relationship of normalized with for varying (a) Normalized ; (b); Normalized .
The Burgers vector component (glide force) is given by reference [39] as:
After normalization, it becomes:
Figure 11 demonstrates the variation in the normalized glide force as parameter under the condition , while considering different cases with . As derived from Equation (41), the glide force magnitude shows direct proportionality to both the stiffness matrix constants of the material and the magnitude of the dislocation’s Burgers vector, indicating that stiffer materials or dislocations with larger Burgers vectors generate stronger glide forces. The trend analysis in Figure 11 clearly shows that the glide force decreases with increasing parameter and increases with increasing parameter , indicating that larger notch geometries result in greater glide forces at a given location, while closer proximity between the dislocation and defect leads to stronger glide forces.
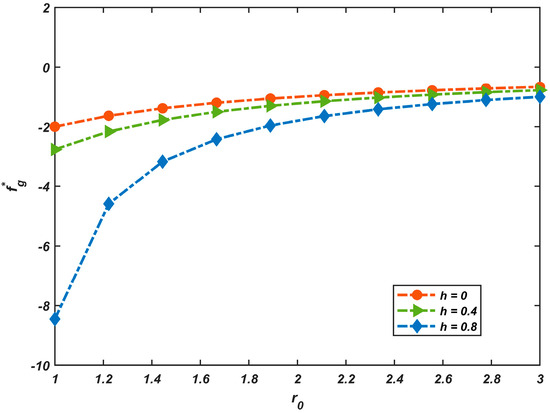
Figure 11.
Relation of normalized driving force with for varying .
This force drives the dislocation to glide towards the free surface along the direction of the Burgers vector. As the dislocation continuously approaches the boundary, its associated stress field redistributes, and the local elastic energy induced by the dislocation in the system gradually decreases. When the dislocation finally reaches the free surface and “escapes” from the crystal, its distortion field vanishes, and the local lattice recovers its integrity. This signifies the accomplishment of a slip displacement equal to one Burgers vector. This process is accompanied by a significant release of elastic energy, exemplifying the system’s evolution towards a lower energy state. Previous studies [40] have directly observed, via TEM, the process where dislocations emitted from a source glide to the surface and are eliminated in submicron Al single crystals. This confirms that if dislocations cannot multiply or stably exist within the crystal, they will ultimately be eliminated by gliding to a free surface.
6. Conclusions
This work explores the interaction between a screw dislocation and a parabolic notch in one-dimensional hexagonal piezoelectric quasicrystals, employing the complex variable approach. Closed-form solutions for both the stress field and electric field are obtained. Numerical analysis reveals the shielding effect induced by the parabolic notch on nearby screw dislocations, predicting the existence of a dislocation-free zone. The J-integral is employed to evaluate both the resultant driving force acting on the screw dislocation and the glide force along the Burgers vector direction. Furthermore, systematic investigations are conducted on the influence of angular position, separation distance, and notch size on the driving force components and glide force. The main conclusions are summarized as follows:
- The phonon and phason stress fields exhibit synergistic enhancement near the defect, while the piezoelectric effect suppresses the local concentration of the electric displacement field. This leads to an opposite distribution trend where the electric displacement decreases in stress concentration zones, with maximum amplitude and variation rate occurring at the notch root.
- The screw dislocation generates a stress singularity, and symmetric stress fields emerge near the free surface of the notch due to image dislocations. The mutual interference between the dislocation and notch causes dramatic changes in local stress gradients. Significant stress concentrations are observed at both the notch root and dislocation core, potentially increasing fracture susceptibility.
- The J-integral analysis demonstrates that the attractive driving force exerted by the notch on the dislocation intensifies markedly with decreasing separation distance and shows a positive correlation with notch size. The angular dependence of force components displays both symmetric and antisymmetric characteristics, fundamentally governed by the geometric symmetry of the notch configuration.
- The screw dislocation glides toward the free surface along the Burgers vector direction, experiencing a glide force inversely proportional to the separation distance. Upon reaching and “escaping” from the surface, a small dislocation-free zone forms. This process releases the lattice distortion and stored elastic energy carried by the dislocation, resulting in a reduction of the total system energy.
Author Contributions
Y.G.: Conceptualization, methodology, writing – original draft. G.L.: Resources, supervision, project administration, funding acquisition. C.W.: Software, validation, writing – review & editing. J.F.: Validation, formal analysis, visualization. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (Grant No. 12162027), the Natural Science Foundation Key Project of Inner Mongolia Autonomous Region (2024ZD21), the First-Class Disciplines Project Inner Mongolia Autonomous Region, China (Grant No. YLXKZX-NSD-001), and Inner Mongolia Normal University Basic Research Operating Expenses (2023JBZD005).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Shechtman, D.; Blech, I.; Gratias, D.; Cahn, F.W. Metallic phase with long-range orientational order and no translational symmetry. Phys. Rev. Lett. 1984, 53, 1951–1953. [Google Scholar] [CrossRef]
- Fan, T.Y. Mathematical Theory of Elasticity of Quasicrystals and Its Applications; Springer: Singapore, 2016. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, G.T.; Liao, H. A plastic analysis of Griffith crack problem in 1D hexagonal piezoelectric quasicrystals. Sci. Rep. 2025, 15, 18769. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Zhao, X.; Lu, S.; Yang, J.; Zhou, Y.; Ding, S. Dynamic Behavior of Interface Cracks in 1D Hexagonal Piezoelectric Quasicrystal Coating–Substrate Structures Subjected to Plane Waves. J. Eng. Mech. 2024, 150, 04024090-1. [Google Scholar] [CrossRef]
- Ma, Y.Y.; Zhou, Y.T.; Zhao, X.F.; Lu, S.N.; Ding, S.H. Analysis of Interface Crack between One-Dimensional Hexagonal Piezoelectric Quasicrystal Coating and Substrate under Love Wave Impact. J. Ningxia Univ. (Nat. Sci. Ed. Chin. Eng.) 2025, 1, 2+16–23. (In Chinese) [Google Scholar]
- Su, M.; Xiao, J.; Feng, G.; Xia, X. Mode-III fracture of a nanoscale cracked hole in one-dimensional hexagonal piezoelectric quasicrystals. Int. J. Mech. Mater. Des. 2022, 18, 423–433. [Google Scholar] [CrossRef]
- Su, M.; Xiao, J. Model III fracture analysis of a nanoscale elliptical hole with four cracks in one-dimensional hexagonal piezoelectric quasicrystals. Eng. Fract. Mech. 2022, 274, 108776. [Google Scholar] [CrossRef]
- Xin, Y.; Xiao, J. An analytic solution of an arbitrary location through-crack emanating from a nano-circular hole in one-dimensional hexagonal piezoelectric quasicrystals. Math. Mech. Solids. 2023, 29, 71–82. [Google Scholar] [CrossRef]
- Liu, X.W.; Yang, Y.L.; Wang, Z.Q. Propagation Behavior of Double Cracks from a Rhombic Hole in One-Dimensional Hexagonal Piezoelectric Quasicrystals. Math. Pract. Theory 2025, 2, 149–157. (In Chinese) [Google Scholar]
- Wang, C.Y.; Liu, G.T. Anti-Plane Problem of Four Secondary Cracks Originating from a Lip-Shaped Hole in One-Dimensional Hexagonal Piezoelectric Quasicrystals. Appl. Math. Mech. 2024, 7, 886–897. (In Chinese) [Google Scholar]
- Zhang, B.C.; Ding, S.H.; Zhang, B.W.; Zhang, L.P. Fracture Behavior of Asymmetric Cracks at an Elliptical Hole Edge in One-Dimensional Hexagonal Piezoelectric Quasicrystal Bimaterials. Sci. Technol. Eng. 2024, 29, 12422–12430. (In Chinese) [Google Scholar]
- Nabarro, F.R.N. Theory of Crystal Dislocations; Oxford University Press: Oxford, UK, 1967. [Google Scholar]
- Yang, S.H.; Ding, D.H. Fundamentals of Dislocation Theory in Crystals; Science Press: Beijing, China, 1998; Volume 2. (In Chinese) [Google Scholar]
- Ding, D.H.; Wang, R.H.; Yang, W.G.; Hu, C.Z. General expressions for the elastic displacement fields induced by dislocations in quasicrystals. J. Phys. Condens. Matter 1995, 7, 5423–5436. [Google Scholar] [CrossRef]
- Pi, J.D.; Zhao, Y.; Li, L.H. Interaction between a Screw Dislocation and Two Unequal Interface Cracks Emanating from an Elliptical Hole in One Dimensional Hexagonal Piezoelectric Quasicrystal Bi-Material. Crystals 2022, 12, 314. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, X.; Ding, S. Analytical Solution of the Interference between Elliptical Inclusion and Screw Dislocation in One-Dimensional Hexagonal Piezoelectric Quasicrystal. Crystals 2023, 13, 1419. [Google Scholar] [CrossRef]
- Jiang, L.J.; Liu, G.T. The interaction between a screw dislocation and a wedge-shaped crack in one-dimensional hexagonal piezoelectric quasicrystals. Chin. Phys. B 2017, 26, 044601. [Google Scholar] [CrossRef]
- Pi, J.D.; Zhou, Y.B.; Liu, G.T. Elastic Analysis of a Moving Screw Dislocation in One-Dimensional Hexagonal Piezoelectric Quasicrystalline Materials. Chin. J. Appl. Mech. 2021, 1, 388–395. [Google Scholar]
- Cui, X.W.; Li, L.H. Interaction Between Screw Dislocations and Cracks in Semi-Infinite One-Dimensional Hexagonal Piezoelectric Quasicrystals. J. Inner Mongolia Norm. Univ. Nat. Sci. Ed. 2018, 47, 465–469. (In Chinese) [Google Scholar]
- Cui, X.W.; Li, L.H. Anti-Plane Problem of Wedge-Shaped Bodies with Screw Dislocations in Finite-Sized One-Dimensional Hexagonal Piezoelectric Quasicrystals. Chin. J. Appl. Mech. 2019, 36, 1058–1062+1257. (In Chinese) [Google Scholar]
- Li, L.H.; Cui, X.W.; Guo, J.H. Interaction between a screw dislocation and an elliptical hole with two asymmetrical cracks in a one-dimensional hexagonal quasicrystal with piezoelectric effect. Appl. Math. Mech. 2020, 41, 899–908. [Google Scholar] [CrossRef]
- Li, L.H.; Zhao, Y. Interaction of a Screw Dislocation with Interface and Wedge-Shaped Cracks in One-Dimensional Hexagonal Piezoelectric Quasicrystals Bimaterial. Math. Probl. Eng. 2019, 1, 1037297. [Google Scholar] [CrossRef]
- Zhao, Y.; Yu, J.; Li, L.H. Screw Dislocations in One-Dimensional Hexagonal Piezoelectric Bimaterials. J. Inner Mongolia Norm. Univ. Nat. Sci. 2019, 48, 200–204. (In Chinese) [Google Scholar]
- Zhao, Y.; Li, L.H. Screw Dislocations in Semi-Infinite One-Dimensional Hexagonal Piezoelectric Bimaterials. Math. Pract. Theory 2019, 49, 184–190. (In Chinese) [Google Scholar]
- Doitrand, A.; Leguillon, D. V-notch crack initiation by the coupled criterion considering plasticity. Int. J. Fracture. 2025, 249, 2. [Google Scholar] [CrossRef]
- Bahrami, B.; Bahadori, A.; Petru, M.; Nejati, M.; Ayatollahi, M.R. Experimental and theoretical assessment of crack kinking in marble stones in the presence of a V-notch under mode I loading. Constr. Build. Mater. 2022, 357, 129371. [Google Scholar] [CrossRef]
- Gou, K.; Mallikarjunaiah, S.M. Finite element study of V-shaped crack-tip fields in a three-dimensional nonlinear strain-limiting elastic body. Math. Mech. Solids. 2023, 28, 2155–2176. [Google Scholar] [CrossRef]
- Iizuka, H.; Tanaka, M. Effects of grain size on wedge-type crack initiation in low-cycle fatigue at high temperature. Mater. High Temp. 1991, 9, 17–22. [Google Scholar] [CrossRef]
- Kazberuk, A.; Savruk, M.P.; Chornen’kyi, A.B. Stress Concentration Near an Elliptic Hole or a Parabolic Notch in a Quasiorthotropic Plane. Mater. Sci. 2016, 52, 295–304. [Google Scholar] [CrossRef]
- Savruk, M.P. Stress Concentration Near Curvilinear Holes and Notches with Nonsmooth Contours. Mater. Sci. 2021, 57, 331–343. [Google Scholar] [CrossRef]
- Ma, L.F.; Hills, D.A. Interaction of a parabolic notch with a generalized singularity. Int. J. Eng. Sci. 2022, 176, 103685. [Google Scholar] [CrossRef]
- Ma, L.F.; Hills, D.A. A wedge of arbitrary angle interacting with a generalized singularity. Int. J. Solids Struct. 2023, 262, 112062. [Google Scholar] [CrossRef]
- Altay, G.; Dokmeci, M.C. On the fundamental Eqs. of piezoelasticity of quasicrystal media. Int. J. Solids Struct. 2012, 49, 3255–3262. [Google Scholar] [CrossRef]
- Li, Y.; Li, Y.; Qin, Q.H.; Yang, L.Z.; Zhang, L.L.; Gao, Y. Axisymmetric bending analysis of functionally graded one-dimensional hexagonal piezoelectric quasi-crystal circular plate. Proc. R. Soc. Lond. A 2020, 476, 20200301. [Google Scholar] [CrossRef] [PubMed]
- Eshelby, J.D. The Force on an Elastic Singularity. Philosophical Transactions of the Royal Society of London. Math. Phys. Sci. Ser. A 1951, 244, 87–112. [Google Scholar]
- Cherepanov, G.P. The Propagation of Cracks in a Continuous Medium.Journal of Applied Mathematics and Mechanics. J. Appl. Math. Mech. 1967, 31, 503–512. [Google Scholar] [CrossRef]
- Rice, J.R. A Path Independent Integral and the Approximate Analysis of Strain Concentration by Notches and Cracks. J. Appl. Mech. 1968, 35, 379–386. [Google Scholar] [CrossRef]
- Bidiansky, B.; Rice, J.R. Conservation Laws and Energy-Release Rates. J. Appl. Mech. 1973, 40, 201–203. [Google Scholar] [CrossRef]
- Stagni, L. Edge dislocation near an elliptic inhomogeneity with either an adhering or a slipping interface a comparative study. Philos. Mag. A 1993, 68, 49–57. [Google Scholar] [CrossRef]
- Oh, S.H.; Legros, M.; Kiener, D.; Dehm, G. In situ observation of dislocation nucleation and escape in a submicrometre aluminium single crystal. Nat. Mater. 2009, 8, 95–100. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).