Hydrostatic-Pressure Modulation of Band Structure and Elastic Anisotropy in Wurtzite BN, AlN, GaN and InN: A First-Principles DFT Study
Abstract
1. Introduction
2. Computational Method
3. Results and Discussion
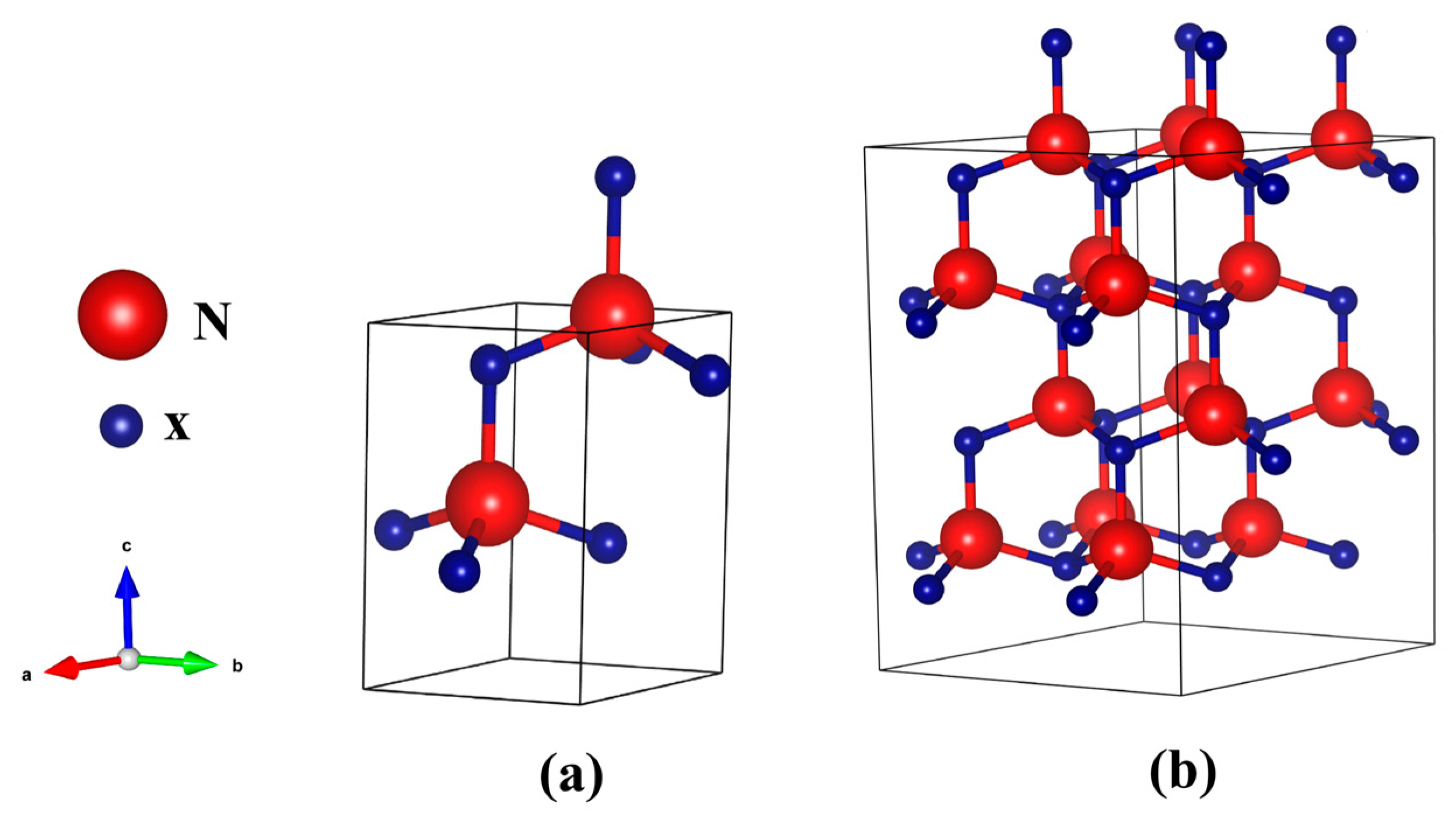
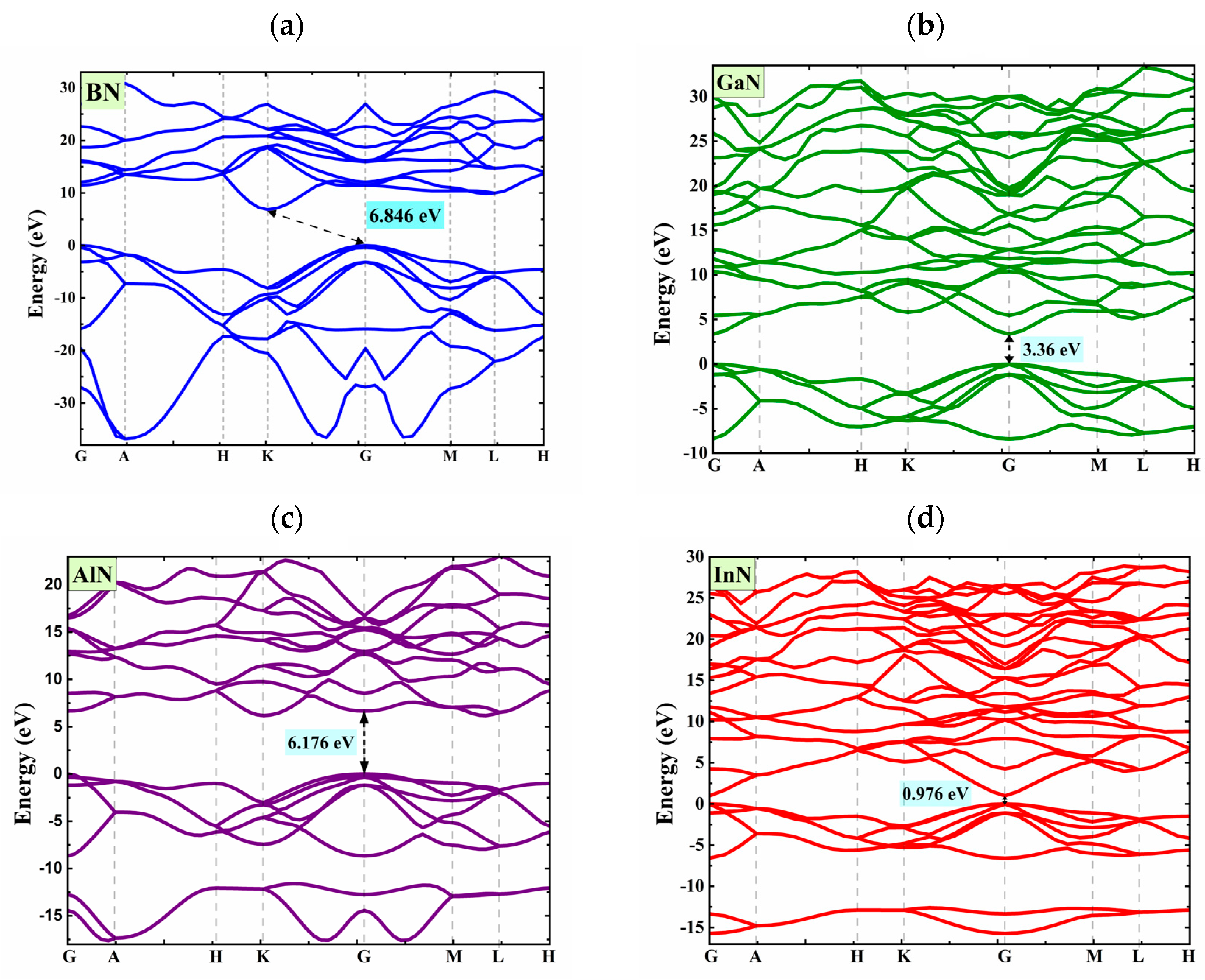
3.1. Bandgap Energy and Structural Parameters of XN Materials
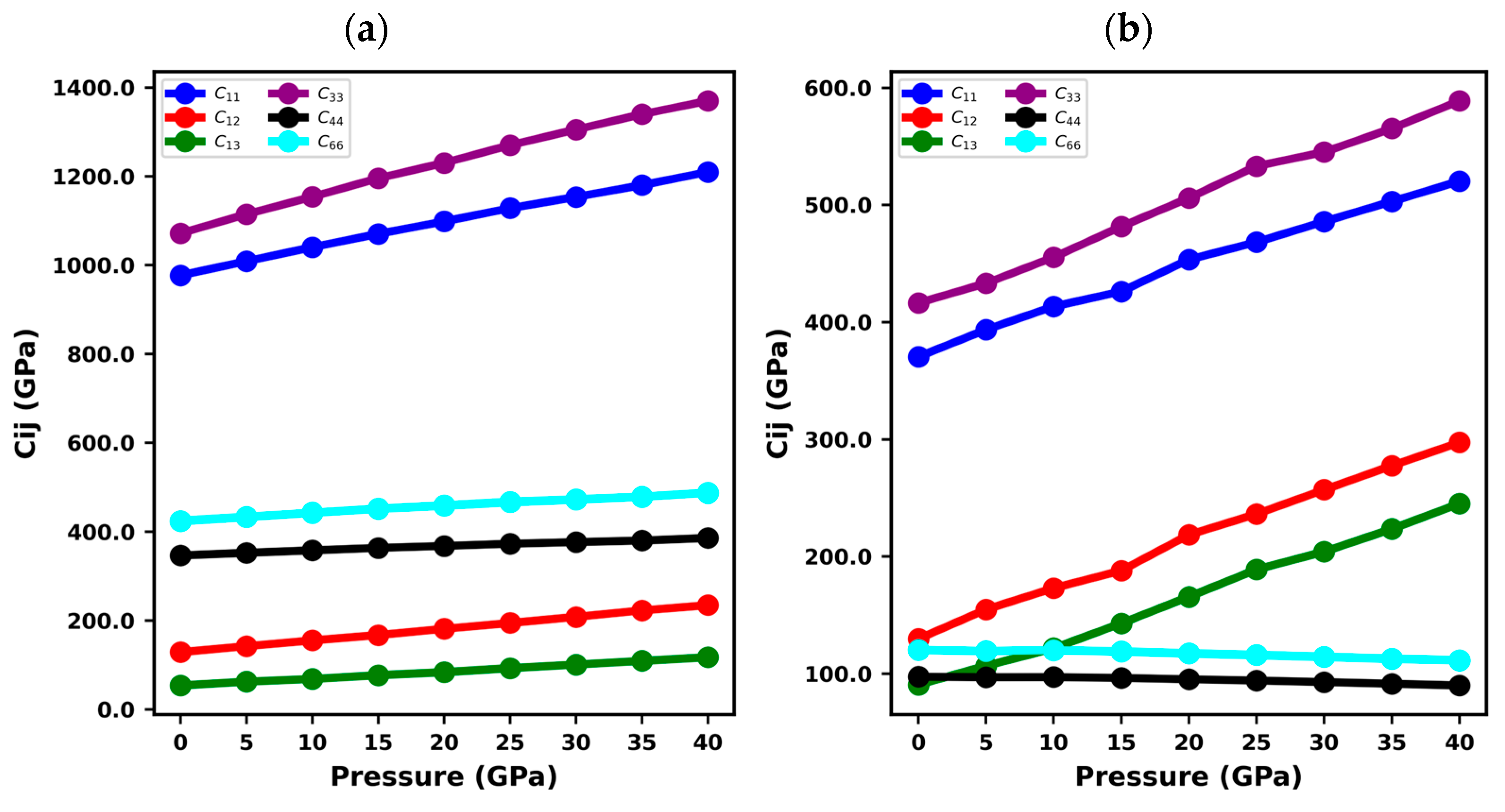
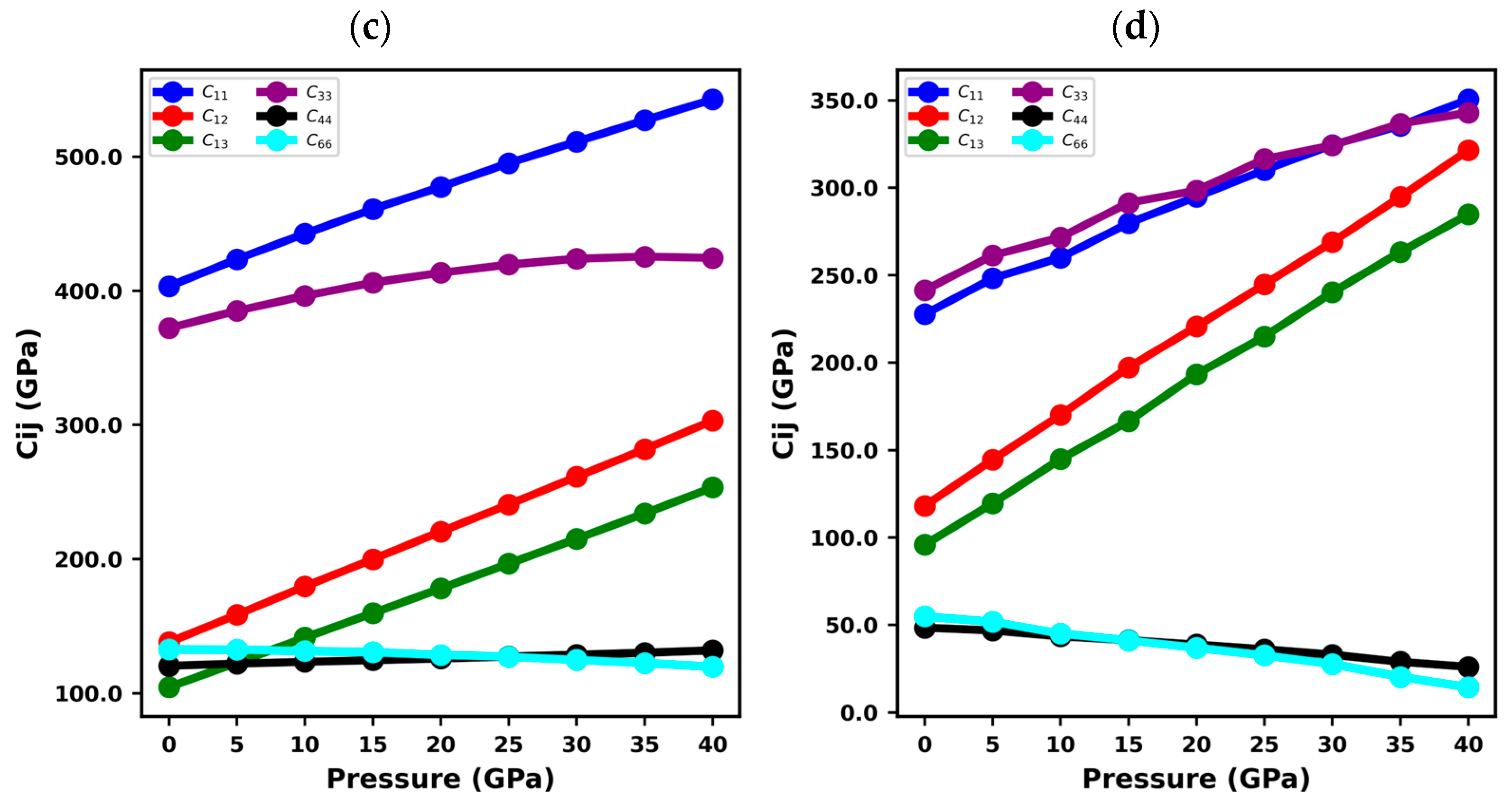
3.2. Elastic Constants of XN Materials
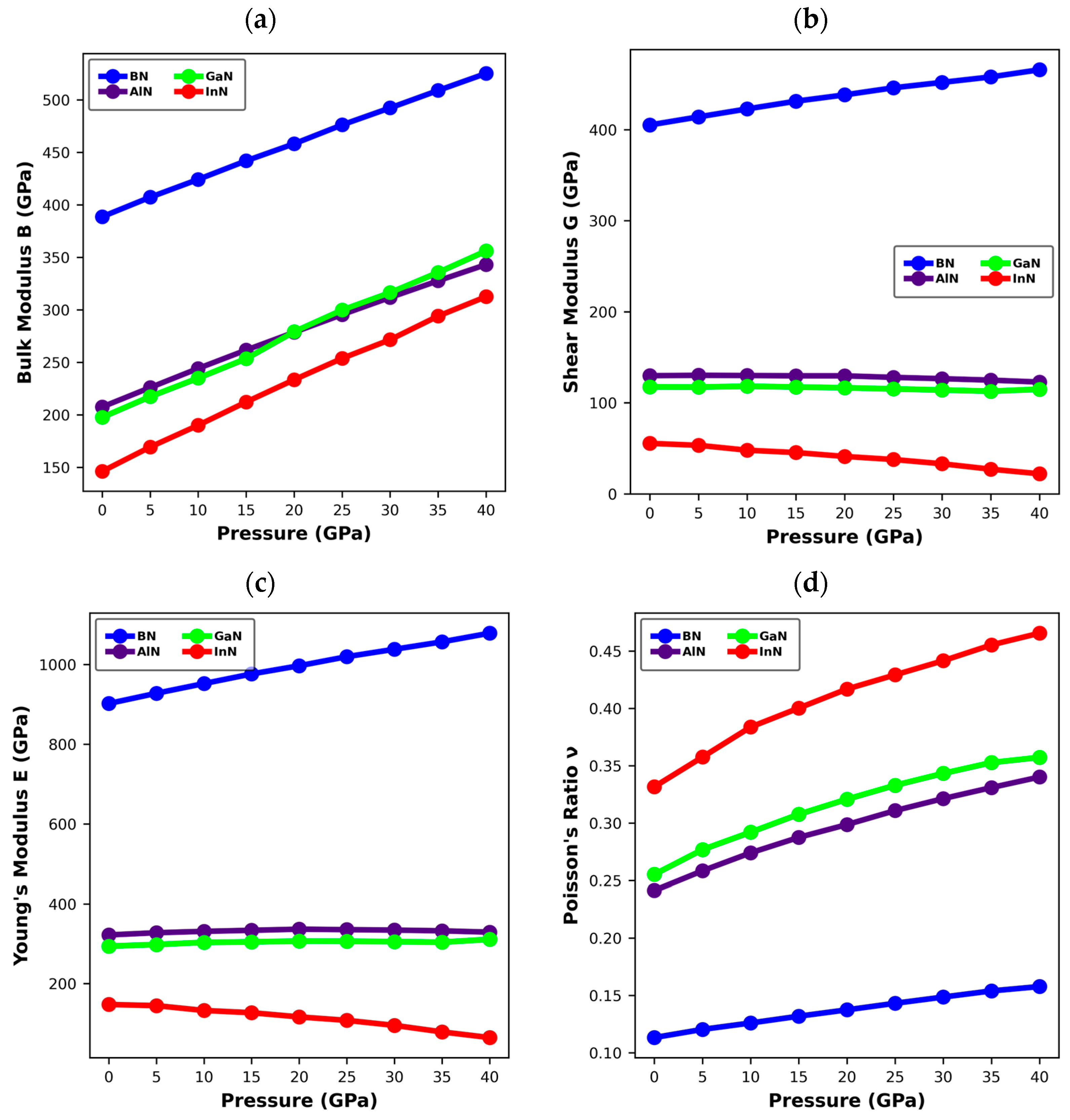
3.3. Mechanical Properties of XN Materials
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gao, S.-P. Cubic, wurtzite, and 4H-BN band structures calculated using GW methods and maximally localized Wannier functions interpolation. Comput. Mater. Sci. 2012, 61, 266–269. [Google Scholar] [CrossRef]
- Wang, Y.-H.; Liang, Y.C.; Samudra, G.S.; Huang, H.; Huang, B.-J.; Huang, S.-H.; Chang, T.-F.; Huang, C.-F.; Kuo, W.-H.; Lo, G.-Q. 6.5 V High Threshold Voltage AlGaN/GaN Power Metal-Insulator-Semiconductor High Electron Mobility Transistor Using Multilayer Fluorinated Gate Stack. IEEE Electron Device Lett. 2015, 36, 381–383. [Google Scholar] [CrossRef]
- Higashiwaki, M.; Matsui, T. Epitaxial growth of high-quality InN films on sapphire substrates by plasma-assisted molecular-beam epitaxy. J. Cryst. Growth 2003, 252, 128–135. [Google Scholar] [CrossRef]
- Cui, Z.; Gao, X.; Zhang, S.; Wang, L. High carrier mobility and polarization sensitivity of AlN/Hf2CO2 heterojunction photodetector. Chin. J. Phys. 2024, 91, 421–431. [Google Scholar] [CrossRef]
- Lu, J.L.; Chen, D.; Yushyna, L. A high power-density and high efficiency insulated metal substrate based GaN HEMT power module. In Proceedings of the 2017 IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 1–5 October 2017. [Google Scholar] [CrossRef]
- Du, J.; Dai, W.; Kou, H.; Wu, P.; Xing, W.; Zhang, Y.; Zhang, C. AlN coatings with high thermal conductivity and excellent electrical properties for thermal management devices. Ceram. Int. 2023, 49, 16740–16752. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, L.; Park, C.; Fay, C.C.; Wang, X.; Ke, C. Mechanical strength of boron nitride nanotube-polymer interfaces. Appl. Phys. Lett. 2015, 107, 253105. [Google Scholar] [CrossRef]
- Shen, L.; Heikman, S.; Moran, B.; Coffie, R.; Zhang, N.Q.; Buttari, D.; Smorchkova, I.P.; Keller, S.; Denbaars, S.P.; Mishra, U.K. AlGaN/AlN/GaN high-power microwave HEMT. IEEE Electron. Device Lett. 2001, 22, 457–459. [Google Scholar] [CrossRef]
- He, J.; Cheng, W.C.; Wang, Q.; Cheng, K.; Yu, H.; Chai, Y. Recent Advances in GaN-Based Power HEMT Devices. Adv. Electron. Mater. 2021, 7, 2001045. [Google Scholar] [CrossRef]
- Abboudi, H.; En-Nadir, R.; Kabatas, B.-M.; El Baraka, A.; Ez-Zejjari, I.; El Ghazi, H.; Sali, A. Tuning Intermediate Band Solar Cell Efficiency: The Interplay of Electric Fields, Composition, Impurities, and Confinement. Nanomaterials 2024, 14, 1858. [Google Scholar] [CrossRef] [PubMed]
- Dutta, R.; White, C.E.; Greenberg, E.; Prakapenka, V.B.; Duffy, T.S. Equation of state of the α-PbO2 and P a3-type phases of GeO2 to 120 GPa. Phys. Rev. B 2018, 98, 144106. [Google Scholar] [CrossRef]
- Mujica, A.; Rubio, A.; Munoz, A.; Needs, R. High-pressure phases of group-IV, III–V, and II–VI compounds. Rev. Mod. Phys. 2003, 75, 863. [Google Scholar] [CrossRef]
- Vurgaftman, I.; Meyer, J.; Ram-Mohan, L.R. Band parameters for III–V compound semiconductors and their alloys. J. Appl. Phys. 2001, 89, 5815–5875. [Google Scholar] [CrossRef]
- Piprek, J. Efficiency models for GaN-based light-emitting diodes: Status and challenges. Materials 2020, 13, 5174. [Google Scholar] [CrossRef] [PubMed]
- Mudassir, S.; Muhammad, J. A review of gallium nitride (GaN) based devices for high power and high frequency applications. J. Appl. Emerg. Sci. 2016, 4, 141–146. [Google Scholar]
- Avrutin, V.; Silversmith, D.J.; Mori, Y.; Kawamura, F.; Kitaoka, Y.; Morkoc, H. Growth of Bulk GaN and AlN: Progress and Challenges. Proc. IEEE 2010, 98, 1302–1315. [Google Scholar] [CrossRef]
- Li, G.; Wang, W.; Yang, W.; Lin, Y.; Wang, H.; Lin, Z.; Zhou, S. GaN-based light-emitting diodes on various substrates: A critical review. Rep. Prog. Phys. 2016, 79, 056501. [Google Scholar] [CrossRef] [PubMed]
- Kuyyalil, J.; Tangi, M.; Shivaprasad, S.M. Effect of interfacial lattice mismatch on bulk carrier concentration and band gap of InN. J. Appl. Phys. 2012, 112, 083521. [Google Scholar] [CrossRef]
- Romanitan, C.; Mihalache, I.; Tutunaru, O.; Pachiu, C. Effect of the lattice mismatch on threading dislocations in heteroepitaxial GaN layers revealed by X-ray diffraction. J. Alloys Compd. 2021, 858, 157723. [Google Scholar] [CrossRef]
- Bhuiyan, A.G.; Sugita, K.; Hashimoto, A.; Yamamoto, A. InGaN Solar Cells: Present State of the Art and Important Challenges. IEEE J. Photovolt. 2012, 2, 276–293. [Google Scholar] [CrossRef]
- Crawford, M.H. Materials Challenges of AlGaN-Based UV Optoelectronic Devices. In Semiconductors and Semimetals; Elsevier: Amsterdam, The Netherlands, 2017; pp. 3–44. [Google Scholar]
- Yadav, N.; Dutta, S.; Narang, K.; Yadav, I.; Pandey, A.; Jha, R.; Padmavati, M.V.G. Effect of Growth Induced Residual Stress in Epitaxial AlN thin film on SiC Substrate for MEMS Applications. Trans. Electr. Electron. Mater. 2025, 26, 125–133. [Google Scholar] [CrossRef]
- Sumiya, M.; Yoshimura, K.; Ohtsuka, K.; Fuke, S. Dependence of impurity incorporation on the polar direction of GaN film growth. Appl. Phys. Lett. 2000, 76, 2098–2100. [Google Scholar] [CrossRef]
- Sintonen, S.; Kivisaari, P.; Pimputkar, S.; Suihkonen, S.; Schulz, T.; Speck, J.S.; Nakamura, S. Incorporation and effects of impurities in different growth zones within basic ammonothermal GaN. J. Cryst. Growth 2016, 456, 43–50. [Google Scholar] [CrossRef]
- Hussain, I.; Ullah, S.; Khan, A.A.; Ahmad, R.; Ahmad, I. Two-dimensional III-nitrides: A comprehensive DFT and thermodynamics studies. Comput. Condens. Matter 2024, 39, e00898. [Google Scholar] [CrossRef]
- Jellil, Z.; Idrissi El Oudrhiri, A.; Jebari, H.; Soussi, A.; Eddekkar, M.; Ez-Zejjari, I.; Ez-Zahraouy, H. Band gap shifting of halide perovskite KSrCl3 from ultra-violet to visible region under pressure for photovoltaic applications. Micro Nanostruct. 2024, 193, 207911. [Google Scholar] [CrossRef]
- Pinhal, G.B.; Marana, N.L.; Fabris, G.S.L.; Sambrano, J.R. Structural, electronic and mechanical properties of single-walled AlN and GaN nanotubes via DFT/B3LYP. Theor. Chem. Acc. 2019, 138, 31. [Google Scholar] [CrossRef]
- Satawara, A.M.; Shaikh, G.A.; Gupta, S.K.; Gajjar, P.N. Structural, electronic and optical properties of hexagonal boron-nitride (h-BN) monolayer: An Ab-initio study. Mater. Today Proc. 2021, 47, 529–532. [Google Scholar] [CrossRef]
- Gasmi, F.Z.; Chemam, R.; Graine, R.; Boubir, B.; Meradji, H. Structural, electronic, and optical properties of the gallium nitride semiconductor by means of the FP-LAPW method. J. Mol. Model. 2020, 26, 356. [Google Scholar] [CrossRef] [PubMed]
- Madelung, O. Semiconductors: Group IV Elements and III-V Compounds; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Matsuoka, T.; Okamoto, H.; Nakao, M.; Harima, H.; Kurimoto, E. Optical bandgap energy of wurtzite InN. Appl. Phys. Lett. 2002, 81, 1246–1248. [Google Scholar] [CrossRef]
- Bagayoko, D.; Franklin, L. Density-functional theory band gap of wurtzite InN. J. Appl. Phys. 2005, 97, 123708. [Google Scholar] [CrossRef]
- Nwigboji, I.H.; Ejembi, J.I.; Malozovsky, Y.; Khamala, B.; Franklin, L.; Zhao, G.; Ekuma, C.E.; Bagayoko, D. Ab-initio computations of electronic and transport properties of wurtzite aluminum nitride (w-AlN). Mater. Chem. Phys. 2015, 157, 80–86. [Google Scholar] [CrossRef]
- Yamashita, H.; Fukui, K.; Misawa, S.; Yoshida, S. Optical properties of AlN epitaxial thin films in the vacuum ultraviolet region. J. Appl. Phys. 1979, 50, 896–898. [Google Scholar] [CrossRef]
- Beladjal, K.; Kadri, A.; Zitouni, K.; Mimouni, K. Bandgap bowing parameters of III-nitrides semiconductors alloys. Superlattices Microstruct. 2021, 155, 106901. [Google Scholar] [CrossRef]
- Gorczyca, I.; Suski, T.; Perlin, P.; Grzegory, I.; Kaminska, A.; Staszczak, G. Hydrostatic Pressure as a Tool for the Study of Semiconductor Properties—An Example of III–V Nitrides. Materials 2024, 17, 4022. [Google Scholar] [CrossRef] [PubMed]
- Güler, E.; Güler, M. High pressure elastic properties of wurtzite aluminum nitrate. Chin. J. Phys. 2014, 52, 1625–1635. [Google Scholar]
- Qin, H.; Kuang, T.; Luan, X.; Li, W.; Xiao, J.; Zhang, P.; Yang, D.; Zhang, G. Influence of Pressure on the Mechanical and Electronic Properties of Wurtzite and Zinc-Blende GaN Crystals. Crystals 2018, 8, 428. [Google Scholar] [CrossRef]
- Paisley, M.J.; Sitar, Z.; Posthill, J.B.; Davis, R.F. Growth of cubic phase gallium nitride by modified molecular-beam epitaxy. J. Vac. Sci. Technol. A Vac. Surf. Film. 1989, 7, 701–705. [Google Scholar] [CrossRef]
- Segall, M.; Lindan, P.J.; Probert, M.a.; Pickard, C.J.; Hasnip, P.J.; Clark, S.; Payne, M. First-principles simulation: Ideas, illustrations and the CASTEPcode. J. Phys. Condens. Matter 2002, 14, 2717. [Google Scholar] [CrossRef]
- Tolba, S.A.; Gameel, K.M.; Ali, B.A.; Almossalami, H.A.; Allam, N.K. The DFT+U: Approaches, Accuracy, and Applications; InTech: Houston, TX, USA, 2018. [Google Scholar]
- Head, J.D.; Zerner, M.C. A Broyden—Fletcher—Goldfarb—Shanno optimization procedure for molecular geometries. Chem. Phys. Lett. 1985, 122, 264–270. [Google Scholar] [CrossRef]
- Dal Corso, A.; Pasquarello, A.; Baldereschi, A. Density-functional perturbation theory for lattice dynamics with ultrasoft pseudopotentials. Phys. Rev. B 1997, 56, R11369–R11372. [Google Scholar] [CrossRef]
- Chung, D.H.; Buessem, W.R. The Voigt-Reuss-Hill Approximation and Elastic Moduli of Polycrystalline MgO, CaF2, β-ZnS, ZnSe, and CdTe. J. Appl. Phys. 1967, 38, 2535–2540. [Google Scholar] [CrossRef]
- Rougab, M.; Gueddouh, A. Electronic and Optical Properties of V-D oped AlN Rock-salt Structure: A First-principles Study Within GGA and GGA+ U Method. J. Supercond. Nov. Magn. 2022, 35, 3661–3669. [Google Scholar] [CrossRef]
- Kirchner-Hall, N.E.; Zhao, W.; Xiong, Y.; Timrov, I.; Dabo, I. Extensive benchmarking of DFT+ U calculations for predicting band gaps. Appl. Sci. 2021, 11, 2395. [Google Scholar] [CrossRef]
- Said, A.; Debbichi, M.; Said, M. Theoretical study of electronic and optical properties of BN, GaN and BxGa1−xN in zinc blende and wurtzite structures. Optik 2016, 127, 9212–9221. [Google Scholar] [CrossRef]
- Neumann, H. J.H. Edgar (ed.). Properties of Group III Nitrides. (EMIS Datareviews Series No. 11). INSPEC, The Institution of Electrical Engineers, London 1994. 302 Seiten, 121 Abbildungen, 77 Tabellen. ISBN 0-85296-818-3. Cryst. Res. Technol. 1995, 30, 910. [Google Scholar] [CrossRef]
- Qin, H.; Luan, X.; Feng, C.; Yang, D.; Zhang, G. Mechanical, Thermodynamic and Electronic Properties of Wurtzite and Zinc-Blende GaN Crystals. Materials 2017, 10, 1419. [Google Scholar] [CrossRef] [PubMed]
- Angerer, H.; Brunner, D.; Freudenberg, F.; Ambacher, O.; Stutzmann, M.; Höpler, R.; Metzger, T.; Born, E.; Dollinger, G.; Bergmaier, A.; et al. Determination of the Al mole fraction and the band gap bowing of epitaxial AlxGa1−xN films. Appl. Phys. Lett. 1997, 71, 1504–1506. [Google Scholar] [CrossRef]
- Wright, A.F.; Nelson, J.S. Consistent structural properties for AlN, GaN, and InN. Phys. Rev. B 1995, 51, 7866–7869. [Google Scholar] [CrossRef] [PubMed]
- Wang, A.J.; Shang, S.L.; Du, Y.; Kong, Y.; Zhang, L.J.; Chen, L.; Zhao, D.D.; Liu, Z.K. Structural and elastic properties of cubic and hexagonal TiN and AlN from first-principles calculations. Comput. Mater. Sci. 2010, 48, 705–709. [Google Scholar] [CrossRef]
- Domagala, J.; Leszczynski, M.; Prystawko, P.; Suski, T.; Langer, R.; Barski, A.; Bremser, M. Strain relaxation of AlxGa1−xN epitaxial layers on GaN and SiC substrates. J. Alloys Compd. 1999, 286, 284–288. [Google Scholar] [CrossRef]
- Stampfl, C.; Van De Walle, C.G. Density-functional calculations for III-V nitrides using the local-density approximation and the generalized gradient approximation. Phys. Rev. B 1999, 59, 5521–5535. [Google Scholar] [CrossRef]
- Paszkowicz, W.; Adamczyk, J.; Krukowski, S.; Leszczyński, M.; Porowski, S.; Sokolowski, J.A.; Michalec, M.; Łasocha, W. Lattice parameters, density and thermal expansion of InN microcrystals grown by the reaction of nitrogen plasma with liquid indium. Philos. Mag. A 1999, 79, 1145–1154. [Google Scholar] [CrossRef]
- Yixi, S.; Xin, J.; Kun, W.; Chaoshu, S.; Zhengfu, H.; Junyan, S.; Jie, D.; Sheng, Z.; Yuanbin, C. Vacuum-ultraviolet reflectance spectra and optical properties of nanoscale wurtzite boron nitride. Phys. Rev. B 1994, 50, 18637. [Google Scholar] [CrossRef] [PubMed]
- Silvetti, M.; Attaccalite, C.; Cannuccia, E. Pressure dependence of electronic, vibrational and optical properties of wurtzite-boron nitride. Phys. Rev. Mater. 2023, 7, 055201. [Google Scholar] [CrossRef]
- Duan, Y.; Qin, L.; Shi, L.; Tang, G. More accurate predictions of band gap tuned by pressure in InN using HSE06 and GW approximations. Comput. Mater. Sci. 2015, 101, 56–61. [Google Scholar] [CrossRef]
- Perlin, P.; Mattos, L.; Shapiro, N.A.; Kruger, J.; Wong, W.S.; Sands, T.; Cheung, N.W.; Weber, E.R. Reduction of the energy gap pressure coefficient of GaN due to the constraining presence of the sapphire substrate. J. Appl. Phys. 1999, 85, 2385–2389. [Google Scholar] [CrossRef]
- Nye, J.F. Physical Properties of Crystals: Their Representation by Tensors and Matrices; Oxford University Press: Oxford, UK, 1985. [Google Scholar]
- Shimada, K.; Sota, T.; Suzuki, K. First-principles study on electronic and elastic properties of BN, AlN, and GaN. J. Appl. Phys. 1998, 84, 4951–4958. [Google Scholar] [CrossRef]
- Polian, A.; Grimsditch, M.; Grzegory, I. Elastic constants of gallium nitride. J. Appl. Phys. 1996, 79, 3343–3344. [Google Scholar] [CrossRef]
- Kim, K.; Lambrecht, W.R.L.; Segall, B. Elastic constants and related properties of tetrahedrally bonded BN, AlN, GaN, and InN. Phys. Rev. B 1996, 53, 16310–16326. [Google Scholar] [CrossRef] [PubMed]
- Ohashi, Y.; Arakawa, M.; Kushibiki, J.-i.; Epelbaum, B.M.; Winnacker, A. Ultrasonic microspectroscopy characterization of AlN single crystals. Appl. Phys. Express 2008, 1, 077004. [Google Scholar] [CrossRef]
- Wright, A.F. Elastic properties of zinc-blende and wurtzite AlN, GaN, and InN. J. Appl. Phys. 1997, 82, 2833–2839. [Google Scholar] [CrossRef]
- Serrano, J.; Bosak, A.; Krisch, M.; Manjón, F.J.; Romero, A.H.; Garro, N.; Wang, X.; Yoshikawa, A.; Kuball, M. InN Thin Film Lattice Dynamics by Grazing Incidence Inelastic X-Ray Scattering. Phys. Rev. Lett. 2011, 106, 205501. [Google Scholar] [CrossRef] [PubMed]
- Eichler, J.; Lesniak, C. Boron nitride (BN) and BN composites for high-temperature applications. J. Eur. Ceram. Soc. 2008, 28, 1105–1109. [Google Scholar] [CrossRef]
- Kurakevych, O.; Solozhenko, V. High-Pressure Design of Advanced BN-Based Materials. Molecules 2016, 21, 1399. [Google Scholar] [CrossRef] [PubMed]
- Yonenaga, I.; Deura, M.; Tokumoto, Y.; Kutsukake, K.; Ohno, Y. Insight into physical processes controlling the mechanical properties of the wurtzite group-III nitride family. J. Cryst. Growth 2018, 500, 23–27. [Google Scholar] [CrossRef]
- Maiz Hadj Ahmed, H.; Benaissa, H.; Zaoui, A.; Ferhat, M. Exploring original properties of GaN-BN alloys using high-throughput ab initio computation. Optik 2022, 261, 169166. [Google Scholar] [CrossRef]
- Savastenko, V.A.; Sheleg, A.U. Study of the elastic properties of gallium nitride. Phys. Status Solidi (A) 1978, 48, K135–K139. [Google Scholar] [CrossRef]
- Yonenaga, I. Hardness, Yield Strength, and Dislocation Velocity in Elemental and Compound Semiconductors. Mater. Trans. 2005, 46, 1979–1985. [Google Scholar] [CrossRef]
- Nowak, R.; Pessa, M.; Suganuma, M.; Leszczynski, M.; Grzegory, I.; Porowski, S.; Yoshida, F. Elastic and plastic properties of GaN determined by nano-indentation of bulk crystal. Appl. Phys. Lett. 1999, 75, 2070–2072. [Google Scholar] [CrossRef]
- Kisielowski, C.; Krüger, J.; Ruvimov, S.; Suski, T.; Ager, J.W.; Jones, E.; Liliental-Weber, Z.; Rubin, M.; Weber, E.R.; Bremser, M.D.; et al. Strain-related phenomena in GaN thin films. Phys. Rev. B 1996, 54, 17745–17753. [Google Scholar] [CrossRef] [PubMed]
- Ueno, M.; Onodera, A.; Shimomura, O.; Takemura, K. X-ray observation of the structural phase transition of aluminum nitride under high pressure. Phys. Rev. B 1992, 45, 10123–10126. [Google Scholar] [CrossRef] [PubMed]
- Gerlich, D.; Dole, S.L.; Slack, G.A. Elastic properties of aluminum nitride. J. Phys. Chem. Solids 1986, 47, 437–441. [Google Scholar] [CrossRef]
- Boch, P.; Glandus, J.C.; Jarrige, J.; Lecompte, J.P.; Mexmain, J. Sintering, oxidation and mechanical properties of hot pressed aluminium nitride. Ceram. Int. 1982, 8, 34–40. [Google Scholar] [CrossRef]
- Lu, Y.-S.; Hsieh, C.-H.; Gwo, S.; Hou, M.T.; Yao, J.-S.; Yeh, J.A. An investigation of the Young’s modulus of single-crystalline wurtzite indium nitride using an atomic force microscopy based micromechanical bending test. Appl. Phys. Lett. 2012, 101, 221906. [Google Scholar] [CrossRef]
- Peng, F.; Han, Y.; Fu, H.; Yang, X. First-principles calculations on structure and elasticity of wurtzite-type indium nitride under pressure. J. Alloys Compd. 2009, 475, 885–888. [Google Scholar] [CrossRef]
- Han, N.T.; Dien, V.K.; Chang, T.-R.; Lin, M.-F. Optical excitations of graphene-like materials: Group III-nitrides. Nanoscale Adv. 2023, 5, 5077–5093. [Google Scholar] [CrossRef] [PubMed]
- Murphy, L.R.; Meek, T.L.; Allred, A.L.; Allen, L.C. Evaluation and Test of Pauling’s Electronegativity Scale. J. Phys. Chem. A 2000, 104, 5867–5871. [Google Scholar] [CrossRef]

| Electronic Configuration | Energy (eV) | ||
|---|---|---|---|
| InN | In | - | |
| N | - | ||
| BN | B | 12 | |
| N | 12.75 | ||
| GaN | Ga | 3.75 | |
| N | 3.5 | ||
| AlN | Al | 3.5 | |
| N | 4.25 | ||
| Structure | Methods | Ref. | |||||
|---|---|---|---|---|---|---|---|
| BN | LDA | 2.52 | 1.29 | 4.17 | 1.07 | 23.03 | This study |
| LDA | 2.50 | 2.07 | 4.169 | 1.09 | - | [47] | |
| LDA+U | 2.46 | 7.71 | 4.07 | 7.66 | 21.39 | This study | |
| GGA | 2.5527 | 0.011 | 4.2215 | 0.15 | 23.82 | This study | |
| Experimental | 2.553 | - | 4.215 | - | - | [48] | |
| GaN | LDA | 3.1554 | 1.06 | 5.1453 | 0.76 | 44.36 | This study |
| LDA | 3.156 | 1.05 | 5.145 | 0.77 | 44.373 | [49] | |
| LDA+U | 3.1249 | 2.02 | 5.0836 | 1.95 | 42.99 | This study | |
| GGA | 3.2245 | 1.10 | 5.2521 | 1.29 | 47.29 | This study | |
| GGA | 3.242 | 1.65 | 5.28 | 1.83 | 48.075 | [49] | |
| Experimental | 3.1893 | - | 5.1851 | - | - | [50] | |
| AlN | LDA | 3.0637 | 1.48 | 4.9011 | 1.58 | 39.84 | This study |
| LDA | 3.084 | 0.83 | 4.948 | 0.64 | - | [51] | |
| LDA+U | 3.0012 | 3.50 | 4.7655 | 4.30 | 36.66 | This study | |
| GGA | 3.1249 | 0.48 | 5.0089 | 0.58 | 42.35 | This study | |
| GGA | 3.12 | 0.32 | 5.00 | 0.40 | - | [52] | |
| Experimental | 3.11 | - | 4.98 | - | - | [53] | |
| InN | LDA | 3.529 | 0.25 | 5.70 | 0.05 | 61.53 | This study |
| LDA | 3.544 | 0.42 | 5.762 | 1.03 | - | [54] | |
| LDA+U | 3.30 | 6.47 | 5.30 | 7.06 | 50.26 | This study | |
| GGA | 3.608 | 2.23 | 5.833 | 2.27 | 65.79 | This study | |
| GGA | 3.614 | 2.40 | 5.883 | 3.15 | - | [54] | |
| Experimental | 3.538 | - | 5.703 | - | - | [55] |
| Structure | Methods | Bandgap Energy (eV) | Ref. |
|---|---|---|---|
| BN | LDA | 4.914 | This study |
| GGA | 5.204 | This study | |
| LDA+U | 6.846 | This study | |
| experimental | 8.7 ± 0.5 | [56] | |
| GaN | LDA | 2.088 | This study |
| GGA | 1.671 | This study | |
| LDA+U | 3.36 | This study | |
| experimental | 3.4 | [30] | |
| AlN | LDA | 4.659 | This study |
| GGA | 4.11 | This study | |
| LDA+U | 6.176 | This study | |
| experimental | 6.2 | [34] | |
| InN | LDA | 1.057 | This study |
| GGA | 0.976 | This study | |
| experimental | 0.7–1.0 | [31] |
| Structure | Ref. | ||||||
|---|---|---|---|---|---|---|---|
| BN | 976.95 | 128.85 | 53.88 | 1071.48 | 346.43 | 424.05 | This study |
| 982 | 134 | 74 | 1077 | 388 | 424 | [61] | |
| GaN | 370.48 | 129.76 | 90.64 | 416.39 | 97.5 | 120.36 | This study |
| 374.35 | 126.56 | 80.85 | 441.94 | 98.86 | 123.89 | [49] | |
| 390 ± 15 | 145 ± 20 | 106 ± 20 | 398 ± 20 | 105 ± 10 | 123 ± 10 | [62] | |
| AlN | 403.34 | 138 | 104.56 | 372.19 | 120.46 | 132.67 | This study |
| 398 | 142 | 112 | 383 | 127 | 128 | [63] | |
| 401.2 ± 0.5 | 135 ± 0.5 | 96.3 ± 22.1 | 368.9 ± 27 | 122.6 ± 0.2 | − | [64] | |
| InN | 227.5 | 118.06 | 95.85 | 241.42 | 48.47 | 54.84 | This study |
| 223 | 115 | 92 | 224 | 48 | − | [65] | |
| 225 ± 7 | 109 ± 8 | 108 ± 8 | 265 ± 3 | 55 ± 3 | − | [66] |
| Structure | B (GPa) | G (GPa) | E (GPa) | ν | Ref. |
|---|---|---|---|---|---|
| BN | 388.72 | 405.17 | 902.09 | 0.113 | This study |
| 397 [69] | 410 ± 30 [69] | 860 ± 40 [69] | 0.12 [70] | - | |
| GaN | 197.705 | 117.47 | 294.15 | 0.252 | This study |
| 195 [71] | 161 [72] | 295 [73] | 0.23 ± 0.06 [74] | - | |
| AlN | 207.59 | 129.8 | 322.24 | 0.241 | This study |
| 207.9 ± 6.2 [75] | 132.8 [75] | 308 [76] | 0.245 [77] | - | |
| InN | 146.25 | 55.49 | 148.65 | 0.33 | This study |
| 152 ± 5 [66] | 43 [71] | 149 ± 5 [78] | 0.359 [79] | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ez-zejjari, I.; Ghazi, H.E.; Belaid, W.; En-nadir, R.; Abboudi, H.; Sali, A. Hydrostatic-Pressure Modulation of Band Structure and Elastic Anisotropy in Wurtzite BN, AlN, GaN and InN: A First-Principles DFT Study. Crystals 2025, 15, 648. https://doi.org/10.3390/cryst15070648
Ez-zejjari I, Ghazi HE, Belaid W, En-nadir R, Abboudi H, Sali A. Hydrostatic-Pressure Modulation of Band Structure and Elastic Anisotropy in Wurtzite BN, AlN, GaN and InN: A First-Principles DFT Study. Crystals. 2025; 15(7):648. https://doi.org/10.3390/cryst15070648
Chicago/Turabian StyleEz-zejjari, Ilyass, Haddou El Ghazi, Walid Belaid, Redouane En-nadir, Hassan Abboudi, and Ahmed Sali. 2025. "Hydrostatic-Pressure Modulation of Band Structure and Elastic Anisotropy in Wurtzite BN, AlN, GaN and InN: A First-Principles DFT Study" Crystals 15, no. 7: 648. https://doi.org/10.3390/cryst15070648
APA StyleEz-zejjari, I., Ghazi, H. E., Belaid, W., En-nadir, R., Abboudi, H., & Sali, A. (2025). Hydrostatic-Pressure Modulation of Band Structure and Elastic Anisotropy in Wurtzite BN, AlN, GaN and InN: A First-Principles DFT Study. Crystals, 15(7), 648. https://doi.org/10.3390/cryst15070648







