Abstract
LK-99, with chemical formula Pb10−xCux(PO4)6O, was recently reported to be a room-temperature superconductor. While this claim has met with little support in a flurry of ensuing work, a variety of calculations (mostly based on density-functional theory) have demonstrated that the system possesses some unusual characteristics in the electronic structure, in particular flat bands. We have established previously that within DFT, the system is insulating with many characteristics resembling the classic cuprates, provided the structure is not constrained to the P3(143) symmetry nominally assigned to it. Here we describe the basic electronic structure of LK-99 within self-consistent many-body perturbative approach, quasiparticle self-consistent GW (QSGW) approximation and their diagrammatic extensions. QSGW predicts that pristine LK-99 is indeed a Mott/charge transfer insulator, with a bandgap gap in excess of 3 eV, whether or not constrained to the P3(143) symmetry. When Pb9Cu(PO4)6O is hole-doped, the valence bands modify only slightly, and a hole pocket appears. However, two solutions emerge: a high-moment solution with the Cu local moment aligned parallel to neighbors, and a low-moment solution with Cu aligned antiparallel to its environment. In the electron-doped case the conduction band structure changes significantly: states of mostly Pb character merge with the formerly dispersionless Cu d state, and high-spin and low spin solutions once again appear. Thus we conclude that with suitable doping, the ground state of the system is not adequately described by a band picture, and that strong correlations are likely. Irrespective of whether this system class hosts superconductivity or not, the transition of Pb10(PO4)6O from being a band insulator to Pb9Cu(PO4)6O, a Mott insulator, and multi-determinantal nature of doped Mott physics make this an extremely interesting case-study for strongly correlated many-body physics.
1. Introduction
A recent paper [1] reported that Cu-doped Pb10(PO4)6O (AKA LK-99, the trademark name given by its discoverers) exhibits a Meissner effect up to 400 K. This rather startling claim [2,3] has met with healthy skepticism in the scientific community, with wide speculation that the levitation they reported was an artifact of some weak ferromagnetic interaction [4,5]. If superconductivity at 400 K were indeed confirmed, it would be a truly remarkable and transformational discovery with major consequences for a wide range of technologies. Unfortunately, recent attempts to find superconductivity in LK-99 have been unsuccessful [4,5,6,7,8,9], damping the initial optimism. There have also been suggestions the presence of Cu2S byproduct can explain the observed drop in resistivity [10]. Nevertheless this materials system is very interesting in its own right as a template for hosting unusual one-particle properties, which as we show here are highly conducive to interesting and exotic many-body effects. In particular we establish, using a self-consistent form of ab initio many-body perturbation theory, the extremely flat valence and conduction bands are highly susceptible to strong correlations owing to spin fluctuations (see Figure 1).
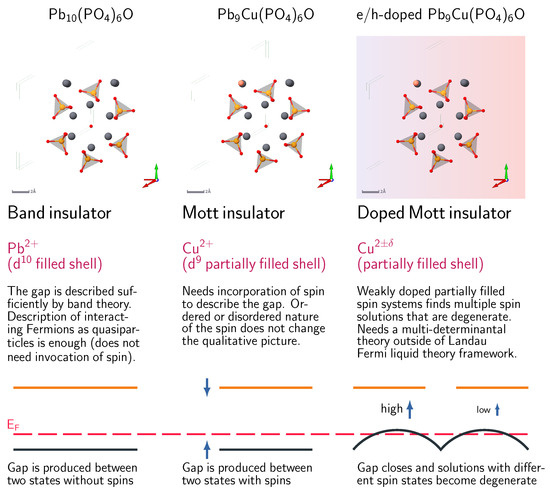
Figure 1.
From band-insulator (Pb10(PO4)6O) to Mott-insulator (Pb9Cu(PO4)6O) to doped Mott insulator: Cartoon of the symmetrised LK-99 structure, viewed in direction slightly off the z axis. Large grey atoms are Pb, pink is Cu, yellow P and red is O. For the doped Pb9Cu(PO4)6O case, the background charge is represented schematically with a shaded background. We show the transition of the compound Pb10(PO4)6O from being a band insulator that is sufficiently described by band theory without the need to invoke spin, to a Mott insulator Pb9Cu(PO4)6O which gaps out the Fermi surface because of the spin fluctuations of the partially filled Cu2+ state with d9 configuration. Further, as the Mott insulator is doped with electrons or holes, we observe the system to have multiple solutions with nearly degenerate high- and low-spin configurations that can not be described by a theory for electronic scattering in the spirit of a single-determinant picture of Landau theory of Fermi liquid. We note that in the many-body literature often the languages for Mott and charge-transfer are confused and debated. We call Pb9Cu(PO4)6O a Mott insulator primarily because a non-magnetic solution of the system does not open a gap, and needs some treatment of the spin fluctuations. Note that, ↑ and ↓ spin symbols between valence and conduction are used for presentation purpose only. The valence and conduction states can be of any spin.
Recent density-functional theory (DFT) calculations [11,12,13,14,15,16,17,18] agree that Pb10(PO4)6O is a band insulator, however, there is little agreement on the metallic/insulating character of Pb9Cu(PO4)6O. As we have established in Ref. [13], various flavors of DFT predict Pb9Cu(PO4)6O to be a Mott/charge transfer insulator, provided the system is relaxed and not constrained to its nominal P3 symmetry, a crucial ingredient of the electronic structure of LK-99 that most other DFT calculations missed. This [13] work also showed the gap to be robust against the most likely kinds of disorder that preserve stoichiometry. Here we use a higher level of theory, the Quasiparticle Self-Consistent GW (QSGW) [19,20] approximation, and affirm the principal result of that work: the pristine system is insulating and the gap is larger than found from density-functionals [15]. It also turns out that relaxation of the P3 symmetry is not at all essential: the energy band structures of the fully relaxed structures and structures constrained to retain P3 symmetry are very similar. Recent synthesis of phase-pure single crystals [21] of Pb9Cu(PO4)6O shows the system to be an insulator and optically transparent, a conclusion in complete consistency with our previous [13] and present studies.
Our study turns to the effect of electron- and hole-doping of Pb9Cu(PO4)6O. Indeed, some remarkable many-body effects emerge in both cases. In the hole doping case, the system can be reasonably approximated by a conventional picture: change in occupation of largely unaltered valence bands. However, two stable magnetic solutions emerge at the QSGW level, a high-spin state and a low-spin state. Electron doping is more exotic because of the magnetic (Cu d) character of the lowest conduction band, as we explain below. At the QSGW level of theory the rigid band approximation breaks down, which leads to somewhat exotic changes in the one-particle spectrum, with higher lying bands hybridizing with the quasi-atomic Cu d state, and give rise to a conduction band consisting several bands, derived mostly from Cu and Pb. As in the hole-doped case, a high-spin and a low-spin state can be stabilized.
The presence of two nearly degenerate spin states suggests that the ground state is a strongly correlated many-body state that lies outside of a band picture, which is limited to a single Slater determinant. In this picture, the correlations arise from spin exchange between the Cu and O (hole doped case) and between Cu and Pb (electron doped case).
2. Results and Discussion
2.1. Lattice Structure
The parent compound Pb9Cu(PO4)6O, AKA LK-99, forms in the hexagonal P3 structure, space group 143. Stoichiometrically, it may be regarded as combinations of formula units (Pb3(PO4)2)3PbO. Six of the Pb (which may be called Pb(6h) using Wykoff conventions) form a staggered set of triangles consistent with three-fold rotational symmetry along the c axis. The other four Pb(4f) atoms lie farther from this axis. Each P is surrounded by four almost equidistant O atoms, in a slightly deformed tetrahedron. From the perspective of chemical bonding, the P form hybrids which bond to an O p orbital and form bond-antibond pairs. Assigning a formal charge of +5 and −2 to P and O, the PO4 unit has a formal charge of . Treating the Pb s states as core, Pb has two valence electrons, so (Pb3(PO4)2) forms a combination of covalent and ionic bonds. PbO also forms an ionic bond; thus the parent compound (Pb3(PO4)2)3PbO is a mixed covalent-ionic insulator. This last O sits in the center of the Pb rings and forms a linear chain on the c-axis. Four sites are available to it, but only one site is occupied. Structural relaxations were performed with the VASP [22], using the SCAN functional [23] (Ref. [13]). The Cu-O| distance is 5.78 Å.
2.2. Energy Band Structure of the Parent LK-99 Compound
By the parent compound we refer to an ideal Pb9Cu(PO4)6O, with O| occupying the lowest energy configuration determined from the SCAN functional, as described in ref. [13]. Relaxations consistent with P3 were considered (symmetry-restricted), and also the system was allowed to fully relax (unrestricted). As noted in that reference, the electronic structure does not depend on which site O| occupies (all four original O (4e) sites are equivalent. Therefore, the choice of which site to occupy does not matter in the 41 atom cell, however, non-equivalent O configurations exist in supercells). Moreover, the Cu-Cu exchange interactions are predicted by SCAN to be much smaller than room temperature (as might be expected in any case owing to the large Cu-Cu separation). Thus, if the Cu have local moments as density-functionals predict, the local moments will have no long range order. Ref. [13] also notes that the electronic structure of both antiferrromagnetic and paramagnetic spin configurations are very similar to the ferromagnetic one, provided in the FM case spin up and spin down are symmetrized. We restrict consideration to the FM case here, keeping in mind that to derive a good description of the electronic structure from it, the majority and minority channels should be symmetrized.
For the single-particle band structure, we use the Quasiparticle Self-Consistent GW approximation in the Questaal package [20,24]. Self-consistency is realized in a quasiparticle sense: the energy-dependent self-energy includes many-body effects, especially plasmon excitations, but the quasiparticlization procedure replaces the dynamical self-energy with a static one to yield an optimized single Slater determinant. Quasiparticlization uses a principle that minimizes some norm of the difference between the interacting G and the noninteracting one [19,25] and it also satisfies a variational principle [26]. Importantly, it has the property that the single-particle band structure should correspond to true excitation energies, in contrast to DFT. Spin orbit coupling is included in these calculations. Note that the fully dynamical self-energy (calculated in the QSGW procedure) contains more than one solution, however, the iterations in the QSGW procedure, often, fluctuate between these multiple solutions and a spin-flip diagram (as contained within dynamical mean field theory approach) is needed to achieve a converged solution that is a probabilistic average of these multiple spin solutions. There is as yet no perturbative approach that includes such a diagram, however, the dynamical self energy in QSGW approach contains these multiple solutions and can be converged to achieve each of them independently.
The energy bands of the parent compound (Figure 2) neatly divide into a band of OP-derived p states well below the Fermi level EF (green), and pair of states of mixed OP+O| character (turquoise) split off from the other O-derived bands, and forming the valence band maximum. Cu is with a lone Cu orbital forming a nearly dispersionless conduction band minimum (red), and finally states of (mostly s) Pb character sitting above it (blue). (Also, see Table 1 and Figure 3 for atomic characters of the low-energy states.) Top panels show QSGW bands for structures relaxed with the SCAN functional subject to a symmetry constraint (see Figure 2a) and fully relaxed (see Figure 2b). There is very little difference in the two cases, except in constrained relaxation the two bands at the valence band maximum are degenerate at A (apart from a slight lifting of degeneracies because of majority and minority spins are not equivalent owing to the ferromagnetic approximation noted above). In the unrestricted relaxation, P3 symmetry is lifted and so is the degeneracy. SCAN is supposed to produce slightly better structures, though we find that the difference between PBEsol and SCAN is unimportant for both the lattice structure and electronic structure. Since the QSGW electronic structure does not depend on the starting electronic potential, the final electronic structure derived from QSGW is independent of whether PBEsol and SCAN is used as starting point in this case.
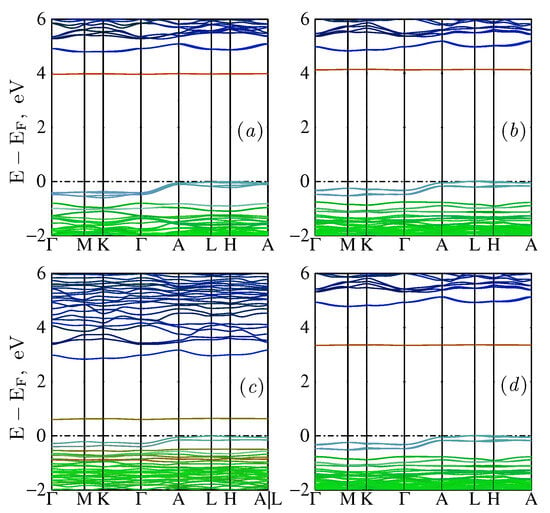
Figure 2.
Energy bands of the parent compound Pb9Cu(PO4)6O: Top panels show calculations in the QSGW approximation for the symmetry-constrained relaxation (a) and the fully relaxed case (b). Panel (c) shows the band structure obtained from the PBEsol functional, using the fully relaxed structure and panel (d) how the band structure is modified from QSGW (a) when ladders are added to the polarizability (QSGŴ) [27]. Red, green, and blue depict Mulliken projections onto Cu, , and Pb orbitals. Turquoise seen in the highest valence bands is a result of
O| mixed in with character. All energy bands include spin orbit coupling.

Table 1.
Percentages of different atomic characters from the low energy electronic states: for the undoped Pb9Cu(PO4)6O, % of atomic characters are shown for the valence (−0.5 eV to ) and conduction states (+4.0 eV to +4.4 eV). For hole-doped Pb9Cu(PO4)6O electronic states within an energy window of −0.5 eV to +0.2 eV are integrated to extract the percentages. For the electron-doped Pb9Cu(PO4)6O energy window of −0.2 eV to +0.3 eV is used. Notably, the kinetic energy of the low energy electronic states increases on hole doping, while remains nearly invariant on electronic doping when compared to the undoped case.
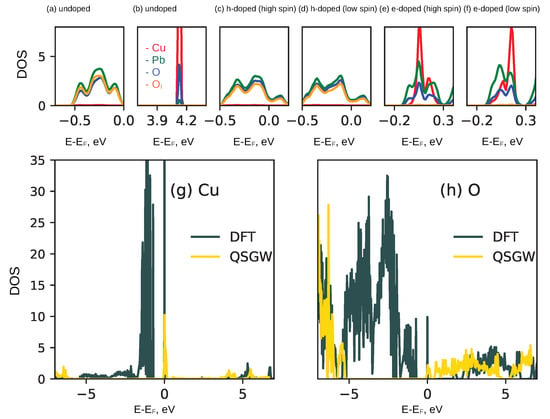
Figure 3.
QSGW electronic density of states: of (a) valence and (b) conduction states of undoped Pb9Cu(PO4)6O and (c) high spin and (d) low spin solutions for the hole doped and (e) high spin and (f) low spin solutions for the electron doped Pb9Cu(PO4)6O. In (g,h) we show the density of states comparisons between QSGW and DFT for Cu and O states for the electron doped case.
The QSGW band structure (Figure 2d) has notable differences with those generated by standard density functionals (Figure 2c). In the latter case, the symmetry-constrained structure is predicted to be metallic; only by breaking symmetry one Cu d state splits off to form the conduction band. Even after a gap forms under relaxation, the gap is small (see Figure 2c), and the conduction band contains much more O character (compare the red color of the QSGW conduction band to the yellowish PBEsol [28] result). Adding U to PBE increases the Cu local moment, shifting and conduction band closer to the QSGW result, the amount depending on the value of U. However, even for U = 5 the gap is still eV. Also note that the gap between higher-lying (Pb-derived) bands and the valence band is much reduced. This reflects a well-known tendency of DFT to underestimate bandgaps. These differences will turn out to be important when doping is considered. Alongside of correcting the band gap (which is effectively an eigenvalue correction issue), these results also show the ability of QSGW approaches in correcting the eigenfunctions which has been shown to have important implications in a range of correlated systems [29].
On the other hand, QSGW has a well-known tendency to overestimate bandgaps by roughly about 10–20%, largely because ladder diagrams are omitted from the polarizability [27]. This tendency is especially pronounced when levels are spin split by exchange interactions between localized spins on a given site, e.g., in NiO, CoO, and La2CuO4. It has been found that adding ladder diagrams largely ameliorates this tendency. [27] Extending QSGW to include ladder diagrams in W we denote QSGŴ, and we consider it here to assess its effect on the ideal LK99 parent compound. The resulting energy band structure, Figure 2d looks quite similar to QSGW, except the unoccupied Cu state is shifted down by ∼0.8 eV. This reduction in the gap is similar to, but slightly less than, what is found for NiO, CoO, CuO, Fe3O4, and La2CuO4 [27]. We also note that the position of this level is very sensitive to small changes in the potential, and as a result the self-energy was difficult to stabilize. But it hints at the extreme sensitivity of the Cu-derived conduction band to small perturbations.
With Cu substituting for Pb, Cu d states must lie at the Fermi level if restricted to nonmagnetic solutions. Indeed calculations show that the Cu d overlap with p states belonging to O| and OP. Cu is formally , the valence band maximum has one hole, making the system metallic. Bonds of both the Cu-d O-p are have a dispersion of ∼0.2 eV or less, and they weakly hybridize with each other. Because of their extremely low dispersion, their kinetic energy is small and both charge and spin easily fluctuate between Cu and the environment. It is noteworthy that any of common bosons responsible for many body effects are strong contenders in this system. First, the electron-phonon interaction can be very strong because of the flat bands, and also because a significant band of phonons involving OP, with energies between 110–140 meV, form part of the PO4 network. (Note that the O| phonons also have rather high energies, between 60–80 meV). Second, charge fluctuations, e.g., between the weakly bonded but spatially separated Cu and O| can be a source of strong instabilities. And finally, the spin fluctuations can be low-energy. This will be particularly evident in the doped cases to be discussed next.
2.3. Doping
To avoid peculiarities of the “chemical personality” of specific dopants, we dope the system by adding a homogeneous nuclear background charge, which must be compensated by adding or removing electrons to keep the unit cell neutral. We consider both electron and hole doping. As check on the appropriateness of uniform background model, we compared the electron-doped case to a system with a real dopant—a F atom substituting for the chain-O, and find it similar to a QSGW calculation in the presence of a homogeneous background, requiring one extra electron.
2.4. Hole-Doped Case
Doping LK-99 with holes acts similarly to doping cuprates or sp semiconductors: the energy bands do not change shape significantly and a hole pocket at the valence band maximum appears. Figure 4 shows the resulting energy band structure with doping of 1/2 electron per formula unit. Perhaps the most surprising result to emerge from QSGW is that two self-consistent solutions can be stabilized with different spin configurations: a “low-moment” configuration with 0.5 in the unit cell, and a “high-moment” configuration with 1.5 . In both cases the Cu moment is very close to the undoped compound (0.81 ), while the remaining moment is distributed over O and Pb. In the low-moment case, spins align antiferrromagnetically to the Cu on average, while they align ferromagnetically in the high-moment case. This strongly hints that the ground state cannot be comprised of a single Slater determinant, and that spin fluctuations are inherently large. Note the subtle differences in the numbers of bands crossing the Fermi energy between the low- (Figure 4a) and high-spin (Figure 4b) solutions.
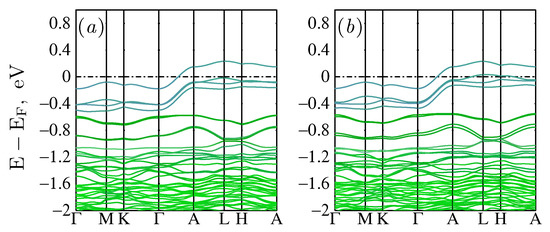
Figure 4.
Hole doped Pb9Cu(PO4)6O: (a) A low-spin solution and a (b) high-spin solution emerge. Colors correspond to the same orbital projections as in Figure 2. The high- and low spin solutions have remarkably similar electronic structure and atomic-characters at the low-energies.
2.5. Electron-Doped Case
A very different picture emerges when LK-99 is doped with electrons. The rigid-band approximation no longer applies. For small doping, electrons occupy the unoccupied Cu d state and reduce the local moment in proportion to the doping. When heavily doped, the splitting between states of Pb s character and the lowest conduction band Cu d character can close. This likely occurs because the gap between Cu and the valence band originates primarily from an exchange splitting as a consequence of the onsite Hubbard interaction, while much of the splitting between the unoccupied Pb(s) and valence band is a consequence of the long-range screened coulomb interaction W [30]. The latter is important in determining the bandgap in sp semiconductors, while the former is largely responsible for the gap in transition metal oxides such as NiO, CoO, CuO and La2CuO4, where the gap closes if the local moment vanishes. When the system is doped, screening increases and the long-ranged part of W is reduced. However, the local screening on Cu (essentially on-site U and J) is much less affected. When Pb-Cu splitting does close, the conduction band involves multiple states, mixing the localized the Cu d state and more dispersive Pb s states (Figure 5) Here also a “low-moment” configuration with 0.66 (Figure 5a), and a “high-moment” configuration with 1.2 (Figure 5b) can be stabilized, with the Cu local moment approximately similar to the parent compound. We note in passing DFT does not capture this effect, as it requires feedback between the screening and the band structure. [31] We show the remarkable differences in the Cu and O projected density of states (Figure 3g,h) between the two approximations, DFT and QSGW, over a large energy window around the Fermi level. The strong renormalization of the DFT electronic bands and spectral weight redistribution can be observed due to the QSGW self-energy corrections. However, electron doping should be taken with some caution. The wide gap mitigates against thermodynamically stable dopants, and it may not be feasible to electron dope this system.
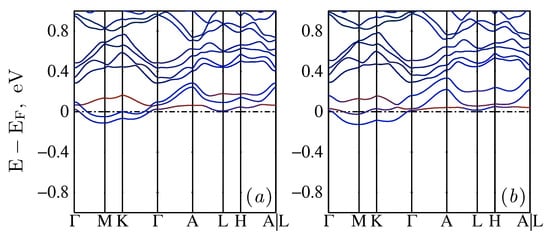
Figure 5.
Electron doped Pb9Cu(PO4)6O: (a) is low-spin solution, (b) high-spin solution. Colors correspond to the same orbital projections as in Figure 2. The high- and low spin solutions have remarkably similar electronic structure and atomic-characters at the low-energies.
3. Conclusions
The original work [13] that established pristine LK-99 is insulating, in a DFT framework, has been confirmed theoretically by several groups, using some form of DFT or a combination of DFT and DMFT [32,33]. This has led these groups to conclude that some form of doping that changes the electron count, is essential for LK-99 to be a metal.
The present work confirms that conclusion at a higher level of theory, and turns to the question of electron and hole doping, within the QSGW framework. Two remarkable results emerge from QSGW that are not found in density-functional theory. The first is the marked change in splitting between Pb states in the conduction band and the O-derived valence band states with doping. This can be understood as a change in the screening as the system becomes metallic. The close relation between bandgaps in sp bonded semiconductors and the long-range form of the screened coulomb interactions has been established for some time [30,34] and the effect of changes in screening on the band structure in such systems systems has been also been reported [31,35]. What is unique in the present case is that bandgaps with two different origins coexist: one of another of semiconductor character (Pb-O) which is sensitive to doping and another of Mott character (Cu-O) which is not. The second remarkable finding is the coexistence of two spin states, with the Cu aligned either parallel or antiparallel to the host. A single d state of a Cu impurity in a , configuration, embedded in a wide-gap semiconducting host has been seen before: it has been observed in Cu-doped ZnO [36,37]. But in the present case flat bands with low kinetic energy allow a moment to be induced on the sp subspace that would not occur in Cu-doped ZnO, and the coexistence of two subspaces with different spin channels is new. In the QSGW approach, the quasiparticlization procedure demands a single Slater determinant; thus the alignment of the two kinds of spins emerges as two distinct solutions. While it was possible to stabilize two distinct spin configurations, there was a strong tendency to flip between them as self-consistency proceeded. This indicates that the spin configurations are nearly degenerate in energy. Self-consistency is clearly essential here: such a result would be problematic with conventional forms of GW, e.g., one-shot GW based on DFT. The crucial role of self-consistency has been discussed recently for several other insulating systems [29,38].
The near-degeneracy of distinct ground states in a one-particle description suggests that the true ground state cannot be described by a single-determinant; and moreover correlations from spin fluctuations between the Cu local moment and delocalized environment are likely to be very strong. This does not by itself indicate a strong propensity for superconductivity, but it does suggest a novel path to strong correlations. In terms of strong correlations, what makes LK-99 unique is its non-dispersive O-like states (hole doped system) that is devoid of almost any Cu character. This is not observed in popular 2D cuprates like La2CuO4 and Nd2CuO4 or 1D cuprates like SrCuO2 or Sr2CuO3. Flat O-like states can host large electron-phonon coupling and/or density wave instabilities. On the contrary, the electron doped situation has non-dispersive states from Cu which can host spin waves. Further, existence of multiple spin solutions make the system intriguing for further research. Multiple spin solutions are observed in systems like NiO and MnF2 [39], several other cuprates and the rare-earth nickelate series. Often, competition between strong multiplet fluctuations and unquenched orbital moments in solid states can lead to bond and spin disproportionation. It would be worth studying those possibilities in LK-99. We believe, the fact that Pb10(PO4)6O is a band insulator, Pb9Cu(PO4)6O is a Mott insulator and the electron- and hole-doped Pb9Cu(PO4)6O can not be described by a single Slater determinant, makes these class of systems a unique playground to explore the transition from band- to Mott-insulator to multi-determinantal nature of weakly doped Mott physics.
4. Methods
We apply quasiparticle self-consistent theory (QSGW) [19], which, in contrast to conventional methods, modifies the charge density and is determined by a variational principle [26]. Further, QSGŴ [27] is a diagrammatic extension of QSGW where the screened coulomb interaction W is computed including excitonic vertex corrections (ladder diagrams) by solving a Bethe–Salpeter equation (BSE) within Tamm-Dancoff approximation [40]. Crucially, both our QSGW and QSGŴ methods are fully self-consistent in both self-energy and the charge density [29]. G, , and are updated iteratively until all of them converge. Such approaches are parameter-free and have no starting point bias.
Author Contributions
Conceptualization, M.v.S. and D.S.D.; Methodology, D.P., S.A. and M.v.S.; Validation, S.L. and D.S.D.; Formal analysis, S.A., D.P. and M.v.S.; Investigation, D.P., S.A., S.L. and D.S.D. All authors have read and agreed to the published version of the manuscript.
Funding
Funding was provided by the Basic Energy Sciences, Division of Materials within the Office of Basic Energy Sciences, U.S. Department of Energy. DD was supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under Grant No. DE-FG02-03ER46066, and the Gordon and Betty Moore Foundation’s EPiQS Initiative through Grant No. GBMF9458, and by the Frontier machine at the Oak Ridge Leadership Computing facility.
Data Availability Statement
All the input file structures and the command lines to launch calculations are rigorously explained in the tutorials available on the Questaal webpage [24] under the terms of the AGPLv3 license. The data for reproducing the doped DFT and QSGW electronic structures from our work are available https://zenodo.org/records/15764941?preview=1&token=eyJhbGciOiJIUzUxMiJ9.eyJpZCI6IjdiMWUzZWM5LTBkNzEtNDVkMC1hY2UyLWE4ZjM3N2FjYzQyMiIsImRhdGEiOnt9LCJyYW5kb20iOiI2MTc1ZWFhZTMxODlkNDAyOTk2YTAwYzA1MDg0MmMwMiJ9.TOglPCzJtF26yafq9sJZvYyZOxCTLddf3blvl5RSrRzS5oungJSXX4HaDFeMc1ljGadknirJKXgPBExJ881sOg"> on zenodo (accessed on 29 June 2025). Further data requests should be made to S.A. and D.P.
Acknowledgments
This work was authored in part by the National Renewable Energy Laboratory for the U.S. Department of Energy (DOE) under Contract No. DE-AC36-08GO28308. Funding was provided by the Basic Energy Sciences, Division of Materials within the Office of Basic Energy Sciences, U.S. Department of Energy. DD was supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under Grant No. DE-FG02-03ER46066, and the Gordon and Betty Moore Foundation’s EPiQS Initiative through Grant No. GBMF9458, and by the Frontier machine at the Oak Ridge Leadership Computing facility. S.A., D.P. and M.v.S. acknowledge the use of the National Energy Research Scientific Computing Center, under Contract No. DE-AC02-05CH11231 using NERSC award BES-ERCAP0021783 and we also acknowledge that a portion of the research was performed using computational resources sponsored by the Department of Energy’s Office of Energy Efficiency and Renewable Energy and located at the National Renewable Energy Laboratory. The views expressed in the article do not necessarily represent the views of the DOE or the U.S. Government. The U.S. Government retains and the publisher, by accepting the article for publication, acknowledges that the U.S. Government retains a nonexclusive, paid-up, irrevocable, worldwide license to publish or reproduce the published form of this work, or allow others to do so, for U.S. Government purposes.
Conflicts of Interest
The authors declare no competing financial or non-financial interests.
References
- Lee, S.; Kim, J.; Kim, H.-T.; Im, S.; An, S.; Auh, K.H. Superconductor Pb10−xCux(PO4)6O showing levitation at room temperature and atmospheric pressure and mechanism. arXiv 2023, arXiv:2307.12037. [Google Scholar]
- Lee, S.; Kim, J.-H.; Kwon, Y.-W. The first room-temperature ambient-pressure superconductor. arXiv 2023, arXiv:2307.12008. [Google Scholar]
- Lee, S.; Kim, J.; Im, S.; An, S.; Kwon, Y.-W.; Ho, A.K. Consideration for the development of room-temperature ambient-pressure superconductor (LK-99). J. Korean Cryst. Growth Cryst. Technol. 2023, 33, 61. [Google Scholar]
- Guo, K.; Li, Y.; Jia, S. Ferromagnetic half levitation of LK-99-like synthetic samples. Sci. China Phys. Mech. Astron. 2023, 66, 107411. [Google Scholar] [CrossRef]
- Timokhin, I.; Chen, C.; Wang, Z.; Yang, Q.; Mishchenko, A. Synthesis and characterisation of LK-99. arXiv 2023, arXiv:2308.03823v2. [Google Scholar]
- Liu, L.; Meng, Z.; Wang, X.; Chen, H.; Duan, Z.; Zhou, X.; Yan, H.; Qin, P.; Liu, Z. Semiconducting Transport in Pb10−xCux(PO4)6O Sintered from Pb2SO5 and Cu3P. Adv. Funct. Mater. 2023, 33, 2308938. [Google Scholar] [CrossRef]
- Kumar, K.; Karn, N.K.; Kumar, Y.; Awana, V. Absence of superconductivity in LK-99 at ambient conditions. ACS Omega 2023, 8, 41737. [Google Scholar] [CrossRef]
- Kumar, K.; Karn, N.; Awana, V. Synthesis of possible room temperature superconductor LK-99: Pb9Cu (PO4)6O. Supercond. Sci. Technol. 2023, 36, 10LT02. [Google Scholar] [CrossRef]
- Wu, H.; Yang, L.; Xiao, B.; Chang, H. Successful growth and room temperature ambient-pressure magnetic levitation of LK-99. arXiv 2023, arXiv:2308.01516. [Google Scholar]
- Jain, P.K. Superionic phase transition of copper (I) sulfide and its implication for purported superconductivity of LK-99. J. Phys. Chem. C 2023, 127, 18253. [Google Scholar] [CrossRef]
- Griffin, S.M. Origin of correlated isolated flat bands in copper-substituted lead phosphate apatite. arXiv 2023, arXiv:2307.16892. [Google Scholar]
- Lai, J.; Li, J.; Liu, P.; Sun, Y.; Chen, X.-Q. First-principles study on the electronic structure of Pb10−xCux(PO4)6O (x = 0, 1). J. Mater. Sci. Technol. 2023, 171, 66–70. [Google Scholar] [CrossRef]
- Kurleto, R.; Lany, S.; Pashov, D.; Acharya, S.; van Schilfgaarde, M.; Dessau, D.S. Pb-apatite framework as a generator of novel flat-band CuO based physics, including possible room temperature superconductivity. arXiv 2023, arXiv:2308.00698. [Google Scholar]
- Si, L.; Held, K. Electronic structure of the putative room-temperature superconductor Pb9Cu (PO4)6O. Phys. Rev. B 2023, 108, L121110. [Google Scholar] [CrossRef]
- Cabezas-Escares, J.; Barrera, N.F.; Lavroff, R.H.; Alexandrova, A.N.; Cardenas, C.; Munoz, F. Electronic structure and vibrational stability of copper-substituted lead apatite LK-99. Phys. Rev. B 2024, 109, 144515. [Google Scholar] [CrossRef]
- Sun, Y.; Ho, K.-M.; Antropov, V. Metallization and spin fluctuations in Cu-doped lead apatite. Phys. Rev. Mater. 2023, 7, 114804. [Google Scholar] [CrossRef]
- Tao, K.; Chen, R.; Yang, L.; Gao, J.; Xue, D.; Jia, C. The 1/4 occupied O atoms induced ultra-flatband and the one-dimensional channels in the Pb9Cux(PO4)6O4 (x= 0, 0.5) crystal. APL Mater. 2024, 12, 021120. [Google Scholar] [CrossRef]
- Jiang, Y.; Lee, S.B.; Herzog-Arbeitman, J.; Yu, J.; Feng, X.; Hu, H.; Călugăru, D.; Brodale, P.S.; Gormley, E.L.; Vergniory, M.G.; et al. Pb9Cu(PO4)6(OH)2: Phonon bands, localized flat-band magnetism, models, and chemical analysis. Phys. Rev. B 2023, 108, 235127. [Google Scholar] [CrossRef]
- Van Schilfgaarde, M.; Kotani, T.; Faleev, S. Quasiparticle Self-Consistent GW Theory. Phys. Rev. Lett. 2006, 96, 226402. [Google Scholar] [CrossRef]
- Pashov, D.; Acharya, S.; Lambrecht, W.R.L.; Jackson, J.; Belashchenko, K.D.; Chantis, A.; Jamet, F.; van Schilfgaarde, M. Questaal: A package of electronic structure methods based on the linear muffin-tin orbital technique. Comp. Phys. Comm. 2020, 249, 107065. [Google Scholar] [CrossRef]
- Puphal, P.; Akbar, M.; Hepting, M.; Goering, E.; Isobe, M.; Nugroho, A.; Keimer, B. Single crystal synthesis, structure, and magnetism of Pb10−xCux(PO4)6O. APL Mater. 2023, 11, 101128. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
- Sun, J.; Ruzsinszky, A.; Perdew, J.P. Strongly constrained and appropriately normed semilocal density functional. Phys. Rev. Lett. 2015, 115, 036402. [Google Scholar] [CrossRef] [PubMed]
- Questaal Code Website. Available online: https://www.questaal.org (accessed on 29 June 2025).
- Kotani, T.; van Schilfgaarde, M.; Faleev, S.V. Quasiparticle self-consistent GW method: A basis for the independent-particle approximation. PRB 2007, 76, 165106. [Google Scholar] [CrossRef]
- Ismail-Beigi, S. Justifying quasiparticle self-consistent schemes via gradient optimization in Baym–Kadanoff theory. J. Phys. Condens. Matter 2017, 29, 385501. [Google Scholar] [CrossRef]
- Cunningham, B.; Gruning, M.; Pashov, D.; Van Schilfgaarde, M. QSGW: Quasiparticle self-consistent GW with ladder diagrams in W. Phys. Rev. B 2023, 108, 165104. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.; Burke, K. Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 2008, 100, 136406. [Google Scholar] [CrossRef]
- Acharya, S.; Pashov, D.; Rudenko, A.N.; Rosner, M.; van Schilfgaarde, M.; Katsnelson, M.I. Importance of charge self-consistency in first-principles description of strongly correlated systems. npj Comput. Mater. 2021, 7, 208. [Google Scholar] [CrossRef]
- Maksimov, E.G.; Mazin, I.I.; Savrasov, S.Y.; Uspenski, Y.A. Excitation spectra of semiconductors and insulators: A density-functional approach to many-body theory. J. Phys. Condens. Matter 1989, 1, 2493. [Google Scholar] [CrossRef]
- Vidal, J.; Botti, S.; Olsson, P.; Guillemoles, J.-F.; Reining, L. Strong Interplay between Structure and Electronic Properties in CuIn(S,Se)2: A First-Principles Study. Phys. Rev. Lett. 2010, 104, 056401. [Google Scholar] [CrossRef]
- Korotin, D.M.; Novoselov, D.Y.; Shorikov, A.O.; Anisimov, V.I.; Oganov, A.R. Electronic correlations in promising room-temperature superconductor Pb9Cu(PO4)6O: A DFT+DMFT study. Phys. Rev. B 2023, 108, L241111. [Google Scholar] [CrossRef]
- Si, L.; Wallerberger, M.; Smolyanyuk, A.; di Cataldo, S.; Tomczak, J.M.; Held, K. Pb10−xCux(PO4)6O: A Mott or charge transfer insulator in need of further doping for (super)conductivity. J. Phys. Condens. Matter 2023, 36, 065601. [Google Scholar] [CrossRef] [PubMed]
- Gruning, M.; Marini, A.; Rubio, A. Density functionals from many-body perturbation theory: The band gap for semiconductors and insulators. J. Chem. Phys. 2006, 124, 154108. [Google Scholar] [CrossRef] [PubMed]
- Neaton, J.B.; Hybertsen, M.S.; Louie, S.G. Renormalization of molecular electronic levels at metal-molecule interfaces. Phys. Rev. Lett. 2006, 97, 216405. [Google Scholar] [CrossRef]
- Dingle, R. Luminescent transitions associated with divalent copper impurities and the green emission from semiconducting zinc oxide. Phys. Rev. Lett. 1969, 23, 579. [Google Scholar] [CrossRef]
- Lany, S.; Zunger, A. Polaronic hole localization and multiple hole binding of acceptors in oxide wide-gap semiconductors. Phys. Rev. B 2009, 80, 085202. [Google Scholar] [CrossRef]
- Grzeszczyk, M.; Acharya, S.; Pashov, D.; Chen, Z.; Vaklinova, K.; van Schilfgaarde, M.; Watanabe, K.; Taniguchi, T.; Novoselov, K.; Katsnelson, M.; et al. Strongly Correlated Exciton-Magnetization System for Optical Spin Pumping in CrBr3 and CrI3. Adv. Mater. 2023, 35, 2209513. [Google Scholar] [CrossRef]
- Acharya, S.; Pashov, D.; Weber, C.; van Schilfgaarde, M.; Lichtenstein, A.I.; Katsnelson, M.I. A theory for colors of strongly correlated electronic systems. Nat. Commun. 2023, 14, 5565. [Google Scholar] [CrossRef]
- Hirata, S.; Head-Gordon, M. Time-dependent density functional theory within the Tamm–Dancoff approximation. Chem. Phys. Lett. 1999, 314, 291. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).