The Temperature Sensitivity of the Piezoelectric Thickness Shear Mode of α-GeO2 Single Crystals
Abstract
1. Introduction
2. Methodology
- −
- Determining, based on experimental measurements, the curves of the evolution of elastic constants as a function of the temperature, as well as the first- and second-order temperature coefficients.
- −
- Researching and calculating the temperature-compensated cut angles of Y-plates in single and double rotations within a temperature range of 25–900 °C.
- −
- Examining the effect of rotation on Y-plates on the emergence of parasitic vibration modes.
2.1. First- and Second-Order Temperature Coefficients of the Resonant Frequency
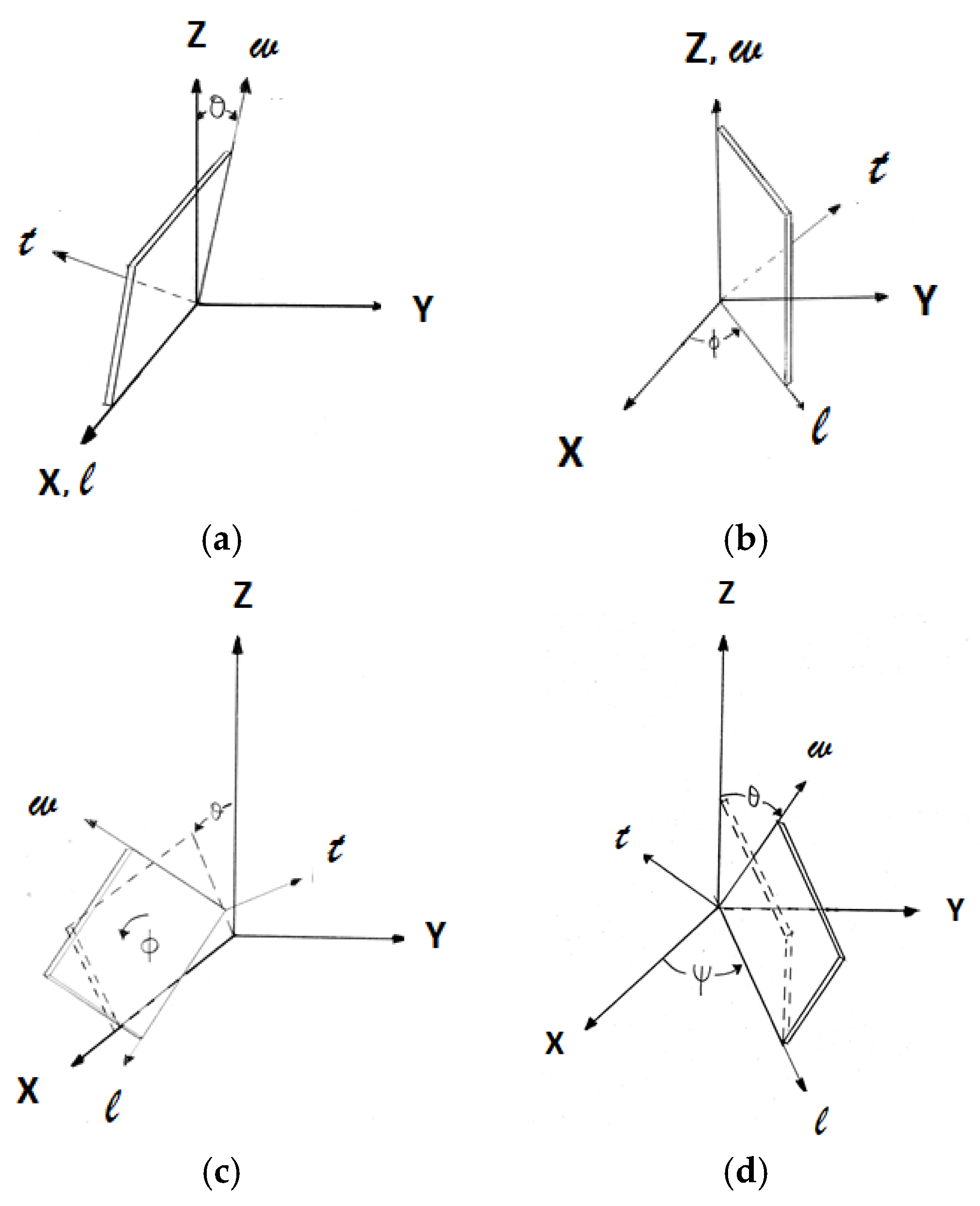
2.2. Rotated Y-Cut Plates
2.3. Elastic Constants of Rotated Y-Cut Plates
2.3.1. Elastic Constants of a Singly Rotated Y-Cut Plate
2.3.2. Elastic Constants of a Doubly Rotated Y-Cut Plate
3. Results and Discussion
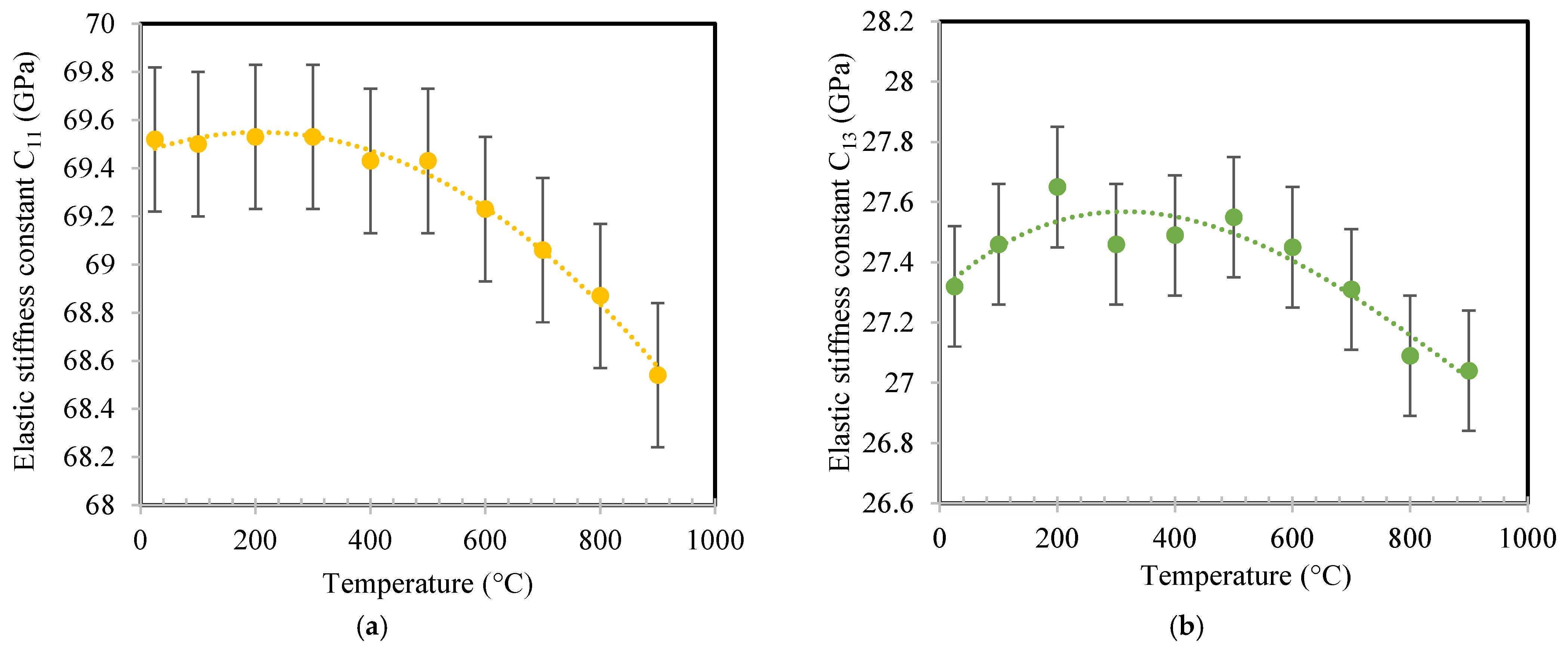
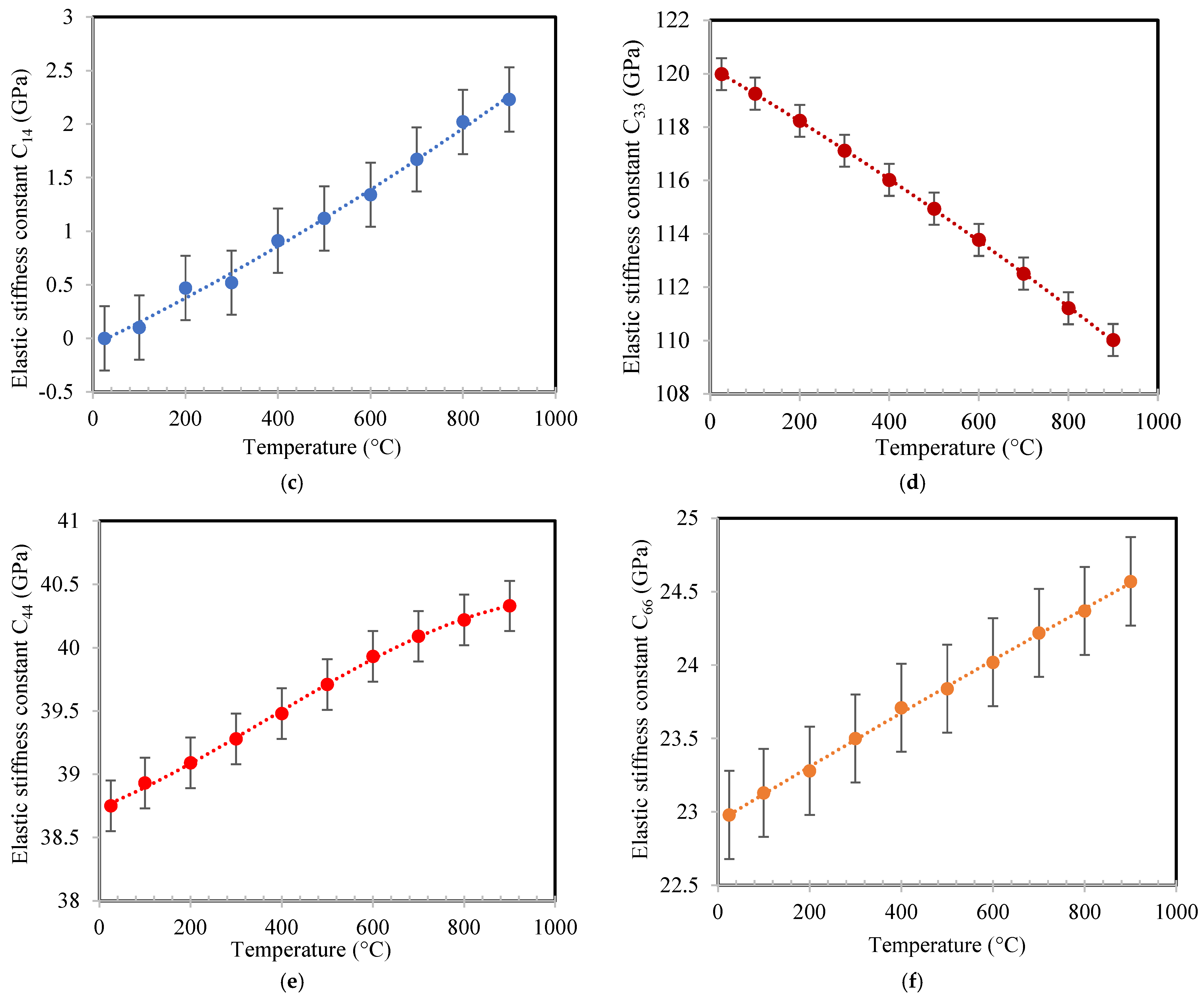
3.1. Temperature-Dependent Elastic Constants of α-GeO2
3.2. Cuts with Zero Temperature Coefficients
3.2.1. Singly Rotated Y-Cut Plate
3.2.2. Doubly Rotated Y-Cut Plate
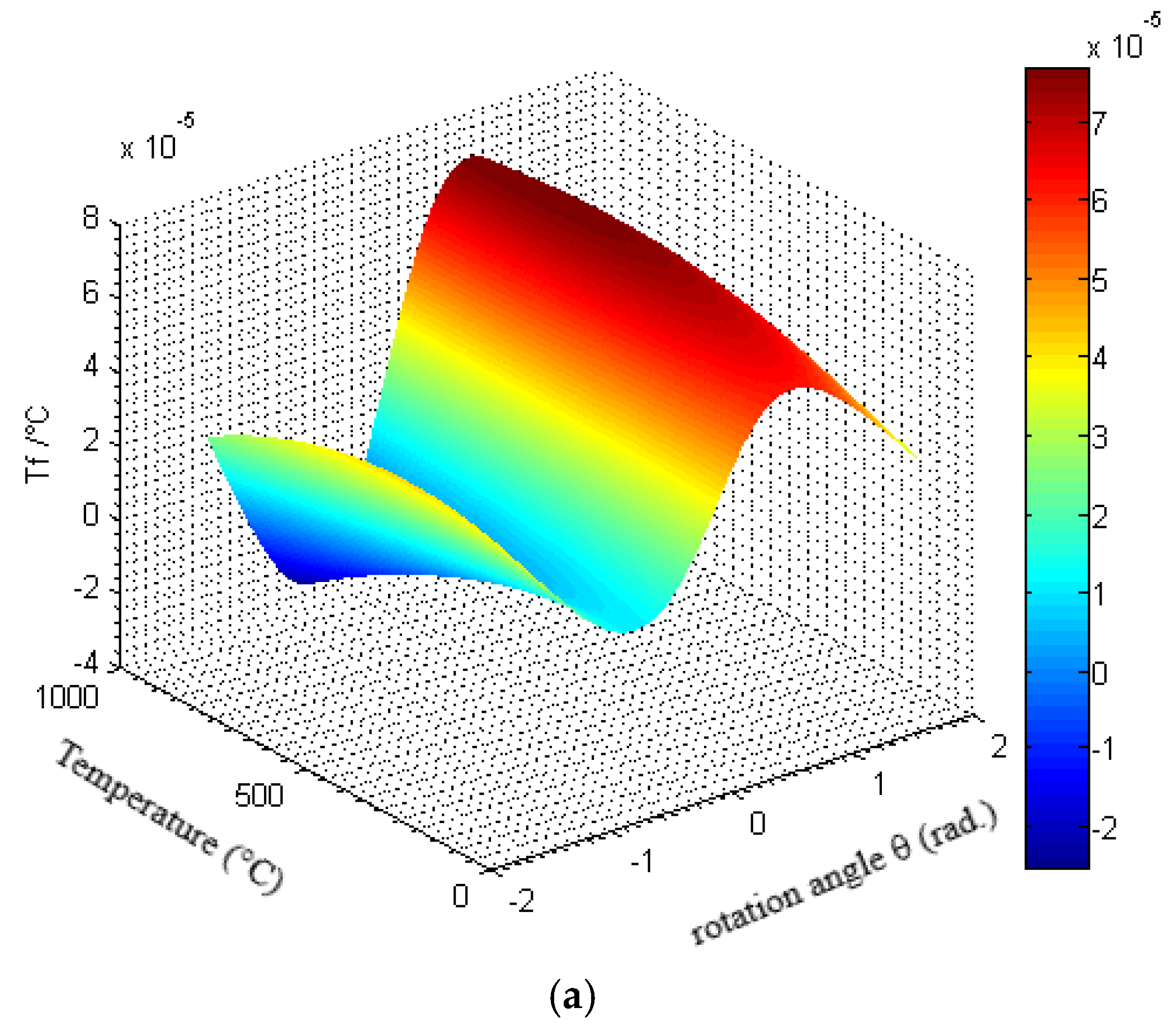
3.3. Second-Order Resonance Frequency Temperature Coefficients for Rotated Y-Plates
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hamidon, M.V.; Skarda, V.; White, N.M.; Krispel, F.; Krempl, P.; Binhack, M. Buff. Fabrication of high temperature surface acoustic wave devices for sensor applications. Sens. Actuators A Phys. 2005, 403, 123–124. [Google Scholar]
- Daniau, W.; Salut, R.; Friedt, J.M.; Pena, A.; Menaert, B.; Armand, P.; Papet, P.; Penarier, A.; Nouvel, P. Experimental demonstration of Surface Acoustic Wave propagation on α-GeO2 for wireless, passive sensor design. In Proceedings of the 2023 IEEE International Frequency Control Symposium-European Frequency (EFTF/IFCS), Toyama, Japan, 15–19 May 2023; IEEE: New York, NY, USA, 2023; pp. 1–4. [Google Scholar] [CrossRef]
- Pena, A.; Felix, C.; Menaert, B.; Boulanger, B. Crystal growth, measurement and modeling of the optical activity of alpha-GeO2. Comparison with alpha-SiO2. arXiv 2025, arXiv:2501.12496. [Google Scholar] [CrossRef]
- Remark, T.; Segonds, P.; Pena, A.; Menaert, B.; Debray, J.; Pujol, M.C.; Boulanger, B. First Measurements of Nonlinear Second-Order Frequency Conversion Phase-Matching Conditions in the Uniaxial Crystal α-GeO2. In Laser Congress 2021 (ASSL, LAC); paper ATh2A.3; Optica Publishing Group: Washington, DC, USA, 2021; Available online: https://opg.optica.org/abstract.cfm?URI=ASSL-2021-ATh2A.3 (accessed on 18 April 2025).
- Remark, T.; Segonds, P.; Pena, A.; Menaert, B.; Debray, J.; Jegouso, D.; Pujol, M.C.; Boulanger, B. Linear and nonlinear optical properties of the piezoelectric crystal α-GeO2. Opt. Mater. Express 2021, 11, 3520–3527. [Google Scholar] [CrossRef]
- Armand, P.; Hermet, P.; Bantignies, J.L.; Haidoux, A.; Maurin, D.; Ménaert, B.; Pena, A.; Papet, P. Optical properties in the infrared range of the birefringent α-GeO2 single crystal. Mat. Res. Bull. 2020, 129, 110881. [Google Scholar] [CrossRef]
- Philippot, E.; Goiffon, A.; Ibanez, A.; Pintard, M. Structure Deformations and Existence of the α-β Transition in MXO4 Quartz-like Materials. J. Solid State Chem. 1994, 110, 356–362. [Google Scholar] [CrossRef]
- Philippot, E.; Palmier, D.; Pintard, M.; Goiffon, A. A General Survey of Quartz and Quartz-like Materials: Packing Distortions, Temperature, and Pressure Effects. J. Solid State Chem. 1996, 123, 1–13. [Google Scholar] [CrossRef]
- Balitsky, D.V.; Balitsky, V.S.; Pisarevley, Y.V.; Philippot, E.; Silvestrova, O.Y.; Pushcharovsky, D.Y. Growth of germanium dioxide single crystals with α-quartz structure and investigation of their crystal structure, optical, elastic, piezoelectric, dielectric and mechanical properties. Ann. Chim. Sci. Mat. 2001, 26, 183–192. [Google Scholar] [CrossRef]
- Krempl, P.W. Piezoelectricity in quartz analogs. J. Phys. IV Fr. 2005, 126, 95–100. [Google Scholar]
- Lignie, A.; Ménaert, B.; Armand, P.; Peña, A.; Debray, J.; Papet, P. Top Seeded Solution Growth and Structural Characterizations of α-Quartz-like Structure GeO2 Single Crystal. Cryst. Growth Des. 2013, 13, 4220–4225. [Google Scholar] [CrossRef]
- Armand, P.; Lignie, A.; Beaurain, M.; Papet, P. Flux-Grown Piezoelectric Materials: Application to α-Quartz Analogues. Crystals 2014, 4, 168–189. [Google Scholar] [CrossRef]
- Lignie, A.; Armand, P.; Papet, P. Growth of piezoelectric water-free GeO2 and SiO2-substituted GeO2 single-crystals. Inorg. Chem. 2011, 50, 9311–9317. [Google Scholar] [CrossRef] [PubMed]
- Lignie, A.; Granier, D.; Armand, P.; Haines, J.; Papet, P. Modulation of quartz-like GeO2 structure by Si substitution: An X-ray diffraction study of Ge1−xSixO2 (0 ≤ x < 0.2) flux-grown single crystals. J. Appl. Cryst. 2012, 45, 272–278. [Google Scholar] [CrossRef]
- Fraysse, G.; Lignie, A.; Hermet, P.; Armand, P.; Bourgogne, D.; Haines, J.; Ménaert, B.; Papet, P. Vibrational origin of the thermal stability in the highly distorted α-quartz-type material GeO2: An experimental and theoretical study. Inorg. Chem. 2013, 52, 7271–7279. [Google Scholar] [CrossRef]
- Papet, P.; Bah, M.; Haidoux, A.; Rufflé, B.; Menaert, B.; Revellez, A.P.; Debray, J.; Armand, P. High temperature piezoelectric properties of flux-grown α-GeO2 single crystal. J. Appl. Phys. 2019, 126, 144102. [Google Scholar] [CrossRef]
- 17.17.220.01; IEEE Standard on Piezoelectricity. IEEE: New York, NY, USA, 1987; Volume 176.
- Bechmann, R. Elastic and Piezoelectric Constants of Alpha-Quartz. Phys. Rev. 1958, 110, 1060. [Google Scholar] [CrossRef]
- Dziuba, R.F.; Weinschel, W.R. Temperature Compensated Crystal Oscillators. IEEE Trans. Instrum. Meas. 1963, 12, 67–77. [Google Scholar]
- Hibbert, D.A. Quartz Crystal Resonators and their Temperature Compensation. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1970, 17, 216–226. [Google Scholar]
- Vig, J.R.; Ballato, A. 4 Frequency Control Devices. Phys. Acoust. 1999, 24, 209–273. [Google Scholar] [CrossRef]
- Tiersten, H.F. Linear Piezoelectric Plate Vibrations; Springer Sciences + Business Media: New York, NY, USA, 1969. [Google Scholar] [CrossRef]
- Newnham, R.E. Properties of Materials: Anisotropy, Symmetry, Structure; OUP Oxford: Oxford, UK, 2005. [Google Scholar]
- Bechmann, R. Frequency-Temperature-Angle Characteristics of AT-Type Resonators Made of Natural and Synthetic Quartz. Proc. IRE 1956, 44, 1600–1607. [Google Scholar] [CrossRef]
- Jiang, X.; Kim, K.; Zhang, S.; Johnson, J.; Salazar, G. High-Temperature Piezoelectric Sensing. Sensors 2014, 14, 144–169. [Google Scholar] [CrossRef]
- Wu, J.; Gao, X.; Chen, J.; Wang, C.M.; Zhang, S.; Dong, S. Review of high temperature piezoelectric materials, devices, and applications. Acta Phys. Sin. 2018, 67, 207701-1–207701-30. [Google Scholar] [CrossRef]
- Lignie, A.; Zhou, W.; Armand, P.; Rufflé, B.; Mayet, R.; Debray, J.; Hermet, P.; Ménaert, B.; Thomas, P.; Papet, P. High-temperature Elastic moduli of Flux-grown alpha-GeO2 Single Crystal. ChemPhysChem 2014, 15, 118–125. [Google Scholar] [CrossRef]


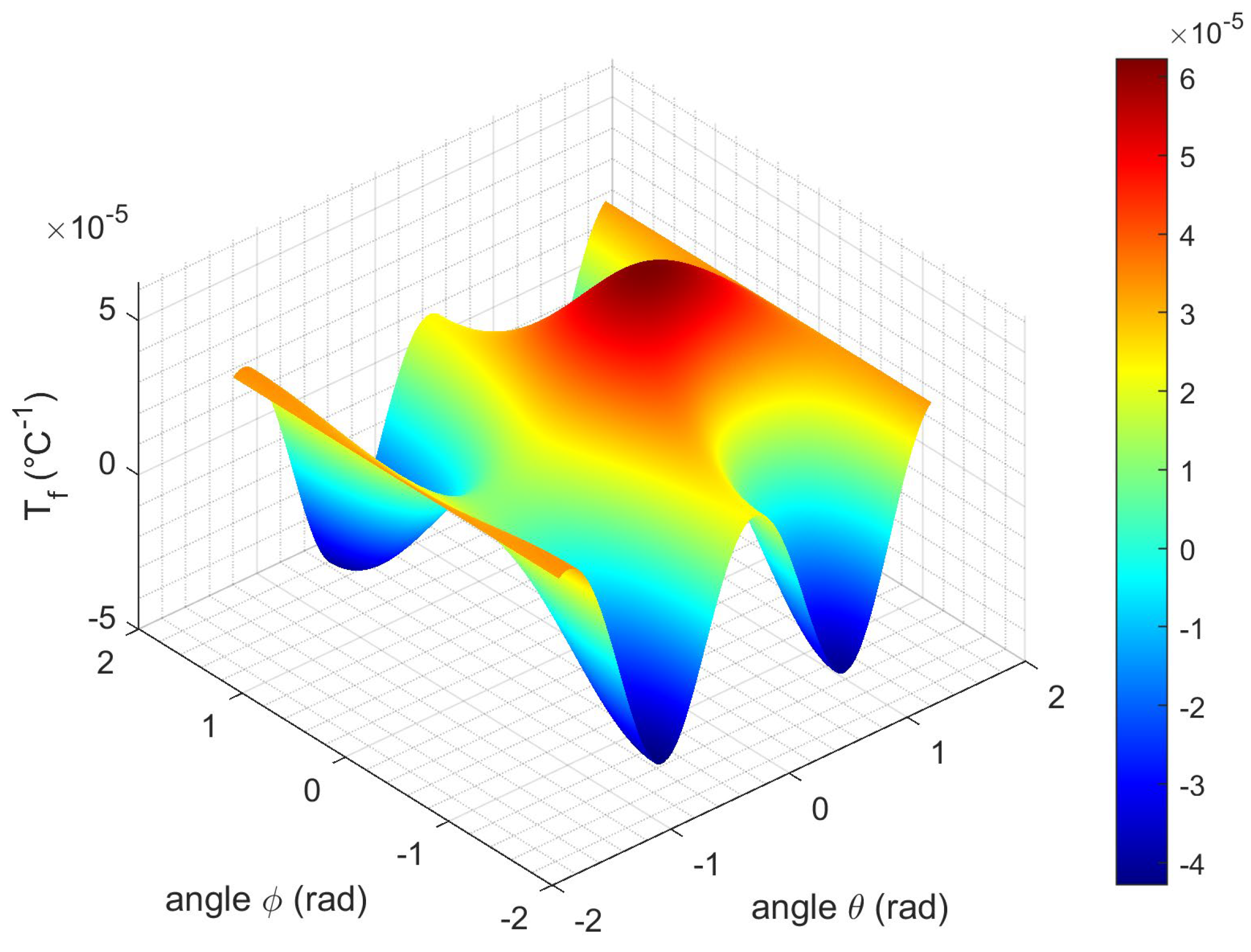
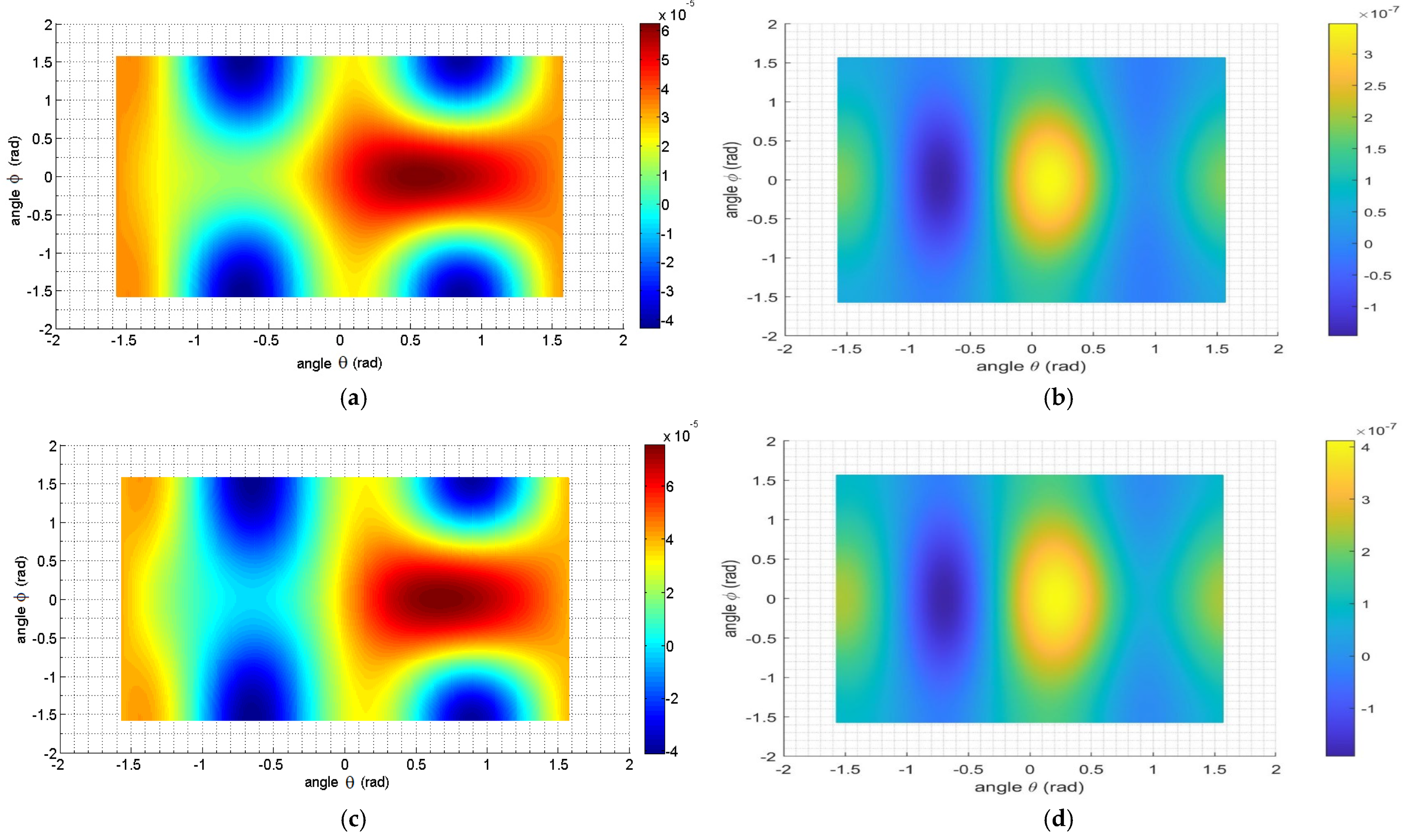

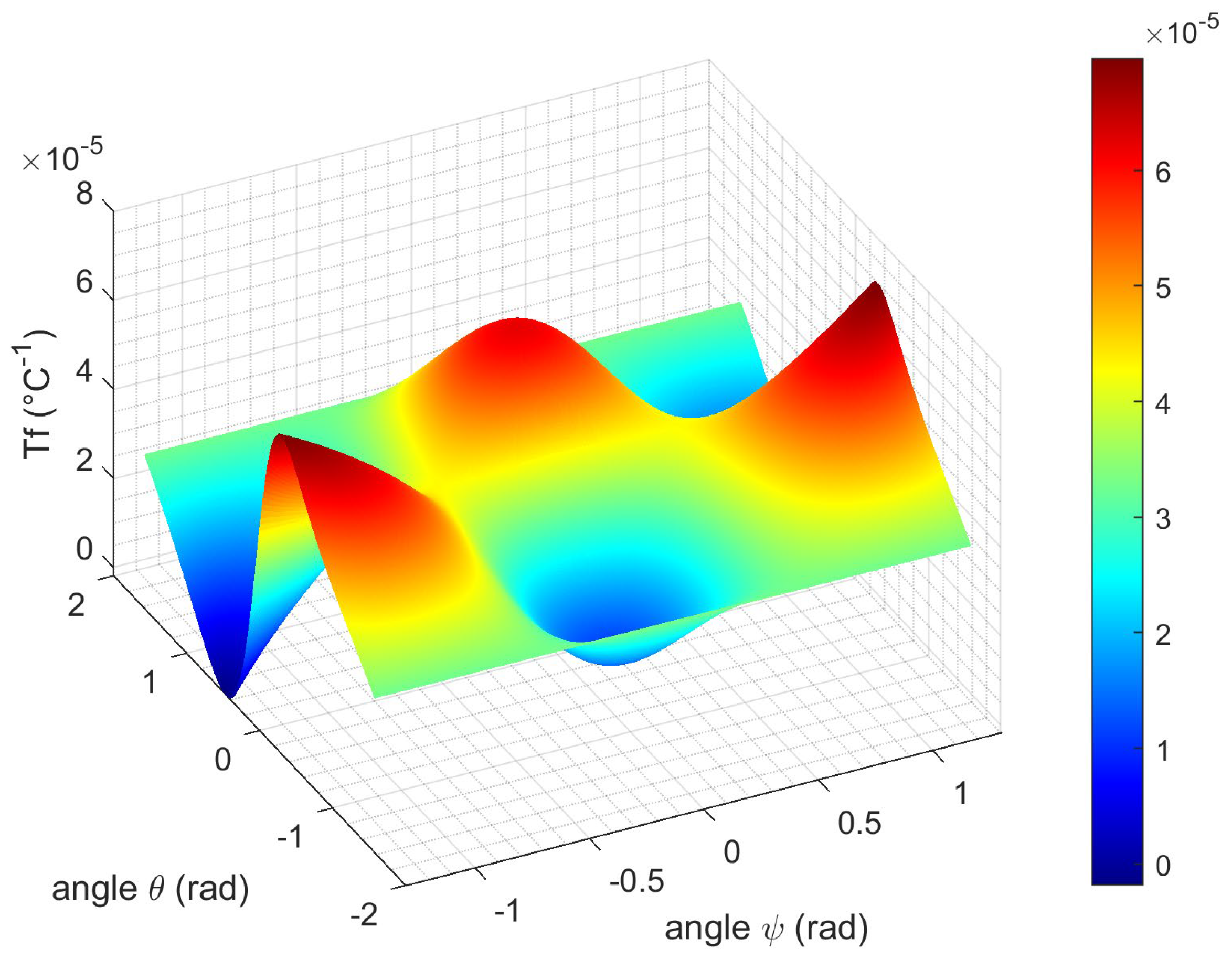
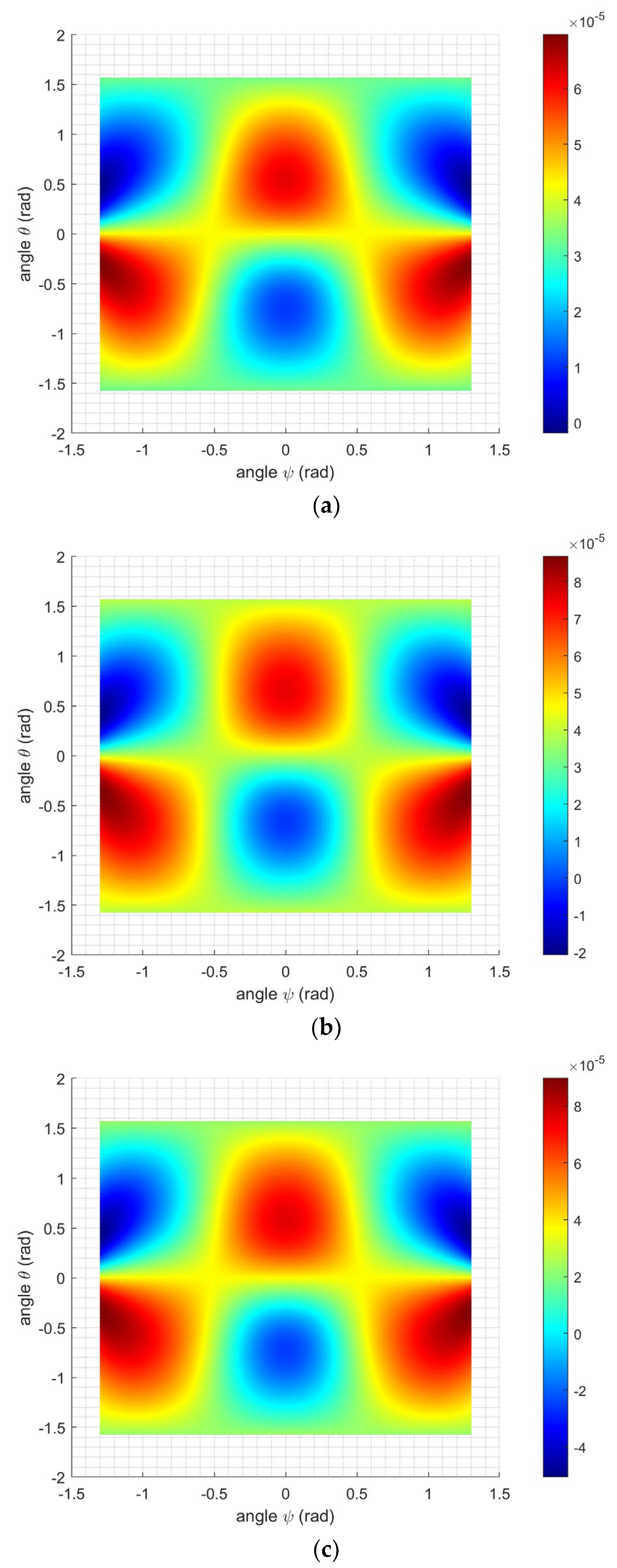
| Elastic Stiffness (Gpa) | First-Order Temperature Coefficients of Cij (ppm°C−1) | Second-Order Temperature Coefficients of Cij (ppm°C−2) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| T = 25 °C | T = 500 °C | T = 900 °C | T = 25 °C | T = 500 °C | T = 900 °C | T = 25 °C | T = 500 °C | T = 900 °C | |
| 69.51 | 69.38 | 68.55 | +3.27 | −14.82 | −48.69 | −0.007 | −0.003 | −0.053 | |
| 27.34 | 27.50 | 27.01 | +60.21 | −26.86 | −54.42 | −0.124 | −0.060 | −0.007 | |
| 0 | 0.91 | 2.04 | +50,266.70 | +2680.22 | +1578.92 | −32.06 | +1.108 | +0.490 | |
| 119.98 | 114.90 | 109.99 | −81.93 | −100.63 | −118.45 | −0.015 | −0.016 | −0.017 | |
| 38.77 | 39.71 | 40.33 | +39.59 | +51.73 | +19.11 | +0.044 | −0.015 | −0.064 | |
| 22.98 | 23.85 | 24.56 | +81.98 | +73.34 | +70.19 | −0.004 | −0.004 | −0.004 | |
| Elastic Stiffness at 25 °C (Gpa) | First-Order Temperature Coefficients of Cij at 25 °C (In Units of ppm°C−1) | Second-Order Temperature Coefficients of Cij at 25 °C (In Units of ppm°C−2) | ||||
|---|---|---|---|---|---|---|
| α-SiO2 [18] | α-GeO2 | α-SiO2 [18] | α-GeO2 | α-SiO2 [18] | α-GeO2 | |
| 86.74 | 69.51 | −48.50 | +3.27 | −0.107 | −0.007 | |
| 11.90 | 27.34 | −550.00 | +60.21 | −1.150 | −0.124 | |
| 17.91 | 0.01 | +101.00 | +50,266.70 | −0.048 | −32.06 | |
| 107.20 | 119.98 | −160.00 | −81.93 | −0.275 | −0.015 | |
| 57.93 | 38.77 | −177.00 | +39.59 | −0.216 | +0.044 | |
| 39.89 | 22.98 | +178.00 | +81.98 | 0.118 | −0.004 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Papet, P.; Armand, P. The Temperature Sensitivity of the Piezoelectric Thickness Shear Mode of α-GeO2 Single Crystals. Crystals 2025, 15, 613. https://doi.org/10.3390/cryst15070613
Papet P, Armand P. The Temperature Sensitivity of the Piezoelectric Thickness Shear Mode of α-GeO2 Single Crystals. Crystals. 2025; 15(7):613. https://doi.org/10.3390/cryst15070613
Chicago/Turabian StylePapet, Philippe, and Pascale Armand. 2025. "The Temperature Sensitivity of the Piezoelectric Thickness Shear Mode of α-GeO2 Single Crystals" Crystals 15, no. 7: 613. https://doi.org/10.3390/cryst15070613
APA StylePapet, P., & Armand, P. (2025). The Temperature Sensitivity of the Piezoelectric Thickness Shear Mode of α-GeO2 Single Crystals. Crystals, 15(7), 613. https://doi.org/10.3390/cryst15070613






