Fractional Vortex Dynamics in Two-Band Superconductors with Linear Normal Strips

Abstract

We investigate the impact of normal linear strips—both perpendicular and parallel to the direction of vortex motion—on the dynamics of fractional vortices in a two-band superconducting slab. In the absence of pinning, composite vortices dominate throughout the sample, while non-composite (dissociated) vortices appear only near the vortex entry edge, with energy dissipation primarily governed by the motion of composite structures. To modulate vortex behavior, we introduce linear regions of locally suppressed superconductivity, oriented either perpendicular or parallel to the vortex trajectory. A single perpendicular strip confines fractional vortices to the injection region, whereas two perpendicular strips stabilize composite vortices in the central domain and induce fractional vortex states near the boundaries. In contrast, parallel strips promote the dissociation of vortices across the entire sample, significantly altering the spatial configuration and dynamics of the vortex matter. Furthermore, the interband correlation coefficient serves as a direct indicator of the degree of spatial overlap between vortices in the two condensates. These findings highlight the critical role of pinning geometry in shaping vortex dynamics and energy dissipation, offering new strategies for controlling flux behavior in multiband superconductors for technological applications.

1. Introduction

Understanding and controlling vortex dynamics in superconductors is crucial for improving their performance in technological applications, such as in magnetic resonance imaging (MRI), particle accelerators, and power transmission systems [1,2,3]. In type-II superconductors, magnetic flux penetrates the material in the form of quantized vortices, whose motion leads to energy dissipation [4,5,6]. One of the main strategies to suppress this dissipation is to immobilize vortices using pinning centers—regions where superconductivity is locally suppressed, such as structural defects, impurities, or non-superconducting inclusions [7,8,9]. These normal regions act as energy minima that trap vortices, reduce their mobility, and enhance the critical current [10,11].

In multiband superconductors, the situation becomes more complex due to the existence of multiple superconducting condensates. In numerous materials such as borocarbides [12], NbSe₂ [13], MgB₂ [14], cuprates [15], heavy fermion systems [16,17], and iron-pnictides [18,19,20], the superconducting (SC) state displays a complex multicomponent character. This behavior arises because superconductivity originates from condensates of electrons belonging to different bands, which can be effectively modeled using multiple coupled order parameters [21]. Each condensate can host vortices that carry only a fraction of the magnetic flux quantum, known as fractional vortices [22,23,24,25,26]. Unlike conventional vortices, fractional vortices can move independently in their respective bands, leading to enhanced energy dissipation and reduced effectiveness of intrinsic pinning. This poses a significant challenge for practical applications, motivating the need for tailored pinning strategies that can stabilize both composite and fractional vortex structures [27,28]. Fractional flux topological excitations [29,30] have gained growing interest because of their link to nonstandard pairing mechanisms [31] and their potential role in the design of topological quantum systems [32]. In two-component superconductors with distinct phase stiffnesses, two thermal transitions may occur: a continuous decoupling of light and heavy vortices (vortex sublattice melting), and a first-order melting of the heavy vortex lattice within a liquid of light vortices—phenomena absent in single-component systems [33]. Half-quantum flux carriers have been observed in intrinsic Josephson junctions of d-wave superconductors [34] and in small rings of Sr₂RuO₄ [35] and $\beta$-Bi₂Pd [36]. In weakly coupled [37] or artificial layered superconductors [38], vortex cores can shift across layers. This allows partial flux even with integer phase windings in each layer. Fractional vortex cores in KFe₂As₂ were recently observed via scanning tunneling microscopy [19]. In Ba1_−xK_xFe₂As₂ ($x\approx 0.77$), vortices with temperature-dependent fractional flux were shown to be mobile and controllable using SQUID magnetometry [20]. A theoretical strategy has been explored to control the dissociation of composite vortices into fractional components and their separation into stationary and fast-moving vortices, through the variation of direct current (DC) and pinning strength [39].

In addition, finite size effects play a crucial role in shaping vortex dynamics in slab geometries, leading to marked changes in the current-voltage characteristics. Experimental and theoretical analyses have shown that confinement and edge barriers can induce nonlinearity and directional vortex motion [40], alter vortex–antivortex interactions [41], and significantly impact nucleation and annihilation processes as revealed in recent numerical simulations [42].

To address this challenge, artificial pinning landscapes have been developed to engineer vortex behavior and enhance superconducting performance. Techniques such as heavy-ion irradiation [43], chemically grown defects [44], and nanostructured perforations [45] have demonstrated remarkable control over vortex arrangements. Yet, in multiband systems, additional features such as domain structures—arising when different superconducting states are nearly degenerate in free energy—introduce new topological elements. These domains, separated by domain walls, can trap vortices and lead to the formation of exotic configurations like vortex sheets, where a conventional vortex splits into two fractional vortices, each carrying half of a quantum of magnetic flux [46,47].

In this context, multiband superconductors offer a rich playground for exploring unconventional vortex matter and pinning phenomena. In the present work, we employ the Ginzburg–Landau theory extended to multiple bands to study the behavior of critical currents and vortex structures in the presence of engineered pinning centers. Our goal is to understand how artificial pinning geometries can influence the mobility and stability of fractional and composite vortices, and to identify configurations that enhance the superconducting performance of multiband materials.

This work is organized as follows. In Section 2, we describe the materials and methods used in our study, including the implementation of the multiband Ginzburg–Landau formalism and the configuration of normal linear strips designed to probe vortex dynamics. Section 3 presents our main results, where we analyze how different geometries of the normal linear strips influence the motion and confinement of both fractional and composite vortices. Finally, in Section 4, we summarize our conclusions and provide a discussion of the implications of our findings.

2. Materials and Methods

In this work, the two-component time-dependent Ginzburg–Landau (TCGL) equations, as presented in [24], are adopted. The Gibbs energy functional of the TCGL model is given in terms of its density energy as follows:

$$\begin{array}{cc}\hfill g=& {\displaystyle \frac{{(\mathbf{B}-{\mathbf{B}}_0)}^2}{8\pi }}+\sum _{j=1,2}\left\{{\displaystyle \frac{1}{2m_j}}{\left|\mathbf{D}{\psi }_j\right|}^2+{\alpha }_j{\left|{\psi }_j\right|}^2\right.\hfill \\ \hfill & \left.+{\displaystyle \frac{1}{2}}{\beta }_j{\left|{\psi }_j\right|}^4\right\}+g_J,g_J=-\Gamma ({\psi }_1^{*}{\psi }_2+{\psi }_1{\psi }_2^{*}),\hfill \end{array}$$

(1)

where the complex gap (condensate) functions of the bands labeled $j=1,2$, are given by ${\psi }_j=\left|{\psi }_j\right|exp\left(i{\theta }_j\right)$. The operator $\mathbf{D}=-\mathbf{i}\hslash \nabla -2e\mathbf{A}/c$ represents the gauge-invariant gradient, while the magnetic field is defined as $\mathbf{B}=\nabla \times \mathbf{A}$. The applied (external) field is denoted by ${\mathbf{B}}_0$, and $g_J$ corresponds to the interband coupling, also known as the Josephson energy (healing coupling). The parameters ${\alpha }_j$, ${\beta }_j$, and $m_j$ are material constants defined as

$$\begin{array}{cc}\hfill & {\alpha }_j=-N\left(0\right)n_j{\chi }_j,{\beta }_j=N\left(0\right){\displaystyle \frac{n_j}{W^2}},\hfill \\ \hfill & m_j={\displaystyle \frac{3W^2}{N\left(0\right)n_j{v}_j^2}},\Gamma =N\left(0\right){\displaystyle \frac{{\lambda }_{12}}{G}},\hfill \\ \hfill & W^2={\displaystyle \frac{8{\pi }^2{T}_c^2}{7\zeta \left(3\right)}},{\chi }_j=\tau -{\displaystyle \frac{S_j}{n_{j}G}},\hfill \end{array}$$

(2)

where $\tau =1-T/T_c$, and $N_j=N\left(0\right)n_j$ represents the band density of states ($DOS$) at the Fermi energy. The total DOS is given by $N\left(0\right)=N_1+N_2$, with the condition $n_1+n_2=1$. The dimensionless coupling constants are defined as ${\lambda }_{ij}=g_{ij}N\left(0\right)$, where $g_{ij}$ are the coupling constants. Additionally, $G={\lambda }_{11}{\lambda }_{22}-{\lambda }_{12}^2$, and $v_j$ denote the Fermi band velocity. The terms $S_1$ and $S_2$ appear in the solution of the linearized gap equation for the critical temperature $T_c$ and are defined similarly to previous work [48].

$$\begin{array}{cc}\hfill & S_1={\lambda }_{22}-n_{1}GS,S_1={\lambda }_{11}-n_{2}GS,\hfill \\ \hfill & S_2={\displaystyle \frac{n_1{\lambda }_{11}+n_2{\lambda }_{22}\pm \sqrt{{(n_1{\lambda }_{11}+n_2{\lambda }_{22})}^2+4n_1{n}_2{\lambda }_{12}^2}}{2n_1{n}_{2}G}}.\hfill \end{array}$$

(3)

The TCGL equations are derived by imposing the stationary condition on the energy functional, while incorporating additional dynamical contributions. This leads to the following equation:

$$\begin{array}{cc}\hfill & {\eta }_1{\displaystyle \frac{\partial {\psi }_1}{\partial t}}={\displaystyle \frac{1}{2m_1}}{\mathbf{D}}^2{\psi }_1+{\alpha }_1{\psi }_1+{\left|{\psi }_1\right|}^2{\psi }_1-\Gamma {\psi }_2,\hfill \\ \hfill & {\eta }_2{\displaystyle \frac{\partial {\psi }_2}{\partial t}}={\displaystyle \frac{1}{2m_2}}{\mathbf{D}}^2{\psi }_2+{\alpha }_2{\psi }_2+{\left|{\psi }_2\right|}^2{\psi }_2-\Gamma {\psi }_1,\hfill \end{array}$$

(4)

where the relaxation constants ${\eta }_j$ are introduced for the respective bands. The corresponding equation, like the Maxwell equation, is given by

$${\displaystyle \frac{c}{4\pi }}\left[\nabla \times \left[\nabla \times \mathbf{A}\right]\right]={\mathbf{J}}_n+{\mathbf{J}}_s,$$

(5)

where ${\mathbf{J}}_s$ represents the super-currents.

$$\begin{array}{c}\hfill {\mathbf{J}}_s=2e\mathrm{Re}\left[{\displaystyle \frac{1}{m_1}}{\psi }_1{\mathbf{D}}^{*}{\psi }_1^{*}+{\displaystyle \frac{1}{m_2}}{\psi }_2{\mathbf{D}}^{*}{\psi }_2^{*}\right],\end{array}$$

(6)

and ${\mathbf{J}}_n$ represents the normal current induced by the electric field

$$\begin{array}{c}\hfill {\mathbf{J}}_n=\sigma \mathbf{E}=-{\displaystyle \frac{\sigma }{c}}{\displaystyle \frac{\partial \mathbf{A}}{\partial t}},\end{array}$$

(7)

with $\sigma$ representing the normal conductivity of the material. Although the characteristic lengths of this model strongly depend on the coupling between the bands, it is still possible to define the coherence length and the penetration depth for each band separately employing the standard Ginzburg–Landau (GL) expressions.

$$\begin{array}{c}\hfill {\xi }_j={\displaystyle \frac{\hslash v_j}{\sqrt{6}W}},{\lambda }_j=\sqrt{{\displaystyle \frac{3c^2}{16\pi N\left(0\right)e^2{n}_j{v}_j^2}}}.\end{array}$$

(8)

It is also possible to define the GL parameter $\kappa$ for each band.

$$\begin{array}{c}\hfill {\kappa }_j={\displaystyle \frac{{\lambda }_j}{{\xi }_j}},{\displaystyle \frac{{\kappa }_2}{{\kappa }_1}}=\sqrt{{\displaystyle \frac{n_1}{n_2}}}{\displaystyle \frac{v_1^2}{v_2^2}}.\end{array}$$

(9)

In the context of a single-band superconductor, the (GL) parameter ${\kappa }_j$ characterizes the type of superconductivity in an isolated band. Specifically, if ${\kappa }_j<1/\sqrt{2}$, the band exhibits type-I superconductivity, which means that it fully expels the magnetic field except at the surface. In contrast, when ${\kappa }_j>1/\sqrt{2}$, the band behaves as a Type II superconductor. A set of material parameters is chosen as ${\lambda }_{11}=2.0$, ${\lambda }_{22}=1.03$, ${\lambda }_{12}={10}^{-4}$, $\alpha =v_1/v_2=0.52$, ${\kappa }_1=10.0$, and $n_1=0.355$. Although these values do not correspond to a specific material, they illustrate a general case in which the vortex sizes differ between bands. With these parameters, it is possible to determine the critical temperature $T_c$ of the superconductor, as well as the individual critical temperatures for each band, considered separately, as

$$T_{cj}=T_c\left(1-{\displaystyle \frac{S_j}{n_{j}G}}\right),$$

(10)

For the selected microscopic parameters, this results in critical temperatures of $T_{c1}=0.9997T_c$ and $T_{c2}=0.9030T_c$. In our calculations, we set the temperature to $T=0.85T_c$, which is sufficiently close to $T_c$ while remaining below both $T_{c1}$ and $T_{c2}$, ensuring that superconductivity is present in both bands. The GL parameters are obtained as ${\kappa }_1=10.0$ and ${\kappa }_2=2.0$, indicating that both bands, when considered separately, exhibit type-II superconductivity. The ratio of the coherence lengths between the two bands is found to be ${\xi }_2/{\xi }_1=2.24$. Following standard terminology, we refer to band $j=1$ as the “strong” band and band $j=2$ as the “weak” band. The magnetic quantum flux ${\Phi }_0$ can be decomposed into two fractional components, approximately given by the expression

$${\varphi }_j={\displaystyle \frac{{\lambda }^2{\Phi }_0}{{\lambda }_j^2}}.$$

(11)

In this context, $\lambda$ represents the effective London penetration depth of the multiband superconductor—that is, the characteristic length scale over which the magnetic field decays inside the material—while ${\lambda }_j$ denotes the partial London penetration depth associated with the j-th band [49]. Using this relation, the fractional flux contributions carried by a single vortex state in each band are determined as ${\varphi }_1=0.72{\Phi }_0$ and ${\varphi }_2=0.28{\Phi }_0$ for the first and second bands, respectively. In numerical simulations, it is convenient to scale all relevant quantities using the characteristic parameters of the strongest band.

$$\begin{array}{cc}\hfill & {\psi }_j=W{\tilde{\psi }}_j,\mathbf{r}={\xi }_1\tilde{\mathbf{r}},\mathbf{A}=A_0\tilde{\mathbf{A}},\hfill \\ & t=t_0\tilde{t},{\eta }_j={\eta }_0^j{\tilde{\eta }}_j,\hfill \end{array}$$

(12)

where

$$\begin{array}{cc}\hfill & A_0={\displaystyle \frac{\hslash c}{2e{\xi }_1}},t_0={\displaystyle \frac{4\pi \sigma {\kappa }_1^2{\xi }_1^2}{c^2}},{\eta }_0^j=n_{j}N\left(0\right)t_0.\hfill \end{array}$$

(13)

The dimensionless form of the TCGL equations is expressed as (where all quantities have been scaled, and the “tilde” notation is omitted for simplicity).

$$\begin{array}{cc}\hfill & {\eta }_1{\displaystyle \frac{\partial {\psi }_1}{\partial t}}={\mathbf{D}}^2{\psi }_1-\left({\chi }_1-{|{\psi }_1|}^2\right){\psi }_1-\gamma {\psi }_2,\hfill \\ \hfill & {\eta }_2{\displaystyle \frac{\partial {\psi }_2}{\partial t}}={\displaystyle \frac{1}{\alpha }}{\mathbf{D}}^2{\psi }_2-\left({\chi }_2-{|{\psi }_2|}^2\right){\psi }_2-{\displaystyle \frac{\gamma }{\alpha }}{\displaystyle \frac{n_1}{n_2}}{\psi }_1.\hfill \end{array}$$

(14)

The gauge-invariant derivative is defined as $\mathbf{D}=-i\nabla -\mathbf{A}$, while the parameter $\gamma$ is given by $\gamma ={\lambda }_{12}/\left(n_{1}G\right)$. For the decay rates, we assume ${\eta }_1={\eta }_2=5.0$. Under these conditions, Equation (5) simplifies to:

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\partial \mathbf{A}}{\partial t}}=\mathrm{Re}\left[{\psi }_1{\mathbf{D}}^{*}{\psi }_1^{*}+{\displaystyle \frac{1}{\alpha }}{\displaystyle \frac{n_2}{n_1}}{\psi }_2{\mathbf{D}}^{*}{\psi }_2^{*}\right]-{\kappa }_1^2\left[\nabla \times \left[\nabla \times \mathbf{A}\right]\right].\hfill \end{array}$$

(15)

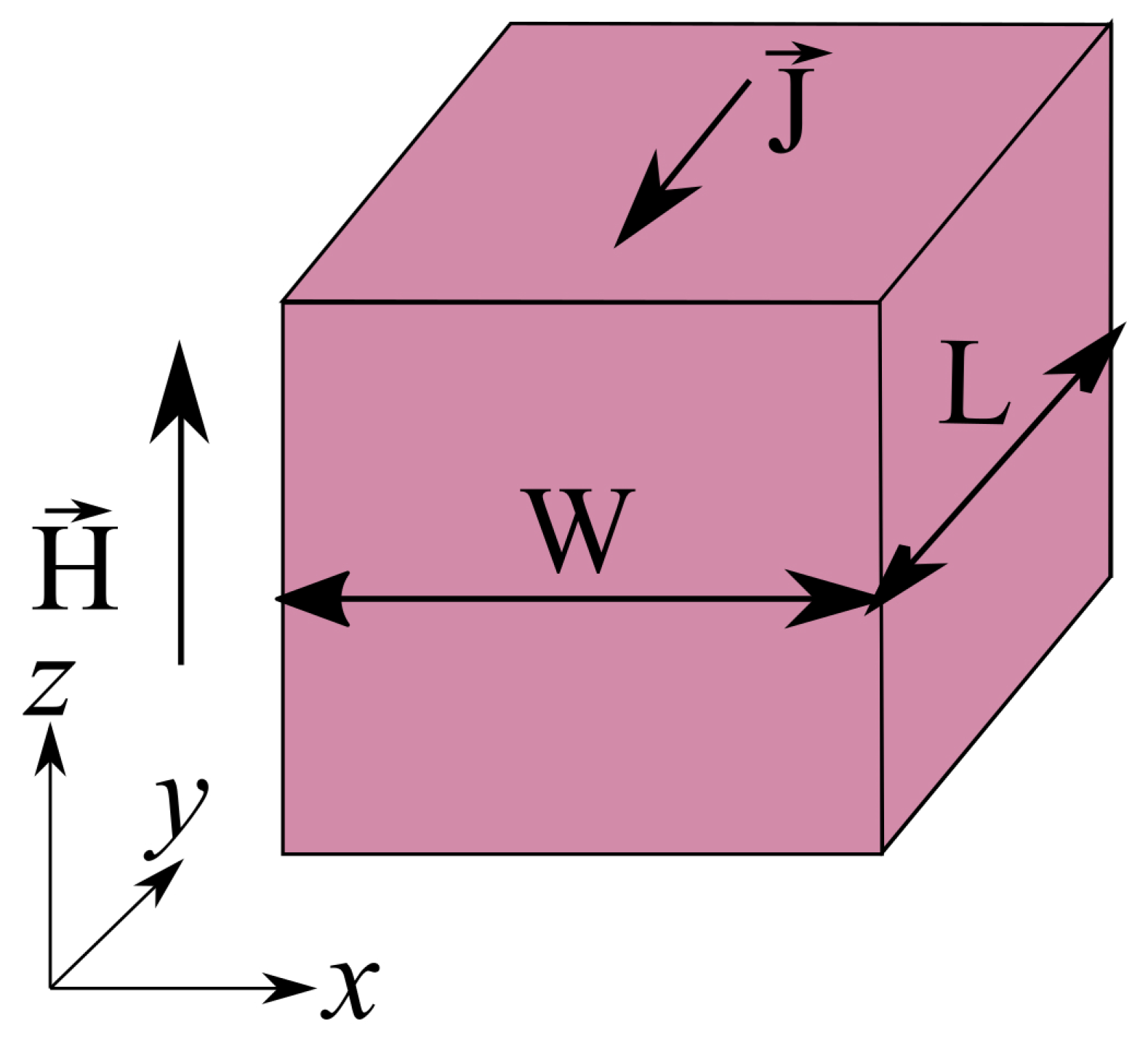
We analyze a system in the form of an infinitely long rectangular slab with cross-sectional dimensions of $L\times W$, considering a slab of infinite length, demagnetization effects are neglected; see Figure 1. The system is effectively reduced to a two-dimensional structure.

The governing Equations (14) and (15) are solved using periodic boundary conditions (Von karma conditions) along the x direction, where $W=300{\xi }_1$, along with the standard Ginzburg–Landau condition.

$$\begin{array}{c}\hfill {\mathbf{D}}_y{\psi }_j=0,\end{array}$$

(16)

and in the y-direction $L=300{\xi }_1$, where the vector component y is perpendicular to the surface of the sample, periodic boundary conditions (Von Karma conditions) are also applied. The numerical solution is implemented on a two-dimensional square grid with uniform spacings $a_x=a_y={\xi }_1=0.1$. The computational method used is the U-$\Psi$ method [10,50,51], combined with a parallelized Euler finite difference algorithm for time evolution. The motion of vortices is driven by an externally applied current with density $\mathbf{j}$ flowing along the $\mathbf{x}$-direction within the sample. In the numerical approach, this current is introduced by incorporating an additional magnetic field $\Delta \mathbf{B}$, which is related to $\mathbf{j}$ through Equation (5). Given the selected geometry, this extra field is oriented along the z-axis and is designed as the total applied field, and takes the values $B=B_0-\Delta B$ for $y<0$ and $B=B_0+\Delta B$ for $y>w$. Considering that $\mathbf{B}=[\nabla \times \mathbf{A}]$ and using Equation (5), the resulting current density is determined as $J={\displaystyle \frac{c\Delta B}{2\pi }}$. Defects in the sample are introduced through the constant $\chi$, which is considered as a spatial function, ${\chi }_J(x,y)$. For a pinning barrier perpendicular to the direction of vortex motion, ${\chi }_J$ is defined as follows:

$${\chi }_J(x,y)=\left\{\begin{array}{cc}\tau -{\displaystyle \frac{S_J}{n_{j}G}},\hfill & \mathrm{out}\mathrm{of}\mathrm{the}\mathrm{region}\mathrm{of}\mathrm{linear}\mathrm{barrier},\hfill \\ -{\displaystyle \frac{S_j}{n_{J}G}},\hfill & \mathrm{in}\mathrm{the}\mathrm{region}\mathrm{of}\mathrm{linear}\mathrm{barrier}\mathrm{along}x\mathrm{and}\mathrm{with}\mathrm{a}\mathrm{width}\Delta y.\hfill \end{array}\right.$$

(17)

For a pinning barrier parallel to the direction of vortex move, ${\chi }_j$ is defined as:

$${\chi }_J(x,y)=\left\{\begin{array}{cc}\tau -{\displaystyle \frac{S_J}{n_{J}G}},\hfill & \mathrm{out}\mathrm{of}\mathrm{the}\mathrm{region}\mathrm{of}\mathrm{linear}\mathrm{barrier},\hfill \\ -{\displaystyle \frac{S_J}{n_{J}G}},\hfill & \mathrm{in}\mathrm{the}\mathrm{region}\mathrm{of}\mathrm{linear}\mathrm{barrier}\mathrm{along}y\mathrm{and}\mathrm{width}\Delta x.\hfill \end{array}\right.$$

(18)

Given the above, we proceed to present the numerical results for our particular system.

In this study, we employed the Pearson correlation coefficient (r) [26] to differentiate non-composite vortex states based on data derived from the order parameters of both the strongest and weakest bands (${\psi }_i$ and $i=1,2$). The correlation coefficient r is expressed in terms of the square modulus of the order parameters of the two condensates, ${\psi }_1$ and ${\psi }_2$, as follows:

$$r={\displaystyle \frac{\mathrm{cov}\left({\left|{\psi }_1\right|}^2,{\left|{\psi }_2\right|}^2\right)}{{\sigma }_1{\sigma }_2}}.$$

(19)

The $\mathrm{cov}(\dots )$ represents the covariance operator, ${\psi }_1$ is the order parameter corresponding to the strongest band, ${\psi }_2$ pertains to the weakest band, and ${\sigma }_{1,2}$ denote the standard deviations of ${\left|{\psi }_{1,2}\right|}^2$.

3. Results

3.1. Two-Band Pinning-Free Superconductor with Large Dimensions

Several studies have shown that fractional vortices are not stable in large-size samples. The main reason lies in the energetic cost associated with separating individual vortices: in extended geometries, the system minimizes its energy when fractional vortices merge to form composite vortices carrying an integer number of magnetic flux quanta. This behavior has been thoroughly analyzed in work such as that by Pina, de Souza Silva, and Milošević (2012) [22], who used a two-component Ginzburg–Landau model to demonstrate that fractional vortex states can only be stabilized under specific conditions and mainly in mesoscopic samples. Complementarily, Maiani, Benfenati, and Babaev (2022) showed that, in general, fractional vortices are energetically unstable in the bulk due to divergent energy contributions, although they may be temporarily stabilized near sample edges [25]. Lin and Reichhardt (2013) further evidenced that fractional vortices can be stabilized through periodic pinning arrays; however, in the absence of such artificial structures, they tend to coalesce into composite vortices [23]. The fractional vortices represent a remarkable feature of multiband superconductivity and their stability is strongly constrained by sample geometry and the presence of external confinement or pinning mechanisms.

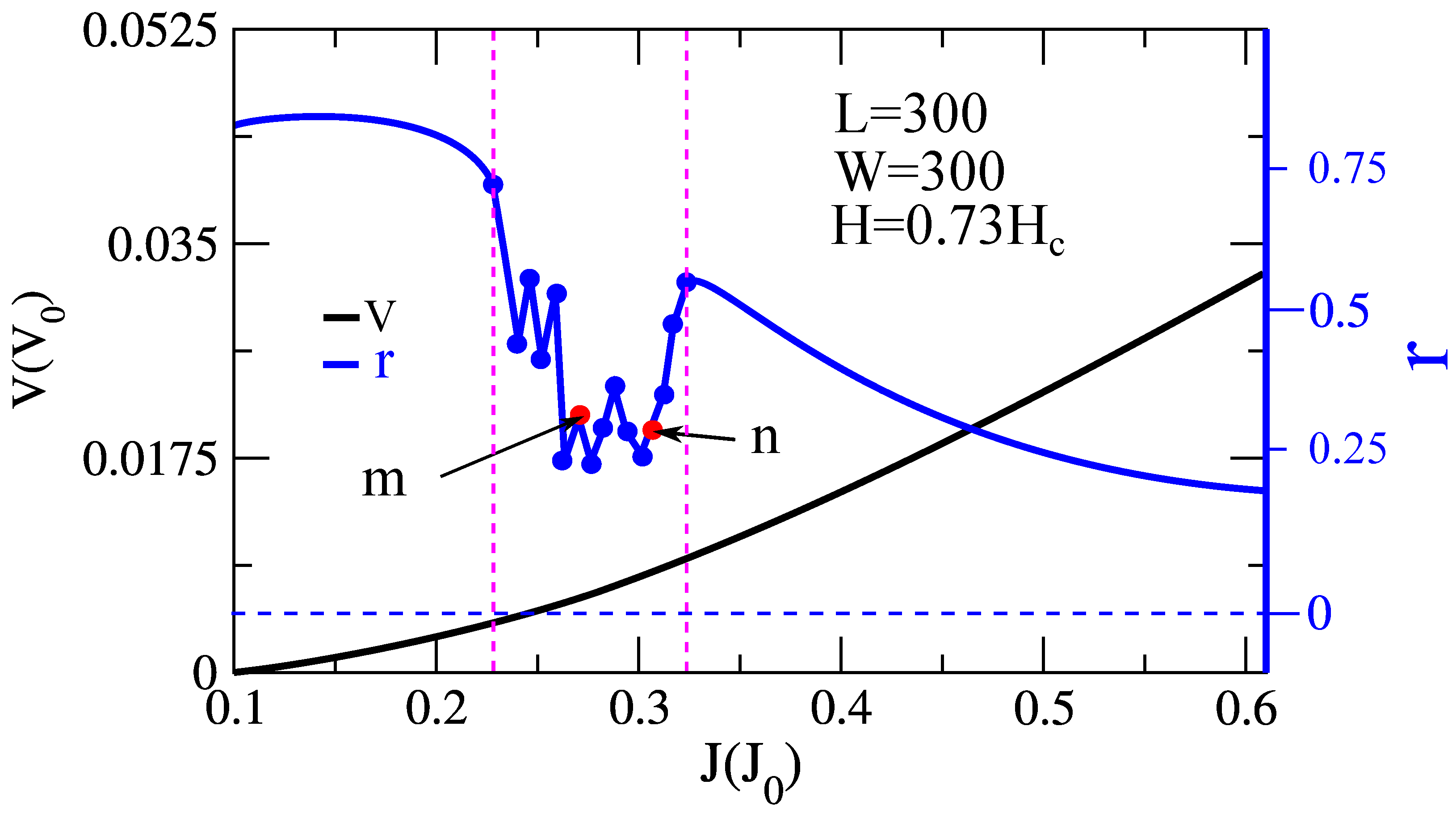
In Figure 2, we show the behavior of the voltage (V) and the correlation coefficient (r) as functions of the applied current density (J). The voltage increases monotonically with J, as expected, due to the progressive motion of vortices entering and traversing the superconducting sample. This behavior reflects the dissipation associated with vortex dynamics as they move toward their equilibrium positions under the influence of the applied current. In the case of an infinite pinning-free superconductor, vortices begin to move with any infinitesimal applied current [39], which leads to a finite induced voltage for all currents greater than zero [49]. However, when the finite geometry of the superconducting sample is taken into account—even without pinning—the vortex motion occurs only above a well-defined threshold current. This phenomenon is attributed to vortex interactions with the sample boundaries; see references [24,26,52,53,54] for more details. Here, a finite voltage emerges only beyond a nonzero critical current and, although the internal characteristics of vortices differ between single-band and multiband superconductors, the physical boundaries of the sample similarly affect vortex dynamics in both situations. Therefore, it is reasonable to assume the existence of a current threshold for the onset of vortex motion in finite-geometry, pinning-free superconductors of both single and two-band types. In our investigation, we explicitly consider the finite dimensions of the sample, where it is possible to observe a similar behavior: the induced voltage remains zero below a threshold current of $J=0.1J_0$, becoming finite above it (see Figure 2). Furthermore, Figure 2 reveals that the voltage increases monotonically with current, indicating faster vortex motion at higher currents, in qualitative agreement with the findings reported in [39,49].

In contrast, the correlation coefficient r, which quantifies the degree of coherence between the superconducting order parameters of the two bands [26], exhibits a non-monotonic behavior. Initially, r decreases as the current increases, indicating a gradual loss of coherence between the bands. This trend can be attributed to the emergence and proliferation of fractional vortices, which originate independently in each band. As the current increases further, the weak band becomes increasingly suppressed, approaching the normal state. In this regime, the number of vortices increases, and the amplitude of the superconducting order parameter in the weak band is strongly reduced, leading to a minimum in the correlation. In the normal state, the superconducting order parameter vanishes, and thus the interband correlation reaches its lowest possible value. Interestingly, the $r\left(J\right)$ curve features a distinct region of accelerated decay, bounded by the magenta dotted lines in Figure 2. Within this region, the dissociation of vortices is particularly pronounced; however, the correlation does not reach zero, indicating that complete decoupling between the bands is not achieved globally. Instead, dissociated vortices appear predominantly in localized regions within the slab, especially near the edges where vortices first penetrate. To gain further insight into this behavior, we analyze the vortex configurations at two representative points on the $r\left(J\right)$ curve. The two characteristic points are m at $J=0.27J_0$ and n at $J=0.30J_0$; both lie within the region where the correlation coefficient r reaches its lowest values. At the point m, the weak band displays significant suppression, and the density of dissociated vortices is maximal. The second point n corresponds to a slightly higher current $J=0.30J_0$. Here, the weak band has transitioned further into the normal state, and the density of dissociated vortices is notably reduced. This suggests that, as the weak band becomes fully normal, the remaining superconducting coherence is governed primarily by the strong band, and the system approaches a state with fewer fractional vortices and reduced interband interaction.

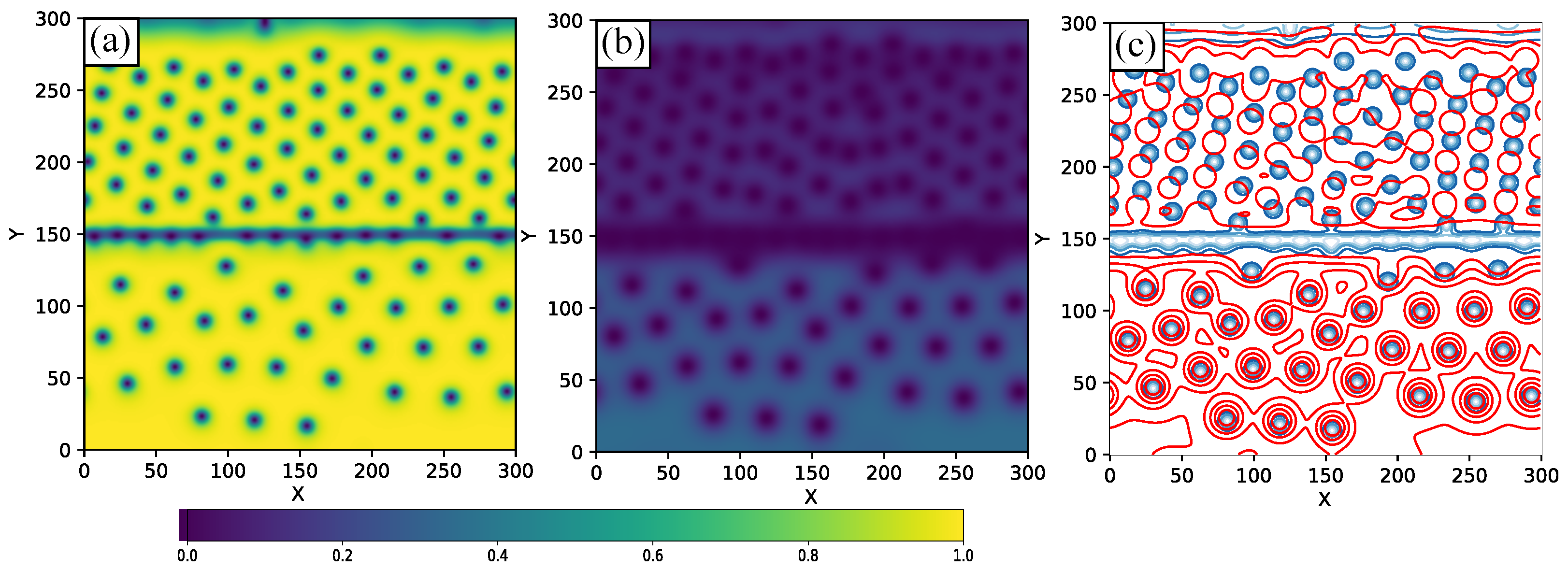
In Figure 3a–c, we show the spatial distribution of the Cooper pair density for the first band (Figure 3a), the second band (Figure 3b), and the total condensate (Figure 3c). From the latter, the vortices are only dissociated in specific regions of the slab. Most vortices are composite, and only small regions near the edges exhibit dissociated vortices. This behavior is consistent with the reduced value of the correlation coefficient r observed at this current density (see point m in Figure 2), which reflects a partial loss of interband coherence in localized regions. Nonetheless, despite the reduced correlation, some degree of spatial overlap between vortex cores still persists. This partial alignment suggests that the Josephson coupling is not negligible and still exerts a binding effect between the condensates, limiting the full decoupling of the vortex positions.

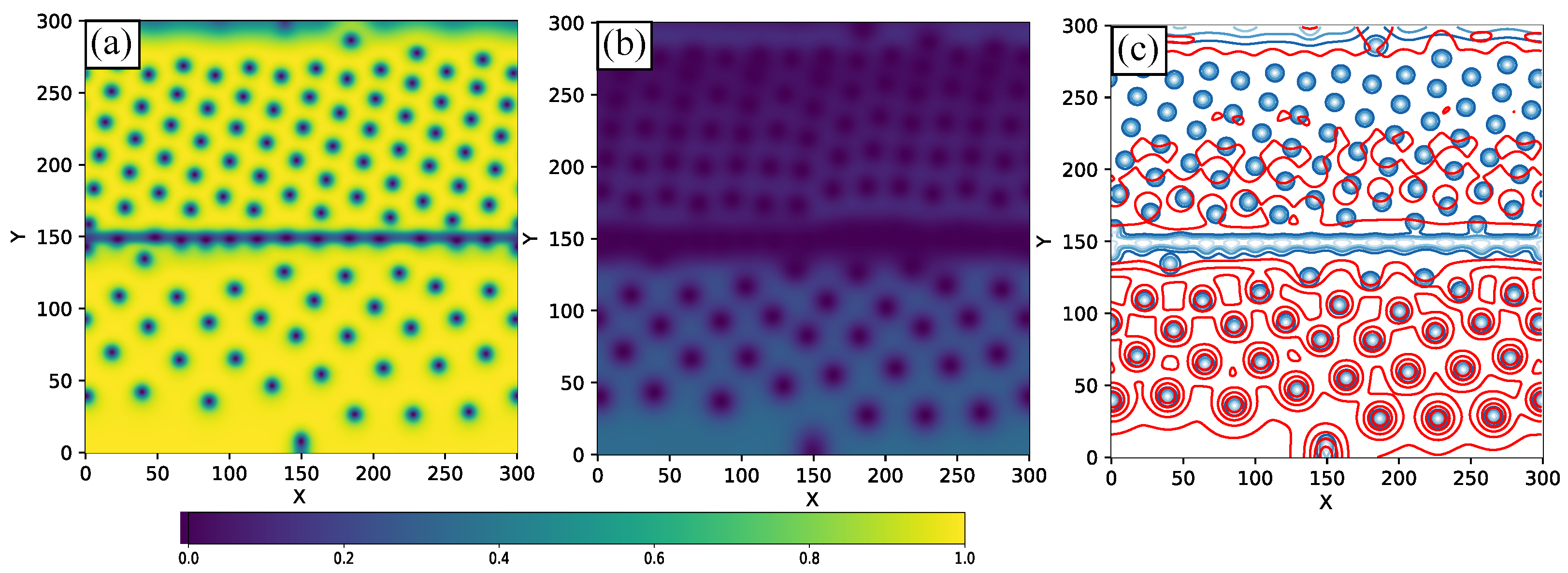
In Figure 4a–c, we present the spatial distribution of the Cooper pair density for the first band, the second band, and the total condensate, respectively, corresponding to point n on the $r\left(j\right)$ curve shown in Figure 2. Compared to the previous case (point m), the normal state in the weaker band is more developed, and a few dissociated vortices are observed when the condensate densities are superimposed in Figure 4c. The vortices in each band have different core sizes, and their interaction with the boundaries through which they penetrate leads to their dissociation. However, most of them recombine as they traverse the sample towards the opposite edge. In larger samples, the increased distance between boundaries reduces the influence of edge effects, allowing the vortices to recombine. This is because the system can relax to a configuration that minimizes the energy, favoring the formation of composite vortices. Moreover, the proximity of the system to the normal state at this higher current density may facilitate tunneling-like processes between vortex states in different bands. As the applied current and external fields continue to increase, the superconducting order parameter in the weaker band becomes increasingly suppressed, pushing the system closer to the normal state. In this regime, we expect the correlation coefficient r to decrease further, signaling the eventual loss of coherence between the bands and the suppression of superconductivity.

In both scenarios discussed thus far, no pinning barriers were introduced into the system. Consequently, the vortices were free to move throughout the sample, subject only to the intrinsic properties of the material and the external fields. In the following section, we investigate how the introduction of pinning barriers affects the vortex states in each superconducting band, analyzing the modified vortex configurations, and we aim to understand how normal linear strips influence the spatial distribution, coherence, and dynamics of vortices in multiband superconductors and the relationship with the correlation coefficient.

3.2. Normal Linear Strips Perpendicular to Vortex Motion

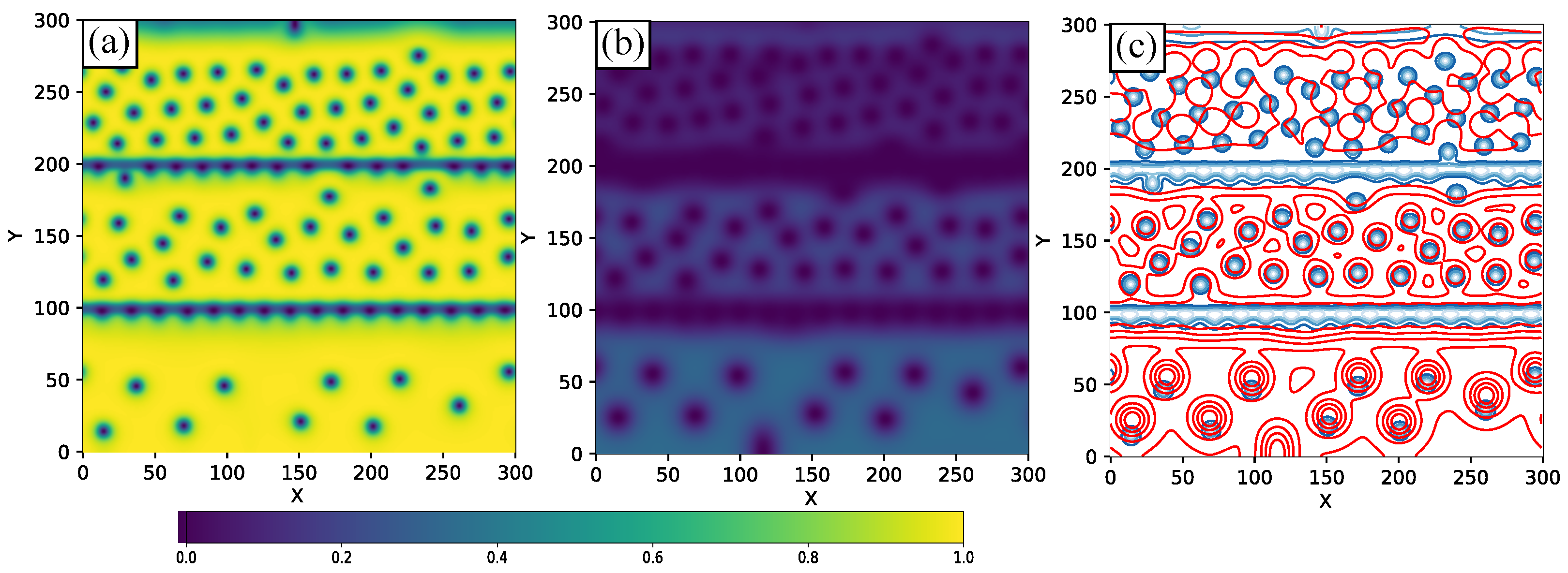
In Figure 5a–c, we show the vortex configurations for both superconducting bands and the total condensate in the presence of normal linear strips located at the center of the sample. The results correspond to the same value of the correlation coefficient r as in point m from the previous analysis, which is lower than the value observed at point n. We observe that in the region above the central strip in the normal state, there is a very low degree of coincidence between the vortex cores in the two bands, indicative of significant vortex dissociation. Below this region, the vortices are composite, with their positions aligned and exhibiting long-range correlations. As expected, no vortices are present within the central normal region, confirming that the normal strips effectively suppress superconductivity locally and prevent vortex nucleation within that zone. However, in a curious way, vortex entry into the superconducting regions occurs preferentially through the sections adjacent to the normal line. This behavior suggests that this normal structure alters the local energy landscape in such a way that it channels vortex motion along specific trajectories, thus modifying the dynamics and spatial distribution of vortices across the sample.

The normal strip constrains the available space for order parameter deformations, introduces asymmetries in the order parameters due to each band’s distinct response, and disrupts long-range vortex interactions. These changes turn intrinsic differences, such as coherence lengths and critical currents, into dominant local factors. In the region just above the strip, this modified energy balance allows vortices to dissociate into independent components. Upon crossing the interface, only those vortices capable of compensating residual deformation energy, synchronizing their phases through the weak remaining coupling, and maintaining local stability are able to recombine. This selection process explains the marked reduction in vortex density observed below the strip. Thus, a simple local discontinuity becomes a powerful probe of quantum behavior, exposing otherwise hidden material properties. The strip not only perturbs the local superconducting state but also induces a global reorganization of the condensate, revealing how controlled imperfections can be used to explore and manipulate quantum states that remain concealed in homogeneous systems.

In Figure 6a–c, we present the Cooper pair density for the first band, the second band, and the total condensate, corresponding to the same vortex state analyzed in the presence of a central pinning barrier, but now for a configuration associated with a value of the correlation coefficient, matching that of point n in Figure 2. At higher current values, the region above the normal strip becomes nearly normal, effectively suppressing superconductivity in both bands. In contrast, the region below the strip remains superconducting in both condensates, although with weakened order parameters. In this lower region, vortices continue to exhibit a composite character, with cores in both bands remaining spatially aligned.

In Figure 7a–c, we show the vortex configurations for both superconducting bands and for the total condensate in the presence of two normal linear strips. The vortex state corresponds to the same current value as point m in Figure 2.

Introducing two normal strips, rather than just one, leads to a more complex evolution of vortex states. While a single strip creates a clear separation between decoupled vortices in the upper region and recombined vortices below, two strips define three distinct regions with gradually changing vortex behavior. The first strip initiates the expected decoupling in the upper zone, but the presence of a second strip modifies this transition. In the intermediate region between the two strips, the system exhibits a partial recovery of coherence between components, resulting in a metastable state with partial vortex recombination. This intermediate response indicates that the system retains some dependence on the unperturbed bulk conditions.

Below the second strip, the filtering effect becomes more stringent: only vortices capable of adapting to both discontinuities persist, leading to an even more pronounced reduction in vortex density compared to the single-strip case. The lower region also exhibits asymmetric decoupling relative to the upper zone, indicating that the system’s response depends on the sequence in which perturbations are applied, not merely on their presence. This history-dependent behavior suggests hysteresis in the processes of vortex coupling and decoupling, highlighting that multiple strips do not simply enhance the effect of a single one—they generate new physical regimes. The second strip acts not only as an additional filter but also as a modifier of the first strip’s influence, enabling a partial reorganization before the system is perturbed again. This sequence of successive constraints allows for a detailed analysis of the stability of interband coupling, revealing how vortex states evolve under structured changes rather than a single abrupt discontinuity. The result is a spatial structure with multiple coherence configurations, providing detailed information about the interactions between bands in weakly coupled superconductors.

Figure 8a–c presents the spatial distribution of the Cooper pair density for the same superconducting system with two normal strips, now at a higher current corresponding to point n in Figure 2. The region above the first normal strip becomes fully normal, with superconductivity completely suppressed. In contrast, the intermediate region between the two strips remains superconducting in both bands and continues to support composite vortices. The vortex cores in both condensates remain spatially aligned, indicating that interband coherence is preserved despite the increased current. This behavior suggests that the intermediate region is less affected by the elevated current, possibly due to its partial isolation from the direct influence of the adjacent normal zones.

Meanwhile, the lower region, below the second strip, maintains the dissociated vortex state observed at lower currents. Vortices in this region remain decoupled, with the core positions in each band no longer overlapping. This persistent dissociation reflects the cumulative impact of the two normal discontinuities, which fragment the condensate and prevent the reestablishment of coherence. Thus, while the upper region transitions fully into the normal state, the middle and lower zones maintain distinct superconducting behaviors, shaped by their relative positions within the structured landscape.

3.3. Linear Pinning Barrier Parallel to the Vortex Motion

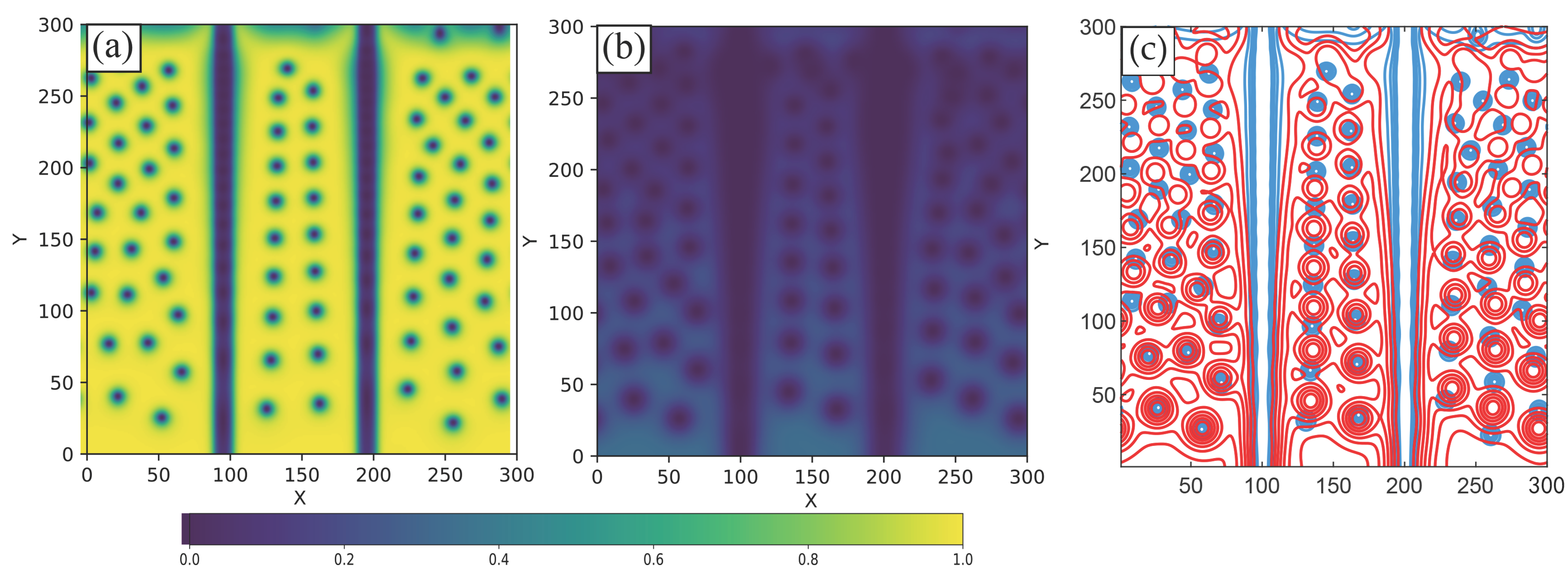
In line with the previous results, we now examine the impact of introducing two normal strips parallel to the direction of vortex motion. To do this, Figure 9a–c show the vortex configurations for the first band, the second band, and the total condensate, respectively, at the current value corresponding to point m. Placing two normal strips parallel to the direction of vortex motion significantly modifies the vortex configurations in the system. The suppression of superconductivity along these strips alters the surrounding energy landscape. This promotes the dissociation of vortices in adjacent superconducting areas, leading to an increased number of fractional vortices across the sample. In several regions, the dissociated vortices maintain their separation as they cross the entire system, without recombining into composite structures. The parallel orientation of the strips ensures a persistent influence along the vortex trajectory, hindering the recovery of spatial overlap between the vortex cores of each band. As a result, the interband coherence remains weak over extended paths, stabilizing fractional vortex states. This behavior reveals how extended directional inhomogeneities can be used to selectively control the coupling between condensates in multiband superconductors.

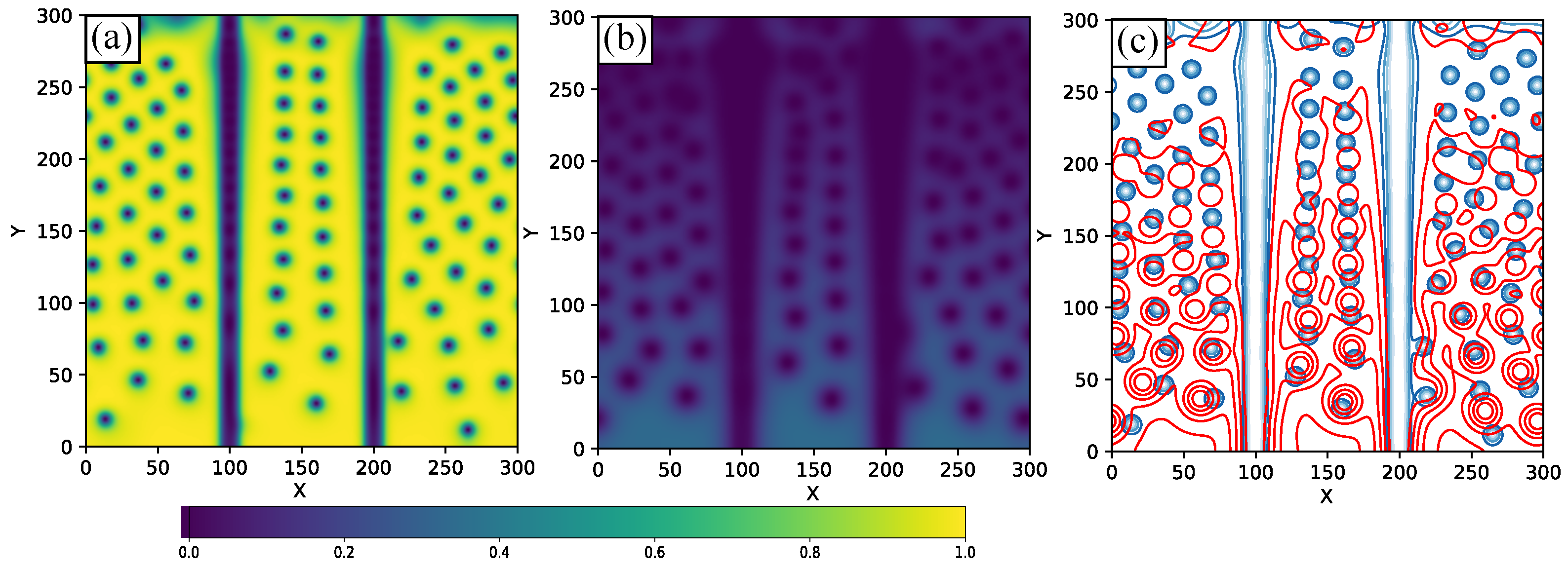
Finally, in Figure 10a–c, we present the vortex configurations corresponding to point n for both superconducting bands and the total condensate. At higher current values, the upper region of the slab transitions fully into the normal state, eliminating superconductivity in both bands. Despite this, in the remaining superconducting portion of the sample, dissociated vortices are observed to traverse the entire system from one edge to the other. This behavior contrasts with the lower-current regime, where partial recombination occurred between the strips.

The increase in current amplifies the disparity in the response of each condensate, weakening the interband coupling and favoring the persistence of fractional vortex states. The presence of two normal strips aligned with the vortex motion further constrains the local coherence recovery, guiding the dissociated vortices along uninterrupted paths. As a result, the entire superconducting region supports independent vortex dynamics in each band, and the interband phase locking becomes negligible over macroscopic distances.

This regime illustrates how the combined effects of structured inhomogeneities and strong driving currents can stabilize the long-range dissociation of vortices, providing a controlled route to access new dynamical states in multiband superconductors.

Discussion: The results obtained provide a detailed characterization of fractional vortex behavior in two-band superconductors under varying confinement conditions. In the absence of pinning barriers, the system exhibits a behavior consistent with predictions in the literature: composite vortices dominate throughout most of the sample, while fractional vortices appear only in small, localized regions—primarily near the edges where vortices enter. This is in line with theoretical and numerical studies suggesting that fractional vortices are generally unstable in extended systems and tend to recombine into composite structures to minimize the total free energy. The Cooper pair density profiles reflect this partial dissociation as a moderate decrease in the interband correlation coefficient r, without complete decoupling. The transition toward partially dissociated states occurs within a well-defined current range, where r decreases significantly but not entirely, indicating that interband coupling—though weakened—still plays a stabilizing role.

The introduction of normal linear barriers perpendicular to the direction of vortex motion dramatically alters this dynamic. A single central barrier creates a clear spatial differentiation: in the upper region above the strip, vortex dissociation is pronounced, while below it, partial recombination occurs. This is a consequence of the local disruption of quantum coherence and the modified energy landscape induced by the discontinuity. The barrier effectively selects vortices capable of compensating residual deformation energy and maintaining local stability across the interface, resulting in a marked reduction in vortex density below the strip. When two such barriers are introduced, the sample is divided into three distinct zones: an upper region with strong dissociation, an intermediate zone where coherence partially recovers, and a lower region with a significant reduction in vortex count. This behavior highlights not only a filtering effect but also a history-dependent response: the system’s evolution is not symmetric or additive—the second barrier reshapes the effects of the first, introducing hysteresis-like features into the coupling and decoupling dynamics.

In contrast, the presence of normal strips aligned parallel to the vortex motion promotes a more global reorganization of the vortex landscape. These parallel barriers suppress superconductivity along extended channels, modifying the surrounding energy environment and facilitating vortex dissociation across the entire system. At low currents, fractional vortices emerge and remain dissociated throughout their trajectory, without recombining into composite entities. At higher currents, this behavior persists even in the remaining superconducting portions of the sample, where dissociated vortices traverse uninterrupted paths from edge to edge. The parallel orientation of the barriers sustains a directional constraint that continuously inhibits coherence recovery, preventing the spatial overlap of vortex cores from different bands. As a result, interband phase locking is suppressed over macroscopic distances, and long-range dissociation becomes the stable configuration.

Taken together, these findings demonstrate how structured inhomogeneities can be used to precisely control interband coupling and vortex behavior in multiband superconductors. Both perpendicular and parallel normal barriers serve as effective tools to induce, tune, and stabilize vortex dissociation, revealing interband dynamics that remain hidden in homogeneous systems. The emergence of metastable states, regions with mixed coherence configurations, and long-range dissociation regimes provides a conceptual and experimental framework for the design of superconducting devices where local control of quantum coherence is essential.

Furthermore, from a point of view of experimental realizations, we point out that $Mg{B}_2$ is a prototypical two-band superconductor where fractional vortices and interband coupling effects have been theoretically predicted and partially explored experimentally [14,55,56,57]. The coexistence of distinct superconducting gaps and weak interband scattering in $Mg{B}_2$ enables the partial decoupling of the order parameter phases, providing favorable conditions for observing vortex dissociation and composite-core deconfinement phenomena. In addition, granular superconductors and artificial Josephson lattices can emulate effective multiband behavior by hosting multiple weakly coupled superconducting condensates. These systems naturally support engineered pinning landscapes and phase discontinuities, which have been shown to stabilize fractional vortices (semifluxons) in controlled experiments [58]. In addition, we note that certain iron-based superconductors, such as $Fe$($Te$,$Se$), have been identified as candidate topological superconductors. Experimental evidence for Majorana bound states in vortex cores and half-quantum vortex configurations has been reported in these systems [59], supporting the idea that topological order can enable fractionalization phenomena closely related to those described in our work.

4. Conclusions

This work presents a detailed analysis of fractional vortex dynamics in two-band superconductors under the influence of linear normal barriers with different orientations. By systematically examining the behavior of vortex configurations in the absence of pinning, as well as in the presence of normal strips placed perpendicular and parallel to the vortex motion, we have characterized the relationship between interband coherence, current-induced dissociation, and spatial constraints introduced by the barriers. In the case without artificial inhomogeneities, our results confirm that composite vortices dominate throughout most of the sample, with dissociated vortices appearing only in small, localized regions. This observation is consistent with theoretical predictions and highlights the stabilizing role of Josephson coupling in maintaining interband coherence under moderate driving currents.

When normal barriers are introduced perpendicular to the vortex motion, they define spatially separated regions with distinct coherence properties. These barriers locally suppress superconductivity, acting as selective filters that prevent the propagation of vortex configurations unable to satisfy the energy balance imposed by the discontinuity. The presence of metastable states and history-dependent responses in these systems reveals the sensitivity of vortex dynamics to spatially structured perturbations. In contrast, barriers aligned parallel to the direction of vortex motion affect the entire system more uniformly. In this configuration, fractional vortices propagate over long distances without recombination, indicating a strong suppression of interband coherence. This behavior demonstrates that extended inhomogeneities along the vortex trajectory are effective tools to stabilize dissociated vortex states across the full extent of the sample.

Overall, our results show that linear normal barriers can be used not only to perturb the superconducting state, but also to actively control the structure and dynamics of vortex matter in multiband systems. This offers a powerful framework for probing the nature of interband interactions and for designing experiments or devices where localized control of coherence and vortex mobility is essential.