Sintering and Electrical Conductivity of Medium- and High-Entropy Calcium-Doped Four B-Site Cation Perovskite Materials
Abstract
1. Introduction
2. Materials and Methods
2.1. Material Synthesis
2.2. Sintering Characterization
2.3. Electrical Conductivity
3. Results
3.1. Configurational Entropy
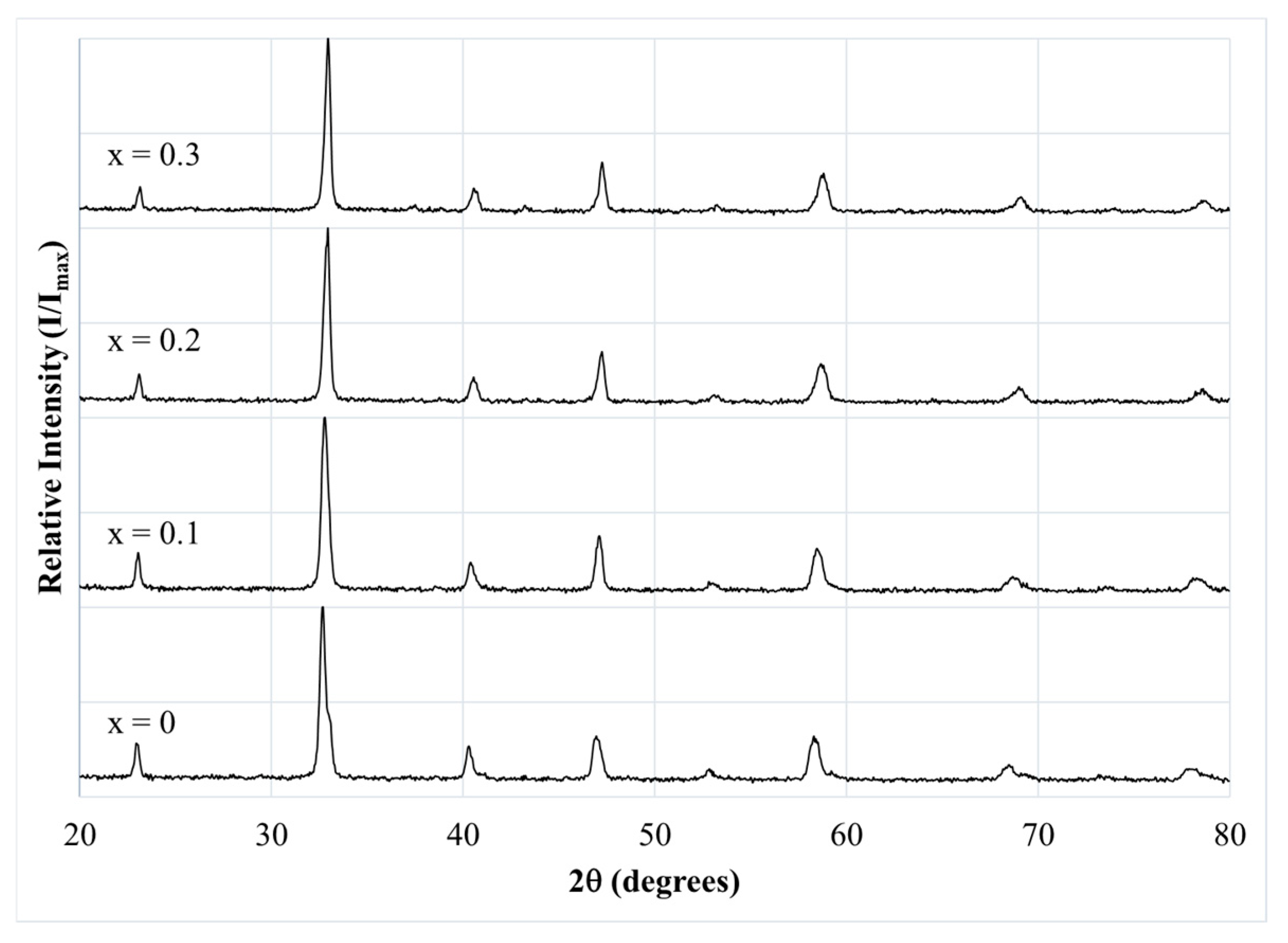
3.2. Structure (X-Ray Diffraction, XRD)
3.3. Sintering Characterization
3.4. Electrical Conductivity
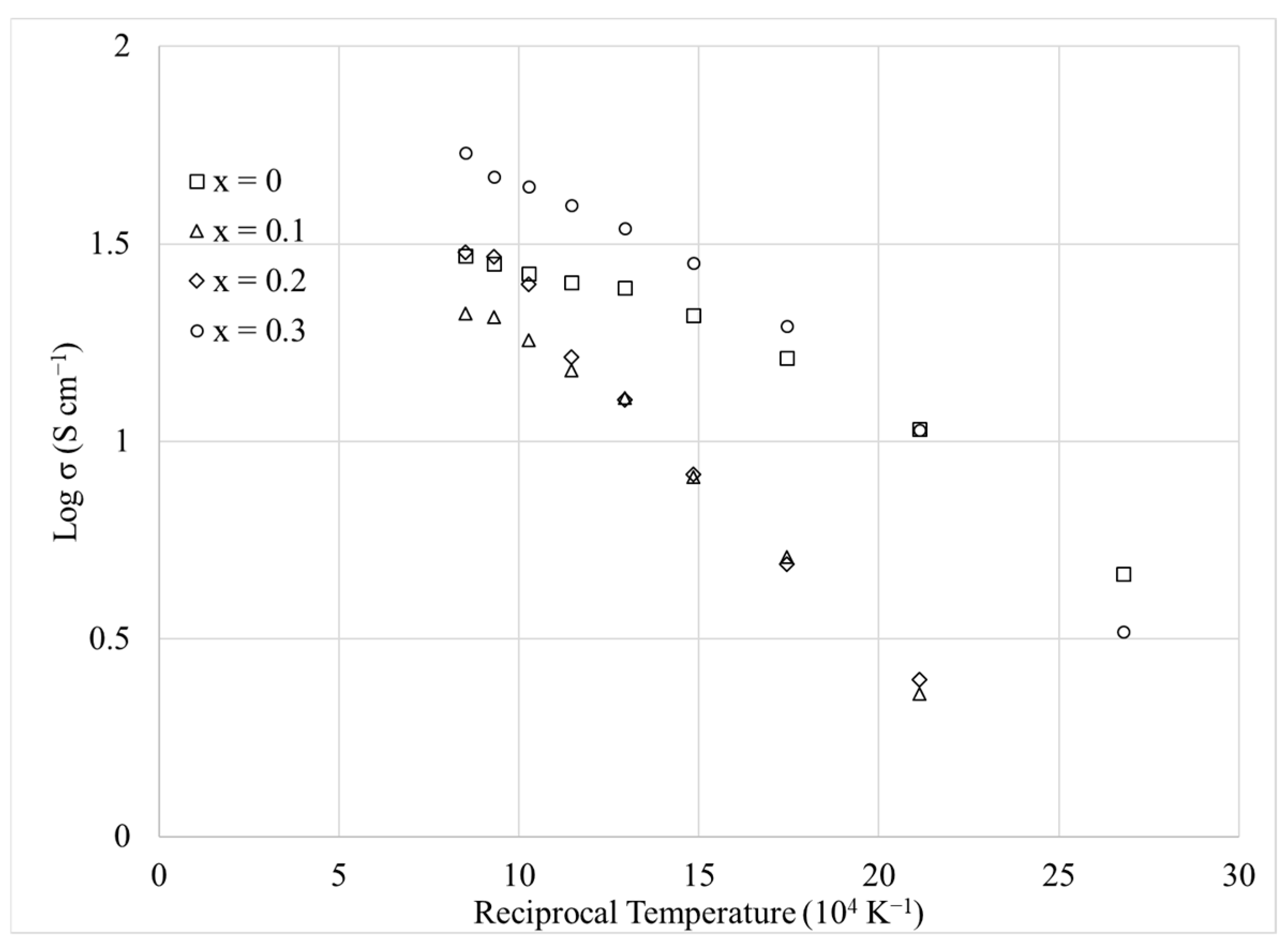
3.5. Activation Energy for Conduction
3.6. Effect of Configurational Entropy
3.7. Discussion of Conduction Mechanism and Practical Implications
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Koc, R.; Anderson, H. Investigation of Strontium-doped La(Cr,Mn)O3 for Solid Oxide Fuel Cells. J. Mater. Sci. 1992, 27, 5837–5843. [Google Scholar] [CrossRef]
- Kolisetty, A.; Fu, Z.; Koc, R. Development of La(CrCoFeNi)O3 System Perovskites as Interconnect and Cathode Materials for Solid Oxide Fuel Cells. Ceram. Intl. 2017, 43, 7647–7652. [Google Scholar] [CrossRef]
- Liu, J.; Deng, C.; Liu, X.; Shao, S.; Zheng, P.; Chen, L.; Wu, P.; Li, H.; Ji, H.; Zhu, W. Single Mo Atoms Stabilized on High-Entropy Perovskite Oxide: A Frontier for Aerobic Oxidative Desulfurization. Inorg. Chem. 2023, 62, 11044–11055. [Google Scholar] [CrossRef]
- Sparlin, D.; Raffaelle, R. Theoretical and Experimental Implications of Self Compensation in the RMO3 Perovskite Structure. Ceram. Trans. 1991, 24, 221–227. [Google Scholar]
- Sehlin, S.; Anderson, H.; Koc, R.; Sparlin, D. Evidence for 2+-4+ Pairing in the (La,Ca)(Cr,Co)O3 Series. Ceram. Trans. 1991, 24, 249–256. [Google Scholar]
- Gajjala, S.R.; Swift, G.; Koc, R. Sintering and Electrical Conductivity of Calcium-Doped Three-Cation Perovskite Materials. J. Mater. Sci. Mater. Eng. 2024, 19, 3. [Google Scholar] [CrossRef]
- Sfirloaga, P.; Poienar, M.; Malaescu, I.; Lungu, A.; Mihali, C.V.; Vlazan, P. Electrical Conductivity of Ca-Substituted Lanthanum Manganites. Ceram. Int. 2018, 44, 5823–5828. [Google Scholar] [CrossRef]
- Sehlin, S.; Anderson, H.; Sparlin, D. Electrical Characterization of the (La, Ca)(Cr, Co)O3 System. Solid State Ion. 1995, 78, 235–243. [Google Scholar] [CrossRef]
- Rost, C.; Sachet, E.; Borman, T.; Moballegh, A.; Dickey, E.; Hou, D.; Jones, J.; Curtarolo, S.; Maria, J. Entropy-Stabilized Oxides. Nat. Commun. 2015, 6, 8485. [Google Scholar] [CrossRef]
- Bérardan, D.; Franger, S.; Dragoe, D.; Meena, A.; Dragoe, N. Colossal Dielectric Constant in High Entropy Oxides. Phys. Status Solidi—Rapid Res. Lett. 2016, 10, 328–333. [Google Scholar] [CrossRef]
- Bérardan, D.; Franger, S.; Meena, A.; Dragoe, N. Room Temperature Lithium Superionic Conductivity in High Entropy Oxides. J. Mater. Chem. A 2016, 4, 9536–9541. [Google Scholar] [CrossRef]
- Zhao, Z.; Xiang, H.; Dai, F.; Peng, Z.; Zhou, Y. (La0.2Ce0.2Nd0.2Sm0.2Eu0.2)2Zr2O7: A Novel High-Entropy Ceramic with Low Thermal Conductivity and Sluggish Grain Growth Rate. J. Mater. Sci. Technol. 2019, 35, 2647–2651. [Google Scholar] [CrossRef]
- Yeh, J.; Chen, S.; Lin, S.; Gan, J.; Chin, T.; Shun, T.; Tsau, C.; Chang, S. Nanostructured High-Entropy Alloys with Multiple Principal Elements: Novel Alloy Design Concepts and Outcomes. Adv. Eng. Mater. 2004, 6, 299–303. [Google Scholar] [CrossRef]
- Miracle, D.; Senkov, O. A Critical Review of High Entropy Alloys and Related Concepts. Acta Mater. 2017, 122, 448–511. [Google Scholar] [CrossRef]
- Murty, B.S.; Yeh, J.W.; Ranganathan, S. High-Entropy Alloys, 1st ed.; Butterworth-Heinemann: London, UK, 2014; pp. 13–25. [Google Scholar]
- Witte, R.; Sarkar, A.; Kruk, R.; Eggert, B.; Brand, R.; Wende, H.; Hahn, H. High-Entropy Oxides: An Emerging Prospect for Magnetic Rare-Earth Transition Metal Perovskites. Phys. Rev. Mater. 2019, 3, 034406. [Google Scholar] [CrossRef]
- Takaba, H.; Kimura, S.; Alam, M. Crystal and Electronic Structures of Substituted Halide Perovskites Based on Density Functional Calculation and Molecular Dynamics. Chem. Phys. 2017, 485–486, 22–28. [Google Scholar] [CrossRef] [PubMed]
- Lufaso, M.; Woodward, P. Prediction of the Crystal Structures of Perovskites Using the Software Program SPuDS. Acta Cryst. B 2001, 57, 725–738. [Google Scholar] [CrossRef]
- Jarin, S.; Yuan, Y.; Zhang, M.; Hu, M.; Rana, M.; Wang, S.; Knibbe, R. Predicting the Crystal Structure and Lattice Parameters of the Perovskite Materials via Different Machine Learning Models Based on Basic Atom Properties. Crystals 2022, 12, 1570. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiaojie, X. Modeling of Lattice Parameters of Cubic Perovskite Oxides and Halides. Heliyon 2021, 7, e07601. [Google Scholar] [CrossRef]
- Shannon, R.D. Revised Effective Ionic Radii and Systematic Studies of Interatomic Distances in Halides and Chalcogenides. Acta Cryst. 1976, A32, 751–767. [Google Scholar] [CrossRef]
- Kim, C.; Rim, Y.; Kim, D.; Kim, H. Combined Effect of the Large Ionic Radius and Low Electronegativity of Lanthanum Additive on Solution-Processed Zinc–Tin–Oxide Thin-Film Transistors. Thin Solid Film. 2013, 56, 291–294. [Google Scholar] [CrossRef]
- Sugiura, Y.; Saito, Y.; Endo, T.; Makita, Y. Effect of the Ionic Radius of Alkali Metal Ions on Octacalcium Phosphate Formation Via Different Substitution Modes. Cryst. Growth Des. 2019, 19, 4162–4171. [Google Scholar] [CrossRef]
- Krok-Kowalski, J.; Rej, H.; Groń, T.; Warczewski, J.; Mydlarz, T.; Okońska-Kozłowska, I. Influence of the Substitution of Cu Ions for Cd Ions on the Crystallographic and Magnetic Properties of Cd1−xCuxCr2Se4 Spinels. J. Magn. Magn. Mater. 1994, 137, 329–338. [Google Scholar] [CrossRef]
- Tiwari, S.; Mishra, A. Effect of Ionic Radii Variation on the Structural, Electrical, Dielectric, and Magnetic Characteristics of Orthochromite RCrO3 (R = La, Y, Gd). J. Supercond. Nov. Magn. 2024, 37, 623–637. [Google Scholar] [CrossRef]
- Heyns, A.; Harden, P. Evidence for the Existence of Cr(IV) in Chromium-Doped Malayaite Cr4+:CaSnOSiO4: A Resonance Raman Study. J. Phys. Chem. Solids 1999, 60, 277–284. [Google Scholar] [CrossRef]
- Pourret, O.; Faucon, M.-P. Cobalt. In Encyclopedia of Geochemistry; Encyclopedia of Earth Sciences Series; White, W.M., Ed.; Springer: Cham, Switzerland, 2018; pp. 1–4. [Google Scholar]
- Huang, Y.; Zhao, B.; Ang, R. Enhanced Thermoelectric Performance and Room-Temperature Spin-State Transition of Co4+ Ions in the Ca3Co4–xRhxO9 System. J. Phys. Chem. C. 2013, 117, 11459–11470. [Google Scholar] [CrossRef]
- Breviglieri, S.; Cavalheiro, É.; Chierice, G. Correlation between Ionic Radius and Thermal Decomposition of Fe (II), Co (II), Ni (II), Cu (II) and Zn (II) Diethanoldithiocarbamates. Thermochim. Acta. 2000, 356, 79–84. [Google Scholar] [CrossRef]
- Štepánková, H.; Kohout, J.; Novak, P.; Lütgemeier, H. Dependence of 57Fe Hyperfine Field in Yttrium Iron Garnet on Ionic Radius of Diamagnetic Defects: NMR Study. Aust. J. Phys. 1998, 51, 437–452. [Google Scholar] [CrossRef]
- Porta, P.; Anichini, A.; Bucciarelli, U. Distribution of Nickel Ions among Octahedral and Tetrahedral Sites in NixZn1–xAl2O4 Spinel Solid Solutions. J. Chem. Soc. Faraday Trans. 1 Phys. Chem. Condens. Phases 1979, 75, 1876–1887. [Google Scholar] [CrossRef]
- Xu, X.; Li, L.; Huang, J.; Fang, X.; Liu, W.; Zhang, N.; Wang, H.; Wang, X. Engineering Ni3+ Cations in NiO Lattice at the Atomic Level by Li+ Doping: The Roles of Ni3+ and Oxygen Species for CO Oxidation. ACS Catal. 2018, 8, 8033–8045. [Google Scholar] [CrossRef]
- Li, H.; Zhou, Y.; Liang, Z.; Ning, H.; Fu, X.; Xu, Z.; Qiu, T.; Xu, W.; Yao, R.; Peng, J. High-Entropy Oxides: Advanced Research on Electrical Properties. Coatings 2021, 11, 628. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, Y.; Xu, Y.; Zhang, H.; Shao, Z.; Wang, Z.; Chen, H. Novel High-Entropy Oxides for Energy Storage and Conversion: From Fundamentals to Practical Applications. Green Energy Environ. 2023, 8, 1341–1357. [Google Scholar] [CrossRef]
- Ma, J.; Liu, T.; Ye, W.; He, Q.; Chen, K. High-Entropy Perovskite Oxides for Energy Materials: A Review. J. Energy Storage 2024, 90, 111890–111913. [Google Scholar] [CrossRef]
- Ning, Y.; Pu, Y.; Wu, C.; Chen, Z.; Zhang, X.; Zhang, L.; Wang, B. Design Strategy of High-Entropy Perovskite Energy-Storage Ceramics: A Review. J. Eur. Ceram. Soc. 2024, 44, 4831–4843. [Google Scholar] [CrossRef]
- Ye, S.; Zhu, J.; Zhu, S.; Zhao, Y.; Li, M.; Huang, Z.; Wang, H.; He, J. Design Strategies for Perovskite-Type High-Entropy Oxides with Applications in Optics. ACS Appl. Mater. Interfaces 2023, 15, 47475–47486. [Google Scholar] [CrossRef]
- Zheng, H.; Liu, Y.; Ma, Z.; Debroye, E.; Ye, J.; Zhang, L.; Liu, T. High-Entropy Perovskite Oxides as a Family of Electrocatalysts for Efficient and Selective Nitrogen Oxidation. ACS Nano 2024, 18, 17642–17650. [Google Scholar] [CrossRef]
- Pechini, M.P. Method of Preparing Lead and Alkaline Earth Titanates and Niobates and Coating Method Using the Same to Form a Capacitor. U.S. Patent 3,330,697, 11 July 1967. [Google Scholar]
- Gajjala, S.R.; Fu, Z.; Koc, R. Investigation of (La1-X,CaX)(Ni0.25Fe0.25Cr0.25Co0.25)O3 for Solid Oxide Fuel Cells Cathode Materials. Ceram. Eng. Sci. Proc. 2019, 39, 85–97. [Google Scholar]
- Chick, L.; Liu, J.; Stevenson, J.; Armstrong, T.; McCready, D.; Maupin, G.; Coffey, G.; Coyle, C. Phase Transitions and Transient Liquid-Phase Sintering in Calcium-Substituted Lanthanum Chromite. J. Am. Ceram. Soc. 1997, 80, 2109–2120. [Google Scholar] [CrossRef]
- Kiebach, R.; Pirou, S.; Aguilera, L.M. A Review on Dual-Phase Oxygen Transport membranes: From Fundamentals to Commercial Deployment. J. Mater. Chem. A 2022, 10, 2152–2195. [Google Scholar] [CrossRef]
- Xinju, L.; Shuoqi, H.; Zhenpan, C. Roles of the A-Site Ca Dopant in Modifying Surface Properties of a Co-Based Perovskite Catalyst for Selective Oxidation of Cyclohexane. Ind. Eng. Chem. Res. 2024, 63, 6087–6099. [Google Scholar]
- Ulyanova, A.V.; Senina, M.O.; Lemeshev, D.O. Dense ceramics based on solid solutions. J. Physics. Conf. Ser. 2021, 1942, 012049. [Google Scholar] [CrossRef]
- Halabi, R.; Simotko, S.; Tsur, Y. The influence of point defects on the sintering of magnesium oxide. J. Am. Ceram. Soc. 2024, 107, 8023–8035. [Google Scholar] [CrossRef]
- Koc, R.; Anderson, H.U. Liquid Phase Sintering of LaCrO3. J. Eur. Ceram. Soc. 1992, 9, 285–292. [Google Scholar] [CrossRef]
- Yokokawa, H.; Sakai, N.; Kawada, T.; Dokiya, M. Thermodynamic Stabilities of Perovskite Oxides for Electrodes and Other Electrochemical Materials. Solid State Ion. 1992, 52, 43–56. [Google Scholar] [CrossRef]
- Mori, M.; Hiei, Y.; Sammes, N.M. Sintering Behavior of Ca- or Sr-Doped LaCrO3 Perovskites Including Second Phase of AECrO4 (AE = Sr, Ca) in Air. Solid State Ion. 2000, 135, 743–748. [Google Scholar] [CrossRef]
- German, R.M.; Suri, P.; Park, S.J. Review: Liquid Phase Sintering. J. Mater. Sci. 2009, 44, 1–39. [Google Scholar] [CrossRef]
- Misusaki, J.; Yoshiro, M.; Yamauchi, S.; Fueki, K. Electrical Conductivity and Seebeck Coefficient of Nonstoichiometric La1-xSrxCoO3-δ. J. Electrochem. Soc. 1989, 136, 2082–2088. [Google Scholar] [CrossRef]
- Kharton, V.; Yaremchenko, A.; Naumovich, E. Research on the Electrochemistry of Oxygen Ion Conductors in the Former Soviet Union. II. Perovskite-Related Oxides. J. Solid State Electrochem. 1999, 3, 303–326. [Google Scholar] [CrossRef]
- Chiba, R.; Yoshimura, F.; Sakurai, Y. An Investigation of LaNi1−xFexO3 as a Cathode Material for Solid Oxide Fuel Cells. Solid State Ion. 1999, 124, 281–288. [Google Scholar] [CrossRef]
- Weber, A.; Ivers-Tiffée, E. Materials and Concepts for Solid Oxide Fuel Cells (SOFCs) in Stationary and Mobile Applications. J. Power Sources 2004, 127, 273–283. [Google Scholar] [CrossRef]
- Dusastre, V.; Kilner, J.A. Optimisation of Composite Cathodes for Intermediate Temperature SOFC Applications. Solid State Ion. 1999, 126, 163–174. [Google Scholar] [CrossRef]
- Waller, D.; Lane, J.A.; Kilner, J.A.; Steele, B.C.H. The Effect of Thermal Treatment on the Resistance of LSCF Electrodes on Gadolinia Doped Ceria Electrolytes. Solid State Ion. 1996, 86, 767–772. [Google Scholar] [CrossRef]






| Cation | Ionic Radius (Oxidation State), nm |
|---|---|
| Lanthanum | 0.117 (+3) [22] |
| Calcium | 0.100 (+2) [23] |
| Chromium | 0.073 (+2) [24], 0.0615 (+3) [25], 0.041 (+4) [26] |
| Cobalt | 0.065 (+2) [27], 0.0545 (+3) [28], 0.053 (+4) [28] |
| Iron | 0.077 (+2) [29], 0.0645 (+3) [30] |
| Nickel | 0.78 (+2) [31], 0.56 (+3) [32] |
| Ca Doping Fraction, x | Relative Density (%) |
|---|---|
| 0 | 90 |
| 0.1 | ~100 |
| 0.2 | ~100 |
| 0.3 | ~100 |
| Material | x = 0 | x = 0.1 | x = 0.2 | x = 0.3 |
|---|---|---|---|---|
| La1−xCax(Co0.25Cr0.25Fe0.25Ni0.25)O3−δ | 28.2 | 20.6 | 29.3 | 46.9 |
| LaCoO3 [50] | 1000 | |||
| LaCrO3 (700 °C) [51] | 0.34 | |||
| LaFeO3 [52] | 0.1 | |||
| LaNiO3 [52] | 40 |
| Ca Doping Fraction, x | Activation Energy, Adiabatic (Figure 7) | Activation Energy, Non-Adiabatic (Figure 8) |
|---|---|---|
| x = 0 | 0.059974 | 0.071685 |
| x = 0.1 | 0.094356 | 0.106063 |
| x = 0.2 | 0.099182 | 0.110888 |
| x = 0.3 | 0.078242 | 0.090037 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Swift, G.; Gajjala, S.R.; Koc, R. Sintering and Electrical Conductivity of Medium- and High-Entropy Calcium-Doped Four B-Site Cation Perovskite Materials. Crystals 2025, 15, 524. https://doi.org/10.3390/cryst15060524
Swift G, Gajjala SR, Koc R. Sintering and Electrical Conductivity of Medium- and High-Entropy Calcium-Doped Four B-Site Cation Perovskite Materials. Crystals. 2025; 15(6):524. https://doi.org/10.3390/cryst15060524
Chicago/Turabian StyleSwift, Geoffrey, Sai Ram Gajjala, and Rasit Koc. 2025. "Sintering and Electrical Conductivity of Medium- and High-Entropy Calcium-Doped Four B-Site Cation Perovskite Materials" Crystals 15, no. 6: 524. https://doi.org/10.3390/cryst15060524
APA StyleSwift, G., Gajjala, S. R., & Koc, R. (2025). Sintering and Electrical Conductivity of Medium- and High-Entropy Calcium-Doped Four B-Site Cation Perovskite Materials. Crystals, 15(6), 524. https://doi.org/10.3390/cryst15060524





