Abstract
Tungsten Inert Gas (TIG) welding is a widespread welding process used in the industry for high-quality joints. However, this welding process suffers from lower productivity. Activated Tungsten Inert Gas (ATIG) is a variant of the TIG that aims to increase the depth penetration capability of conventional TIG welding. This is achieved by applying a thin coating of activating flux material onto the workpiece surface before welding. This work investigates the effect of the thermophysical properties of individual metallic oxide fluxes on 316L stainless steel weld morphology. Four levels of current intensity (120, 150, 180, 200 A) are considered. The weld speed up to 15 cm/min and arc length of 2 mm are maintained constant. Thirteen oxides were tested under various levels of current intensity in addition to multiple thermophysical properties combinations, and the depth penetration (D) and the aspect ratio (R) were recorded. This process has provided 52 combinations (13 oxides * 4 currents). Based on the numerical observations, linear and nonlinear models for describing the effect of the thermophysical parameters on the weld characteristics were tuned using a particle swarm optimization algorithm. While the linear model provided good prediction accuracy, the nonlinear exponential model outperformed the linear one for the depth yielding a mean absolute percentage error of 17%, a coefficient of determination of 0.8266, and a root mean square error of 0.9665 mm. The inverse optimization process, where the depth penetration ranged from 1.5 mm to 12 mm, thus covering a large spectrum of industries, the automotive, power plants, and construction industries, was solved to determine the envelopes’ lower and upper limits of optimal oxide thermophysical properties. The results that allowed the design of the fluxes to be used in advance were promising since they provided the oxide designer with the numerical ranges of the oxide components to achieve the targeted depths. Future directions of this work can be built around investigating additional nonlinear models, including saturation and dead-zone, to efficiently estimate the effect of the thermophysical properties on the welding process of other materials.
1. Introduction
Austenitic stainless steels, known as 300 series, contain mostly 18% chromium and 8% nickel. The austenitic or austenite phase is a solid solution of carbon and iron. Austenitic stainless steels are the most diversified and widespread family [1] owing to their excellent corrosion resistance and mechanical properties. This type of steel is widely used in industries such as construction, automotive, and food processing [2]. The microstructure is a stable austenite phase, with a face-centered cubic (FCC) crystal structure. Austenitic stainless steels are widely used in various industries, including conventional and nuclear power plants, due to their excellent corrosion resistance and mechanical properties at elevated temperatures [3,4]. Welding is the most common fabrication method for assembling parts. Among several fusion welding processes, TIG is a commonly used technique in various industries, including chemical and petrochemical, aerospace, and marine. TIG joins similar or dissimilar materials. A TIG weld joint is considered a high-quality joint. However, its main disadvantage is the limitation related to the thickness of up to 3 mm welded in one single pass. ATIG is a promising alternative technique. The ATIG process uses the same equipment as the TIG process, except that a thin paste layer is deposited before welding. Two main mechanisms were proposed to explain the higher weld penetration achieved with the ATIG technique in a single pass.
- -
- Inverse Marangoni convection [5] occurs when a surfactant element in a weld pool favors the molten metal movement from the weld edges to the center of the weld pool, leading to a penetrated weld and narrower weld bead, as shown in Figure 1.
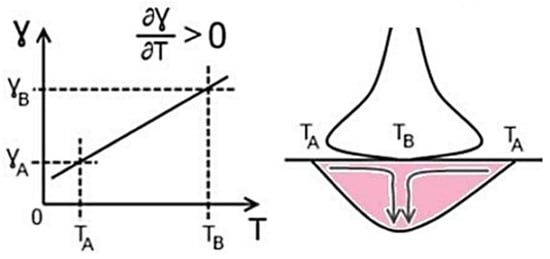 Figure 1. Inverse Marangoni convection mechanism.
Figure 1. Inverse Marangoni convection mechanism. - -
- The second mechanism is related to the migration of elements from the weld pool to the arc welding (see Figure 2). These elements react with the outer arc electrons and contribute to retracting the arc welding, enhancing the current density provided to the weld bead [6].
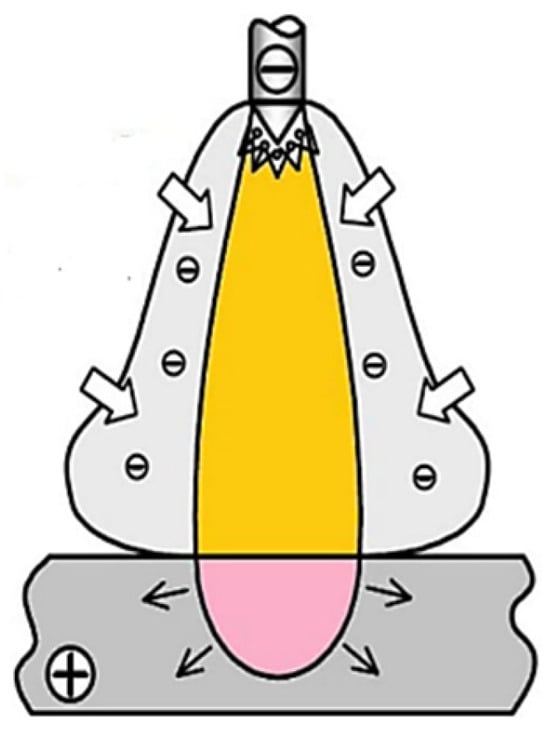 Figure 2. Arc constriction mechanism.
Figure 2. Arc constriction mechanism.
Many studies have been conducted to optimize the welding parameters and maximize depth penetration. Others focus on optimizing the welding parameters to ensure good mechanical properties. Aljufri et al. [7] investigated the impact of shielding gas flow on TIG welding of 304 stainless steel. Increasing the gas flow rate to 13 L/min resulted in an average tensile stress of 47.50 MPa, strain of 0.189, elastic modulus of 2525 MPa, and hardness of 105.52 HBW. Further increasing the gas flow rate to 18 L/min led to an average tensile stress of 49.69 MPa, strain of 0.192, modulus of elasticity of 2597 MPa, and hardness of 106.704 HBW. Based on the research findings, it was observed that the weld area exhibited an increase in hardness values due to the heat generated during the welding process. Research using artificial intelligence technology is being actively conducted in the manufacturing field. In welding, work on fusion welding quality prediction using robust optimization tools has been led since the early decades. Artificial neural network algorithms have been increasingly used to predict welding morphology and mechanical properties [8]. Based on measurement and estimation of the weld bead geometry in arc welding processes, machine learning and deep learning are used for predictive quality of welds. The intelligent design of robotic welding process parameters using learning-based methods has been used to ensure the sustainability and reliability of welded structures. The welding processes’ efficiency and accuracy have been proven to increase significantly by using machine learning algorithms. Artificial intelligence can find solutions to the adaptability and repeatability of welds [9]. In solid state welding, Srinivasan et al. [10] investigate the impact of the tool’s shoulder diameter, pin profile, and rotational and traverse speeds on the mechanical properties of the friction stir welded namely Ti–6Al–4 V alloy joints. The central composite design (CCD) concept of response surface methodology (RSM) has been applied. They claim that the optimized values of 25 mm shoulder diameter, having a taper cylindrical pin geometry employed at a tool traverse speed of 40 mm min−1 and a rotational speed of 1400 rpm, give rise to a largest tensile strength of 809.8 MPa and yield a strength of 778.7 MPa and percentage of elongation of 6.9%. John Solomon et al. [11] studied the effect of friction stir welding (FSW) parameters such as tool rotation speed, traverse speed, tilt angle, and the employed tool to optimize tensile strength and elongation percentage of the AZ80 AMg alloy joints. Response surface methodology was used. The cylindrical geometry at a tilt angle of 0.630, rotational speed of 962.077 rpm, and tool traverse speed of 2.105 mm s−1 achieved the highest tensile strength of 195.299 MPa.
Fasil et al. [12] investigated the Tungsten Inert Gas-Metal Inert Gas (TIG-MIG) hybrid welding parameters on EN24 mild steel to ensure a sound weld by understanding the relationships between the material properties and the welding conditions. The appropriate welding parameters were a MIG welding current of 200 A, MIG welding voltage of 15 V, TIG welding current of 200 A, TIG welding voltage of 18 V, and welding travel speed of 5 mm/s. The significant process parameters were investigated using ANOVA. MIG welding current and MIG welding voltage were important factors, with percentage contributions of 44.19% and 49.20%, respectively. Cynthia et al. [13] worked on TIG-MIG hybrid welding of AISI 1008 mild steel joints. A combined gray relational system theory and the Taguchi method were used for process optimization to obtain a set of process parameters that maximizes both ultimate tensile strength and 0.2% yield strength for structural applications. From the results, the gas flow rate had the most significant influence on the responses, with a percentage contribution of 39.77%. Bishub et al. [14] focused on single-pass welding of Inconel 825 strips employing TIG welding. They used Box–Behnken design to investigate the ultimate tensile strength of weld through 27 experiments. The welding current is the most contributing input parameter, followed by welding speed. Higher heat input with low welding speed increases the deposition rate and ensures more strength in the weldment. The maximum UTS achieved is 701.73 MPa at an optimal welding current up to 120 A, a welding speed of 180 mm/min, shield gas up to 12 L/min, and an arc length of 2.24 mm. Nabendu [15] applied the gray–Taguchi method for process optimization. This technique allows for multi-objective optimization, which is beneficial in evaluating weld quality through mechanical characteristics such as ultimate tensile strength, yield strength, and percentage elongation. Adirek et al. [16] implemented a fractional factorial experimental design followed by a central composite design to optimize the TIG welding parameters on AISI 304 stainless steel. The optimal welding current was up to 136 A, with a welding speed equal to 13 cm/min, a wire feed rate of 93 cm/min, and a length of arc of 2.5 mm. They claim that fractional factorial experimental design followed by a central composite design approach enhances the reliability of the results and provides a robust framework for future research in welding optimization. Pratheesh et al. [17] optimized pulsed-TIG welding parameters using the Taguchi method to improve the weld tensile strength of aluminum alloy 6013. The pulsed-TIG welding procedure is used on the welding surface to lower the heat-affected zone and hence the strength of the weld. Welding current and gas flow rate have been discovered to affect response output measures such as weld tensile strength.
Ghumman et al. [18] investigated the surface roughness, hardness, and tensile strength of welds produced by a single-pass TIG welding process in austenitic stainless-steel 3 mm plates (AISI 316L). The experiments were conducted using a Taguchi L9 orthogonal array. The results indicated an optimum tensile strength of 624.92 MPa, achieved at the parametric combination of 100 A current, voltage of 16 V, and gas flow rate of 6 L/min. The microhardness results indicated an optimum value of 319.2 HV, achieved at the parametric combination of a current of 125 A, 16 V of voltage, and a gas flow rate of 9 L/min. A minimum surface roughness of 7.33 µm was attained at 125 A intensity current, a voltage of 16 V, and a gas flow rate of 9 L/min. Hedhibi et al. [19] used the particle swarm optimization (PSO) method to investigate thirteen metallic oxides to find the optimum oxide combination to enhance ATIG welding morphology for mild steel to 316L stainless steel joints. This increased penetration depth by 1.84 times, maintained mechanical properties, and improved energy absorption and hardness. Jay et al. [20] used multi-response optimization route by integrating response surface methodology with the JAYA optimization algorithm to optimize the ATIG welding process parameters for carbon steels.
Sivakumar et al. [21] used the gray relational analysis (GRA) to optimize welding process parameters for ATIG welding of a 6.5 mm thick Inconel 625 plate. The effect of welding current, torch travel speed, and arc gap on weld penetration depth, weld cross-sectional area, weld bead width, and microhardness. The following recommended settings, such as 300 A welding current, 90 mm/min torch travel speed, and 5 mm arc gap, as the best-optimized parameters.
Kumaar et al. [22] conducted the optimization of process parameters for ATIG welding of 10 mm thick Inconel 617 material. Process parameters considered in this study include weld current, weld torch travel speed (mm/min), arc gap (mm), and a flux powder silicon dioxide (SiO2)% and titanium dioxide (TiO2)% combination. They concluded that weld current of 290 A, weld torch travel speed of 50 mm/min with an arc gap of 1 mm, and 100% TiO2 as flux allows for obtaining the maximum depth penetration up to 7.04 mm and the aspect ratio of 0.437. They highlighted that weld current is the most significant factor affecting the weld depth penetration, depth-to-width ratio, and weld cross-sectional area. This study used PSO and the Genetic Algorithm (GA) to enhance the welding process. Sivakumar et al. [23] conducted experiments on Inconel 625 by ATIG welding. They concluded that the optimum input parameters, such as welding current (300 A), torch travel speed (75 mm/min), and arc gap (1 mm), lead to an optimum output of hardness of 262 HB and an aspect ratio of 0.421. Sekar et al. [24] employed Taguchi-based gray relational analysis to optimize multiple welding parameters, including welding current, welding speed, arc gap, and gas flow rate. They concluded that welding speed plays a major role in affecting penetration depth and aspect ratio in multi-objective optimization for super duplex stainless steel (SAF2507). Tomaž et al. [25] present the results of research into the application of activating fluxes in ATIG welding austenitic stainless steel 316L with a thickness of 6 mm. The findings indicate that the ATIG process, particularly with a mixture of BC-31 and Quick TIG fluxes, yields superior mechanical properties. Many articles have already been published that focus on ATIG and AMIG welding of stainless steel, but none make the connection between the thermophysical properties of metal oxides and ATIG weld morphology. Since the problem of modeling the relationship between the thermal properties of various oxides and, respectively, weld depth penetration and weld depth aspect ratio is known to be complex, irregular, and multidimensional (with many factors influencing many outputs), quantifying this relationship is a computationally hard optimization problem, usually difficult to solve using classical optimization tools. By utilizing this algorithm, the model can accurately adjust parameters to closely match the physical phenomena of welding processes influenced by the thermophysical properties of oxides. The present work is dedicated to studying the effects of the thermophysical properties on the ATIG weld bead morphology of 6 mm thick 316 L stainless steel. Weld morphology prediction using the optimization method was conducted. PSO is an efficient optimization algorithm that excels at finding global optima (against local optima solutions) in complex, multidimensional spaces. PSO is well suited to this problem. The PSO algorithm refines the model’s parameters to better reflect the actual welding outcomes as influenced by the oxides’ thermophysical properties. Consequently, the novelty of this work is to capture the influence of various oxides’ thermal properties on weld characteristics. This approach helps in identifying the most critical factors and ensuring that the model’s focus is on accurately capturing these key influences, leading to more accurate quantification of weld depth penetration and aspect ratio. This work contains a large database that can be used by researchers and industries to develop flux for other materials. This work can serve as a new research approach in the development of materials science. This work contributes to enhancing the knowledge of ATIG welding processes and provides a solid foundation for further research and practical applications in the welding sector.
2. Materials and Methods
2.1. Materials
Table 1 depicts the chemical composition and the melting point of stainless steel 316L.

Table 1.
Chemical composition (weight %) and melting point (°C) of 316L stainless steel.
We notice that the spherical powders with an average size in the range of 325 mesh, with a purity of 99%, were used. The oxides selected for the current study belong to three categories: acidic, basic, and amphoteric oxides. The main selection criteria were their thermal properties, such as melting temperature, boiling point, and enthalpy of formation. For instance, from the point of view of melting point, some oxides are close to the 316L stainless steel melting point, others have very low melting temperatures, and others have high melting temperatures to establish a relation between the depth welds and the aspect ratio and the oxides’ thermal properties. The second interesting oxide property to study is surface tension, as shown in Table 2. The oxide’s surface tension varies between 80 and 800 mN/m. Finally, the oxides’ first ionization energy ranges between 9.43 and 12.10 eV. We note that the first ionization energy affects arc welding by increasing the arc temperature and enhancing the heat provided to the weld pool. The selected thermophysical properties of the deposited powders are listed in Table 2.

Table 2.
Metallic oxides thermophysical properties [26].
2.2. Welding Procedure
The welding machine used is the TIG from ESAB manufacturer with a motorized carriage that allows us to approach the automatic welding to make sure that the weld is performed at a constant speed and the constant length of arc welding, as shown in Figure 3. The shielding gas used is Argon.

Figure 3.
TIG welding machine with a motorized carriage.
Experiments consist of welding a 20 cm line on a rectangular plate of 6 mm thickness. Before welding, the 100 mm × 200 mm × 6 mm plates were cleaned with acetone. The powders have been heated separately in a furnace at 100 °C for 1 h to eliminate humidity. Acetone (or methanol), a volatile product, is poured onto the oxide in a 1:1 ratio and gently mixed until it has a paint-like consistency, easy to spread on the edges of the plates to be welded. The thickness of the flux layer is measured using the micrometric method. This method allows for the flux layer thickness measurement with an error limit of 5 microns. In this method, the thickness of the flux layer is determined by taking at least three measurements. The supposed thickness of the paste layer was estimated to be 0.4 mm, as shown in Figure 4. The mean coating density of flux was about 4–5 mg/cm2.
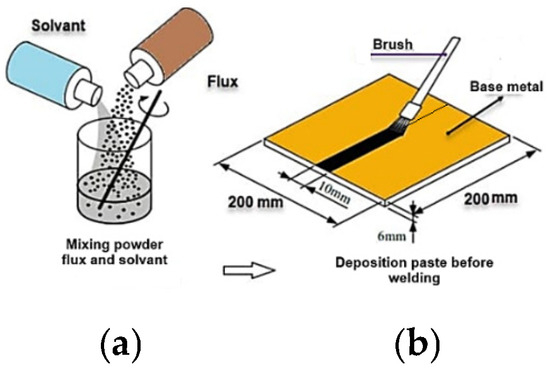
Figure 4.
Flux preparation (a) and paste deposition before welding (b).
The joints were executed with a square butt weld design without edge preparation. Both plates were clamped with a zero gap distance. The welding parameters are listed in Table 3.

Table 3.
Welding conditions.
We note that the intensity current levels (120, 150, 180, 200 A) cover various levels of electric current used in workshops and industries. Maintaining all other welding parameters constant, each current level provides the workpiece with the heat necessary to conduct the welding operation. The heat provided activates the oxygen available in the oxides by releasing oxygen to play its role as the surfactant element in the weld pool. So, the oxygen can be liberated or not, depending on the energy conveyed to the weld pool.
After welding, the samples were cut far from the welding starting point to be sure that the arc welding was stabilized. Three coupons were taken from each weld line as shown in Figure 5. Each run is conducted twice, and the reported results are an average of 6 measurements. The weld morphology of both TIG and ATIG welding has been analyzed. The selected coupons were etched using Glyceregia solution (15 cc HCl + 5 cc HNO3 + 10 cc glycerol). The weld aspect was checked using Motic Images Plus version 2.0 software integrated with an optical microscope.
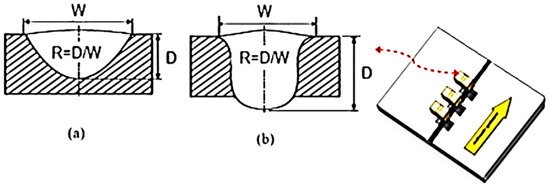
Figure 5.
Morphology parameters of partially penetrated weld bead (a) and fully penetrated weld bead (b).
2.3. Methodology
In welding processes, obtaining a weld joint of required properties is a critical issue in various domains, including the automotive industry, aerospace, construction, and manufacturing. In fact, for these domains, the weld bead geometry, mechanical properties, and distortion features should be in certain acceptable ranges to prevent any possible deterioration during the welded systems’ use. However, determining the optimal parameters for the welding process remains a significant challenge because of the complex relationships between various factors, including the thermophysical properties of the fluxes, which help in the welding process. Variables such as enthalpy of formation, melting point flux, flux surface tension, and welding current must be carefully selected to produce weld depth and the weld aspect ratio to achieve a full penetration in a single pass. In addition, the diversity of materials being welded, ranging from traditional steels to advanced alloys, may cause additional complexity as each material has its own thermal and mechanical properties, necessitating carefully calibrated welding conditions specific to each material. In this section, a systematic and comprehensive approach combining experimental analysis, mathematical modeling, computational methods, and advanced optimization techniques for accurately capturing the complex relationships between the welding process inputs and outputs will be detailed. The flowchart of the overall framework is depicted in Figure 6 below.
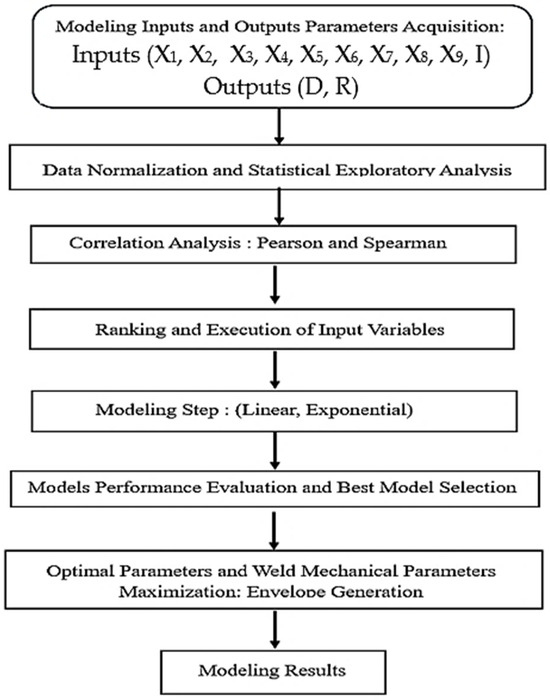
Figure 6.
Welding process optimization: flowchart of the general framework.
Step 1: Data acquisition
Several experiments were conducted to collect data for the welding process modeling and optimization. Although conducting one experiment is time consuming and logistically difficult, the research team has conducted a total of 52 experiments, which has allowed a high level of flexibility during the various models’ implementation. Therefore, multiple combinations of input parameters were generated, namely X1, X2, …, X9, the welding current, I, and two outputs, namely, the weld depth (D) and aspect ratio (R). The thirteen metallic oxides, along with their thermophysical properties in terms of the input variables (the welding current is not included since it is considered as an external parameter to the oxide itself), are depicted in Table 4 below.

Table 4.
Input variables related to metallic oxides.
The names of the variables as well as their meanings are summarized in Table 5.

Table 5.
Inputs and outputs of the AISI 316L stainless steel welding process.
Step 2: Data normalization and exploratory analysis
Data normalization and statistical exploratory analysis play crucial roles in modeling and optimizing a welding process. Usually, data (inputs and outputs) are set at different scales in magnitude and units. Normalization ensures that all inputs and outputs are scaled to a common range, which may eliminate the effects of the differences and may contribute to alleviating the computational burden during the model calibration. This step is particularly important in welding process modeling, where variables such as melting point flux, boiling point flux, welding current, depth, aspect ratio, and material properties may vary widely in scale. Normalized data may improve the performance of the modeling algorithms by eliminating disproportionality that may influence the results. In addition, statistical exploratory analysis complements normalization by providing insights into data patterns, distributions, and visible relationships among variables. Techniques such as descriptive statistics and visualizations may help identify key factors influencing weld quality and potential outliers or inconsistencies in the data. In this study, all data are normalized according to the following equation [27,28]:
XN is the normalized value inside the interval [0, 1], X is the original variable (in its natural scale), Xmin and Xmax are, respectively, the minimum and maximum values of the original variable.
Note that after the modeling and optimization task is performed, a denormalization process will be performed to set up the decision variables (the models’ inputs) to their original scales.
Step 3: Correlation analysis: Pearson vs. Spearman
The Pearson and Spearman correlation study [29] involves the calculation of coefficients that statistically measure and evaluate the strength and direction of relationships between the variables in the welding process. However, before calculating those factors, the causality between two variables should be justified, since a high value of correlation does not mean the existence of this relationship. Pearson and Spearman are known to be two common measures of correlation, although they are substantially different. The Pearson correlation is usually used to measure the linear relationship between two variables under the assumption of normal distribution. In contrast, the Spearman correlation assesses the monotonic relationship (either increase or decrease), which may not be linear (it may be curvilinear), using the principle of data ranking. Through several applications, Spearman was found to be efficient in non-parametric and nonlinear relationships. Spearman correlation has the merit of performing even in the case where the data distributions are skewed. Combining Pearson and Spearman can provide a comprehensive understanding of the relationships in the welding process under investigation in this study, since it involves complex datasets with hidden and complex features.
Step 4: Ranking and exclusion of input variables
In the case of multiple inputs, the selection of the significant input variables is a critical issue since it may impact the complexity of the model. Indeed, considering all variables together may lead to a high computational burden under non-guaranteed accuracy improvement. The best way to prevent this issue is first to rank the inputs in their increasing order of correlation metrics with the considered output. However, the user experience may help here in selecting the best inputs. Additionally, if two inputs are mutually correlated, their respective effects may be redundant. Therefore, one of the two correlated inputs should be excluded to prevent redundancy.
Step 5: Modeling step
The relationships between the oxides’ parameters and the weld depth and aspect ratio are complex, involving linear and nonlinear behaviors. Although we studied other models such as Gaussian, power, and sigmoid, we found that the exponential model was the best in terms of accuracy. Therefore, we adopted the exponential model, and we will conduct an in-depth study of its calibration and performance analysis. The linear regression model is well known to capture linear relationships and may serve as a baseline model (benchmark). Overall, to the best of our knowledge, the nonlinear models cited previously, including the exponential one, were not investigated in the literature, and their adoption through this paper may represent a meaningful contribution in the field of welding modeling and optimization.
In this study, two types of models are considered. Although the regression model was previously considered under specific assumptions, to the best of the authors’ knowledge, nonlinear models such as the exponential model were not considered in the past. Therefore, investigating the exponential relationships between the inputs and the outputs may be considered an innovation in the field of welding processes. Considering the models’ inputs (X1–X9) and the welding current (I) and the model outputs as Y (which may be the welding depth, D, or the aspect ratio, R), and without loss of generality, the investigated models are described as follows [30,31].
To optimally tune the model parameters, a swarm intelligence technique is used. PSO is a nature-inspired metaheuristic optimization technique widely used for solving complex optimization problems, such as the welding process optimization. PSO works under the process of simulating the social behavior of a flock of birds or a school of fish searching for food. In the context of calibrating the coefficients of a welding model that relates a set of inputs to an output, PSO can be employed to minimize an objective function such as the error between predicted and observed outputs while optimizing the coefficients of the model. PSO usually involves 6 steps, namely [32,33]:
- Initialization: A swarm (group) of particles is initialized randomly inside an interval ranging from the lower limit to the upper limit of the coefficient. However, random initialization may be replaced by manual initialization if the user has an idea about the coefficient’s probable value. In PSO, each particle represents a potential solution of the optimization problem coded as the particle position.
- Fitness Evaluation: The fitness of each particle is evaluated based on an objective function, such as the mean squared error (MSE) between the welding process model’s predicted outputs and the actual observed outputs.
- Update Personal Best and Global Best: Each particle keeps records of its personal best position (“P”) and the swarm collectively maintains a global best position (“G”) based on the best fitness values achieved. During the search process, each process tends to imitate the global best particle among the swarm and to track its previous best discoveries if no improved position is found.
- Velocity and Position Update: Each particle updates its velocity and position based on its personal best, the global best, and its current velocity. The particle moves equations involve three components: current velocity, past own visited position, and the position of the global best particle. Based on this combination, each particle illustrates the social behavior and the cognitive behavior.
- Iteration: The optimization process is repeated for a preset number of iterations until a convergence criterion is met, such as when the change in global best fitness value falls below a threshold or if there is no improvement in the discovered solution for a certain number of iterations. Those conditions are usually known as the possible stopping criteria.
- Output: After stopping, the PSO algorithm provides the global best position (position of the global best particle among the swarm), which represents the optimized model coefficients of the welding process.
The PSO operation is illustrated by the following velocity (Equation (4)), position (Equation (5)), and fitness function evaluation (Equation (6)) equations.
where
- is the velocity of particle i at iteration k.
- is the inertia weight for controlling the impact of the previous velocity.
- are the acceleration coefficients for cognitive and social components.
- , are the random numbers uniformly distributed in [0, 1].
- is the best position of particle i.
- is the global best position.
- is the current position of particle i.
- is the observed output for the j-th data point.
- is the model-predicted output for the j-th data point given the coefficients .
- n is the number of data points.
The PSO algorithm was implemented in MATLAB R2020 using the built-in particle swarm function. The key parameters were configured via the optima options function as follows: the swarm size was set to 100 particles, and the maximum number of iterations was set to 200. These settings were chosen based on preliminary tuning to ensure a balance between convergence speed and solution quality. The cognitive and social coefficients, along with inertia weight, were maintained at their MATLAB default values (1.49 and 0.729, respectively), which are consistent with values recommended in the literature for general-purpose optimization. This configuration provided robust convergence for the welding process optimization problem while remaining computationally efficient.
Although the advantages of the PSO algorithm used in this study to tune the models’ parameters, several assumptions were considered, and inherent limitations should be highlighted. It was assumed that the objective function landscape is continuous and sufficiently smooth for the PSO to explore effectively. The PSO parameters—such as swarm size, cognitive and social coefficients, and inertia weight—were selected based on the literature recommendations and preliminary tuning, but no global sensitivity analysis was performed to test their optimality. Additionally, the PSO algorithm was executed under the assumption that the welding process responses (weld depth and aspect ratio) are deterministic and not significantly affected by external noise or process disturbances. Another limitation of the PSO is its sensitivity to the initialization problem and its ability to converge to sub-optimal solutions (mainly in the context of a non-convex search space). These aspects will be addressed in future work to improve the robustness and generalizability of the proposed approach.
3. Results and Discussions
3.1. Weld Morphology
Table 6 depicts the weld morphology for TIG and ATIG welds obtained for intensity currents 120, 150, 180, and 180 A levels. Thirteen oxides were tested and evaluated in terms of depth penetration weld and aspect ratio. We notice that the welds performed by 120 and 150 A lead partial depth penetration. The welds with oxides SrO, ZrO2, MgO, and CaO exhibit a partial depth penetration regardless of the intensity current, even with 180 or 200 A.

Table 6.
Depth weld and aspect ratio for TIG and ATIG welds for four levels of intensity current.
In the case of the 120- or 150-intensity current, the energy provided by the arc welding to the weld pool is not enough to liberate the active element, such as oxygen, and allow it to play its role as a surfactant element; consequently, the depth penetration is partial. However, for the remaining oxides tested, such as SiO2, TiO2, Fe2O3, Cr2O3, ZnO, Mn2O3, V2O5, MoO3, and Co3O4, the weld was fully penetrated with variation and variance in the depth beads. Table 7 depicts the morphology of TIG and ATIG welds performed with 180 A intensity current and 15 cm/min welding speed. The width of the TIG weld bead is greater than that of the ATIG weld, regardless of the type of oxide used. In the case of TIG welding, the molten metal moves outward from the weld pool center to the edges, leading to wide and shallow weld morphology. However, in ATIG welds carried out with SiO2, Ti2O, Fe2O3, Cr2O3, ZnO, Mn2O3, V2O5, MoO3, and Co3O4 oxides, the welds are fully penetrated (see Table 6).

Table 7.
Weld beads using different metallic oxides flux with 180 A, 15 cm/min.
Table 8 shows that the size of the weld is proportional to the current intensity regardless of the oxide type. It seems that under a 200 A intensity current, the oxygen surfactant element is largely liberated. The inverse Marangoni convection is more pronounced.

Table 8.
Weld beads performed at 150–180–200 A current intensity, and welding speed 15 cm/min.
3.2. Statistical Exploratory Analysis and Correlation Study
A statistical exploratory analysis has been conducted to obtain an overall idea about the data distribution by calculating each variable’s mean, median, standard deviation, and range, including the inputs and the outputs. The values of the obtained statistical metrics are provided in Table 9.

Table 9.
Statistical metrics of the data.
As depicted in Table 9, the statistical metrics are on different scales, which may require normalizing the data to prevent any unbalanced contributions in the overall model involving multiple variables. In addition, the histograms (Figure 7) of the two outputs (D and R) may indicate that the experiments were conducted under two different conditions. This is clear in both histograms, which exhibit two normal distributions.
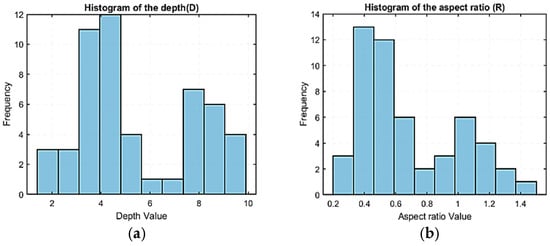
Figure 7.
Histograms of the depth (D) (a) and the aspect ratio (R) data (b).
As the study is about modeling the effect of multiple inputs (X1, X2, X3, X4, X5, X6, X7, X8, X9, and I) on two outputs (D and R) considered separately, it is crucial to select the most significant inputs to prevent unnecessary complexity of the models. For this aim, the most relevant inputs are selected according to three complementary criteria. Namely, the correlation (Pearson and Spearman), the user expertise, and any additional constraints. First, the input variables are selected based on their correlation coefficients with the two outputs. The two correlation matrices were calculated, and they are depicted in Figure 8 below. It can be noticed from the matrices that X2, X3, X4, X7, X9, and I are the most correlated (in absolute value) with the outputs (D and R). Additionally, as per the user’s expertise, the other variables were excluded because they may have the same effect as one of the selected inputs. For example, X1 is highly correlated with X3 (0.85 Spearman correlation), and X5 is well correlated with X2 and X3 (respectively, 0.77 and 0.56 in Spearman). In addition, X8 was excluded because of its high correlation with X2 and X3. The process of exclusion is typically adopted to prevent redundancy and unnecessary model complexity, which may induce additional computational burden. In addition, the three input variables—X5 (surface tension flux), X6 (ionization potential), and X8 (boiling point of flux—Melting point of base metal)—were excluded based on domain expertise. The decision was driven by several considerations. First, X5 (oxide surface tension) is inherently difficult to quantify consistently, as surface tension effects depend on dynamic weld pool conditions that vary during arc operation and may not be accurately captured by a static material property. Similarly, X6 (ionization potential), while relevant in arc physics, tends to have a secondary influence on bead geometry compared to more dominant parameters such as thermal conductivity or oxide layer behavior. Its effect is typically indirect and moderated by the shielding gas and arc current settings, which remained constant in this study. Finally, X8, representing the difference between the boiling point of the flux and the melting point of the base metal, showed limited variation across the tested oxides and was found to contribute minimally to prediction accuracy in preliminary trials. Through this domain expertise approach, a certain level of trade-off between the model accuracy and complexity is ensured. It is worth noting also that the welding current (I) is the most influential input as it has higher correlations with both the depth (D) and the aspect ratio (R). The Pearson correlation (D, I) and (R, I) are, respectively, 0.73 and 0.57, and the Spearman correlation is 0.72 and 0.48. Although the Pearson correlation has exhibited high values for the selected inputs with the outputs, the Spearman correlation has also shown nonlinear relationships, which may stipulate a high competitiveness between linear and nonlinear models. In what follows, we will detail the progressive steps of implementing two different types of models, namely, linear and exponential, as described in Equations (2) and (3).
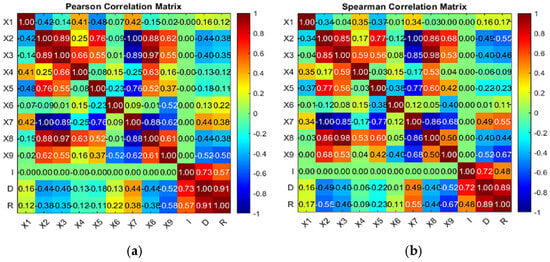
Figure 8.
Pearson (a) and Spearman (b) correlation of the data.
3.3. Models’ Development
The modeling of the relationships between the selected inputs and, separately, the weld depth (D) and the aspect ratio (R), was conducted by implementing four models. The dataset was randomly divided into two subsets: 75% (39 samples) were used for the model training, and the remaining 25% (13 samples) were used for the model’s validation. Note that the 25% data points used in the validation/testing phase were not used in the training phase. Therefore, they are completely new (not previously seen by the model).
To evaluate the quality of the models, three performance metrics were calculated. Those metric equations are provided as follows [34]:
Mean absolute percentage error () indicates the accuracy of the model’s predictions by measuring the average absolute percentage error between the predicted and actual values.
Coefficient of determination (R2) represents the proportion of the variance in the dependent variable (D or R) that can be predicted by independent variables. It indicates how well the model fits the data, with values closer to 1 indicating a better fit.
Root mean square error (RMSE) measures the average magnitude of the error between predicted and actual values, with a lower RMSE indicating better model performance
where and represent, respectively, the predicted and the actual (reported) values.
Note here that the above performance metrics were calculated for the training data (in-sample), the validation data (out-of-sample), and all the data. The results are summarized in Table 10 and Table 11. As shown in Table 10, the nonlinear exponential model is found to outperform the linear model in training data and all data predictions for both the depth and aspect ratio. However, the linear model is found to perform better for the validation data. As the size of the validation data was relatively limited (13 samples), the nonlinear model outperformed with a high number of samples.

Table 10.
Modeling and prediction performance measures for D.

Table 11.
Modeling and prediction performance measures for aspect ratio R.
A detailed analysis of the prediction performance reveals discrepancies between predicted and actual values for both weld depth (D) and aspect ratio (R), highlighting areas for model improvement. While the linear and exponential models showed acceptable performance for weld depth, with R2 values above 0.80 and MAPE around 17% on training data, both models experienced reduced accuracy on validation data, suggesting relatively limited generalization. The exponential model, although slightly better on training data, performed worse on validation (R2 = 0.6136, MAPE = 17.09%), indicating potential overfitting. For aspect ratio, the models performed less robustly overall, with the exponential model achieving good training results (R2 = 0.7428, MAPE = 20.16%) but showing a significant drop on validation (R2 = 0.2518, MAPE = 45.06%). These discrepancies likely stem from nonlinear interactions between process variables, oxide behavior, and inherent experimental variability, such as arc instability, surface preparation inconsistencies, or unmeasured factors like the operator behavior or the instruments/machines’ potential errors. Future work will focus on expanding the dataset, incorporating replicates, and exploring advanced modeling techniques such as ensemble learning or neural networks to enhance predictive reliability and reduce error propagation.
The exponential model coefficients presented in Table 10 and Table 11, while primarily empirical, reflect underlying physical phenomena in welding metallurgy. Each coefficient pair (ai, bi) corresponds to a specific oxide and captures its contribution to the weld bead geometry. For example, oxides with large negative values of ai and positive bi generally indicate materials that enhance arc constriction and increase energy density, thereby promoting deeper penetration. Conversely, oxides with coefficients indicating weaker exponential growth or decay suggest limited influence on arc behavior or less efficient surface activation. The signs and magnitudes of these coefficients align with known behaviors of oxides in the ATIG process—for instance, TiO2 and SiO2 tend to promote penetration by stabilizing the arc and modifying surface tension gradients, which is reflected in their more pronounced coefficient values. While the model is not mechanistic, the trends in the coefficients offer insights into the thermophysical and chemical interactions at the weld pool surface, emphasizing the role of flux composition in modulating heat flow and bead shape.
The phenomenon in ATIG welding is very complex. However, as the manuscript states, the two mechanisms are responsible for increasing depth penetration at the expense of the weld width. Experiments conclude that the depth of penetration is affected by the amount of oxygen content during welding, as it favors the influence of inverse Marangoni convection and the arc constriction. Increasing current intensity increases the heat supplied to the workpiece; it allows the release of oxygen, which will play its role as a surfactant element. The thermal properties, such as the oxide’s enthalpy energy and the oxide’s melting point, are crucial for the amount of oxygen liberated. For instance, the oxides that have a melting temperature close to that of the workpiece to be welded significantly affect the shape and the morphology of the weld bead. Oxides with a surface tension greater than 500 mN/m poorly wet the weld pool metal, which contributes to a decrease in the width of the bead and have insufficient effective participation in the weld pool metal melt. Oxides with a surface tension below 260 mN/m are characterized by low melting and boiling temperatures, decompose during welding, and saturate the welding arc with gaseous products of the oxide flux (oxygen anions and metal cations). This contributes to some reduction in the effectiveness of the action of oxide fluxes on the morphology of welded seams and the occurrence of mechanisms of action of fluxes associated with physical processes occurring in the welding arc. Owing to the complexity of the phenomena that occurred during a welding operation, we remark a slight variability in the aspect ratio results. This is observable when the whole dataset is used (52 samples). Based on the obtained results, the nonlinear exponential model will be adopted in what follows, and further analysis based on that model will be performed. The scatter plots of the depth (D) modeling are provided in Figure 9, Figure 10 and Figure 11 for the training, validation, and all datasets.
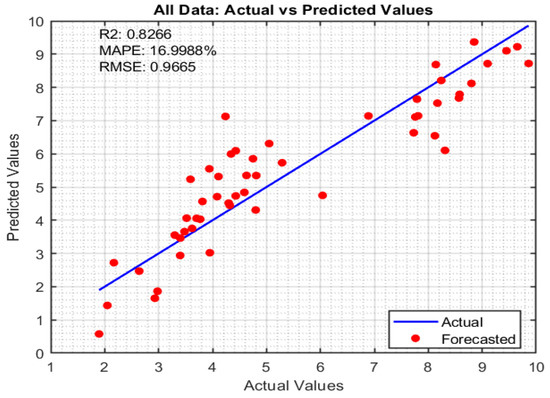
Figure 9.
Scatter plot of depth D (all data).
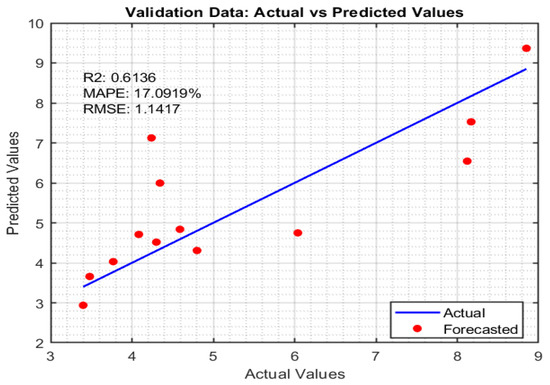
Figure 10.
Scatter plot of depth D (training data).
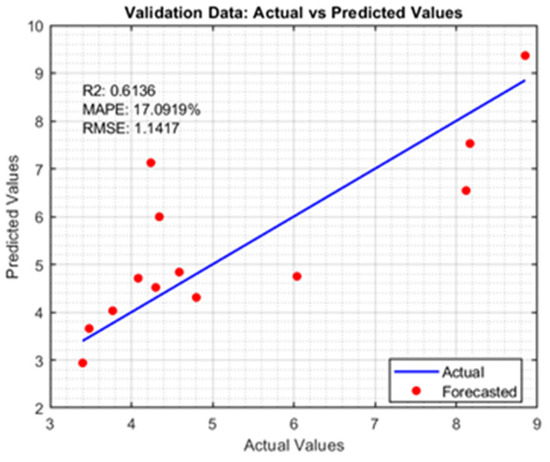
Figure 11.
Scatter plot of the depth D (validation data).
The scatter plots of the aspect ratio (R) modeling are provided in Figure 12, Figure 13 and Figure 14 for the training, validation, and all datasets.
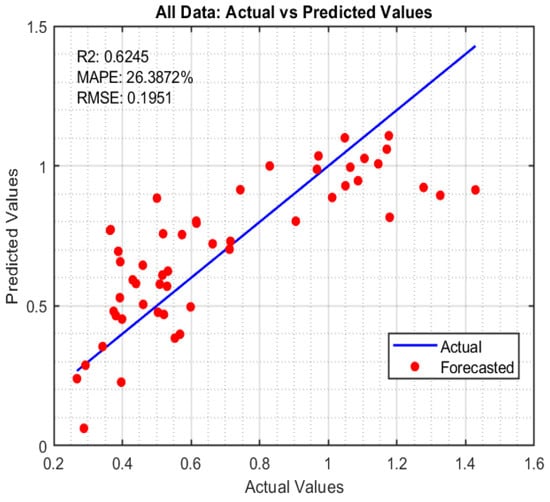
Figure 12.
Scatter plot of R (all data).
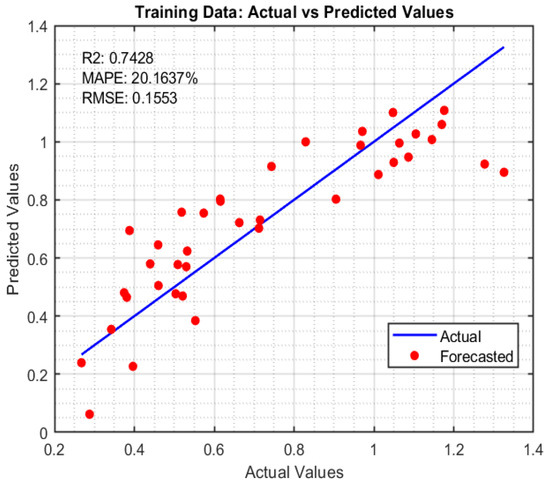
Figure 13.
Scatter plot of R (training data).
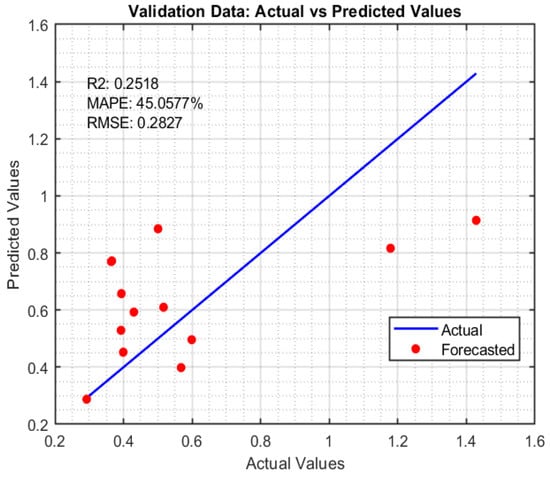
Figure 14.
Scatter plot of R (validation data).
The morphology of 316L SS welded joints obtained by ATIG welding depends on such thermophysical properties of oxides as the melting point “Tmo”, boiling point “Tbo” and temperature ranges “Tbo–Tmo”, surface tension (σ), and ionization potential “Ui”. The oxygen content in the oxide and its oxides’ thermophysical properties play an important role in the effectiveness of the formation of welded joints.
The mechanism of action of fluxes in ATIG 316L stainless steel welding can proceed according to several mechanisms in combination, and the predominance of the action of any of them depends on many factors, starting from the chemical composition of the flux and its thermophysical properties and ending with the conditions and parameters of the TIG welding mode. The outliers are probably due to some reduction in the effectiveness of the action of oxide fluxes on the morphology of welded joints and the occurrence of mechanisms of action of fluxes associated with physical processes occurring in the welding arc. The residuals are normally distributed. The errors are random and normally distributed. It implies that the model captures the main patterns and sources of variation in the data and that the errors are random and independent, which indicates the accuracy of the model.
Based on Table 10 results, the numerical equations of the depth (D) and the aspect ratio (R) are provided as follows (Equations (10) and (11)).
As the above models are calibrated using normalized values for either the inputs and outputs, the obtained depth (D) and aspect ratio (R) should be denormalized to their original scales according to the following Equations (12) and (13):
3.4. Application to a Design Problem
Oxides play a critical role in welding operations since they are known to influence weld quality, assure welding process stability, and improve the metallurgical characteristics of the parts being welded. Usually, oxides are intentionally introduced through fluxes and coatings. In arc welding, oxide layers on the base metal have a high impact on weld penetration. In addition, fluxes containing oxides help stabilize the arc and protect the weld from atmospheric contamination. Moreover, oxides in filler materials can modify weld composition, improving mechanical properties such as hardness and corrosion resistance. From this perspective, determining the flux (oxide) composition is a challenging problem for the welding operator. In practice, the weld depth varies from one application to another. For instance, the required penetration depth for welding beads varies from one industry to another. The optimal penetration depth is usually determined so that it fulfills several constraints, including integrity, safety, and current operative standards. For example, in the electric power generation domain, welds must meet stringent regulations to ensure structural reliability under extreme conditions, often requiring deep penetration welds of at least 80–100% of the material thickness, typically ranging from 3 to 10 mm, depending on the component such as turbine blades [35]. The automotive industry, while also prioritizing strength and durability, typically employs welds with penetration depths of 40–80%, translating to 1.5 to 5 mm, depending on the material and location, such as chassis reinforcement, trim, and or exhaust systems [36]. In the construction, ship, and heavy machinery sectors, deep penetration welds of 75–100% are necessary for load-bearing structures, often requiring depths of 5 to 12 mm to withstand high stresses and vibrations [37].
In this subsection, based on the model developed and validated in Section 2.2, we expect to solve the inverse optimization problem where the targeted weld depths from various industries are given. The objective is to determine the optimal composition of the oxides and the optimal current under which the welding is carried out. In this case, we will solve the optimization problem where the model, along with its coefficients, are known (since they were optimally tuned in the previous step). The optimization decision variables are now the variables X2, X3, X4, X7, X9, and I. Using the particle swarm optimization (PSO) technique and all the decision variables as normalized inside the interval [0, 1], we expect to minimize the quadratic error between the targeted depth (Dtarget) and the depth provided by the model depending on the decision variables. This problem, referred to as a design one, is therefore constrained since its variables are to be found in the range 0 to 1. At the end of the design problem-solving, the normalized design parameters will be converted again to their normal/regular values through a denormalization process as described in Equation (14) below [38].
The results of the design problem involving three different industries (power plant, automotive, and construction) are provided in Table 7 below. The design parameters for the three industries are optimized as normalized and then converted to their original scales. The error between the predicted depth and the targeted depth is found to be small. The current under which each weld should be performed is rounded to the nearest integer value, as tuning the current during the welding operation cannot provide values with an accuracy of 1% or even 10%. Therefore, the current values are selected to be entire. As illustrated in Table 12, for the power plant industry, the current yielded by the model is 146.6 A. However, it was rounded to the nearest standardized value of 150 A.

Table 12.
Design results of fluxes/oxides for selected industries.
Through this design problem-solving, the welding operator can select the oxide type in advance and proceed to prepare the adequate ones related to the industry while considering the targeted depth as prescribed by the relevant standards. During the welding operation, the welding current, as a critical parameter, can be tuned optimally on the welding machine.
The inverse optimization problem was run for the range of depths covering most industries to generate an envelope for the oxide design parameters. The considered range covers depths ranging from 1.5 mm to 12 mm. Using a step of 0.5 mm, 22 runs were carried out. The obtained results are shown in Table 13.

Table 13.
Design parameters of the oxide components envelopes covering depths from 1.5 mm to 12 mm.
The experimental results of the study allow for the determination of the influence of the physical and chemical properties of individual oxides forming a flux, in particular for 316L stainless steel welded joints, and the effect of these properties on the morphology of welds and the mechanism of action of the flux. The results depicted in Table 12 of the envelope reveal recommendations for oxide properties for different thicknesses ranging from 1.5 mm to 12 mm. These results from the calculation on the envelope can serve as data for researchers and industries to make a judicious choice of oxides to use during welding operations to improve their product while saving on material and electricity consumption.
The scalability of the proposed PSO-based modeling and inverse optimization framework is a key consideration for its application in broader manufacturing contexts. While this study focused on a specific material and set of welding conditions, the methodology is inherently adaptable to other alloys and welding configurations, provided that appropriate process data are collected. However, practical implementation in real-world manufacturing environments presents challenges such as process variability, sensor integration, and system robustness. One promising direction is the integration of the developed models with real-time weld monitoring systems, using sensors such as infrared cameras, voltage/current probes, or optical emission spectrometers to dynamically track weld quality. These data could feed into an adaptive control system, enabling in-process parameter adjustment based on model predictions. Such a closed-loop system would enhance consistency and quality in automated welding applications.
4. Conclusions
In the present work, the thermophysical properties of oxide and four current intensity levels (120, 150, 180, and 200 A) have been considered to optimize the ATIG weld depth and the weld aspect ratio of a 6 mm 316L SS material. Thirteen oxides have been tested. This study allows the forecasting of the morphology of ATIG 316L SS welds based on the selected oxides. In the current study, the welding process of ATIG 316L SS was modeled and optimized through several steps. First, after a careful correlation study, the most relevant welding parameters were selected according to their effect on the weld depth and aspect ratio. Second, based on 52 experiments, a linear classical regression model and a novel exponential nonlinear model were optimally calibrated and validated. Since the exponential model was found to outperform the linear one, an engineering design problem was solved as an inverse optimization framework. For this aim, the targeted depths of various industries, including power plants, automotive, and construction, and covering values ranging from 1.5 mm to 12 mm, were considered. The obtained results have allowed to generation of lower and upper limits of the envelopes for each one of the oxide compositions based on the most influential input parameters (X2, X3, X4, X7, and X9) as well as the range of the welding current to be used. Through this study, the obtained results were found to be promising, and therefore, they may be extended to other models and target other industries to solve the problem of the envelope, which consists of finding the ranges of the design parameters to keep the depths inside certain limits. The nonlinear exponential model outperformed the linear one for the depth, yielding a mean absolute percentage error of 17%, a coefficient of determination of 0.8266, and a root mean square error of 0.9665 mm. The inverse optimization process, for the depth penetration ranging from 1.5 mm to 12 mm, allows the determination of the input oxides’ thermophysical properties ranges. The main contributing input thermophysical properties ranges were specified to achieve full penetration in a single pass.
670 °C < Oxide melting point (TM) < 2826 °C
2134 °C < Oxide boiling point (TB) < 2701 °C
140 °C < Oxide boiling and melting points difference flux (TB–TM) < 1585 °C
35 °C < |Base metal boiling point—Oxide melting point (TM)| < 2191 °C
90 °C < |Oxide melting point flux (Tm)–Base metal melting point| < 200 °C
While the present study demonstrates the effectiveness of the selected swarm intelligence (SI) (PSO) approach in optimizing the ATIG welding process parameters, it is important to indicate that no direct comparison was made with other well-established optimization techniques such as Genetic Algorithms (GAs), Simulated Annealing (SA), or response surface methodology (RSM). The primary objective was to investigate the applicability and performance of the chosen SI method within the context of welding optimization, rather than to conduct a comparative study. Nonetheless, future research will benefit from a comprehensive comparative analysis involving multiple optimization technique, other types of models (Gaussian, power, and sigmoid), and statistical analysis (e.g., ANOVA, confidence intervals) to assess the significance of each oxide’s effect on weld depth and aspect ratio to further validate the robustness and superiority of the swarm intelligence framework in welding applications. In addition, given the adaptability of the swarm intelligence approach and the general structure of the PSO model, it can be calibrated to suit different alloys with varying thermal and metallurgical properties, such as stainless steel, aluminum alloys, or titanium. Similarly, the model can be adapted to alternative welding processes, including Gas Tungsten Arc Welding (GTAW), Metal Inert Gas (MIG) welding, or hybrid laser-arc welding, by redefining the process-specific input parameters and objective functions.
Author Contributions
Conceptualization, K.T. and S.B.; methodology, K.T. and S.B.; software, K.T. and S.B.; validation, K.T. and S.B.; formal analysis, K.T. and S.B.; investigation, K.T. and S.B.; resources, K.T. and S.B.; data curation, K.T. and S.B.; writing—original draft preparation, K.T. and S.B.; writing—review and editing, K.T. and S.B.; visualization, K.T. and S.B.; supervision, K.T. and S.B. All authors have read and agreed to the published version of the manuscript.
Funding
The authors extend their appreciation to Prince Sattam bin Abdulaziz University for funding this research work through the project number (PSAU/2024/01/31063).
Data Availability Statement
The data used to support the findings of this study are included within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Nouri, A.; Wen, C. Stainless steels in orthopedics. In Structural Biomaterials—Properties, Characteristics and Selection, Woodhead Publishing Series in Biomaterials; Woodhead Publishing: Cambridge, UK, 2021; pp. 67–101. [Google Scholar]
- Singh, C.; Lee, T.; Lee, K.H.; Kim, Y.S.; Huang, E.-W.; Jain, J.; Liaw, P.K.; Lee, S.Y. Exceptional fatigue-resistant austenitic stainless steel for cryogenic applications. Appl. Mater. Today 2024, 38, 102195. [Google Scholar] [CrossRef]
- Fashu, S.; Trabadelo, V. A critical review on development, performance and selection of stainless steels and nickel alloys for the wet phosphoric acid process. Mater. Des. 2023, 227, 111739. [Google Scholar] [CrossRef]
- Gary, S.W.; Shigeharu, U. Structural Alloys for Nuclear Energy Applications, Chapter 8—Austenitic Stainless Steels; Odette, G.R., Zinkle, S.J., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 293–347. [Google Scholar]
- Leconte, S.; Paillard, P.; Chapelle, P.; Henrion, G.; Saindrenan, J. Effect of oxide fluxes on activation mechanisms of tungsten inert gas process. Sci. Techno. Weld. Join. 2006, 11, 389–397. [Google Scholar] [CrossRef]
- Patel, N.P.; Sharma, D.K.; Upadhyay, G.H. Effect of Activated Fluxes on Weld Penetration and Mechanism Responsible for Deeper Penetration of Stainless Steels—A Review. In Current Advances in Mechanical Engineering; Lecture Notes in Mechanical Engineering (LNME); Springer: Singapore, 2021; pp. 737–746. [Google Scholar]
- Aljufri, A.; Sofyan, S.; Muhammad, R.; Reza, P.; Indra, M. Influence of shielding gas flow on the TIG welding process using stainless steel 304 material. J. Weld. Tech. 2024, 6, 38–45. [Google Scholar] [CrossRef]
- Kim, I.-S.; Lee, M.-G.; Jeon, Y. Review on Machine Learning Based Welding Quality Improvement. Int. J. Precis. Eng. Manuf.-Smart Technol. 2023, 1, 219–226. [Google Scholar] [CrossRef]
- Mahadevan, R.R.; Jagan, A.; Pavithran, L.; Shrivastava, A.; Selvaraj, S.K. Intelligent welding by using machine learning techniques. Mater. Today Proc. 2021, 26, 7402–7410. [Google Scholar] [CrossRef]
- Srinivasan, D.; Sevvel, P.; Dhanesh, B.S.D.; Vasanthe, R. Optimization of parameters and formulation of numerical model employing GRA–PCA and RSM approach for friction stir welded Ti–6Al–4V alloy joints. Mater. Res. Express 2024, 11, 056511. [Google Scholar] [CrossRef]
- John Solomon, I.; Sevvel, P.; Gunasekaran, J.; Vasanthe Roy, J. Parametric-based optimization of friction stir welded wrought AZ80A Mg alloy employing response surface methodology. Mater. Res. Express 2023, 10, 116514. [Google Scholar] [CrossRef]
- Tesfaye, F.K.; Getaneh, A.M. The grey-based Taguchi method was used to enhance the TIG-MIG hybrid welding process parameters for mild steel. Invent. Discl. 2024, 4, 100016. [Google Scholar] [CrossRef]
- Abima, C.S.; Akinlabi, S.A.; Madushele, N.; Fatoba, O.S.; Akinlabi, E.T. Multi-objective optimization of process parameters in TIG-MIG welded AISI 1008 steel for improved structural integrity. Int. J. Adv. Manuf. Technol. 2021, 118, 3601–3615. [Google Scholar] [CrossRef]
- Choudhury, B.; Chandrasekaran, M.; Devarasiddappa, D. Development of ANN modeling for estimation of weld strength and integrated optimization for GTAW of Inconel 825 sheets used in aero engine components. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 308. [Google Scholar] [CrossRef]
- Ghosh, N. Effect of GTAW process parameters on AISI 304L austenitic stainless steels and optimization using Grey-Taguchi technique. Can. Metall. Q. 2024, 1–10. [Google Scholar] [CrossRef]
- Adirek, B.; Wasawat, N.; Nuttachat, W. Optimization of Tungsten Inert Gas Welding Process Parameters for AISI 304 Stainless Steel. Defect Diffus. Forum 2022, 417, 23–28. [Google Scholar]
- Pratheesh, K.S.; Anand, K.; Rajesh, R.; Ashwin, S. Optimization of Tungsten Inert Gas Welding Process Parameters on AA6013. In Materials, Design, and Manufacturing for Sustainable Environment; Lecture Notes in Mechanical Engineering(LNME); Springer: Singapore, 2022; pp. 381–396. [Google Scholar] [CrossRef]
- Vora, J.J.; Abhishek, K.; Srinivasan, S. Attaining optimized A-TIG welding parameters for carbon steels by advanced parameter-less optimization techniques: With experimental validation. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 261. [Google Scholar] [CrossRef]
- Ghumman, K.Z.; Ali, S.; Khan, N.B.; Khan, M.H.; Ali, H.T.; Ashurov, M. Optimization of TIG welding parameters for enhanced mechanical properties in AISI 316L stainless steel welds. Int. J. Adv. Manuf. Technol. 2025, 136, 353–365. [Google Scholar] [CrossRef]
- Hedhibi, A.C.; Touileb, K.; Djoudjou, R.; Ouis, A.; Alrobei, H.; Ahmed, M.M.Z. Mechanical Properties and Microstructure of TIG and ATIG Welded 316L Austenitic Stainless Steel with Multi-Components Flux Optimization Using Mixing Design Method and Particle Swarm Optimization (PSO). Materials 2021, 14, 7139. [Google Scholar] [CrossRef] [PubMed]
- Sivakumar, J.; Vasudevan, M.; Korra, N.N. Systematic Welding Process Parameter Optimization in Activated Tungsten Inert Gas (A-TIG) Welding of Inconel 625. Trans. Indian Inst. Met. 2022, 73, 555–569. [Google Scholar] [CrossRef]
- Kumaar, S.S.; Korra, N.N.; Devakumaran, K.; Kumar, G. Optimization of Process Parameters for the A-TIG Welding of Inconel 617 using Particle Swarm Optimization (PSO) and Genetic Algorithm (GA). Surf. Rev. Lett. 2022, 29, 2250136. [Google Scholar] [CrossRef]
- Sivakumar, J.; Korra, N.N. Optimization of Welding Process Parameters for Activated Tungsten Inert Welding of Inconel 625 Using the Technique for Order Preference by Similarity to Ideal Solution Methodology. Arab. J. Sci. Eng. 2021, 46, 7399–7409. [Google Scholar] [CrossRef]
- Sekar, C.B.; Boopathy, S.R.; Vijayan, S.R.; Rao, S.R.K. Multi-objective optimization of welding parameters using Taguchi-based grey relation analysis in activated TIG(ATIG), welding on SAF2507 super duplex stainless steel. AIP Conf. Proc. 2021, 2395, 30007. [Google Scholar] [CrossRef]
- Vuherer, T.; Bajić, D.; Manjgo, M.; Bjelajac, E.; Skumavc, A.; Orožim, U.; Lojen, G. Comparison of ATIG welding powders and their influence on mechanical properties. Zavar. I Zavarene Konstr. 2024, 69, 99–110. [Google Scholar] [CrossRef]
- Mills, K.C. Recommended Values of Thermophysical Properties for Selected Commercial Alloys; National Physical Laboratory 472 and ASM International; Woodhead Publishing Limited: Cambridge, UK, 2002. [Google Scholar]
- Cabello-Solorzano, K.; Ortigosa de Araujo, I.; Peña, M.; Correia, L.; Tallón-Ballesteros, A.J. The Impact of Data Normalization on the Accuracy of Machine Learning Algorithms: A Comparative Analysis. In Proceedings of the 18th International Conference on Soft Computing Models in Industrial and Environmental Applications (SOCO 2023), Salamanca, Spain, 5–7 September 2023; Springer: Cham, Switzerland, 2023; Volume 750, pp. 344–353. [Google Scholar] [CrossRef]
- Singh, D.; Singh, B. Feature-wise normalization: An effective way of normalizing data. Pattern Recognit. 2022, 122, 108307. [Google Scholar] [CrossRef]
- de Winter, J.C.F.; Gosling, S.D.; Potter, J. Comparing the Pearson and Spearman correlation coefficients across distributions and sample sizes: A tutorial using simulations and empirical data. Psychol. Methods 2016, 21, 273–290. [Google Scholar] [CrossRef] [PubMed]
- Azadi Moghaddam, M.; Kolahan, F. Optimization of A-TIG Welding Process Using Simulated Annealing Algorithm. J. Adv. Manuf. Syst. 2020, 19, 869–891. [Google Scholar] [CrossRef]
- Pu, Y.; Rong, Y.; Chen, J.; Mao, Y. Accelerated Identification Algorithms for Exponential Nonlinear Models: Two-Stage Method and Particle Swarm Optimization Method. Circuits Syst. Signal Process. 2022, 41, 2636–2652. [Google Scholar] [CrossRef]
- Kozinski, O.; Kotyrba, M.; Volna, E. Improving the production efficiency based on algorithmization of the planning process. Appl. Syst. Innov. 2023, 6, 77. [Google Scholar] [CrossRef]
- Touileb, K.; Djoudjou, R.; Ouis, A.; Hedhibi, A.C.; Boubaker, S.; Ahmed, M.M.Z. Particle Swarm Method for Optimization of ATIG Welding Process to Joint Mild Steel to 316L Stainless Steel. Crystals 2023, 13, 1377. [Google Scholar] [CrossRef]
- Wu, J.; Azarm, S. Metrics for quality assessment of a multiobjective design optimization solution set. J. Mech. Des. 2001, 123, 18–25. [Google Scholar] [CrossRef]
- Poblano-Salas, C.D.; Barceinas-Sanchez, J.D.O.; Sanchez-Jimenez, J.C. Failure analysis of an AISI 410 stainless steel airfoil in a steam turbine. Eng. Fail. Anal. 2011, 18, 68–74. [Google Scholar] [CrossRef]
- Mishra, A. Automotive Materials: An Overview. Int. Res. J. Eng. Technol. (IRJET) 2020, 7, 4852–4857. [Google Scholar]
- Liu, J.; Cheng, Y.; Jing, X.; Liu, X.; Chen, Y. Prediction and optimization method for welding quality of components in ship construction. Sci. Rep. 2024, 14, 9353. [Google Scholar] [CrossRef] [PubMed]
- Date, C.J. Denormalization. In Database Design and Relational Theory; Apress: Berkeley, CA, USA, 2019; pp. 161–182. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).





















