The Missing Structures of Pasteur’s Aspartates
Abstract
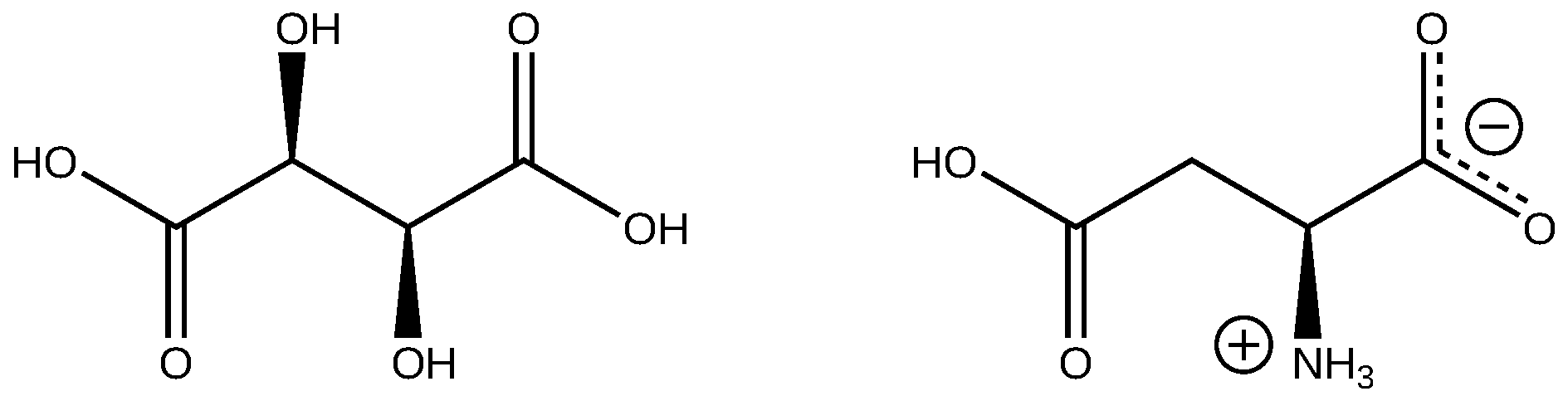
1. Introduction
2. Materials and Methods
2.1. Synthesis and Crystallization
2.2. X-Ray Crystal Structure Determinations
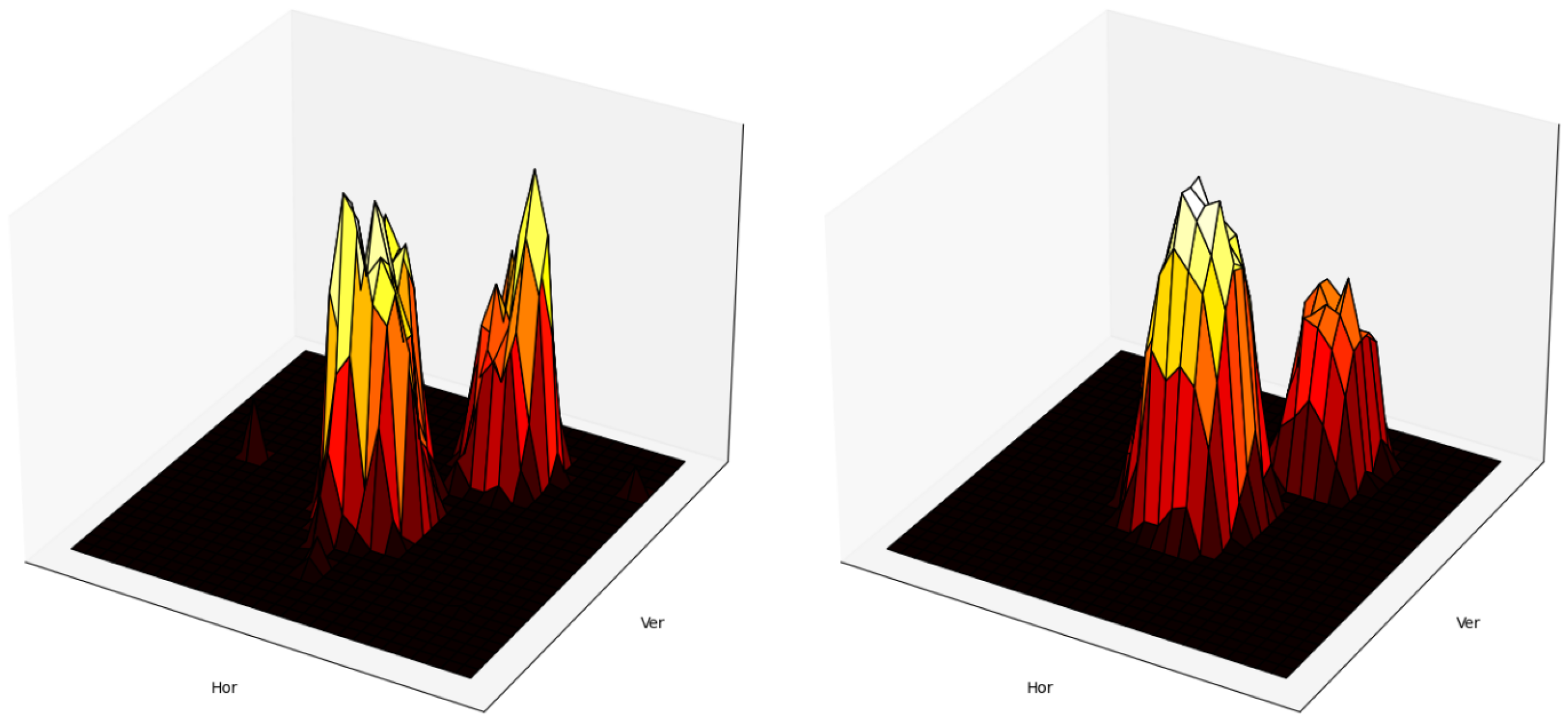
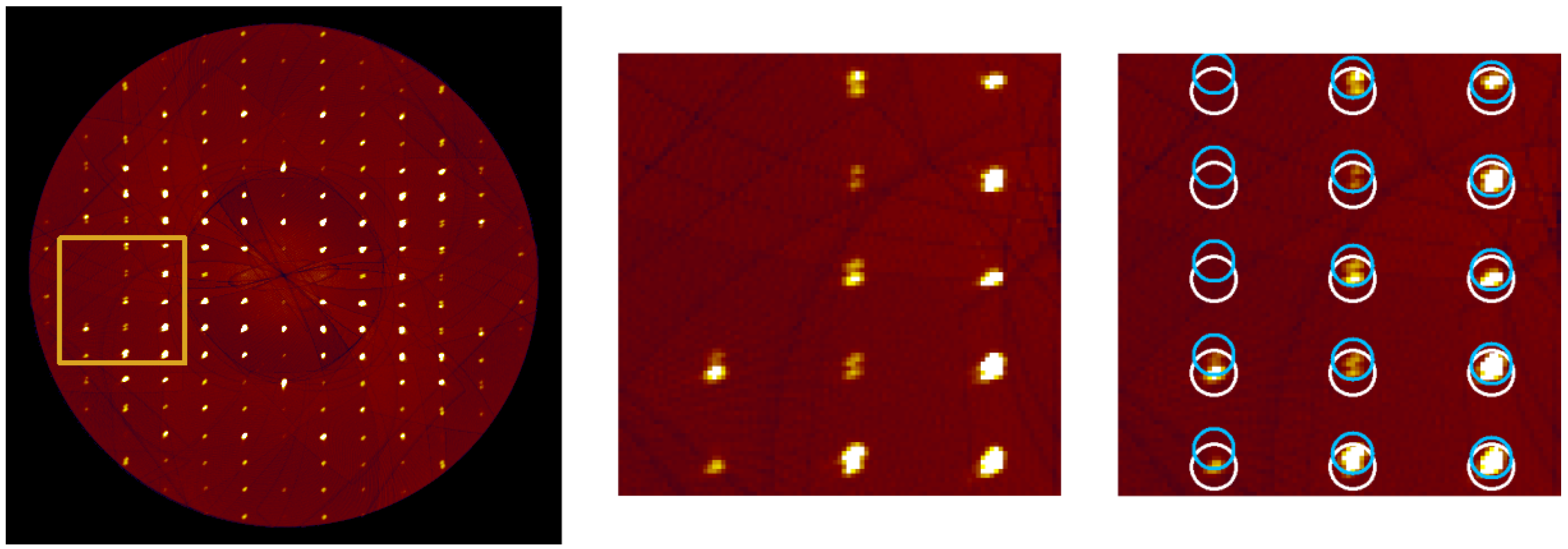
2.3. Twinning in Compound 1
2.4. Twinning in Compound 2
2.5. Absolute Structure of Compound 1
3. Results and Discussion
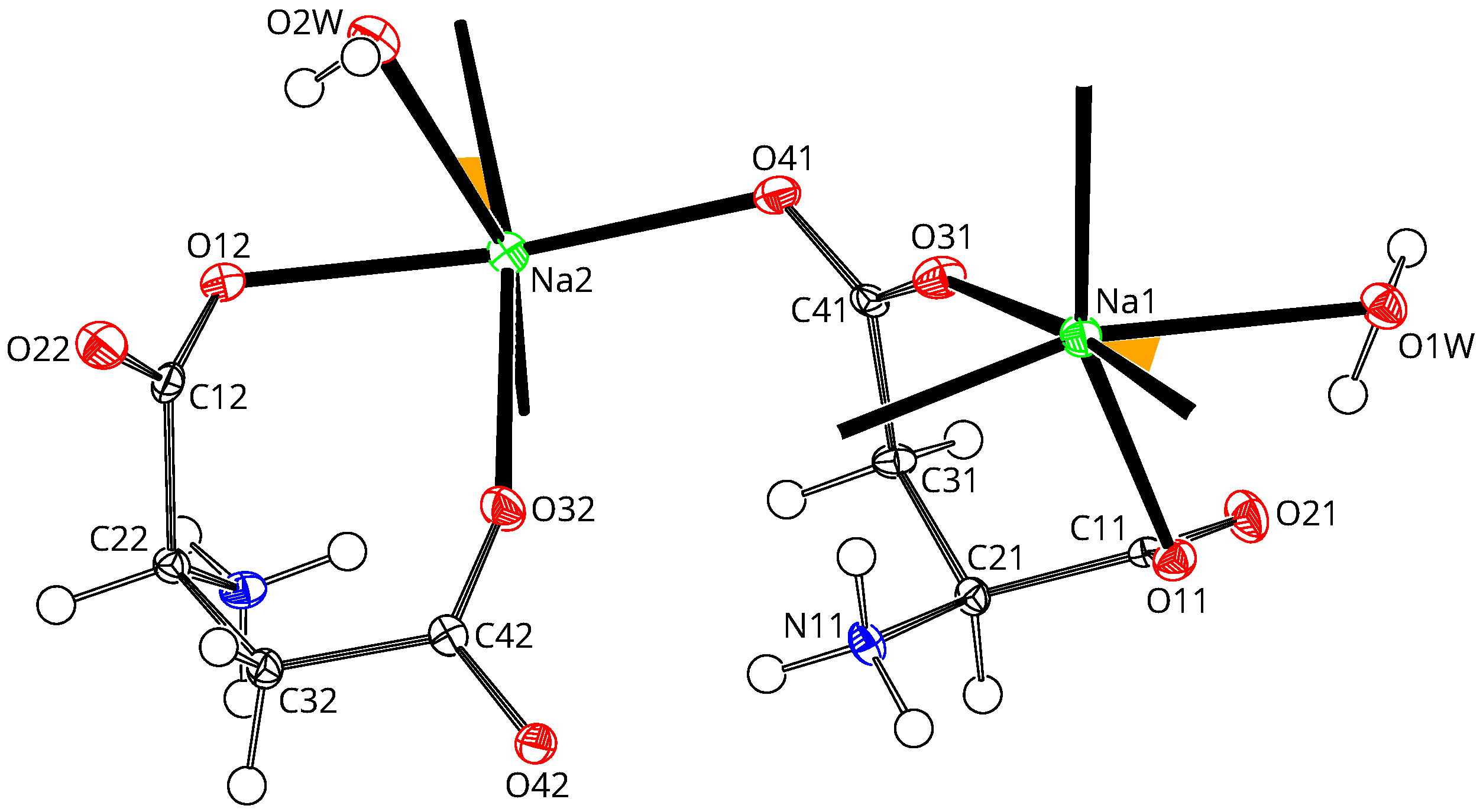
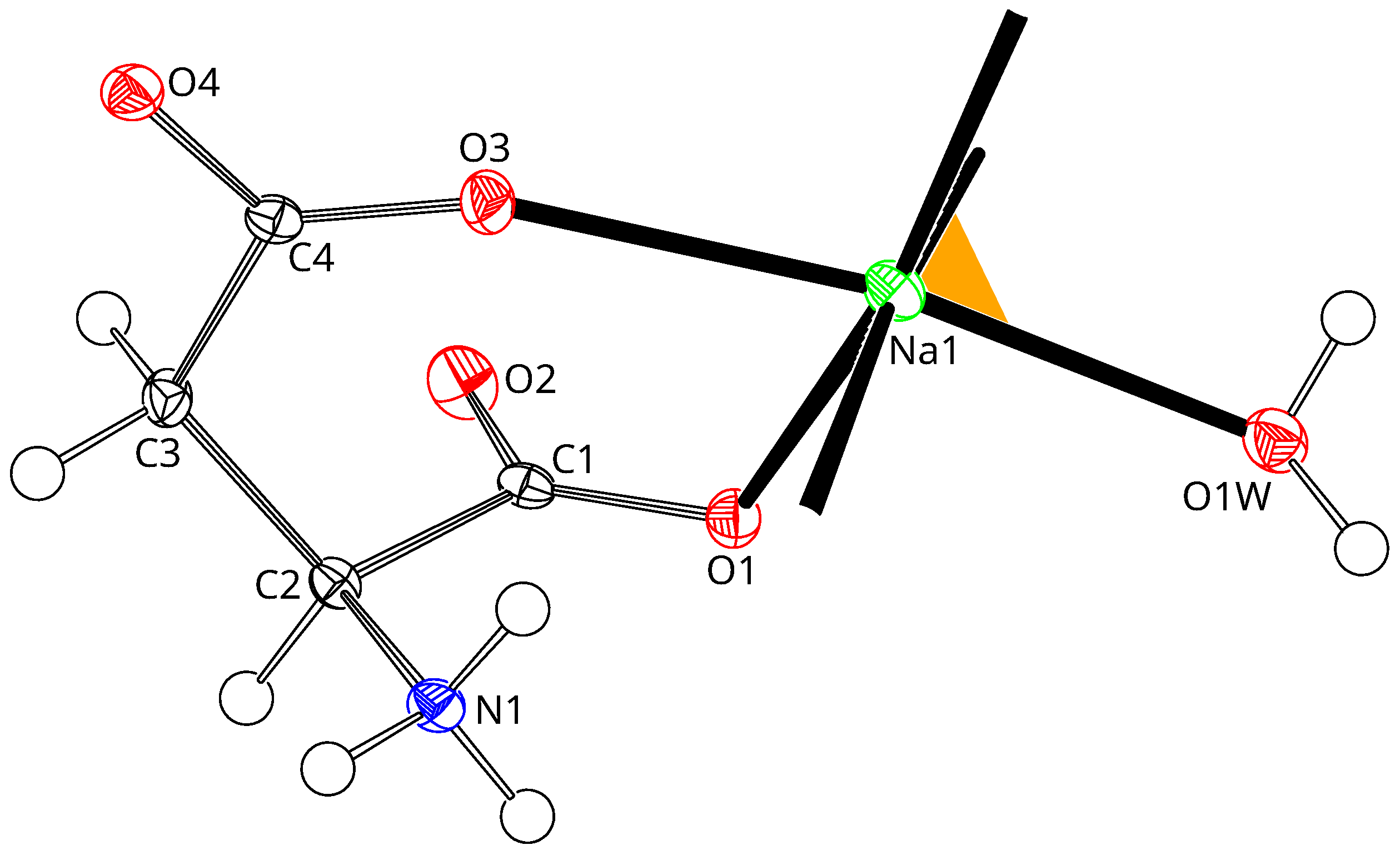
3.1. Sodium Coordination
3.2. Amino Acid Conformations
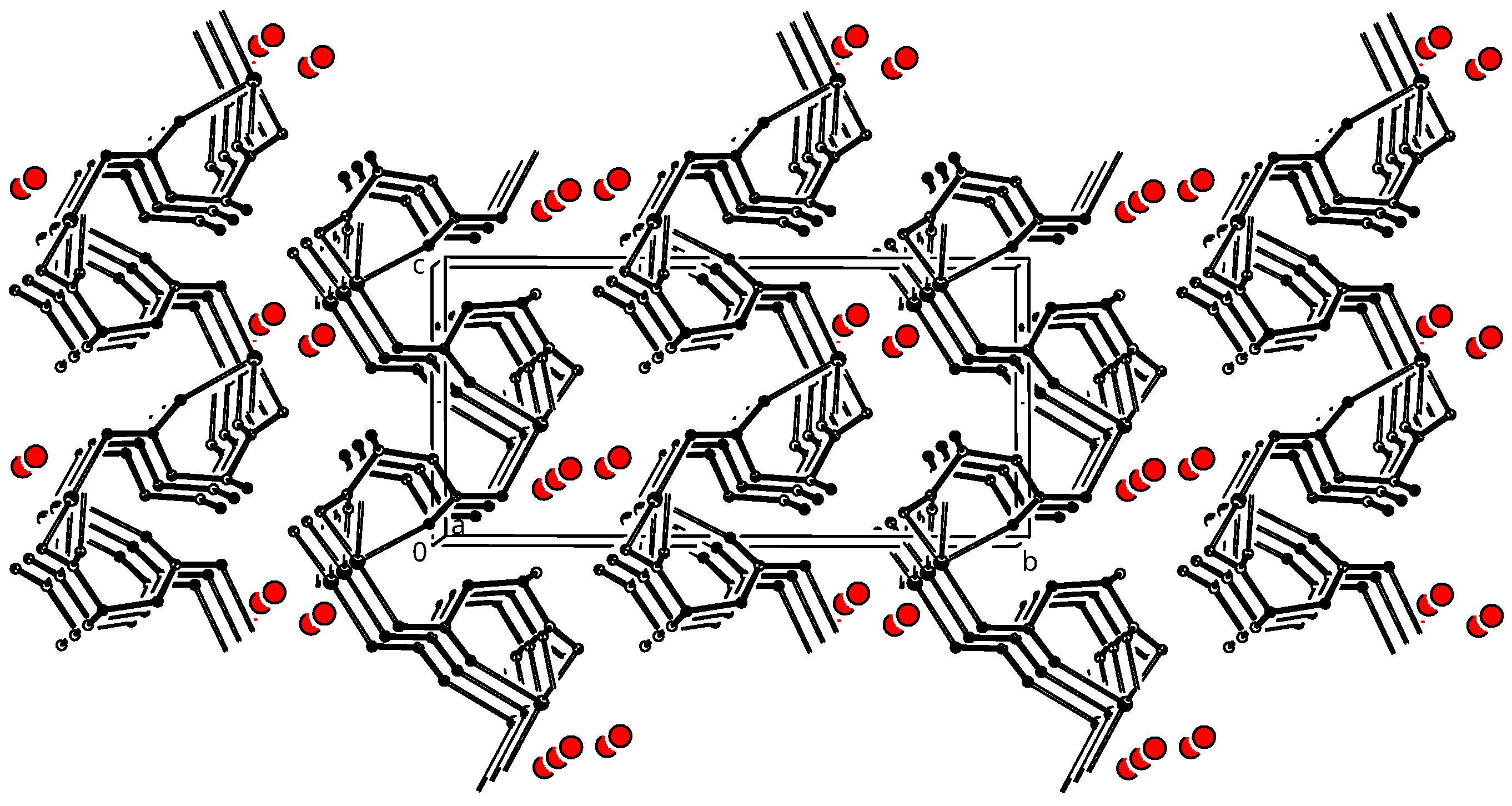
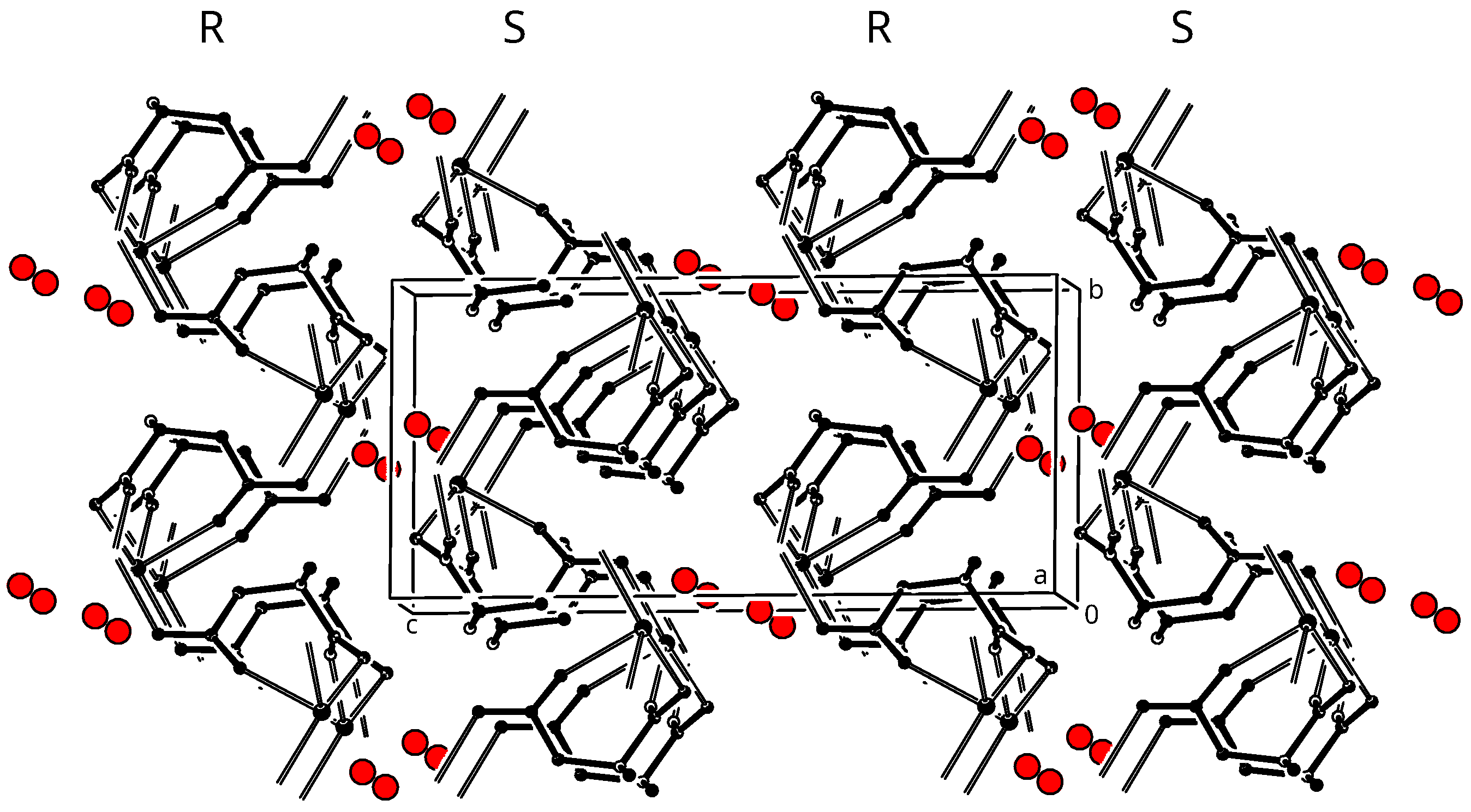
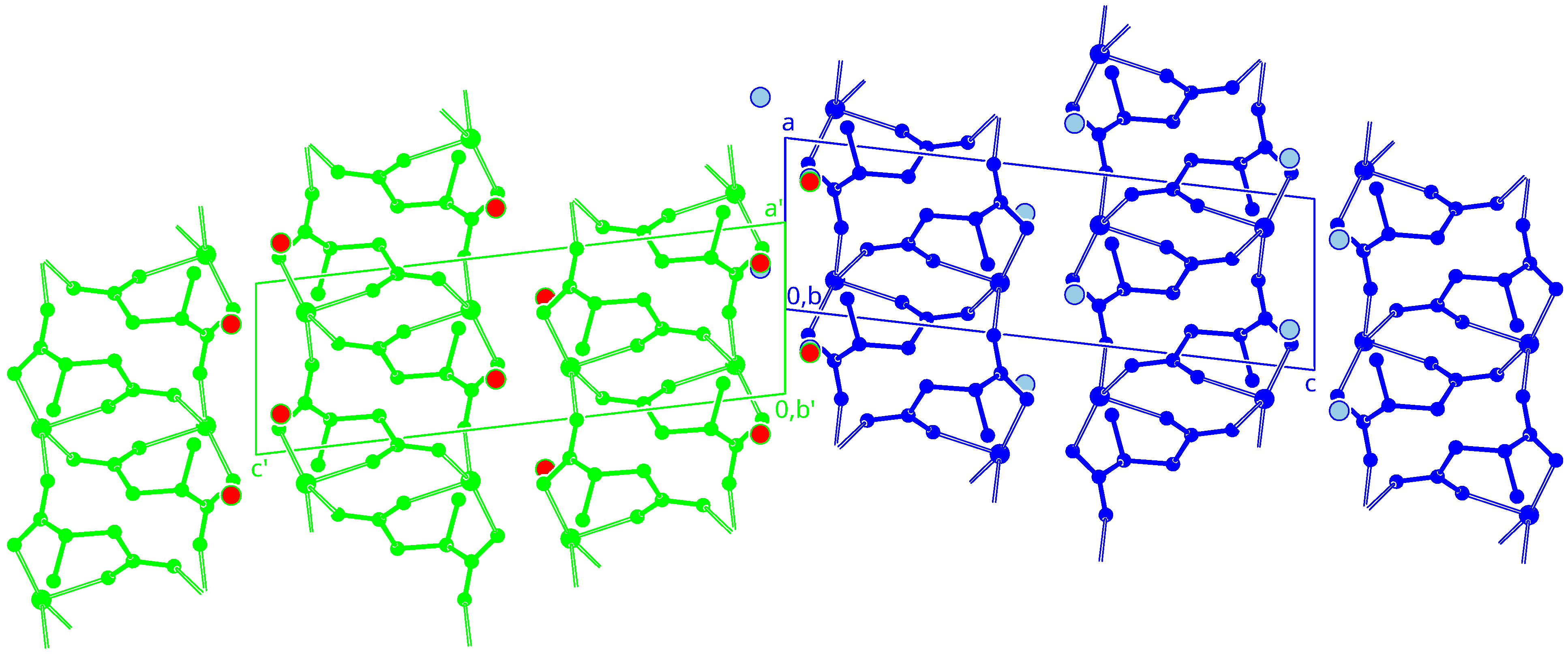
3.3. Crystal Packing
3.4. Twinning Model for Enantiopure Compound 1
3.5. Twinning Model for Racemic Compound 2
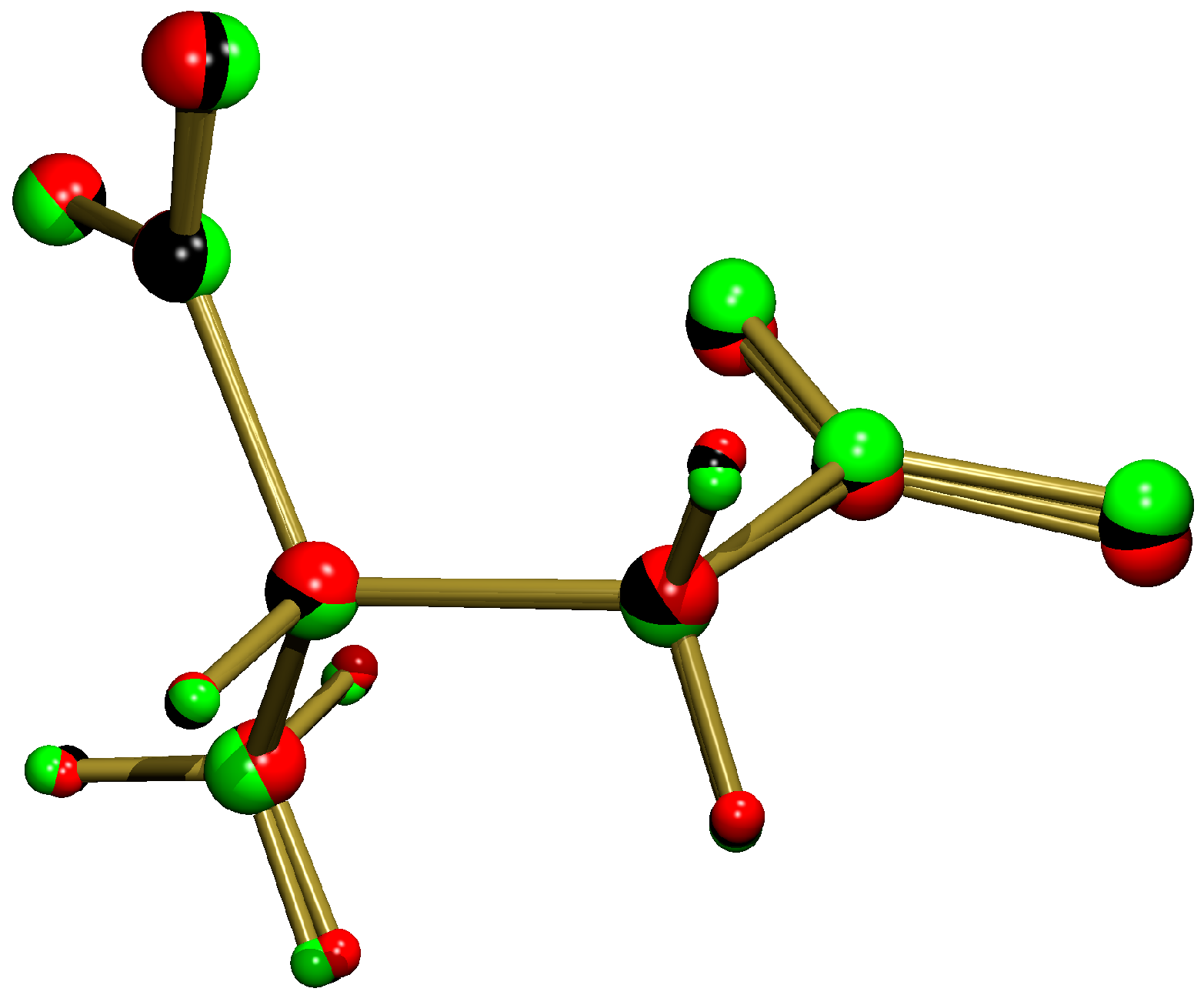
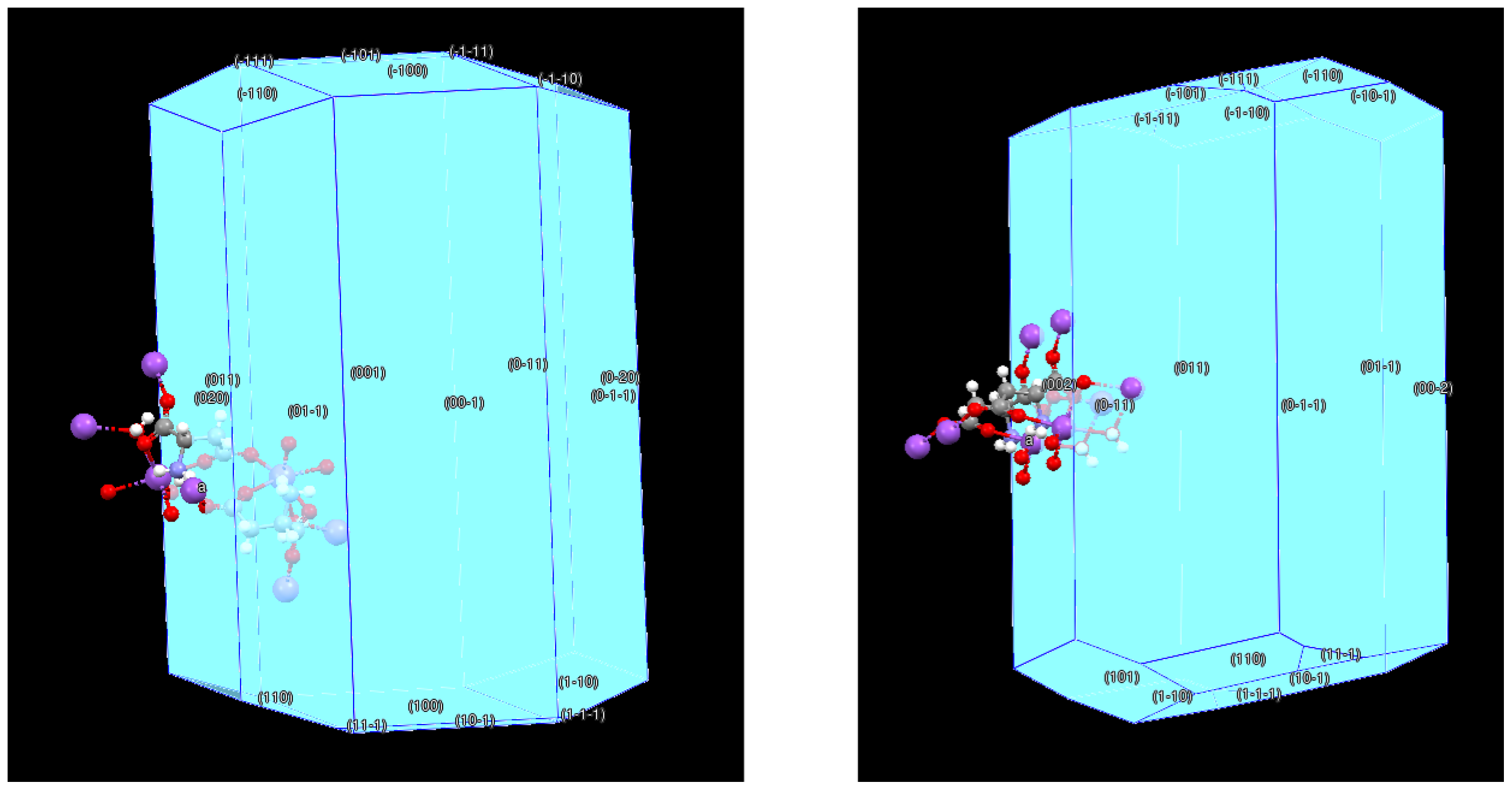
3.6. BFDH Morphology
3.7. Non-Standard Unit Cell Parameters
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Flack, H.D. Louis Pasteur’s discovery of molecular chirality and spontaneous resolution in 1848, together with a complete review of his crystallographic and chemical work. Acta Crystallogr. Sect. A 2009, 65, 371–389. [Google Scholar] [CrossRef] [PubMed]
- Gal, J. Pasteur and the art of chirality. Nat. Chem. 2017, 9, 604–605. [Google Scholar] [CrossRef] [PubMed]
- Rietveld, I.B.; Painsecq, F.; Jandl, C.; Stam, D.; Coquerel, G. In the Footsteps of Pasteur: Finding Conglomerates by Using State-of-the-Art Electron Diffraction. Cryst. Growth Des. 2024, 24, 5893–5897. [Google Scholar] [CrossRef]
- Bernal, J.D. Science and Industry in the Nineteenth Century; Routledge & Kegan Paul: London, UK, 1953. [Google Scholar]
- Gal, J. Louis Pasteur, Chemical Linguist: Founding the Language of Stereochemistry. Helv. Chim. Acta 2019, 102, e1900098. [Google Scholar] [CrossRef]
- Jacques, J. The Molecule and Its Double; McGraw-Hill: New York, NY, USA, 1993. [Google Scholar]
- Jacques, J.; Collet, A.; Wilen, S.H. Enantiomers, Racemates, and Resolutions; Krieger Pub. Co.: Malabar, FL, USA, 1994. [Google Scholar]
- Rekis, T. Crystallization of chiral molecular compounds: What can be learned from the Cambridge Structural Database? Acta Crystallogr. Sect. B 2020, 76, 307–315. [Google Scholar] [CrossRef]
- Groom, C.R.; Bruno, I.J.; Lightfoot, M.P.; Ward, S.C. The Cambridge Structural Database. Acta Crystallogr. Sect. B 2016, 72, 171–179. [Google Scholar] [CrossRef]
- Pasteur Vallery-Radot, R. Oeuvres de Pasteur. Tome Premier: Dissymétrie Moléculaire; Masson et cie: Paris, France, 1922; pp. 169–171. [Google Scholar]
- Grattarola, G. Asparaginsäure Natronsalze. Z. Krist.—Cryst. Mater. 1892, 20, 620. [Google Scholar] [CrossRef]
- Groth, P. Chemische Krystallographie, Dritter Teil; Verlag von Wilhelm Engelmann: Leipzig, Germany, 1910; p. 277. [Google Scholar]
- Schmidbaur, H.; Classen, H.G.; Helbig, J. Aspartic and Glutamic Acid as Ligands to Alkali and Alkaline-Earth Metals: Structural Chemistry as Related to Magnesium Therapy. Angew. Chem. Int. Ed. Engl. 1990, 29, 1090–1103. [Google Scholar] [CrossRef]
- Fleck, M.; Petrosyan, A.M. Salts of Amino Acids: Crystallization, Structure and Properties; Springer: Cham, Switzerland, 2014. [Google Scholar] [CrossRef]
- Herbst-Irmer, R.; Sheldrick, G.M. Refinement of Twinned Structures with SHELXL97. Acta Crystallogr. Sect. B 1998, 54, 443–449. [Google Scholar] [CrossRef]
- Sevvana, M.; Ruf, M.; Usón, I.; Sheldrick, G.M.; Herbst-Irmer, R. Non-merohedral twinning: From minerals to proteins. Acta Crystallogr. Sect. D 2019, 75, 1040–1050. [Google Scholar] [CrossRef]
- Dudev, M.; Wang, J.; Dudev, T.; Lim, C. Factors Governing the Metal Coordination Number in Metal Complexes from Cambridge Structural Database Analyses. J. Phys. Chem. B 2006, 110, 1889–1895. [Google Scholar] [CrossRef] [PubMed]
- Bock, C.W.; Markham, G.D.; Katz, A.K.; Glusker, J.P. The Arrangement of First- and Second-shell Water Molecules Around Metal Ions: Effects of Charge and Size. Theor. Chem. Accounts 2006, 115, 100–112. [Google Scholar] [CrossRef]
- Ruggiero, M.T.; Sibik, J.; Erba, A.; Zeitler, J.A.; Korter, T.M. Quantification of cation–anion interactions in crystalline monopotassium and monosodium glutamate salts. Phys. Chem. Chem. Phys. 2017, 19, 28647–28652. [Google Scholar] [CrossRef]
- Duisenberg, A.J.M. Indexing in single-crystal diffractometry with an obstinate list of reflections. J. Appl. Crystallogr. 1992, 25, 92–96. [Google Scholar] [CrossRef]
- Schreurs, A.M.M.; Xian, X.; Kroon-Batenburg, L.M.J. EVAL15: A diffraction data integration method based on ab initio predicted profiles. J. Appl. Crystallogr. 2010, 43, 70–82. [Google Scholar] [CrossRef]
- Duisenberg, A.J.M. Diffractometry and reflection profiles of anisotropic mosaic and split crystals. Acta Crystallogr. Sect. A 1983, 39, 211–216. [Google Scholar] [CrossRef]
- Sheldrick, G.M. SHELXT—Integrated space-group and crystal-structure determination. Acta Crystallogr. Sect. A 2015, 71, 3–8. [Google Scholar] [CrossRef]
- Sheldrick, G.M. Crystal structure refinement with SHELXL. Acta Crystallogr. Sect. C 2015, 71, 3–8. [Google Scholar] [CrossRef]
- Spek, A.L. Structure validation in chemical crystallography. Acta Crystallogr. Sect. D 2009, 65, 148–155. [Google Scholar] [CrossRef]
- Parsons, S.; Flack, H.D.; Wagner, T. Use of intensity quotients and differences in absolute structure refinement. Acta Crystallogr. Sect. B 2013, 69, 249–259. [Google Scholar] [CrossRef]
- Hooft, R.W.W.; Straver, L.H.; Spek, A.L. Determination of absolute structure using Bayesian statistics on Bijvoet differences. J. Appl. Crystallogr. 2008, 41, 96–103. [Google Scholar] [CrossRef]
- Schmidbaur, H.; Bach, I.; Wilkinson, D.L.; Müller, G. Metal ion binding by amino acids. Preparation and crystal structures of lithium hydrogen L-aspartate hydrate and potassium hydrogen L-aspartate dihydrate. Chem. Berichte 1989, 122, 1427–1431. [Google Scholar] [CrossRef]
- Kitaĭgorodskiĭ, A.I. Molecular Crystals and Molecules; Academic Press: New York, NY, USA, 1973. [Google Scholar]
- Robinson, K.; Gibbs, G.V.; Ribbe, P.H. Quadratic Elongation: A Quantitative Measure of Distortion in Coordination Polyhedra. Science 1971, 172, 567–570. [Google Scholar] [CrossRef]
- Alvarez, S.; Avnir, D.; Llunell, M.; Pinsky, M. Continuous symmetry maps and shape classification. The case of six-coordinated metal compounds. New J. Chem. 2002, 26, 996–1009. [Google Scholar] [CrossRef]
- Duisenberg, A.J.M.; Kroon-Batenburg, L.M.J.; Schreurs, A.M.M. An intensity evaluation method: EVAL-14. J. Appl. Crystallogr. 2003, 36, 220–229. [Google Scholar] [CrossRef]
- Stöger, B.; Pokorny, B.; Lumpi, D.; Zobetz, E.; Fröhlich, J. The twinning of two closely related phenylisoxazoles interpreted according to order-disorder theory. Z. Krist.—Cryst. Mater. 2013, 228, 106–112. [Google Scholar] [CrossRef]
- Marzouki, M.A.; Souvignier, B.; Nespolo, M. Twinning of aragonite—The crystallographic orbit and sectional layer group approach. Acta Crystallogr. Sect. A 2015, 71, 195–202. [Google Scholar] [CrossRef]
- Herbstein, F.H. Twinned crystals. III. γ-o-Nitroaniline. Acta Crystallogr. 1965, 19, 590–595. [Google Scholar] [CrossRef]
- Lutz, M.; Kroon-Batenburg, L.M.J. Order-Disorder in Diaquobis(salicylato)copper(II) Revisited. Croat. Chem. Acta 2018, 91, 289–298. [Google Scholar] [CrossRef]
- Le Page, Y. The derivation of the axes of the conventional unit cell from the dimensions of the Buerger-reduced cell. J. Appl. Crystallogr. 1982, 15, 255–259. [Google Scholar] [CrossRef]
- Le Page, Y. Mallard’s law recast as a Diophantine system: Fast and complete enumeration of possible twin laws by [reticular] [pseudo] merohedry. J. Appl. Crystallogr. 2002, 35, 175–181. [Google Scholar] [CrossRef]
- Nespolo, M.; Ferraris, G. Hybrid twinning—A cooperative type of oriented crystal association. Z. Krist.—Cryst. Mater. 2005, 220, 317–323. [Google Scholar] [CrossRef]
- Lutz, M.; Klein, T.J.S.d.; Huijben, J. 5-Iodouracil: Structure of a reflection twin. Acta Crystallogr. Sect. C 2015, 71, 912–915. [Google Scholar] [CrossRef] [PubMed]
- Hartman, P. On the Morphology of Growth Twins. Z. Krist.—Cryst. Mater. 1956, 107, 225–237. [Google Scholar] [CrossRef]
- Kitamura, M.; Hosoya, S.; Sunagawa, I. Re-investigation of the re-entrant corner effect in twinned crystals. J. Cryst. Growth 1979, 47, 93–99. [Google Scholar] [CrossRef]
- Winn, D.; Doherty, M.F. Modeling crystal shapes of organic materials grown from solution. AIChE J. 2000, 46, 1348–1367. [Google Scholar] [CrossRef]
- Macrae, C.F.; Edgington, P.R.; McCabe, P.; Pidcock, E.; Shields, G.P.; Taylor, R.; Towler, M.; van de Streek, J. Mercury: Visualization and analysis of crystal structures. J. Appl. Crystallogr. 2006, 39, 453–457. [Google Scholar] [CrossRef]
- Donnay, J.D.H.; Harker, D. A new law of crystal morphology extending the Law of Bravais. Am. Mineral. 1937, 22, 446–467. [Google Scholar]
- Blatov, V.A.; Shevchenko, A.P.; Proserpio, D.M. Applied Topological Analysis of Crystal Structures with the Program Package ToposPro. Cryst. Growth Des. 2014, 14, 3576–3586. [Google Scholar] [CrossRef]
- Hammersley, A.P.; Bernstein, H.J.; Westbrook, J.D. International Tables for Crystallography, Volume G; Springer: Dordrecht, The Netherlands, 2005; pp. 444–458. [Google Scholar]



| 1 (Enantiopure) | 2 (Racemic) | |
|---|---|---|
| sum formula | C4H8NNaO5 | C4H8NNaO5 |
| formula weight | 173.10 | 173.10 |
| crystal system | monoclinic | monoclinic |
| space group | (no. 4) | (no. 14) |
| a [Å] | 5.27592(17) | 5.2977(2) |
| b [Å] | 16.174(2) | 7.7195(3) |
| c [Å] | 7.7051(8) | 16.4812(8) |
| [°] | 90.734(3) | 96.588(2) |
| V [Å3] | 657.43(11) | 669.56(5) |
| Z | 4 | 4 |
| [] | 1.749 | 1.717 |
| [] | 0.21 | 0.21 |
| T [K] | 150(2) | 150(2) |
| crystal size [mm] | ||
| [Å] | 0.71073 | 0.71073 |
| [Å−1] | 0.71 | 0.71 |
| meas. refl. | 25,442 | 31,302 |
| unique refl. | 3832 | 1997 |
| obs. refl. [] | 3781 | 1939 |
| 0.030 | 0.029 | |
| no. parameters | 214 | 121 |
| no. restraints | 7 | 0 |
| a, b † | 0.0349, 0.0647 | 0.0422, 0.1553 |
| R1/wR2 (obs. refl.) | 0.0219/0.0561 | 0.0261/0.0712 |
| R1/wR2 (all refl.) | 0.0222/0.0562 | 0.0267/0.0715 |
| S | 1.114 | 1.083 |
| Parsons z [26] (SHELXL) | 0.01(7) [1802 pairs] | – |
| [e/Å3] | −0.17/0.29 | −0.28/0.36 |
| Structure | Atom Name | [30] | [30] | CSM [31] | Symmetry |
|---|---|---|---|---|---|
| 1 | Na1 | 1.044 | 136.09 | 2.381 | (0.32 Å) |
| Na2 | 1.049 | 144.10 | 2.387 | (0.26 Å) | |
| 2 | Na1 | 1.053 | 159.26 | 2.620 | (0.32 Å) |
| 1 (mol. 1, x = 1) | 1 (mol. 2, x = 2) | 2 * | Li [28] | K [28] | ||
|---|---|---|---|---|---|---|
| O1x–C1x–C2x–N1x | −0.1(2) | −0.5(2) | −0.53(12) | −28.5(2) | −32.7(3) | |
| O2x–C1x–C2x–N1x | 177.49(16) | 176.17(16) | 178.78(8) | 153.12(15) | 150.84(17) | |
| N1x–C2x–C3x–C4x | 62.8(2) | 56.2(2) | 57.97(10) | −70.7(2) | −62.6(2) | |
| C2x–C3x–C4x–O3x | 13.7(2) | 16.8(3) | 15.48(13) | 3.0(2) | −1.2(3) | |
| C2x–C3x–C4x–O4x | −167.39(16) | −163.77(16) | −165.32(8) | −175.23(18) | 178.82(18) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kersten, D.J.C.; Lutz, M. The Missing Structures of Pasteur’s Aspartates. Crystals 2025, 15, 521. https://doi.org/10.3390/cryst15060521
Kersten DJC, Lutz M. The Missing Structures of Pasteur’s Aspartates. Crystals. 2025; 15(6):521. https://doi.org/10.3390/cryst15060521
Chicago/Turabian StyleKersten, Damian J. C., and Martin Lutz. 2025. "The Missing Structures of Pasteur’s Aspartates" Crystals 15, no. 6: 521. https://doi.org/10.3390/cryst15060521
APA StyleKersten, D. J. C., & Lutz, M. (2025). The Missing Structures of Pasteur’s Aspartates. Crystals, 15(6), 521. https://doi.org/10.3390/cryst15060521







