Abstract
The emergence of artificial neural networks and the widespread application of process analytical technology (PAT) have founded a robust foundation for neural network applications in crystallization research. This study investigated benzophenone antisolvent crystallization kinetics through online monitoring of the crystallization process via PAT tools and kinetics fitting via neural networks. The antisolvent crystallization process was simulated by integrating network-based kinetics with population balance. The findings suggest that benzophenone exhibits size-independent growth in water–methanol systems. The neural network-based model demonstrates improved performance (a consistent 50 ± 5% enhancement in prediction accuracy (R2) over empirical kinetic models) in predicting crystallization kinetics. Furthermore, the network-based process model achieved remarkable agreement with the experimental crystal size distribution, showing smaller deviation (1.1%), less than that of traditional empirical models (5.29%). This work proposed a robust crystallization process model combining PAT tools and artificial neural networks, enabling rapid crystallization kinetics determination and accurate process simulations.
1. Introduction
Crystallization is an important operation for separation and purification in chemical production processes [1,2,3,4,5]. Among the typical crystallization processes, antisolvent crystallization is one of the most popular crystallization techniques in the pharmaceutical industry [6,7], which works particularly well for substances that are heat-sensitive or have a small temperature effect on solubility [2,8].
The development and optimization of the antisolvent crystallization process depend on the understanding of the crystallization kinetics, which is significantly important for the control of crystal polymorphism, the regulation of crystal morphology, the management of particle size, and the preparation of eutectic crystals [4,6,8,9,10]. In practice, extensive trial-and-error experiments are often conducted to obtain accurate growth and nucleation kinetics data [11]. For complex antisolvent crystallization systems, constructing an accurate kinetic model can be very time-consuming.
The current widespread use of process analytical technology (PAT) tools provides a remarkable foundation in rapidly acquiring sufficient data for kinetic studies [12]. For example, ATR-FTIR spectroscopy can collect information on the solution concentration and thus monitor the supersaturation online, while EasyViewer from Mettler Toledo can provide real-time particle size distributions during the crystallization process. Such PAT tools facilitate rapid data collections for the kinetics study of anticrystallization processes.
For kinetics modeling, moment-based methods are widely used according to the population balance to give traditional empirical models of crystallization processes. However, the accuracy of empirical kinetic models is usually not good enough due to the unmatured mechanism theories of both nucleation and crystal growth.
In recent years, artificial neural networks have been increasingly applied in the field of crystallization especially in process modeling and predictive control [13,14,15,16,17,18]. Chen et al.’s physics-informed deep learning framework successfully solved population balance model problems for particle distribution prediction undergoing aggregation and breakage [14]. Wu’s work further demonstrated PINNs’ effectiveness in identifying the growth parameters in continuous oscillatory baffle crystallizers [16]. Wu, Zheng et al. constructed a physical information recurrent neural network (PIRNN), recurrent neural network (RNN), and autoencoder recurrent neural network (AERNN) model, respectively, and designed a predictive control strategy based on the above models for the batch cooling crystallization process [15,17]. Artificial neural networks, as a data-driven information mining technique [19], can approximate any continuous function [20] and thus may be a potential substitute for the empirical kinetic equations when sufficient data are available. However, there is little literature about the application of neural networks on crystallization kinetics, especially for volume-varied antisolvent crystallization processes.
Benzophenone and its derivatives are widely employed in pharmaceuticals, organic light-emitting materials, novel photo initiators, coatings, biomaterials, and UV filter applications [21,22,23,24,25,26,27]. Given that the crystal morphology of benzophenone in a methanol–water mixture is well suited for crystal size distribution analysis using PAT tools and benzophenone’s solubility in different solvents varies rather widely [28,29,30,31], antisolvent crystallization with methanol as the good solvent and water as the antisolvent can be considered an appropriate approach.
The goal of this study is to discover the possibility of neural networks to replace empirical kinetic equations in antisolvent crystallization process simulation. Firstly, PAT tools are utilized to monitor the solution concentration and crystal size distribution during antisolvent crystallization, providing original experimental data. Subsequently, the original experimental data are correlated according to empirical kinetic models by using the method of moments. Sufficient process data acquired by PAT tools are used to train neural networks to form a specific neural network-based kinetic model, exhibiting ability to predict crystallization kinetics, i.e., nucleation and crystal growth rates. Finally, process simulations using the empirical kinetic equations with fitted parameters and the trained neural network-based kinetic model will be run separately. The results will be compared in a validation antisolvent crystallization process of benzophenone to evaluate the accuracy of both models. Figure 1 describes the framework for the construction and validation of the neural network-based kinetic model for the antisolvent crystallization of benzophenone.
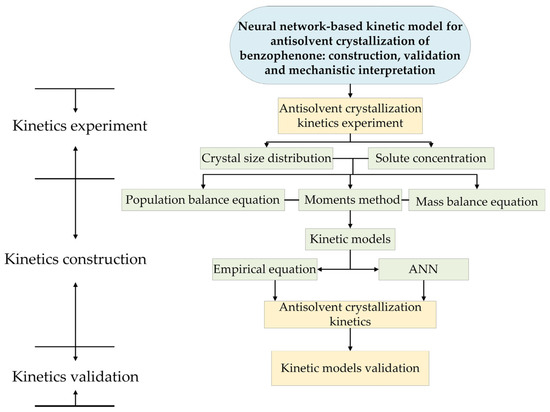
Figure 1.
Framework for the construction and validation of the neural network-based kinetic model for antisolvent crystallization of benzophenone.
2. Experimental Section
2.1. Materials
Benzophenone was purchased from Tianjin Heowns Biochemical Technology Co., Ltd. (Tianjin, China) with 99% purity. Methanol was obtained from Tianjin Kermel Chemical Reagent Co., Ltd. (Tianjin, China) with 99.5% purity. All chemicals were used without being further purified.
2.2. Antisolvent Crystallization Kinetics Experiment
In this study, methanol is the good solvent and water is the antisolvent. Figure 2 depicts the equipment used in the antisolvent crystallization experiments. An unsaturated solution of benzophenone in methanol with a certain concentration was filled in a jacked crystallizer. The antisolvent, water, was added into the crystallizer by a peristaltic pump at adjustable rates. The mixture was stirred using a two-blade paddle to make it homogeneous. When the solution became supersaturated, a certain amount of benzophenone crystals with size ranging from 150 to 250 μm were introduced as seeds. After the addition of antisolvent finished, stirring continued for another 30 min to consume the residue supersaturation before completing the experiment.
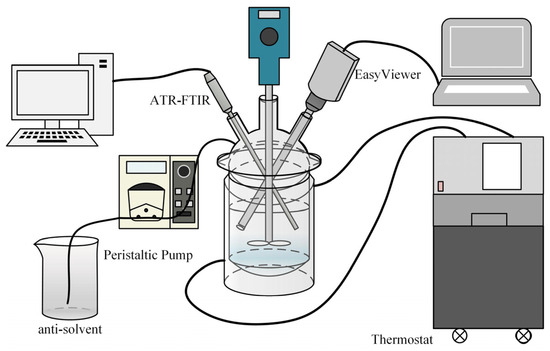
Figure 2.
The setup of antisolvent crystallization experiments of benzophenone.
During the crystallization process, the concentration of the solution was measured online by ATR-FTIR spectroscopy (React IR 15, Mettler Toledo, Redmond, WA, USA) based on the pre-determined standard curve and solubility curves (SI, Figures S2 and S3). The morphology and crystal size distribution of the crystals precipitated in the solution were monitored by EasyViewer (EasyViewer 400, Mettler Toledo, Giessen, Germany). Both ATR tools were configured with a sampling interval of 30 s. A thermostat was used to keep the entire crystallization system at 20 °C.
A total of 33 antisolvent crystallization kinetics experiments of benzophenone were conducted, from which 26 valid datasets were obtained after rigorous screening (the experimental parameters are detailed in SI, Table S1). With a constant total antisolvent mass (91 g), the three additive rates of antisolvent in Table S1 yielded inversely proportional experimental durations, consequently generating three datasets of varying sizes. To systematically evaluate kinetic model performance, the 26 datasets were partitioned as follows: (1) 20 randomly selected datasets were used for kinetic parameter regression and neural network training; (2) the remaining 6 datasets served as a validation set to assess the reliability of the kinetic parameters and the generalization capability of the trained neural network.
3. Model Theory
3.1. Population Balance Equation
The population balance equation explaining the antisolvent crystallization process with seeds at constant temperature is given by Equation (1) when ignoring primary nucleation, agglomeration, and breakage [32,33].
where L is the chord length of crystals, μm; n is the crystal particle density function, #/(μm*mL); G is the crystal growth rate, μm/min. V is the volume of the ternary mixed solution, mL.
3.2. Method of Moments
The moments are defined as follows [32,33,34,35]:
where Li is the chord length at the midpoint of the i-th chord length channel interval, μm; ∆Li is the length of the i-th chord length channel interval, μm; ni is the crystal particle density function within the i-th chord length channel interval, #/(μm*mL); NE is the number of chord length channels; mj is the j-th order moment, μmj.
The population balance equation can be transformed from a partial differential form to an ordinary differential form using the method of moments.
For the size-independent growth process, the moment equation is as follows.
While for a size-dependent growth process, the moment equation can be given as follows:
Combining the moment equations, kinetic experimental data can be used to solve the growth rate.
The first four moments, m0, m1, m2, and m3, represent the number of crystals per unit solution volume, the total chord length per unit solution volume, the total crystal area per unit solution volume, and the total crystal volume per unit solution volume, respectively. Using the third-order moment can calculate the mass of precipitated crystals.
where ρ is the density of the ternary mixed solution, g/mL; kv = 1 [7], since benzophenone crystals are cubic, as shown in Figure 3.

Figure 3.
Morphology of benzophenone crystals.
3.3. Mass Balance
Solute mass balance during the crystallization process
mseed is the mass of the crystal seeds, g; mcrystals is the mass of crystals precipitated during the crystallization process, g; Csolute and Msolvent are the mass concentration (g/g solvent) of the solute and the mass of the binary solvent mixture (g), respectively; the 0 in the footer represents the initial time. The solute’s mass can be used to calculate the third-order moment.
The antisolvent crystallization process considers the effect of the varying volume of the solution on the crystal size distribution. Thus, the ternary solution mixture of the crystallization process needs to perform the mass balance.
Ranti is the additive rate of antisolvent, mL/min.
By applying mass balance principles, the solute concentration data from ATR-FTIR can be quantitatively correlated with the measurements obtained by EasyViewer, producing a crystal size distribution that reflects both solution-phase concentration changes and solid-phase particulate evolution. The equations for this methodology are as follows:
where ni,easyviewer is the chord length distribution obtained by EasyViewer; Li is the chord length at the midpoint of the i-th chord length channel interval, μm; ∆Li is the length of the i-th chord length channel interval, μm; wpi is the crystal volume distribution, %; mcrystals is the mass of crystals precipitated during the crystallization process; V is the volume of the ternary mixed solution, mL.
3.4. Growth Rate
3.4.1. Size-Independent Growth
Size-independent growth indicates that the growth rate of crystals is not a function of the crystal size. Through systematic comparison between predictions from different empirical growth models and experimental growth rates, the empirical kinetic equation for the size-independent growth model is established as follows [36,37].
where Gt represents the time-dependent growth coefficient, which is equal to the growth rate when growth is independent of particle size. r is the mass ratios of antisolvent and solvent. ω is the average input agitation power [38], K is the power number, related to the type of stirrer and the Reynolds number in the crystallizer. In this work, we take K = 1. Nr is the rotational speed of the stirring paddle, rad/s; Dc is the diameter of the stirring paddle, m; kg, g, g1, and g2 are size-independent growth kinetic factors that need to be fitted. C* is the solubility of the solute in solvent mixture (g/g solution) and is calculated using the following equation: C* = 0.464e(−r/0.116) + 0.01. This expression is derived from Equation (S2) in the Supplementary Materials. ∆C is the absolute supersaturation (g/g solvent).
Bringing Equation (11) into Equation (4) and setting j = 3 yields
The size-independent growth rate at each discrete time can be calculated from the experimental data and Equation (14) using the third moment (j = 3). This approach avoids potential mistakes in crystal size distribution data due to the accuracy of measurements. The kinetics parameters of the time-independent growth rate function can be fitted by Equation (11).
3.4.2. Size-Dependent Growth
For size-dependent growth, the growth rate varies for crystals with different sizes at the same time. The crystal growth rate is expressed as the product of the time-dependent growth coefficient and crystal size-dependent function.
Various empirical size-dependent growth models are listed below.
Bransom (BR) model [39]:
Canning and Randolph (CR) model [40]:
Mydlarz and Joenes (MJ2) model [41]:
Mydlarz and Jones (MJ3) model [42]:
where a, b are the kinetic parameters in the size-dependent growth rate function.
The following equations are obtained by merging the size-dependent growth rate models mentioned above into Equation (5) when setting j to 3.
BR model:
CR model:
MJ2 model:
MJ3 model:
The experimental data can be used to fit the kinetic parameters in Equations (11), (16)–(19). Similar to size-independent growth, the growth rate is determined using the third-order moments (j = 3), avoiding measurement errors that come with crystal size distribution data.
3.5. Nucleation Rate
The nucleation rate is the change in the number of crystals per unit volume of the solution [37].
where B is the nucleation rate, #/(mL min). The following empirical kinetic equation for the nucleation rate was adopted for antisolvent crystallization [36].
where S is the supersaturation; ω is the average input agitation power; r is the mass ratios of antisolvent and solvent; ks, α, β, γ are the nucleation rate kinetic parameters.
3.6. Artificial Neural Network
3.6.1. Construction of Artificial Neural Network
A total of six neural networks were designed to approximate a size-independent growth rate, a nucleation rate, and the time-dependent growth coefficients associated with four different size-dependent growth models. The structure of the neural network for kinetics in this work is built as follows. There are three neurons in the input layer, which correspond to the input variables’ dimensions (ω, r, and ∆C or S); the output layer has one neuron, which corresponds to the output variable (G, Gt, and B). The network has seven hidden layers. Each of the hidden layers comprises a fully connected layer, an activation function, and a dropout to mitigate overfitting. The number of neurons in these fully connected layers follows a symmetrical spindle-shaped configuration: 16, 32, 64, 96, 64, 32, 16, forming a structure that increases and then decreases. The structure of the neural network is shown in Figure 4. The fork neuron represents the neuron that is randomly kicked out by the dropout.
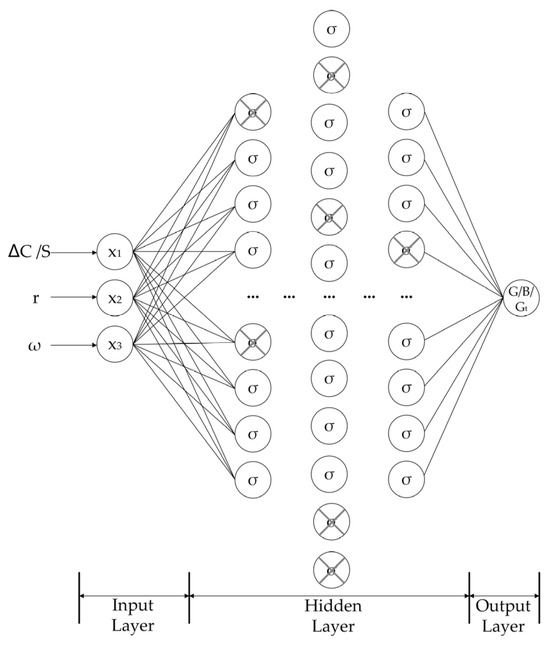
Figure 4.
The structure of the neural network.
3.6.2. Training of Artificial Neural Network
The training of artificial neural networks is essentially an optimization process that requires iterative optimization to find the most suitable neural network structure parameters. The networks of this study are trained by supervised learning. All input layer data were normalized using min–max scaling to the [0, 1] range. This preprocessing approach not only accelerates network convergence but also inherently mitigates the amplitude impact of measurement noise. The output layer results were inversely transformed for loss function computation. As illustrated in Equation (27), loss function is formulated as a mean squared error (MSE) between the output of a neural network and its corresponding ground truth. A total of six such MSE-based loss functions are developed, corresponding, respectively, to the size-independent growth rate, the nucleation rate, and four time-dependent growth coefficients included in the size-dependent growth models. In order to minimize the loss functions, gradient optimization algorithms are used to modify the network structure parameters. The loss evolution during the training of the neural network used to approximate the time-dependent growth coefficient in the size-dependent growth model (BR model) is shown in Figure 5. It shows that the loss curve drops rapidly at the beginning, indicating good convergence. Fluctuations appear later, but the overall trend remains stable, suggesting effective model training.
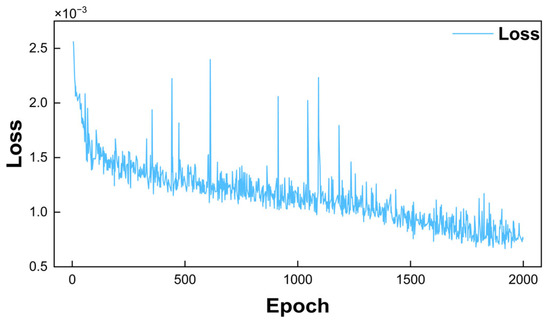
Figure 5.
Training loss of network approximating time-dependent growth coefficient (BR model).
The Python-based Pytorch library was used to build and train the neural network, and GPU acceleration was used for neural network training. The Adam algorithm from torch.optim was utilized for gradient optimization.
3.7. Parameter Fitting
3.7.1. Kinetic Parameter Fitting
To determine the kinetic parameters for size-independent growth, a gradient optimization method was used to minimize the difference between the calculated results of Equation (11) and the size-independent growth rate obtained from Equation (14).
For size-dependent growth, the gradient optimization method was also used to minimize the difference between (dm3/dt) + m3 d(lnV)/dt calculated from the experimental data and the results of Equations (20)–(23), determining the time-dependent coefficients of the growth rates. Then, using Equation (11), the kinetic parameters of the empirical crystal growth models were fitted.
Equation (24) was used to calculate the nucleation rate, and the gradient optimization method was used to minimize the differences between the nucleation rate and the result of Equation (25) calculation when determining the nucleation kinetic parameters.
3.7.2. Crystal Size Distribution Data Processing
The crystal size distribution incorporating concentration information, as calculated through Equations (9) and (10), fundamentally depends on the chord length distribution data acquired from EasyViewer measurements. To validate the reliability of CLD data obtained from EasyViewer, we conducted parallel measurements by combining online EasyViewer monitoring with offline Mastersizer 3000 during crystallization. The results demonstrate good agreement (R2 = 0.89) between the CLD-derived crystal size distribution and Malvern measurements, with detailed comparative curves and statistical analysis provided in the Supporting Materials (Figure S5 and Table S5).
Although some studies have directly used the CLD for kinetic analysis [43,44], considering the inherent characterization differences between the CLD and actual CSD, we applied gradient optimization to the CLD data, which included solution concentration information. The reconstructed crystal size distribution (CSD) was further constrained by embedding physical information such as the non-negativity and monotonicity of each moment into a composite objective function, thereby ensuring the final crystal size distribution simultaneously satisfies both experimental measurements and physical information.
3.7.3. Fitting the Change Rate of Crystal Size Distribution in Process Simulation
To optimize the change in the CSD, a gradient optimization method was employed, minimizing the two objectives and one constraint condition: (1) objective one: the difference between the third-order moment calculated from the crystal size distribution using the method of moments and the third-order moment that was obtained from the change rate of the third-order moment as defined by Equations (14) and (20)–(23); (2) objective two: the difference between the final experimental crystal size distribution when the antisolvent addition finished and that calculated from the crystal size distribution at the next time step; and (3) constraint condition: the concentration calculated from the crystal size distribution and mass balance must be larger than or equal to the solubility.
3.8. Process Simulation
Kinetic experimental data were used as the validation set for network training and kinetic parameters fitting. The initial conditions for process simulation such as the crystal size distribution, solution concentration, and solution volume at the moment of crystal seeding were first introduced.
By applying the method of moments and mass balance, the change rates for both the concentration and solution volume were determined.
The size-independent versus size-dependent growth rates were obtained using either an empirical kinetic model containing the fitted parameters or a trained neural network containing kinetic information. The change rate of the third-order moment (dm3/dt) and the third-order moment at the next time step were calculated. The change rate of the crystal size distribution (dn/dt) was determined by the fitting method described in Section 3.7.3. The transformed population balance equations (ODEs) were solved using an ODE solver, giving the crystal size distribution, solution concentration, and solution volume at the next time step. This iterative process continued until all the discrete time points were processed. The detailed simulation workflow is shown in Figure 6.
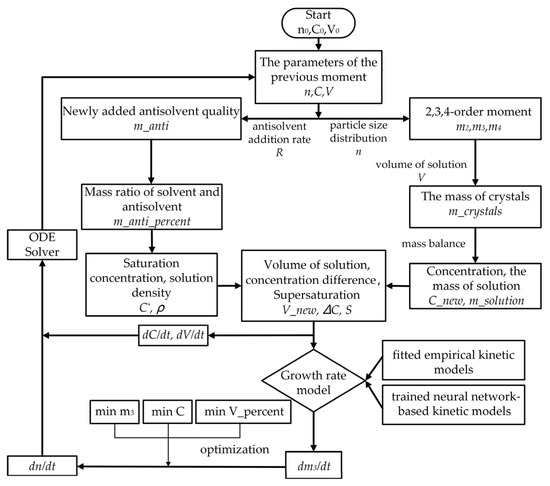
Figure 6.
Flowchart of the kinetic simulation.
4. Results and Discussion
4.1. Kinetic Fitting
4.1.1. Fitting Results of Growth Rate
- (1)
- Size-dependent growth
Figure 7 shows the fitting of the experimental growth rates (blue points, 20 sets grouped in rectangles) using the BR model (Equation (20), red lines). The experimental growth rates were calculated using the experimental crystal size distribution and solution volume data according to Section 3.4.2. The fitting results show good agreement with the experimental data with an R2 close to 1, indicating the accuracy of the calculated growth rates and model parameters.
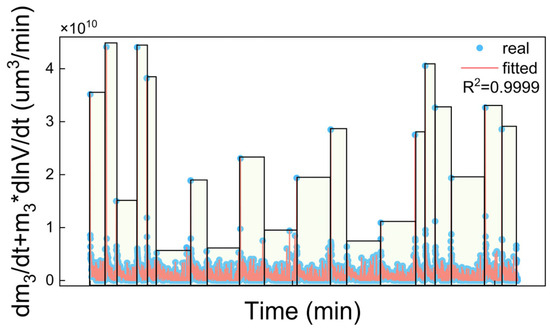
Figure 7.
BR growth model fitting results using 20 sets of experimental data.
In each set of data, the curves in Figure 7 exhibited a rapid declining to zero. The time span varied due to different rates of antisolvent addition. Figure 8 demonstrates the m3 results under different antisolvent addition rates. It shows that m3 increased rapidly when the crystallization began but the increasing rate dropped quickly during the antisolvent crystallization. This agrees with the curve trends in Figure 7 due to the change rate of m3 (dm3/dt) being positively correlated to the growth rate. Moreover, the antisolvent addition rate (R) is positively correlated with the 3-order moment (m3). Under conditions of constant total antisolvent dosage, a higher addition rate leads to increased antisolvent input per unit time, which significantly elevates the system supersaturation, and this enhanced supersaturation promotes the nucleation and growth process, resulting in an increase in the m3 value.
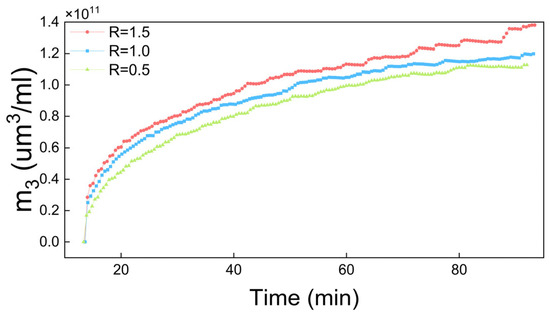
Figure 8.
Third-order moments under three different antisolvent addition rates.
Similar fits were carried out using the other three size-dependent growth models, all of which showed good agreement with the data, similar to the BR model, which also performed excellently. The calculated dm3/dt + m3 dlnV/dt values from Equations (20)–(23) were compared with the experimental measurements to obtain the time-dependent growth coefficients (Gt) and kinetic parameters through gradient optimization. The fitted kinetic parameters in the size-dependent growth models are shown in Table 1.

Table 1.
Fitting results of the kinetic parameters.
Figure 9 compares the fitting of Gt by the empirical growth kinetics and neural network. Gt_BR_experimental represents the Gt fitted from the experimental data using BR model fitting (Equation (20)). Gt_BR_num is the numerical calculated Gt using the empirical kinetic equation (Equation (11)) in which the parameters (listed in Table 1) were obtained by fitting Equation (11) to the Gt_BR_experimental results. Gt_BR_net is the predicted Gt by the trained neural network, which is used to approximate the time-dependent growth coefficients associated with the size-dependent growth model (BR model). The kinetic parameters fitted from 20 sets of experimental data are listed in Table 1 and the R2, evaluated using 20 sets and a single set of experimental data, for both the empirical kinetic model and neural network-based model are compared in Table 2. The MAE and RMSE are listed in Table S2 (SI). Such fittings based on the other size-dependent growth models are similar to those of the BR model and the fitting results are also listed in Table 1 and Table 2. A comprehensive evaluation of the statistical metrics (R2 in Table 2; MAE and RMSE in Table S2, SI) shows that the neural network-based model achieves significantly better agreement with 20 sets of experimental data compared to the empirical kinetic models. This reveals the robustness of the neural network-based kinetic model and the potential of its applications in crystallization process simulations. By the way, the neural network-based model and the empirical kinetic model have similar fitted results, when fitting with one set of experimental data, according to the R2 value and the (b) of Figure 9, indicating that both models are capable of effectively capturing the growth behavior in individual experiments.
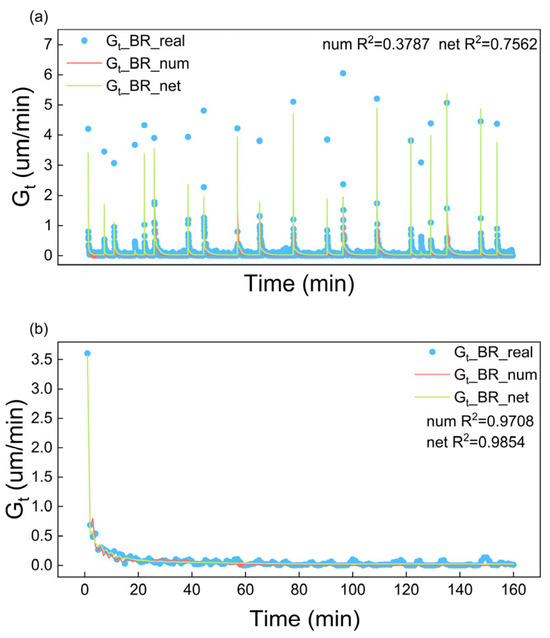
Figure 9.
Fitting of Gt based on BR model by both empirical growth kinetics and artificial neural network-based kinetics using (a) 20 sets of experimental data and (b) 1 set of experimental data.

Table 2.
R2 values of the kinetic models.
- (2)
- Size-independent growth
Similarly, for the size-independent growth mechanism, Gt (=G) was obtained from the experimental CSD according to Equation (14). Subsequently, the empirical kinetic model (Equation (11)) was fitted to give the parameters (Table 1) and the neural network-based growth model was trained. The R2 for both the empirical kinetic model and neural network-based growth model are listed in Table 2 and the MAE and RMSE are listed in Table S2 (SI).
For size-independent growth kinetics modeling, kinetic parameter fitting in empirical kinetic models (3–5 min) shows comparable computational requirements to neural network training (12–15 min) when considering the entire modeling process. While the large parameter space of the neural network increases its training cost, the empirical kinetic model requires additional time for equation form selection (e.g., power-law vs. exponential functions). The overall computational cost is therefore similar, although neural networks have a slightly higher computational cost compared to empirical kinetic models.
Figure 10 illustrates the comparison of experimental growth rates to those being calculated according to both the fitted empirical kinetic model and trained neural network-based growth model. The comparison is performed under two cases: using 20 sets of experimental data and using a single set of experimental data. The figure and R2 reveal that the neural network-based kinetic model is superior to the empirical size-independent growth model, especially the fitting with 20 sets of experimental data. The neural network-based kinetic model and empirical size-independent growth model demonstrated comparable fitting accuracy with single-dataset training, while the former showed superior performance when extended to 20 datasets, revealing the empirical model’s limitations in generalizability.
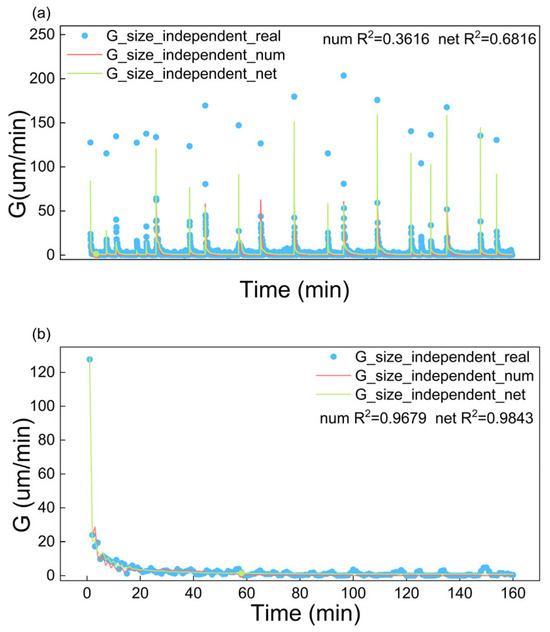
Figure 10.
Fitting of Gt based on size-independent model by both empirical growth kinetics and neural network-based kinetics using (a) 20 sets of experimental data and (b) 1 set of experimental data.
4.1.2. Fitting Results of Nucleation Rate
Figure 11 shows the fitting of the experimental nucleation rates according to the empirical nucleation kinetics and neural network-based nucleation model. The experimental nucleation rates calculated using Equation (24) (blue scatters) exhibited significant variability, primarily attributed to the measurement errors inherent in the instruments of EasyViewer. The nucleation rate kinetic parameters (listed in Table 1) were fitted by substituting the experimentally calculated nucleation rates, S, r, and ω, into Equation (25). According to the fitting R2, MAE, and RMSE (Table 2 and Table S2, SI), both the empirical nucleation kinetic model and neural network-based model gave marked deviations from the experimental observations. Despite extensive efforts to test numerous empirical kinetic equations, it is hard to obtain perfect fittings with experimental data. This might rely on a persistent limitation in traditional kinetic studies that must give an explicit function. In contrast, the neural network-based that do not require time-consuming determination of the functional form are more advantageous.
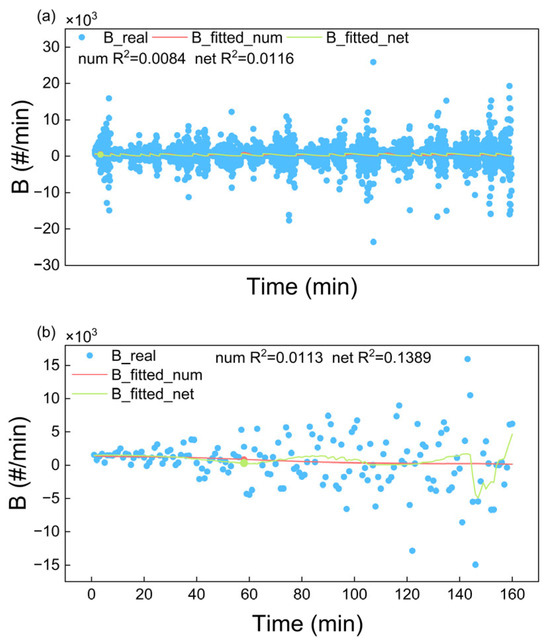
Figure 11.
Fitting of nucleation rates by using both empirical nucleation kinetics and neural network-based kinetics using (a) 20 sets of experimental data and (b) 1 set of experimental data.
4.2. The Results of Process Simulation
To validate the kinetics, both the fitted empirical kinetic models and trained neural network-based kinetic models were employed to simulate the whole antisolvent crystallization process of benzophenone. As shown in Figure 12, each category—empirical and neural network-based—consists of five individual models. Throughout the entire simulation process, the simulation results of the concentration, solution volume, and crystal size distribution predicted by four models—size-independent and size-dependent (BR), each with empirical and neural network-based kinetics—were compared with the validation experiment results at each discrete time point, as shown in Figure 13, Figure 14 and Figure 15. The corresponding R2 values, MAE, and RMSE, which quantify the agreement between the simulation and experimental results, are summarized in Table 3, Table S3 (SI), and Table S4 (SI). The other size-dependent models’ simulation results can be found in the Supplementary Materials.
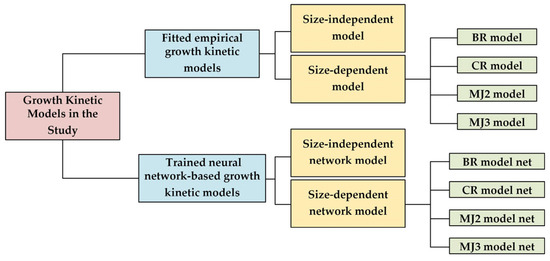
Figure 12.
The growth kinetic models in this study.
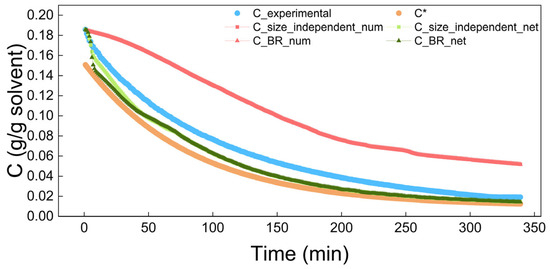
Figure 13.
Comparison of the concentration in the size-independent and size-dependent (BR) process simulations.
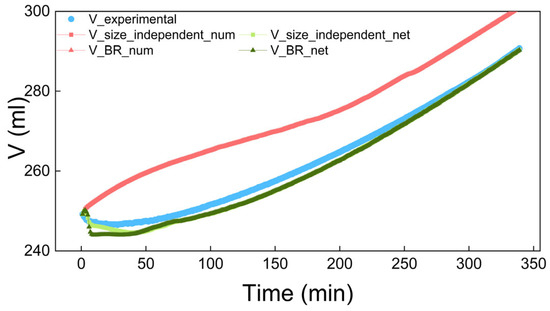
Figure 14.
The solution volume in the size-independent and size-dependent (BR) process simulations.
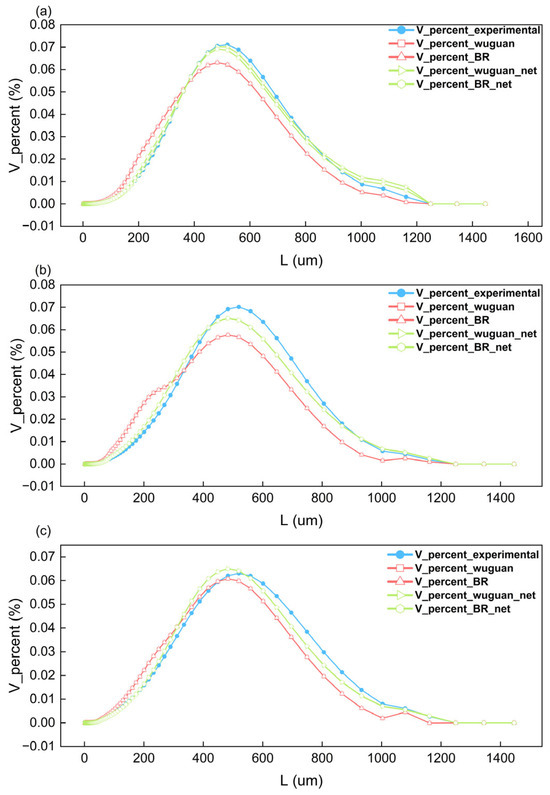
Figure 15.
The crystal size distribution in the size-independent and size-dependent (BR) process simulations at 15 min (a), 90 min (b), and 180 min (c).

Table 3.
R2 values of process simulation results.
In Figure 13 and Figure 14, the blue scatter plots represent the experimental data for the concentration and solution volume, respectively, while the orange scatter plot in Figure 13 indicates solubility. The area between the blue scatter plot and orange scatter plot is the metastable zone in Figure 13. The red and green dotted lines represent the simulation results based on empirical and neural network-based kinetics. Notably, the red dotted lines almost completely overlap, while the green dotted lines closely match both the experimental data and each other, though with slightly less overlap than the red lines.
In Figure 15, the blue dotted line graph depicts the crystal size distribution during the experimental process; the red dotted line graph depicts the crystal size distribution results from the kinetic simulation embedded with the empirical kinetic equation; and the green dotted line graph represents the crystal size distribution obtained from the kinetic simulation with the neural network embedded.
The simulation results show that the growth rates predicted by the neural network are more accurate than those calculated using empirical kinetic equations. As a result, the neural network’s kinetic simulation results match the experimental results better. This indicates that in the study of crystallization kinetics, neural networks, with their advantages of accuracy, versatility, and robustness, can replace empirical kinetic equations. Furthermore, the results in the figure show that whether there is size-independent or size-dependent growth, the solution concentration, solution volume, and crystal size distribution obtained from kinetic simulations are very similar. This implies that the antisolvent crystallization of benzophenone in the water–methanol system may be dominated by size-independent growth.
5. Conclusions
Benzophenone was employed as the model substance to conduct a kinetics study of the antisolvent crystallization process, involving both traditional empirical kinetic models and neural network-based models.
PAT tools such as ATR-FTIR and EasyViewer were used to acquire data on the solution concentration and crystal size distribution during a series of antisolvent crystallization experiments. Based on the calibration curves, ATR-FTIR was found to be applicable to provide rapid online monitoring of the solution concentration (thus supersaturation) and solution density (thus solution volume). However, the direct results of EasyViewer are not precise enough to determine the CSD. The raw CSD was modified before being applied to kinetic study by an optimization process that contains two objectives and constraint of mass balance.
Twenty sets of kinetic experimental data were utilized to fit the empirical kinetic models, including four size-dependent growth equations, one size-independent growth equation, and one nucleation equation by using the gradient optimization method. Using the same data as the training set, this study also built neural networks based on the Pytorch library in Python 3.9.18 (PyCharm 2023.2.3), obtaining one trained nucleation rate network and five trained growth rate networks. By comparing the experimental growth rate and nucleation rate to those calculated by the models, it was discovered that the neural network-based kinetic models were almost twice as good as the empirical kinetic models, exhibiting high accuracy, generalizability, and robustness.
The remaining kinetic experimental data were used as a validation set for process simulations. The simulation results using size-dependent and size-independent models were similar, revealing that the antisolvent crystallization process of benzophenone in the methanol–water system matches the size-independent growth mechanism. Furthermore, the neural network-based model predicted the CSD more accurately than the empirical kinetic models, with an R2 of 0.9890 versus 0.9471 in the size-independent case, enabling rapid crystallization kinetics determination and accurate process simulations. Therefore, the performance of the neural network in the process simulations supports its viability as a replacement for empirical kinetic equations.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/cryst15050464/s1. Figure S1: ATR-FTIR spectra of benzophenone in water-methanol mixture with various concentrations; Figure S2: The relationship between infrared peak height and benzophenone concentration; Figure S3: The solubility of benzophenone in different antisolvent solvent mass ratios; Figure S4: The density of saturated ternary mixture solution in different antisolvent solvent mass ratios; Figure S5 The comparative curves between the CLD-derived crystal size distribution and Malvern measurements; Figure S6: Comparison of the concentration in the size-independent and size-dependent process simulations (a) CR, (b) MJ2, (c) MJ3; Figure S7: The solution volume in the size-independent and size-dependent process simulations (a) CR, (b) MJ2, (c) MJ3; Figure S8: The crystal size distribution in the size-independent and size-dependent (CR) process simulations at (a) 15-min, (b) 90-min, (c) 80-min; Figure S9: The crystal size distribution in the size-independent and size-dependent (MJ2) process simulations at (a) 15-min, (b) 90-min, (c) 80-min; Figure S10: The crystal size distribution in the size-independent and size-dependent (MJ3) process simulations at (a) 15-min, (b) 90-min, (c) 80-min; Table S1: The process parameters in antisolvent crystallization kinetic experiment; Table S2: MAE and MRSE values of the kinetic models under 20 sets of experimental data; Table S3: MAE values of process simulation results; Table S4: RMSE values of process simulation results; Table S5: The statistical analysis metrics between the CLD-derived crystal size distribution and Malvern measurements; Equation (S1): The equation of the height of the infrared characteristic peak of the benzophenone versus concentration relationship; Equation (S2): The equation of solubility versus mass ratio of antisolvent and solvent; Equation (S3): The density of saturated ternary mixture solution versus mass ratio of antisolvent and solvent.
Author Contributions
Conceptualization, Y.D., S.X. and C.X.; methodology, Y.D., S.X. and C.X.; software, Y.D.; validation, Y.D.; formal analysis, Y.D., S.X. and C.X.; data curation, Y.D.; writing—original draft preparation, Y.D.; writing—review and editing, Y.D., S.X., C.X., Y.S., X.Z. and Y.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article; further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Mostafa Nowee, S.; Abbas, A.; Romagnoli, J.A. Antisolvent Crystallization: Model Identification, Experimental Validation and Dynamic Simulation. Chem. Eng. Sci. 2008, 63, 5457–5467. [Google Scholar] [CrossRef]
- Muthancheri, I.; Long, B.; Ryan, K.M.; Padrela, L.; Ramachandran, R. Development and Validation of a Two-Dimensional Population Balance Model for a Supercritical CO2 Antisolvent Batch Crystallization Process. Adv. Powder Technol. 2020, 31, 3191–3204. [Google Scholar] [CrossRef]
- Omar, H.M.; Rohani, S. Crystal Population Balance Formulation and Solution Methods: A Review. Cryst. Growth Des. 2017, 17, 4028–4041. [Google Scholar] [CrossRef]
- Pawar, N.; Agrawal, S.; Methekar, R. Modeling, Simulation, and Influence of Operational Parameters on Crystal Size and Morphology in Semibatch Antisolvent Crystallization of α-Lactose Monohydrate. Cryst. Growth Des. 2018, 18, 4511–4521. [Google Scholar] [CrossRef]
- Ramisetty, K.A.; Pandit, A.B.; Gogate, P.R. Ultrasound-Assisted Antisolvent Crystallization of Benzoic Acid: Effect of Process Variables Supported by Theoretical Simulations. Ind. Eng. Chem. Res. 2013, 52, 17573–17582. [Google Scholar] [CrossRef]
- Jia, S.; Yang, P.; Gao, Z.; Li, Z.; Fang, C.; Gong, J. Recent Progress in Antisolvent Crystallization. Cryst. Eng. Commun. 2022, 24, 3122–3135. [Google Scholar] [CrossRef]
- Abbas, A.; Romagnoli, J.; Widenski, D. Modeling of Crystallization Processes. In Process Systems Engineering; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2010; pp. 239–285. ISBN 978-3-527-63120-9. [Google Scholar]
- Rosenbaum, T.; Tan, L.; Dummeldinger, M.; Mitchell, N.; Engstrom, J. Population Balance Modeling To Predict Particle Size Distribution upon Scale-Up of a Combined Antisolvent and Cooling Crystallization of an Active Pharmaceutical Ingredient. Org. Process Res. Dev. 2019, 23, 2666–2677. [Google Scholar] [CrossRef]
- Kumar, R.; Thakur, A.K.; Banerjee, N.; Kumar, A.; Gaurav, G.K.; Arya, R.K. Liquid Antisolvent Crystallization of Pharmaceutical Compounds: Current Status and Future Perspectives. Drug Deliv. Transl. Res. 2023, 13, 400–418. [Google Scholar] [CrossRef]
- Orehek, J.; Češnovar, M.; Teslić, D.; Likozar, B. Mechanistic Crystal Size Distribution (CSD)-Based Modelling of Continuous Antisolvent Crystallization of Benzoic Acid. Chem. Eng. Res. Des. 2021, 170, 256–269. [Google Scholar] [CrossRef]
- Zhou, G.X.; Fujiwara, M.; Woo, X.Y.; Rusli, E.; Tung, H.-H.; Starbuck, C.; Davidson, O.; Ge, Z.; Braatz, R.D. Direct Design of Pharmaceutical Antisolvent Crystallization through Concentration Control. Cryst. Growth Des. 2006, 6, 892–898. [Google Scholar] [CrossRef]
- Trampuž, M.; Teslić, D.; Likozar, B. Process Analytical Technology-Based (PAT) Model Simulations of a Combined Cooling, Seeded and Antisolvent Crystallization of an Active Pharmaceutical Ingredient (API). Powder Technol. 2020, 366, 873–890. [Google Scholar] [CrossRef]
- Lima, F.A.R.D.; Rebello, C.M.; Costa, E.A.; Santana, V.V.; Moares, M.G.F.d.; Barreto, A.G.; Secchi, A.R.; Souza, M.B.d.; Nogueira, I.B.R. Improved Modeling of Crystallization Processes by Universal Differential Equations. Chem. Eng. Res. Des. 2023, 200, 538–549. [Google Scholar] [CrossRef]
- Chen, X.; Wang, L.G.; Meng, F.; Luo, Z.-H. Physics-Informed Deep Learning for Modelling Particle Aggregation and Breakage Processes. Chem. Eng. J. 2021, 426, 131220. [Google Scholar] [CrossRef]
- Wu, G.; Yion, W.T.G.; Dang, K.L.N.Q.; Wu, Z. Physics-Informed Machine Learning for MPC: Application to a Batch Crystallization Process. Chem. Eng. Res. Des. 2023, 192, 556–569. [Google Scholar] [CrossRef]
- Wu, S.; Xia, H. Parameter Identification of Multi-Dimensional PBE Growth Model Based on PINN. In Proceedings of the 2024 43rd Chinese Control Conference (CCC), Kunming, China, 28–31 July 2024; pp. 1372–1377. [Google Scholar]
- Zheng, Y.; Wang, X.; Wu, Z. Machine Learning Modeling and Predictive Control of the Batch Crystallization Process. Ind. Eng. Chem. Res. 2022, 61, 5578–5592. [Google Scholar] [CrossRef]
- Lima, F.A.R.D.; de Moraes, M.G.F.; Barreto, A.G.; Secchi, A.R.; Grover, M.A.; de Souza, M.B. Applications of Machine Learning for Modeling and Advanced Control of Crystallization Processes: Developments and Perspectives. Digit. Chem. Eng. 2025, 14, 100208. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, Y.; Zhang, H. Recent Advances in Stochastic Gradient Descent in Deep Learning. Mathematics 2023, 11, 682. [Google Scholar] [CrossRef]
- Ojha, V.K.; Abraham, A.; Snášel, V. Metaheuristic Design of Feedforward Neural Networks: A Review of Two Decades of Research. Eng. Appl. Artif. Intell. 2017, 60, 97–116. [Google Scholar] [CrossRef]
- Blazevicius, D.; Grigalevicius, S. A Review of Benzophenone-Based Derivatives for Organic Light-Emitting Diodes. Nanomaterials 2024, 14, 356. [Google Scholar] [CrossRef]
- Dorman, G.; Prestwich, G.D. Benzophenone Photophores in Biochemistry. Biochemistry 1994, 33, 5661–5673. [Google Scholar] [CrossRef]
- Surana, K.; Chaudhary, B.; Diwaker, M.; Sharma, S. Benzophenone: A Ubiquitous Scaffold in Medicinal Chemistry. Med. Chem. Commun. 2018, 9, 1803–1817. [Google Scholar] [CrossRef] [PubMed]
- Heurung, A.R.; Raju, S.I.; Warshaw, E.M. Benzophenones. Dermatitis 2014, 25, 3–10. [Google Scholar] [CrossRef] [PubMed]
- Boscá, F.; Miranda, M.A. New Trends in Photobiology (Invited Review) Photosensitizing Drugs Containing the Benzophenone Chromophore. J. Photochem. Photobiol. B Biol. 1998, 43, 1–26. [Google Scholar] [CrossRef]
- Zhao, W.; He, Z.; Lam, J.W.Y.; Peng, Q.; Ma, H.; Shuai, Z.; Bai, G.; Hao, J.; Tang, B.Z. Rational Molecular Design for Achieving Persistent and Efficient Pure Organic Room-Temperature Phosphorescence. Chem 2016, 1, 592–602. [Google Scholar] [CrossRef]
- Zhang, B.; Song, L.; Feng, C.; Tian, W. Study on Synthesis, Optical Properties and Application of Benzophenone Derivatives. Chem. Sel. 2022, 7, e202203948. [Google Scholar] [CrossRef]
- Ouyang, J.; Na, B.; Xiong, G.; Xu, L.; Jin, T. Corrigendum to “Determination of Solubility and Thermodynamic Properties of Benzophenone in Different Pure Solvents. J. Chem. Eng. Data 2018, 63, 4809–4810. [Google Scholar] [CrossRef]
- Ouyang, J.; Na, B.; Xiong, G.; Xu, L.; Jin, T. Determination of Solubility and Thermodynamic Properties of Benzophenone in Different Pure Solvents. J. Chem. Eng. Data 2018, 63, 1833–1840. [Google Scholar] [CrossRef]
- Azizian, S.; Haydarpour, A. Solubility of Benzophenone in Binary Alkane + Carbon Tetrachloride Solvent Mixtures. J. Chem. Eng. Data 2003, 48, 1476–1478. [Google Scholar] [CrossRef]
- Ouyang, J.; Liu, L.; Zhou, L.; Liu, Z.; Li, Y.; Zhang, C. Solubility, Dissolution Thermodynamics, Hansen Solubility Parameter and Molecular Simulation of 4-Chlorobenzophenone with Different Solvents. J. Mol. Liq. 2022, 360, 119438. [Google Scholar] [CrossRef]
- Hulburt, H.M.; Katz, S. Some Problems in Particle Technology: A Statistical Mechanical Formulation. Chem. Eng. Sci. 1964, 19, 555–574. [Google Scholar] [CrossRef]
- Marchisio, D.L.; Pikturna, J.T.; Fox, R.O.; Vigil, R.D.; Barresi, A.A. Quadrature Method of Moments for Population-Balance Equations. AIChE J. 2003, 49, 1266–1276. [Google Scholar] [CrossRef]
- McGraw, R. Description of Aerosol Dynamics by the Quadrature Method of Moments. Aerosol Sci. Technol. 1997, 27, 255–265. [Google Scholar] [CrossRef]
- Trifkovic, M.; Sheikhzadeh, M.; Rohani, S. Kinetics Estimation and Single and Multi-Objective Optimization of a Seeded, Anti-Solvent, Isothermal Batch Crystallizer. Ind. Eng. Chem. Res. 2008, 47, 1586–1595. [Google Scholar] [CrossRef]
- Ashraf, A.B.; Rao, C.S. Multiobjective Temperature Trajectory Optimization for Unseeded Batch Cooling Crystallization of Aspirin. Comput. Chem. Eng. 2022, 160, 107704. [Google Scholar] [CrossRef]
- Widenski, D.J.; Abbas, A.; Romagnoli, J.A. Use of Predictive Solubility Models for Isothermal Antisolvent Crystallization Modeling and Optimization. Ind. Eng. Chem. Res. 2011, 50, 8304–8313. [Google Scholar] [CrossRef]
- Liu, P.; Yang, L.; Ma, Y.; Zhang, Y.; Wang, H.; Cheng, J.; Yang, C. Continuous Antisolvent Crystallization of L-Histidine: Impact of Process Parameters and Kinetic Estimation. Ind. Eng. Chem. Res. 2024, 63, 2831–2841. [Google Scholar] [CrossRef]
- Bransom, S.H. Factors in the Design of Continuous Crystallizer. Br. Chem. Eng. 1960, 5, 838–843. [Google Scholar]
- Canning, T.F.; Randolph, A.D. Some Aspects of Crystallization Theory: Systems That Violate McCabe’s Delta L Law. AIChE J. 1967, 13, 5–10. [Google Scholar] [CrossRef]
- Mydlarz, J.; Jones, A.G. On Modelling the Size-Dependent Growth Rate of Potassium Sulphate in an Msmpr Crystallizer. Chem. Eng. Commun. 1990, 90, 47–56. [Google Scholar] [CrossRef]
- Mydlarz, J.; Jones, A.G. On the Estimation of Size-Dependent Crystal Growth Rate Functions in MSMPR Crystallizers. Chem. Eng. J. Biochem. Eng. J. 1993, 53, 125–135. [Google Scholar] [CrossRef]
- Zhao, W.; Li, B.; Liu, S.; Deng, Y.; Zhang, R.; Jiang, Y. Kinetic Study of Complicated Anti-Solvent and Cooling Crystallization of Disodium 5′-Ribonucleotide. Particuology 2023, 73, 103–112. [Google Scholar] [CrossRef]
- Trifkovic, M.; Sheikhzadeh, M.; Rohani, S. Multivariable Real-Time Optimal Control of a Cooling and Antisolvent Semibatch Crystallization Process. AIChE J. 2009, 55, 2591–2602. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).