119Sn Element-Specific Phonon Density of States of BaSnO3
Abstract
1. Introduction
2. Materials and Methods
2.1. Synthesis
2.2. Neutron Diffraction
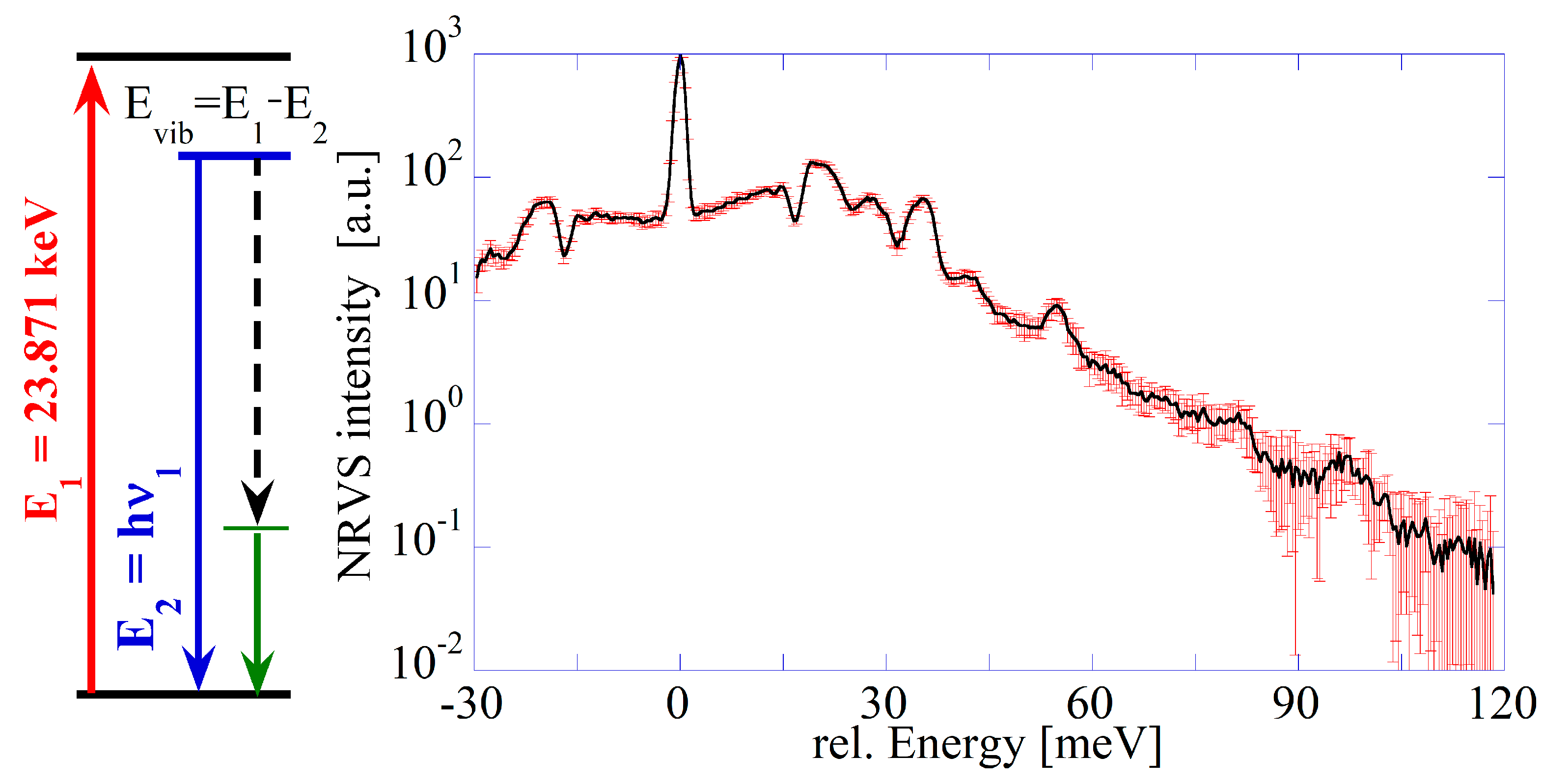
2.3. Nuclear Resonance Vibration Spectroscopy
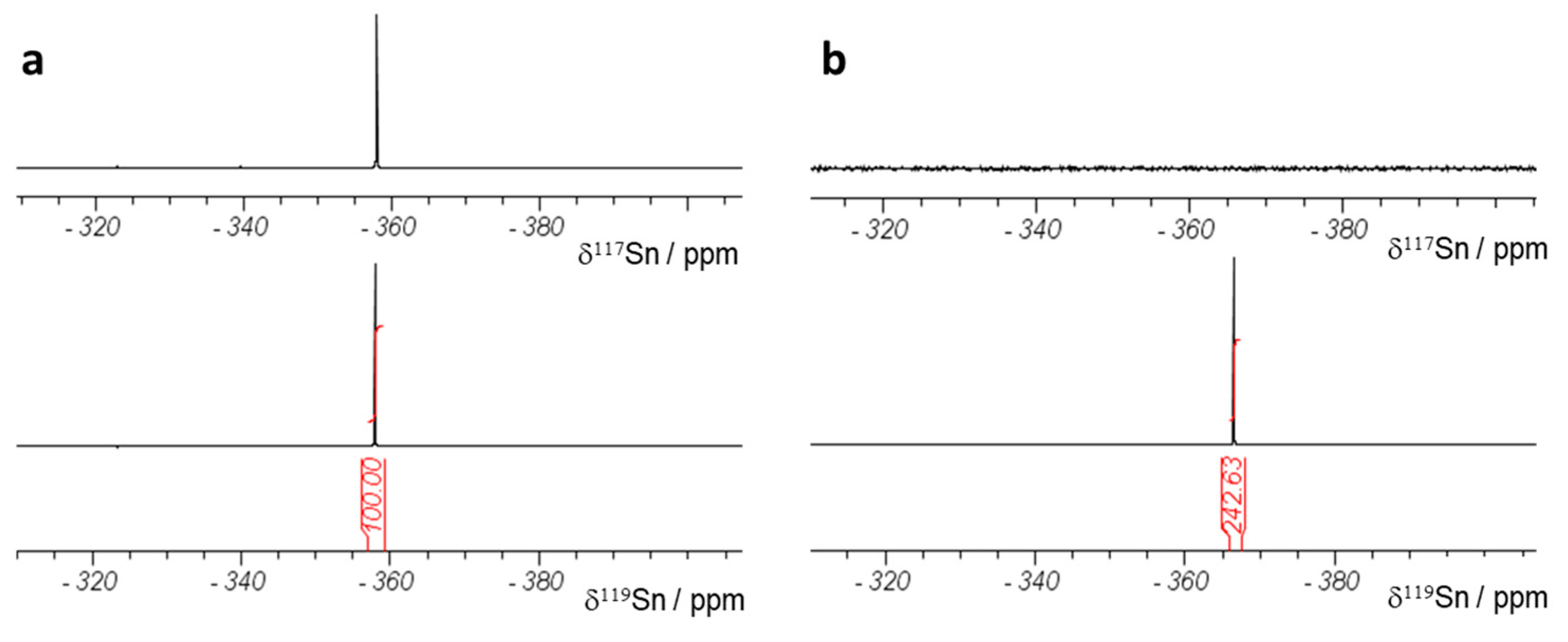
2.4. Nuclear Magnetic Resonance Spectroscopy (NMR)
2.5. Theoretical Calculation of Total and Partial Vibrational Density of States (PVDOS)
3. Results
3.1. Crystallographic Structure
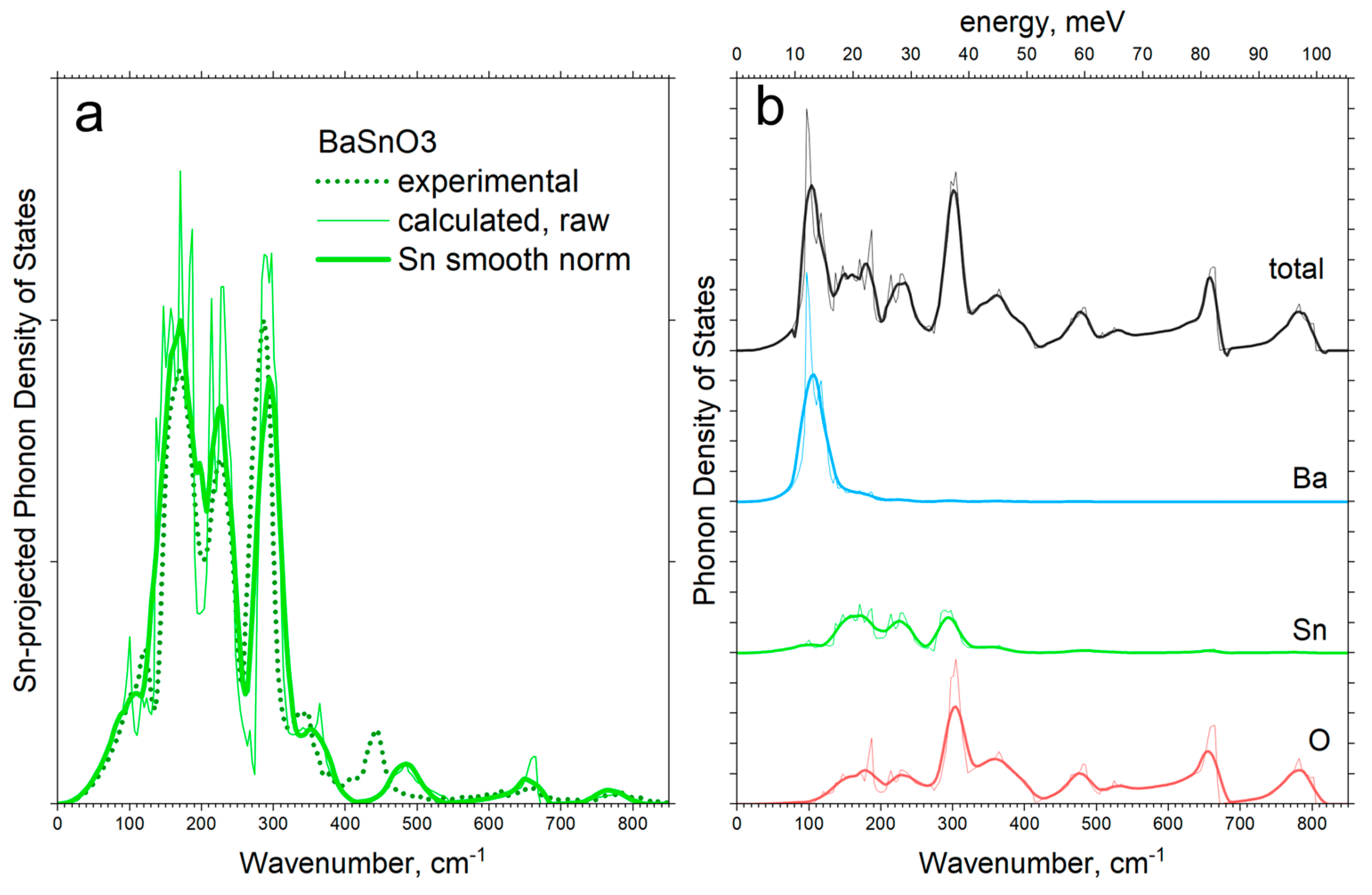
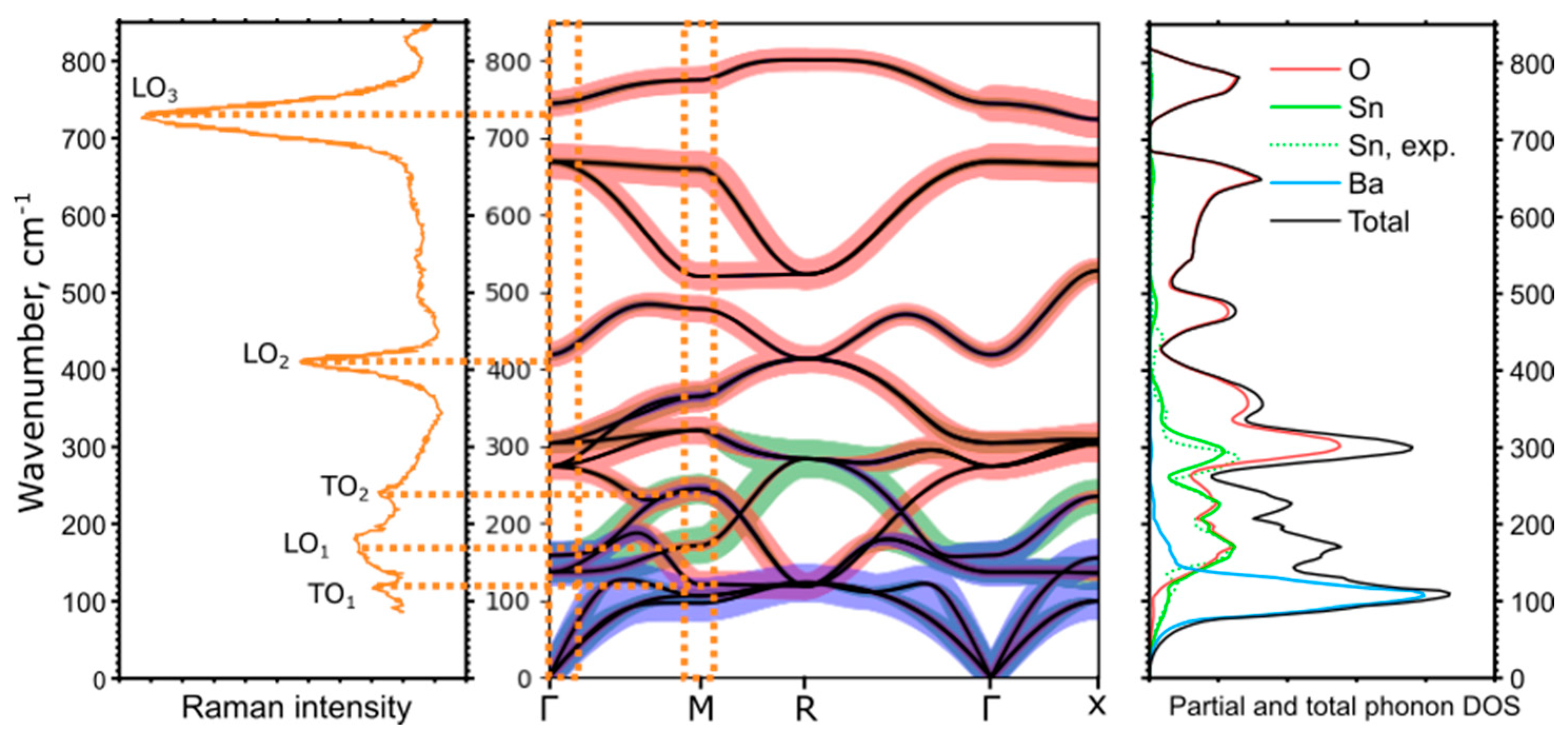
3.2. Experimental and Calculated PVDOS
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DOS | Density of States |
| NAC | Non-Analytical Contribution |
| NMR | Nuclear Magnetic Resonance |
| NRIXS | Nuclear Resonant Inelastic X-ray Scattering |
| NRVS | Nuclear Resonance Vibration Spectroscopy |
| PVDOS | Partial Vibration Density of States |
| TO | Transversal Optical |
| LO | Longitudinal Optical |
References
- Fresenius, C.R.; Bullock, J.L. A System of Instruction in Quantitative Chemical Analysis (1860); Kessinger Publishing: Whitefish, MT, USA, 1860; p. 704. [Google Scholar]
- Gordiz, K.; Muy, S.; Zeier, W.G.; Shao-Horn, Y.; Henry, A. Enhancement of ion diffusion by targeted phonon excitation. Cell Rep. Phys. Sci. 2021, 2, 100431. [Google Scholar] [CrossRef]
- Muy, S.; Schlem, R.; Shao-Horn, Y.; Zeier, W.G. Phonon–Ion Interactions: Designing Ion Mobility Based on Lattice Dynamics. Adv. Energy Mater. 2020, 11, 2002787. [Google Scholar] [CrossRef]
- Gao, Y.; Huang, J.; Cheng, J.; Bo, S.-H. Correlate phonon modes with ion transport via isotope substitution. Sci. China Chem. 2023, 66, 768–777. [Google Scholar] [CrossRef]
- Braun, A.; Chen, Q. Experimental neutron scattering evidence for proton polaron in hydrated metal oxide proton conductors. Nat. Commun. 2017, 8, 15830. [Google Scholar] [CrossRef] [PubMed]
- Chen, Q.; Braun, A.; Yoon, S.; Bagdassarov, N.; Graule, T. Effect of lattice volume and compressive strain on the conductivity of BaCeY-oxide ceramic proton conductors. J. Eur. Ceram. Soc. 2011, 31, 2657–2661. [Google Scholar] [CrossRef]
- Chen, Q.; Huang, T.-W.; Baldini, M.; Hushur, A.; Pomjakushin, V.; Clark, S.; Mao, W.L.; Manghnani, M.H.; Braun, A.; Graule, T. Effect of Compressive Strain on the Raman Modes of the Dry and Hydrated BaCe0.8Y0.2O3Proton Conductor. J. Phys. Chem. C 2011, 115, 24021–24027. [Google Scholar] [CrossRef]
- Wang, H.; Braun, A.; Cramer, S.P.; Gee, L.B.; Yoda, Y. Nuclear Resonance Vibrational Spectroscopy: A Modern Tool to Pinpoint Site-Specific Cooperative Processes. Catalysts 2021, 11, 909. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, H.; Xiao, Y.; Vogt, S.; Thauer, R.K.; Shima, S.; Volkers, P.I.; Rauchfuss, T.B.; Pelmenschikov, V.; Case, D.A.; et al. Characterization of the Fe Site in Iron–Sulfur Cluster-Free Hydrogenase (Hmd) and of a Model Compound via Nuclear Resonance Vibrational Spectroscopy (NRVS). Inorg. Chem. 2008, 47, 3969–3977. [Google Scholar] [CrossRef]
- Pelmenschikov, V.; Birrell, J.A.; Pham, C.C.; Mishra, N.; Wang, H.; Sommer, C.; Reijerse, E.; Richers, C.P.; Tamasaku, K.; Yoda, Y.; et al. Reaction Coordinate Leading to H2 Production in [FeFe]-Hydrogenase Identified by Nuclear Resonance Vibrational Spectroscopy and Density Functional Theory. J. Am. Chem. Soc. 2017, 139, 16894–16902. [Google Scholar] [CrossRef]
- Lin, J.-F.; Tse, J.S.; Alp, E.E.; Zhao, J.; Lerche, M.; Sturhahn, W.; Xiao, Y.; Chow, P. Phonon density of states of Fe2O3across high-pressure structural and electronic transitions. Phys. Rev. B 2011, 84, 064424. [Google Scholar] [CrossRef]
- Chumakov, A.I.; Barla, A.; Rüffer, R.; Metge, J.; Grünsteudel, H.F.; Grünsteudel, H.; Plessel, J.; Winkelmann, H.; Abd-Elmeguid, M.M. Nuclear inelastic scattering of synchrotron radiation by 119Sn. Phys. Rev. B 1998, 58, 254–257. [Google Scholar] [CrossRef]
- Barla, A.; Rüffer, R.; Chumakov, A.I.; Metge, J.; Plessel, J.; Abd-Elmeguid, M.M. Direct determination of the phonon density of states inβ−Sn. Phys. Rev. B 2000, 61, R14881–R14884. [Google Scholar] [CrossRef]
- Giefers, H.; Tanis, E.A.; Rudin, S.P.; Greeff, C.; Ke, X.; Chen, C.; Nicol, M.F.; Pravica, M.; Pravica, W.; Zhao, J.; et al. Phonon density of states of metallic Sn at high pressure. Phys. Rev. Lett. 2007, 98, 245502. [Google Scholar] [CrossRef]
- Edla, R.; Nowak, D.; Hauschild, D.; Sergueev, I.; Pareek, D.; Gutay, L.; Heske, C.; Weinhardt, L.; Stankov, S. Lattice Dynamics of Cu2ZnSn(Sx,Se1-x)4 Kesterite Thin-Film Solar Cells Studied by Nuclear Inelastic Scattering. J. Phys. Chem. C Nanomater. Interfaces 2024, 128, 17483–17491. [Google Scholar] [CrossRef]
- Bauer, G.S.; European Nucl, S.O.C. SINQ as a versatile alternative neutron source. In Proceedings of the 3rd International Topical Meeting on Research Reactor Fuel Management (RRFM ‘99), Bruges, Belgium, 28–30 March 1999; pp. 1–9. [Google Scholar]
- Fischer, P.; Frey, G.; Koch, M.; Könnecke, M.; Pomjakushin, V.; Schefer, J.; Thut, R.; Schlumpf, N.; Bürge, R.; Greuter, U.; et al. High-resolution powder diffractometer HRPT for thermal neutrons at SINQ. Phys. B Condens. Matter 2000, 276–278, 146–147. [Google Scholar] [CrossRef]
- Fischer, W.E. SINQ—The spallation neutron source, a new research facility at PSI. Phys. B 1997, 234, 1202–1208. [Google Scholar] [CrossRef]
- Toby, B.H.; Von Dreele, R.B. GSAS-II: The genesis of a modern open-source all purpose crystallography software package. J. Appl. Crystallogr. 2013, 46, 544–549. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, Y.; Wang, X.; Jalan, B.; Chen, S.; Hou, Y. Roles of Point Defects in Thermal Transport in Perovskite Barium Stannate. J. Phys. Chem. C 2018, 122, 11482–11490. [Google Scholar] [CrossRef]
- Baron, A.Q.R.; Tanaka, Y.; Miwa, D.; Ishikawa, D.; Mochizuki, T.; Takeshita, K.; Goto, S.; Matsushita, T.; Kimura, H.; Yamamoto, F.; et al. Early commissioning of the SPring-8 beamline for high resolution inelastic X-ray scattering. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2001, 467–468, 627–630. [Google Scholar] [CrossRef]
- Yoda, Y. X-ray beam properties available at the nuclear resonant scattering beamline at SPring-8. Hyperfine Interact. 2019, 240, 72. [Google Scholar] [CrossRef]
- Benczer-Koller, N.; Fink, T. Lifetime and decay of the 23.8 keV state of 119Sn. Nucl. Phys. A 1971, 161, 123–128. [Google Scholar] [CrossRef]
- Gee, L.B.; Wang, H.; Cramer, S.P. NRVS for Fe in Biology: Experiment and Basic Interpretation. Methods Enzymol. 2018, 599, 409–425. [Google Scholar] [CrossRef] [PubMed]
- Sturhahn, W. CONUSS and PHOENIX: Evaluation of nuclear resonant scattering data. Hyperfine Interact. 2000, 125, 149–172. [Google Scholar] [CrossRef]
- Frackowiak, D. The Jablonski diagram. J. Photochem. Photobiol. B Biol. 1988, 2, 399. [Google Scholar] [CrossRef]
- Sougrati, M.T.; Jouen, S.; Hannoyer, B. Relative Lamb-Mossbauer factors of tin corrosion products. Hyperfine Interact. 2006, 167, 4. [Google Scholar] [CrossRef]
- Sturhahn, W.; Chumakov, A. Lamb–Mössbauer factor and second-order Doppler shift from inelastic nuclear resonant absorption. Hyperfine Interact. 1999, 123/124, 809–824. [Google Scholar] [CrossRef]
- Kim, B.G.; Jo, J.Y.; Cheong, S.W. Hybrid functional calculation of electronic and phonon structure of BaSnO. J. Solid. State Chem. 2013, 197, 134–138. [Google Scholar] [CrossRef]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Buongiorno Nardelli, M.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 2017, 29, 465901. [Google Scholar] [CrossRef] [PubMed]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baseggio, O.; Bonfa, P.; Brunato, D.; Car, R.; Carnimeo, I.; Cavazzoni, C.; de Gironcoli, S.; Delugas, P.; Ferrari Ruffino, F.; et al. Quantum ESPRESSO toward the exascale. J. Chem. Phys. 2020, 152, 154105. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Prandini, G.; Marrazzo, A.; Castelli, I.E.; Mounet, N.; Marzari, N. Precision and efficiency in solid-state pseudopotential calculations. NPJ Comput. Mater. 2018, 4, 72. [Google Scholar] [CrossRef]
- Togo, A.; Chaput, L.; Tadano, T.; Tanaka, I. Implementation strategies in phonopy and phono3py. J. Phys. Condens. Matter 2023, 35, 353001. [Google Scholar] [CrossRef]
- Togo, A. First-principles Phonon Calculations with Phonopy and Phono3py. J. Phys. Soc. Jpn. 2023, 92, 012001. [Google Scholar] [CrossRef]
- Aggoune, W.; Eljarrat, A.; Nabok, D.; Irmscher, K.; Zupancic, M.; Galazka, Z.; Albrecht, M.; Koch, C.; Draxl, C. A consistent picture of excitations in cubic BaSnO3 revealed by combining theory and experiment. Commun. Mater. 2022, 3, 12. [Google Scholar] [CrossRef]
- Bjørheim, T.S.; Løken, A.; Haugsrud, R. On the relationship between chemical expansion and hydration thermodynamics of proton conducting perovskites. J. Mater. Chem. A 2016, 4, 5917–5924. [Google Scholar] [CrossRef]
- Phelan, D.; Han, F.; Lopez-Bezanilla, A.; Krogstad, M.J.; Gim, Y.; Rong, Y.; Zhang, J.; Parshall, D.; Zheng, H.; Cooper, S.L.; et al. Structural properties of barium stannate. J. Solid. State Chem. 2018, 262, 142–148. [Google Scholar] [CrossRef]
- Alagdal, I.A.; West, A.R. Oxygen stoichiometry, conductivity and gas sensing properties of BaSnO3. J. Mater. Chem. C 2016, 4, 4770–4777. [Google Scholar] [CrossRef]
- Cui, J.; Zhang, Y.; Wang, J.; Zhao, Z.; Huang, H.; Zou, W.; Yang, M.; Peng, R.; Yan, W.; Huang, Q.; et al. Oxygen deficiency induced strong electron localization in lanthanum doped transparent perovskite oxide BaSnO3. Phys. Rev. B 2019, 100, 165312. [Google Scholar] [CrossRef]
- Jaim, H.M.I.; Lee, S.; Zhang, X.; Takeuchi, I. Stability of the oxygen vacancy induced conductivity in BaSnO3 thin films on SrTiO3. Appl. Phys. Lett. 2017, 111, 172102. [Google Scholar] [CrossRef]
- Stanislavchuk, T.N.; Sirenko, A.A.; Litvinchuk, A.P.; Luo, X.; Cheong, S.W. Electronic band structure and optical phonons of BaSnO3 and Ba0.97La0.03SnO3 single crystals: Theory and experiment. J. Appl. Phys. 2012, 112, 044108. [Google Scholar] [CrossRef]
- Bévillon, É.; Chesnaud, A.; Wang, Y.; Dezanneau, G.; Geneste, G. Theoretical and experimental study of the structural, dynamical and dielectric properties of perovskite BaSnO3. J. Phys. Condens. Matter 2008, 20, 145217. [Google Scholar] [CrossRef]
- Tummers, B.; van der Laan, J.; Huyser, K. DataThief III. 2006. Available online: https://www.datathief.org/ (accessed on 29 April 2025).
- Kreuer, K.D. Proton conductivity: Materials and applications. Chem. Mater. 1996, 8, 610–641. [Google Scholar] [CrossRef]
- Song, X.; Wang, G.; Zhou, L.; Yang, H.; Li, X.; Yang, H.; Shen, Y.; Xu, G.; Luo, Y.; Wang, N. Oxide Perovskite BaSnO3: A Promising High-Temperature Thermoelectric Material for Transparent Conducting Oxides. ACS Appl. Energy Mater. 2023, 6, 9756–9763. [Google Scholar] [CrossRef]
- Cramer, S.P. X-Ray Spectroscopy with Synchrotron Radiation; Springer Nature Switzerland: Cham, Switzerland, 2020; p. 400. [Google Scholar]

| BaSnO3, wR = 5.11% | |||
| T, K | 1 K | 100 K | 200 K |
| a, Å | 4.11016(7) | 4.11113(10) | 4.11329(11) |
| Ba occ. | 1 0.970(3) 0.975(3) | ||
| Sn occ. | |||
| O occ. | |||
| Uiso(Ba), Å2 | 0.00167(12) | 0.00272(17) | 0.00402(18) |
| Uiso(Sn), Å2 | 0.00068(10) | 0.00120(15) | 0.00184(16) |
| U11(O), Å2 | 0.00498(11) | 0.00571(17) | 0.00768(19) |
| U33(O), Å2 | 0.00228(21) | 0.00299(31) | 0.0033(3) |
| PVDOS Peak Position [cm−1] | Assignment | |||
|---|---|---|---|---|
| This Work Exp. | This Work Calc. | Ref. [43] | Ref. [43] | Ref. [44] |
| 105, 122 | 100, 120 | 115 | TO1 | Ba-SnO3 translation |
| 153, 170, 185 | 150, 170, 187 | 150–170 | LO1 | |
| 216, 227, 240 | 214, 229, 240 | 238 | TO2 | O-Sn-O bending |
| 275, 295, 310 | 266, 288, 297 | |||
| 334, 347 | 340 | |||
| 409 | - | 408 | LO2 | Sn-O3 torsion |
| 433, 446 | 426, 441 very low | |||
| 465, 487 | 465, 483 | |||
| 655 | 662 | |||
| - | - | 724 | LO3 | Sn-O stretching |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rulev, A.; Wang, H.; Erat, S.; Aycibin, M.; Rentsch, D.; Pomjakushin, V.; Cramer, S.P.; Chen, Q.; Nagasawa, N.; Yoda, Y.; et al. 119Sn Element-Specific Phonon Density of States of BaSnO3. Crystals 2025, 15, 440. https://doi.org/10.3390/cryst15050440
Rulev A, Wang H, Erat S, Aycibin M, Rentsch D, Pomjakushin V, Cramer SP, Chen Q, Nagasawa N, Yoda Y, et al. 119Sn Element-Specific Phonon Density of States of BaSnO3. Crystals. 2025; 15(5):440. https://doi.org/10.3390/cryst15050440
Chicago/Turabian StyleRulev, Alexey, Hongxin Wang, Selma Erat, Murat Aycibin, Daniel Rentsch, Vladimir Pomjakushin, Stephen P. Cramer, Qianli Chen, Nobumoto Nagasawa, Yoshitaka Yoda, and et al. 2025. "119Sn Element-Specific Phonon Density of States of BaSnO3" Crystals 15, no. 5: 440. https://doi.org/10.3390/cryst15050440
APA StyleRulev, A., Wang, H., Erat, S., Aycibin, M., Rentsch, D., Pomjakushin, V., Cramer, S. P., Chen, Q., Nagasawa, N., Yoda, Y., & Braun, A. (2025). 119Sn Element-Specific Phonon Density of States of BaSnO3. Crystals, 15(5), 440. https://doi.org/10.3390/cryst15050440







