Microstructure Evolution and the Influence on Residual Stress in Metal Additive Manufacturing with Analytics †
Abstract
1. Introduction
2. Methodology
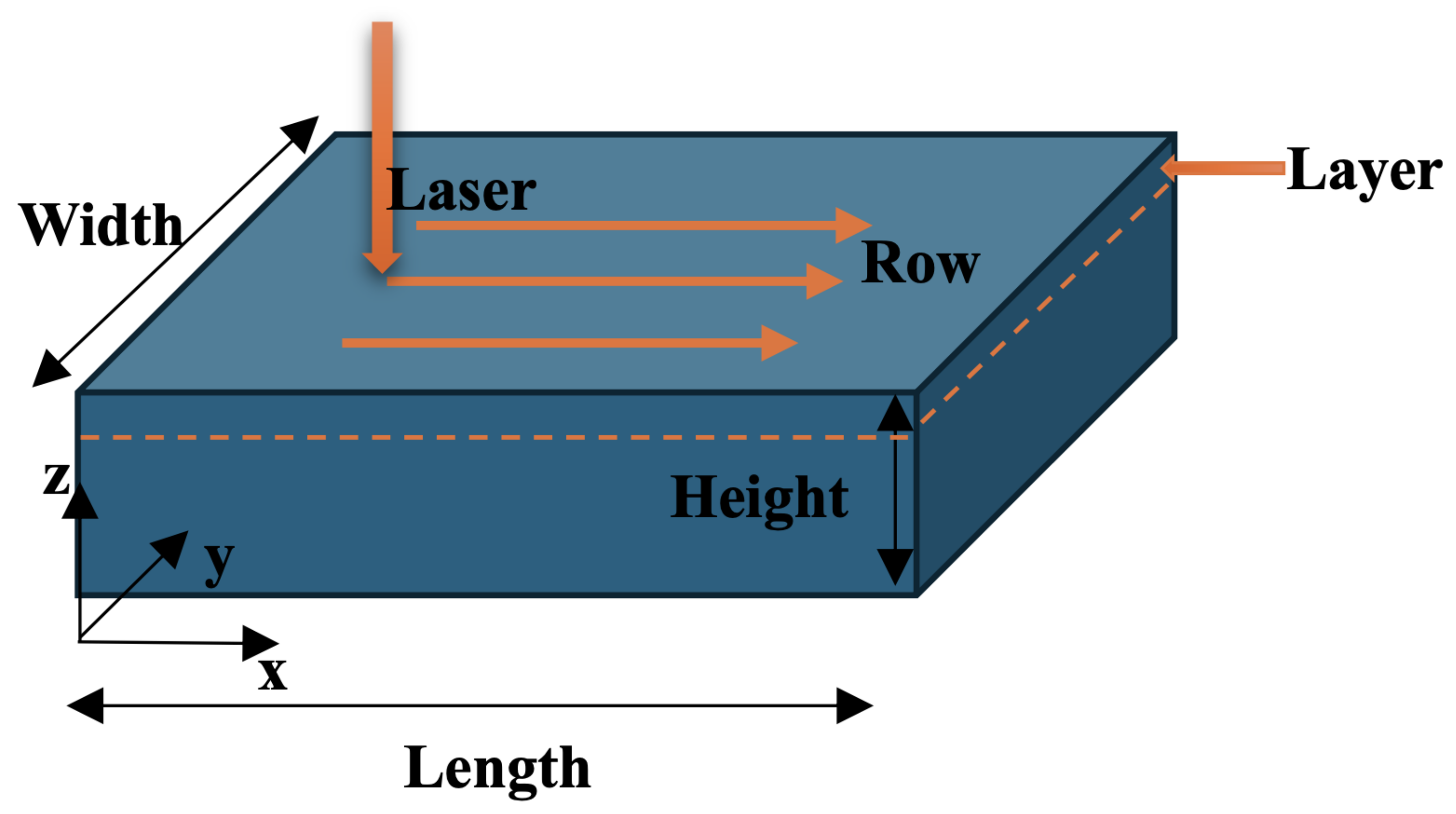
2.1. Thermal Profile
- -
- V: laser scanning velocity
- -
- P: laser power
- -
- K: thermal conductivity
- -
- c: heat capacity
- -
- : laser absorption coefficient
- -
- : thermal diffusivity
- -
- : density
- -
- R: distance between the heat source and the analysis location
- -
- : thermal conductivity of the powder
- -
- h: heat convection coefficient
- -
- : emissivity
- -
- : Stefan-Boltzmann constant
2.2. Texture
2.3. Grain Size
2.4. Microstructure-Affected Materials Properties
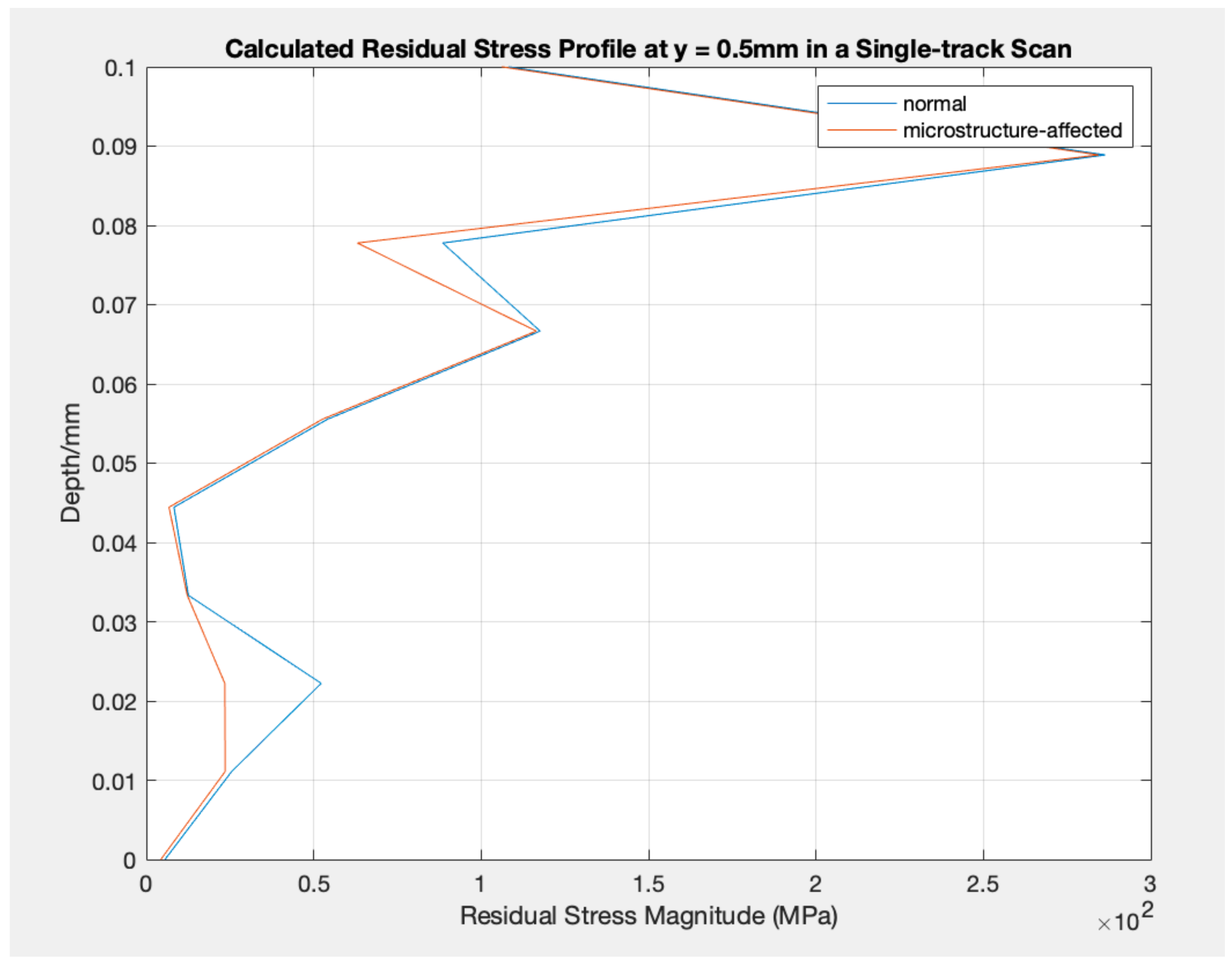
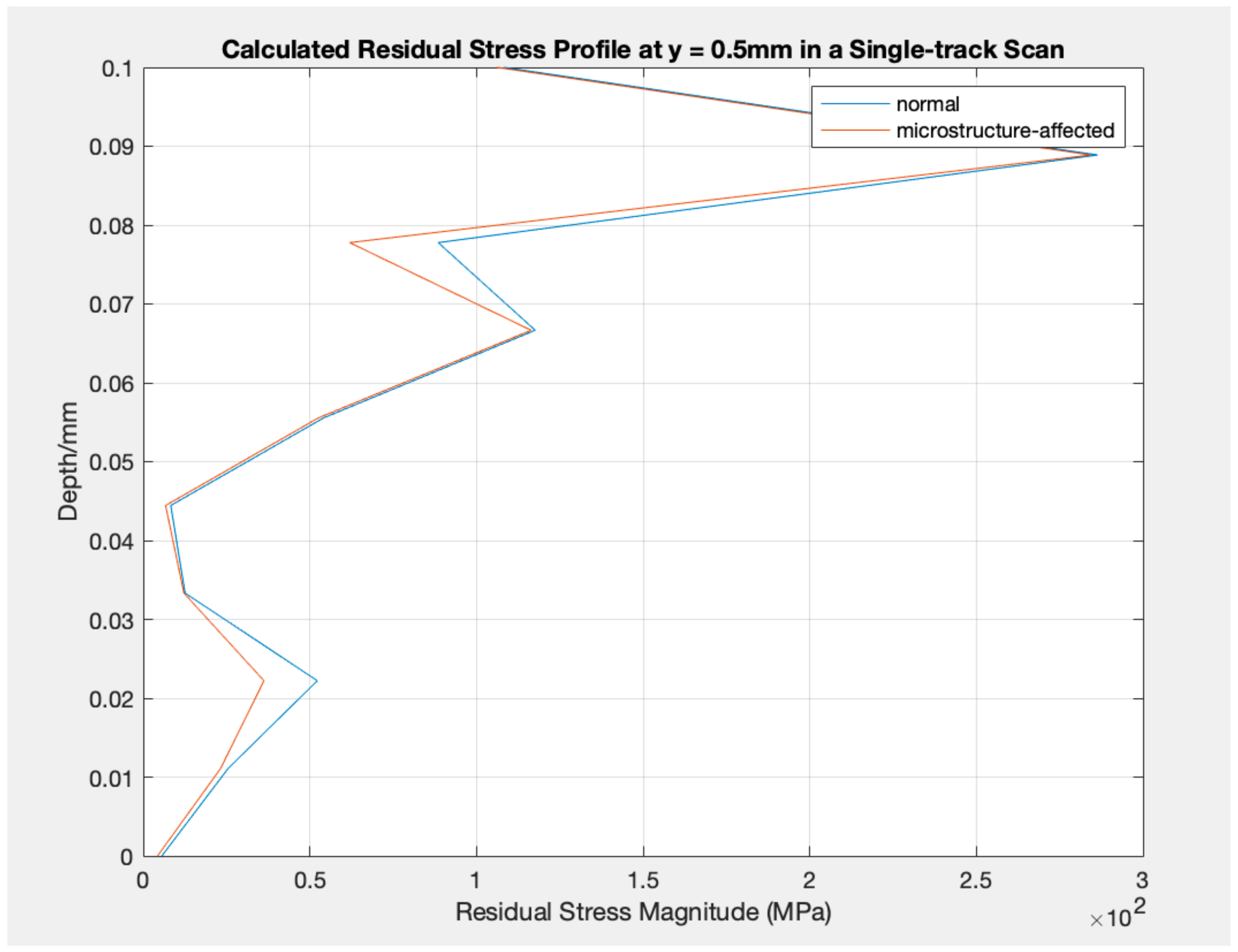
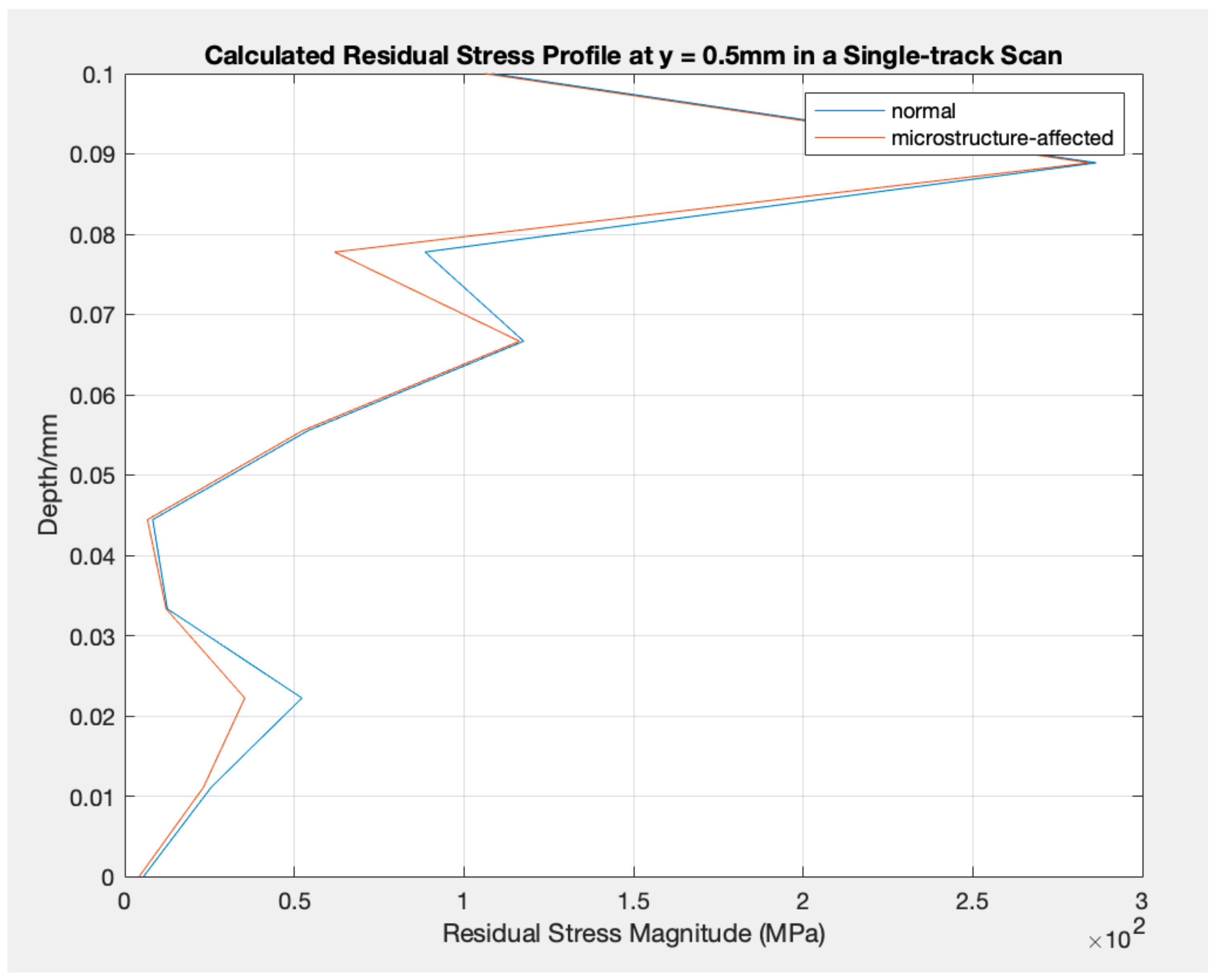
2.5. Residual Stress
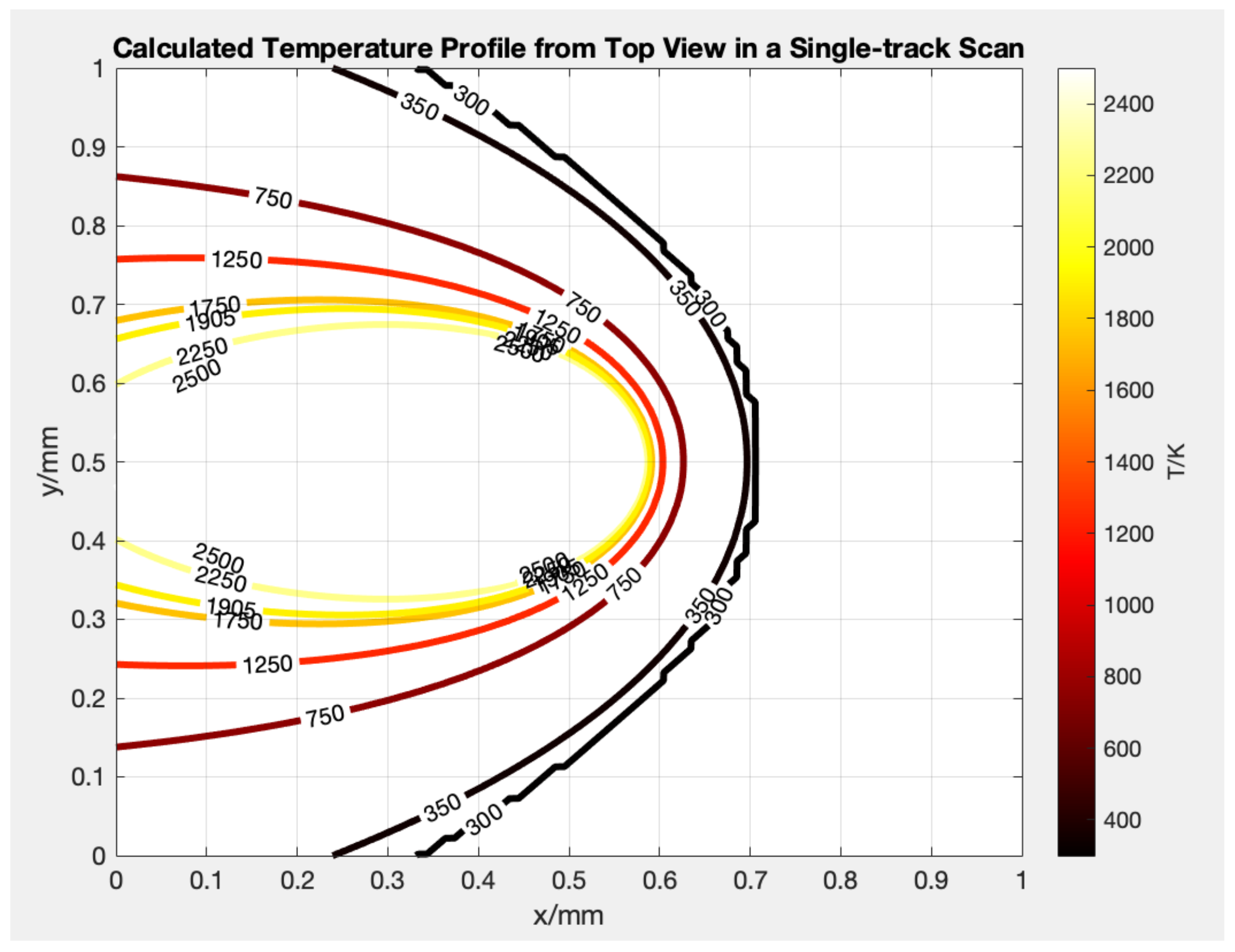
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AM | Additive Manufacturing |
| LPBF | Laser powder bed fusion |
| CET | Columnar-to-equiaxed transition of crystallographic orientation |
| FEM | Finite element method |
| AI | Artificial intelligence |
| BCC | Body-centered cubic |
| HCP | Hexagonal close packed |
| P | Laser power |
| T | Temperature |
| Laser absorption coefficient | |
| x, y, z | Coordinates |
| V | Laser scanning velocity |
| R | Distance from the heat source to the point of analysis |
| K | Thermal conductivity |
| Coordinates of the heat source | |
| Thermal diffusivity | |
| Room temperature | |
| c | Heat capacity |
| Density | |
| Heat of conduction | |
| Heat of convection | |
| Heat of radiation | |
| A | Area of each heat sink on the melt pool surface |
| Powder thermal conductivity | |
| T | Temperature change |
| h | Heat convection coefficient |
| Radiation emissivity | |
| Stefan-Boltzmann constant | |
| G | Thermal gradient vector |
| Solidification rate | |
| n | Exponent |
| ∅ | Certain value in Hunt’s model |
| m | Specific crystallographic orientation vector of the seed crystal that gives the maximum value of |
| PX | Polycrystal base |
| Number of possible seed crystals | |
| Melting temperature | |
| Bulk thermal conductivity | |
| nn, kk | Columnar/equiaxed transition coefficient |
| X, Y, Z | Coordinate axis |
| JMAK | Johnson-Mehl-Avrami-Kolmogorov |
| Thermal expansion coefficient | |
| , | Thermal stress in the xx and zz directions |
| G | Green’s function |
| Poisson’s Ratio | |
| E | Elastic modulus |
| Strain | |
| Volume fraction of dynamically recrystallized material | |
| Peak strain | |
| Initial grain size | |
| Activation energy | |
| Materials constants | |
| q | Cooling rate |
| n | Newly formed grain number |
| I | Nucleation rate per unit volume |
| Stiffness constants | |
| Complicance constants |
References
- Huang, W.; Garmestani, H.; Liang, S.Y. Microstructure Evolution and the Influence on Material Properties of Residual Stress in Additive Manufacturing with Analytics for a Green Future. In Proceedings of the TMS 2025 154th Annual Meeting & Exhibition Supplemental Proceedings, Las Vegas, NV, USA, 23–27 March 2025; TMS 2025; The Minerals, Metals & Materials Series. Springer: Berlin/Heidelberg, Germany, 2025; pp. 244–253. [Google Scholar]
- DebRoy, T.; Wei, H.; Zuback, J.; Mukherjee, T.; Elmer, J.; Milewski, J.; Beese, A.M.; Wilson-Heid, A.d.; De, A.; Zhang, W. Additive manufacturing of metallic components–process, structure and properties. Prog. Mater. Sci. 2018, 92, 112–224. [Google Scholar] [CrossRef]
- Frazier, W.E. Metal additive manufacturing: A review. J. Mater. Eng. Perform. 2014, 23, 1917–1928. [Google Scholar] [CrossRef]
- Herzog, D.; Seyda, V.; Wycisk, E.M.; Emmelmann, C. Additive manufacturing of metals. Acta Mater. 2016, 117, 371–392. [Google Scholar] [CrossRef]
- Blakey-Milner, B.; Gradl, P.; Snedden, G.; Brooks, M.; Pitot, J.; Lopez, E.; Leary, M.; Berto, F.; Du Plessis, A. Metal additive manufacturing in aerospace: A review. Mater. Des. 2021, 209, 110008. [Google Scholar] [CrossRef]
- Aboulkhair, N.T.; Simonelli, M.; Parry, L.; Ashcroft, I.; Tuck, C.; Hague, R. 3D printing of Aluminium alloys: Additive Manufacturing of Aluminium alloys using selective laser melting. Prog. Mater. Sci. 2019, 106, 100578. [Google Scholar] [CrossRef]
- Ligon, S.C.; Liska, R.; Stampfl, J.; Gurr, M.; Mülhaupt, R. Polymers for 3D Printing and Customized Additive Manufacturing. Chem. Rev. 2017, 117, 10212–10290. [Google Scholar] [CrossRef]
- Wang, X.; Jiang, M.; Zhou, Z.; Gou, J.; Hui, D. 3D printing of polymer matrix composites: A review and prospective. Compos. Part B-Eng. 2017, 110, 442–458. [Google Scholar] [CrossRef]
- Chen, Z.; Li, Z.; Li, J.; Liu, C.; Lao, C.; Fu, Y.; Liu, C.; Yang, L.; Wang, P.; Yi, H. 3D printing of ceramics: A review. J. Eur. Ceram. Soc. 2019, 39, 661–687. [Google Scholar] [CrossRef]
- Bourell, D.; Kruth, J.P.; Leu, M.; Levy, G.; Rosen, D.; Beese, A.M.; Clare, A. Materials for additive manufacturing. CIRP Ann. 2017, 66, 659–681. [Google Scholar] [CrossRef]
- Ngo, T.D.; Kashani, A.R.; Imbalzano, G.; Nguyen, K.T.; Hui, D. Additive manufacturing (3D printing): A review of materials, methods, applications and challenges. Compos. Part Eng. 2018, 143, 172–196. [Google Scholar] [CrossRef]
- Bartlett, J.L.; Li, X. An overview of residual stresses in metal powder bed fusion. Addit. Manuf. 2019, 27, 131–149. [Google Scholar] [CrossRef]
- Megahed, M.; Mindt, H.W.; N’Dri, N.A.; Duan, H.; Desmaison, O. Metal additive-manufacturing process and residual stress modeling. Integr. Mater. Manuf. Innov. 2016, 5, 61–93. [Google Scholar] [CrossRef]
- Staub, A.; Spierings, A.B.; Wegener, K. Correlation of meltpool characteristics and residual stresses at high laser intensity for metal lpbf process. Adv. Mater. Process. Technol. 2018, 5, 153–161. [Google Scholar] [CrossRef]
- Noronha, P.J.; Wert, J.J. An Ultrasonic Technique for the Measurement of Residual Stress. J. Test. Eval. 1975, 3, 147–152. [Google Scholar] [CrossRef]
- Chung, D.D.L. Thermal analysis of carbon fiber polymer-matrix composites by electrical resistance measurement. Thermochim. Acta 2000, 364, 121–132. [Google Scholar] [CrossRef]
- Krause, T.W.; Clapham, L.; Pattantyus, A.; Atherton, D.L. Investigation of the stress-dependent magnetic easy axis in steel using magnetic Barkhausen noise. J. Appl. Phys. 1996, 79, 4242–4252. [Google Scholar] [CrossRef]
- Ager, J.W.; Drory, M.D. Quantitative measurement of residual biaxial stress by Raman spectroscopy in diamond grown on a Ti alloy by chemical vapor deposition. Phys. Rev. B Condens. Matter 1993, 48 4, 2601–2607. [Google Scholar] [CrossRef]
- Wu, A.S.; Brown, D.W.; Kumar, M.; Gallegos, G.F.; King, W.E. An Experimental Investigation into Additive Manufacturing-Induced Residual Stresses in 316L Stainless Steel. Metall. Mater. Trans. A 2014, 45, 6260–6270. [Google Scholar] [CrossRef]
- Wang, Z.; Denlinger, E.R.; Michaleris, P.; Stoica, A.D.; Ma, D.; Beese, A.M. Residual stress mapping in Inconel 625 fabricated through additive manufacturing: Method for neutron diffraction measurements to validate thermomechanical model predictions. Mater. Des. 2017, 113, 169–177. [Google Scholar] [CrossRef]
- Prime, M.B. Cross-sectional mapping of residual stresses by measuring the surface contour after a cut. J. Eng. Mater. Technol.-Trans. Asme 2001, 123, 162–168. [Google Scholar] [CrossRef]
- Mokhtarishirazabad, M.; McMillan, M.; Vijayanand, V.D.; Simpson, C.; Agius, D.; Truman, C.E.; Knowles, D.A.; Mostafavi, M. Predicting residual stress in a 316L electron beam weld joint incorporating plastic properties derived from a crystal plasticity finite element model. Int. J. Press. Vessel. Pip. 2022, 201, 104868. [Google Scholar] [CrossRef]
- Kapoor, K.; Yoo, Y.S.J.; Book, T.A.; Kacher, J.; Sangid, M.D. Incorporating grain-level residual stresses and validating a crystal plasticity model of a two-phase Ti-6Al-4 V alloy produced via additive manufacturing. J. Mech. Phys. Solids 2018, 121, 447–462. [Google Scholar] [CrossRef]
- Huang, W.; Wang, W.; Ning, J.; Garmestani, H.; Liang, S.Y. Analytical Model of Quantitative Texture Prediction Considering Heat Transfer Based on Single-Phase Material in Laser Powder Bed Fusion. J. Manuf. Mater. Process. 2024, 8, 70. [Google Scholar] [CrossRef]
- Huang, W.; Garmestani, H.; Liang, S.Y. Analytical prediction of texture of multi-phase materials in laser powder bed fusion. J. Manuf. Mater. Process. 2024, 8, 234. [Google Scholar]
- Ji, X.; Mirkoohi, E.; Ning, J.; Liang, S.Y. Analytical modeling of post-printing grain size in metal additive manufacturing. Opt. Lasers Eng. 2020, 124, 105805. [Google Scholar] [CrossRef]
- Wang, W.; Ning, J.; Liang, S.Y. Prediction of lack-of-fusion porosity in laser powder-bed fusion considering boundary conditions and sensitivity to laser power absorption. Int. J. Adv. Manuf. Technol. 2021, 112, 61–70. [Google Scholar] [CrossRef]
- Johnson, G.R. A Constitutive Model and Data for Metals Subjected to Large Strains, high strain rates and high temperatures. In Proceedings of the 7th International Symposium on Ballistics, The Hague, Netherlands, 19–21 April 1983. [Google Scholar]
- Lee, H.J.; Ni, H.; Wu, D.T.; Ramirez, A.G. Grain size estimations from the direct measurement of nucleation and growth. Appl. Phys. Lett. 2005, 87, 124102. [Google Scholar] [CrossRef]
- Özel, T.; Llanos, I.; Soriano, J.; Arrazola, P.J. 3D finite element modelling of chip formation process for machining inconel 718: Comparison of fe software predictions. Mach. Sci. Technol. 2011, 15, 21–46. [Google Scholar] [CrossRef]
- Kobayashi, T.; Simons, J.; Brown, C.; Shockey, D. Plastic flow behavior of Inconel 718 under dynamic shear loads. Int. J. Impact Eng. 2008, 35, 389–396. [Google Scholar] [CrossRef]
- Kobryn, P.A.; Semiatin, S.L. Microstructure and texture evolution during solidification processing of Ti–6Al–4V. J. Mater. Process. Technol. 2003, 135, 330–339. [Google Scholar] [CrossRef]
- Welsch, G.; Boyer, R.; Collings, E. Materials Properties Handbook: Titanium Alloys; ASM International: Almere, The Netherlands, 1993. [Google Scholar]
- Avrami, M. Kinetics of phase change. I General theory. J. Chem. Phys. 1939, 7, 1103–1112. [Google Scholar] [CrossRef]
- Avrami, M. Kinetics of phase change. II transformation-time relations for random distribution of nuclei. J. Chem. Phys. 1940, 8, 212–224. [Google Scholar] [CrossRef]
- Avrami, M. Granulation, phase change, and microstructure kinetics of phase change. III. J. Chem. Phys. 1941, 9, 177–184. [Google Scholar] [CrossRef]
- Faleiros, A.; Rabelo, T.N.; Thim, G.P.; Oliveira, M.A.S. Kinetics of phase change. Mater. Res.-Ibero-Am. J. Mater. 2000, 3, 51–60. [Google Scholar] [CrossRef]
- Cahn, J.W. Transformation kinetics during continuous cooling. Acta Metall. 1956, 4, 572–575. [Google Scholar] [CrossRef]
- Umemoto, M.; Hai Guo, Z.; Tamura, I. Effect of cooling rate on grain size of ferrite in a carbon steel. Mater. Sci. Technol. 1987, 3, 249–255. [Google Scholar] [CrossRef]
- Ikehata, H.; Nagasako, N.; Furuta, T.; Fukumoto, A.; Miwa, K.; Saito, T. First-principles calculations for development of low elastic modulus Ti alloys. Phys. Rev. B 2004, 70, 174113. [Google Scholar] [CrossRef]
- Howard, C.J.; Kisi, E.H. Measurement of single-crystal elastic constants by neutron diffraction from polycrystals. J. Appl. Crystallogr. 1999, 32, 624–633. [Google Scholar] [CrossRef]
- Heldmann, A.; Hoelzel, M.; Hofmann, M.; Gan, W.; Schmahl, W.W.; Griesshaber, E.; Hansen, T.W.; Schell, N.; Petry, W. Diffraction-based determination of single-crystal elastic constants of polycrystalline titanium alloys. J. Appl. Crystallogr. 2019, 52, 1144–1156. [Google Scholar] [CrossRef]
- Mirkoohi, E.; Tran, H.C.; Lo, Y.L.; Chang, Y.C.; Lin, H.; Liang, S.Y. Analytical mechanics modeling of residual stress in laser powder bed considering flow hardening and softening. Int. J. Adv. Manuf. Technol. 2020, 107, 4159–4172. [Google Scholar] [CrossRef]
- Cho, J.Y.; Xu, W.; Brandt, M.; Qian, M. Selective laser melting-fabricated Ti-6Al-4V alloy: Microstructural inhomogeneity, consequent variations in elastic modulus and implications. Opt. Laser Technol. 2019, 111, 664–670. [Google Scholar] [CrossRef]




| Model Inputs | Value | Unit |
|---|---|---|
| Surrounding Temperature () | 20 | |
| Melting Temperature () | 1655 | |
| Density () | 4428 | kg/m3 |
| Modulus of Elasticity (E) | 60.78 | GPa |
| Poisson’s Ratio () | 0.34 | 1 |
| Bulk Thermal Conductivity () | 5–35 | W/(mK) |
| Powder Thermal Conductivity () | 0.21 | W/(mK) |
| Heat Capacity (C) | 500–800 | J/(KgK) |
| Heat Convection Coefficient (h) | 24 | W/(m2K) |
| Radiation Emissivity () | 0.9 | 1 |
| Stefan-Boltzmann Constant () | 5.67 × | W/(m2K) |
| Columnar/Equiaxed Transition Coefficient (nn) | 3.2 | 1 |
| Columnar/Equiaxed Transition Coefficient (kk) | 1 | |
| Laser Absorption Value | 0.818 | 1 |
| Part Length (L) | 4 | mm |
| Part Width (W) | 1 | mm |
| Part Height (H) | 0.5 | mm |
| Number of Heat Sinks (S) | 9 | 1 |
| Layer Thickness | 50 | m |
| Hatching Space | 50 | m |
| Hall-Petch Material Constant (k) | 230 | m0.5 MPa |
| Hall-Petch Material Constant () | 737 | MPa |
| ID | Layers | Rows |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 2 | 2 |
| 3 | 3 | 3 |
| 4 | 4 | 4 |
| 5 | 5 | 5 |
| (GPa) | (GPa) | (GPa) | (GPa) | |
|---|---|---|---|---|
| 1 | 106.580 | 114.330 | 108.660 | 109.857 |
| 2 | 106.380 | 106.700 | 119.300 | 110.793 |
| 3 | 105.020 | 106.050 | 129.340 | 113.470 |
| 4 | 104.880 | 104.890 | 141.160 | 116.977 |
| 5 | 104.870 | 106.210 | 130.030 | 113.703 |
| 1 | 0.464 | 0.497 | 0.195 | 0.199 | 0.209 | 0.199 |
| 2 | 0.463 | 0.464 | 0.195 | 0.218 | 0.195 | 0.218 |
| 3 | 0.457 | 0.461 | 0.192 | 0.237 | 0.194 | 0.237 |
| 4 | 0.456 | 0.456 | 0.192 | 0.258 | 0.192 | 0.258 |
| 5 | 0.456 | 0.462 | 0.192 | 0.238 | 0.194 | 0.238 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, W.; Garmestani, H.; Liang, S.Y. Microstructure Evolution and the Influence on Residual Stress in Metal Additive Manufacturing with Analytics. Crystals 2025, 15, 435. https://doi.org/10.3390/cryst15050435
Huang W, Garmestani H, Liang SY. Microstructure Evolution and the Influence on Residual Stress in Metal Additive Manufacturing with Analytics. Crystals. 2025; 15(5):435. https://doi.org/10.3390/cryst15050435
Chicago/Turabian StyleHuang, Wei, Hamid Garmestani, and Steven Y. Liang. 2025. "Microstructure Evolution and the Influence on Residual Stress in Metal Additive Manufacturing with Analytics" Crystals 15, no. 5: 435. https://doi.org/10.3390/cryst15050435
APA StyleHuang, W., Garmestani, H., & Liang, S. Y. (2025). Microstructure Evolution and the Influence on Residual Stress in Metal Additive Manufacturing with Analytics. Crystals, 15(5), 435. https://doi.org/10.3390/cryst15050435








