Process Optimization Simulation of Residual Stress in Martensitic Steel Considering Phase Transformation

Abstract

The solid phase transformation of martensitic steel during heat treatment will affect the stress and temperature. Previous residual stress prediction models ignore the effect of phase transition on residual stress. In order to predict residual stress accurately, a residual stress calculation method considering solid phase transition was presented. The measures to reduce residual stress in quenching medium, cooling rate, and the starting temperature and tempering temperature of the martensitic transformation were studied. The experimental results show that residual stress decreases after air cooling. In a certain range, residual stress can be reduced during heat treatment by decreasing the cooling rate and the martensite start temperature. The recommended tempering temperature is 380 °C.

1. Introduction

Martensitic steel is extensively utilized in transportation and mechanical components because of its favorable characteristics, including excellent plasticity, extended service life, and high strength [1,2,3,4,5]. Martensitic steel undergoes the martensitic transformation during heat treatment. Residual stress is affected by the martensitic transformation [6,7,8,9]. The martensitic transformation can lead to volume and yield strength changes, which will affect the residual stress of martensitic steel after heat treatment [10,11]. The residual stress produced in the heat treatment process affects the dimensional stability, fatigue strength, stress corrosion resistance and crack resistance of the member [12,13]. Therefore, the accurate prediction of residual stress is very important. The experimental method can only measure the local residual stress of martensitic steel, which has limitations. The residual stress field of martensitic steel can be obtained by finite element simulation, and the residual stress of martensitic steel components can be predicted. A residual stress model that takes into account the martensitic transformation is crucial for accurately forecasting residual stress, which in turn is essential for optimizing the heat treatment process to control the residual stress in martensitic steel.

By optimizing the heat treatment process (such as quenching and tempering), the residual stress during the martensitic transformation can be effectively controlled, thereby improving the fatigue strength and toughness of the material. By reducing residual stress or providing a favorable residual stress state, the service life of structural components can be significantly extended and the risk of failure reduced. Economic aspects can be improved by optimizing processes to reduce later repair and replacement costs. In areas such as the aviation, automotive, and energy sectors, there are extremely high demands on material properties, and optimizing residual stress is critical to meeting these demands. By controlling residual stress, material characteristics can be customized to meet performance requirements in specific applications.

Some studies have measured residual stress in martensitic steels by experimental tests. The effects of different quenching rates on residual stress were studied by X-ray diffraction [14]. Although these experiments provide valuable information for understanding the distribution of residual stress, it is often difficult to fully reflect the residual stress state under actual process conditions due to the complexity of experimental conditions and samples. The finite element analysis method has been used to simulate stress evolution during the martensitic transformation [15]. Although these numerical models can predict the distribution of residual stress fairly well, they often rely on empirical parameters and simplified assumptions, and the results may not be accurate enough. In some studies, the multi-scale model method is used to try to combine the relationship between microstructure and macroscopic properties to investigate the effect of the martensitic transformation on residual stress more comprehensively. However, these methods are often computationally complex and require large amounts of experimental data to verify their accuracy. Most of the current research focuses on martensitic steels with specific alloy composition, such as some low-alloy steels, while the research on high-alloy martensitic steels is relatively rare. The effects of different alloy compositions on the phase transformation process and residual stress are significantly different, but systematic comparative studies are insufficient. There are few studies on the effect of new process on the martensitic transformation and residual stress in the current literature, and many studies are still located in the traditional process conditions, lacking in-depth discussion under modern manufacturing technology. In this study, an improved finite element method, combined with the phase field model and the thermo-mechanical coupling method, is used to simulate the residual stress generation in the martensitic transformation process more accurately. This method can better consider the effect of local microstructure change on stress state. This will help optimize the heat treatment process for specific materials. This study will explore the effects of advanced heat treatment processes on the martensitic transformation and residual stress, which will not only enrich theoretical research but also help guide practical industrial applications.

The prediction of residual stress involves thermodynamics, phase transformation dynamics, and elastoplastic mechanics [16,17]. The residual stress model should take into account various factors, including heat transfer, metallurgy, and mechanics [18,19]. For martensitic steel, the martensitic transformation has only been considered in a few studies on welding [20,21,22]. Wang et al. [23] utilized ABAQUS 2022 to determine the residual stress distribution in welded joints of martensitic steel. Similarly, Zubairuddin et al. [24] employed SYSWELD to analyze the stress and deformation in martensitic steel. Although the martensitic transformation was considered, latent heat was also ignored. Deng et al. [25] obtained the stress field of martensitic steel through simulation but did not consider the effect of martensitic phase transition. In their research, the effects of volume change and yield strength variation resulting from the martensitic transformation were taken into account, whereas plasticity and latent heat were disregarded. The martensitic transformation can cause large volume expansion [26]. Chen et al. [27] found in their research that large volume strain during heat treatment has a significant impact on residual stress. The effect of phase transition on residual stress was neglected in previous studies of residual stress models. In order to predict the residual stress more accurately, a residual stress prediction model considering phase transition is proposed [28,29]. Therefore, the effect of phase transition should be considered in finite element simulation to accurately predict the residual stress of martensitic steel.

A residual stress prediction method considering phase change is proposed. The measures to control the residual stress are discussed in terms of quenching medium, cooling rate, and the starting temperature and tempering temperature of the martensitic transition.

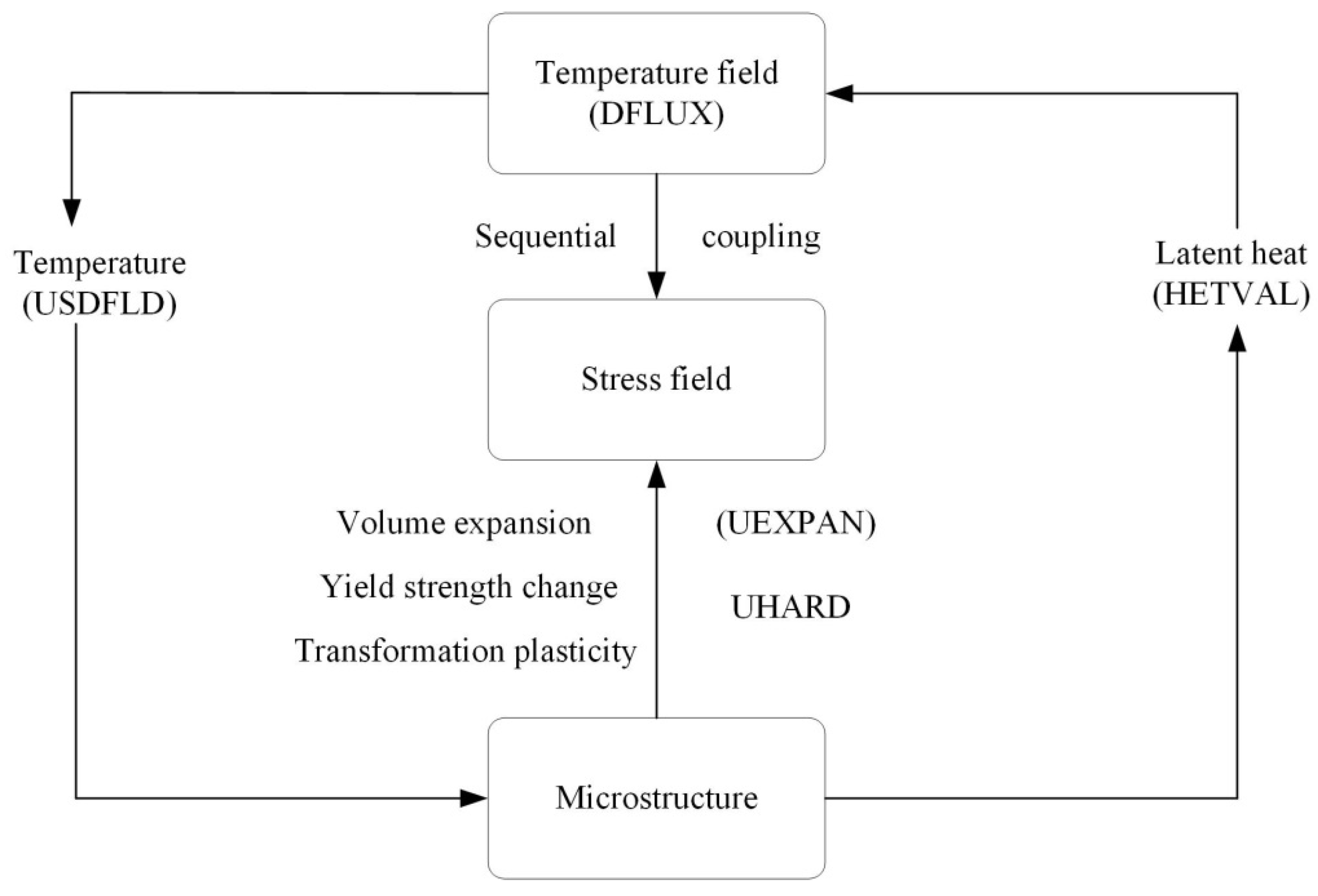
2. Calculation Method of Residual Stress Considering Martensitic Transformation

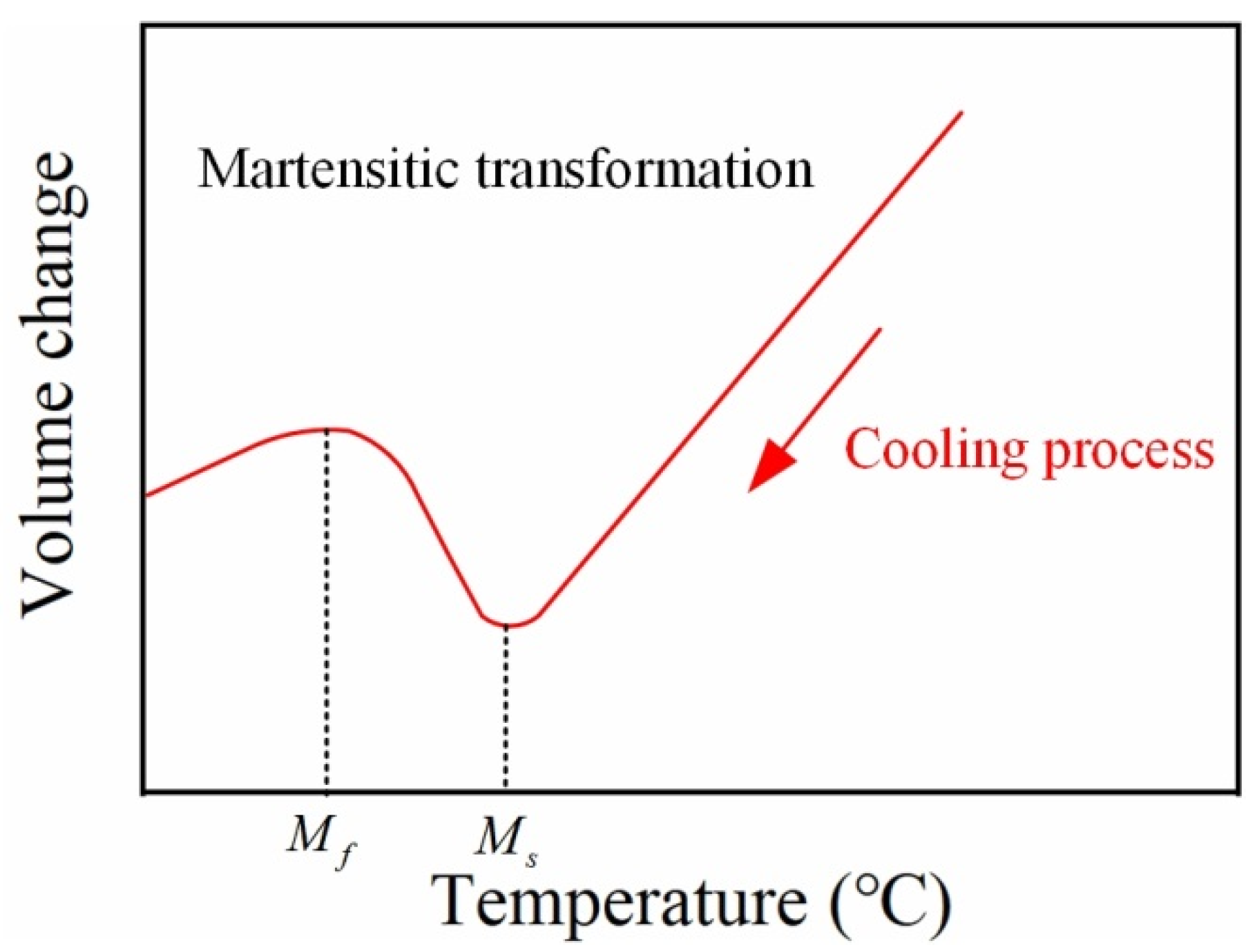
2.1. Microstructure Field Calculation

The sample analyzed in this paper is low-carbon martensitic steel after quenching. Consequently, the martensitic transformation is incorporated into the microstructure calculations with the martensite volume fraction following the Koistinen–Marburger equation [10]:

$${\phi }_{\mathrm{M}}=1-\exp \left[-\alpha (M_s-T)\right]$$

(1)

${\phi }_{\mathrm{M}}$ is the martensite volume fraction; M_s is the martensitic transformation point; T is temperature; α is a constant which is 0.011.

2.2. Temperature Field Calculation

The calculation equation of the whole temperature field is written as [30]

$$\rho c \left({\phi }_{\mathrm{M}},T\right) Ṫ =\nabla \left[k\left({\phi }_{\mathrm{M}},T\right)\cdot \nabla T\right]+\stackrel{.}{Q}$$

(2)

ρ is material density; c is heat capacity; k is the heat transfer coefficient; T is temperature; $Ṫ$ is the partial of temperature with respect to time; $\nabla$ is the gradient operator; $\stackrel{.}{Q}$ is the latent heat of phase transformation per unit time.

Q is the latent heat of phase transformation, calculated by the formula

$$Q=\Delta H\cdot {\stackrel{.}{\phi }}_{\mathrm{M}}$$

(3)

ΔH is the heat released during the decomposition of austenite per unit volume; ${\stackrel{.}{\phi }}_{\mathrm{M}}$ is the martensitic phase variable per unit time.

The boundary condition is defined as follows [11]:

$$k\left[{\displaystyle \frac{\partial T}{\partial x}}{l}_x+{\displaystyle \frac{\partial T}{\partial y}}{l}_y+{\displaystyle \frac{\partial T}{\partial z}}{l}_z\right]=h(T-T_{\infty })$$

(4)

l_x, l_y, and l_z are direction cosines in the x, y, and z directions, respectively; h is the surface heat transfer coefficient; T and T_∞ are the surface and ambient temperatures, respectively.

2.3. Stress Field Calculation

The thermal elastoplastic behavior of martensitic steel during the quenching process is a nonlinear problem addressed using incremental theory. In this analysis, the Von-Mises yield criterion, isotropic hardening conditions, and the Prandtl–Reuss flow rule are implemented. The volume change of martensitic steel is illustrated in Figure 1. The total strain increment is defined in the following manner [31]:

$$\Delta {\epsilon }_{\mathit{ij}}=\Delta {\epsilon }_{\mathit{ij}}^{\mathrm{e}}+\Delta {\epsilon }_{\mathit{ij}}^{\mathrm{p}}+\Delta {\epsilon }_{\mathit{ij}}^{\mathrm{t}\mathrm{h}}+\Delta {\epsilon }_{\mathit{ij}}^{\mathrm{t}\mathrm{r}}+\Delta {\epsilon }_{\mathit{ij}}^{\mathrm{t}\mathrm{p}}$$

(5)

$\Delta {\epsilon }_{\mathit{ij}}^{\mathrm{e}}$, $\Delta {\epsilon }_{\mathit{ij}}^{\mathrm{p}}$, $\Delta {\epsilon }_{\mathit{ij}}^{\mathrm{t}\mathrm{h}}$, $\Delta {\epsilon }_{\mathit{ij}}^{\mathrm{t}\mathrm{r}}$, and $\Delta {\epsilon }_{\mathit{ij}}^{\mathrm{t}\mathrm{p}}$ are elastic strain increment, plastic strain increment, thermal strain increment, phase change plastic increment, and phase change plastic strain increment, respectively.

The material exhibits uniform mechanical and physical properties in all directions, allowing the increments of microstructure strain and thermal strain to be expressed as follows [32]:

$$\Delta {\epsilon }_{\mathit{ij}}^{\mathrm{tr}}={\phi }_{\mathrm{M}}\left[{\epsilon }_{\mathrm{M}}(T+\Delta T)-{\epsilon }_{\mathrm{A}}\left(T+\Delta T\right)\right]$$

(6)

$$\Delta {\epsilon }_{\mathit{ij}}^{\mathrm{th}}={\phi }_{\mathrm{M}}\left[{\epsilon }_{\mathrm{M}}(T+\Delta T)-{\epsilon }_{\mathrm{M}}\left(T\right)\right]$$

(7)

${\epsilon }_{\mathrm{M}}$ is the relative strain of the martensitic microstructure; ${\epsilon }_{\mathrm{A}}$ is the relative strain of the austenitic microstructure.

In line with the GJ theory, the Lebond formula is employed to compute transformation plasticity [33,34]:

$$\mathrm{d}{\epsilon }^{\mathrm{tr}}={\displaystyle \frac{3}{2}}\mathit{KSf}\left(\epsilon \right)\epsilon$$

(8)

S is the stress deviation; K is the coefficient of transformation plasticity; ε is the rate of transformation plasticity; f(ε) is the kinetic formula of transformation plasticity.

2.4. Simulation Route

In simulations that take into account the martensitic transformation, the influence of phase transitions on stress is integrated into the constitutive equation and implemented through an ABAQUS user subroutine. The simulated route is shown in Figure 2. First, ABAQUS 2022 is utilized to create a 3D model, wherein heat-related material properties are entered into the material parameter editing interface. Next, during the simulation, the martensite fraction is determined based on temperature and the Koistinen–Marburger formula [34]. Subsequently, the latent heat generated by the phase transition is incorporated into the HETVAL subroutine as an internal heat source [35]. The changes in phase transformation plasticity and yield strength are addressed by the UHARD subroutine, while the impact of volume change on stress is managed by the UEXPAN subroutine. This model is applicable to metals undergoing martensitic phase transitions. The finite element model constructed in this study is mainly applicable to metal materials with uniform material properties. The material parameters used in the model are based on references, and its physical and mechanical properties have been verified in a number of experiments. However, for heterogeneous materials or composites, models need to be adjusted accordingly to account for the effects of material interfaces and polyphase structures. The finite element model in the present study is mainly designed for regular circular geometries and is suitable for structures with symmetry and uniform loading conditions. However, for complex asymmetries or geometries with sharp corners, the model requires mesh optimization and parameter adjustment to ensure the accuracy of the analysis results.

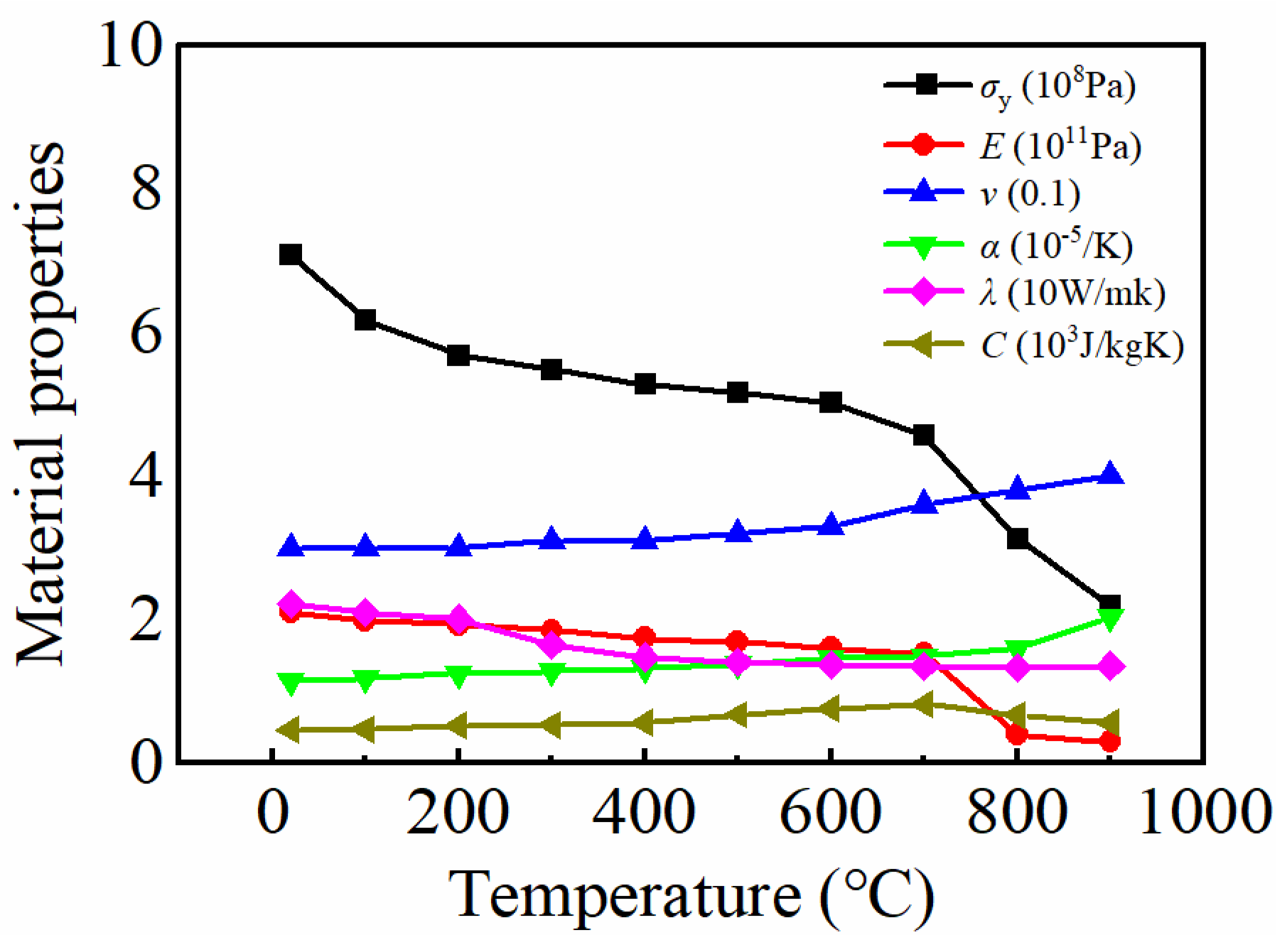
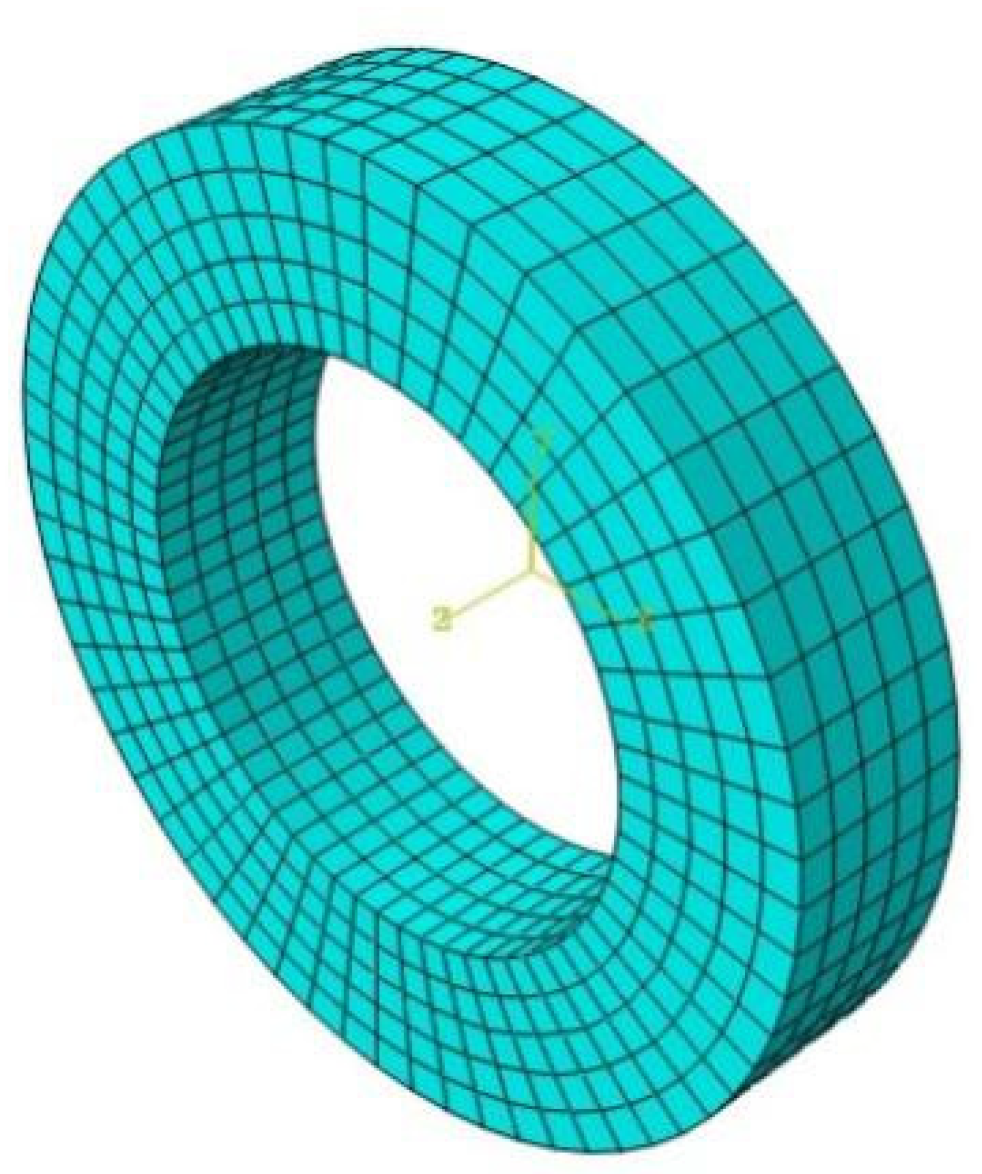
2.5. Calculation Model and Parameters

The thermal and physical properties of martensitic steel involved in the model and mechanical property parameters are shown in Figure 3. In metallurgical and mechanical calculations, the temperature-dependent properties of materials should be considered first. The corresponding thermal property data (such as thermal conductivity λ, specific heat capacity C) and mechanical properties parameters (such as yield stress σ_y, elastic modulus E, Poisson ratio ν, linear thermal expansion coefficient α). The density of martensitic steel changes little with temperature. It is considered that the density of martensitic steel during quenching is 7800 kg·m⁻³. The heat transfer coefficient used in the model is based on martensitic steel as outlined in reference [36]. The thermal conductivity of air cooling is 0.025 W(m·K), the thermal conductivity of oil cooling is 0.2 W(m·K), and the thermal conductivity of water cooling is 0.6 W(m·K). The martensitic steel model is constructed using finite element analysis software ABAQUS 2022, as depicted in Figure 4. The thermodynamic coupling finite element method is used to simulate the interaction between temperature and stress fields, especially the stresses caused by phase transitions and temperature gradients during heat treatment. The dimensions of the ring are 100 × 100 × 50 mm³, with a cell size of 2 mm, resulting in a total of 62,500 cells. In finite element analysis, the mesh size is the key factor that affects the calculation accuracy and convergence. Smaller mesh sizes often provide more accurate results but significantly increase computational costs. Therefore, it is necessary to conduct grid sensitivity analysis to determine the appropriate mesh size and ensure the reliability and computational efficiency of the model results. In order to ensure the accuracy of the model results, a grid sensitivity analysis was carried out. Three different mesh sizes (coarse mesh, medium mesh, and fine mesh) were selected for simulation calculation. The key parameters include maximum stress, maximum displacement, etc. The results show that with the decrease in mesh size, the changes in key parameters tend to be stable, indicating that the model results converge gradually. Through the grid sensitivity analysis, the middle grid was selected as the final model grid to balance the calculation accuracy and efficiency. The boundary conditions of the temperature field were convection boundary conditions, and the initial temperature was set at room temperature (20 °C). To validate the accuracy of the model, data from the literature were employed for comparison. The model validation in this study mainly relies on experimental data in the existing literature. Specifically, we selected the key parameters of stress and strain in the literature for comparison. During the verification process, the model simulation results were compared with experimental results in the literature under the same conditions, such as temperature, pressure, and other environmental variables. In order to evaluate the accuracy of the model, we use the mean square error as an evaluation index. The results show that the mean square error between the predicted value of the model and the experimental data is 0.05, which indicates that the model has good fitting performance. Although there is no independent experimental verification in this study, the validity of the model is preliminarily verified by comparing it with a number of data from the literature. Future studies will include further experimental validation to consolidate the reliability of the model. In addition, we plan to expand the data source to cover more experimental conditions to fully evaluate the suitability and stability of the model. Current models have indeed been developed primarily for specific types of martensitic steel materials and their specific component geometry. The ring workpiece has symmetry and uniformity, which makes it possible to simplify the calculation when analyzing the stress distribution. The symmetrical geometry helps to understand and predict the distribution of residual stress, especially on the inner and outer surfaces of the ring.

3. Heat Treatment Process Regulates Residual Stress

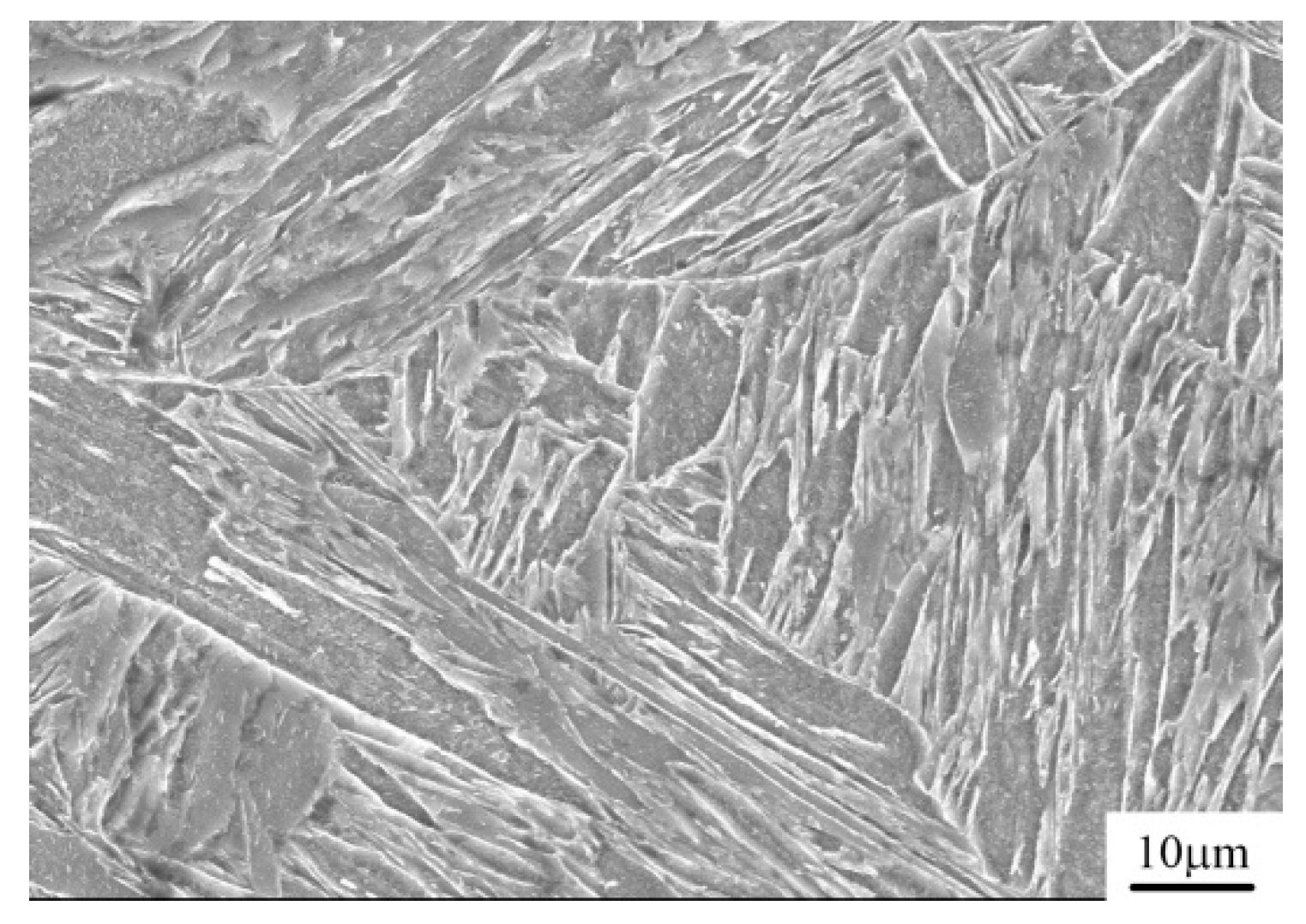
3.1. Microstructure

The microstructure of low-carbon martensitic steel is composed of martensitic lath and residual austenite as shown in Figure 5. After tempering, the lath martensite structure is tempered martensite structure, and the structure is the smallest, and there is a small amount of dispersed carbide.

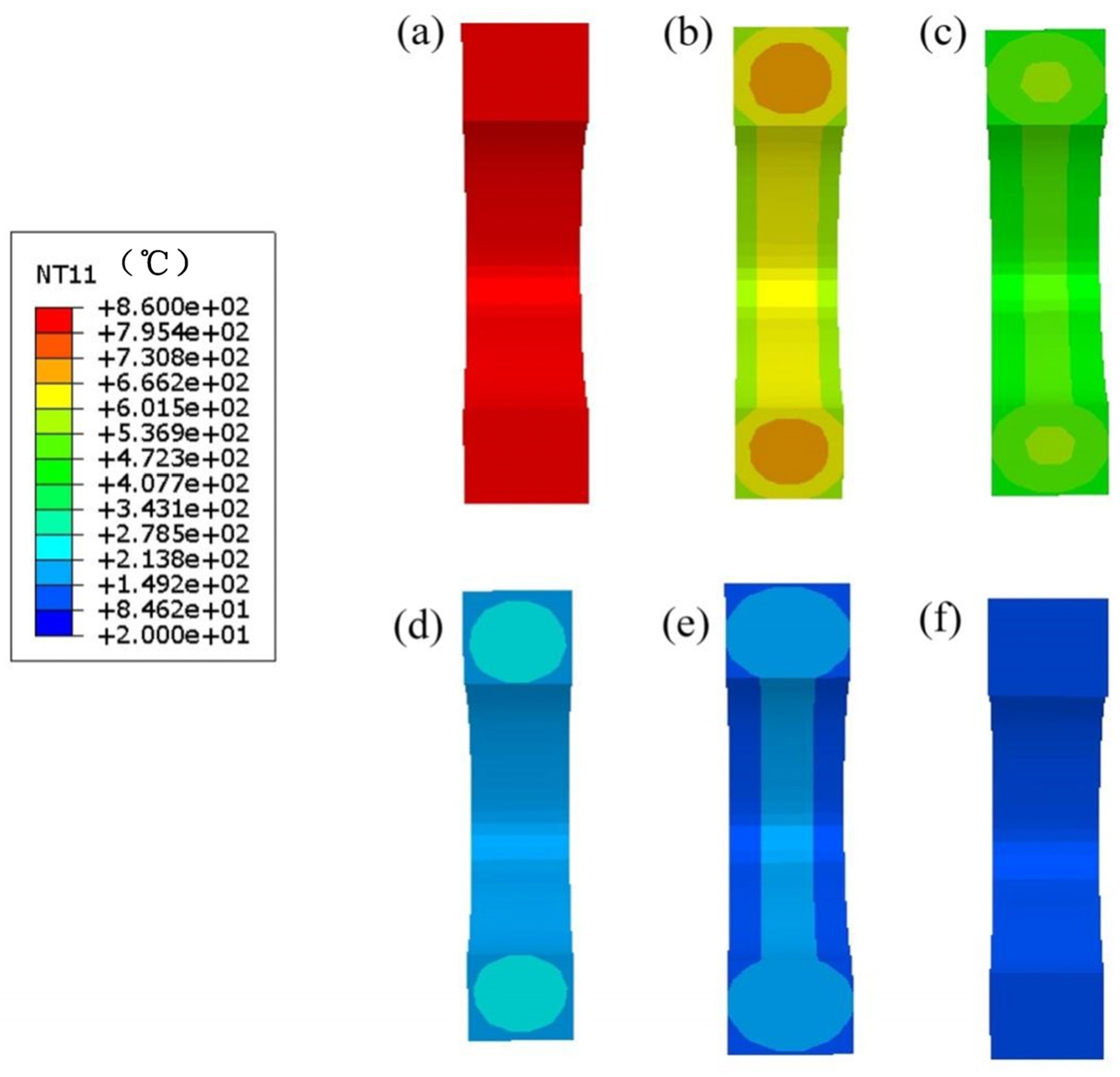
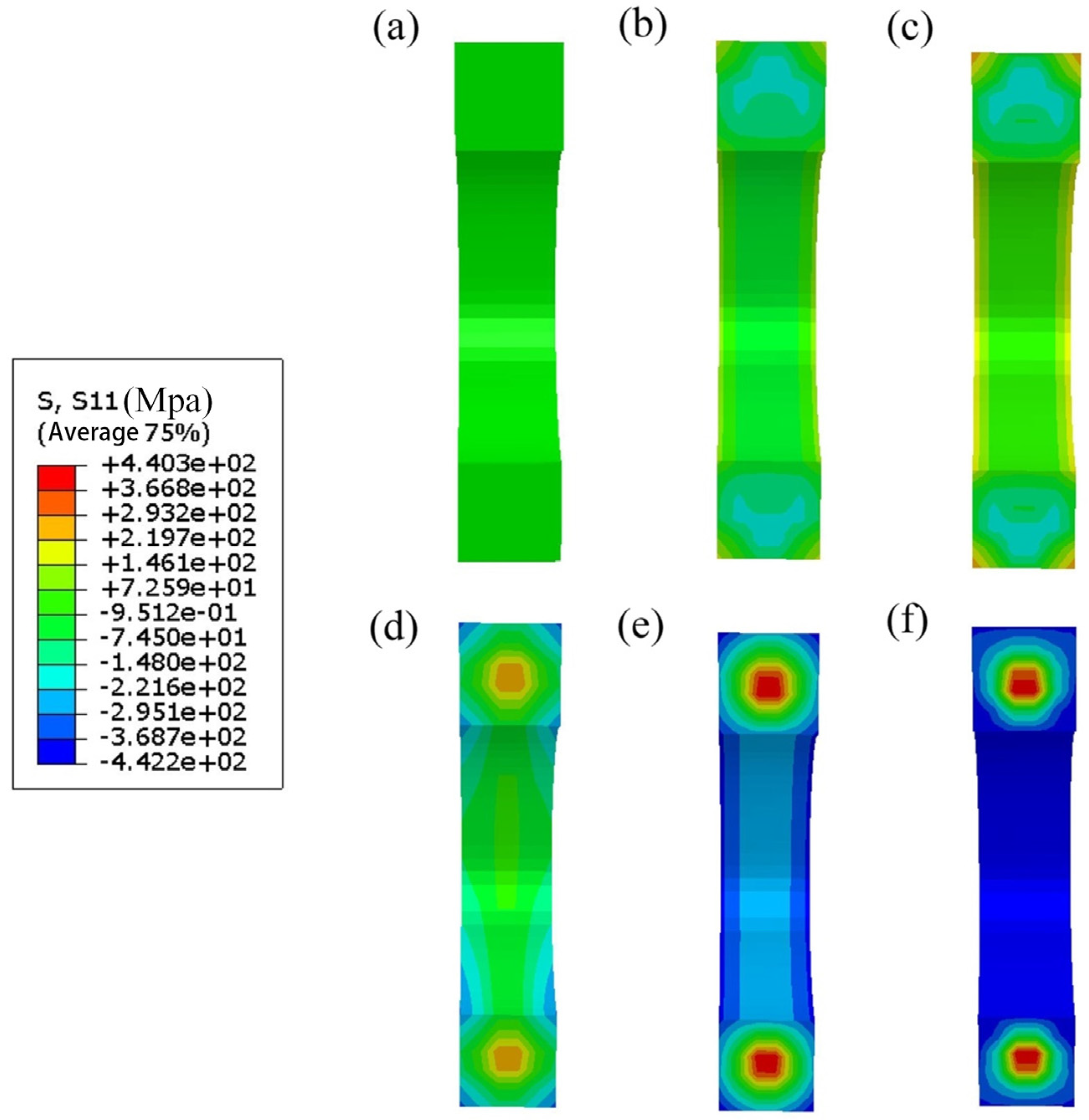
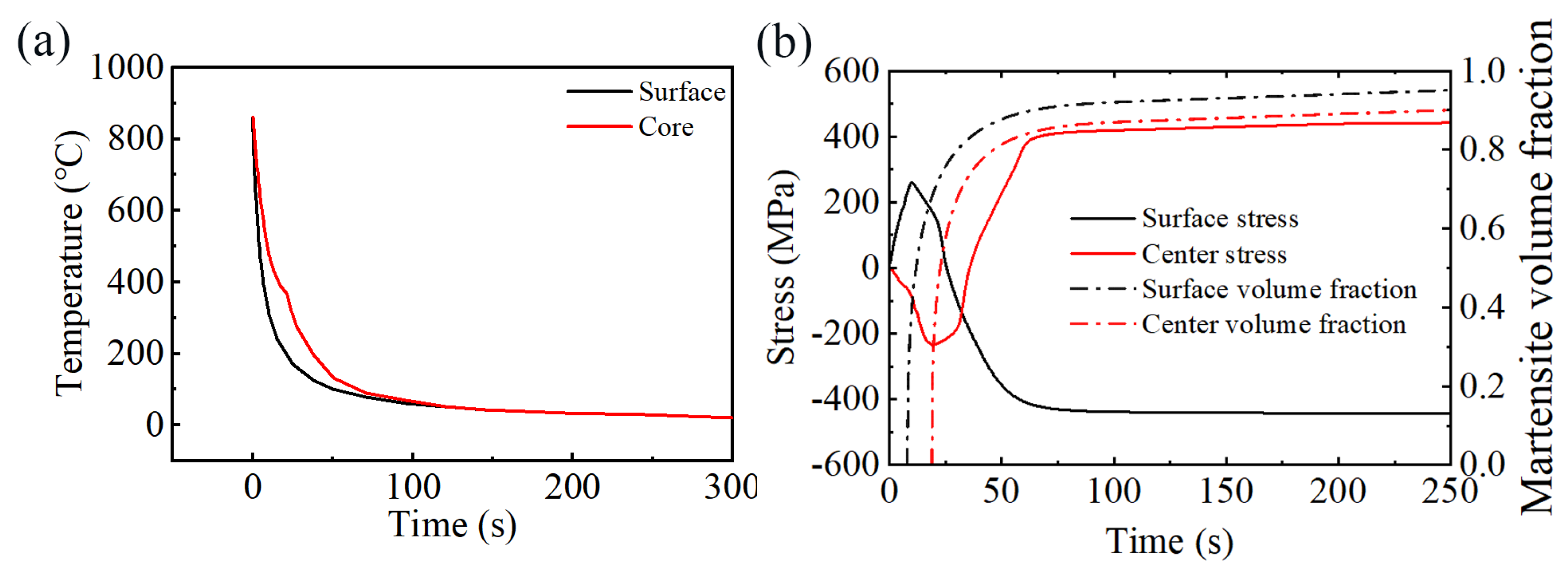
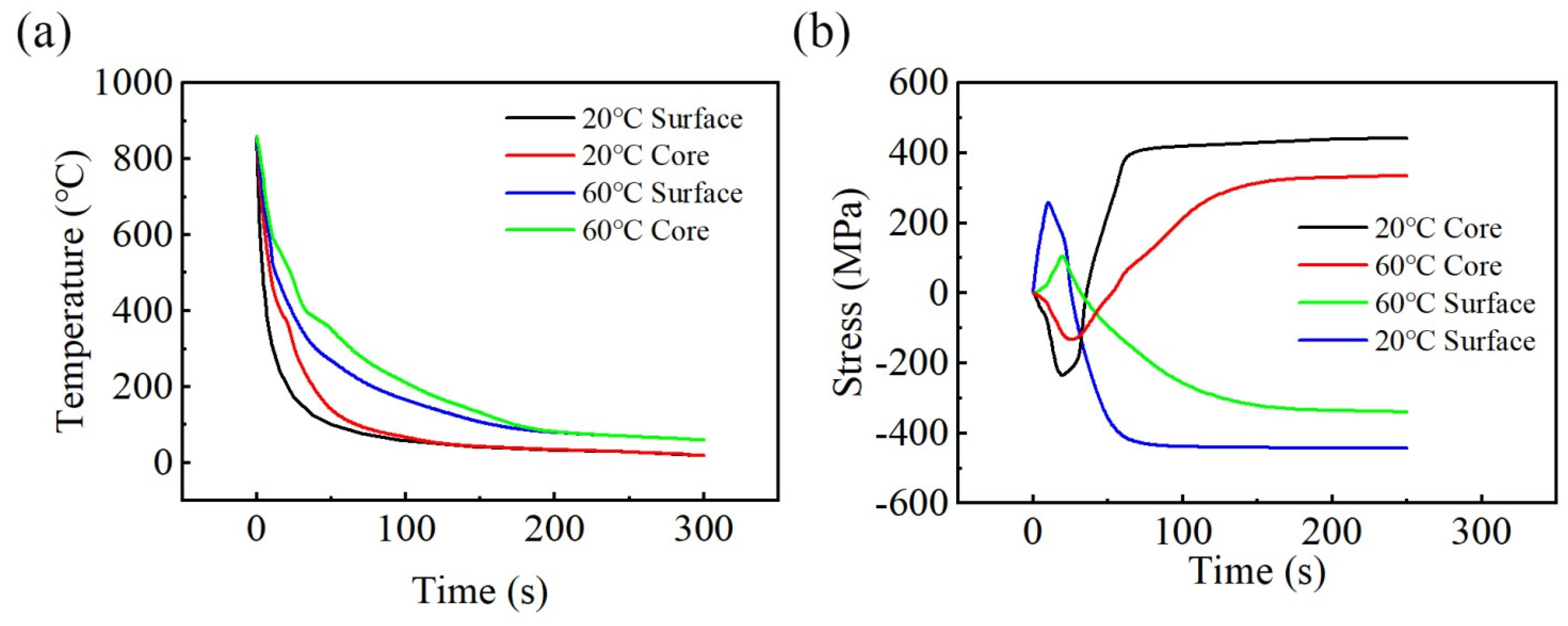
3.2. Temperature and Stress During Quenching

Figure 6 shows the temperature field variation of martensitic steel during water quenching at 20 °C. When the sample is water-quenched, the temperature of sample edge drops the fastest followed by the surface. The core of the sample is not in direct contact with the medium and relies on heat conduction. Therefore, the sample remains at a very high temperature. With the quenching, the core temperature of the sample decreases gradually. Due to the different cooling rates of the core and surface of the sample, an uneven temperature field is generated. When the quenching time is 300 s, the temperature of the core and surface gradually tends to be consistent with that of the medium.

Figure 7 shows the change in the stress field of martensitic steel during water quenching at 20 °C. When the sample just enters the water, the surface cools rapidly and shrinks, resulting in tensile residual stress. Under conditions of synchronous shrinkage, compressive residual stress is generated at the surface. As quenching time progresses, the temperature of the core gradually decreases, and its cooling rate exceeds that of the surface. Consequently, the core begins to shrink. At this point, the surface temperature is low, and its strength is high, leading to an increased restraining effect from the core. This results in a gradual increase in residual stress within the core, while the residual stress at the surface decreases. As the core continues to shrink, it transitions from compressive residual stress to tensile residual stress at 25 s, while the surface shifts from an initial state of tensile residual stress to compressive residual stress. Ultimately, a stress state characterized by inner tension and outer compression is established. Throughout the quenching process, the stress values for both the core and surface increase progressively. Upon the completion of quenching, the tensile residual stress in the core can reach 440 MPa, while the compressive residual stress at the surface can reach −442 MPa.

The analysis above indicates that the evolution paths of the temperature field and stress field in martensitic steel during quenching differ significantly. To monitor the changes in temperature and stress at key locations during the quenching process, nodes are selected at the surface and at the center of the core. As shown in Figure 8a, the exothermic effect of phase transformation is distinctly observable around 385 °C. Over time, the temperature difference between the surface and the core gradually reduces. Although the temperature of the sample continues to decrease, there are no significant changes in residual stress during the later stages of quenching, as shown in Figure 8b.

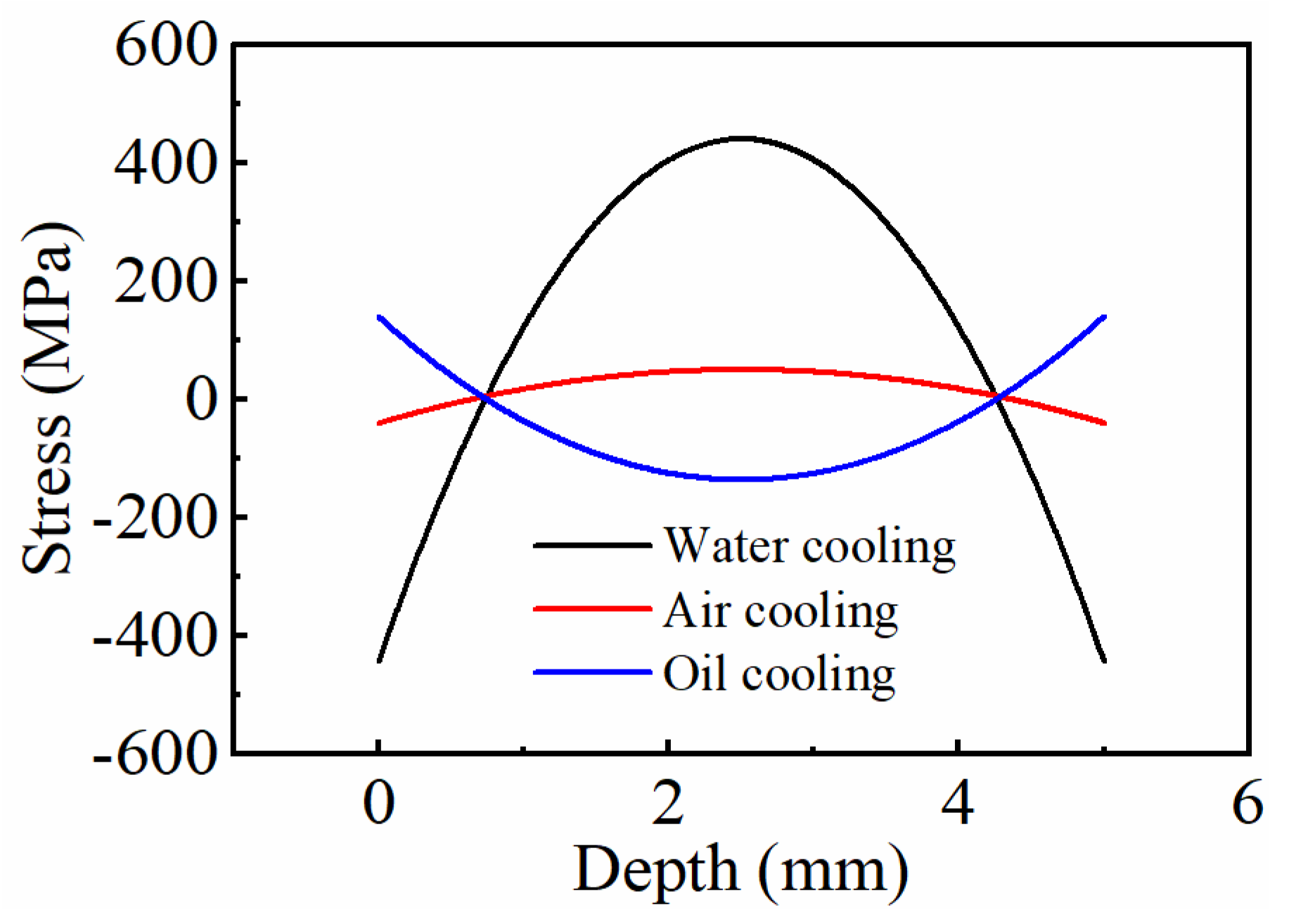
3.3. Influence of Quenching Medium on Residual Stress

Different quenching media have different cooling capacity for the sample and the corresponding quenching stress is also different. In this excerpt, three different cooling media are used for calculation and comparative study. Assuming the hardenability of the sample is large enough, the whole martensitic microstructure can be obtained even if it is air-cooled. The distribution of residual stress during the cooling process of martensitic steel is analyzed, revealing that the stress distribution after quenching varies with different cooling media, as illustrated in Figure 9. In the case of air cooling, which is relatively gentle, the temperature difference between the surface and the core remains small. For oil cooling, the temperature difference is also modest due to the slower cooling rates, resulting in tensile residual stress at the surface and compressive residual stress in the core. Conversely, water quenching involves a rapid cooling rate, producing a substantial temperature gradient within the sample. As a result, the residual stress levels are markedly higher following water quenching.

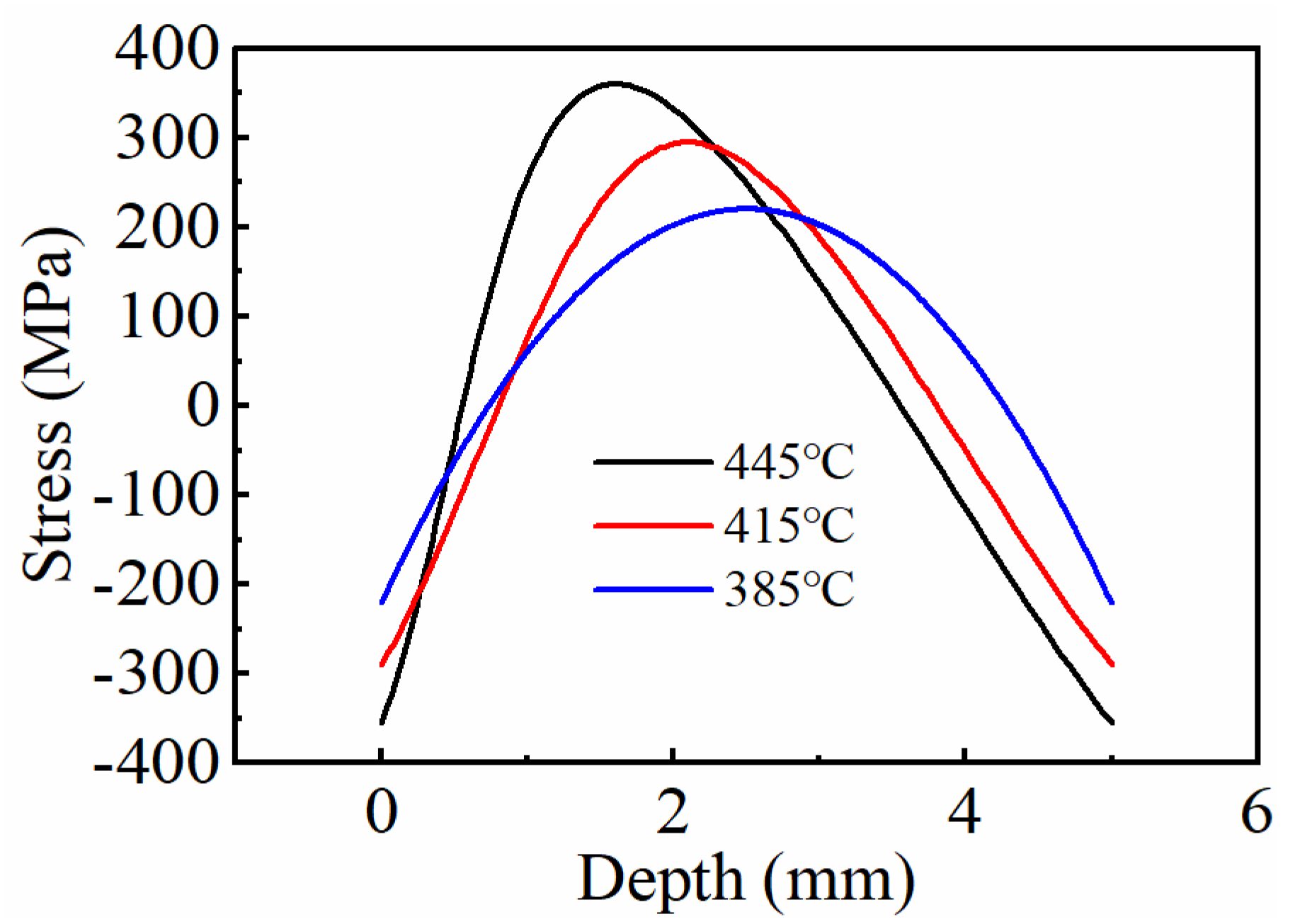
3.4. Influence of Cooling Rate on Residual Stress

The residual stress distribution after quenching in water at 20 °C, 40 °C, 60 °C, and 80 °C, respectively, are shown in Figure 10 and

Table 1. The influence of quenching temperatures on residual stress.

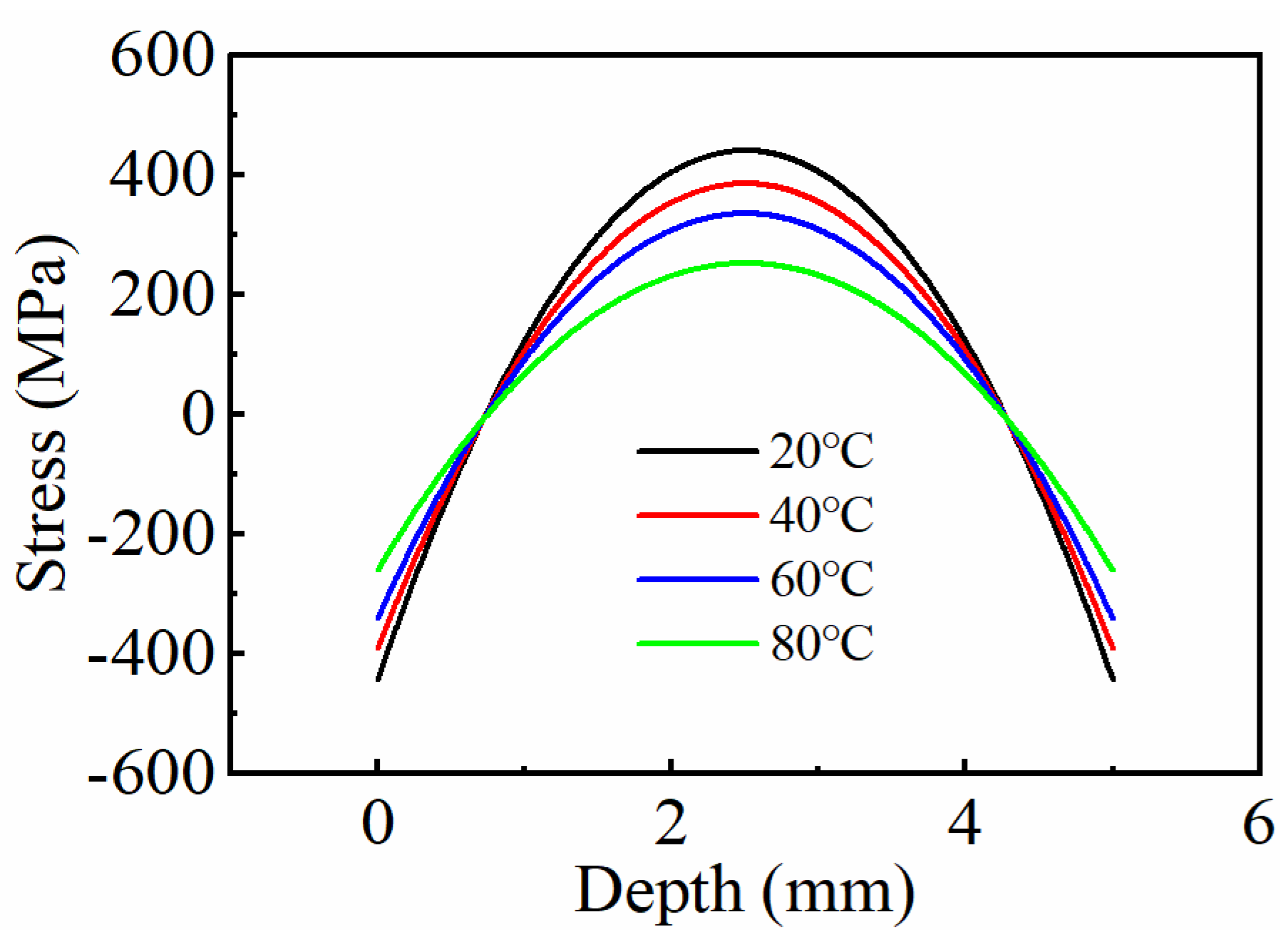
Quenching Temperatures (°C)	20	40	60	80
Surface residual stresses (MPa)	−442	−390	−340	−260
Core residual stresses (MPa)	439	384	334	251

. In Table 1, quenching temperature refers to the temperature of the water in which the quenching is carried out. The temperature selected is the commonly used quenching temperature of martensitic steel. The quenching residual stress at the four temperatures presents a symmetrical distribution. The residual stress value is higher when the quenching temperature is 20 °C. The surface stress is 440 MPa and the heart stress is −442 MPa. When quenching temperature is 60 °C, surface and core residual stresses are 335 MPa and −340 MPa. When the quenching temperature rises to 80 °C, the residual stress of the sample does not exceed 260 MPa. The results indicate that as the quenching temperature decreases, the temperature difference between the specimen and the cooling medium increases. Consequently, lowering the cooling rate can lead to a reduction in the residual stress of martensitic steel.

Figure 11 illustrates the evolution of temperature and stress at the surface and core of the sample following water quenching at 20 °C and 60 °C. When the sample is initially submerged in water, the cooling rate at 60 °C is lower than that at 20 °C. According to the stress evolution curves, both quenching temperatures result in tensile residual stress at the surface and compressive residual stress at the core upon entering the water. As quenching time progresses, the stress at the surface transitions from tensile to compressive, while the core stress shifts from compressive to tensile.

Figure 12 and

Table 2. The influence of Ms on the residual stress.

Starting temperature of martensitic transformation (°C)	445	415	385
Finishing temperature of martensitic transformation (°C)	270	240	210

present the impact of varying transition starting temperatures on residual stress. The peaks of tensile and compressive stresses are influenced by the transition starting temperature. As the transition starting temperature rises, the stress levels gradually increase. Consequently, the peak of tensile stress shifts towards the center, while the phase change stress decreases. The combination of thermal stress and phase change stress contributes to an increase in surface compressive stress. Thus, lowering the starting temperature for the martensitic transformation is advantageous for reducing residual stress.

Residual stress is inevitably generated during phase transition. Tempering can effectively reduce the residual stress. Tempering temperature refers to the temperature at which the metal is heated after tempering. The residual stress at 320 °C, 350 °C, and 380 °C without tempering is calculated. The evolution of residual stress under four conditions is shown in Figure 13 and

Table 3. The influence of tempering temperatures on the residual stress.

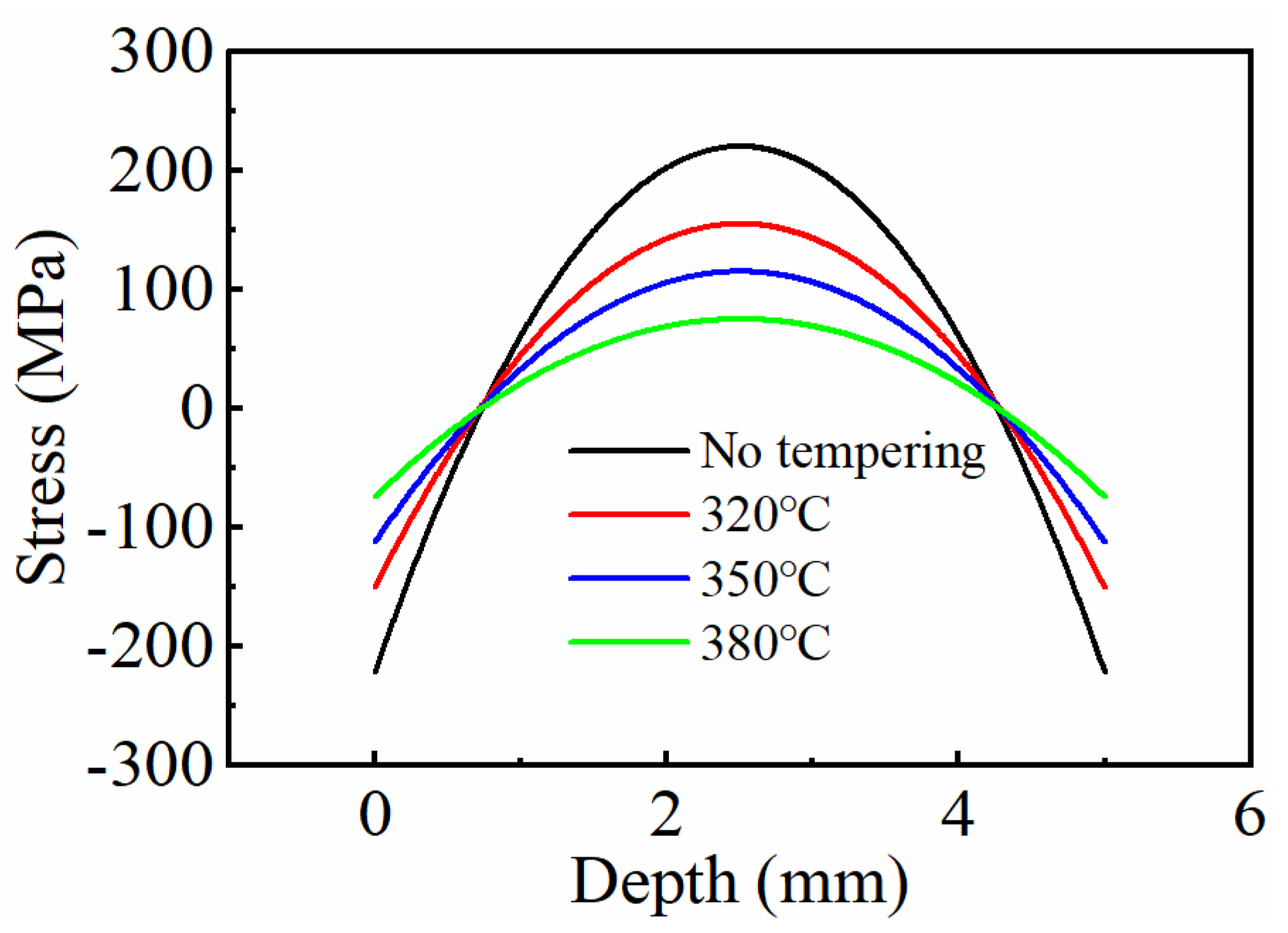
Tempering Temperatures (°C)	No Tempering	320	350	380
Surface residual stresses (MPa)	−221	−150	−112	−74
Core residual stresses (MPa)	220	154	114	74

. In Table 3, the tempering temperature is understood as the heating temperature of the material. Although the overall stress distribution trend is not obvious after tempering, the stress after tempering is lower than that before tempering. Tempering reduces the internal stress of martensitic steel, especially the residual stress with uneven distribution. The residual stress decreases with the increasing tempering temperature.

4. Conclusions

A method of residual stress prediction considering phase transition is proposed. The measures to reduce residual stress are discussed in terms of quenching medium, cooling rate, and the initial temperature and tempering temperature of the martensitic transformation by finite element simulation. The residual stress generated after quenching varies depending on the type of cooling medium used. In the case of air cooling, the residual stress in martensitic steel is lower, and the distribution of this stress is more uniform. An investigation into the residual stress of martensitic steel following tempering at 320 °C, 350 °C, and 380 °C reveals that increasing the tempering temperature leads to a reduction in residual stress. The optimal tempering temperature suggested is 380 °C. The findings indicate that lowering the initial temperature of phase transition helps to decrease residual stress. It is recommended to set the initial phase transition temperature at 385 °C. The reliability of the model is highly dependent on the material constitutive relationship and experimental data, but in some cases, the relevant parameters are difficult to obtain or inaccurate, which affects the prediction results. A combination of macro-scale and micro-scale modeling methods is used to more accurately capture stress distribution and phase transition processes inside the material. In order to further promote the application of martensitic steel and other types of steel, the residual stress forms of different alloy components and heat treatment processes on other steels such as low-alloy steel and high-strength steel and their effects on material properties were studied, and optimized treatment schemes were sought. The effects of different cooling rates, temperatures, and media on the residual stress and microstructure of martensitic steel and other steels during phase transformation were systematically studied in order to explore the best heat treatment process. Long-term fatigue tests and environmental stress tests are carried out to evaluate the performance and potential failure mode of martensitic steel under actual working conditions, providing a more reliable reference for industrial applications.