Next Article in Journal
Constitutive Equation and Heat Distortion Behavior of TA4 Titanium Alloy
Next Article in Special Issue
Effect of Molecular Perturbation on Polymorphism: The Case of 8-Halotheophyllines (8-Cl-Tph and 8-Br-Tph)
Previous Article in Journal
Impact of KOH Wet Treatment on the Electrical and Optical Characteristics of GaN-Based Red μLEDs
Previous Article in Special Issue
Advancements in the Research on the Preparation and Growth Mechanisms of Various Polymorphs of Calcium Carbonate: A Comprehensive Review
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Crystals
Volume 15
Issue 4
10.3390/cryst15040289
crystals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Polymorphism and the Phenomenon of Whole-Molecule Disorder Revealed in a Novel Dipodal Thiopyridine Ligand

by
Simran Chaudhary
,
Renny Maria Losus
and
Liliana Dobrzańska
*
Faculty of Chemistry, Nicolaus Copernicus University in Toruń, Gagarina 7, 87-100 Toruń, Poland
*
Author to whom correspondence should be addressed.
Crystals 2025, 15(4), 289; https://doi.org/10.3390/cryst15040289
Submission received: 9 March 2025 / Revised: 17 March 2025 / Accepted: 19 March 2025 / Published: 22 March 2025
(This article belongs to the Special Issue Crystalline Materials: Polymorphism)
Browse Figures
Versions Notes

Abstract

:
We report two polymorphs (α and β) of a novel bipodal ligand, 1,4-bis(thiopyridine)benzene, which were isolated from the same methanolic solution. Single-crystal X-ray analyses revealed the phenomenon of positional whole-molecule disorder occurring in form α, which comes down to packing disorder. Computational calculations were carried out to compare the crystal lattice energies of the isolated polymorphs. The energetically more stable form β has a higher packing efficiency and shows an increased number of hydrogen bonds compared with both components of form α, the packing of which is dominated by van der Waals interactions. Supportive bulk studies, such as thermal analysis and powder X-ray diffraction, were also performed.

Graphical Abstract

1. Introduction

Studies on polymorphism [1], the ability of a compound to crystallize in two or more crystalline forms differing by molecular conformation [2,3,4], molecular arrangement, or both, is highly important, from both a scientific and an industrial point of view, as sometimes, slight differences in the crystal structures of polymorphs can lead to entirely different properties [5]. This phenomenon is particularly relevant within the pharmaceutical industry, where the appearance of different forms can have serious repercussions on the API (active pharmaceutical ingredient), including changes in drug properties, such as the dissolution rate, solubility, chemical stability, melting point, color, and even biological performance, including efficacy and toxicity. Therefore, selecting an API’s solid form is a crucial step [6].
Though there are a lot of reports in the literature on polymorphism, gaining control over the desired polymorphic form is still far from being understood. Computational studies such as crystal structure predictions (CSPs), which are under continuous development to complement the experimental screening of solid forms, help to identify the most likely formed polymorphic phases, and to understand the crystallization behavior at the molecular level [7,8,9]. However, determining the crystal structures of metastable polymorphs through computational prediction methods has been considered difficult, particularly in flexible molecules, as these methods are still in their infancy [10,11].
In continuation of our studies on polymorphism taking place in dipodal N-donor ligands containing an aromatic core [12], we isolated polymorphs of 1,4-bis(thiopyridine)benzene (Scheme 1). Interestingly, one of the forms (α) showed whole-molecule disorder, a phenomenon which occurs when a molecule in a crystal can occupy multiple orientations or positions. Depending on the energy of the adapted molecular orientations, we could expect either a 50:50 molecular disorder ratio for the same energy, or differentiation based on the energy gap; for example, the whole-molecule disorder revealed for (1-adamantyl)methyl-1-adamantanecarboxylate shows 95/5 occupancies of the components [13]. One of the most studied systems showing whole-molecule disorder is (C60—Ih) fullerene [14,15]. However, the phenomenon is not encountered so often. Mostly, the two components are related by pseudo two-fold symmetry, as reported, for example, for 2-(2-thien-yl)-1-(2-pyrazin-yl)ethene and 2-(2-thien-yl)-1-(2-quinoxalin-yl)ethene [16], but there are also cases where the components are not related by a symmetry operation, such as for 4,4′-sulfonyl-bis[N-(4-nitro-phenyl-methylene)benzen-amine] [17]. In a very recent paper, whole-molecule disorder was revealed for one out of three molecules in 8-nitrobenzothiazinone [18]. Our studies were elaborated by applying computational methods, as well as via supportive studies on bulk material, such as PXRD and thermal analyses.

2. Materials and Methods

2.1. Reagents and Materials

All commercially available chemicals and solvents were of reagent grade, and were used without further purification. The new ligand 1,4-bis(thiopyridine)benzene was synthesized via a procedure adapted from the synthesis of 2-benzenesulfonyl-pyridine [19]. A 25 mL flask was charged with 4-bromopyridine hydrochloride (1.45 g, 7.5 mmol), 1,4-benzenedithiol (0.5 g, 3.5 mmol), and DMF (5 mL). K2CO3 (2.21 g, 16 mmol) was added, and the mixture was heated to 110 °C and stirred for 24 h. The resulting mixture was extracted using water and ethyl acetate. The organic layer was washed with water, dried over MgSO4, filtered, and concentrated to give the pure product as a yellow solid. Yield = 88%. 1H NMR (CDCl3, 700 MHz): δ = 7.15 (d, 4H), 7.62 (t, 4H), 8.47 (s, 4H) ppm; 13C NMR (CDCl3, 100 MHz): δ = 149.8, 148.5, 135.3, 132.1, 121.7 ppm. MP = 133–135 °C.
By slow evaporation at room temperature, 1,4-Bis(thiopyridine)benzene (10 mg) was re-crystallized from methanol and THF (10 mL). Crystals of forms α and β were obtained after a few days from the same methanolic solution, and were used for SCXRD analysis. The latter form was also isolated from a THF solution.

2.2. Measurements

1H and 13C NMR spectra of the ligand were recorded on a Bruker Avance III 700 and 400 instrument, respectively, and referenced to residual solvent peaks. The melting point was collected with a Stuart SMP50 automated melting point apparatus, starting at a temperature of 30 °C and ramping up at 2 °C/min.
PXRD analyses were performed on a Philips X’pert diffractometer using CuKα radiation. The samples were measured at ambient temperature in a 2θ range of 4–45°, at a scan speed of 4°/min. PXRD data were investigated using the Powder Cell, version 2.4 [20] and Profex, version 4.3.4 [21] software packages.
Thermal analyses (TGA, heat flow-calibrated DTA) were carried out on a Perkin Elmer Pyris STA9 analyzer at a heating rate of 2 °C min−1, under dry nitrogen with a flow rate of 20 mL min−1.

2.3. Computational Studies

Hirshfeld surface analysis [22] was conducted using CrystalExplorer 21 [23], which serves as an important tool for gaining additional insight into the intermolecular interaction of molecular crystals. The directions and strengths of intermolecular interactions within the molecular crystal were mapped onto Hirshfeld surfaces. Two-dimensional fingerprint plots of all the interactions present in forms α and β were generated in the range of 0.4–2.8 Å, including reciprocal contacts. The same program was used for calculating the crystal lattice energies and their decomposition into 4 terms: electrostatic, exchange, induction, and dispersion, by applying the CE-B3LYP energy model. Moreover, PIXEL [24,25,26] was also used to calculate the crystal lattice energies. The molecular wavefunctions for CrystalExplorer and molecular electron densities for Pixel were calculated using Gaussian 16 [27] at the B3LYP/6-31G(d,p) and MP2/6-31G** levels, respectively. A comparison of the molecular packing similarity was performed using Mercury [28], by calculating the positional differences between a cluster of 15 molecules in each structure, and using the program XPac [29,30], the strategy of which comes down to a comparison of the intermolecular angular parameters, to indicate the similarity of compounds at the level of so-called supramolecular constructs of different dimensionality. Moreover, it calculates the dissimilarity index ‘x’ with a value equal to 0, corresponding to perfect geometrical similarity. The computational studies for α were performed on both isolated components (major—αa, and minor—αb).

2.4. Structure Determination

Single-crystal X-ray diffraction data were collected on an XtaLAB Synergy-S Dualflex diffractometer equipped with monochromated CuKα radiation (λ = 1.54184). The crystals were mounted on a nylon loop and coated with Paratone-N oil. Data collection was carried out at 100(2) K to minimize solvent loss, possible structural disorder, and thermal motion effects. Cell refinement and data reduction was performed by using the corresponding diffractometer’s software package (CrysAlisPro Software System, version CrysAlisPro 1.171.43.120a; Rigaku, Oxford, UK). The structures were solved by using direct methods with SHELXS-2019/3 [31], and refined by using full-matrix least-squares methods based on F2 by using SHELXL-2019/3 [32]. All non-hydrogen atoms were refined anisotropically. All H atoms were positioned geometrically with C-H = 0.95 Å (aromatic), and refined as riding, with Uiso (H) = 1.2 Ueq (C). The programs Mercury [28] and POV-Ray were both used to prepare molecular graphics. A summary of the data collection and structure refinement parameters is provided in Table 1. The crystallographic data for α and β have been deposited at the Cambridge Crystallographic Data Centre: CCDC 2429692-2429693, respectively. These data can be obtained free of charge from the Cambridge Crystallographic Data Centre via http://www.ccdc.cam.ac.uk/structures (accessed on 22 January 2025).

3. Results and Discussion

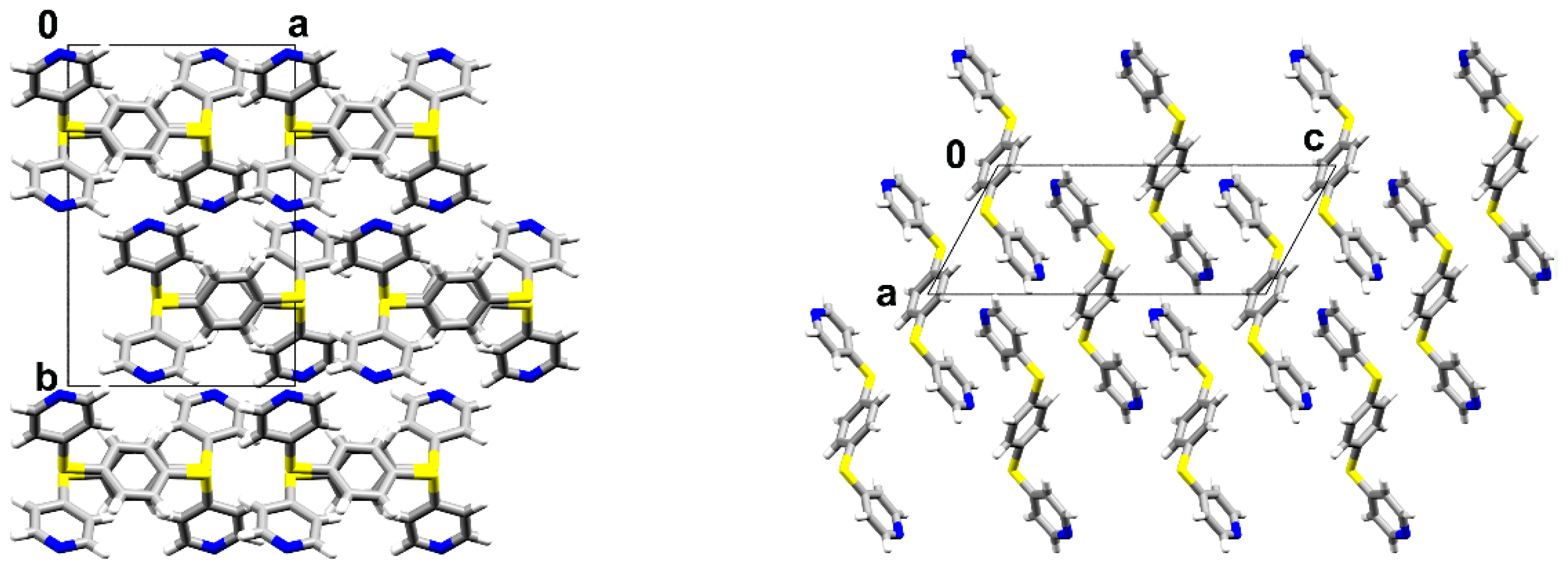
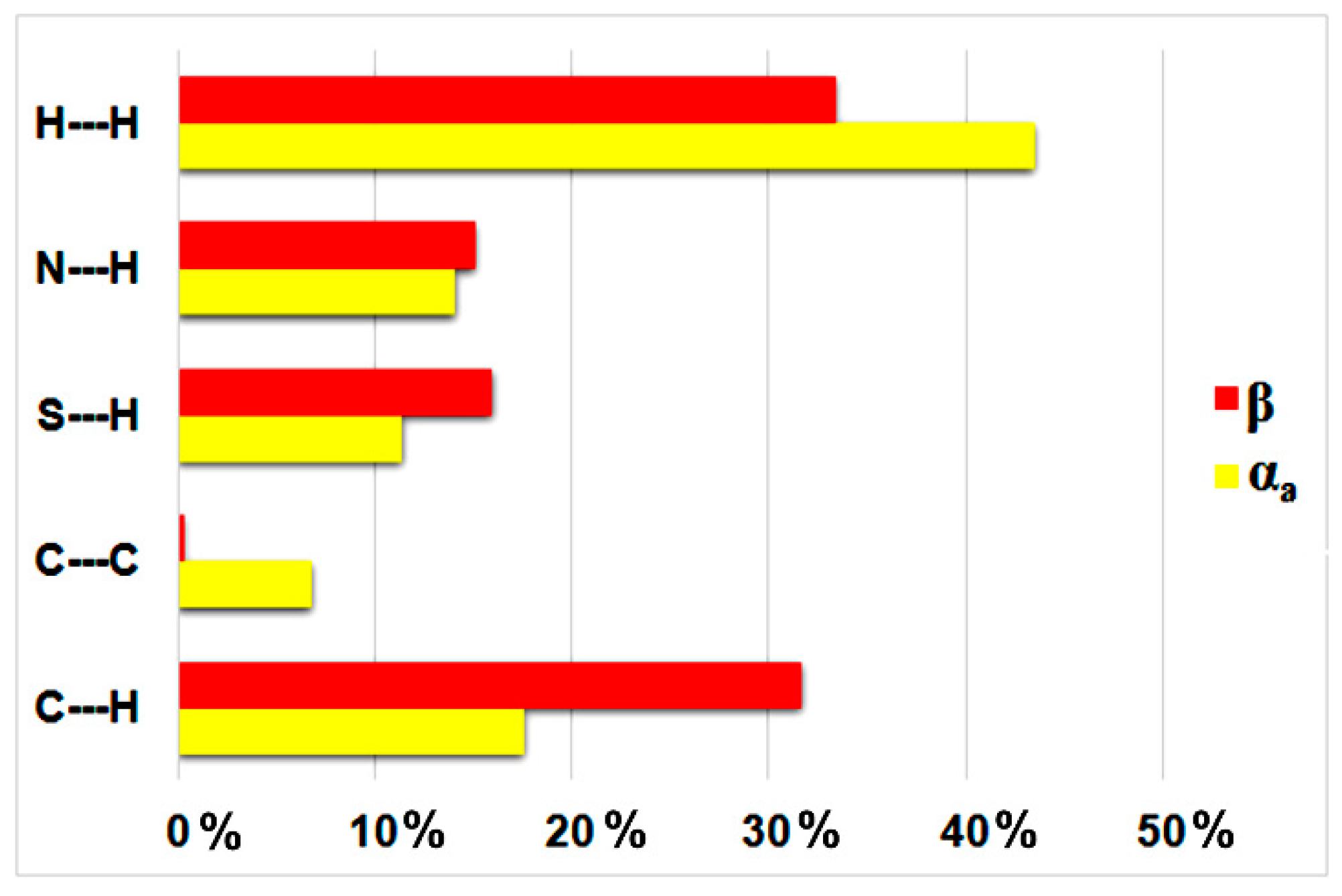
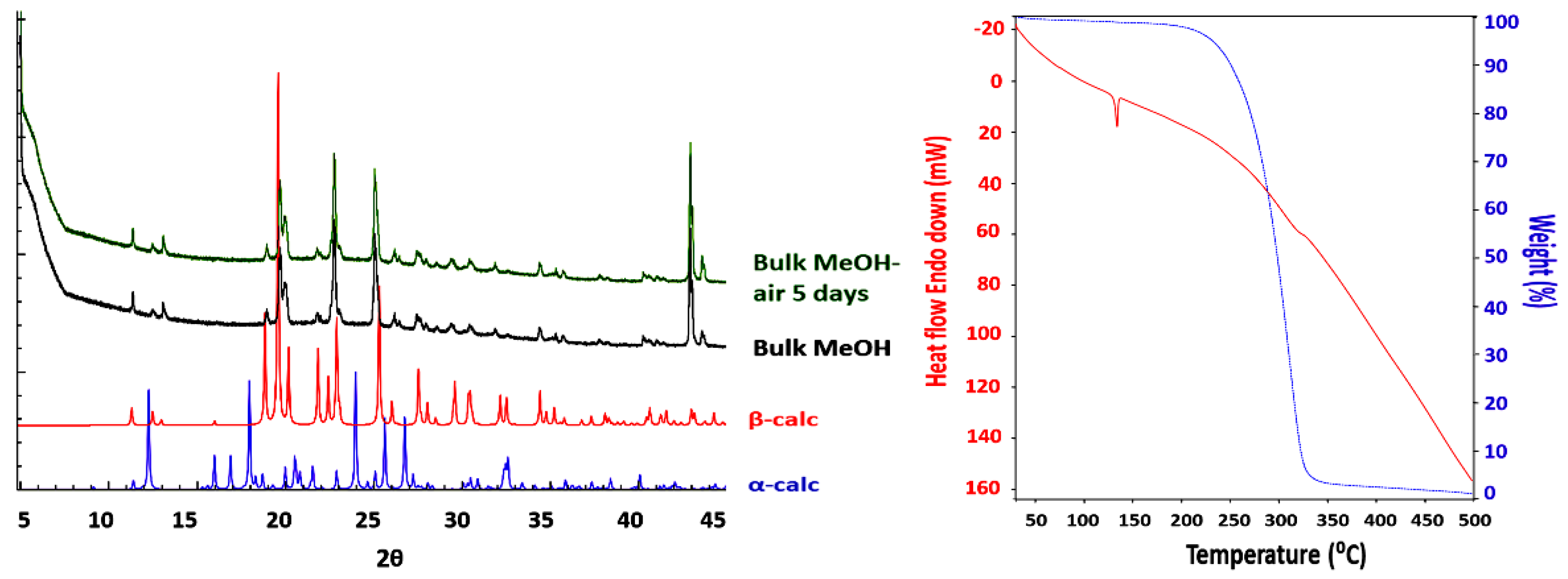
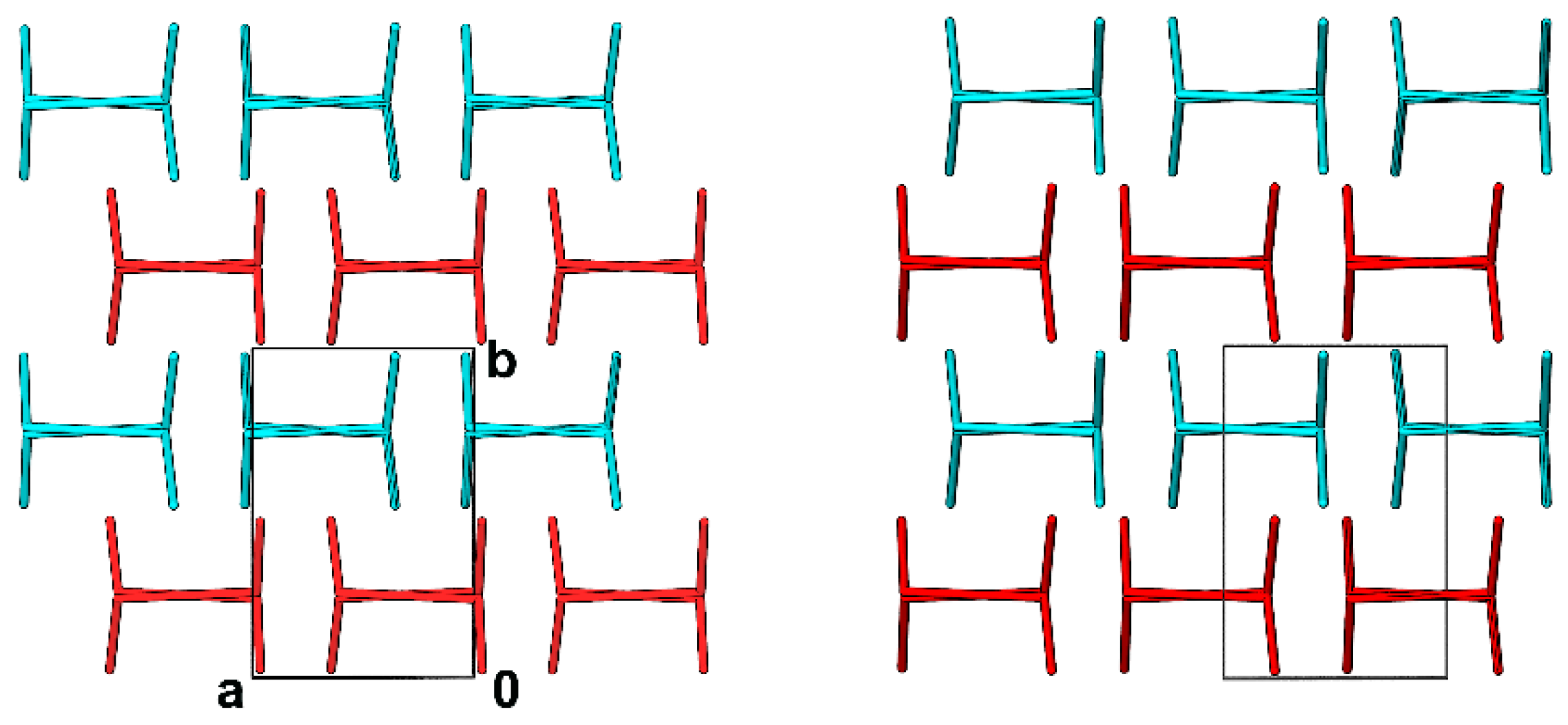
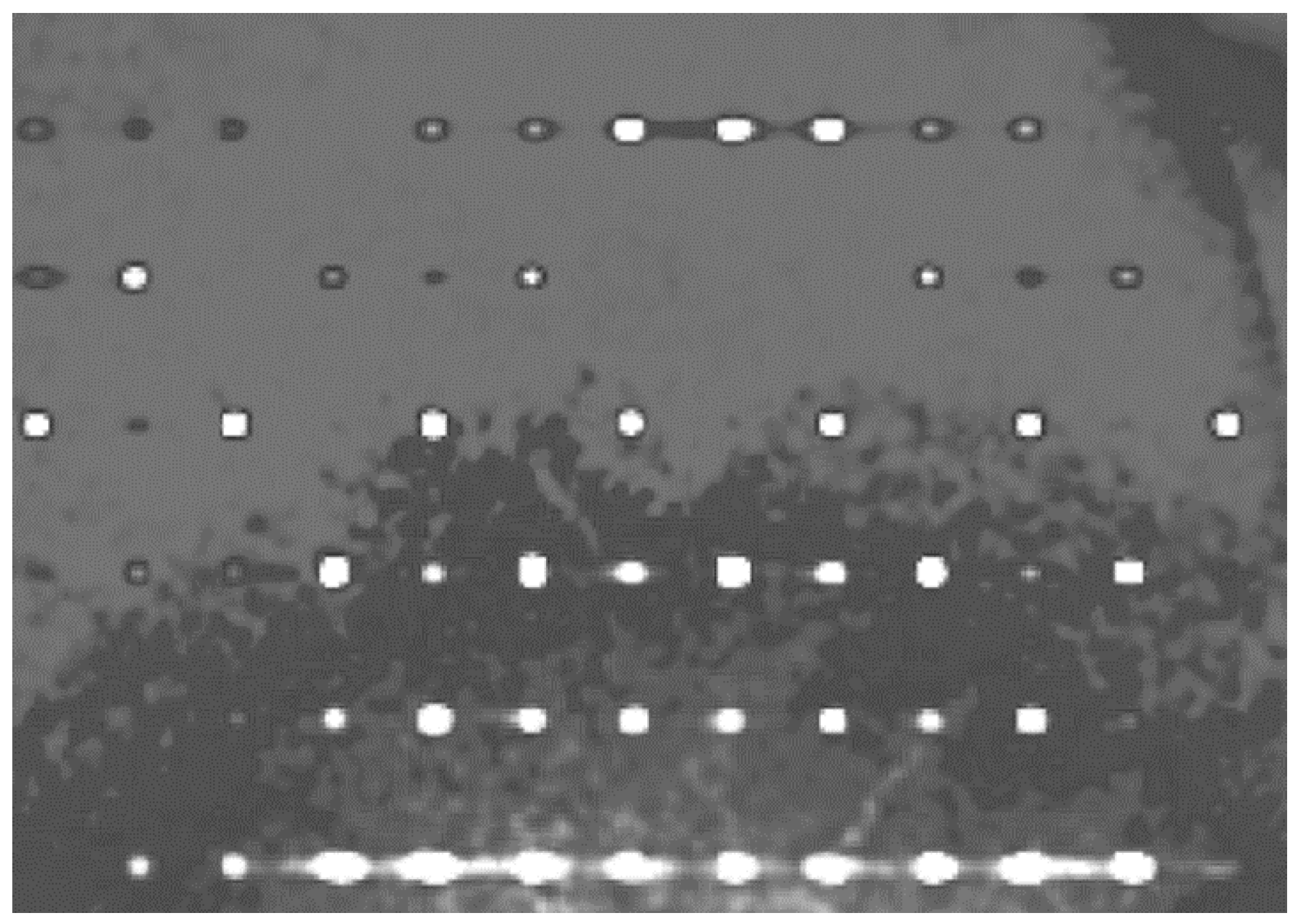
3.1. Crystal Structures and Studies on Bulk

SCXRD revealed that both isolated polymorphs, α and β, crystallize in the same P21/c space group of the monoclinic system. Form α contains one molecule of 1,4-bis(thiopyridine)benzene in the asymmetric unit (Figure 1), unlike form β, which contains half a molecule, with the other half being generated by an inversion center. Interestingly, α shows whole-molecule disorder, with occupancies of the components estimated to have a 93:7 ratio. We have separated both components (major—αa, and minor—αb) and used these in further comparisons.
The bond lengths and angles of the molecules in αa and β do not deviate from typical values for comparable molecular fragments, as revealed by a geometry check performed with the application Mogul [33]. The geometry of αb is not perfect, as a result of its low occupancy input.
The molecules in these two polymorphs adopt pretty much the same ‘anti-’ conformation, showing a slight change in the orientation of the pyridine rings, which results from differences in packing and, accordingly, distinct sets of intermolecular interactions. The angles between the mean planes of the benzene ring and the pyridine rings are 81/82° and 84° in αa and β, respectively. On the other hand, the angles between the mean planes of the pyridine rings in αa and β are 9° and 0°, respectively.
The molecular arrangements in αa and β are very distinct (Figure 2). Both programs XPac and Mercury indicated no packing similarities between these two phases.
The intermolecular interactions in both polymorphs involve an abundant net of C-H---N hydrogen bonds, leading to the formation of 3D supramolecular assemblies, supported in αa by π-π interactions formed between the pyridine rings (N18), with a distance of 3.619 Å (Table 2). Moreover, it seems that S---S interactions [34] are also involved in stabilizing the molecular arrangements in β, with a distance of 3.5541(6) Å, which is shorter than the sum of their van der Waals radii (3.66 Å) [35]. In the case of αa, these distances are a bit longer, namely 3.7321(6) Å.
To quantify the contributions of the different contacts, a Hirshfeld analysis was performed, allowing for the generation of fingerprint plots for αa and β and the determination of the relative contributions of intermolecular contacts to the Hirshfeld surface [23]. These indicated that β is clearly dominated by weak hydrogen bonds, whereas αa is dominated by van der Waals forces and further stabilized by weak hydrogen bonding and π-π interactions. The latter are absent in β (Figure 3).

3.2. Polymorph Stability

The crystal lattice energy calculations (Table 3) carried out with CrystalExplorer indicated a lower stability of αa compared to form β (ca. 9 kJ/mol), which is in accordance with the calculated packing efficiencies (70.1 versus 71.6%) and densities (1.398 g/cm3 versus 1.429 g/cm3).
PXRD studies performed on the bulk crystalline material indicated dominancy of the β phase (the powder pattern did not change after leaving the sample exposed to air for 5 days). It seems that α converts rather quickly to β (the crystal measured was taken from the solution). The bulk sample did not undergo any transitions in a temperature range from room temperature up to the melting point, as shown on the DTA curve (Figure 4).

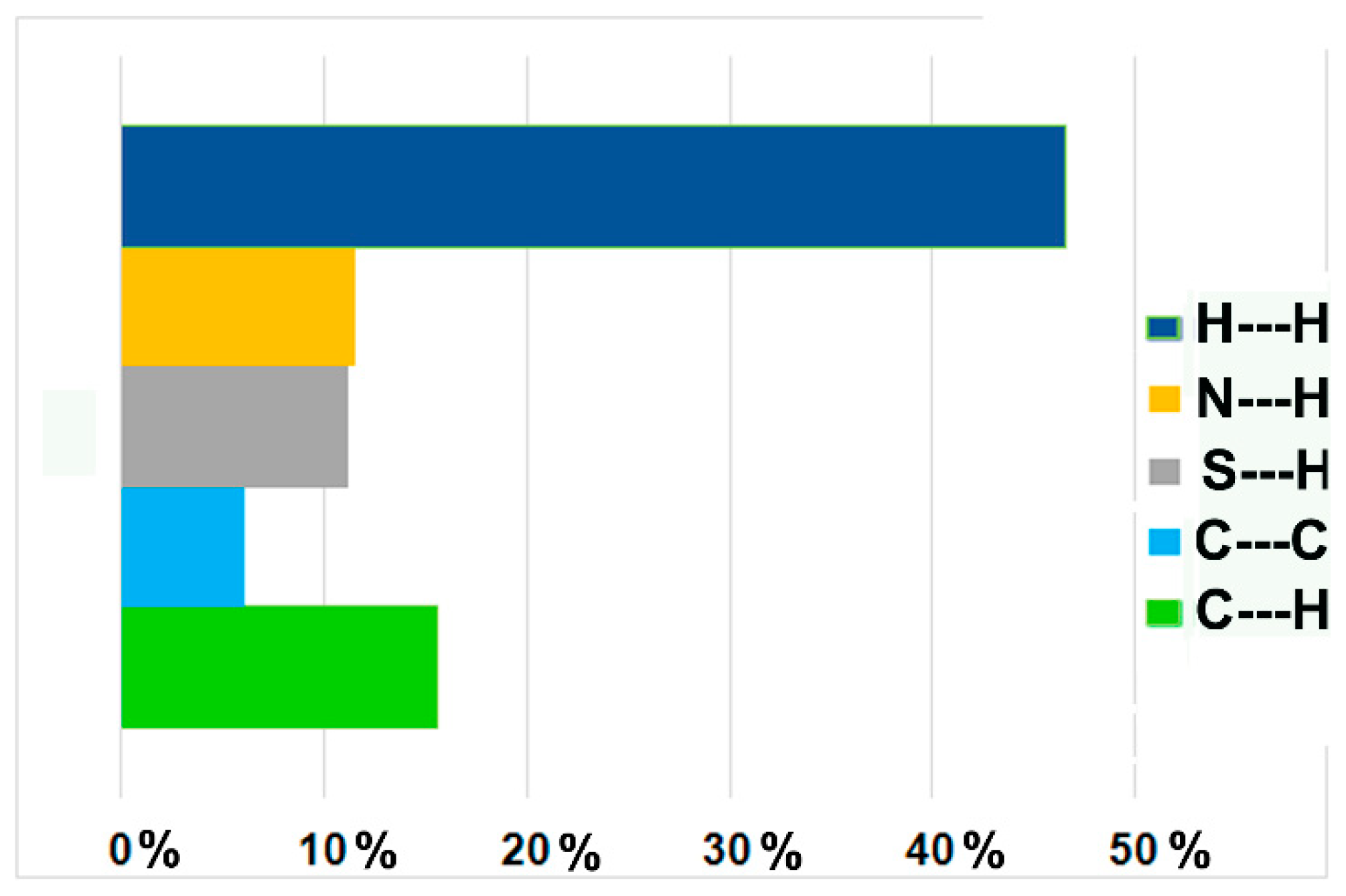
3.3. Whole-Molecule Disorder

There are claims that whole-molecule disorder does not exist, and that the phenomenon could be overlooked twinning or some other structure-related issue. In the presented case, the model with whole-molecule disorder gave us the best output.
Comparison of the packing modes of the ligand molecules in αa and αb (Figure 5) indicates that the difference between the major and the minor component lies mostly in the mutual position of the AB layers formed by the ligands parallel to the ac plane. This is also evident from the results generated by the program XPack, which was used to estimate the similarity of the molecular arrangements, and is especially handy in the case of isostructural systems or polymorphs. It indicated the formation of 2D supramolecular constructs (meaning the presence of matching layers that show differences in the way they are stacked), and calculated a dissimilarity index equal to 1.7, which indicates high similarity between both components. For clarification, this value is in the range of those obtained upon replacement of small substituents in crystal structures such as Cl with Br (x = 1) and Me with CF3 (x = 2.8) [36]. The program Mercury also estimated a high similarity between αa and αb, showing overlap of 8 molecules out of 15, with an RMS deviation of 0.063 Å (the standard settings were used, selecting the molecules with 20% tolerance for bonds and angles).
Both components (major αa and minor αb) show different sets of intermolecular interactions. This is obviously a rough estimate for αb, as it concerns a component with a very low input in the crystal formed. Hirshfeld analyses performed with CrystalExplorer indicated that the packing of αb is dominated by van der Waals interactions to a higher extent than is the case for αa, and that it shows a lower input of H bonding (Figure 6). This observation is supported by calculated enrichment ratios [37], indicating dominance of C-H---N interactions in αa, with a value of 1.47, versus 1.11 in αb (see also Table 4; the same labeling was applied for both components), and slight dominance of H---H contacts in αb (1.07 versus 1.03).
Hydrogen bonds involving the C17A and C6A atoms, as well as S7A---S14A interactions (3.725 Å) in αb, result in the formation of 2D supramolecular layers parallel to the ac plane, a motive which is also present in αa. Interestingly, new very short contacts occur between the AB layers, involving C9A and N18A, as well as very short π-π contacts between the pyridine rings (N18A) of the layers, defined as such with a distance of ca. 2.86 Å, as a result of changes in their mutual position. The shortness of the new contacts could indicate that the αb component is just a local defect, in particular, a stacking fault, which could also be perceived as stacking disorder. This interpretation is supported by the lines of diffuse scattering occurring along the reciprocal b* axis (Figure 7).
This molecular arrangement leads molecules to encounter large repulsive forces, as was shown by applying the standard set of programs, such as CrystalExplorer and PIXEL [38] (Table 5).
As we were aware that we were dealing with some sort of artificial, faulty structure, we checked what the shortest reported π-π distances were, and we found some structures of coordination compounds showing the presence of π-π distances of similar length, namely 2.94 Å (refcode ZOMSEB) and 2.96 Å (refcode OXUDES0). We also selected two organic molecules (hits: ECUTUR09, NPOFNP09) showing slightly longer, but still quite short, π-π distances of ca. 3.1 Å, and performed analogous crystal lattice energy calculations using the suite of standard programs. The results generated via CrystalExplorer and Pixel were similar to those obtained for αb (Table 6). A high repulsion term indicated unfavorable structural arrangements.
These results, obtained for earlier reported crystal structures containing short π-π distances, raise the question of whether αb is nothing more than a local defect, or whether it would be possible to isolate it as an independent polymorph.
This is, to some extent, reminiscent of the issue concerning the elusive form II of aspirin, which was broadly discussed for many years [39,40,41,42] before, finally, phase II was isolated [43]. The difference between form I and II of aspirin also lies in the mutual arrangement of 2D layers stabilized via C-H---O interactions. However, both of these phases form separated domains, leading to the phenomenon of intergrowth polymorphism. Applying XPack to check the similarities of the phases in aspirin’s forms I and II indicated the formation of 2D constructs with x = 0.8.

4. Conclusions

Two polymorphs of a novel heterocyclic ligand, namely 1,4-bis(thiopyridine)benzene, were isolated. The energetically more stable form is dominated by hydrogen bonds, whereas the less stable form is dominated by van der Waals interactions. The positional whole-molecule disorder observed in phase α reveals the presence of stacking faults, whereby a shift in the molecular layers causes an increase in the repulsion forces, as a result of shortening of the distances between the molecules in these layers, such as the centroid–centroid distance between the pyridine rings, and C-H---N interactions. As structures with similarly short π-π distances have been reported before, one might wonder whether the minor ‘faulty’ component could be isolated as an independent polymorph. It would be the least stable form from those presented, with the lowest input of hydrogen bonds, the packing of which is dominated by van der Waals interactions. We are currently trying to tackle this issue with other computational methods, and are also trying to figure out what the minimal possible distance would be for π-π stacking of aromatic rings in the rich world of a molecular kaleidoscope.

Author Contributions

Conceptualization, L.D.; software, S.C., R.M.L. and L.D.; investigation, S.C., R.M.L. and L.D.; writing—original draft preparation, L.D. and S.C.; editing, R.M.L.; visualization, L.D., S.C. and R.M.L. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Science Centre—Poland, grant number 2014/14/E/ST5/00611.

Data Availability Statement

Data are contained within the article.

Acknowledgments

All authors would like to thank the ‘Excellence Initiative—Research University’ program for funding the research group of Crystal Engineering and Advanced Solid-State Characterization.

Conflicts of Interest

The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

  1. Cruz-Cabeza, A.J.; Reutzel-Edens, S.M.; Bernstein, J. Facts and Fictions about Polymorphism. Chem. Soc. Rev. 2015, 44, 8619–8635. [Google Scholar] [CrossRef]
  2. Nangia, A. Conformational Polymorphism in Organic Crystals. Acc. Chem. Res. 2008, 41, 595–604. [Google Scholar]
  3. Cruz-Cabeza, A.J.; Bernstein, J. Conformational Polymorphism. Chem. Rev. 2014, 114, 2170–2191. [Google Scholar]
  4. Sengupta, B.; Beasley, M.; Mason, B. Conformational Polymorphism in Organic Crystals: Structural and Functional Aspects—A Review. Curr. Res. Mater. Chem. 2019, 1, 104. [Google Scholar]
  5. Purohit, R.; Venugopalan, P. Polymorphism: An Overview. Resonance 2009, 14, 882–893. [Google Scholar]
  6. Lee, E.H. A Practical Guide to Pharmaceutical Polymorph Screening & Selection. Asian J. Pharm. Sci. 2014, 9, 163–175. [Google Scholar]
  7. Price, S.L. Computational Prediction of Organic Crystal Structures and Polymorphism. Int. Rev. Phys. Chem. 2008, 27, 541–568. [Google Scholar]
  8. Wu, E.J.; Kelly, A.W.; Iuzzolino, L.; Lee, A.Y.; Zhu, X. Unprecedented Packing Polymorphism of Oxindole: An Exploration Inspired by Crystal Structure Prediction. Angew. Chem. Int. Ed. 2024, 63, e202406214. [Google Scholar]
  9. Beran, G.J.O. Frontiers of Molecular Crystal Structure Prediction for Pharmaceuticals and Functional Organic Materials. Chem. Sci. 2023, 14, 13290–13312. [Google Scholar] [CrossRef]
  10. Dudek, M.K.; Drużbicki, K. Along the Road to Crystal Structure Prediction (CSP) of Pharmaceutical-like Molecules. CrystEngComm 2022, 24, 1665–1678. [Google Scholar]
  11. Nikhar, R.; Szalewicz, K. Reliable Crystal Structure Predictions from First Principles. Nat. Commun. 2022, 13, 3095. [Google Scholar] [CrossRef] [PubMed]
  12. Chaudhary, S.; Kędziera, D.; Rafiński, Z.; Dobrzańska, L. Solvent-Induced Polymorphism in Dipodal N-Donor Ligands Containing a Biphenyl Core. RSC Adv. 2023, 13, 30625–30632. [Google Scholar]
  13. Milić, D.; Alešković, M.; Matkovic-Calogovic, D.; Mlinarić-Majerski, K. (1-Adamantyl)Methyl Esters: Whole-Molecule Disorder in the Crystal Structure of (1-Adamantyl)Methyl-1-Adamantanecarboxylate. Croat. Chem. Acta 2009, 82, 833–839. [Google Scholar]
  14. Dorset, D.L.; McCourt, M.P. Disorder and the Molecular Packing of C60 Buckminsterfullerene: A Direct Electron-Crystallographic Analysis. Acta Crystallogr. Sect. A 1994, 50, 344–351. [Google Scholar]
  15. David, W.I.F.; Ibberson, R.M.; Matthewman, J.C.; Prassides, K.; Dennis, T.J.S.; Hare, J.P.; Kroto, H.W.; Taylor, R.; Walton, D.R.M. Crystal Structure and Bonding of Ordered C60. Nature 1991, 353, 147–149. [Google Scholar] [CrossRef]
  16. Ichharam, V.; Boeyens, J.C.A. Structural Analysis of 2-(2-Thienyl)-1-(2-Pyrazinyl)Ethene [C10H8N2S] and 2-(2-Thienyl)-1-(2-Quinoxalinyl)Ethene [C14H10N2S]. Cryst. Eng. 2001, 4, 171–178. [Google Scholar]
  17. Cox, P.J.; Wardell, J.L. 4,4′-Sulfonyl-Bis[N-(4-Nitro-Phenyl-Methylene)Benzen-Amine. Acta Crystallogr. Sect. C Cryst. Struct. Commun. 2003, 59, 706–708. [Google Scholar] [CrossRef]
  18. Seidel, R.W.; Goddard, R.; Schlegel, T.U.; Richter, A.; Rudolph, I.; Imming, P. Polymorphism and Whole-Molecule Disorder of an Antitubercular 8-Nitrobenzothiazinone. J. Chem. Crystallogr. 2024, 1–10. [Google Scholar] [CrossRef]
  19. Trankle, W.G.; Kopach, M.E. Green Chemical Synthesis of 2-Benzenesulfonyl-Pyridine and Related Derivatives. Org. Process Res. Dev. 2007, 11, 913–917. [Google Scholar]
  20. Kraus, W.; Nolze, G. POWDER CELL—A Program for the Representation and Manipulation of Crystal Structures and Calculation of the Resulting X-Ray Powder Patterns. J. Appl. Crystallogr. 1996, 29, 301–303. [Google Scholar]
  21. Doebelin, N.; Kleeberg, R. Profex: A Graphical User Interface for the Rietveld Refinement Program BGMN. J. Appl. Crystallogr. 2015, 48, 1573–1580. [Google Scholar] [CrossRef] [PubMed]
  22. Spackman, M.A.; Jayatilaka, D. Hirshfeld Surface Analysis. CrystEngComm 2009, 11, 19–32. [Google Scholar] [CrossRef]
  23. Spackman, P.R.; Turner, M.J.; McKinnon, J.J.; Wolff, S.K.; Grimwood, D.J.; Jayatilaka, D.; Spackman, M.A. CrystalExplorer: A Program for Hirshfeld Surface Analysis, Visualization and Quantitative Analysis of Molecular Crystals. J. Appl. Crystallogr. 2021, 54, 1006–1011. [Google Scholar] [CrossRef]
  24. Gavezzotti, A. Calculation of Intermolecular Interaction Energies by Direct Numerical Integration over Electron Densities. 2. An Improved Polarization Model and the Evaluation of Dispersion and Repulsion Energies. J. Phys. Chem. B 2003, 107, 2344–2353. [Google Scholar] [CrossRef]
  25. Gavezzotti, A. Non-Conventional Bonding between Organic Molecules. the “halogen Bond” in Crystalline Systems. Mol. Phys. 2008, 106, 1473–1485. [Google Scholar] [CrossRef]
  26. Reeves, M.G.; Wood, P.A.; Parsons, S. MrPIXEL: Automated Execution of Pixel Calculations via the Mercury Interface. J. Appl. Crystallogr. 2020, 53, 1154–1162. [Google Scholar] [CrossRef] [PubMed]
  27. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
  28. MacRae, C.F.; Sovago, I.; Cottrell, S.J.; Galek, P.T.A.; McCabe, P.; Pidcock, E.; Platings, M.; Shields, G.P.; Stevens, J.S.; Towler, M.; et al. Mercury 4.0: From Visualization to Analysis, Design and Prediction. J. Appl. Crystallogr. 2020, 53, 226–235. [Google Scholar] [CrossRef]
  29. Gelbrich, T.; Hursthouse, M.B. A Versatile Procedure for the Identification, Description and Quantification of Structural Similarity in Molecular Crystals. CrystEngComm 2005, 7, 324–336. [Google Scholar] [CrossRef]
  30. Gelbrich, T.; Hursthouse, M.B. Systematic Investigation of the Relationships between 25 Crystal Structures Containing the Carbamazepine Molecule or a Close Analogue: A Case Study of the XPac Method. CrystEngComm 2006, 8, 448–460. [Google Scholar] [CrossRef]
  31. Sheldrick, G.M. A Short History of SHELX. Acta Crystallogr. Sect. A 2008, 64, 112–122. [Google Scholar] [CrossRef]
  32. Sheldrick, G.M. Crystal Structure Refinement with SHELXL. Acta Crystallogr. Sect. C Struct. Chem. 2015, 71, 3–8. [Google Scholar] [CrossRef] [PubMed]
  33. Bruno, I.J.; Cole, J.C.; Kessler, M.; Luo, J.; Momerwell, W.D.S.; Purkis, L.H.; Smith, B.R.; Taylor, R.; Cooper, R.I.; Harris, S.E.; et al. Retrieval of Crystallographically-Derived Molecular Geometry Information. J. Chem. Inf. Comput. Sci. 2004, 44, 2133–2144. [Google Scholar]
  34. Antonijević, I.S.; Janjić, G.V.; Milčić, M.K.; Zarić, S.D. Preferred Geometries and Energies of Sulfur-Sulfur Interactions in Crystal Structures. Cryst. Growth Des. 2016, 16, 632–639. [Google Scholar]
  35. Bondi, A. Van Der Waals Volumes and Radii. J. Phys. Chem. 1964, 68, 441–451. [Google Scholar]
  36. Gelbrich, T.; Threlfall, T.L.; Hursthouse, M.B. XPac Dissimilarity Parameters as Quantitative Descriptors of Isostructurality: The Case of Fourteen 4,5′-Substituted Benzenesulfonamido-2-Pyridines Obtained by Substituent Interchange Involving CF3/I/Br/Cl/F/Me/H. CrystEngComm 2012, 14, 5454–5464. [Google Scholar] [CrossRef]
  37. Jelsch, C.; Ejsmont, K.; Huder, L. The Enrichment Ratio of Atomic Contacts in Crystals, an Indicator Derived from the Hirshfeld Surface Analysis. IUCrJ 2014, 1, 119–128. [Google Scholar]
  38. Munday, L.B.; Solares, S.D.; Chung, P.W. Generalized Stacking Fault Energy Surfaces in the Molecular Crystal RDX. Philos. Mag. 2012, 92, 3036–3050. [Google Scholar] [CrossRef]
  39. Ouvrard, C.; Price, S.L. Toward Crystal Structure Prediction for Conformationally Flexible Molecules: The Headaches Illustrated by Aspirin. Cryst. Growth Des. 2004, 4, 1119–1127. [Google Scholar]
  40. Vishweshwar, P.; McMahon, J.A.; Oliveira, M.; Peterson, M.L.; Zaworotko, M.J. The Predictably Elusive Form II of Aspirin. J. Am. Chem. Soc. 2005, 127, 16802–16803. [Google Scholar]
  41. Bond, A.D.; Boese, R.; Desiraju, G.R. On the Polymorphism of Aspirin. Angew. Chem. Int. Ed. 2007, 46, 615–617. [Google Scholar]
  42. Bond, A.D.; Boese, R.; Desiraju, G.R. On the Polymorphism of Aspirin: Crystalline Aspirin as Intergrowths of Two “Polymorphic” Domains. Angew. Chem. Int. Ed. 2007, 46, 618–622. [Google Scholar]
  43. Bond, A.D.; Solanko, K.A.; Parsons, S.; Redder, S.; Boese, R. Single Crystals of Aspirin Form II: Crystallisation and Stability. CrystEngComm 2011, 13, 399–401. [Google Scholar]
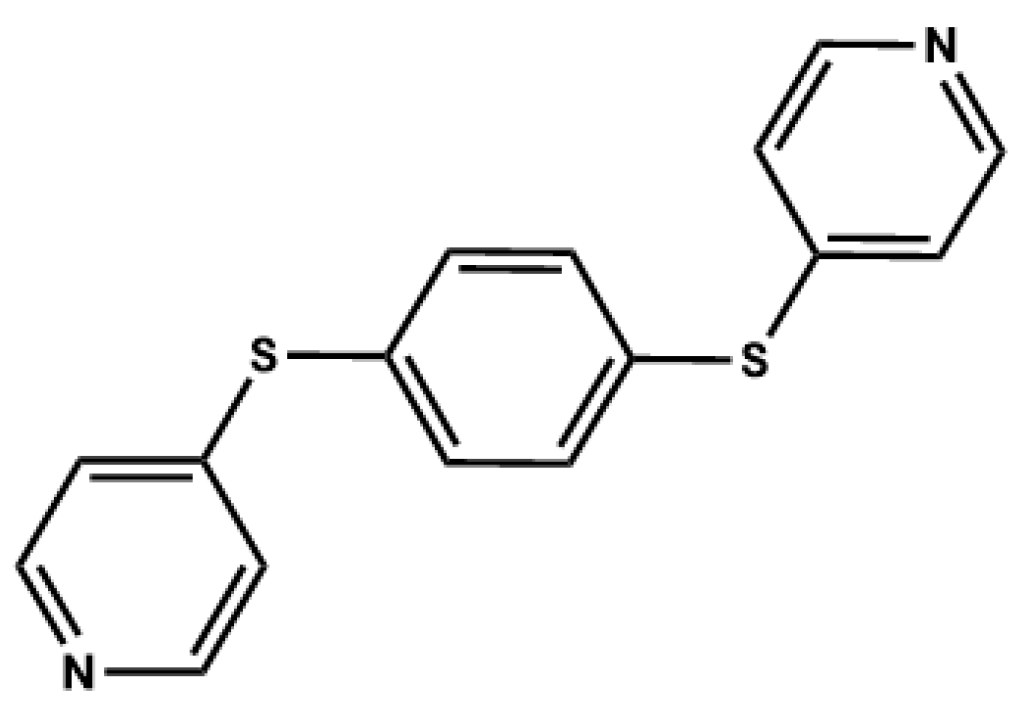
Crystals 15 00289 sch001
Scheme 1. Representation of 1,4-bis(thiopyridine)benzene.
Scheme 1. Representation of 1,4-bis(thiopyridine)benzene.
Crystals 15 00289 sch001
Crystals 15 00289 g001
Figure 1. On left: molecular structure of αa with atomic displacement plot shown at 50% probability; on right: overlay of αa with β (in green: αa, in blue: β, RMSD = 0.2081 Å).
Figure 1. On left: molecular structure of αa with atomic displacement plot shown at 50% probability; on right: overlay of αa with β (in green: αa, in blue: β, RMSD = 0.2081 Å).
Crystals 15 00289 g001
Crystals 15 00289 g002
Figure 2. Packing diagram shown along c axis for αa and along b axis for β.
Figure 2. Packing diagram shown along c axis for αa and along b axis for β.
Crystals 15 00289 g002
Crystals 15 00289 g003
Figure 3. Estimated contributions of selected intermolecular forces stabilizing the formation of αa and β.
Figure 3. Estimated contributions of selected intermolecular forces stabilizing the formation of αa and β.
Crystals 15 00289 g003
Crystals 15 00289 g004
Figure 4. (On left): powder patterns; (on right): heat flow-calibrated DTA curve.
Figure 4. (On left): powder patterns; (on right): heat flow-calibrated DTA curve.
Crystals 15 00289 g004
Crystals 15 00289 g005
Figure 5. Simplified packing representation of ligand molecules in αa and αb.
Figure 5. Simplified packing representation of ligand molecules in αa and αb.
Crystals 15 00289 g005
Crystals 15 00289 g006
Figure 6. Estimated contributions (percentages) of selected intermolecular forces stabilizing formation of αb.
Figure 6. Estimated contributions (percentages) of selected intermolecular forces stabilizing formation of αb.
Crystals 15 00289 g006
Crystals 15 00289 g007
Figure 7. Reconstruction of reciprocal lattice plane 0kl.
Figure 7. Reconstruction of reciprocal lattice plane 0kl.
Crystals 15 00289 g007
Table 1. Crystal data and details of refinement parameters for crystal structures α and β.
Table 1. Crystal data and details of refinement parameters for crystal structures α and β.
Compound Referenceαβ
Chemical formulaC16H12N2S2C16H12N2S2
Formula mass296.40296.40
Crystal systemmonoclinicmonoclinic
Space groupP21/cP21/c
a/Å10.5963(3)7.6480(2)
b/Å14.4449(3)5.85520(10)
c/Å10.0761(3)17.5179(5)
α/°9090
β/°113.933(3)118.578(4)
γ/°9090
Unit cell volume/Å31409.67(7)688.89(4)
Temperature/K100(2)100(2)
No. of formula units per unit cell, Z42
Radiation typeCuKαCuKα
Absorption coefficient, μ/mm−13.3293.406
No. of reflections measured143276681
No. of independent reflections29041385
Rint0.03110.0324
Final R1 values (I > 2σ(I))0.03240.0290
Final wR(F2) values (I > 2σ(I))0.09280.0768
Final R1 values (all data)0.03680.0299
Final wR(F2) values (all data)0.09580.0773
Goodness of fit on F21.0751.088
Table 2. Hydrogen bonding parameters for αa and β.
Table 2. Hydrogen bonding parameters for αa and β.
CompoundD-H---AH---A (Å)D---A (Å)D-H---A (°)
αaC9-H9---N1 i2.793.466(2)129
C10-H10---N1 i2.923.530(2)123
C13-H13---N1 ii2.673.509(2)148
C17-H17---N1 iii2.733.548(2)145
C6-H6---N18 iv2.923.642(2)134
C12-H12---N18 v2.563.390(2)147
βC5-H5---N1 i2.993.471(2)112
C6-H6---N1 i2.863.414(2)118
C10-H10---N1 ii2.573.446(2)153
Symmetry codes (αa): (i) 1 − x, −y, −z, (ii) 1 − x, 1/2 + y, 1/2 − z, (iii) x − 1, 1/2 − y, z − 3/2, (iv) 1 + x, 1/2 − y, 3/2 + z, (v) −x, 1 − y, −1 − z; (β): (i) 2 − x, y − 1/2, 1/2 − z, (ii) x − 1, 3/2 − y, z − 1/2.
Table 3. The results of the crystal lattice energy calculations for αa and β (kJ/mol units).
Table 3. The results of the crystal lattice energy calculations for αa and β (kJ/mol units).
CrystalExplorerE_eleE_polE_disE_repE_tot
Tonto wavefunction calc.
αa−55.6−9.9−154.680.5−139.7
β−52.6−10.3−160.074.2−148.8
Gaussian wavefunction calc.
αa−57.4−10.1−154.680.6−141.6
β−54.8−10.4−160.074.3−150.9
Table 4. Hydrogen bonding parameters for αb.
Table 4. Hydrogen bonding parameters for αb.
D-H---AH---A (Å)D---A (Å)D-H---A (°)
C17A-H17A---N1A i2.853.628(3)140
C6A-H6A---N18A ii2.783.597(3)144
C9A-H9A---N18A iii2.222.943(3)132
Symmetry codes: (i) x − 1, 1/2 − y, z − 3/2, (ii) 1 + x, 1/2 − y, 3/2 + z (iii) −x, y − 1/2, −z − 3/2.
Table 5. The results of the crystal lattice energy calculations for αb (kJ/mol units).
Table 5. The results of the crystal lattice energy calculations for αb (kJ/mol units).
CrystalExplorerE_eleE_polE_disE_repE_tot
Tonto wavefunction calc.
−122.1−10.8−160.2235.6−57.5
Gaussian wavefunction calc.
−124.9−11.1−160.2236.2−60.0
Pixel−156.1−94−218.9476.87.8
Table 6. The results of the crystal lattice energy calculations for ECUTUR09 and NPOFNP09 (kJ/mol units).
Table 6. The results of the crystal lattice energy calculations for ECUTUR09 and NPOFNP09 (kJ/mol units).
E_eleE_polE_disE_repE_tot
ECUTUR09
Pixel−178.3−80.5−264.1519.7−3.2
CrystalExplorer−153.5−6.6−217.1296.2−81.0
NPOFNP09
Pixel−137.8−57.4−218.9418.34.3
CrystalExplorer−120.2−5.7−187.3234.7−78.5
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Chaudhary, S.; Losus, R.M.; Dobrzańska, L. Polymorphism and the Phenomenon of Whole-Molecule Disorder Revealed in a Novel Dipodal Thiopyridine Ligand. Crystals 2025, 15, 289. https://doi.org/10.3390/cryst15040289

AMA Style

Chaudhary S, Losus RM, Dobrzańska L. Polymorphism and the Phenomenon of Whole-Molecule Disorder Revealed in a Novel Dipodal Thiopyridine Ligand. Crystals. 2025; 15(4):289. https://doi.org/10.3390/cryst15040289

Chicago/Turabian Style

Chaudhary, Simran, Renny Maria Losus, and Liliana Dobrzańska. 2025. "Polymorphism and the Phenomenon of Whole-Molecule Disorder Revealed in a Novel Dipodal Thiopyridine Ligand" Crystals 15, no. 4: 289. https://doi.org/10.3390/cryst15040289

APA Style

Chaudhary, S., Losus, R. M., & Dobrzańska, L. (2025). Polymorphism and the Phenomenon of Whole-Molecule Disorder Revealed in a Novel Dipodal Thiopyridine Ligand. Crystals, 15(4), 289. https://doi.org/10.3390/cryst15040289

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop