Enhancing Light Absorption in Perovskite Solar Cells Using Au@Al₂O₃ Core–Shell Nanostructures: An FDTD Simulation Study

Abstract

Adding plasmonic nanostructures to perovskite solar cells (PSCs) can boost light absorption, but often at the cost of new electronic losses. Based on 3D FDTD simulations, this study demonstrates how Au@Al₂O₃ core-shell nanostructures can overcome this fundamental trade-off through a dual function of the Al₂O₃ shell, namely its moderate refractive index and excellent passivating properties. In addition, the geometry of Au@Al₂O₃ core–shell nanostructure is optimized to produce a maximum short-circuit current density ($J_{sc}$) of 25 mA cm⁻². The simulations provide mechanism-level design rules that link dielectric choice and geometry to near-field localization and far-field coupling in perovskite absorbers. An experimentally testable parameter window is reported rather than device-level performance claims, with explicit discussion of energy partitioning and stability caveats associated with plasmonic loss in Au and interfacial chemistry.

1. Introduction

Perovskite solar cells (PSCs) have emerged as one of the most promising next-generation photovoltaic technologies, garnering immense attention due to their remarkable progress in power conversion efficiency (PCE) and their exceptional optoelectronic properties [1]. Since their inception, certified efficiencies have rapidly surpassed 25%, positioning them as direct competitors to established thin-film technologies [1]. This remarkable progress is rooted in the intrinsic advantages of perovskite materials, which include high absorption coefficients across the visible spectrum, long carrier diffusion lengths, and tunable bandgaps [1]. However, to move beyond current efficiency plateaus and address commercialization challenges, researchers are actively exploring advanced light management strategies to further enhance photon absorption, particularly in the near-infrared (NIR) region where the material’s performance typically wanes [2].

Among these strategies, the integration of plasmonic nanostructures represents a particularly effective approach for enhancing light-harvesting capabilities [1,2]. By leveraging the unique optical properties of metallic nanoparticles, it is possible to manipulate light at the nanoscale to increase absorption within the thin active layer of the PSC [3]. This is typically achieved through two primary mechanisms: far-field scattering, which increases the optical path length of incident light, and near-field enhancement, where intense, localized electromagnetic fields boost the absorption rate in the surrounding semiconductor [1,2]. Consequently, a wide range of nanostructure geometries, including nanorods [4] and nano-octahedrons [5], have been explored to tailor these plasmonic effects.

However, the direct incorporation of bare metallic nanoparticles into the perovskite layer presents a fundamental trade-off. While optically beneficial, the metal-semiconductor interface is a double-edged sword; it can act as a highly active site for non-radiative charge recombination, which quenches excitons and creates significant electronic losses that can negate any optical gains [6]. This issue is compounded by parasitic absorption within the metal itself, where the plasmon energy dissipates as heat rather than contributing to photocurrent generation [2]. Therefore, a critical challenge in designing plasmonic PSCs is to harness the optical benefits of the nanoparticles while simultaneously mitigating these detrimental electronic effects at the interface.

To address this challenge, the core–shell architecture has emerged as a highly effective solution [6,7]. In this design, a dielectric shell is conformally coated onto the metallic core, serving as a physical and electronic barrier between the metal and the perovskite active layer. This insulating shell effectively passivates the metal surface, preventing direct contact and thereby suppressing charge recombination and exciton quenching [6,7]. This strategy allows for the preservation of the plasmon-generated carriers, ensuring that the optical enhancement translates into a net increase in device performance. Common materials explored for this purpose include silica (SiO₂) [7] and titania (TiO₂) [6], which encapsulate the metal core to manage the critical interface.

The selection of the shell material is paramount, as it must satisfy two distinct and crucial functions: it must possess the ideal refractive index to tune the localized surface plasmon resonance (LSPR) into the perovskite’s weak absorption window, and it must provide excellent electronic passivation to protect the interface. Conventional materials, however, fall short of meeting both criteria simultaneously. For instance, Au@TiO₂ nanostructures provide strong LSPR tuning but introduce potential stability issues due to the photocatalytic nature of TiO₂ [6]. Conversely, Au@SiO₂ offers good passivation, but its low refractive index limits its LSPR tuning capabilities [7]. This presents a clear research gap for a shell material with a more balanced profile. Aluminum oxide (Al₂O₃) has recently emerged as an exceptionally promising candidate from an electronic standpoint. Studies have demonstrated that an ultra-thin layer of Al₂O₃ deposited via atomic layer deposition (ALD) can effectively passivate the perovskite surface, chemically protecting it from humidity-induced degradation while reducing electronic defects [8]. Despite its proven effectiveness as a passivating agent, the potential of Al₂O₃ as an optical component for tuning plasmon resonances has remained largely unexplored. This untapped optical potential is particularly compelling because its material properties are uniquely suited to address the aforementioned challenges. Specifically, the moderate refractive index of Al₂O₃ ($n\approx 1.77$) positions it perfectly to provide the balanced LSPR tuning that both SiO₂ and TiO₂ cannot. A systematic study is therefore necessary to confirm its optical advantage and maximize this advantage through geometrical optimization of the nanostructure. In this work, the optical properties of the Au@Al₂O₃ core-shell nanostructure are explored based on the Finite-Difference Time-Domain (FDTD) method, thereby providing the optical justification for a material already known for its superior electronic properties.

Gold nanocubes provide strong and spectrally tunable localized surface plasmon resonances (LSPRs); the peak energy and linewidth shift with the dielectric constant of the surrounding medium, which enables controlled red/NIR tuning through a moderate-index shell [9]. Amorphous Al₂O₃ (typical thin-film $n\approx 1.6$–$1.8$ in the visible) supplies this dielectric environment and forms conformal, pinhole-free coatings by atomic layer deposition (ALD). In perovskite stacks, ultrathin ALD-Al₂O₃ layers have been shown to passivate surface defects, suppress halide migration, and improve tolerance to moisture and oxygen, leading to enhanced operational stability [10]. Compared with TiO₂ shells, Al₂O₃ also avoids UV-photocatalytic pathways that can degrade perovskite/ETL interfaces under illumination [11,12]. These optical and materials considerations motivate the Au@Al₂O₃ choice used throughout this study.

Representative simulation studies have reported band-limited optical gains in perovskite thin films when the localized surface plasmon resonance (LSPR) is placed near the absorber edge and parasitic metal loss is constrained by the dielectric environment. Using 3D FDTD, Jangjoy and Matloub analyzed dielectric–metal–dielectric triple core–shell spheres in ultrathin PSCs and mapped nonmonotonic trends versus core size and shell thickness under AM1.5G normalization [13]. Talebi et al. employed FDTD (MEEP) to decouple antireflection effects of dielectric nanoparticles from plasmonic near-field enhancement of Au nanostructures and performed layer-resolved optical budgeting [14]. The present work examines Au@Al₂O₃ nanocube arrays embedded in the perovskite and identifies an intermediate coverage window that increases active-layer absorptance while explicitly bounding Au loss under the AM1.5G reference.

State-of-the-art $\gamma$-CsPbI₃ devices already exhibit near-flat external quantum efficiency (EQE) approaching ∼90% across 400–725 nm with integrated photocurrents around 20–21 mA cm⁻², leaving limited headroom for broadband gain in that range [15,16]. Consequently, the present optical design targets a band-limited enhancement at the red edge, where the perovskite absorption weakens, while keeping metal losses bounded by a moderate-index Al₂O₃ shell. This framing aligns the simulations with contemporary benchmarks and clarifies that predicted current gains represent optical upper bounds rather than device-level $J_{sc}$ claims [15,16].

2. Simulation Methodology and Device Structure

2.1. Theoretical Framework of the FDTD Method

The FDTD method is a fundamental and powerful numerical algorithm for solving Maxwell’s equations directly in the time domain [17]. First introduced in a seminal 1966 paper by Kane S. Yee, this technique has become a cornerstone of computational electrodynamics, particularly for modeling the complex light-matter interactions found in nanophotonics and plasmonics [18,19].

The method is based on the direct discretization of Maxwell’s time-dependent curl equations. In a source-free, linear, and isotropic medium, these are given by Faraday’s law of induction and the Ampere-Maxwell law [18]:

$$\nabla \times \mathbf{E}=-\mu {\displaystyle \frac{\partial \mathbf{H}}{\partial t}}$$

(1)

$$\nabla \times \mathbf{H}=\epsilon {\displaystyle \frac{\partial \mathbf{E}}{\partial t}}+\sigma \mathbf{E}$$

(2)

where $\mathbf{E}$ is the electric field, $\mathbf{H}$ is the magnetic field, $\epsilon$ is the permittivity, $\mu$ is the permeability, and $\sigma$ is the electrical conductivity of the medium.

The core of the FDTD method is the Yee algorithm, which discretizes space and time using a staggered Cartesian grid (the ‘Yee cell’) [18]. In this scheme, the vector components of the electric and magnetic fields are positioned at half-step intervals from each other in both space and time. This ‘leapfrog’ arrangement allows for the use of central-difference approximations for the spatial and temporal derivatives, resulting in a set of explicit, second-order accurate update equations [17]. For example, the update equation for the $E_x$ component can be expressed in a simplified form as:

$$\begin{array}{cc}\hfill E_x^{n+1}{{|}_{i,j,k}=C_a·E_x^n|}_{i,j,k}& +C_b·\left({\displaystyle \frac{H_z^{n+1/2}{{|}_{i,j+1/2,k}-H_z^{n+1/2}|}_{i,j-1/2,k}}{\Delta y}}\right.\hfill \\ \hfill & \left.-{\displaystyle \frac{H_y^{n+1/2}{{|}_{i,j,k+1/2}-H_y^{n+1/2}|}_{i,j,k-1/2}}{\Delta z}}\right)\hfill \end{array}$$

(3)

where n is the time step index, $(i,j,k)$ are the spatial grid indices, $\Delta y$ and $\Delta z$ are the grid spacings, and $C_a$ and $C_b$ are coefficients dependent on the material properties and time step $\Delta t$. The magnetic field components are updated in a similar fashion at half-time steps. This ‘marching-on-in-time’ process simulates the propagation of electromagnetic waves through the defined geometry step-by-step [18].

Once the FDTD simulation yields the time-dependent electric field distribution $\mathbf{E}(r,t)$, a Fourier transform is applied to obtain the frequency-domain field $\mathbf{E}(r,\omega )$. From this, the power absorbed per unit volume ($P_{abs}$) within a material can be calculated using the following relation [20,21]:

$$P_{abs}(r,\omega )={\displaystyle \frac{1}{2}}\omega \mathrm{Im}\left(\epsilon (r,\omega )\right){\left|\mathbf{E}(r,\omega )\right|}^2$$

(4)

where $\omega$ is the angular frequency and $\mathrm{Im}\left(\epsilon \right)$ is the imaginary part of the material’s complex permittivity, which is related to optical loss. The total absorption in the active layer, $A_{active}\left(\lambda \right)$, is then found by integrating $P_{abs}$ over the volume of the active layer and normalizing by the incident power. This spectral absorptance is then used to calculate the theoretical maximum short-circuit current density, $J_{sc}$, as defined in Equation (5).

The accuracy of FDTD simulations, especially for plasmonic systems, is critically dependent on the spatial discretization [22,23]. A sufficiently fine mesh is required to accurately resolve the rapid spatial variations of the localized surface plasmon fields near metallic nanostructures. Convergence studies, where the mesh size is systematically reduced, are essential to ensure the results are independent of the discretization and accurately reflect the underlying physics [22].

2.2. FDTD Simulation Implementation

The numerical simulations in this work were performed using the Finite-Difference Time-Domain (FDTD) method. FDTD is a robust and widely used computational technique for solving Maxwell’s equations directly in the time domain, which allows for the accurate modeling of light-matter interactions across a broad spectrum with a single simulation run. Its suitability and high accuracy for modeling periodic plasmonic systems, provided that simulation parameters such as mesh refinement are carefully handled, have been extensively validated [22]. This makes it particularly well-suited for analyzing the optical properties and electromagnetic field distributions in complex plasmonic systems, and all simulations were conducted using a commercially available FDTD solver.

2.3. Operational Settings and Data Acquisition for the FDTD Simulations

A single periodic unit cell is modeled, with periodic boundaries in the in-plane directions and perfectly matched layers (PML) along the surface normal to emulate an infinite array and open space. A normally incident broadband plane-wave source (300–800 nm) is employed. For reproducibility, the source parameters, boundary selections, and monitor placement are kept identical across all designs.

To resolve strong field gradients and reduce staircasing at interfaces, a mesh-override region is applied to cover the metal–dielectric interfaces and the entire perovskite layer. Conformal and nonuniform meshing are enabled in the simulation region so the mesh is finest where fields vary rapidly and coarser elsewhere to fit workstation memory.

Two frequency-domain power monitors placed on the incidence and exit planes provide the spectral reflectance $R\left(\lambda \right)$ and transmittance $T\left(\lambda \right)$. The device absorptance is computed as $A_{\mathrm{total}}\left(\lambda \right)=1-R\left(\lambda \right)-T\left(\lambda \right)$. The layer-resolved absorptance in the perovskite, $A_{\mathrm{active}}\left(\lambda \right)$, is computed with a material-absorption analysis restricted to the perovskite volume. All spectra are exported on the same wavelength grid together with near-field maps for interpretation.

As a lightweight credibility check that does not require additional long runs, the energy-balance residual $|1-R\left(\lambda \right)-T\left(\lambda \right)-A_{\mathrm{total}}\left(\lambda \right)|$ is reported and remains within a small numerical tolerance over 300–800 nm in the reported simulations.

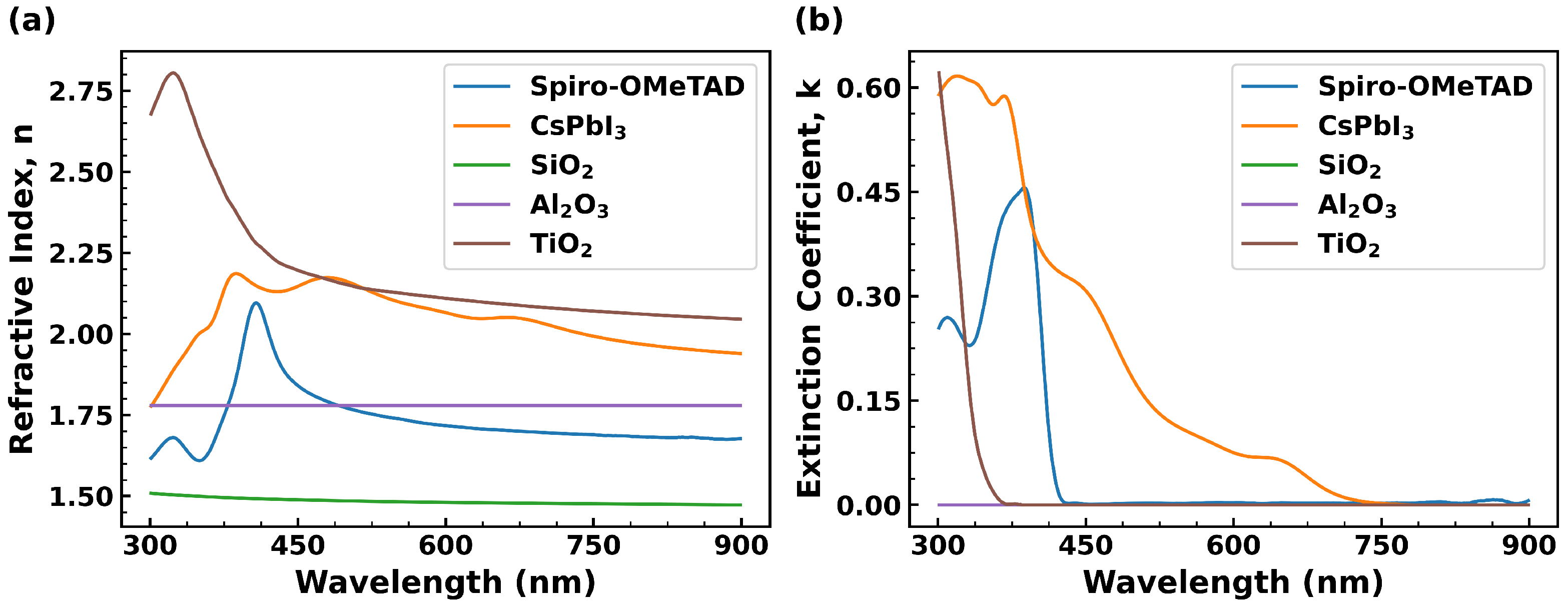
2.4. Geometrical Model and Optical Constants

The device architectures simulated in this study are illustrated in Figure 1. The primary focus is a classic n-i-p planar perovskite solar cell (PSC) incorporating plasmonic core–shell nanostructures, hereafter referred to as the Core–Shell Structure (Figure 1a). This architecture is a widely adopted and representative model for investigating interfacial effects and light management strategies in high-efficiency PSCs [24]. The multilayer stack consists of Indium Tin Oxide (ITO, 100 nm) as the transparent front electrode, followed by a Tin Oxide (SnO₂, 30 nm) Electron Transport Layer (ETL), a Perovskite (PVK, 500 nm) active layer, a Spiro-OMeTAD (250 nm) Hole Transport Layer (HTL), and a Gold (Au, 30 nm) back electrode.

Embedded within the perovskite active layer is a two-dimensional periodic array of Au@Al₂O₃ core–shell nanostructures. Each individual nanostructure consists of a cubic Au core with an edge length ‘d’ conformally coated by an Al₂O₃ shell of thickness ‘c’, as detailed in the inset of Figure 1a. The array is arranged in a square lattice with a period P. To describe the packing compactness, the dimensionless ‘Surface Coverage Fraction’ ($\varphi$) is defined as the ratio of the nanoparticles’ base area to the unit cell’s area, i.e., $\varphi ={(d+2c)}^2/P^2$. A larger value of $\varphi$ thus corresponds to a denser, more tightly packed array.

To evaluate the effectiveness of the proposed design, its performance is compared against two reference architectures. The first is a planar cell without any nanoparticles, which serves as the baseline for absorption and is referred to as the Flat Structure (Figure 1b). The second, termed the Pure Core Structure (Figure 1c), incorporates an array of bare Au nanocubes without the Al₂O₃ shell. This allows for the isolation and quantification of the specific contribution of the dielectric shell.

The accuracy of FDTD simulations is critically dependent on the optical constants (complex refractive index, n and k) of the materials used. The spectral data for the key materials in this model are shown in Figure 2. The optical constants for Gold (Au) were based on well-established experimental data from the literature, consistent with the values compiled by Palik [25]. The complex refractive indices for the new Electron Transport Layer (SnO₂) were taken from established literature values for thin films. The data for the perovskite active layer (CsPbI₃), the shell (Al₂O₃), and the Hole Transport Layer (Spiro-OMeTAD) were based on experimental data reported in Ball’s previous work [26].

The panels report wavelength-dependent dispersion $(n,k)$ for all layers used in the simulations on the same sampling grid as the FDTD monitors to avoid interpolation bias in post-processing. These data should be read as inputs to Maxwell solves, not as fitted outputs. The Au dataset controls the plasmon linewidth and skin depth; the perovskite and Al₂O₃ dispersions together set the local dielectric environment that tunes the LSPR position, while transport-layer $(n,k)$ determine residual parasitic channels.

2.5. Front- Versus Back-Interface Placement: Quantitative Control and Design Rationale

To assess the interface location objectively, the Au@Al₂O₃ nanocube array was translated either to the illuminated ITO/perovskite front interface or kept embedded toward the perovskite/HTL (‘back’) side, while geometry, meshing, boundaries, sources, and monitor sampling were held identical. The observable for comparison is the perovskite-layer absorptance $A_{\mathrm{active}}\left(\lambda \right)$, integrated under AM1.5G to obtain the optical upper-bound short-circuit current density, $J_{sc}^{\mathrm{upper}}$ (Equation (5)). As shown in Figure 3, the front placement increases reflectance over the short-to-mid visible and slightly depresses $A_{\mathrm{active}}\left(\lambda \right)$ near the band edge, yielding $J_{sc}^{\mathrm{upper}}=24.61$ mA cm⁻², whereas the embedded/back placement attains $24.90$ mA cm⁻²; the difference is $0.29$ mA cm⁻² (≈1.2%). These data indicate that the embedded/back configuration better preserves light incoupling while enabling a band-limited, shell-tuned gain at the red/near-IR edge where CsPbI₃ absorption weakens.

This placement choice is also consistent with contemporary $\gamma$-CsPbI₃ device benchmarks: when absorber thickness and front optics are optimized (anti-reflection or nano-texturing), external quantum efficiency is nearly flat across 500–725 nm and the EQE-integrated photocurrent is already ∼20–21 mA cm⁻², leaving limited broadband headroom in that range [15,16]. The present optical design therefore targets thickness/AVT-limited scenarios and emphasizes embedded/back placement to realize a red-edge $\Delta J_{sc}^{\mathrm{upper}}$ without incurring the front-side reflectance and parasitic-loss penalties.

2.6. Simulation Parameters and Data Calculation

A single unit cell of the periodic nanoparticle array was simulated with periodic boundaries in $x,y$ and perfectly matched layers (PMLs) in z. A broadband plane-wave source (300–800 nm) impinged normally. Frequency–domain power monitors placed flush with the incidence and exit planes yielded the spectral reflectance $R\left(\lambda \right)$ and transmittance $T\left(\lambda \right)$; a material-absorption analysis group restricted to the perovskite provided the active-layer absorptance $A_{\mathrm{active}}\left(\lambda \right)$. The total device absorptance was evaluated as $A\left(\lambda \right)=1-R\left(\lambda \right)-T\left(\lambda \right)$. The same domain, boundary, monitor geometry and sampling were used for all designs so that differences reflect only the structures.

The short-circuit current density is evaluated under the AM1.5G reference spectrum to ensure methodological comparability across studies and consistency with photovoltaic rating practice. AM1.5G denotes the standardized global (hemispherical) irradiance on a 37° sun-facing tilted plane at an air mass of 1.5 and a total irradiance of 1000 W m⁻², as defined by IEC 60904-3 and ASTM G173 and disseminated by NREL. While the atmospheric air mass varies during the day, AM1.5G serves as the terrestrial reference for flat–plate PV characterization and solar–simulator classification; it is therefore used here to compute the upper–bound $J_{sc}$ from $A_{\mathrm{active}}\left(\lambda \right)$ via Equation (5) [27,28,29].

A non-uniform, adaptive mesh was employed, with significant refinement around the Au@Al₂O₃ nanoparticle, particularly at the metal–dielectric interface, to accurately resolve the strong near-field gradients associated with the LSPR. This meshing strategy is crucial for ensuring the convergence and accuracy of the simulation results [22].

Assuming an internal quantum efficiency (IQE) of 100%, the AM1.5G-integrated upper-bound short-circuit current density is

$$J_{sc}=q\mathit{\int }{\displaystyle \frac{\lambda }{hc}}{A}_{\mathrm{active}}\left(\lambda \right)I_{\mathrm{AM}1.5\mathrm{G}}\left(\lambda \right)\mathrm{d}\lambda$$

(5)

where q is the elementary charge, h is Planck’s constant, c is the speed of light, $A_{\mathrm{active}}\left(\lambda \right)$ is the perovskite-layer absorptance from the simulation, and $I_{\mathrm{AM}1.5\mathrm{G}}\left(\lambda \right)$ is the reference spectral irradiance. It is intended for method-to-method comparability rather than direct device $J_{sc}$ prediction.

3. Results and Discussion

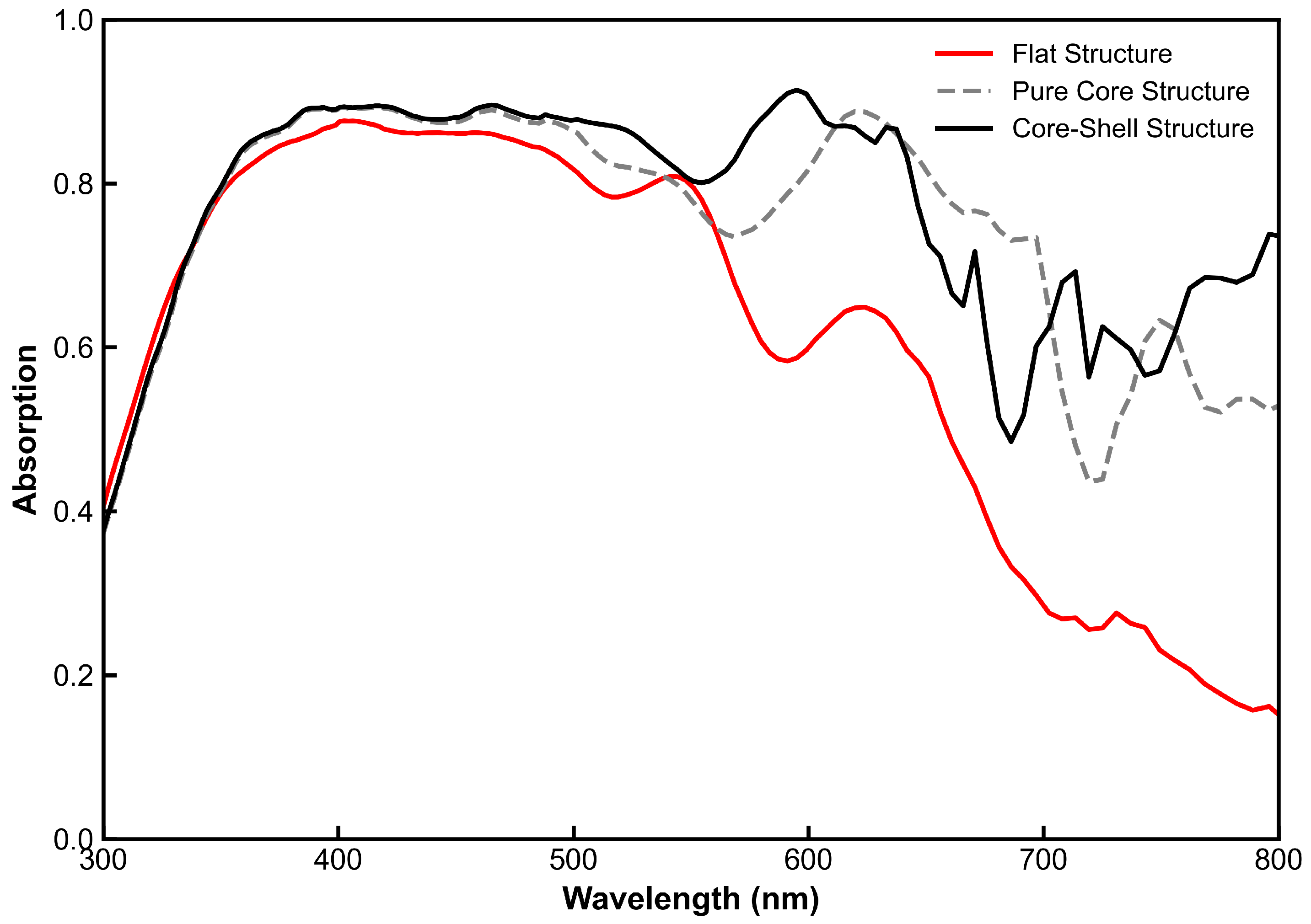
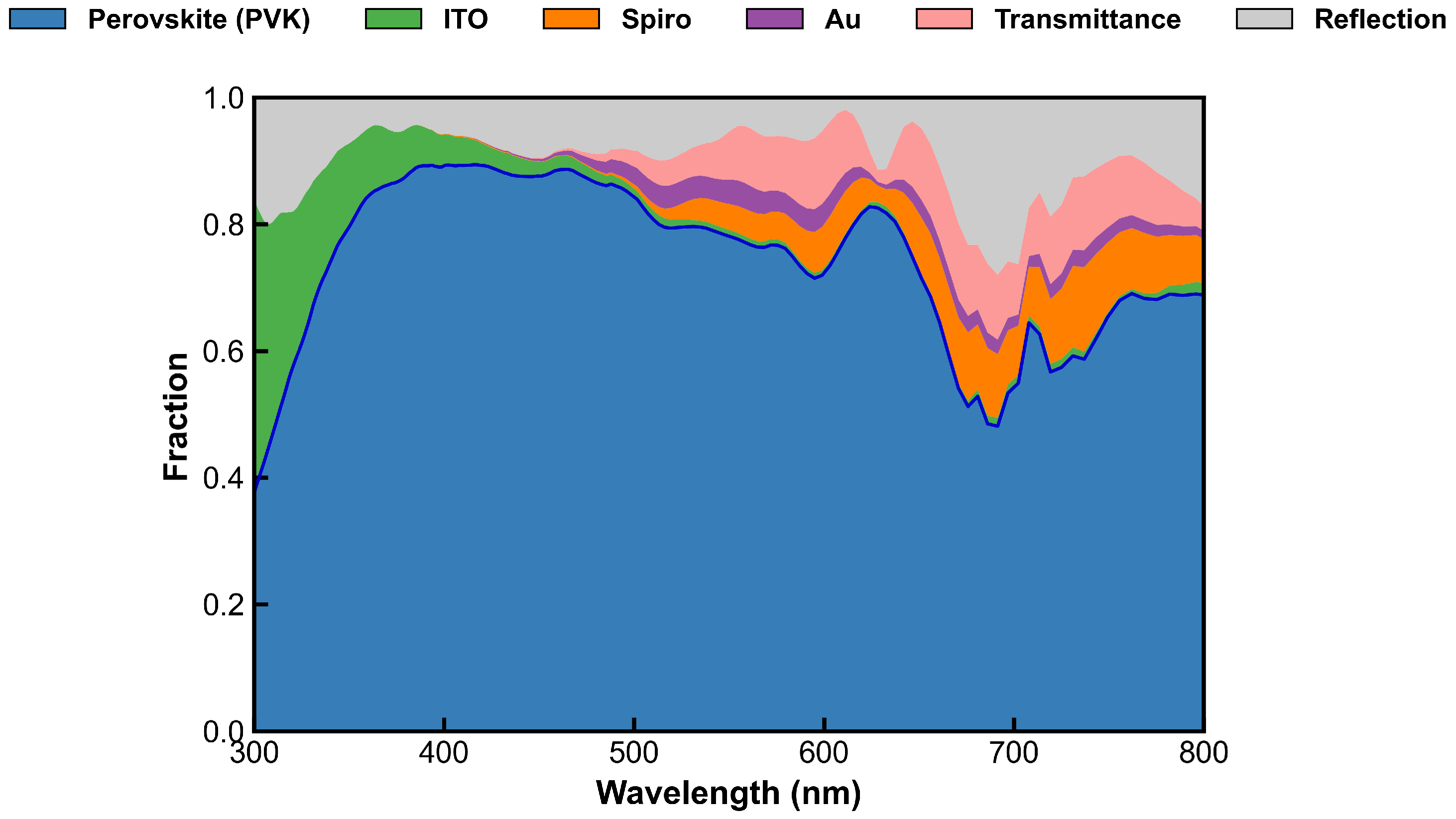
3.1. Optical Properties and the Dual-Function Role of the Al₂O₃ Shell

The simulated absorption spectra for the Core–Shell, Flat, and Pure Core structures are compared in Figure 4. The curves report the perovskite-layer absorptance $A_{\mathrm{active}}\left(\lambda \right)$ (normalized to incident power) for the baseline Flat, the bare-Au Pure Core, and the Au@Al₂O₃ Core–Shell structures under identical domain, boundaries, and source settings. The key signature is a deliberate red-shift of the enhancement band into ∼680–800 nm where the perovskite is intrinsically weaker, indicating that the shell’s moderate index retunes the LSPR to a spectrally useful window while keeping metal loss bounded. A comparison between the Pure Core Structure and the Flat Structure shows that the bare Au nanocubes alone provide a significant absorption boost due to their intrinsic plasmonic resonance [2]. The subsequent addition of the Al₂O₃ shell in the Core–Shell Structure introduces a distinct red-shift of this resonance [9], which strategically redistributes the plasmonic enhancement. Specifically, while the absorption of the Core–Shell structure is slightly reduced in the 550–600 nm range compared to the Pure Core structure, it exhibits a noticeably enhanced absorption profile in the longer wavelength region from approximately 680 nm to 800 nm. This trade-off is the hallmark of the red-shift effect: the enhancement is shifted to the deeper NIR, where the perovskite’s intrinsic absorption is weaker and thus in greater need of enhancement. This targeted enhancement is a direct result of the Al₂O₃ shell’s moderate refractive index, which provides a more effective means to red-shift the Localized Surface Plasmon Resonance (LSPR) into the perovskite’s weaker absorption window than conventional shells. For instance, high-index TiO₂ shells, while offering strong red-shifting, can suffer from photocatalytic degradation effects, whereas low-index SiO₂ shells provide insufficient resonance tuning [30].

The physical origin of this enhancement is visualized in the electric field intensity map in Figure 5. The map reveals several distinct electromagnetic ‘hotspots’, which are the regions where the field intensity is significantly higher than in the surrounding medium. These hotspots are precisely localized at the sharp corners of the nanocubes and, notably, in the narrow gaps between adjacent nanoparticles. The intensity within these hotspots is several times greater than the average field intensity in the bulk perovskite, confirming a powerful light-concentrating effect.

This intense field localization is a known feature of plasmonic nanocubes, often attributed to the ‘lightning rod effect’ where sharp geometries concentrate the electromagnetic field [31]. However, the characteristics of these hotspots—their intensity, size, and spatial distribution—are critically modulated by the dielectric shell material. The shell’s refractive index directly governs the LSPR condition and the efficiency of near-field coupling to the surrounding perovskite. While a low-index shell like SiO₂ would result in weaker, less-coupled hotspots, the moderate refractive index of Al₂O₃ provides an ideal balance. It is perfectly suited to create hotspots that are both highly intense and spatially distributed to maximize interaction with the perovskite active layer, which aligns with the superior absorption shown in Figure 4. However, creating such high-energy regions at a metal-semiconductor interface is a double-edged sword, as it also creates a high risk for carrier recombination. Herein lies the core dual advantage of the Au@Al₂O₃ system: the Al₂O₃ shell performs a crucial dual function. Optically, it tunes the LSPR to generate these hot spots. Electronically, its excellent field-effect passivation capabilities, proven to be effective at perovskite interfaces [10,32], shield the newly generated carriers from the metallic core. This ensures that the hot-carrier dynamics favor efficient charge transfer to the perovskite rather than being lost to non-radiative recombination at the metal surface [33]. This simultaneous optical and electrical contribution within a single core-shell structure represents a highly effective design principle for plasmonic devices [34].

To provide more direct visual evidence of how this LSPR mechanism translates into wavelength-dependent and position-dependent absorption, this study mapped the power absorbed per unit volume ($P_{abs}$) at various cross-sections of the active layer. Figure 6 presents a 3 × 3 grid of these maps, comparing the spatial distribution of absorption at three distinct wavelengths and at z-positions corresponding to the top, middle, and bottom of the nanocubes.

A systematic analysis of these maps reveals several key insights. First, the magnitude of absorption is strongly wavelength-dependent, as indicated by the vastly different colorbar scales spanning several orders of magnitude. The peak absorption density at the resonant wavelength of 600 nm (e.g., top slice, ∼$2\times {10}^{18}$) is orders of magnitude greater than at 450 nm (∼$3\times {10}^{17}$) and 360 nm (∼$1.5\times {10}^{16}$ in the same units). This provides unambiguous quantitative proof that the overall device enhancement is overwhelmingly driven by the LSPR effect, rather than being a minor perturbation.

Second, the spatial patterns differ significantly between resonant and non-resonant conditions. At the shorter wavelengths of 360 nm and 450 nm, where the perovskite material itself is strongly absorbing, the $P_{abs}$ is relatively diffuse. The absorption is highest at the ‘top’ slice (closest to the incident light) and progressively decreases towards the ‘bottom’, consistent with Beer-Lambert law behavior in a non-plasmonic film. In contrast, at the resonant wavelength of 600 nm, the absorption pattern becomes highly structured and localized. Intense absorption ‘hotspots’ emerge, which are most prominent at the ‘top’ and ‘bottom’ surfaces of the nanocubes. This extreme field localization is a hallmark of plasmonic nanocubes, attributed to the ‘plasmonic lightning rod effect,’ where the high curvature of sharp geometric features causes a dramatic concentration of the electromagnetic field [35,36,37]. The deliberate choice of a nanocube geometry is therefore a design strategy to engineer these hotspots and maximize light-matter interaction precisely where it is needed most [37]. The ’middle’ slice at 600 nm shows a weaker, more ring-like absorption pattern around the cubes, consistent with a cross-section of the near-field surrounding the nanoparticles.

This detailed visualization provides direct evidence of the dominant role of near-field enhancement in the designed system, particularly at the LSPR wavelength. This mechanism, where energy is absorbed in the immediate vicinity of the nanoparticle, is distinct from far-field scattering, which becomes more significant for light trapping at longer wavelengths by increasing the optical path length within the active layer [2,38]. The maps in Figure 6 confirm that the optimized geometry effectively leverages the near-field lightning rod effect to drive absorption enhancement in the target spectral window. In addition to the top-view near-field maps in Figure 6, complementary visualizations are provided in the Supplementary Information Section S4 (Figure S1) shows a pseudo-3D rendering of the electric-field intensity at the dipolar LSPR together with an x–z side-view map of the normalized absorbed-power density in the perovskite layer, which illustrate the vertical confinement and volumetric distribution of the optical energy around the Au@Al₂O₃ core–shell nanocube.

3.2. Comparative Analysis of Shell Materials for Optimal LSPR Tuning and Stability

The selection of the dielectric shell material is a critical design choice that dictates both the optical enhancement profile and the long-term stability of the plasmonic device. To demonstrate the significance of shell material on optical performance, a comparative FDTD simulation was performed to compute the total device absorption for Au nanocubes coated with three shell materials of distinct dielectric properties: low-index silica (SiO₂, $n\approx 1.5$), moderate-index alumina (Al₂O₃, $n\approx 1.77$), and high-index titania (TiO₂, $n\approx 2.5$). The results, presented in Figure 7, reveal a complex, non-monotonic relationship between the shell’s refractive index and the resulting absorption enhancement. While all three materials improve absorption, their effectiveness varies significantly across the near-infrared (NIR) spectrum. In the crucial 550–650 nm window, the Au@Al₂O₃ structure exhibits the highest absorption, suggesting its moderate refractive index creates an optimally positioned plasmon resonance for this range. Beyond 650 nm, although the high-index Au@TiO₂ structure shifts some resonant features to longer wavelengths, it suffers from a detrimental absorption dip near 700 nm. The Au@Al₂O₃ structure, in contrast, provides a more consistent and robust broadband enhancement across the entire 550–800 nm region without such a severe performance gap. The Au@SiO₂ structure consistently shows the weakest performance throughout the NIR, confirming its limited tuning capability.

The observed spectral shifts are governed by a fundamental principle of plasmonics: the LSPR peak wavelength is highly sensitive to the refractive index of the surrounding medium, with a higher refractive index inducing a stronger red-shift [9,39]. While this principle explains the general trend, the superior performance of Al₂O₃ in the 550–650 nm range stems from a synergistic balance of optimal resonance positioning and efficient energy coupling. The moderate refractive index of Al₂O₃ not only tunes the dominant LSPR peak squarely into this target window but also acts as an effective optical impedance matching layer between the air and the high-index perovskite, minimizing reflection and maximizing in-coupling. Furthermore, it facilitates efficient near-field energy transfer into the perovskite, avoiding the ‘field screening’ effect of a low-index shell like SiO₂ and the suboptimal field delocalization caused by a high-index shell like TiO₂. This explains why the low-index SiO₂ shell provides an insufficient red-shift, failing to tune the plasmon resonance effectively into the NIR region where the perovskite absorber is weakest. Conversely, the high-index TiO₂ shell produces a very strong red-shift, which is optically potent. However, this optical advantage is overshadowed by a critical material instability. TiO₂ is a well-known photocatalyst that, under UV illumination, generates electron-hole pairs that can catalytically decompose the adjacent perovskite material, leading to irreversible device degradation [40]. This inherent chemical incompatibility makes TiO₂ an unsuitable candidate for stable, long-lasting PSCs. Therefore, Al₂O₃ emerges as the optimal trade-off. Its moderate refractive index provides a substantial and well-positioned LSPR enhancement—far superior to SiO₂—while its chemical inertness and lack of photocatalytic activity ensure the electronic integrity and long-term stability of the perovskite interface, a conclusion supported by comparative studies of dielectric coatings [14]. All curves are computed with the same array geometry and boundary/source settings; only the shell material is varied. The plotted quantity is the total device absorptance $A_{\mathrm{total}}\left(\lambda \right)=1-R\left(\lambda \right)-T\left(\lambda \right)$ so that differences reflect shell-dependent optical coupling. Al₂O₃ produces a stable, broadband rise across 550–800 nm without the mid-band dip seen for TiO₂, consistent with its optimum refractive index that provides LSPR placement and impedance matching without photocatalytic penalties.

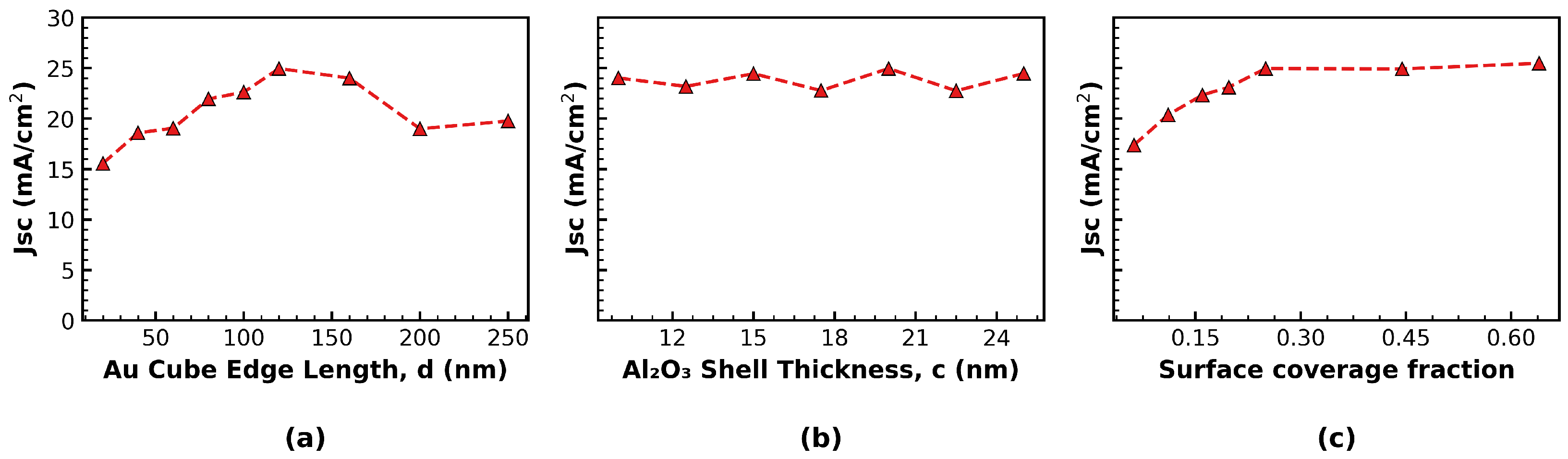
3.3. Optimization of Nanostructure Geometry

To translate these optical benefits into maximum device performance, the nanostructure geometry is systematically optimized against the final device metric: the short-circuit current density ($J_{sc}$). As shown in Figure 8a, the $J_{sc}$ is highly sensitive to the Au core size, peaking at approximately 25 mA cm⁻² for a 120 nm core. This optimum represents a critical balance between competing physical effects: larger particles more effectively scatter light and red-shift the LSPR to match the solar spectrum, but they also suffer from increased parasitic absorption and efficiency-reducing higher-order multipole radiation. In contrast, smaller particles are dominated by near-field absorption but have less impact on far-field light trapping [41]. The finding of an optimum at 120 nm aligns perfectly with this theoretical framework for maximizing useful light enhancement in thin-film solar cells.

Interestingly, the $J_{sc}$ is relatively insensitive to the Al₂O₃ shell thickness within the 10–25 nm range (Figure 8b). This is an advantageous finding from a fabrication standpoint, implying a robust process window. This tolerance is compatible with advanced deposition techniques like atomic layer deposition (ALD), which offers precise, sub-nanometer control over conformal coatings, even on complex nanostructures [42]. It suggests that a 10 nm shell is already sufficient to provide the necessary electronic passivation, with its LSPR tuning effect being secondary to the dominant influence of the core size in this regime.

The array’s Surface Coverage Fraction ($\varphi$), however, significantly impacts performance (Figure 8c), creating a notable interplay between optical enhancement and electronic transport. The calculated $J_{sc}$ steadily increases with higher coverage, which is optically intuitive. However, a closer inspection of Figure 8c reveals a more subtle and profound finding: while the $J_{sc}$ continues to rise, the rate of enhancement diminishes at higher coverage values. At a surface coverage of $\varphi \approx 0.25$, the system has already achieved over 90% of the maximum possible optical enhancement observed in the simulations. More importantly, this optical ‘sweet spot’ coincides almost perfectly with the optimal geometry for electronic performance reported by Xu et al., who achieved their record-breaking efficiency with a porous insulator that had an approximately 25% reduced contact area (equivalent to $\varphi \approx 0.25$) [43]. This alignment is not a mere coincidence; it suggests that the Au@Al₂O₃ system is not governed by a simple trade-off, but rather by a concurrent optimum.

The underlying physics, as explained by recent device models [44], is that the PIC structure simultaneously triggers multiple benefits: (1) The insulating Al₂O₃ provides superior passivation, boosting ${\mathrm{V}}_{oc}$; (2) The structure enhances perovskite crystallinity, which increases carrier mobility and lifetime, thus maintaining a high FF despite the reduced contact area; (3) The array itself provides powerful light trapping, which optically compensates for the reduced absorber volume, maintaining a high ${\mathrm{J}}_{sc}$. This work provides direct optical evidence for this third mechanism. It demonstrates that a concurrent optimum is achievable because the optical enhancement is already near-saturated at the exact point where the electronic properties are maximized. This transforms the design challenge from a compromise into a convergence towards a single, optimal geometry.

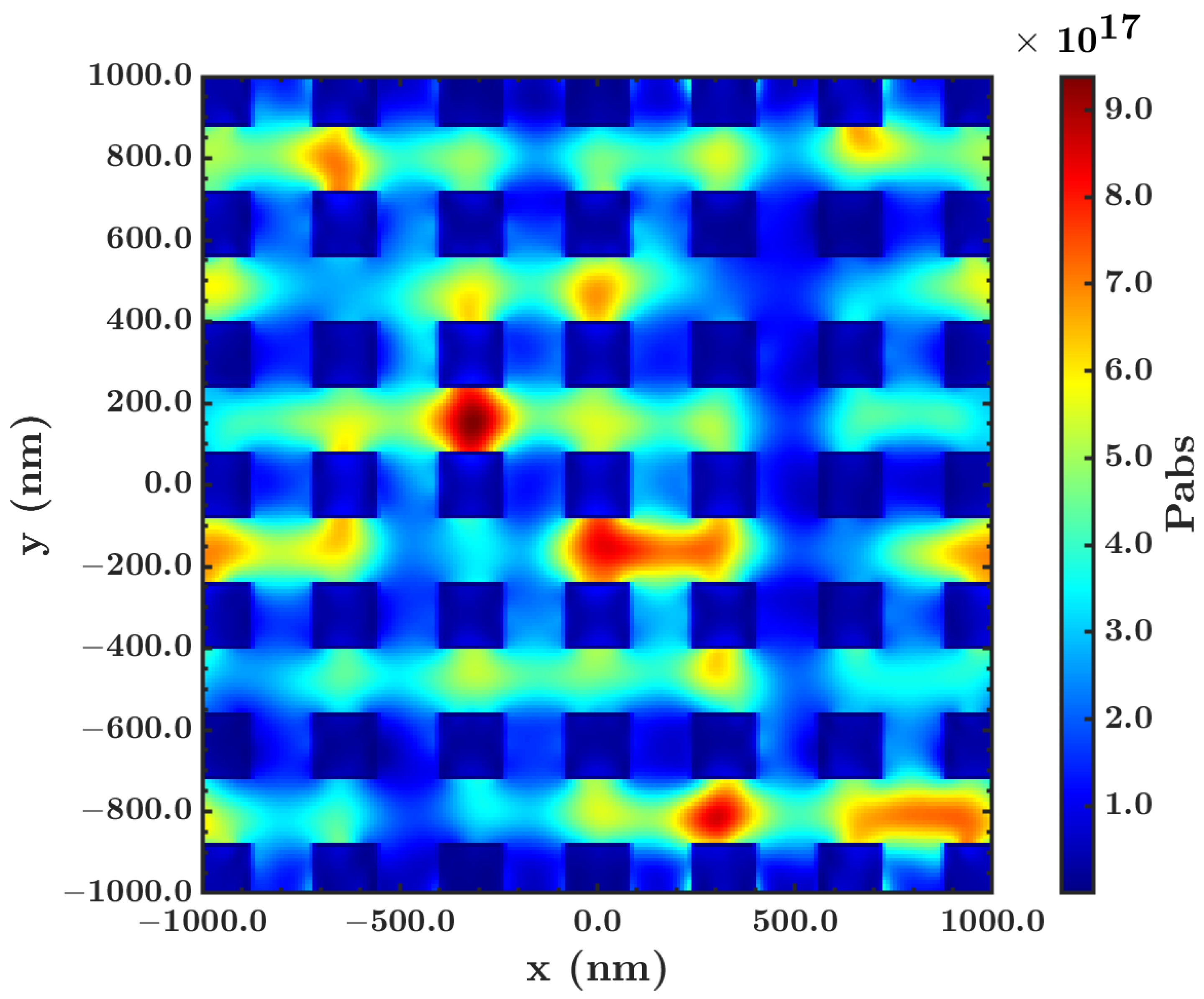
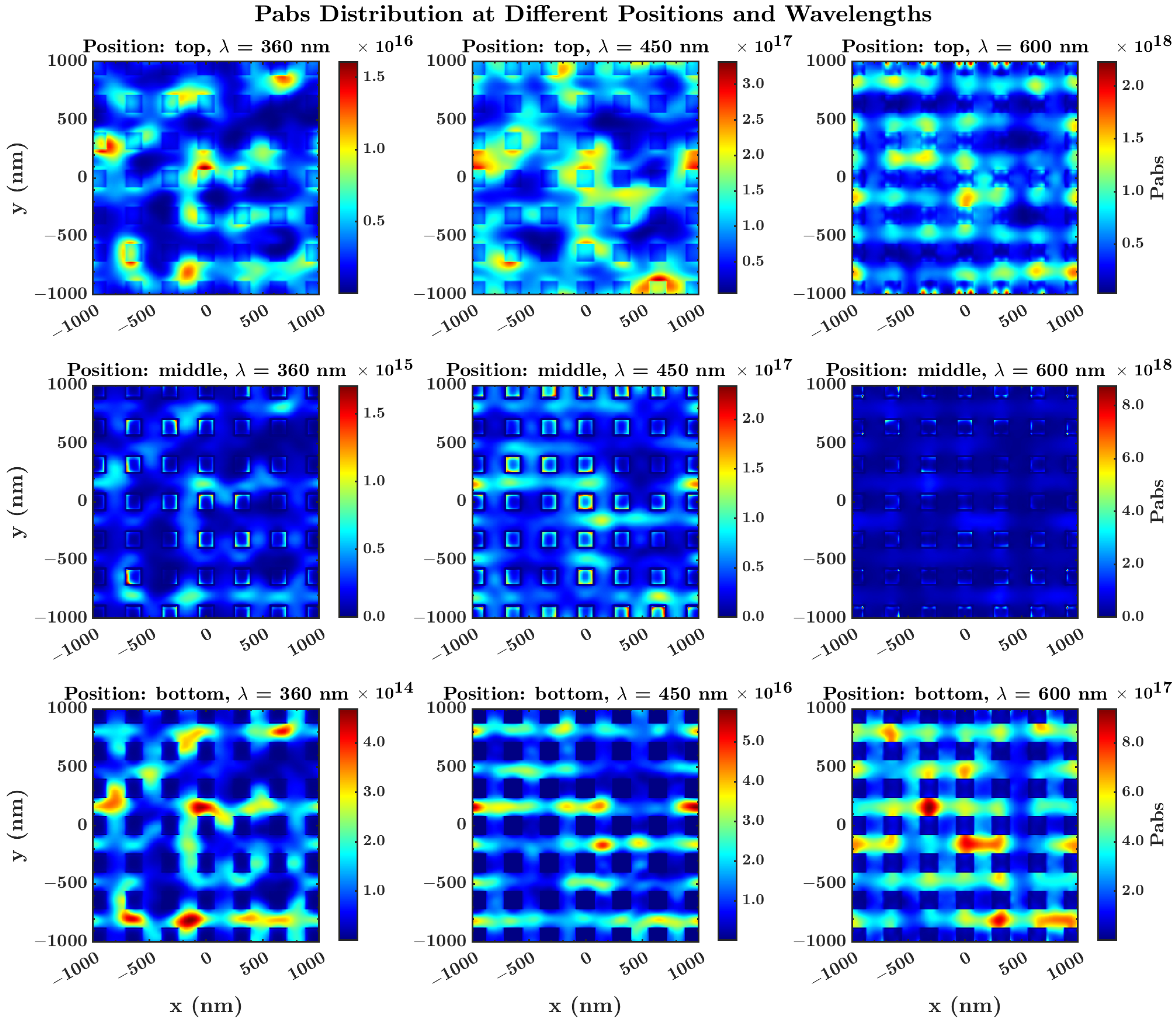
3.4. Impact on Device Performance and Energy Distribution

The integration of these optimized Au@Al₂O₃ arrays substantially improves device performance through a combination of near-field enhancement, far-field scattering, and anti-reflection effects [30,45]. The synergy between these near- and far-field effects is a key strategy for optimizing modern solar cell designs [38]. A critical aspect of plasmonic design is managing the trade-off between desired absorption in the semiconductor and undesirable parasitic absorption (Ohmic loss) in the metal itself [33]. Figure 9 provides insight into this energy distribution, showing the spectral absorption contribution of each layer in the optimized device. The stacked traces are constructed so that $A_{\mathrm{active}}\left(\lambda \right)+A_{\mathrm{others}}\left(\lambda \right)+T\left(\lambda \right)+R\left(\lambda \right)=1$ on the common wavelength grid; hence the area at any $\lambda$ sums to unity and directly partitions incident energy. The PVK (perovskite) trace corresponds to $A_{\mathrm{active}}\left(\lambda \right)$ used in Equation (5). The Au contribution remains a minority channel over 300–800 nm in the explored window, confirming that the Al₂O₃ shell effectively constrains Ohmic loss while promoting useful absorption in the active layer.

Crucially, the plot demonstrates that the absorption enhancement occurs predominantly within the perovskite (PVK) layer, while parasitic absorption in the Au nanoparticles remains comparatively low across the spectrum. This confirms the effectiveness of the optimized design. The Al₂O₃ shell is vital in mediating this balance. Its unique properties not only tune the LSPR for maximum enhancement in the PVK layer but also passivate the Au core, ensuring that the enhanced energy is funneled into charge carrier generation rather than being lost to non-radiative recombination or parasitic heating. This effective management of energy pathways, which relies on the interplay of multipole resonances in the nanoparticle lattice [46], is fundamental to achieving a net gain in solar cell efficiency and showcases the superiority of the Au@Al₂O₃ system [47].

3.5. From Optical Behavior to Design Rules and a Testable Parameter Window

3.5.1. Design Rules Distilled from the Simulations

The parametric scans over core size, shell thickness, and surface coverage allow a set of practical design rules to be formulated for Au@Al₂O₃ nanocube arrays in perovskite solar cells.

(i)

Dielectric-shell tuning. Place the dipolar LSPR in the red/near-IR where the perovskite absorption weakens; this is achieved by a moderate-index shell that red-shifts and narrows the resonance [2,9].

(ii)

Packing fraction. Use an intermediate surface coverage so that useful scattering and near-field localization are maintained while near-field overlap and metal loss remain bounded; the present scans indicate an optimum near $\varphi \approx 0.25$, consistent with trends observed for plasmonic light management in photovoltaics [2].

(iii)

Core size. Select a core dimension that provides the targeted LSPR placement without excessive linewidth broadening; within the explored parameter space, Au cubes near $d\sim 120$ nm meet this condition.

(iv)

Shell thickness and materials role. Use a thin Al₂O₃ shell to provide both dielectric tuning and interfacial passivation; ultrathin ALD-Al₂O₃ layers are widely reported as effective passivation/barrier layers in perovskite stacks [10,48].

3.5.2. Operational Window and Testable Predictions

The results define a practical window in which Au@Al₂O₃ arrays increase the perovskite-layer absorptance while keeping parasitic Au loss controlled: core dimensions centered near $d\sim 120$ nm, intermediate coverage around $\varphi \approx 0.25$, and a thin Al₂O₃ coating sufficient for dielectric tuning and passivation. Two experimental checks follow directly: (a) the LSPR red-shifts monotonically with shell-thickness increase (dielectric-environment control) [9]; and (b) the active-layer EQE gain peaks at intermediate coverage, consistent with the balance between scattering and metal absorption established for plasmonic photovoltaics [2].

3.6. Model-Based Scenarios and Observable Signatures

For window- or building-integrated photovoltaics (BIPV) concepts specified by an average visible transmittance (AVT), the present Au@Al₂O₃ nanocube-array model defines two immediately computable observables: the visible-band transmittance $T\left(\lambda \right)$ used to evaluate AVT and the perovskite active-layer absorptance $A_{\mathrm{active}}\left(\lambda \right)$, which serves as an upper-bound proxy for the external quantum response. Within the explored geometry–dielectric window for embedded Au@Al₂O₃ cubes, a band-limited rise of $A_{\mathrm{active}}\left(\lambda \right)$ is expected near the tuned localized surface plasmon resonance (LSPR) while the target AVT is maintained at fixed thickness, consistent with simulation-focused treatments of semitransparent perovskite solar cells and thin-PV light management [49,50]. Two representative use-cases are summarized in

Table 1. Representative model-based scenarios for the Au@Al₂O₃ nanocube array.

Scenario	Simulation Outputs	Expected Spectral Signature
Semitransparent (BIPV concept)	$T\left(\lambda \right)$ for AVT; $A_{\mathrm{active}}\left(\lambda \right)$	AVT preserved at fixed thickness; red/NIR rise of $A_{\mathrm{active}}$ near the tuned LSPR.
Ultrathin opaque	$A_{\mathrm{active}}\left(\lambda \right)$; $J_{sc}^{\mathrm{upper}}$ via Equation (5) under AM1.5G	Upper-bound $\Delta J_{sc}$ from AM1.5G integration; bounded Au loss.

, which distinguishes semitransparent BIPV concepts from ultrathin opaque designs in terms of their key simulation outputs and expected spectral signatures.

When the absorber thickness is constrained (ultrathin perovskite), the same design window primarily enhances $A_{\mathrm{active}}\left(\lambda \right)$ around the LSPR, as indicated in the “Ultrathin opaque” row of Table 1. The upper-bound short-circuit current density $J_{sc}^{\mathrm{upper}}$ is obtained by integrating $A_{\mathrm{active}}\left(\lambda \right)$ under the Air Mass 1.5 Global (AM1.5G) reference spectrum via Equation (5). Translation from $J_{sc}^{\mathrm{upper}}$ to device $J_{sc}$ requires explicit transport and recombination modeling and is outside the optical scope. This evaluation pipeline follows standard practice in optical simulation (finite-difference time-domain, FDTD, and transfer-matrix method, TMM) and aligns with IEC 60904-3/ASTM G173 definitions and the NREL reference dataset [21,27,28,29,50].

Plasmonic tuning by a moderate-index Al₂O₃ shell and the balance between near-field concentration and metal loss are well established in the perovskite–plasmonics literature; recent numerical studies and reviews employ FDTD/TMM workflows consistent with the present approach to embedded Au@Al₂O₃ arrays [50,51].

3.7. Comparative Discussion with Representative Simulation Studies

A focused comparison with recent simulation work helps contextualize the present parameter window and the layer-resolved energy budget under the AM1.5G convention. Jangjoy and Matloub investigated dielectric–metal–dielectric triple core–shell spherical nanoparticles embedded in ultra-thin perovskite absorbers using 3D FDTD, reporting non-monotonic responses of the AM1.5G-integrated upper bound to core size and shell thickness [13]. Those trends corroborate the general expectation that dielectric environment and geometric scale govern the placement and linewidth of the LSPR; however, the triple-shell motif and spherical symmetry complicate a direct read-across to periodic arrays where inter-particle coupling and coverage become decisive. In contrast, the present nanocube arrays employ a single, moderate-index Al₂O₃ shell that retunes the resonance into the red/near-IR while allowing coverage to be varied independently. Within this geometry–dielectric space, the simulated spectra identify an intermediate packing fraction at which the band-limited rise of $A_{\mathrm{active}}\left(\lambda \right)$ is maximized and the Au contribution remains bounded, a behavior that is read directly from the upper-bound $J_{sc}$ sweeps and the layer-resolved power partition already reported in the figures.

A complementary perspective is provided by Talebi et al., who used FDTD (MEEP) to examine dielectric nanoparticles (including Al₂O₃) in concert with Au nanopyramids and to separate anti-reflection effects from plasmonic near-field enhancement via channel-resolved optical budgeting [14]. That study emphasizes front-surface architectures and clarifies when reflection suppression dominates the gain, whereas the present configuration embeds Au@Al₂O₃ within the perovskite so that near fields couple directly into the absorber volume. Under otherwise comparable FDTD boundary/source conventions and AM1.5G normalization, the layer-resolved analysis here shows that the desired enhancement is concentrated in the perovskite channel over a LSPR-centered band, while metal loss remains a minority pathway across 300–800 nm. Taken together, these contrasts motivate the specific choices made here—nanocube geometry, a single Al₂O₃ shell, and explicit coverage control—and explain why the resulting parameter window is both practically simple and mechanistically transparent: it links a moderate-index shell and intermediate packing to red/near-IR absorptance gains in the active layer without tipping the balance toward parasitic Au heating.

3.8. Implications and Limitations

The derived design rules offer a mechanistic framework, while the following discussion outlines their broader implications and remaining limitations within the optical model.

Layer-resolved spectra show that the desired enhancement predominantly resides in the perovskite active layer, while parasitic channels—Ohmic loss in Au and minor absorption in transport layers—remain bounded within the explored parameter window. This balance is consistent with plasmonic light-management theory for photovoltaics, where near-field concentration and scattering benefits can coexist with metal losses [2]. From a stability perspective, the Al₂O₃ shell electrically and chemically separates Au from the perovskite and has been widely used as an ultrathin passivation and barrier layer in perovskite stacks; however, long-term device stability also depends on interfacial chemistry and UV stress at oxide contacts, which is outside the scope of purely optical modeling [10,11,12,48].

The analysis is optical and does not model charge transport, ion migration, or chemical degradation. Accordingly, the outcome is framed as a parameter window that balances active-layer enhancement against parasitic channels rather than as a device-lifetime claim. A practical validation path includes layer-resolved EQE (to confirm $A_{\mathrm{active}}$ trends), photothermal mapping under 1-sun-equivalent bias (to assess metal-induced heating), UV/humidity stress tests at ETL/perovskite interfaces, and encapsulation trials using ultrathin ALD-Al₂O₃ for barrier/passivation [2,10,12].

Within the red/near-IR where CsPbI₃ absorption weakens, the simulations indicate a localized, shell-tuned gain that is consistent with recent experimental EQE plateaus across 500–725 nm and integrated photocurrents near 20–21 mA cm₋₂ [15,16]. Accordingly, the reported ∼25 mA cm⁻² represents an optical limit under ideal collection rather than a practical single-junction $J_{sc}$ target for pure CsPbI₃ devices [15,16].

4. Conclusions

In this work, the optical potential of Au@Al₂O₃ core-shell nanostructures for enhancing perovskite solar cells was systematically investigated and optimized using three-dimensional FDTD simulations. The findings indicate that an optimized array with a 120 nm Au core yields an upper-bound short-circuit current density near 25 mA cm⁻² under the stated AM1.5G conventions. This enhancement is not the result of a single physical effect but stems from a synergistic balance of multiple mechanisms, including optimal plasmon resonance positioning, enhanced impedance matching, and efficient near-field energy coupling, which together motivate Al₂O₃ as a moderate-index shell and an ultrathin passivation layer.

At a surface coverage of approximately 25%, the simulated optical enhancement approaches its maximum, consistent with reported optimal geometries for porous insulator contacts (PICs). This suggests a practical geometry window, and the optical trends are consistent with the physical picture underlying the PIC concept. The simulations indicate that the Al₂O₃ shell serves a dual function—dielectric tuning of the LSPR and interfacial passivation—supporting a balance between field enhancement and parasitic loss.

In summary, this study provides mechanism-level design guidance that links dielectric choice and geometry to near-field localization and far-field coupling in perovskite absorbers. By establishing a clear optimization pathway and providing a deeper physical understanding of the interplay between optical enhancement and electronic performance, this work furnishes crucial theoretical guidance for the experimental fabrication of next-generation plasmonic devices. A geometry–dielectric parameter window is identified in which Au@Al₂O₃ core–shell arrays increase active-layer absorptance while keeping parasitic loss controlled, serving as mechanism-based guidance with clear experimental tests.