Interpretation of Copper Rolling Texture Components Development Based on Computer Modeling
Abstract
1. Introduction
2. Crystallographic Models of Plastic Deformation—Short Review
2.1. Fully Constrained Deformation, Taylor–Bishop–Hill Approach
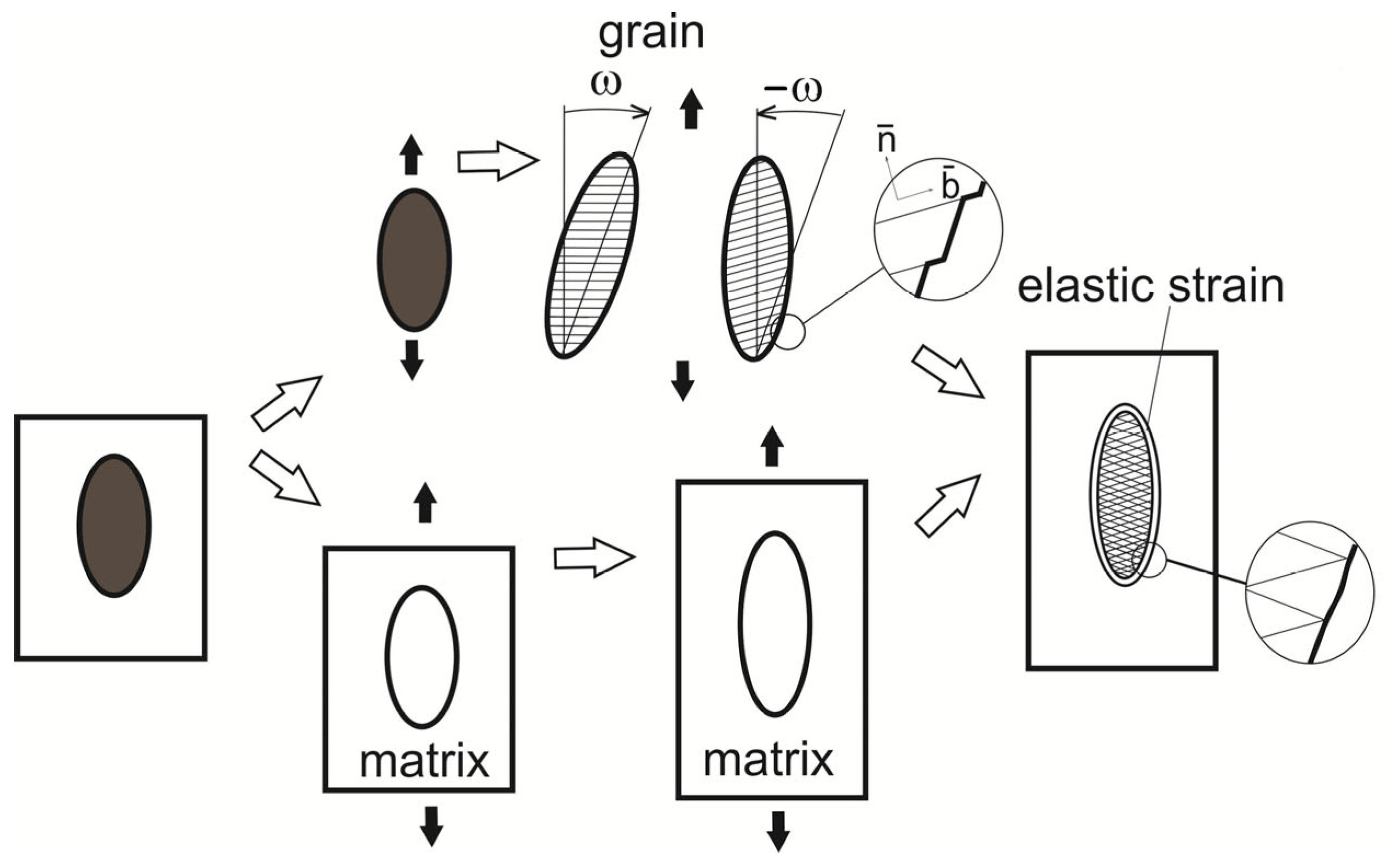
2.2. Models with Relaxation of Selected Strain Components
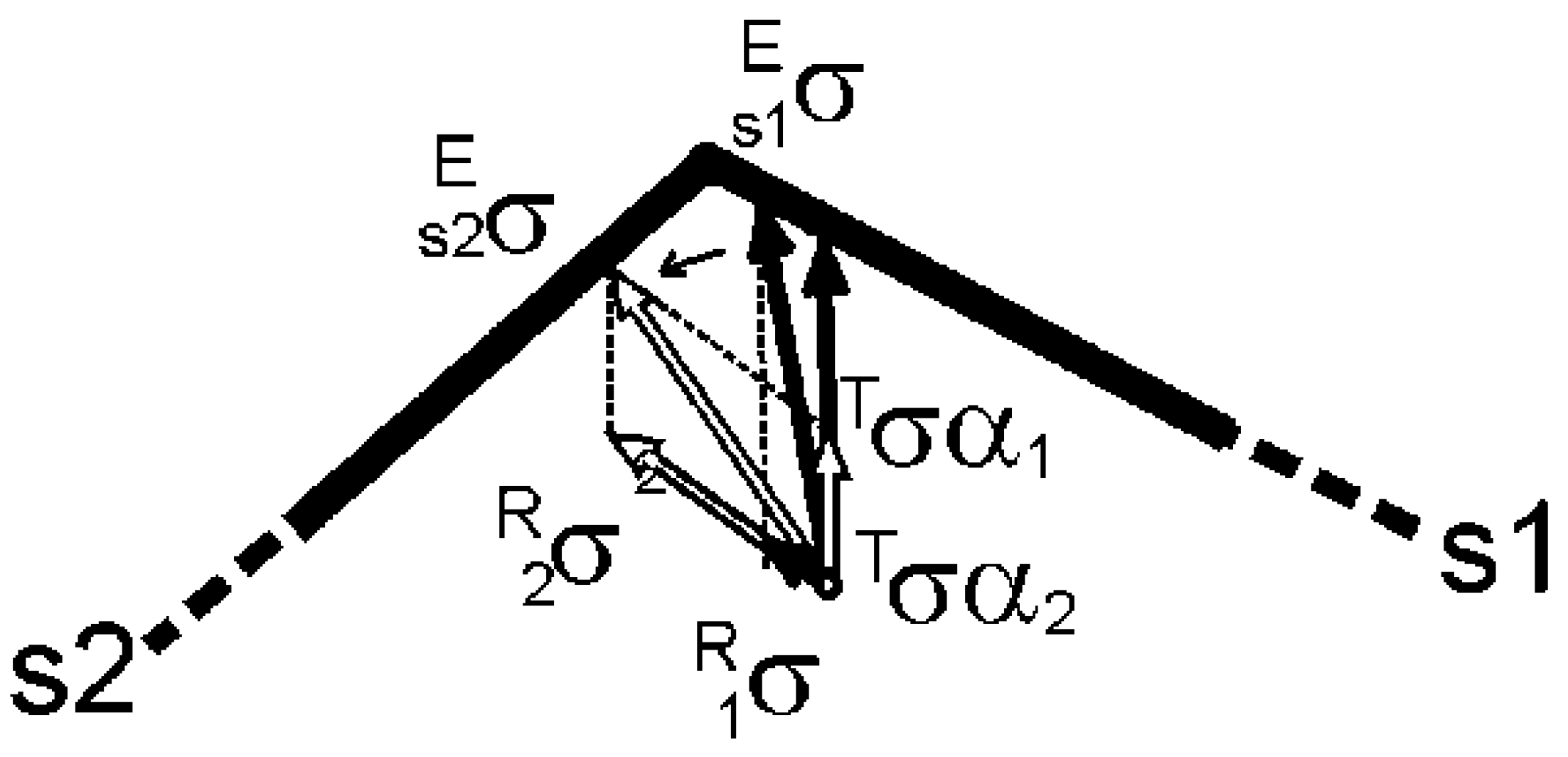
2.3. Sachs-Type Models
2.4. Self-Consistent Approach
2.5. The Fluctuating Stress State (FSS) Model
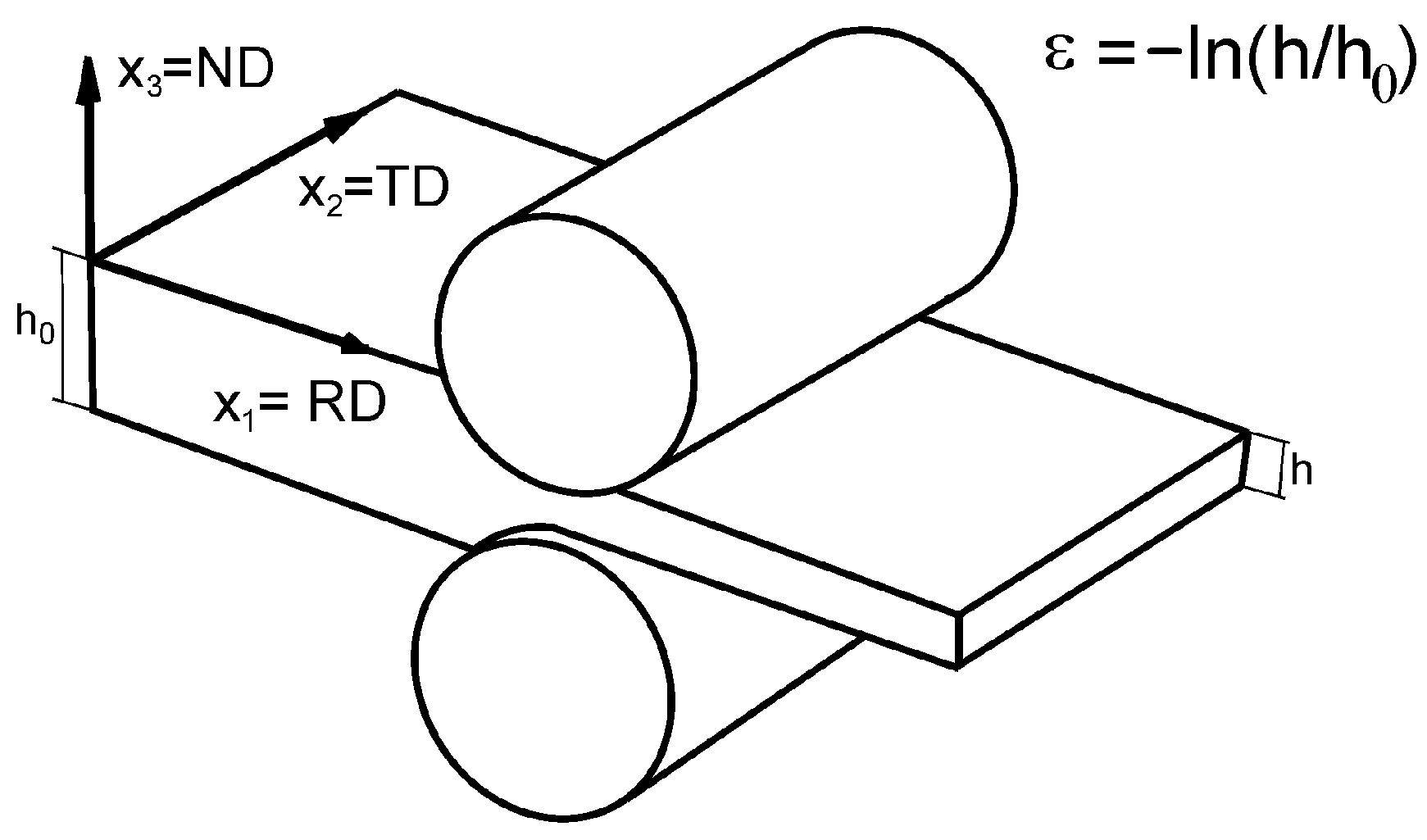
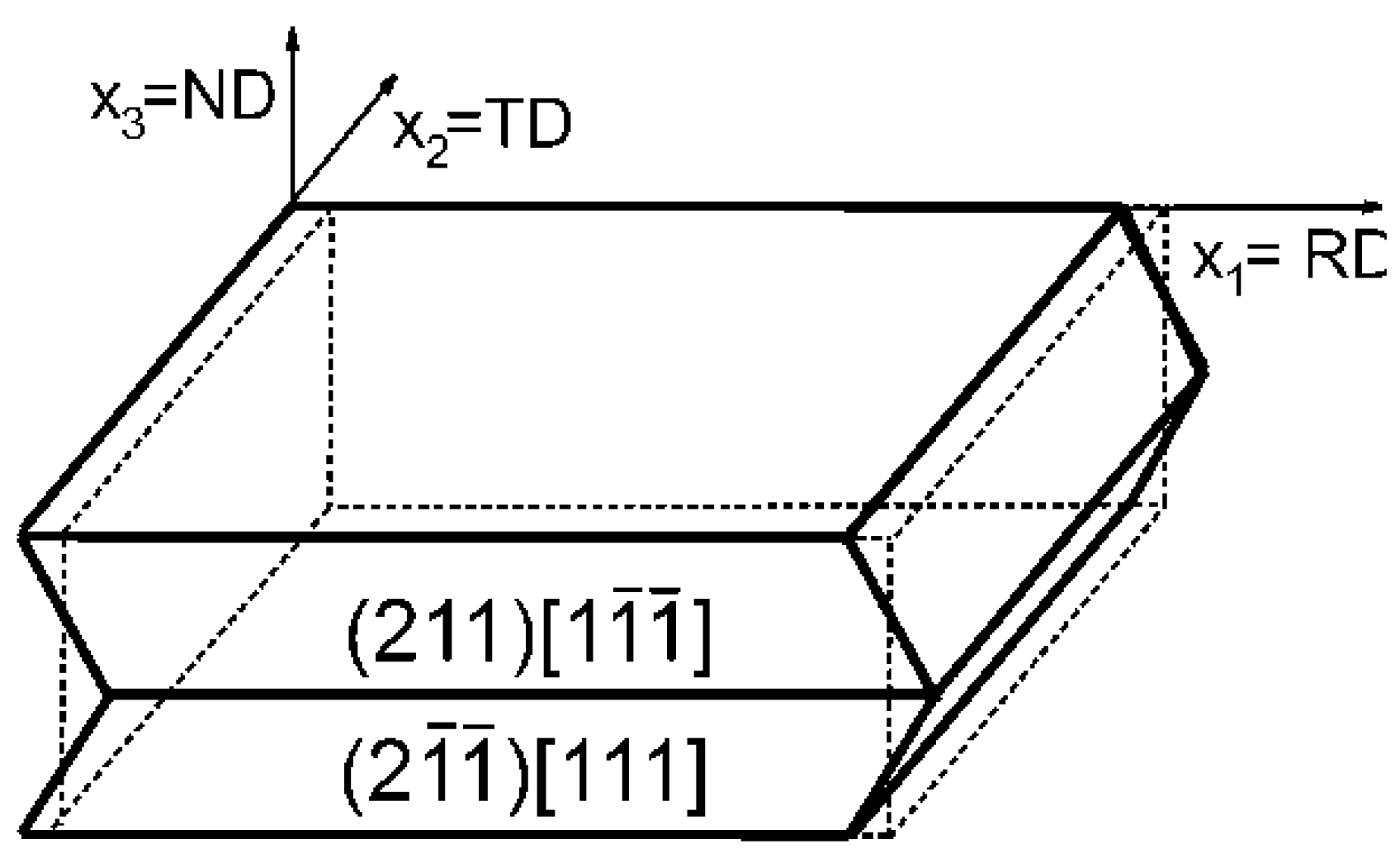
2.6. Boundary Conditions
3. Calculation Procedure
4. Results
4.1. Rolling Textures Developed for Fully Constrained Deformation (Grains Group No. 1)
4.2. Rolling Textures Developed for Partially Constrained Deformation (Grains Group No. 2)
4.3. Rolling Textures Developed for Partially Constrained Deformation (Grains Group No. 3)
4.4. Rolling Textures Developed for Partially Constrained Deformation (Grains Group No. 4)
4.5. Rolling Textures Developed for Grains from Group No. 5
5. Discussion
5.1. B Component
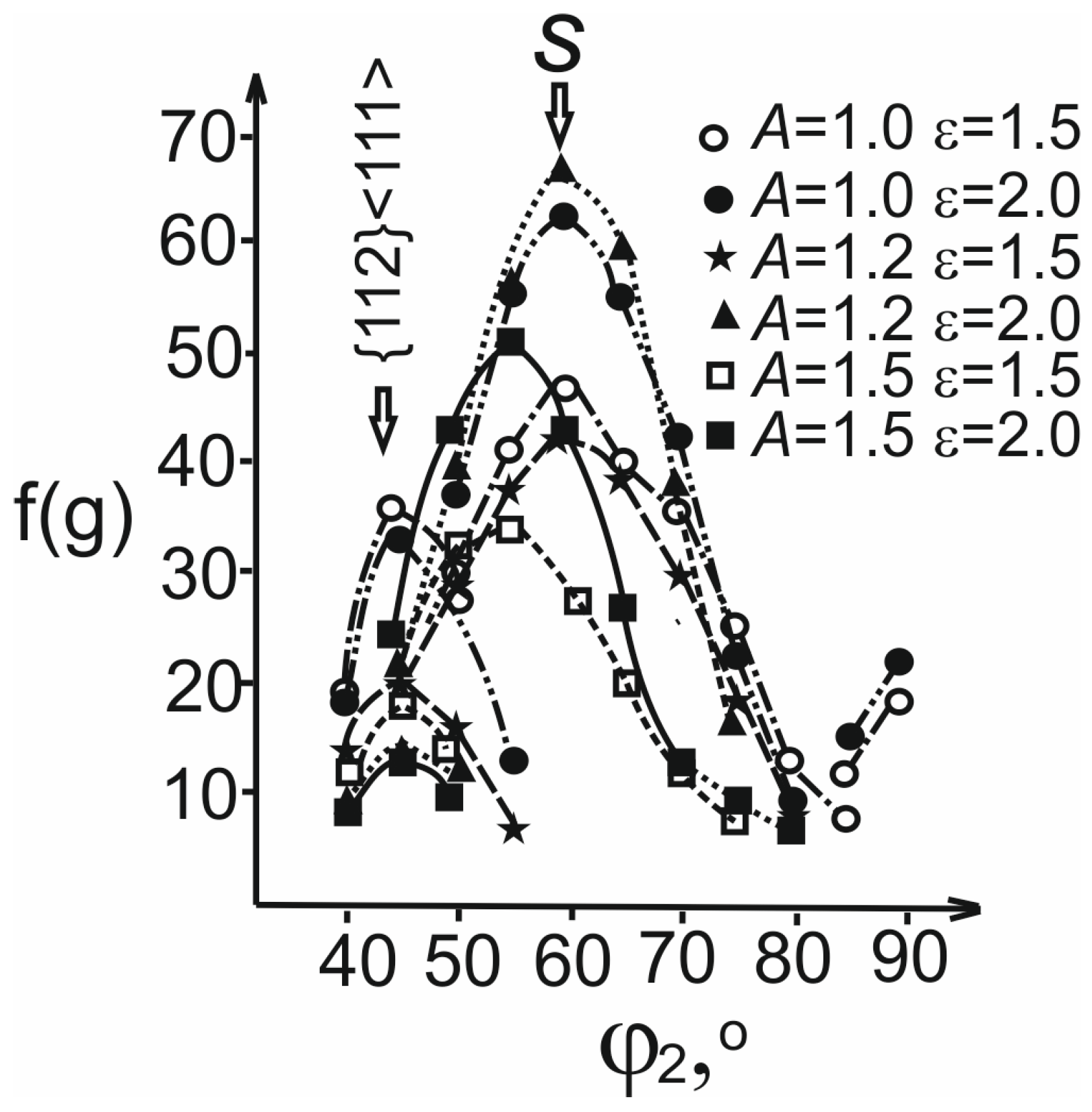
5.2. S Component
5.3. Cu Component
5.4. Weak Components
5.5. G Component
5.6. Cube Components
5.7. False Components
5.8. Strain Effect
6. Conclusions
- -
- Development of the B component is associated with relaxation of the shear strain occurring in the rolling plane.
- -
- Development of the S component is associated with flat grains in which the shear strains (in the plane perpendicular to the transverse direction) and (in the plane perpendicular to the rolling direction) are relaxed.
- -
- Development of the Cu component is associated with relaxation of the shear strain , characteristic for elongated grains, and for flat grains in which is additionally relaxed.
- -
- The effect of slip system strain hardening anisotropy on the shares of individual components depends on the deformation constraints applied to the rolled bar. The slip systems hardening anisotropy significantly affects the volume fraction of the S and Cu components under relaxation of and shears, and of the B component under the relaxation of (at least) and shears. Under the relaxation of only, its effect on the Cu component is insignificant.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Glossary of abbreviations and symbols | |
| CPFE | Crystal Plasticity Finite Element |
| FCC | face centered cubic |
| FEM | finite element method |
| FSS | Fluctuating Stress State |
| ODF | orientation distribution function |
| RC | Relaxed Constrains |
| RD | Rolling Direction |
| ND | Normal Direction |
| TD | Transverse Direction |
| RP | Rolling Plane |
| SFE | stacking fault energy |
| SO(3) | name of the Lie group |
| TBH | Taylor-Bishop-Hill |
| D(υ) | misorientaton distribution number |
| f(g) | ODF intensity for a given orientation g |
| h | final thickness of the rolled strip |
| h0 | initial thickness of the rolled strip |
| L1 | length of the grain; i.e., its size along RD |
| L2 | width of the grain; i.e., its size along TD |
| L3 | thickness of the grain; its size along ND |
| A = | the strain hardening anisotropy parameter |
| D | the distance of a grain boundary strong influence on the deformation of its interior |
| unit slip direction vector (i.e., parallel to the Burgers vector of the slipping dislocations), for the slip system s | |
| ij component of microscopic plastic deformation of grain | |
| component of macroscopic plastic deformation of the polycrystalline sample | |
| maximum intensity of the texture components (calculated value) | |
| strain hardening matrix describing hardening of the system s as a result of a strain in the system h | |
| subspace of the Euler space, defined in the Ref. [90] | |
| elements of the strain hardening matrix related to the group of mutually coplanar systems and those non-coplanar systems, whose dislocations do not create strong obstacles to the dislocations movement, | |
| elements of the strain hardening matrix related to the group of mutually non-coplanar systems, whose dislocations do create strong obstacles to the dislocations movement, | |
| dyadic product of the unit slip direction vector and the unit vector normal to the slip plane, for the slip system s | |
| unit vector normal to the slip plane calculated for the slip system s | |
| α | the stress scale factor |
| simple shear deformation in this slip system s | |
| assumed strain increase in each slip system for single step of the computer model used | |
| ε | rolling true strain (in thickness) |
| p | number of mutually independent slip systems |
| local stress acting on a grain | |
| external stress imposed on a grain | |
| critical shear stress for slip system s | |
| initial value of , assumed to be the same for each slip system s | |
| υ | misorientation |
| Euler angles (here in the Bunge convention) | |
| Superscripts | |
| right | |
| q | number of the slip systems combination |
| left | |
| T | Tucker (stress) tensor |
| R | reaction (stress) |
| E | effective value (of stress) |
| Subscripts | |
| left | |
| s1, s2 | (stress) activated slip system no. 1, 2 |
| 1, 2 | (stress) acting in slip system no. 1, 2 but not activated them |
| Texture components | |
| B | {011}<211> |
| S | ~{123}<634> |
| Cu | {112}<111>, {4 4 11}<11 11 8> |
| G | {011}<100> |
| W | {001}<100> |
| rW | {025}<100> |
| α-fiber | texture fiber |
| β-fiber | texture fiber |
References
- de Souza, C.R.; de Monlevade, E.F. Effect of Cold Rolling Path on the Deformation Textures of C10300 Copper. Mater. Res. 2021, 24, e20200332. [Google Scholar] [CrossRef]
- Long, D.; Liu, S.; Zhu, J.; Zhang, J.; Yuan, X. Texture and Microstructure Evolution of Ultra-High Purity Cu-0.1al Alloy under Different Rolling Methods. Crystals 2021, 11, 1113. [Google Scholar] [CrossRef]
- Lee, J.; Jeong, H.; Lee, G.; Jung, T. Mechanical Properties, Microstructure, and Texture Evolution of Copper Sheets Subjected to Differential Speed Rolling Process. Mater. Res. Express 2022, 9, 106503. [Google Scholar] [CrossRef]
- Gao, Y.; Guo, T.; Feng, R.; Qian, D.; Huang, D.; Zhang, G.; Ling, D.; Ding, Y. High Strength High Conductivity Copper Prepared by C-ECAP and Cryo-Rolling. Mater. Charact. 2024, 208, 113665. [Google Scholar] [CrossRef]
- Qin, J.; Li, X.; Wang, D.; Zhou, C.; Hu, T.; Wang, J.; Wang, Y.; Hu, Y. Microstructure and Texture Evolution in Cold-Rolled and Annealed Oxygen-Free Copper Sheets. Materials 2024, 17, 2202. [Google Scholar] [CrossRef] [PubMed]
- Roters, F.; Eisenlohr, P.; Bieler, T.R.; Raabe, D. Crystal Plasticity Finite Element Methods. In Materials Science and Engineering; Wiley-Vch: Weinheim, Germany, 2010. [Google Scholar]
- Roters, F.; Eisenlohr, P.; Hantcherli, L.; Tjahjanto, D.D.; Bieler, T.R.; Raabe, D. Overview of Constitutive Laws, Kinematics, Homogenization and Multiscale Methods in Crystal Plasticity Finite-Element Modeling: Theory, Experiments, Applications. Acta Mater. 2010, 58, 1152–1211. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, R.; Yao, Y.; Min, N.; Li, W.; Diao, A. The Effect of Multi-Step Tempering and Partition Heat Treatment on 25Cr2Ni3MoV Steel’s Cryogenic Strength Properties. Materials 2024, 17, 518. [Google Scholar] [CrossRef]
- Byrska-Wójcik, D.; Ostachowska, M.; Gibek, J.; Wierzbanowski, K.; Wróbel, M.; Błoniarz, R.; Baczmański, A. Texture Homogenization in Aluminium during Multi-Pass Asymmetric and Symmetric Rolling with Tilted and Flat Material Entry. J. Mater. Process. Technol. 2025, 338, 118796. [Google Scholar] [CrossRef]
- Uniwersał, A.; Wróbel, M.; Wierzbanowski, K.; Wroński, S.; Baczmański, A. Mechanical and Microstructural Characteristics of Polycrystalline Copper Rolled Asymmetrically to a High Deformation Level. Mater. Charact. 2019, 148, 214–223. [Google Scholar] [CrossRef]
- Wroński, S.; Wierzbanowski, K.; Bacroix, B.; Chauveau, T.; Wróbel, M. Effect of Asymmetric Rolling on Mechanical Characteristics, Texture and Misorientations in Ferritic Steel. J. Cent. South Univ. 2013, 20, 1443–1455. [Google Scholar] [CrossRef]
- Crumbach, M.; Pomana, G.; Wagner, P.; Gottstein, G. A Taylor Type Deformation Texture Model Considering Grain Interaction and Material Properties. Part I—Fundamentals. In Recrystallization and Grain Growth; Springer: Berlin/Heidelberg, Germany, 2001; Volume 1 and 2. [Google Scholar]
- Gallardo-Basile, F.J.; Naunheim, Y.; Roters, F.; Diehl, M. Lath Martensite Microstructure Modeling: A High-Resolution Crystal Plasticity Simulation Study. Materials 2021, 14, 691. [Google Scholar] [CrossRef]
- Van Houtte, P.; Li, S.; Engler, O. Taylor-Type Homogenization Methods for Texture and Anisotropy. In Continuum Scale Simulation of Engineering Materials; Wiley-Vch: Weinheim, Germany, 2004. [Google Scholar]
- Hibbard, W.R., Jr.; Yen, M.K. Wire Textures of Copper and Its Binary Alpha Solid Solution Alloys with Aluminum, Nickel and Zinc. Trans. AIME 1948, 175, 126–141. [Google Scholar]
- Heye, W.; Wassermann, G. Die Entstehung der Walztexturen der Kubisch Flächenzentrierten Metalle Durch Gleiten, Mechanische Zwillingsbildung und die Bildung Beschränkter Fasertexturen. Int. J. Mater. Res. 1968, 59, 616–624. [Google Scholar] [CrossRef]
- Łatas, W.; Wróbel, M. Computer Simulation of the Rolling Texture Development for the High and Medium Stacking Fault Energy. Arch. Metall. 1995, 40, 263–281. [Google Scholar]
- Van Houtte, P.; Delannay, L.; Kalidindi, S.R. Comparison of Two Grain Interaction Models for Polycrystal Plasticity and Deformation Texture Prediction. Int. J. Plast. 2002, 18, 359–377. [Google Scholar] [CrossRef]
- Taylor, G.I. Plastic Strain in Metals. Twenty-Eighth May Lecture to the Institute of Metals 1938. J. Inst. Met. 1938, 62, 307–324. Available online: http://pajarito.materials.cmu.edu/documents/Taylor_1938.pdf (accessed on 1 August 2025).
- Taylor, G.I. Verformung Und Fliessen Des Festkörpers. In IUTAM Coloquium; Madrid, R.L., Grammel, S.V., Eds.; Springer: Berlin/Heidelberg, Germany, 1956; p. 3. [Google Scholar]
- Mises, R.V. Mechanik Der Plastischen Formänderung von Kristallen. ZAMM—J. Appl. Math. Mech./Z. Angew. Math. Mech. 1928, 8, 161–185. [Google Scholar] [CrossRef]
- Schmid, E. Yield Point of a Crystals: Critical Shear Stress Law. In Proceedings of the 14th International Congress of Theoretical and Applied Mechanics, Delft, The Netherlands, 30 August–4 September 1976; p. 342. [Google Scholar]
- Bishop, J.F.W.; Hill, R. XLVI. A Theory of the Plastic Distortion of a Polycrystalline Aggregate under Combined Stresses. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1951, 42, 414–427. [Google Scholar] [CrossRef]
- Bishop, J.F.W.; Hill, R. CXXVIII. A Theoretical Derivation of the Plastic Properties of a Polycrystalline Face-Centred Metal. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1951, 42, 1298–1307. [Google Scholar] [CrossRef]
- Chin, G.Y.; Mammel, W.L. Generalization and Equivalence of the Minimum Work (Taylor) and Maximum Work (Bishop-Hill) Principles for Crystal Plasticity. Trans. TMS-AIME 1969, 245, 1211–1214. [Google Scholar]
- Van Houtte, P. On the Equivalence of the Relaxed Taylor Theory and the Bishop-Hill Theory for Partially Constrained Plastic Deformation of Crystals. Mater. Sci. Eng. 1982, 55, 69–77. [Google Scholar] [CrossRef]
- Honneff, H. Berechnung der Orientierungsänderungen und Texturentwicklung Beim Walzen Kristalliner Festkörper Mit Hilfe Eines Modifizierten Taylor-Modells; Technische Hochschule: Aachen, Germany, 1980. [Google Scholar]
- Honneff, H.; Mecking, H. A Method for the Determination of the Active Slip Systems and Orientation Changes During Single Crystal Deformation. In Textures of Materials; Springer: Berlin/Heidelberg, Germany, 1978. [Google Scholar]
- Mecking, H. Computer Simulation of Texture Development. In Proceedings of the 6th International Conference on Textures of Materials (ICOTOM6), Tokyo, Japan, 28 September–3 October 1981; Nagashima, S., Ed.; Iron and Steel Institute: Tokyo, Japan, 1981; Volume 1, pp. 53–66. [Google Scholar]
- Kocks, U.F.; Canova, G.R. How Many Slip Systems, and Which? In Deformation of Polycrystals, Mechanisns and Microstructures; Hansen, N., Horsewell, A., Humphreys, F.J., Eds.; Riso National Laboratory: Roskilde, Denmark, 1981; pp. 35–44. [Google Scholar]
- Kocks, U.F.; Chandra, H. Slip Geometry in Partially Constrained Deformation. Acta Metall. 1982, 30, 695–709. [Google Scholar] [CrossRef]
- Rocks, U.F.; Canova, G.R.; Jonas, J.J. Yield Vectors in f.c.c. Crystals. Acta Metall. 1983, 31, 1243–1252. [Google Scholar] [CrossRef]
- van Houtte, P. Adaption of the Taylor Theory to the Typical Substructure of Some Cold-Rolled Fcc Metals. In Proceedings of the 6th International Conference on Textures of Materials (ICOTOM6), Tokyo, Japan, 28 September–3 October 1981; Nagashima, S., Ed.; Iron and Steel Institute: Tokyo, Japan, 1981; pp. 428–437. [Google Scholar]
- Van Houtte, P. Some Recent Developments in the Theories for Deformation Texture Prediction. In Proceedings of the 7th International Conference on Texture of Materials (ICOTOM7), Noordwijkerhout, The Netherlands, 17–21 September 1984; pp. 7–23. [Google Scholar]
- Mecking, H. Deformation of Polycrystals. In Proceedings of the 5th International Conference on the Strength of Metals and Alloys (ICSMA5), Achen, Germany, 27–31 August 1979; Haasen, P., Gerold, V., Kostorz, G., Eds.; Pergamon Press: Oxford, UK, 1979; Volume 3, pp. 1573–1594. [Google Scholar]
- Fortunier, R.; Driver, J.H. Grain Reorientations in Rolled Aluminium Sheet: Comparison with Predictions of Continuous Constraints Model. Acta Metall. 1987, 35, 1355–1366. [Google Scholar] [CrossRef]
- Daniel, D.; Jonas, J.J. Texture and Anisotropy of Plastic Properties in Deep Drawing Steels. Texture Stress Microstruct. 1991, 14, 1165–1171. [Google Scholar] [CrossRef]
- Gingell, A.D.B.; Fundenberger, J.J.; Verdu, C.; Maurice, C.; Driver, J.H. Microscopic Aspects of Heterogeneous Deformation in Aluminium-Magnesium Alloy 5182. Rev. Metall. Cah. D’Inf. Tech. 1997, 94, 1457–1465. [Google Scholar] [CrossRef]
- Duggan, B.J.; Quadir, M.Z.; Tse, Y.Y. Deformation Bands in Texture Formation in Cold and Warm Rolling Interstitial-Free Steel, in Advanced X-Ray Techniques in Research and Industry. In Advanced X-Ray Techniques in Research and Industry; Singh, A.K., Ed.; IOS Press: Amsterdam, Australia; Berlin/Heidelberg, Germany; Oxford, UK; Tokyo, Japan; Washington, DC, USA, 2005; pp. 66–68. [Google Scholar]
- Verlinden, B.; Driver, J.; Samajdar, I.; Doherty, R. Modelling. In Thermo-Mechanical Processing of Metallic Materials; Cahn, R.W., Ed.; Elsevier: New York, NY, USA, 2007. [Google Scholar]
- Suwas, S.; Gurao, N.P. Development of Microstructures and Textures by Cross Rolling. In Comprehensive Materials Processing: Thirteen Volume Set; Elsevier: New York, NY, USA, 2014; Volume 3. [Google Scholar]
- Wróbel, M.; Dymek, S.; Blicharski, M.; Gorczyca, S. The Development of Dislocation Structure and Texture in Rolled Copper (001)[110] Single Crystals. Texture Stress Microstruct. 1988, 10, 67–75. [Google Scholar] [CrossRef]
- Wrobel, M.; Dymek, S.; Blicharski, M.; Gorczyca, S. Dislocation Microstructure and Texture Development in Rolled Copper Single Crystals. Z. Fuer Met./Mater. Res. Adv. Tech. 1994, 85, 415–425. [Google Scholar] [CrossRef]
- Van Houtte, P.; Delannay, L.; Samajdar, I. Quantitative Prediction of Cold Rolling Textures in Low-CarbonSteel by Means of the Lamel Model. Texture Stress Microstruct. 1999, 31, 109–149. [Google Scholar] [CrossRef]
- Van Houtte, P.; Li, S.; Seefeldt, M.; Delannay, L. Deformation Texture Prediction: From the Taylor Model to the Advanced Lamel Model. Int. J. Plast. 2005, 21, 589–624. [Google Scholar] [CrossRef]
- Honneff, H.; Mecking, H. Analysis of the Deformation Texture at Different Rolling Conditions. In Proceedings of the 6th International Conference on Textures of Materials (ICOTOM 6), Tokyo, Japan, 28 September–3 October 1981; Nagashima, S., Ed.; Iron and Steel Institute: Tokyo, Japan, 1981; pp. 347–355. [Google Scholar]
- Hamada, J.I.; Ono, J.I.; Inoue, H. Effect of Texture on R-Value of Ferritic Stainless Steel Sheets. ISIJ Int. 2011, 51, 1740–1748. [Google Scholar] [CrossRef]
- Hamada, J.I.; Agata, K.; Inoue, H. Estimation of Planar Anisotropy of the R- Value in Ferritic Stainless Steel Sheets. Mater. Trans. 2009, 50, 752–758. [Google Scholar] [CrossRef]
- Liu, Y.S.; Van Houtte, P. Simulation of Deformation Textures in Cold-Rolled Molybdenum Sheets by the Taylor-Bishop-Hill Theory. Int. J. Refract. Met. Hard Mater. 2001, 19, 209–216. [Google Scholar] [CrossRef]
- Tóth, L.S.; Molinari, A.; Raabe, D. Modeling of Rolling Texture Development in a Ferritic Chromium Steel. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 1997, 28, 2343–2351. [Google Scholar] [CrossRef]
- Raphanel, J.L.; Van Houtte, P. Simulation of the Rolling Textures of b.c.c. Metals by Means of the Relaxed Taylor Theory. Acta Metall. 1985, 33, 1481–1488. [Google Scholar] [CrossRef]
- Zankl, G. Magnetische und Elektronenmikroskopische Untersuchungen Zum Plastischen Verhalten von Vielkristallinem Nickel. Z. Naturforschung—Sect. A J. Phys. Sci. 1963, 18, 795–809. [Google Scholar] [CrossRef]
- Schwink, C.H.; Vorbrugg, W. Experimentelle und Theoretische Untersuchungen Zum Plastischen Verhalten Kubisch-Flächenzentrierter Vielkristalle. Z. Naturforschung—Sect. A J. Phys. Sci. 1967, 22, 626–642. [Google Scholar] [CrossRef]
- Hirsch, J.; Lücke, K. Overview No. 76. Mechanism of Deformation and Development of Rolling Textures in Polycrystalline f.c.c. Metals-II. Simulation and Interpretation of Experiments on the Basis of Taylor-Type Theories. Acta Metall. 1988, 36, 2883–2904. [Google Scholar] [CrossRef]
- Sachs, G. Zur Ableitung Einer Fließbedingung. In Mitteilungen der Deutschen Materialprüfungsanstalten; Springer: Berlin/Heidelberg, Germany, 1929. [Google Scholar]
- Tucker, G.E.G. Discussion on Preferred Orientation. J. Inst. Metals 1953, 82, 655–656. [Google Scholar]
- Tucker, G.E.G. Comment on “Rolling Textures in f.c.c. and b.c.c. Metals”. Acta Metall. 1964, 12, 1093–1094. [Google Scholar] [CrossRef]
- Leffers, T. Computer Simulation of the Plastic Deformation in Face Centered Cubic Polycrystals and the Rolling Texture Derived. Phys. Status Solidi (B) 1968, 25, 337–344. [Google Scholar] [CrossRef]
- Leffers, T. A Kinematical Model for the Plastic Deformation of Face Centered Cubic Polycrystals. Ph.D. Thesis, Riso Report No. 302, Wiley-Vch: Riso, Denmark, 1975. [Google Scholar]
- Leffers, T. The Shortcomings of the Taylor Model in the Description of the Plastic Deformation of Real Polycrystals. In Textures of Materials; Springer: Berlin/Heidelberg, Germany, 1978. [Google Scholar]
- Leffers, T. Modified Sachs approach to the plastic deformation of polycrystals as a realistic alternative to the Taylor model. In Energy Technology Review; Elsevier: New York, NY, USA, 1980. [Google Scholar]
- Hansen, N.; Horsewell, A.; Leffers; Lilholt, H. Deformation of Polycrystals: Mechanisms and Microstructures. In Deformation of Polycrystals: Mechanisms and Microstructures; Risø National Laboratory: Roskilde, Denmark, 1981; pp. 55–71. [Google Scholar]
- English Oxford Dictionary. Available online: https://www.oed.com/search/dictionary/?scope=Entries&q=self-consistent (accessed on 2 November 2024).
- Bordoloi, R.B.; Bordoloi, R.; Konwer, R.; Konwer, M.; Dubey, R.K.; Saikia, J.; Baruah, D.; Konwaar, H.; Baruah, G.D. Self Consistency of Universal Laws Appearing in Different Contexts. Asian J. Phys. 2015, 24, 181–187. [Google Scholar]
- Tarpey, T.; Flury, B. Self-Consistency: A Fundamental Concept in Statistics. Stat. Sci. 1996, 11, 229–243. [Google Scholar] [CrossRef]
- Curie, P. Propriétés Magnétiques Des Corps à Diverses Températures. Ann. Chim. Phys. 1895, 5, 289–405. [Google Scholar]
- Weiss, P. L’hypothèse Du Champ Moléculaire et La Propriété Ferromagnétique. J. Phys. Theor. Appl. 1907, 6, 661–690. [Google Scholar] [CrossRef]
- Eshelby, J.D. The Determination of the Elastic Field of an Ellipsoidal Inclusion, and Related Problems. In Collected Works of J. D. Eshelby; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Kröner, E. Zur Plastischen Verformung des Vielkristalls. Acta Metall. 1961, 9, 155–161. [Google Scholar] [CrossRef]
- Hill, R. Continuum Micro-Mechanics of Elastoplastic Polycrystals. J. Mech. Phys. Solids 1965, 13, 89–101. [Google Scholar] [CrossRef]
- Hutchinson, J.W. Elastic-Plastic Behavior of Polycrystalline Metals and Composites. Proc. R. Soc. Ser. A Math. Phys. Sci. 1970, 319, 247–272. [Google Scholar] [CrossRef]
- Berveiller, M.; Zaoui, A. Some Applications of the Self-Consistent Scheme in the Field of Plasticity and Texture of Metallic Polycrystals. In Large Deformations of Solids: Physical Basis and Mathematical Modelling; Springer: Berlin/Heidelberg, Germany, 1986. [Google Scholar]
- Molinari, A.; Canova, G.R.; Ahzi, S. A Self Consistent Approach of the Large Deformation Polycrystal Viscoplasticity. Acta Metall. 1987, 35, 2983–2994. [Google Scholar] [CrossRef]
- Lebensohn, R.A.; Tomé, C.N. A Self-Consistent Anisotropic Approach for the Simulation of Plastic Deformation and Texture Development of Polycrystals: Application to Zirconium Alloys. Acta Metall. Mater. 1993, 41, 2611–2624. [Google Scholar] [CrossRef]
- Nagel, E. The Reduction of Theories. In The Structure of Science. Problems in the Logic of Scientific Explanation; Harcourt, Brace & World: New York, NY, USA, 1961; pp. 336–397. [Google Scholar]
- Batterman, R.W. Reduction. In Encyclopedia of Philosophy; Macmillan: Detroit, MI, USA, 2006; Volume 8, pp. 282–287. [Google Scholar]
- Clausen, B.; Lorentzen, T.; Leffers, T. Self-Consistent Modelling of the Plastic Deformation of F.C.C. Polycrystals and Its Implications for Diffraction Measurements of Internal Stresses. Acta Mater. 1998, 46, 3087–3098. [Google Scholar] [CrossRef]
- Zattarin, P.; Baczmański, A.; Lipiński, P.; Wierzbanowski, K. Modified Self Consistent Model for Time Independent Plasticity of Polycrystalline Material. Arch. Metall. 2000, 45, 163–184. [Google Scholar]
- Kot, P.; Baczmański, A.; Gadalińska, E.; Wroński, S.; Wroński, M.; Wróbel, M.; Bokuchava, G.; Scheffzük, C.; Wierzbanowski, K. Evolution of Phase Stresses in Al/SiCp Composite during Thermal Cycling and Compression Test Studied Using Diffraction and Self-Consistent Models. J. Mater. Sci. Technol. 2020, 36, 176–189. [Google Scholar] [CrossRef]
- Wierzbanowski, K.; Wroński, M.; Leffers, T. FCC Rolling Textures Reviewed in the Light of Quantitative Comparisons between Simulated and Experimental Textures. Crit. Rev. Solid State Mater. Sci. 2014, 39, 391–422. [Google Scholar] [CrossRef]
- Franciosi, P.; Berveiller, M.; Zaoui, A. Latent Hardening in Copper and Aluminium Single Crystals. Acta Metall. 1980, 28, 273–283. [Google Scholar] [CrossRef]
- Franciosi, P. Etude Théorique et Expérimentale du Comportement Élastoplastique des Monocristaux Métalliques se Déformant Par Glissement: Modélisation Pour un Chargement Complexe Quasi Statique; Universite Paris-Nord: Paris, France, 1984. [Google Scholar]
- Stupkiewicz, S.; Petryk, H. A Minimal Gradient-Enhancement of the Classical Continuum Theory of Crystal Plasticity. Part II: Size Effects. Arch. Mech. 2016, 68, 487–513. [Google Scholar]
- Kocks, U.F. The Relation between Polycrystal Deformation and Single-Crystal Deformation. Metall. Mater. Trans. 1970, 1, 1121–1143. [Google Scholar] [CrossRef]
- Backofen, W.A. Deformation Processing; Addison-Wesley: Reading, MA, USA, 1972. [Google Scholar]
- Leffers, T. Computer Simulation of the Plastic Deformation in Face Centered Cubic Polycrystals and the Rolling Texture Derived; Riso Report No 184; Danish Atomic Energy Commission: Riso, Denmark, 1968. [Google Scholar]
- Tome, C.; Canova, G.R.; Kocks, U.F.; Christodoulou, N.; Jonas, J.J. The Relation between Macroscopic and Microscopic Strain Hardening in F.C.C. Polycrystals. Acta Metall. 1984, 32, 1637–1653. [Google Scholar] [CrossRef]
- Hirsch, J.; Lücke, K. Overview No. 76. Mechanism of Deformation and Development of Rolling Textures in Polycrystalline f.c.c. Metals-I. Description of Rolling Texture Development in Homogeneous CuZn Alloys. Acta Metall. 1988, 36, 2863–2882. [Google Scholar] [CrossRef]
- Hirsch, J.; Aryshesnkij, E.; Konovalov, S. Slip System Selection and Taylor Factor Evolution in FCC Metals. SSRN Electron. J. 2020, 3618715. [Google Scholar] [CrossRef]
- Daniel, D.; Jonas, J.J. Measurement and Prediction of Plastic Anisotropy in Deep-Drawing Steels. Metall. Trans. A 1990, 21, 331–343. [Google Scholar] [CrossRef]
- Raabe, D. Computational Materials Science, The Simulation of Materials Microstructures and Properties; Wiley-Vch: Weinheim, Germany, 1998. [Google Scholar]
- Saint-Venant, A.J.C.B. Memoire Sur La Torsion Des Prismes. Mem. Divers. Savants 1855, 14, 233–560. [Google Scholar]
- Love, A.E.H. Treatise on Mathematical Theory of Elasticity, 4th ed.; Dover Publications Inc.: New York, NY, USA, 1944. [Google Scholar]
- Bunge, H.J. Texture Analysis in Material Science; Butterworths: London, UK, 1982. [Google Scholar]
- Wróbel, M.; Łatas, W. Computer Simulation of the Rolling Texture Development for the High and Medium Stacking Fault Energy FCC Metals, Part 2, Theoretical Analysis of Orientation Stability. Arch. Metall. 1995, 40, 333–344. [Google Scholar]
- Hansen, J.; Pospiech, J.; Lücke, K. Tables for Texture Analysis of Cubic Crystals; Springer: Berlin/Heidelberg, Germany, 1978. [Google Scholar]
- Pospiech, J.; Lücke, K. The Rolling Textures of Copper and α-Brasses Discussed in Terms of the Orientation Distribution Function. Acta Metall. 1975, 23, 997–1007. [Google Scholar] [CrossRef]
- Wierzbanowski, K.; Clement, A. Rotation Field and Continuity Equation for Texture Evolution. Cryst. Res. Technol. 1984, 19, 201–212. [Google Scholar] [CrossRef]
- Uniwersał, A.; Wroński, M.; Wróbel, M.; Wierzbanowski, K.; Baczmański, A. Texture Effects Due to Asymmetric Rolling of Polycrystalline Copper. Acta Mater. 2017, 139, 30–38. [Google Scholar] [CrossRef]
- Marin, M.; Ellahi, R.; Vlase, S.; Bhatti, M.M. On the Decay of Exponential Type for the Solutions in a Dipolar Elastic Body. J. Taibah Univ. Sci. 2020, 14, 534–540. [Google Scholar] [CrossRef]


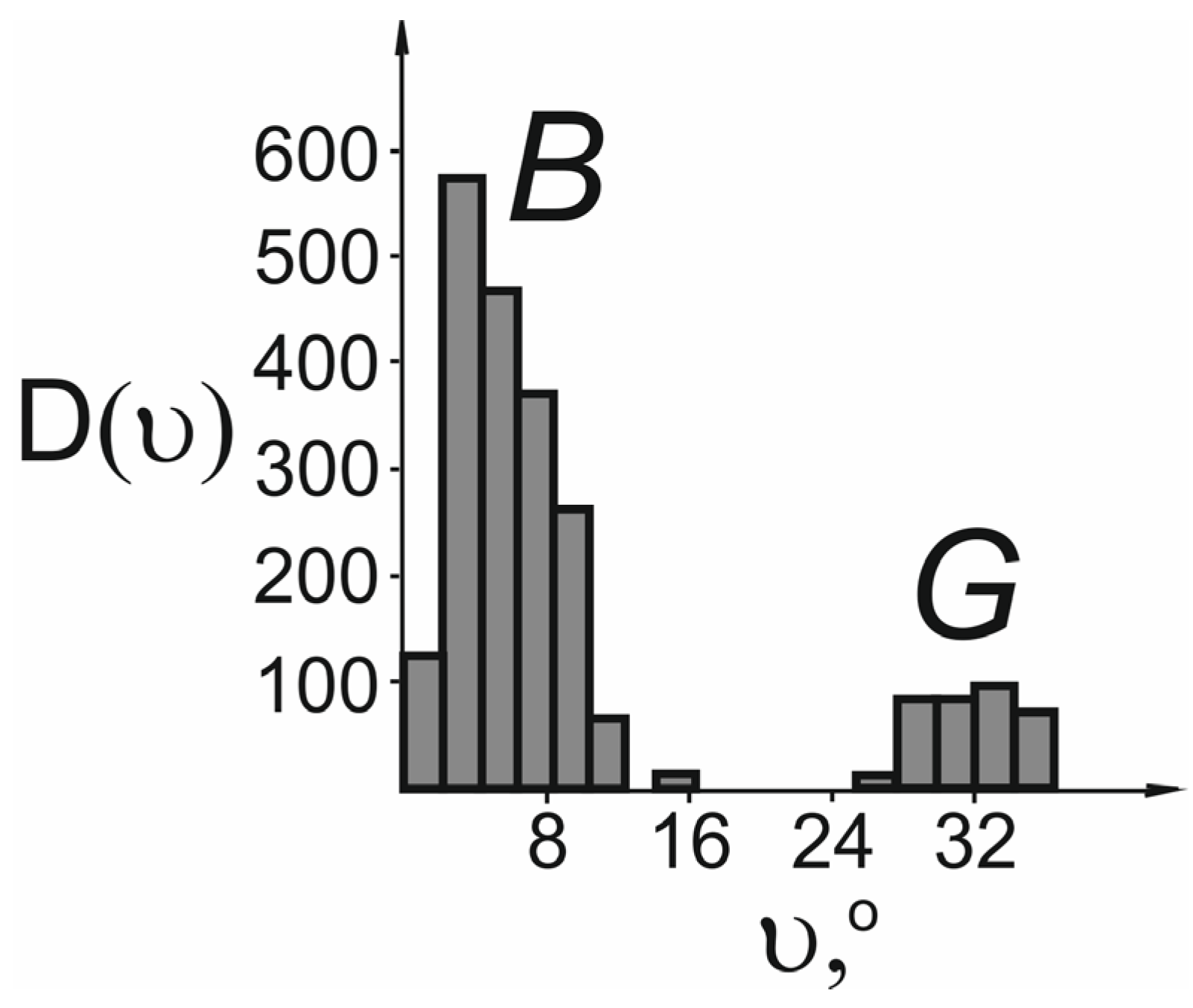
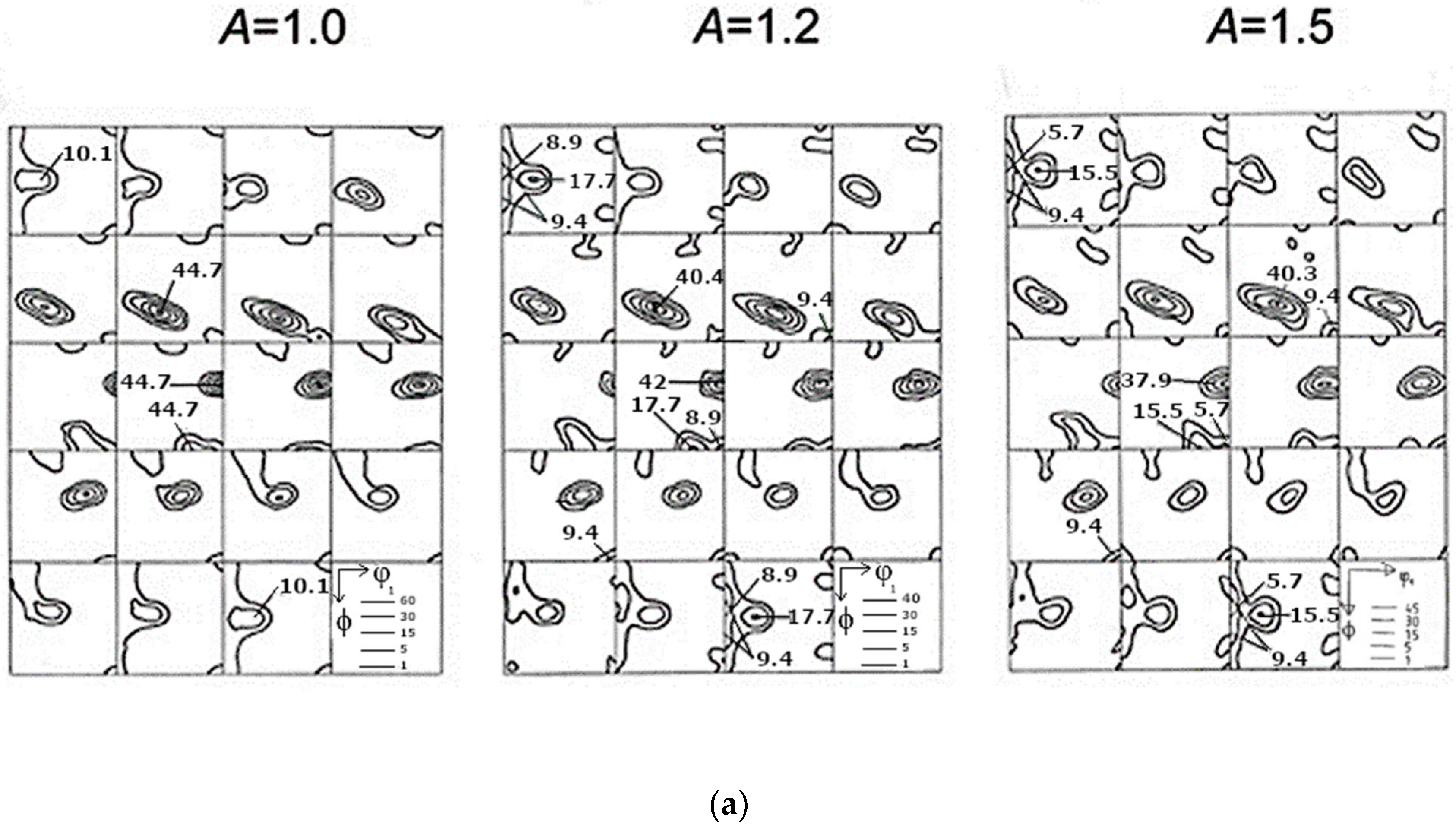
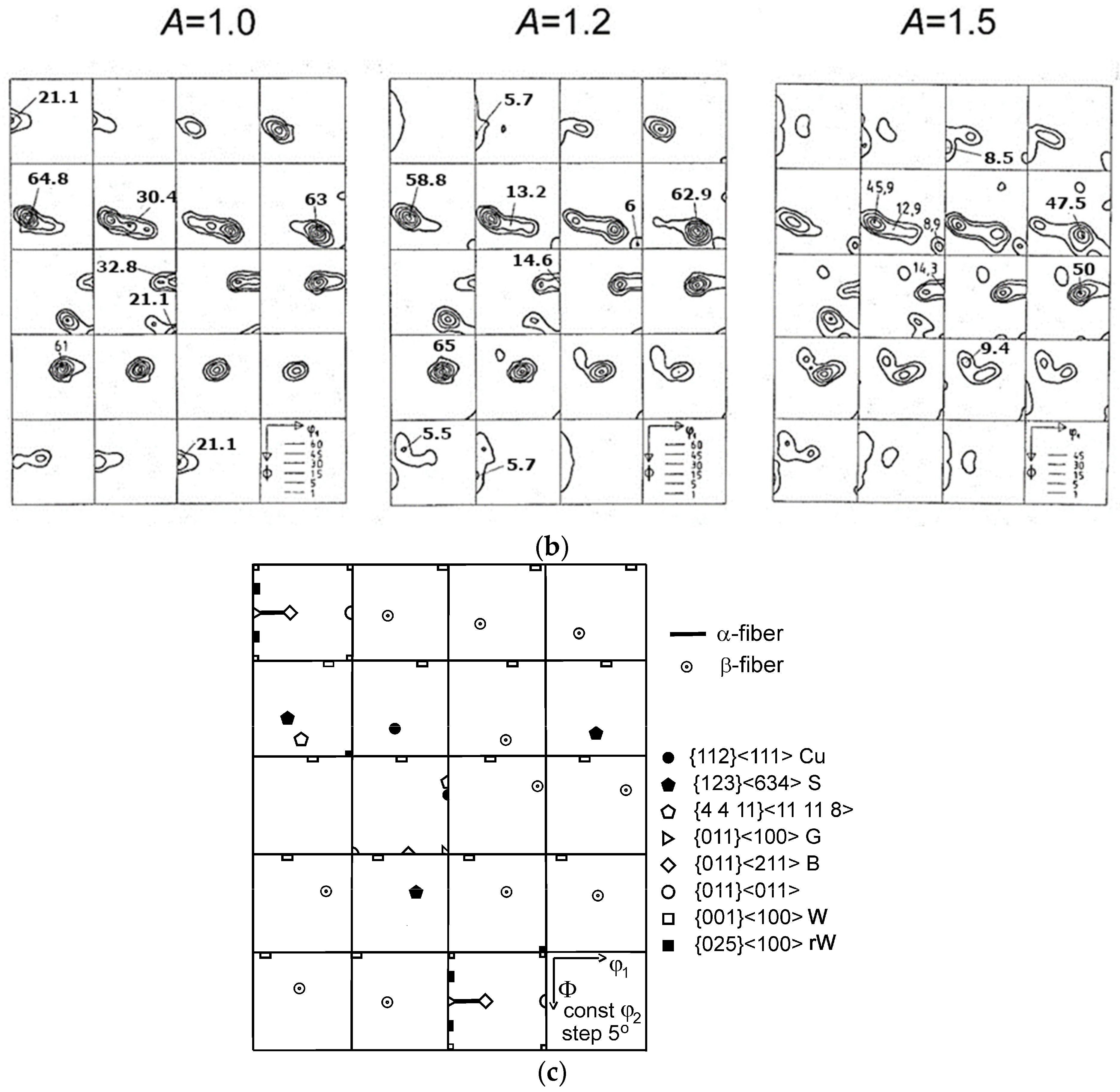
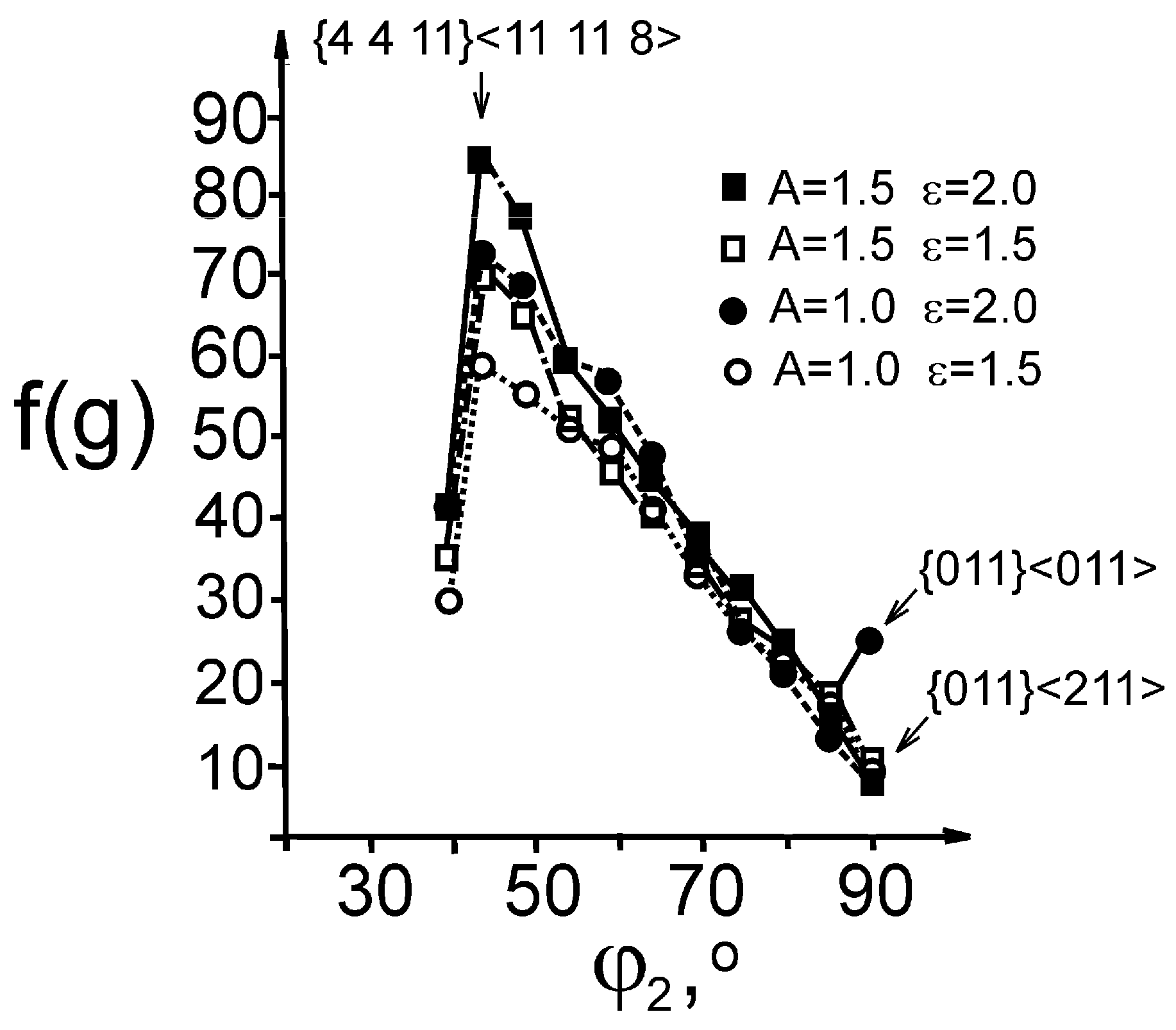


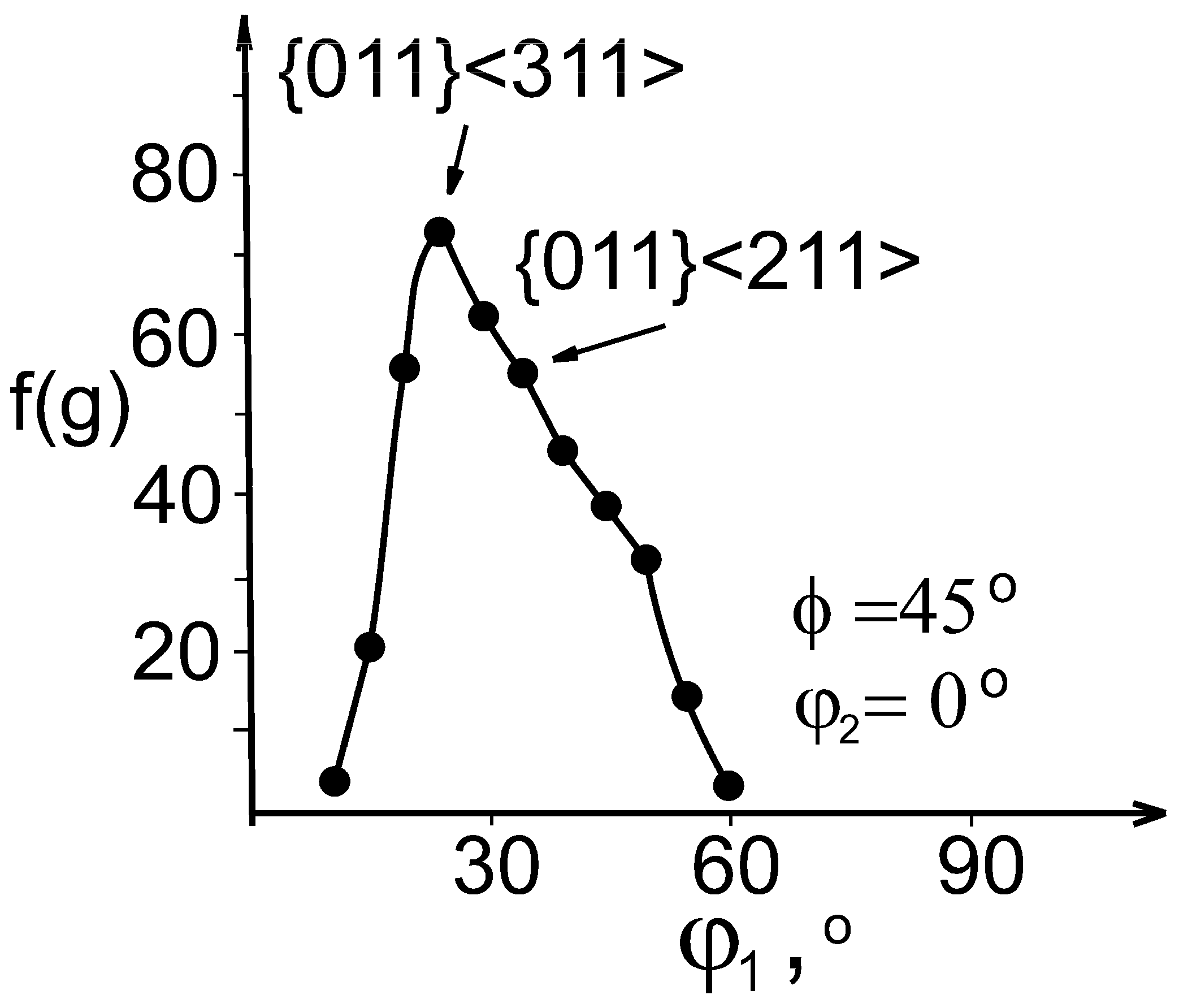

| Grains Group No. | |
|---|---|
| 1 | --- |
| 2 | |
| 3 | |
| 4 | |
| 5 |
| Grains Group No. | Texture Component | The Maximum Position | |||||
|---|---|---|---|---|---|---|---|
| A = 1 | A = 1.2 | A = 1.5 | |||||
| 1 | {4 4 11}<11 11 8> | 90 | 27 | 45 | 70.2 | 80.3 | 81.4 |
| {011}<011> | 90 | 45 | 90 | 22.9 | - | - | |
| 2 | {112}<111> | 90 | 35 | 45 | 44.7 | 42.0 | - |
| {447}<778> | 90 | 39 | 45 | - | - | 37.9 | |
| {011}<311> | 25 | 45 | 90 | 10.1 | 17.7 | 15.5 | |
| {011}<100> | 0 | 45 | 90 | - | 8.9 | 5.7 | |
| {025}<100> | 0 | 22 | 90 | 4.2 | - | - | |
| {047}<100> | 0 | 30 | 90 | - | 9.4 | 9.4 | |
| {001}<100> | 0 | 0 | 90 | 3.9 | 1.9 | 2.9 | |
| 3 | {539}<3 10 5> | 53 | 33 | 59 | 61.0 | - | - |
| {537}<132> | 57 | 40 | 59 | - | 65.0 | - | |
| {324}<275> | 58 | 42 | 56 | - | - | 50.0 | |
| {112}<111> | 90 | 35 | 45 | 32.8 | 14.6 | 14.3 | |
| {011}<100> | 0 | 45 | 90 | 21.1 | - | - | |
| {519}<091> | 13 | 30 | 79 | - | 5.5 | ||
| {317}<1 11 2> | 26 | 24 | 72 | - | - | 9.4 | |
| 4 | {011}<311> | 25 | 45 | 90 | 72.4 | - | - |
| {516}<394> | 37 | 40 | 79 | - | 53.5 | - | |
| {313}<163> | 38 | 47 | 72 | - | - | 46.7 | |
| {011}<655> | 50 | 45 | 90 | - | - | 28.2 | |
| A | Volume Fraction [%] 10° | |
|---|---|---|
| ε = 1.5 | ε = 2.0 | |
| 1.00 | 36.5 | 42.9 |
| 1.05 | 38.4 | 43.9 |
| 1.10 | 38.0 | 43.5 |
| 1.15 | 38.1 | 43.1 |
| 1.20 | 37.8 | 42.9 |
| 1.50 | 37.2 | 42.3 |
| A | Volume Fraction [%] 10° | |
|---|---|---|
| ε = 1.5 | ε = 2.0 | |
| 1.00 | 22.0 | 26.4 |
| 1.05 | 21.5 | 24.4 |
| 1.10 | 21.5 | 24.4 |
| 1.15 | 21.6 | 24.5 |
| 1.20 | 21.2 | 24.4 |
| 1.50 | 18.8 | 21.6 |
| A | Volume Fraction [%] 10° | |
|---|---|---|
| ε = 1.5 | ε = 2.0 | |
| 1.00 | 52.1 | 62.7 |
| 1.05 | 58.9 | 73.7 |
| 1.10 | 61.2 | 76.3 |
| 1.15 | 61.8 | 75.9 |
| 1.20 | 59.9 | 74.5 |
| 1.50 | 42.5 | 56.4 |
| A | Volume Fraction [%] 5° | |
|---|---|---|
| ε = 1.5 | ε = 2.0 | |
| 1.00 | 9.0 | 8.5 |
| 1.05 | 5.4 | 4.6 |
| 1.10 | 4.6 | 3.4 |
| 1.15 | 4.0 | 2.8 |
| 1.20 | 3.6 | 2.4 |
| 1.50 | 3.4 | 2.6 |
| A | Volume Fraction [%] 10° | |
|---|---|---|
| ε = 1.5 | ε = 2.0 | |
| 1.00 | 27.7 | 46.4 |
| 1.05 | 26.2 | 45.1 |
| 1.10 | 24.6 | 42.8 |
| 1.15 | 22.7 | 39.9 |
| 1.20 | 20.4 | 36.0 |
| 1.50 | 10.1 | 15.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Łatas, W.; Wróbel, M.; Wierzbanowski, K.; Byrska-Wójcik, D. Interpretation of Copper Rolling Texture Components Development Based on Computer Modeling. Crystals 2025, 15, 1011. https://doi.org/10.3390/cryst15121011
Łatas W, Wróbel M, Wierzbanowski K, Byrska-Wójcik D. Interpretation of Copper Rolling Texture Components Development Based on Computer Modeling. Crystals. 2025; 15(12):1011. https://doi.org/10.3390/cryst15121011
Chicago/Turabian StyleŁatas, Wiesław, Mirosław Wróbel, Krzysztof Wierzbanowski, and Dorota Byrska-Wójcik. 2025. "Interpretation of Copper Rolling Texture Components Development Based on Computer Modeling" Crystals 15, no. 12: 1011. https://doi.org/10.3390/cryst15121011
APA StyleŁatas, W., Wróbel, M., Wierzbanowski, K., & Byrska-Wójcik, D. (2025). Interpretation of Copper Rolling Texture Components Development Based on Computer Modeling. Crystals, 15(12), 1011. https://doi.org/10.3390/cryst15121011





