Optical and Vibrational Properties of AlN Nanoparticles with Different Geometries: A DFT and TD-DFT Study

Abstract

In this work, by using density functional theory (DFT) and time-dependent DFT (TD-DFT) a comprehensive theoretical study on the structural, electronic, optical, and vibrational properties of aluminum nitride (Al_xN_x) nanoparticles (NPs) is presented. More than thirty nanostructures were constructed based on an initial cubic-like Al₄N₄ building block, including one-dimensional (1D), two-dimensional (2D), and three-dimensional (3D) configurations, as well as asymmetric and defected geometries (also known as exotic geometries). The absorption spectrum was evaluated using the CAM-B3LYP functional while geometry optimizations and vibrational frequencies were performed using the PBE functional. All calculations were performed using the triple-ζ valence plus polarization basis set def2-TZVP. The optical spectra revealed strong geometry-dependent modulation of absorption, with red-shifted and broadened UV–Vis features emerging in elongated and low-symmetry geometries. IR analysis indicates a growing number and intensity of vibrational modes with increasing dimensionality, particularly in the 300–470 cm⁻¹ range, which corresponds to Al–N stretching and bending vibrations. Testing different exchange–correlation functionals showed that CAM-B3LYP is a good choice for excited-state calculations, matching well with the EOM-CCSD functional, which, while offering higher precision, imposes significantly higher computational requirements. Overall, the results demonstrate that structural variation in Al_xN_x NPs leads to tunable optoelectronic and spectroscopic behavior. These findings and calculations highlight the potential of AlN-based nanomaterials for applications in ultraviolet photonics, sensors, and future nanoscale optoelectronic devices.

1. Introduction

Industrial growth, population expansion, and ongoing technological evolution have significantly intensified environmental challenges, particularly with respect to fossil fuel consumption and global energy demands [1]. One of the most urgent worldwide concerns is climate change, which is still directly related to excessive CO₂ emissions from human activities such as industrial operations, electricity generation, and transportation [2]. Decarbonization tactics are therefore becoming increasingly important in the pursuit of environmental sustainability in the short and long run [3]. Since they provide scalable, clean alternatives to fossil fuels, renewable energy sources and especially solar energy are essential to these initiatives [4,5]. A major factor in this shift is the creation of high-performance photovoltaic materials [6]. Materials based on AlN NPs have emerged as promising candidates due to their excellent thermal stability, wide bandgap, and potential applications in optoelectronics and UV-based energy harvesting systems [7,8].

Nanotechnology, as one of the fastest-evolving scientific fields, continues to enable the development of novel materials with advanced functionalities for energy conversion and environmental sustainability [9,10]. Because of their tunable optical and electrical capabilities that are fueled by quantum confinement effects, semiconductor nanoparticles, also known as quantum dots (QDs), have garnered a lot of attention in this context [11]. Aluminum nitride (AlN), a wide-bandgap semiconductor, has shown remarkable potential at the nanoscale for use in ultraviolet (UV) light-emitting diodes, high-frequency transistors, optoelectronic devices, and nanoscale sensors [12,13]. AlN NPs are especially well-suited for harsh-environment applications as well as next-generation photonic and energy systems due to their high thermal conductivity, chemical inertness, and superior dielectric qualities. AlN QDs are also being researched for incorporation into solar systems, where their optical characteristics can be modified to improve energy harvesting effectiveness and UV absorption [14,15].

QDs based on group III–V nitrides, and particularly AlN, have attracted increasing attention due to their unique combination of wide bandgap, high thermal and chemical stability, and strong exciton binding energies [16]. Among these, AlN QDs stand out for their deep UV photoluminescence properties making them suitable for UV-emitting devices, biosensing, and secure optical communication systems [17]. In addition, nitrogen-rich AlN nanostructures exhibit enhanced optical performance due to strong quantum confinement and reduced surface defects [18]. A variety of synthesis techniques—such as solvothermal processing, chemical vapor deposition, laser ablation, and pulsed electron beam deposition—have been explored to produce AlN nanomaterials with controlled size and morphology [19,20]. These synthesis routes directly influence the resulting optical gap, crystallinity, and surface-state distribution. Recent studies have also highlighted the potential of AlN nanomaterials in ultraviolet photodetectors, piezoelectric nano-generators, and dielectric layers in high-power electronics [21,22]. Despite this growing body of experimental work, the fundamental understanding of the size- and shape-dependent electronic and optical properties of AlN nanoparticles remains incomplete. Theoretical approaches such as density functional theory (DFT) and time-dependent DFT (TD-DFT) can offer valuable insights into the relationship between structure, stability, and optical response at the nanoscale [23,24].

In this study, we examine a comprehensive theoretical investigation of the structural, electronic, and optical properties of AlN nanoparticles by employing DFT [22,25] and TD-DFT methods [26]. This work builds on an initial cubic-like Al₄N₄ NP, by which new configurations can be constructed when it is elongated along one, two, and three perpendicular directions. These nanostructures were optimized to ensure geometric and vibrational stability, and their optical properties were evaluated through the simulated ultraviolet–visible (UV–Vis) absorption spectra. The calculations for the examined NPs include the determination of the absorption spectrum (AS), the binding energy (BE), and the highest occupied-lowest unoccupied molecular orbital (HOMO-LUMO) gap. The influence of nanoparticle size and morphology on the optical gap and oscillator strength was examined in detail. This study aims to provide new insights into the nanoscale behavior of AlN-based quantum dots, with potential implications for UV photonics, high-power electronics, and quantum optoelectronic applications.

Despite the growing interest in AlN-based nanomaterials, the fundamental relationship between nanoparticle geometry and optoelectronic behavior remains poorly understood. Previous DFT studies have mostly focused on size effects or bulk-derived properties, while the influence of geometric dimensionality and symmetry breaking on the optical and vibrational response of Al_xN_x clusters has not been systematically explored. The present work aims to address this gap by focusing the research on how the geometric dimensionality and symmetry breaking in Al_xN_x nanoparticles influence their electronic delocalization, optical excitation energies, and infrared-active vibrational modes. By combining DFT and TD-DFT simulations across one-, two-, and three-dimensional configurations, this contribution seeks to identify general structure–property relationships and to clarify how morphological variation governs the optical and vibrational fingerprints of AlN nanostructures. These insights are expected to support the rational design of AlN-based materials for ultraviolet photonic and sensing applications

2. Materials and Methods

In this study, the optical and structural properties of more than 30 different nanoparticles were ascertained using DFT and TD-DFT. After an elongation of the initial cubic-like nanostructure along one, two, and three perpendicular directions, the examined nanostructures were created, and their structural stability was examined. Early research on stable conformations has led to stable morphologies. The triple-ζ quality def2-TZVP basis set [27] was used to perform the geometry optimizations using the gradient corrected functional of Perdew, Burke, and Ernzerhof (PBE) [28]. Then, using TD-DFT on the ground state geometries, the ultraviolet-visible absorption spectra and the lowest singlet vertical excitation energies of each investigated NP were determined. The hybrid CAM-B3LYP (Coulomb-attenuating method) functional [29], which is known for its accurate excitation energy prediction, was used as the exchange–correlation functional in the TD-DFT calculations for all systems under consideration. To verify the dynamical stability of the optimized geometries and examine the IR-active vibrational modes, harmonic vibrational frequency calculations were also performed on them at the PBE/def2-TZVP level. It should be noted that preliminary tests using different functionals were carried out on smaller NPs to validate the selection, because experimental absorption spectra for the suggested nanostructures were not available. The predicted absorption spectra were compared with the high-precision EOM-CCSD functional [30] to choose the best functional because EOM-CCSD requires significantly more computing time. The calculated absorption spectra were constructed using a script that represents each excitation as a Gaussian function with a standard deviation (broadening) of 0.1 eV and centered on the TD-DFT computed excitation energy. To approximate the peak form observed empirically, the latter value was chosen. Relevantly, the vibrational spectra were plotted with the use of a script that represents each vibration as a Gaussian function, with its center on the vibrational frequency considering a standard deviation (broadening) of 10 cm⁻¹. All DFT and TD-DFT calculations presented in this work—including geometry optimizations, vibrational frequency analysis, and absorption spectra simulations—were performed using the TURBOMOLE 7.6 software package [31] with various exchange–correlation functionals (e.g., PBE and CAM-B3LYP). For benchmarking purposes, high-level excited-state calculations at the EOM-CCSD level were carried out on smaller reference structures (such as Al₄N₄) using the Gaussian 16 Rev. c.01.software package [32], owing to its robust implementation of correlated wavefunction methods. These models were designed to probe how directional connectivity and geometric bending influence electronic delocalization and optical response. Such motifs are also consistent with bent or branched AlN nanoclusters occasionally observed in plasma-assisted and gas-phase aggregation experiments. The L-, T-, and S-shaped geometries were selected as representative asymmetric configurations that allow systematic reduction in structural symmetry while preserving comparable composition. The letter symbols indicate the initial configuration made with the cubic-like Al₄N₄ as presented in Figure 1. After geometry optimization these shapes changed. Similar structures were studied for other nanoparticles such as ScN [33], MgS [34], and CaS [35]. The different shapes of those NPs are stable and exhibit a great variety in their absorption and vibrational spectrum. These models were designed to probe how directional connectivity and geometric bending influence electronic delocalization and optical response. Such motifs are also consistent with bent or branched AlN nanoclusters occasionally observed in plasma-assisted and gas-phase aggregation experiments. Eventually, it would be very interesting to study the combinations of those cubic-like NPs.

3. Results and Discussion

Our benchmark results validate our functional choice for extended Al_xN_x structures by confirming previous findings on the Al₄N₄ prototype, where CAM-B3LYP closely reproduces both first and second singlet excitation energies and oscillator strengths compared to EOM-CCSD, with deviations of less than 0.1 eV [36]. This is clear from the collected results in

Table 1. The Al₄N₄ NP comparison of the first and the second excitation energy for the different functionals.

Functional	1st Excitation (eV)	Osc. Strength	2nd Excitation (eV)	Osc. Strength
PBE	0.755	0.0153	2.632	0.120
B3LYP	1.160	0.0210	3.09	0.114
CAM-B3LYP	1.610	0.0240	3.77	0.117
PBE0	1.320	0.0264	3.26	0.132
M06-2X	1.660	0.0219	3.72	0.078
EOM-CCSD	1.557	0.0350	3.664	0.198

where the first two calculated resonances using several different well-known functionals are presented. This pattern aligns with previous benchmarking investigations on III–V nitride clusters, including ScN NPs [33]. In addition, the use of Al_xN_x NPs in high-power applications is supported by the excellent dielectric properties and high thermal stability of bulk AlN ceramics, which have been well documented in the literature [34]. These results are consistent with those of Moustris et al. [35] on exotic and defective calcium nanoclusters. AlN NPs have also shown biocompatibility and anticancer activity in experiments [12]. Recent magnesium-based nanostructures have also been studied for these properties using surface-mode analysis and vibrational fingerprinting [36]. It should also be mentioned that among the latest DFT studies on AlN-based clusters, sol–gel mechanisms for AlN formation and IR-based drug delivery modeling on tetragonal AlN, complement the present work, where size-dependent and shape-dependent analysis of optical and vibrational properties are provided [37,38]. As already mentioned, the agreement between our CAM-B3LYP TD-DFT results and the reference EOM-CCSD data reinforces our computational approach [15], while the vibrational tunability of these systems is confirmed by the growing density of IR-active modes across 1D, 2D, and 3D geometries [34,35]. IR intensities (in km/mol) are reported as obtained from the TD-DFT calculations.

3.1. Al_xN_x Nanoparticles

This work expands on the current knowledge of AlN nanoclusters and offers theoretical justification for their use in optoelectronics, sensing, and possibly biomedical applications by combining geometric variation, optical absorption, and infrared signatures. As can be seen from Figure 1, the initial cubic building block of the form Al₄N₄ served as the basis for all the nanostructures under study. The geometry optimization for the Al₄N₄ nanocluster, as presented in Figure 1, showed that it exhibits a quasi-cubic arrangement with near-ideal angular geometry. Most internal angles approach the ideal 90°, with only slight deviations where an angle of ∼82° was measured, reflecting the structural stability and low strain in the optimized configuration. By elongating this building block, new stable structures with intriguing optical characteristics could be produced. As a result, the formed Al_xN_x nanostructures can be divided into three categories. The first category includes elongated nanoparticles along one direction (1D). The second includes nanoparticles of the general form Al₁₆N₁₆ which were created after elongation of the initial cubic unit along two and three directions and thus forming a group of exotic nanostructures composed of nanostructures with several familiar shapes. The third category of the studied NPs includes the Al₃₂N₃₂ nanostructures. The nanostructures of this group were formed by the elongation of the initial cubic unit along one, two, and three perpendicular directions. An exotic NP was also examined for this case. This exotic nanostructure was created by the extraction of one cubic unit from the center of the two-dimensional Al₃₆N₃₆ case. In addition, larger Al_xN_x NPs were also examined, where x = 36 and x = 40. The examination of the computed optical characteristics of the suggested NPs revealed some intriguing results which trigger potential uses of the suggested nanostructures.

Figure 1. The initial cubic-like building block Al₄N₄ after its geometry optimization. Gray color corresponds to the Al atom while blue to the N atom. (a) Side view of the cube and (b) a 45-degree perspective of the cubic unit.

Figure 1. The initial cubic-like building block Al₄N₄ after its geometry optimization. Gray color corresponds to the Al atom while blue to the N atom. (a) Side view of the cube and (b) a 45-degree perspective of the cubic unit.

3.1.1. One-Directional Al_xN_x NPs

As already mentioned, the AlN NPs were divided into four categories where the first category of nanostructures was created by elongation of the initial cubic-like building block, Al₄N₄, along one direction. The general form of the created NPs is Al_xN_x, where x = 8, 16 for this case. As can be seen from Figure 2, the structure with x = 8 consists of two cubic-like building blocks, and the structure with x = 16 consists of four corresponding cubes. These structures can be considered stable as there were not any imaginary frequencies due to geometry optimization. The computational results for Al₄N₄, Al₈N₈, and Al₁₆N₁₆-1D, showed that each NP exhibits distinct optical and vibrational behavior as a function of its size and composition.

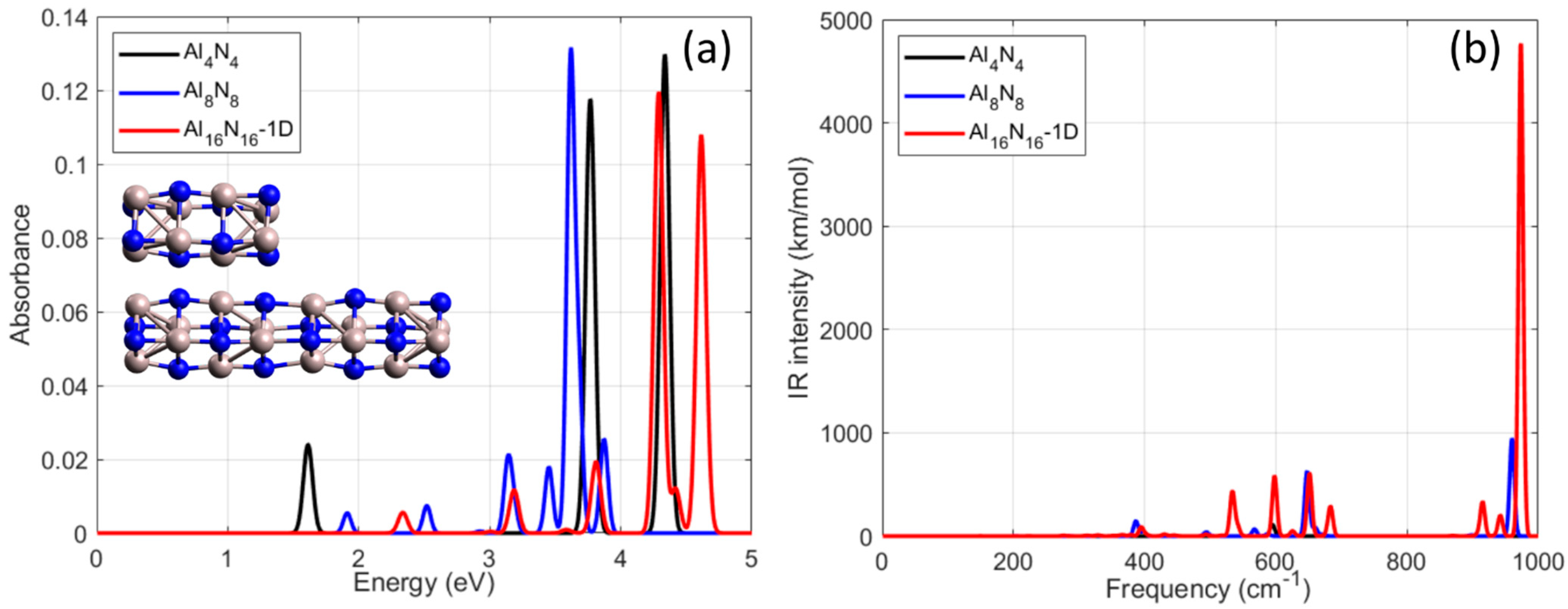
The computed UV–Vis absorption spectra for Al₄N₄, Al₈N₈, and Al₁₆N₁₆-1D are shown in Figure 2a. The smallest cluster, Al₄N₄, exhibits a strong and narrow absorption maximum at 4.48 eV, together with weaker features at 1.34 eV and 3.14 eV. Al₈N₈ presents its most intense peak at 3.62 eV, while the elongated Al₁₆N₁₆-1D nanostructure displays a broader spectral profile with multiple overlapping transitions spanning the 3.18–4.62 eV region. As the geometry becomes more extended and less symmetric, the number and distribution of allowed excitations increase, reflecting enhanced orbital mixing and a higher density of accessible excited states. Importantly, the evolution of the main absorption features across these three clusters is not monotonic: although Al₈N₈ shows a lower-energy peak relative to Al₄N₄, the dominant transition in Al₁₆N₁₆-1D shifts back toward higher energies (~4.5 eV). This behavior indicates that the optical response is governed primarily by geometry-induced symmetry breaking and orbital redistribution rather than by particle size alone. All spectra are normalized to their maximum intensity for consistent comparison.

Figure 2. (a) The UV–visible spectra for the Al_xN_x NPs, where x = 4, 8, 16 when considered after elongation along one direction. Figure legend indicates the color that represents each line of the plot. The inset in the plot presents the examined NPs for x = 8 and for x = 16. (b) The vibrational spectra for the Al_xN_x (x = 4, 8, 16) when considered after elongation along one direction. Figure legend indicates the color that represents each line of the plot.

Figure 2. (a) The UV–visible spectra for the Al_xN_x NPs, where x = 4, 8, 16 when considered after elongation along one direction. Figure legend indicates the color that represents each line of the plot. The inset in the plot presents the examined NPs for x = 8 and for x = 16. (b) The vibrational spectra for the Al_xN_x (x = 4, 8, 16) when considered after elongation along one direction. Figure legend indicates the color that represents each line of the plot.

The infrared (IR) spectra of Al₄N₄, Al₈N₈, and Al₁₆N₁₆-1D nanostructures were computed through harmonic frequency analysis and are depicted in Figure 2b. All systems show well-defined IR-active modes within the low- to mid-frequency range, 300–700 cm⁻¹, corresponding primarily to Al–N stretching and bending vibrations. The smallest structure, Al₄N₄, exhibits its most intense vibrational mode at 595 cm⁻¹ with an IR-intensity value of 111 km/mol. The Al₈N₈ nanostructure shows increased IR activity, presenting strong peaks at 387 cm⁻¹ and 568 cm⁻¹ and a prominent maximum at 648 cm⁻¹. These shifts indicate structural reorganization and enhanced polarizability upon elongation. The Al₁₆N₁₆-1D NP demonstrates the most complex vibrational profile among the three. A series of strong IR peaks is observed at 394 cm⁻¹, 534 cm⁻¹, 598 cm⁻¹, and 651 cm⁻¹ which reaches an IR-intensity of nearly 610 km/mol, which closely matches the strongest peak observed in Al₈N₈, indicating comparable vibrational activity in the high-frequency Al–N stretching region. In addition, there is another resonance mode at 683 cm⁻¹ with an IR-intensity value of 290 km/mol. This enhancement is indicative of cooperative vibrational coupling across the extended chain structure, likely due to increased collective displacement of Al–N units. The gradual increase in both number and intensity of IR-active modes with the length of the nanoparticle reflects the increased vibrational complexity and the relevant decrease in symmetry in elongated configurations. Importantly, no imaginary frequencies were detected in any of the structures, confirming their dynamic stability. Extending the analysis to the higher-frequency range, that is 700–1000 cm⁻¹, distinct differences become evident among the three examined nanoparticles. The Al₄N₄ NP (black line) shows negligible activity in these regions. In contrast, the Al₈N₈ nanostructure, which is indicated by the blue line, exhibits a very intense vibrational mode at 960 cm⁻¹, reaching 947 km/mol. Similarly, the elongated towards one direction Al₁₆N₁₆-1D system (red line) presents a sharp peak at 974 cm⁻¹ with an intensity of about 4767 km/mol, which represents the strongest feature across the entire spectrum. This comparative analysis highlights a non-monotonic evolution of high-frequency IR activity according to which the smallest cluster Al₄N₄ shows suppressed activity, the intermediate Al₈N₈ demonstrates the most intense response, while the elongated Al₁₆N₁₆-1D regains equally strong IR activity near 1000 cm⁻¹. These results provide a comprehensive vibrational fingerprint for 1D Al_xN_x NPs and can serve as reference data for future experimental IR or Raman spectroscopic investigations aimed at identifying such nanostructures. These vibrational fingerprints provide valuable information for experimentalists aiming to detect or identify Al_xN_x nanostructures via IR or Raman spectroscopy. Furthermore, the correlation between structure length and peak positions suggests that vibrational analysis could serve as a sensitive probe of size and morphology at the nanoscale.

3.1.2. Elongated Al₁₆N₁₆ NPs Along Two or Three Directions

In all elongated and shape-modified Al₁₆N₁₆ nanostructures, the spectra of which are presented in Figure 4a,b, similar red-shift behavior was observed, with the main absorption bands ranging from approximately 3.2 to 4.6 eV depending on geometry. The spectra were presented in normalized form for comparison of relative spectral profiles. 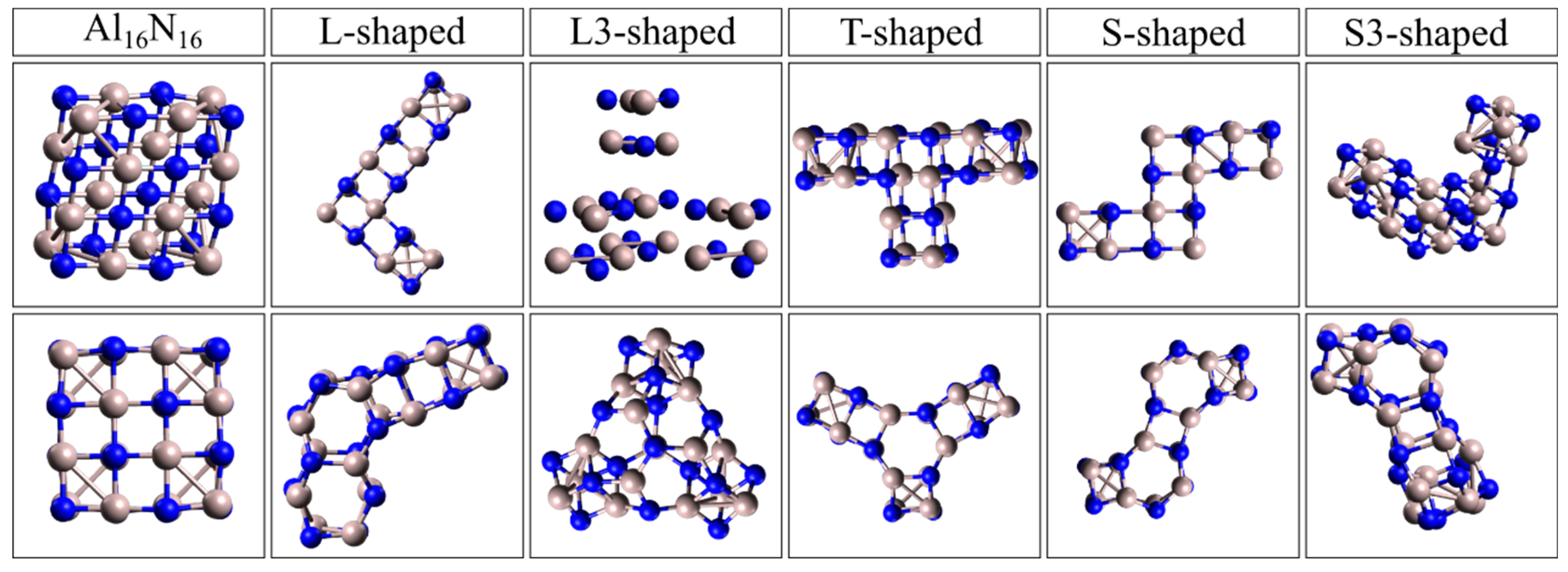The second category of the examined NPs consists of nanostructures which have the general form Al₁₆N₁₆ and were created from the initial cubic cell after its elongation along two and three directions. The first group of this category includes NPs which form some familiar two-dimensional shapes such as an S shape, an L shape, or a T shape. These geometries with their representative names are presented in Figure 3. In the same figure the form of the nanostructure after the geometry optimization is also presented below the initial shape. This set of configurations includes optimized geometries extended along two perpendicular directions or formed into non-linear, asymmetric shapes, such as L-shaped, T-shaped, and cross-like motifs as shown in detail in Figure 3. For the cases of L-shaped and S-shaped geometries a modification where the extension was along three perpendiculars directions was also examined. These cases were named L3 and S3, respectively. The UV–Vis absorption spectra of the examined elongated and shape-modified Al₁₆N₁₆ nanostructures were separated into two groups for better view and are presented in Figure 4a,b.

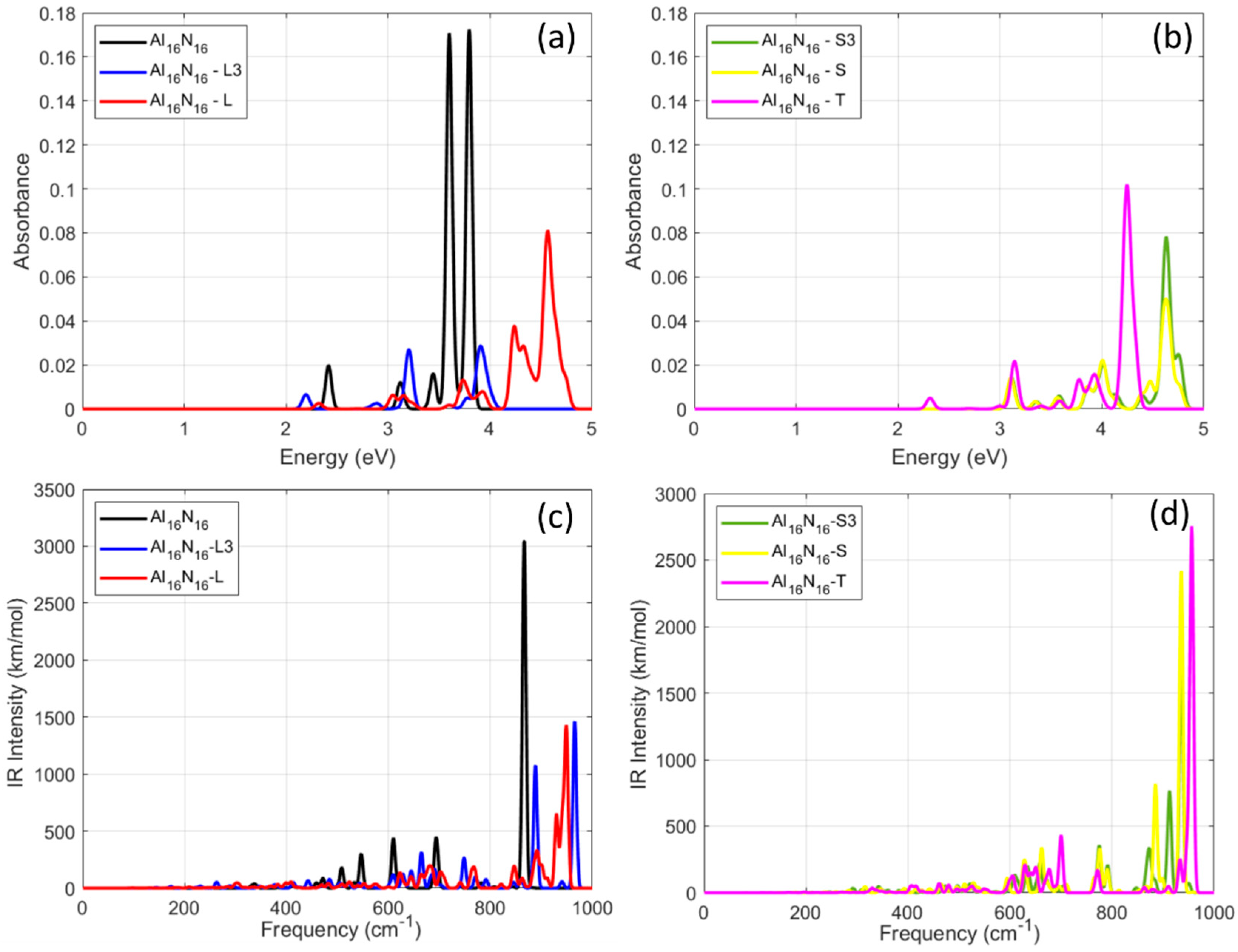
The initial Al₁₆N₁₆ cluster exhibits two intense, narrow absorption peaks centered at 3.60 eV and 3.78 eV, corresponding to localized π–π* transitions [39]. Upon geometric transformation, these sharp peaks broaden and shift. For example, the L-type shape displays a major absorption maximum at 4.57 eV, with reduced intensity and additional low-energy features appearing near 4.2–4.4 eV. Similarly, the T-shaped Al₁₆N₁₆–T geometry shows a strong peak at 4.24 eV, with multiple satellite transitions below 3.14 eV. The Al₁₆N₁₆–S3 configuration exhibits the most spectrally complex profile, with absorbance widely distributed between 3.15 and 4.63 eV, suggesting a high density of permitted transitions and enhanced electronic delocalization. On the other hand, the Al₁₆N₁₆-L3 and Al₁₆N₁₆-S variants show intermediate optical activity and moderate peak splitting. Interestingly, the number and spread of absorption bands increase while the intensity of the main peaks decreases in comparison to the symmetric reference (initial) structure. This underscores the influence of asymmetric geometry and anisotropy on the electronic excitation landscape. These findings imply that precise control over the UV absorption properties of Al₁₆N₁₆ nanoclusters can be achieved by adjusting their geometry. Designing nanoscale optoelectronic components that need particular spectral signatures could make use of this tunability.

Figure 3. The second group of NPs created after elongation of the initial cubic-like building block Al₄Ν₄ along two or three perpendicular directions forming well-known shapes. Gray color corresponds to the Al atom while blue to the N atom. The top row consists of the initial nanostructures, and the bottom row includes the nanostructures after geometry optimization. On the top of each column the relevant name of the nanostructure appears.

Figure 3. The second group of NPs created after elongation of the initial cubic-like building block Al₄Ν₄ along two or three perpendicular directions forming well-known shapes. Gray color corresponds to the Al atom while blue to the N atom. The top row consists of the initial nanostructures, and the bottom row includes the nanostructures after geometry optimization. On the top of each column the relevant name of the nanostructure appears.

Figure 4. (a,b) The UV–vis spectra for the second group of nanostructures, with familiar shapes, when considered after elongation along two or three perpendicular directions. (c,d) The vibrational spectra for the second group of nanostructures, with familiar shapes, when considered after elongation along two perpendicular directions. Figure legend in each plot indicates the color that represents each examined case.

Figure 4. (a,b) The UV–vis spectra for the second group of nanostructures, with familiar shapes, when considered after elongation along two or three perpendicular directions. (c,d) The vibrational spectra for the second group of nanostructures, with familiar shapes, when considered after elongation along two perpendicular directions. Figure legend in each plot indicates the color that represents each examined case.

The vibrational spectra of the Al₁₆N₁₆-based nanostructures with two-dimensional and three-dimensional exotic geometries are presented in Figure 4c,d. As in the case of the absorption spectra, the plots were separated into two groups for better view. All configurations exhibit IR-active modes mainly in the 250–1000 cm⁻¹ region, consistent with Al–N stretching and bending vibrations, as has been previously reported for AlN-based clusters and ceramics. The reference structure Al₁₆N₁₆ shows four strong resonance frequencies. These resonances were calculated at 510 cm⁻¹ with an IR-intensity of 162 km/mol, at 547 cm⁻¹ with IR-intensity of 300 km/mol, at 609 cm⁻¹ with IR-intensity 428 km/mol, and at 695 cm⁻¹ with IR-intensity 430 km/mol. The strongest covariance frequency, however, occurred at 867 cm⁻¹ with an IR-intensity value of 3042 km/mol, which marks the highest intensity observed over the whole series. These correspond to collective vibrations of the Al–N bond associated with symmetric displacement patterns. The Al₁₆N₁₆-L geometry exhibits a broader and denser vibrational profile, with multiple moderate intensity peaks spanning a range of 625–950 cm⁻¹, including strong resonance frequencies at 681, 891, 929, and 949 cm⁻¹ with corresponding IR-intensity values of 197, 330, 654, and 1431 km/mol. This reflects the increased vibrational degrees of freedom introduced by the angular deformation of the cluster. For the case of Al₁₆N₁₆-T, a characteristic IR maximum appears at 956 cm⁻¹ with a corresponding IR-intensity value of 2754 km/mol and a secondary resonance at 700 cm⁻¹ with IR-intensity value of 433 km/mol, which closely resembles the profile of the Al₁₆N₁₆-S structure. However, an increased number of medium intensity modes is also evident between 605 and 680 cm⁻¹.

For the Al₁₆N₁₆-L3 case, as shown by the blue line in Figure 4c, a dominant resonance peak is observed at 966 cm⁻¹ with an intensity of 1462 km/mol, accompanied by two additional resonances at 888 cm⁻¹ (1069 km/mol) and 665 cm⁻¹ (314 km/mol). At lower frequencies, further excitations appear at 645 cm⁻¹ and 609 cm⁻¹, with intensities of 154 and 119 km/mol, respectively. Significant frequency variations are also observed for the nanostructures with S-type geometries, Al₁₆N₁₆–S3 and Al₁₆N₁₆–S. For the S3-shaped nanostructure, the strongest resonance was calculated at 936 cm⁻¹ with an IR-intensity value of 1823 km/mol. Furthermore, another two strong resonances were located at 913 cm⁻¹ and 774 cm⁻¹, with intensities of 766 and 346 km/mol, respectively. Additional notable features include peaks at 871 cm⁻¹ (315 km/mol) and 634 cm⁻¹ (199 km/mol). For the case of the S-shaped nanostructure, the strongest resonance occurs at 936 cm⁻¹ with a high intensity of 2415 km/mol. Another two strong modes appeared at 885 cm⁻¹ (817 km/mol) and 777 cm⁻¹ (317 km/mol). Moreover, several smaller but distinct modes were observed in the range 595–710 cm⁻¹. Across all configurations, the number of IR-active modes systematically increases with geometric complexity, while the intensity distribution broadens. This trend reflects the increasing structural anisotropy and reduced symmetry. Importantly, no imaginary frequencies were detected in any of the cases, confirming the vibrational stability of the optimized nanostructures.

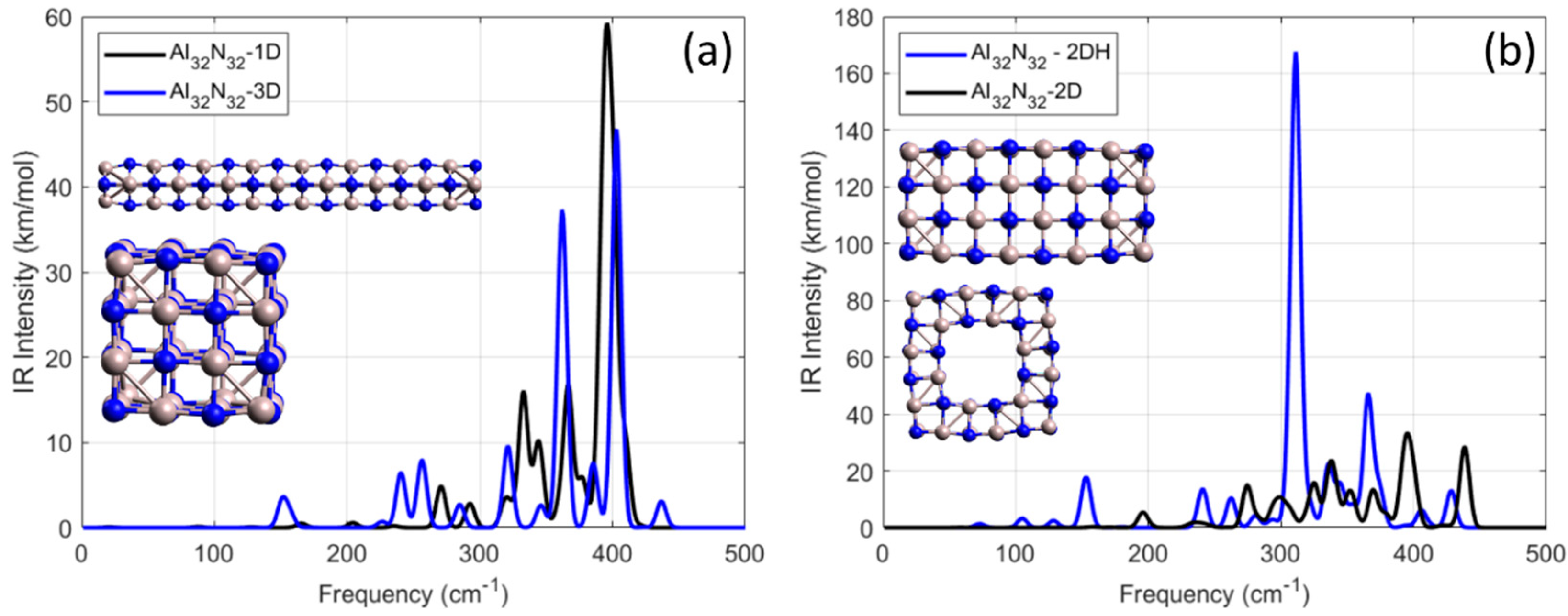
3.1.3. Geometries of Al₃₂N₃₂ Along One, Two, and Three Directions

The third category of the examined AlN NPs includes various geometries of the general form Al₃₂N₃₂. In particular, the examined nanostructures were formed after elongation of the initial cubic-like building block Al₄N₄ along one, two, and three directions, named as Al₃₂N₃₂-1D, Al₃₂N₃₂-2D, and Al₃₂N₃₂-3D, respectively. Also, the defective with a hole exotic NP of the same form, Al₃₂N₃₂, named as Al₃₂N₃₂-2DH was also examined. The vibrational spectra of these nanoparticles which were separated into two groups for better clearance are shown in Figure 5, and their optimized geometries are shown as inset in each plot.

For the case of Al₃₂N₃₂, which was created after elongation of the original cubic Al₄N₄ building block along two vertical directions, the four strongest resonance frequencies were calculated at 394, 438, 337, and 325 cm⁻¹ with corresponding IR-intensity values of 34, 28, 23, and 15 km/mol. For the case of Al₃₂N₃₂-1D, the strongest resonance was calculated at 396 cm⁻¹ with an IR-intensity value of 59 km/mol, almost three times smaller than the strongest frequency resonance of defected Al₃₂N₃₂-2DH, which was calculated at 311 cm⁻¹ with an IR-intensity value of 168 km/mol. In addition, the frequencies at which the resonance peaks from the defected Al₃₂N₃₂–2DH occur were within a range between 152 and 428 cm⁻¹. In conclusion, as structural dimensionality increases, the number of IR-active modes grows, but the maximum IR-intensity peaks were calculated for the 2D system, suggesting an optimal balance between symmetry and vibrational delocalization. All structures were dynamically stable, with no imaginary frequencies observed.

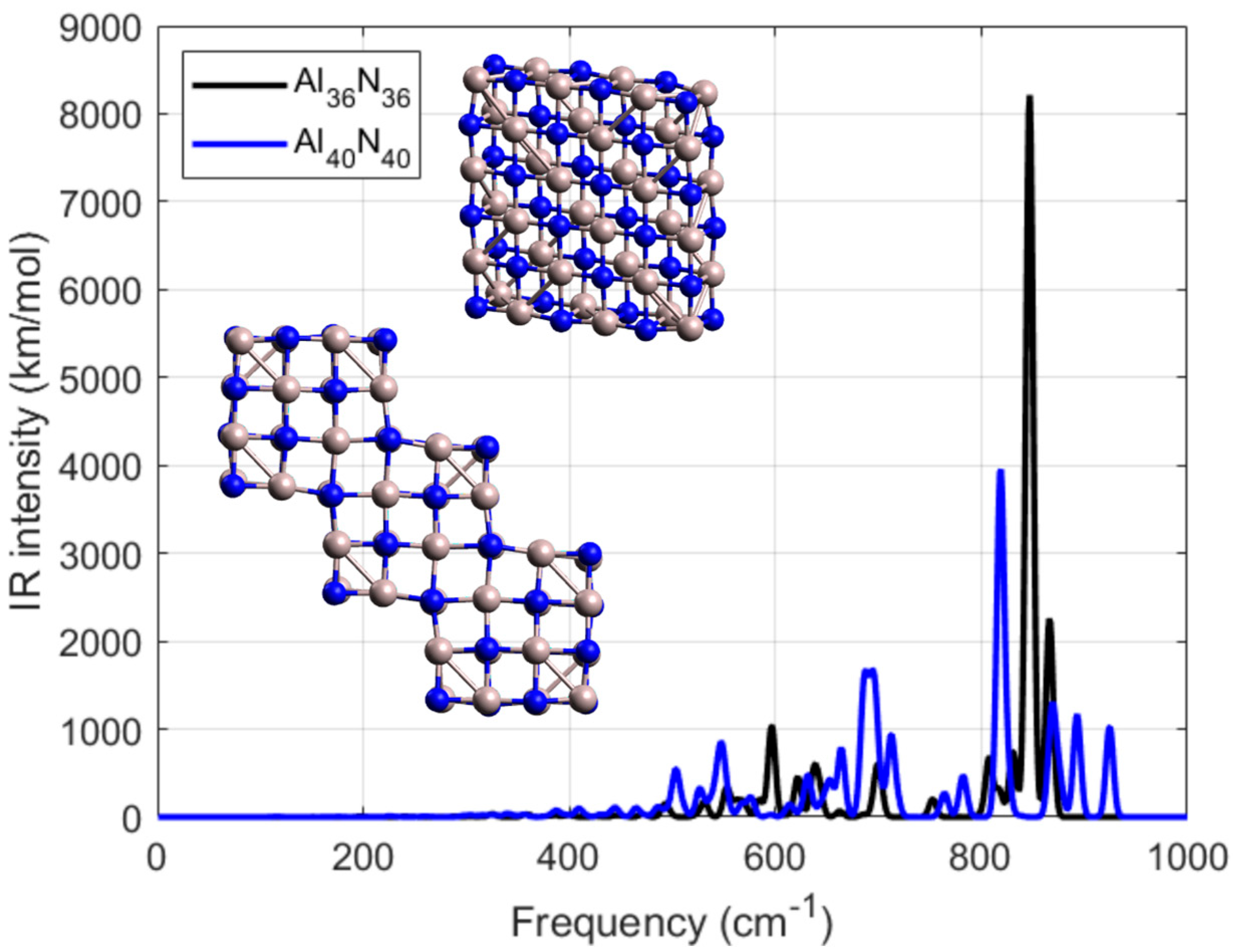
3.1.4. Geometries of Al₃₆N₃₆ and Al₄₀N₄₀

The fourth category of AlN NPs which was examined in this work included geometries of Al_xN_x, where x = 36 and x = 40. The IR spectra of these studied nanostructures, named as Al₃₆N₃₆ and Al₄₀N₄₀, respectively, are shown in Figure 6. In the same figure their geometries are also presented as inset. Both NPs were created from the same initial cubic-like building block Al₄N₄ and were extended along two perpendicular directions. It must be noted that the absorbance spectrum was not calculated due to its high computational time and relevantly high computational resources. Our study regarding the absorbance spectrum was limited according to the affordable computational resources to the previous category of examined structures where x = 16.

The Al₃₆N₃₆ NP, which is presented with the black line in Figure 6, shows a strong vibrational mode for frequency 596 cm⁻¹ with 1029 km/mol. Close to this mode, there was another one with frequency 638 cm⁻¹ with 596 km/mol. Another couple of resonances were found for frequencies 622 cm⁻¹ and 552 cm⁻¹ with relevant IR-intensity values 442 km/mol and 328 km/mol, respectively. In contrast, Al₄₀N₄₀ shows significantly stronger and sharper IR features, with a dominant peak at 694 cm⁻¹ reaching an intensity of 1671 km/mol—about 0.5 times stronger than the highest peak of Al₃₆N₃₆. Furthermore, Al₄₀N₄₀ displayed strong resonances at 503 cm⁻¹ with 541 km/mol, at 547 cm⁻¹ with 850 km/mol, and 664 cm⁻¹ with 753 km/mol. In the higher-frequency region between 700 and 1000 cm⁻¹, both nanostructures display pronounced IR-active resonances. For Al₃₆N₃₆, a dominant sharp mode appears at 847 cm⁻¹ with an intensity of 8212 km/mol, clearly exceeding the intensity of its lower-frequency features. In contrast, Al₄₀N₄₀ shows a broader distribution of resonances in the same spectral window, with characteristic peaks at 695 cm⁻¹ (1167 km/mol) and 819 cm⁻¹ (3957 km/mol). These high-frequency modes are mainly attributed to Al–N stretching vibrations and their stronger manifestation in Al₃₆N₃₆ highlights the dependence of vibrational sharpness on cluster geometry. When compared with the lower-frequency domain, the spectral evolution in this region confirms that increasing nanoparticle size enhances the number of active modes while modulating the intensity profile, leading to a richer and more complex vibrational response. These findings indicate that increasing the size of the nanoparticle not only enhances the number of vibrational modes but also amplifies the IR activity, which could be advantageous for applications requiring high IR responsiveness, such as sensing or optothermal modulation. Overall, the comparative analysis highlights the structural and spectroscopic evolution from Al₃₆N₃₆ to Al₄₀N₄₀ and confirms the correlation between atomic complexity and vibrational spectrum.

3.2. Stability and Binding Energy

To quantitatively evaluate the energetic stability of the optimized Al_xN_x NPs, the binding energy (BE) per formula unit (f.u.) was calculated using both self-consistent field (SCF) energies and zero-point vibrational energy (ZPE)-corrected values. It should be noted that the binding energies reported here are referenced to isolated Al and N atoms to ensure internal consistency among different cluster geometries. While this convention may overestimate absolute cohesive values, it accurately reflects relative stability trends across the studied Al_xN_x nanoparticles. A comparison with molecular Al–N references was also performed and yielded smaller absolute magnitudes but similar formation energy trends, confirming that stability increases with cluster size and dimensionality before reaching a near-saturation regime beyond Al₁₆N₁₆. The binding energy was calculated using the following formula:

$${{\mathrm{E}}_{\mathrm{B}}(\mathrm{A}\mathrm{l}}_{\mathrm{x}}{\mathrm{N}}_{\mathrm{X}})=\mathrm{x}\mathrm{E}\left(\mathrm{A}\mathrm{l}\right)+\mathrm{x}\mathrm{E}\left(\mathrm{N}\right)-\mathrm{E}{(\mathrm{A}\mathrm{l}}_{\mathrm{x}}{\mathrm{N}}_{\mathrm{X}})$$

where the index x indicates each examined formula of the structure (formula unit), E(Al) is the energy of isolated atoms of Al, E(N) is the energy of isolated atoms of N, and E(Al_xN_x) is the total energy of the NP. The BE per f.u., (E_b), is thus given by the following relation:

$${{{{\mathrm{E}}_{\mathrm{b}}(\mathrm{A}\mathrm{l}}_{\mathrm{x}}{\mathrm{N}}_{\mathrm{X}})=\mathrm{E}}_{\mathrm{B}}(\mathrm{A}\mathrm{l}}_{\mathrm{x}}{\mathrm{N}}_{\mathrm{X}})/\mathrm{x}=\mathrm{E}\left(\mathrm{A}\mathrm{l}\right)+\mathrm{E}\left(\mathrm{N}\right)-\mathrm{E}{(\mathrm{A}\mathrm{l}}_{\mathrm{x}}{\mathrm{N}}_{\mathrm{X}})/\mathrm{x}$$

As shown in

Table 2. HOMO–LUMO (HL) gaps and binding energies per f.u. of Al_xN_x NPs.

Examined NPs	HL Gap (eV)	Binding Energy per f.u. (eV)	Binding Energy per f.u. with ZPE (eV)
Al4N4	0.63	7.38	7.24
Al8N8	1.11	8.63	8.47
Al16N16–1D	1.23	9.23	9.06
Al16N16	1.56	9.39	9.22
Al16N16–L3	1.00	9.14	8.97
Al16N16–L	1.36	9.27	9.10
Al16N16–S3	1.84	9.30	9.12
Al16N16–S	1.84	9.29	9.11
Al16N16–T	1.29	9.19	9.02
Al32Ν32–1D	1.15	9.52	9.35
Al32Ν32–2D	1.85	9.78	9.60
Al32Ν32–3D	1.35	9.89	9.72
Al32Ν32–2DH	1.70	9.59	9.41
Al36N36	1.85	9.86	9.68
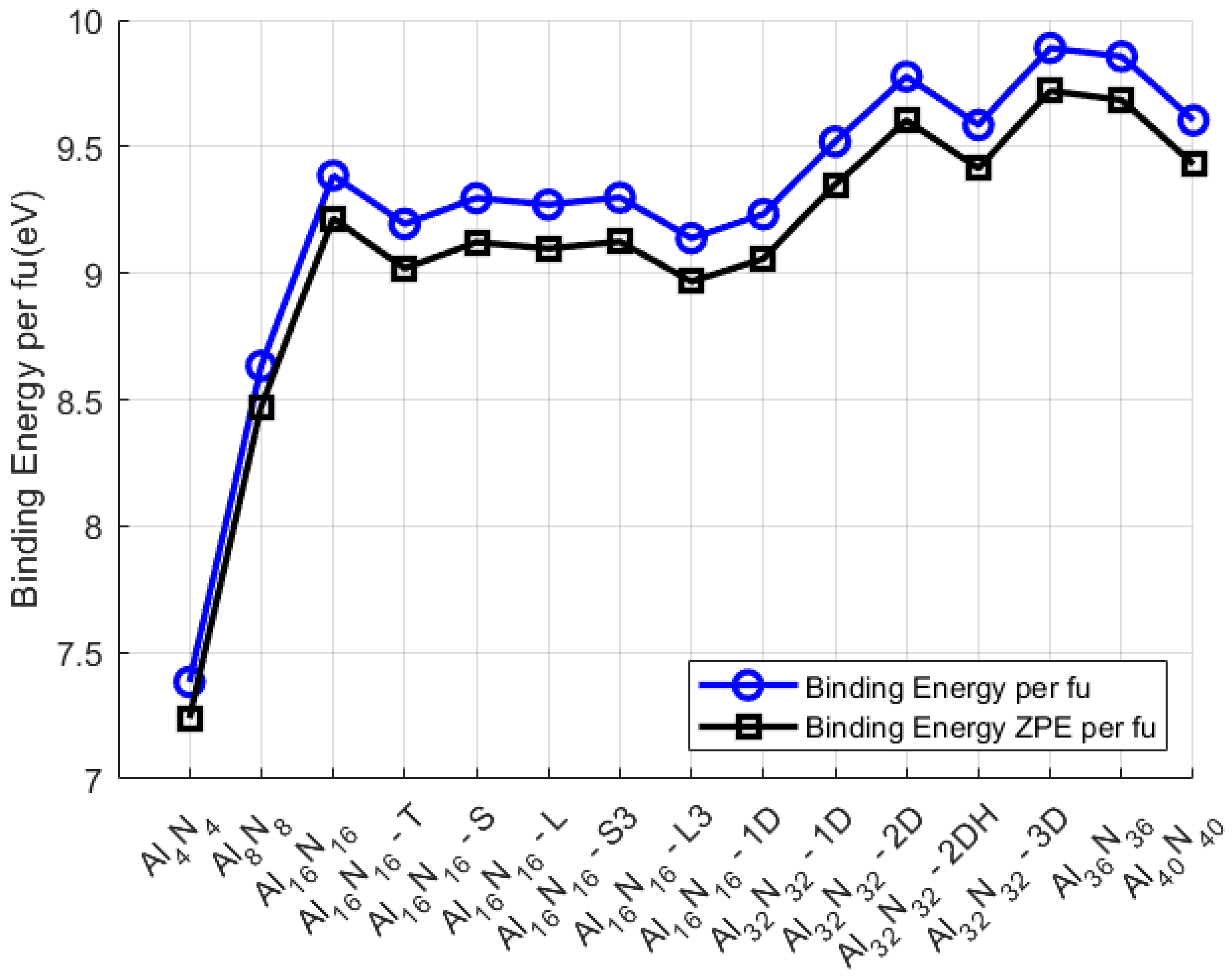
Al40Ν40	1.54	9.60	9.43

, the binding energy per formula unit (BE/f.u.) and the ZPE-corrected BE/f.u. exhibit consistent trends across the entire set of Al_xN_x nanostructures. The BE/f.u. increases significantly from 7.38 eV for the smallest system, Al₄N₄, to values ranging between 9.39 eV and 9.89 eV for mid- to large-sized systems. In more detail, 9.39 eV for Al₁₆N₁₆, 9.89 eV for Al₃₂N₃₂–2D, and 9.86 eV for Al₃₆N₃₆ NPs. This sharp initial rise highlights the thermodynamic advantage of assembling larger clusters, where more Al–N bonds per formula unit contribute to the overall stability. After Al₁₆N₁₆, the BE/f.u. values plateau, with only subtle variations across different geometric arrangements and dimensionalities. Among the exotic Al₁₆N₁₆ NPs, the nanostructures with more compact or symmetric geometries (e.g., Al₁₆N₁₆-S3, Al₁₆N₁₆-S) tend to exhibit slightly higher BE/f.u., suggesting more favorable local bonding environments. Similarly, in the Al₃₂N₃₂ series, the 2D structure yields the highest BE/f.u., reinforcing the energetic preference for planar growth in this size regime. While the BE/f.u. for Al₄₀N₄₀ appears slightly reduced compared to Al₃₆N₃₆, this deviation is likely due to surface relaxation effects and geometric strain in the extended framework. ZPE corrections uniformly reduce the BE/f.u. values by approximately 0.14–0.20 eV per formula unit, with the largest relative impact observed for smaller systems such as Al₄N₄ and Al₈N₈. Despite this reduction, the ordering of structural stability remains consistent, confirming the robustness of the energetic landscape. The proximity of the corrected and uncorrected values supports the validity of using BE/f.u. without ZPE in large-scale screenings where computational efficiency is critical.

Τhe evolution of the HOMO–LUMO gap across the studied nanoparticles depends not only on particle size but also strongly on dimensionality and geometry. While an overall stabilization trend is observed with increasing cluster size, specific configurations such as the 1D Al₃₂N₃₂ nanorod exhibit a slight gap reduction (1.23 → 1.15 eV) due to enhanced orbital delocalization and reduced quantum confinement along the elongated axis. This indicates that electronic structure modulation in Al_xN_x clusters arises from a combination of size and symmetry effects. Ιt should be noted that the HOMO–LUMO gaps reported here represent a molecular-level electronic separations characteristic of finite Al_xN_x clusters rather than bulk semiconductor band gaps. Their smaller values compared to the ~6 eV band gap of bulk AlN originate from quantum confinement and surface-state effects, where unsaturated Al–N bonds and surface polarization introduce localized states that narrow the effective gap. A more quantitative description would require quasiparticle corrections (e.g., ΔSCF- Delta-Self-Consistent-Field or GW methods), which are beyond the present scope but planned for future benchmarking studies. Specifically, HL gaps of 0.63 eV, 1.11 eV, and 1.23 eV were calculated for Al₄N₄, Al₈N₈, and Al₁₆N₁₆-1D, respectively. Two-dimensional structures exhibit systematically higher HL gaps than their 1D, 3D, or exotic counterparts. For instance, the Al₃₂N₃₂-2D NP exhibits a HL gap of 1.85 eV, while the 3D variant of the same size shows a significantly lower value of 1.35 eV. Notably, the largest HL gaps were found in Al₁₆N₁₆-S3, Al₁₆N₁₆-S, and Al₃₆N₃₆, further confirming the stabilizing effects of optimized bonding and dimensionality. Overall, this combined analysis of BE/f.u. and HL gap elucidates the interplay between thermodynamic and electronic stability across different Al_xN_x nanostructures, providing valuable insights for their future application in optoelectronic and energy-related technologies.

Figure 7 displays the binding energy per formula unit (BE/f.u.) for all examined Al_xN_x nanostructures, both with and without zero-point vibrational energy (ZPE) correction. A notable trend is observed: as the nanoparticle size increases, the BE/f.u. generally rises, with a plateau-like behavior forming beyond Al₁₆N₁₆, followed by a secondary upward shift around the Al₃₂N₃₂ series. This pattern reflects the increasing local bonding efficiency and stabilization as the systems grow in dimensional complexity and atom number. The steep initial increase in BE/f.u., from 7.38 eV for Al₄N₄ to 9.38 eV for Al₁₆N₁₆, suggests that the early growth stages significantly enhance thermodynamic stability. Beyond this point, the BE/f.u. values stabilize, indicating a saturation in the bonding contribution per formula unit—particularly evident in exotic Al₁₆N₁6 NPs where dimensional elongation or shape changes do not drastically affect average bond energetics.

Nanostructures with 32 atoms per element show a second stability enhancement, peaking at 9.78 eV/f.u. for Al₃₂N₃₂-2D, which likely benefits from extended delocalization and optimized coordination environments. Interestingly, the BE/f.u. slightly decreases in the largest systems (Al₃₆N₃₆ and Al₄₀N₄₀), suggesting a minor energetic cost associated with further structural complexity or less efficient packing. For comparison, the optical properties of Sc₄N₄ nanoparticle [33] exhibited a significantly higher binding energy per formula unit (10.45 eV) than the Al₄N₄ prototype examined here (7.38 eV), indicating stronger cohesive interactions in the Sc-based system. This difference of over 3 eV/f.u. reflects the more ionic character and robust Sc–N bonding, which also translated to higher excitation energies and blue-shifted absorption peaks. Such comparisons underscore the distinct bonding nature and optical response between early transition metal nitrides and main group III–V nanoclusters.

As expected, incorporating ZPE corrections results in a systematic downward shift of 0.14–0.20 eV/f.u., consistent across all nanostructures. While small in absolute magnitude, this correction is particularly relevant for low-mass systems, where vibrational contributions are proportionally more significant. Crucially, the parallel behavior between the SCF-derived and ZPE-corrected BE/f.u. trends validates the robustness of the energetic ordering and supports the use of uncorrected BE/f.u. values as reliable, fast stability indicators—especially in high-throughput or large-scale screenings. Overall, the per-formula-unit normalization offers a clearer comparison across different sized systems, highlighting how structural elongation and dimensionality influence intrinsic stability independently of total atom count.

4. Conclusions

In this work, DFT and TD-DFT methods were used to conduct a systematic computational analysis of the structural, electronic, and vibrational characteristics of aluminum nitride (Al_xN_x) nanostructures. Based on the initial cubic-like building block Al₄N₄, a variety of geometries were created and elongated along one, two, and three perpendicular directions, as well as exotic asymmetric configurations forming well-known shapes such as L-shaped and T-shaped nanostructures. All geometries were first optimized at the PBE/def2-TZVP level of theory. These geometries were then employed for harmonic vibrational frequency analysis and excited-state TD-DFT calculations at the CAM-B3LYP/def2-TZVP level. The vibrational spectra showed no imaginary frequencies, confirming that all configurations were dynamically stable.

The optical absorption spectra revealed clear quantum confinement effects, with red-shifted and broadened UV–Vis absorption features observed as the size and complexity of the nanostructures increased. The elongated and asymmetric structures exhibited enhanced spectral richness and tunable excitation energies, particularly in the 2.5–4.5 eV region, demonstrating their potential for ultraviolet photonic applications. Vibrational analysis showed that the number and intensity of IR-active modes increased with geometric dimensionality and asymmetry. The strongest IR bands were found in the 800–950 cm⁻¹ range, corresponding to Al–N stretching and bending vibrations, with the 2D and certain 3D structures exhibiting the highest infrared intensities.

The evolution of the HOMO–LUMO gap across the studied Al_xN_x nanoparticles is governed by both particle size and structural dimensionality. While larger clusters generally show electronic stabilization, the gap does not increase monotonically with size. Instead, geometry and symmetry play a decisive role: elongated and low-symmetry configurations exhibit enhanced orbital delocalization and reduced quantum confinement, leading to smaller gaps despite their larger atomic content. This multidimensional dependence highlights that electronic structure modulation in Al_xN_x systems arises from the interplay between size, geometry, and dimensionality rather than size alone.

The appropriateness of CAM-B3LYP for characterizing the excited-state behavior of these systems was validated by benchmarking several exchange–correlation functionals against the results of EOM-CCSD. It has been demonstrated that the structural changes investigated in this work significantly alter optical and vibrational signatures, offering helpful recommendations for the functional design and future experimental identification of AlN-based nanomaterials.

Overall, this work highlights the potential use of Al_xN_x nanostructures in ultraviolet optoelectronics, sensors, and potentially biomedical applications by highlighting their structural stability and optoelectronic versatility. Future studies could examine surface functionalization, solvent effects, or substitutional doping to further customize these characteristics of the examined nanostructures to meet the demands of targeted applications.