A Long-Wave Infrared Circularly Polarized Photodetector Based on an Array of Trapezoidal Silicon Pillars
Abstract
1. Introduction
2. Materials and Methods
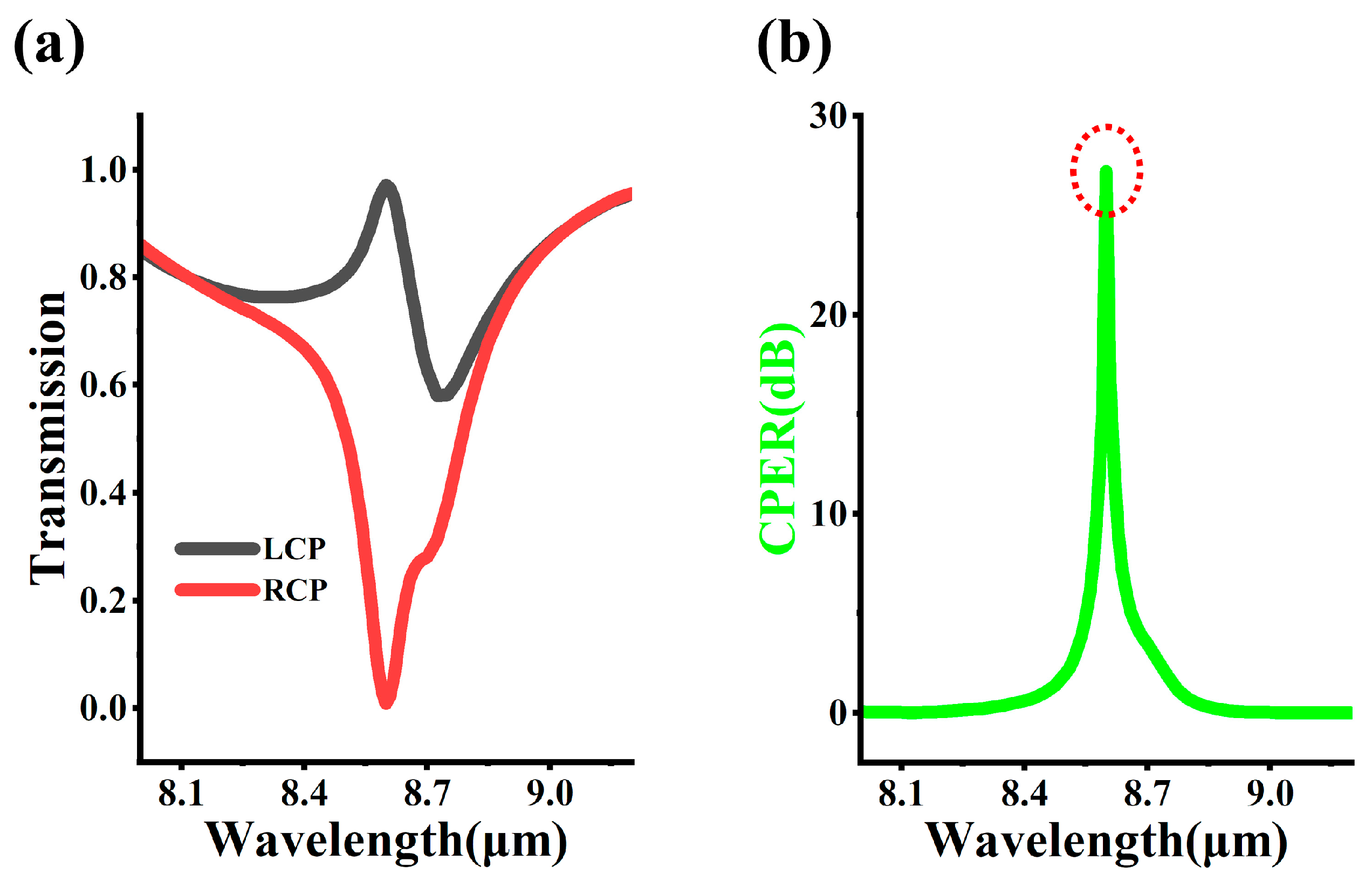
3. Results
3.1. The Influence of Geometric Structures in Metasurfaces
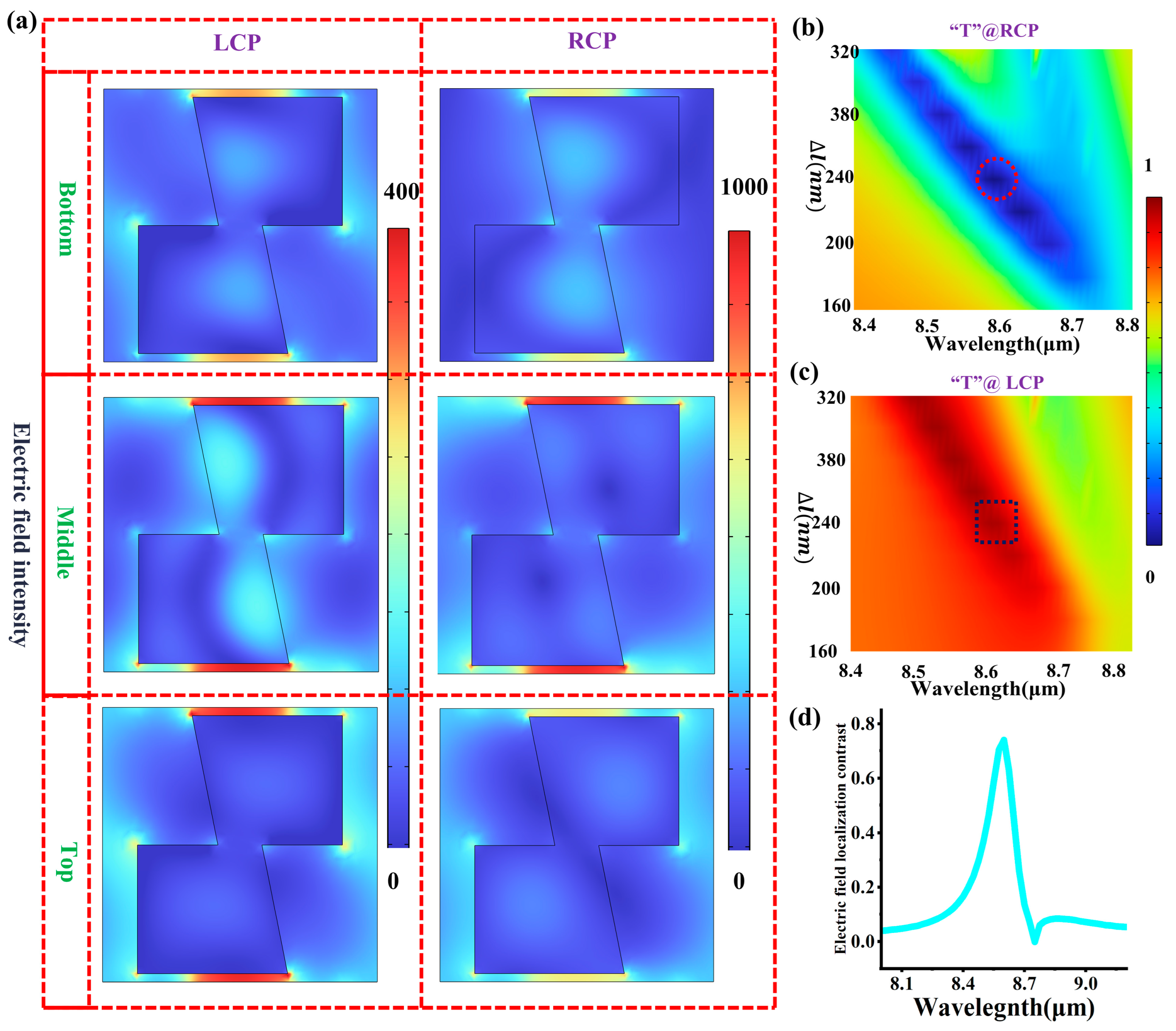
3.2. Analysis of the Electric Field Distribution of Metasurfaces
3.3. The Influence of the Thickness of the Support Layer (hs)
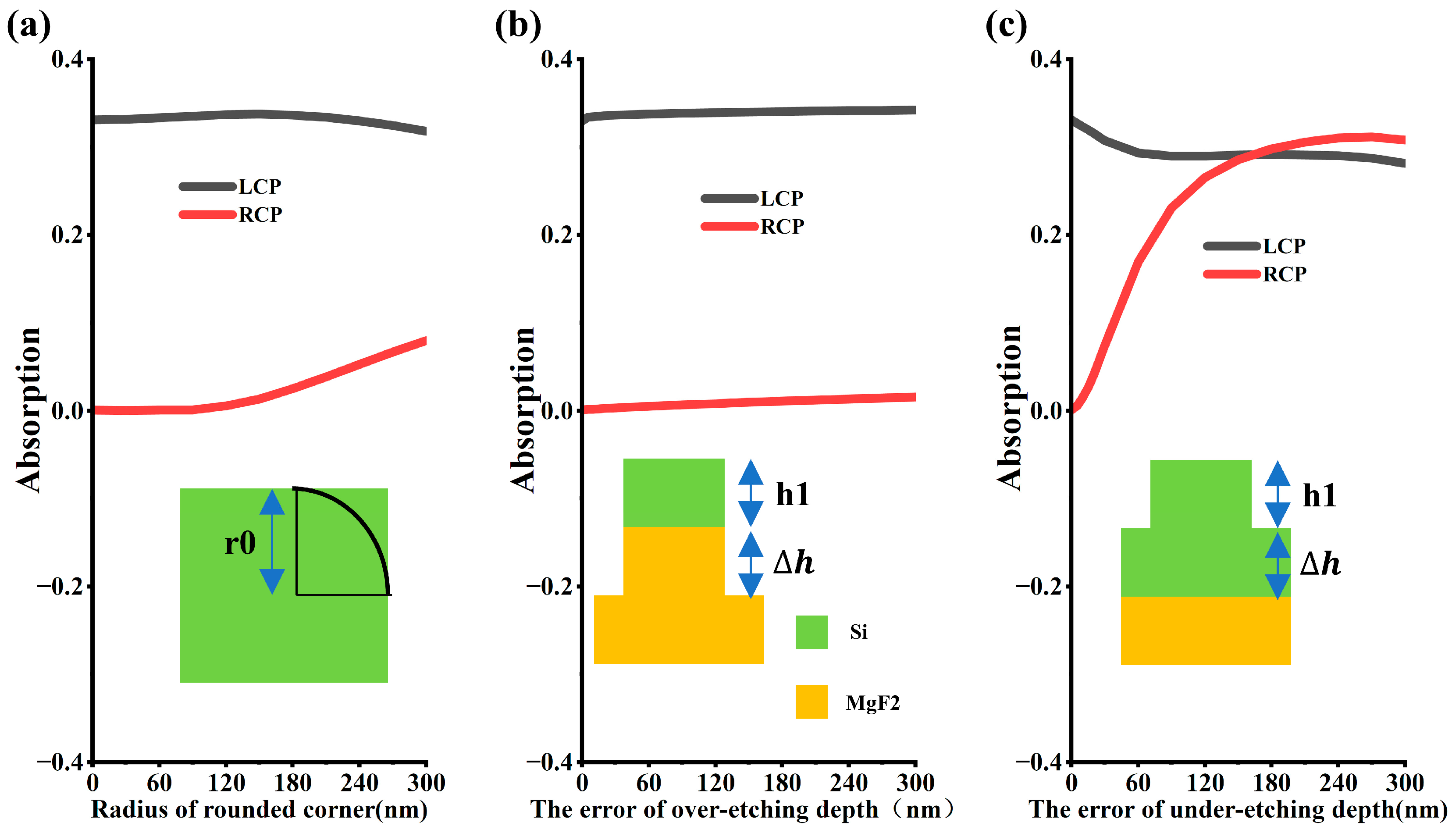
3.4. Analysis of Potential Process Errors
4. Discussion
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Smith, W.H.; Born, J.; Cochran, W.D.; Gelfand, J. Spectroscopic photoelectric imaging Fabry-Perot interferometer—Its development and preliminary observational results. Appl. Opt. 1976, 15, 717–724. [Google Scholar] [CrossRef]
- Pathak, A. Elements of Quantum Computation and Quantum Communication; Taylor & Francis: Abingdon, UK, 2013. [Google Scholar]
- King, M.D.; Kaufman, Y.J.; Tanré, D.; Nakajima, T. Remote sensing of tropospheric aerosols from space: Past, future and present. Bull. Am. Meteorol. Soc. 1999, 80, 2229–2259. [Google Scholar] [CrossRef]
- Rudolph, W.; Kempe, M. Trends in optical biomedical imaging. Opt. Acta Int. J. Opt. 1997, 44, 1617–1642. [Google Scholar] [CrossRef]
- Sambles, J.R. Polarized Light in Optics and Spectroscopy. Opt. Acta Int. J. Opt. 1991, 38, 1204–1205. [Google Scholar] [CrossRef]
- Liu, Y.; Ling, X.; Yi, X.; Zhou, X.; Luo, H.; Wen, S. Realization of polarization evolution on higher-order Poincare sphere with metasurface. Appl. Phys. Lett. 2014, 104, 191110. [Google Scholar] [CrossRef]
- Wei, Z.; Cao, Y.; Su, X.; Gong, Z.; Li, H. Highly efficient beam steering with a transparent metasurface. Opt. Express 2013, 21, 10739–10745. [Google Scholar] [CrossRef] [PubMed]
- Arbabi, A.; Arbabi, E.; Horie, Y.; Kamali, S.M.; Faraon, A. Planar metasurface retroreflector. Nat. Photonics 2017, 11, 415–420. [Google Scholar] [CrossRef]
- Liu, C.; Wang, H.; Zhao, R.; Lei, Y.; Dong, S.; Cai, Y.; Zhou, W.; Wang, Y.; Huang, L.; Xu, K.M. Multi-plane vectorial holography based on a height tunable metasurface fabricated by femtosecond laser direct writing. Photonics Res. 2024, 12, 8. [Google Scholar] [CrossRef]
- Li, S.; Chen, C.; Wang, G.; Ge, S.; Zhao, J.; Ming, X.; Zhao, W.; Li, T.; Zhang, W. Metasurface Polarization Optics: Phase Manipulation for Arbitrary Polarization Conversion Condition. Phys. Rev. Lett. 2025, 134, 023803. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Liu, W.; Cheng, H.; Chen, S.; Tian, J. Tunable dual-band asymmetric transmission for circularly polarized waves with graphene planar chiral metasurfaces. Opt. Lett. 2016, 41, 3142–3145. [Google Scholar] [CrossRef] [PubMed]
- Ma, C.; Yu, P.; Jing, Z.; Zhu, Y.; Li, P.; Wang, W.; Xu, H.; Zhang, Y.; Pan, L.; Choi, T.-Y.; et al. Circular polarization-selective optical, photothermal, and optofluidic effects in chiral metasurfaces. Photonics Res. 2024, 12, 331. [Google Scholar] [CrossRef]
- Jang, J.; Park, M.; Park, Y. Non-interleaved chiral metasurfaces and neural networks enhance the spatial resolution of polarimetry. Light Sci. Appl. 2024, 13, 53. [Google Scholar] [CrossRef]
- Wang, C.; Cheng, X.; Wang, R.; Hu, X.; Wang, C. Flexibly Designable 2D Chiral Metasurfaces with Pixelated Topological Structure Based on Machine Learning. Laser Photonics Rev. 2024, 18, 2300958. [Google Scholar] [CrossRef]
- Gromyko, D.; Loh, J.S.; Feng, J.; Qiu, C.W.; Wu, L. Enabling All-to-Circular Polarization Up-Conversion by Nonlinear Chiral Metasurfaces with Rotational Symmetry. Phys. Rev. Lett. 2025, 134, 023804. [Google Scholar] [CrossRef]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 247–257. [Google Scholar] [CrossRef]
- Greenfield, N.J.; Fasman, G.D. Computed circular dichroism spectra for the evaluation of protein conformation. Biochemistry 1969, 8, 4108. [Google Scholar] [CrossRef] [PubMed]
- Berova, N.; Nakanishi, K.; Woody, R.W. Circular Dichroism: Principles and Applications. In Circular Dichroism Principles Applications; John Wiley & Sons: Hoboken, NJ, USA, 2000. [Google Scholar]
- Zhang, R.; Zhang, Z.; Fan, Y.; Zhang, H.; Chu, J. Single-Layer Transmissive Chiral Plasma Metasurface with High Circular Polarization Extinction Ratio in Visible Wavelength. Nanomaterials 2023, 13, 813. [Google Scholar] [CrossRef]
- Ye, Y.; Li, X.; Zhuang, F.; Chang, S.W. Homogeneous circular polarizers using a bilayered chiral metamaterial. Appl. Phys. Lett. 2011, 99, 031111. [Google Scholar] [CrossRef]
- Cheng, B.; Zou, Y.; Song, G. Full-Stokes polarization short-wave infrared photodetector based on the doubly regulated dielectric metasurfaces. Optik 2025, 322, 172198. [Google Scholar] [CrossRef]
- Tang, Y.; Xie, B.; Liu, H.; Zhang, Y.; Cheng, H.; Chen, S. Mirror Symmetry Broken of Sound Vortex Transmission in a Single Passive Metasurface via Phase Coupling. Phys. Rev. Lett. 2024, 132, 6. [Google Scholar] [CrossRef] [PubMed]
- Shen, Z.; Huang, D.; Lin, X. Dual-band chirality-selective absorbing by plasmonic metasurfaces with breaking mirror and rotational symmetry. Opt. Express 2023, 31, 12. [Google Scholar] [CrossRef]
- Petronijevic, E.; Cesca, T.; Scian, C.; Mattei, G.; Voti, R.L.; Sibilia, C.; Belardini, A. Demonstration of extrinsic chirality in self-assembled asymmetric plasmonic metasurfaces and nanohole arrays. Sci. Rep. 2024, 14, 17210. [Google Scholar] [CrossRef]
- Levanon, N.; Indukuri, S.C.; Frydendahl, C.; Bar-David, J.; Han, Z.; Mazurski, N.; Levy, U. Angular Transmission Response of In-Plane Symmetry-Breaking Quasi-BIC All-Dielectric Metasurfaces. ACS Photonics 2022, 9, 3642–3648. [Google Scholar] [CrossRef]
- Gordon, I.E.; Rothman, L.S.; Hargreaves, R.J.; Hashemi, R.; Karlovets, E.V.; Skinner, F.M.; Conway, E.K.; Hill, C.; Kochanov, R.V.; Tan, Y.; et al. The HITRAN2020 molecular spectroscopic database. J. Quant. Spectrosc. Radiat. Transf. 2022, 277, 107949. [Google Scholar] [CrossRef]
- Beer, R. TES on the aura mission: Scientific objectives, measurements, and analysis overview. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1102–1105. [Google Scholar] [CrossRef]
- Brown, G.J.; Szmulowicz, F.; Linville, R.; Saxler, A.; Mahalingham, K.; Lin, C.H.; Kuo, C.H.; Hwang, W.Y. Type-II superlattice photodetector on a compliant GaAs substrate. IEEE Photonics Technol. Lett. 2002, 12, 684–686. [Google Scholar] [CrossRef]
- Koyama, M.; Kudo, J.; Iguchi, Y.; Inada, H.; Muramatsu, Y.; Kumihashi, I.; Sano, M. Indium Gallium Arsenide/Gallium Arsenide Antimonide Type II Superlattice Photodetector That Can Utilize Night Airglow. Sens. Mater. 2024, 36, 2183–2197. [Google Scholar]
- Wu, Y.; Li, J.; Zhang, Z.Q.; Chan, C.T. Effective medium theory for magnetodielectric composites: Beyond the long-wavelength limit. Phys. Rev. 2006, B74, 085111, Erratum in Phys. Rev. 2015, B92, 199901. [Google Scholar] [CrossRef]
- Chang, L.; Ho, C.C.; Wei, H.S.; Wu, G.Y. Effective medium theory with dimensionality reduction for band structures of photonic crystals. J. Appl. Phys. 2007, 101, 2059. [Google Scholar] [CrossRef]
- Gao, Z.; Wang, P.; Xu, Z.; Zhao, T. Chiral metasurface absorber with near-infrared excitation-induced dual circular dichroism. Opt. Laser Technol. 2024, 175, 110826. [Google Scholar] [CrossRef]
- Toftul, I.; Tonkaev, P.; Koshelev, K.; Lai, F.; Song, Q.; Gorkunov, M.; Kivshar, Y. Chiral Dichroism in Resonant Metasurfaces with Monoclinic Lattices. Phys. Rev. Lett. 2024, 133, 216901. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; He, C.; Deng, Z.; Li, X.; Li, X.; Zhang, Z.; Sui, X.; Li, N.; He, W.; Chen, F. Optical chirality of all dielectric q-BIC metasurface with symmetry breaking. Nanophotonics 2025, 14, 559–569. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Zhang, X.; Liu, J.; Feng, H.; Li, M.; Yang, S.; Jia, Y.; Meng, H.; Gao, Y. A multifunction tunable terahertz chiral metasurface based on graphene and photosensitive silicon. Opt. Mater. 2024, 150, 115177. [Google Scholar] [CrossRef]
- Raza, F.; Chen, R.; Ma, Y. Fano-modulated chiral metasurface for near-infrared sensing via bound states in the continuum. J. Appl. Phys. 2024, 136, 243103. [Google Scholar] [CrossRef]
- Han, J.; Jang, H.; Lim, Y.; Kim, S.; Lee, J.; Jun, Y.C. Chiral Emission from Optical Metasurfaces and Metacavities. Adv. Photonics Res. 2024, 5, 2400060. [Google Scholar] [CrossRef]
- Asefa, S.A.; Seong, M.; Lee, D. Design of Bilayer Crescent Chiral Metasurfaces for Enhanced Chiroptical Response. Sensors 2025, 25, 915. [Google Scholar] [CrossRef] [PubMed]



| Structure | Publication | Wavelength (μm) | CD | CPER (dB) |
|---|---|---|---|---|
| π-shaped [32] | 2024 | 1.55, 2.55 | 0.7, 0.75 | ~10, ~10 |
| Monoclinic Lattices [33] | 2024 | 1.6 | 0.3 | / |
| Broken circle [34] | 2025 | 1.35 | 0.17 | / |
| Graphene and silicon [35] | 2024 | 250 | 0.9 | 9 |
| Double Si columns [36] | 2024 | 1.01 | ~0.9 | 6 |
| Swastika-shaped [37] | 2024 | 0.53 | 0.26 | 3 |
| Double-layered gold [38] | 2025 | 1.25 | 0.55 | ~8 |
| This work | 8.6 | ~1 | 27 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, B.; Zou, Y.; Liang, T.; Ye, A.; Zhai, K.; Lv, L. A Long-Wave Infrared Circularly Polarized Photodetector Based on an Array of Trapezoidal Silicon Pillars. Crystals 2025, 15, 993. https://doi.org/10.3390/cryst15110993
Cheng B, Zou Y, Liang T, Ye A, Zhai K, Lv L. A Long-Wave Infrared Circularly Polarized Photodetector Based on an Array of Trapezoidal Silicon Pillars. Crystals. 2025; 15(11):993. https://doi.org/10.3390/cryst15110993
Chicago/Turabian StyleCheng, Bo, Yuxiao Zou, Taohua Liang, Ansheng Ye, Kunpeng Zhai, and Longfeng Lv. 2025. "A Long-Wave Infrared Circularly Polarized Photodetector Based on an Array of Trapezoidal Silicon Pillars" Crystals 15, no. 11: 993. https://doi.org/10.3390/cryst15110993
APA StyleCheng, B., Zou, Y., Liang, T., Ye, A., Zhai, K., & Lv, L. (2025). A Long-Wave Infrared Circularly Polarized Photodetector Based on an Array of Trapezoidal Silicon Pillars. Crystals, 15(11), 993. https://doi.org/10.3390/cryst15110993






