First-Principles Investigation of Pressure-Induced Structural, Elastic, and Vibrational Properties of In₃Sc

Abstract

This study reports a first-principles investigation of the structural, mechanical, electronic, and vibrational properties of In₃Sc in several crystal structures: AuCu₃ (Pm$\overline{3}$m), Al₃Ti (I4/mmm), Ni₃Sn (P6₃/mmc), and BiF₃ (Fm$\overline{3}$m), with a focus on pressure effects. Calculated equilibrium lattice constants, bulk, shear, and Young’s moduli show good agreement with experimental and theoretical data, especially for the cubic AuCu₃ phase. Elastic constants, examined with the Born stability criteria, reveal that the cubic (SG 221), tetragonal (SG 139), and hexagonal (SG 194) phases are mechanically stable at zero pressure, while the BiF₃-type cubic (SG 225) is unstable. Pressure-dependent variations in lattice parameters, bulk modulus, and elastic moduli, captured by polynomial fits, demonstrate stiffening effects and pressure-induced phase transitions. Band structures and density of states confirm metallicity in all stable phases, with In–Sc hybridization governing bonding. Phonon dispersions and Grüneisen parameters, calculated under compression, establish the dynamical stability of the mechanically stable structures and provide insight into vibrational and thermal behavior. Debye temperature and sound velocities highlight favorable thermal-transport features. Altogether, the results clarify the intrinsic mechanical and thermodynamic response of In₃Sc, supporting its potential as a promising intermetallic for structural and functional use under extreme conditions.

1. Introduction

Intermetallic compounds are an important class of ordered alloys formed between metallic or semi-metallic elements in definite stoichiometries [1,2,3,4]. They generally exhibit high hardness, elevated melting points, excellent thermal stability, and resistance to hot corrosion, which makes them promising candidates for structural applications under extreme environments [5,6,7].

Among them, AB₃-type compounds with the AuCu₃ prototype are of particular interest because their simple cubic ordering leads to distinctive bonding, mechanical responses, and, in some cases, exotic physical phenomena [8,9,10]. Scandium-based AB₃ compounds form a notable subgroup within this family. Al₃Sc, for example, has been widely studied for its remarkable strengthening effect in Al alloys, with first-principles calculations revealing its electronic structure, elastic properties, and thermodynamic stability [11,12]. Ga₃Sc has also been investigated and reported to exhibit metallic bonding and ductile character, although systematic computational studies remain scarce [13].

The indium–scandium (In–Sc) binary system is comparatively less explored. The intermetallic compound In₃Sc was first reported by Yatsenko et al. [14] and later confirmed by Palenzona et al. [15]. Despite these reports, little is known about its intrinsic physical properties. Unlike Al₃Sc or Ga₃Sc, In₃Sc has not been systematically characterized in terms of its structural stability, electronic structure, mechanical behavior, or vibrational properties, particularly under pressure.

Pressure is a fundamental variable in materials science because it reduces interatomic distances, alters bonding states, and strongly affects electronic and vibrational properties [16,17,18]. For AB₃ compounds, high-pressure studies have revealed significant modifications in elastic constants, phonon spectra, and phase stability [19,20]. Thus far, no comprehensive theoretical investigation of In₃Sc under such conditions has been reported.

To address this gap, we employ density functional theory (DFT) calculations [21,22,23] to study In₃Sc in four prototype structures: AuCu₃ (Pm$\overline{3}$m), Al₃Ti (I4/mmm), Ni₃Sn (P6₃/mmc), and BiF₃ (Fm$\overline{3}$m). We evaluate equilibrium structural parameters, elastic constants, and Born stability criteria to establish mechanical robustness, analyze pressure-induced variations in lattice parameters and moduli, and investigate electronic structures to elucidate the bonding character. In addition, phonon dispersions, Grüneisen parameters, and Debye temperatures are calculated to assess vibrational and thermodynamic stability.

This work provides the first systematic theoretical framework for In₃Sc, offering insights into its mechanical, electronic, and vibrational behavior under pressure, and laying the groundwork for future experimental and computational studies on this compound.

2. Materials and Methods

The calculations were carried out within the framework of density functional theory (DFT) [21], as implemented in the Vienna Ab initio Simulation Package (VASP 5.4.4.) [23,24]. Exchange–correlation effects were described using the generalized gradient approximation (GGA) in the Perdew–Burke–Ernzerhof (PBE) functional [25], Van der Waals interactions were accounted for using the empirical dispersion correction method developed by Grimme (DFT-D3) with zero-damping function [26]. The interaction between valence electrons and ionic cores was treated using the projector-augmented wave (PAW) method [27], with scandium (Sc) and indium (In) valence configurations 3d¹4s² and 4d¹⁰5s²5p¹, respectively. A plane-wave cutoff energy of 520 eV was adopted to guarantee convergence of total energies to within 1 meV per formula unit. An electronic energy convergence criterion of 10⁻⁶ eV was employed for the self-consistent field (SCF) calculations to ensure accurate total energy determination. Brillouin zone integrations were performed using Monkhorst–Pack grids [28], with dense k-point meshes selected according to the symmetry of each considered phase: 20 × 20 × 20 for Pm$\overline{3}$m and Fm$\overline{3}$m, 12 × 12 × 16 for I4/mmm, and 21 × 20 × 4 for P6₃/mmc.

All atomic positions and lattice parameters were optimized at each selected volume by minimizing the Hellmann–Feynman forces and the stress tensor components. Convergence was achieved when the forces on each atom were less than 0.002 eV/Å and the residual stresses were below 0.1 GPa. The equilibrium bulk modulus and its pressure derivative were extracted by fitting the calculated energy–volume data to the Murnaghan equation of state [29].

The elastic constants were calculated using density functional perturbation theory (DFPT) [30,31]. In this approach, the stress–strain relationship is obtained from the linear response of the system to small strains, enabling direct evaluation of the full elastic tensor. From the computed elastic constants, various mechanical parameters were derived, allowing assessment of elastic stability and anisotropy.

Phonon dispersion relations were calculated using the supercell finite-displacement method, as implemented in the Phonopy package version 2.8.1. [32]. Supercells of size 2 × 2 × 2 were constructed to obtain the dynamical matrices, and phonon frequencies were evaluated by diagonalization. The vibrational density of states (VDOS), mode symmetries at the Γ point, and Grüneisen parameters were also derived. In all simulations, spin–orbit coupling was omitted, as prior studies have demonstrated that its effect on structural and vibrational properties of related intermetallics is insignificant [33].

3. Results

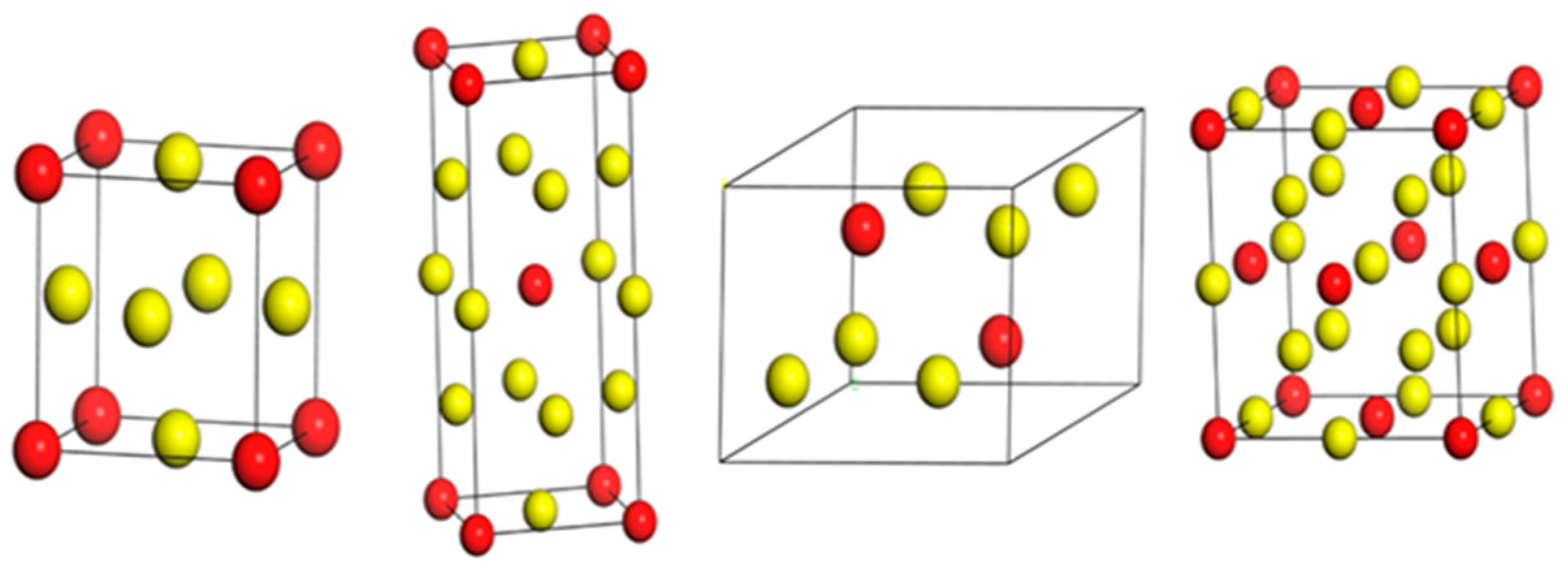
3.1. Structural Properties and Stability of In₃Sc

In order to investigate the structural properties and intrinsic stability of In₃Sc, we studied its behavior in four representative crystal structures: Cu₃Au, Al₃Ti, Ni₃Sn, and BiF₃, as shown in Figure 1. Each of these configurations represents a distinct lattice symmetry, offering insights into the interplay between atomic arrangement, electronic interactions, and mechanical response.

The Cu₃Au-type structure (Pm$\overline{3}$m, SG 221) [34] is established as the ground state of In₃Sc, and notably, serves as a reference for analyzing the stability of other polymorphs. It crystallizes in a simple cubic lattice with one formula unit per primitive cell. The Sc atom occupies the 1a Wyckoff position, while the three In atoms are located at the 3c sites (

Table 1. Atomic Positions of In₃Sc in various crystal structures.

Crystal Structure	Wyckoff Position	Element	x        y        z	Number of Atoms per Unit Cell
AuCu3 Cubic Pm$\overline{3}$m (221)	1a 3c	Sc In	0        0        0 0      ½        ½	4
Al3Ti Tetragonal I4/mmm (139)	2a 2b 4d	Sc In In	0        0        0 ½        ½      0 ½       0        ¾	8
Ni3Sn Hexagonal P63/mmc (194)	2c 6h	Sc In	1/3        2/3        ¼ 0.840534    0.68169   ¼	8
BiF3 Cubic Fm$\overline{3}$m (225)	2a 4b 8c	Sc In In	0        0        0 ½        0        0 ¼        ¾        ¾	16

). Owing to its high cubic symmetry, this structure exhibits nearly isotropic bonding, resulting in a uniform electron density distribution and minimal internal strain.

The Al₃Ti-type structure (I4/mmm, SG 139) [35] is a body-centered tetragonal phase containing two formula units per cell. In this configuration, the Sc atom occupies the 2a site, while the In atoms are distributed over the 2b and 4d Wyckoff positions (Table 1). The lowering of symmetry compared to the cubic phase introduces anisotropic bonding and lattice distortions, which directly affect elastic constants and lead to direction-dependent electronic band dispersion.

The Ni₃Sn-type structure (P6₃/mmc, SG 194) [36] corresponds to a hexagonal arrangement with two formula units per unit cell. In this phase, Sc occupies the 2a site, and In atoms reside at the 6h positions (Table 1). The layered stacking sequence produces strong in-plane bonding within the basal plane but weaker coupling along the c-axis.

Finally, the BiF₃-type structure (Fm$\overline{3}$m, SG 225) [37] is a high-symmetry cubic polymorph with four formula units per unit cell. Sc atoms are located at the 4a sites, while In atoms occupy the 24e sites (Table 1). This phase is structurally more complex than the AuCu₃-type and generally appears at elevated pressures.

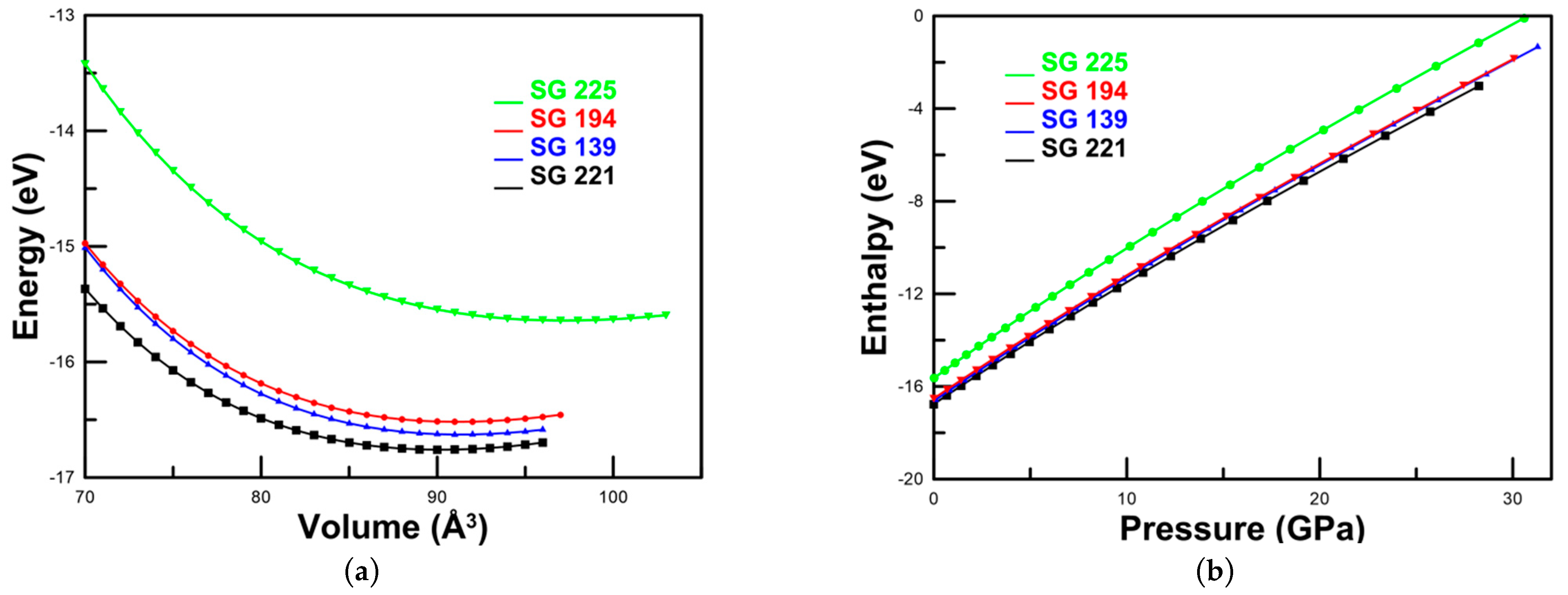
3.2. Energy-Volume and Pressure-Dependent Stability

The thermodynamic stability of each phase was analyzed through energy–volume (E–V) and enthalpy–pressure (H–P) relationships (Figure 2a and Figure 2b, respectively). The E–V curves identify the equilibrium volume V₀ as the point of minimum total energy. The cubic Pm$\overline{3}$m phase exhibits the lowest energy, confirming it as the most stable configuration at ambient conditions. The tetragonal phase, however, is nearly degenerate with the cubic one, showing only a minor energy difference, which indicates that both phases are energetically favorable. Consistently, the calculated enthalpies of the cubic (SG 221) and tetragonal (SG 139) structures are almost indistinguishable across the entire investigated pressure range. This near-degeneracy suggests that the two polymorphs may coexist or compete as stable configurations under compression.

Table 2. Structural properties of In3Sc in the AuCu₃, Al₃Ti, Ni₃Sn, and BiF₃ structures.

Phase Name		a [Å]	b [Å]	c [Å]	B0 [GPa]	B0’	V(Å3)	E(eV)/(f.u)	Ef(eV/(f.u)
AuCu3	This work	4.481			61.145	4.933	90.033	−16.760433	−1.41146
	Exp.	4.479 [15]
		4.77 [38]
		4.46 [14]
	Others	4.532 [39]			55.04 [40]	4.97 [41]
					65.05 [40]	5.01 [41]
					72.89 [40]	4.96 [41]
Al3Ti	This work	4.335	4.335	9.683	62.368	4.781	91.317	−16.629193	−1.280220
Ni3S	This work	6.333	6.333	5.239	60.886	4.697	91.144	−16.519126	−1.170153
BiF3	This work	7.294			49.527	4.705	97.303	−15.64290	−0.293927

summarizes the equilibrium lattice parameters, bulk modulus (B₀), its pressure derivative (B₀′), unit-cell volumes, total energy at equilibrium (E) and formation energy (Ef), alongside available experimental and theoretical data for In₃Sc in the four investigated phases. As shown in Table 2, In₃Sc in the AuCu₃-type (Pm$\overline{3}$m) structure has an equilibrium lattice parameter of 4.481 Å, which matches almost exactly the experimental value of 4.479 Å [15]. This result also lies between other experimental determinations, namely 4.46 Å [14] and 4.77 Å [38]. In comparison with theoretical work, our value is slightly smaller than the lattice constant of 4.532 Å reported in Ref. [39], reflecting possible differences in the exchange–correlation functional and computational parameters. The bulk modulus (61.15 GPa) is consistent with previous theoretical predictions ranging from 55.04 to 72.89 GPa [40]. Relative to the other prototypes, In₃Sc-AuCu₃ is 23% stiffer than In₃Sc-BiF₃ (49.53 GPa), while differing by less than 2% from In₃Sc-Al₃Ti (62.37 GPa) and In₃Sc-Ni₃Sn (60.89 GPa). Its unit-cell volume (90.0 ų) is the smallest among all phases, confirming its compact lattice. The calculated pressure derivative of the bulk modulus (B₀′) for the AuCu₃-type phase is 4.933, which shows excellent agreement with the reported values in Reference [41]. The small deviation (<2%) indicates that our fitted equation of state reproduces the computational compressibility trend reported in [41] with high accuracy, confirming the reliability of our structural optimization.

For In₃Sc in the Al₃Ti-type (I4/mmm) structure, the lattice constants a = 4.335 Å and c = 9.683 Å yield a unit-cell volume of 91.3 ų. This is ~1.4% larger than in AuCu₃, consistent with a slight increase in compressibility. However, the bulk modulus (62.37 GPa) is 2% larger than in In₃Sc-AuCu₃ and 2.4% higher than in In₃Sc-Ni₃Sn, showing comparable or even slightly stronger incompressibility. Compared with In₃Sc-BiF₃, the tetragonal phase is 26% stiffer with ~6% smaller volume.

In the Ni₃Sn-type (P6₃/mmc) structure, In₃Sc exhibits a = 6.333 Å and c = 5.239 Å, corresponding to a unit-cell volume of 91.1 ų—virtually identical to Al₃Ti (difference of 0.2%). The bulk modulus (60.89 GPa) is only 2.4% smaller than Al₃Ti and 0.4% smaller than AuCu₃, highlighting near-equivalent stiffness. By contrast, it is 23% stiffer and ~6.4% denser than In₃Sc–BiF₃, making it mechanically more robust.

The BiF₃-type (Fm$\overline{3}$m) structure of In₃Sc departs significantly from this trend. With a = 7.294 Å, its unit-cell volume reaches 97.3 ų [14], about 8% larger than In₃Sc-AuCu₃ and 6–7% larger than In₃Sc-Al₃Ti and In₃Sn-Ni₃Sn. The bulk modulus (49.53 GPa) is markedly reduced, being 19–26% smaller than in the other three prototypes, reflecting enhanced structural softness and compressibility. In comparing the total and formation energies listed in Table 2, the AuCu₃-type structure is the most stable, followed by the Al₃Ti-type and Ni₃Sn-type structures, with the BiF₃-type being the least stable phase.

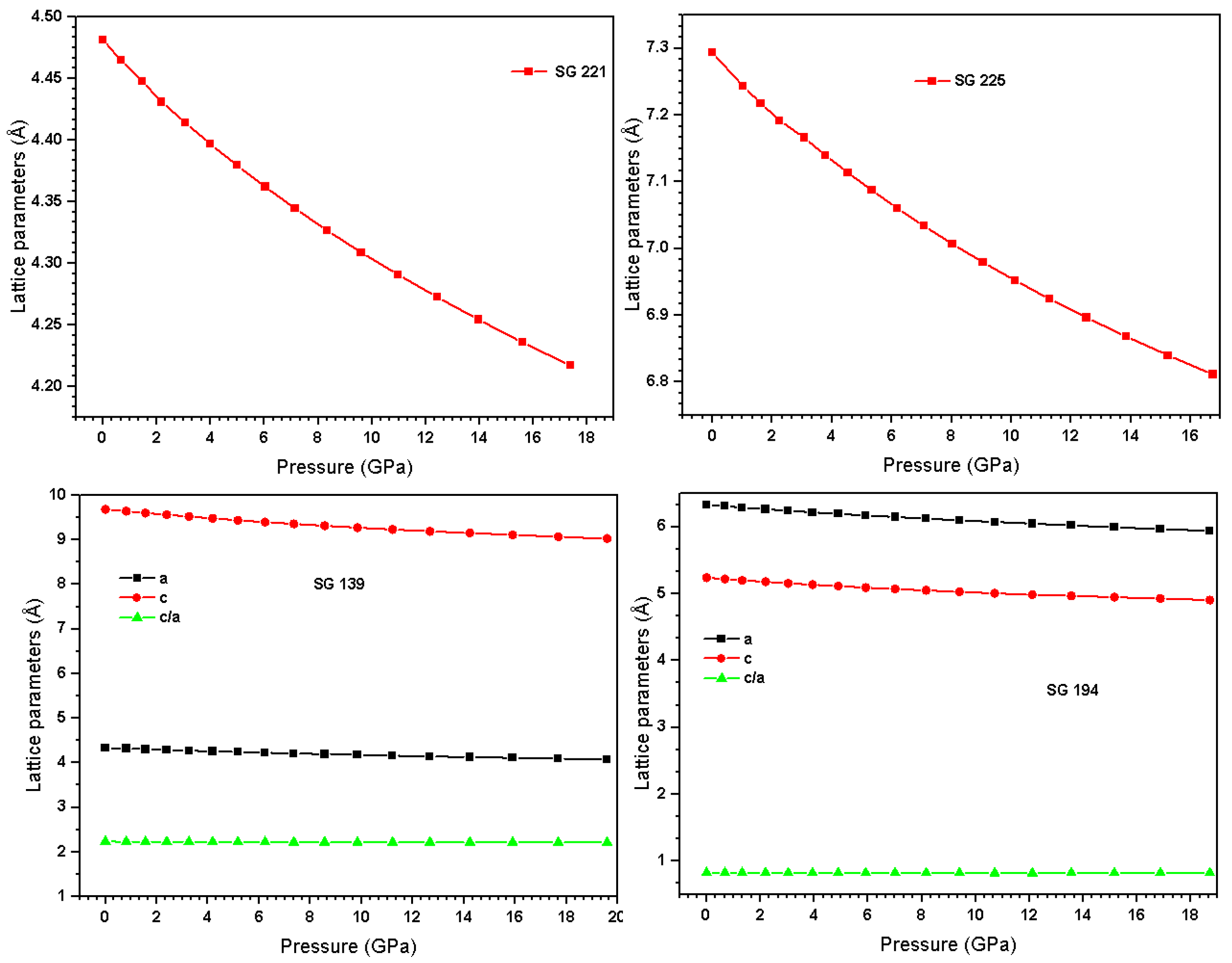
3.3. Lattice Parameters Evolution Under Pressure

The response of lattice parameters to hydrostatic pressure provides critical insights into the mechanical and electronic behavior of In₃Sc, as illustrated in Figure 3. In this study, we focus on a pressure range of 0–20 GPa, which is relevant for typical high-pressure experiments using a Diamond Anvil Cell (DAC). Common pressure-transmitting media such as methanol-ethanol-water remain hydrostatic only up to ~8–10 GPa. Higher pressures require DACs with larger diamonds and gas-loading techniques, accessible to only a few specialized groups. This range ensures that the calculations are directly comparable to standard experimentally achievable pressures, consistent with standard practices in high-pressure research (e.g., MALTA, CRC Press) [42,43,44]. For cubic structures, compression is nearly isotropic due to the equivalence of all bond directions, while lower-symmetry tetragonal and hexagonal phases exhibit anisotropic contraction along different crystallographic axes. This anisotropy arises from differences in bond stiffness, atomic packing, and electronic density distributions along distinct lattice directions.

For the cubic Pm$\overline{3}$m (SG 221) phase, the lattice parameter evolution under pressure is described by the polynomial fit:

$${\displaystyle \raisebox{1ex}{$a$}\!\left/ \!\raisebox{-1ex}{$a_0$}\right.}\left(P\right)= 1 - 0.0047P +0.8227\times {10}^{-4} P^2$$

(1)

(Similarly, the cubic Fm$\overline{3}$m (SG 225) phase, which has a larger unit cell and slightly lower packing efficiency, exhibits:

$${\displaystyle \raisebox{1ex}{$a$}\!\left/ \!\raisebox{-1ex}{$a_0$}\right.}\left(P\right)= 1 - 0.0056P +1.0475\times {10}^{-4} P^2$$

(2)

For the hexagonal P63/mmc (SG 194) phase, the a and c-axes compress at different rates, reflecting directional differences in bond stiffness:

$${\displaystyle \raisebox{1ex}{$a$}\!\left/ \!\raisebox{-1ex}{$a_0$}\right.}\left(P\right)= 1 - 0.0045P +0.6796\times {10}^{-4} P^2, and$$

$${\displaystyle \raisebox{1ex}{$c$}\!\left/ \!\raisebox{-1ex}{$c_0$}\right.}\left(P\right)=1-0.0051P+0.9666\times {10}^{-4} P^2$$

(3)

The ratio of lattice parameters along the c and a-axes evolves as:

$${\displaystyle \raisebox{1ex}{$c$}\!\left/ \!\raisebox{-1ex}{$c_0$}\right.}\left(P\right)= 0.8275 - 5.2500\times {10}^{-4}P +2.4364\times P^2$$

(4)

indicating that the c-axis compresses faster than the basal plane. In the tetragonal I4/mmm (SG 139) phase, a similar anisotropic trend is observed:

$${\displaystyle \raisebox{1ex}{$a$}\!\left/ \!\raisebox{-1ex}{$a_0$}\right.}\left(P\right)= 1 - 0.0043P +0.6506\times {10}^{-4} P^2, and$$

$${\displaystyle \raisebox{1ex}{$c$}\!\left/ \!\raisebox{-1ex}{$c_0$}\right.}\left(P\right)=1-0.0051P+0.8600\times {10}^{-4} P^2$$

(5)

$${\displaystyle \raisebox{1ex}{$c$}\!\left/ \!\raisebox{-1ex}{$a$}\right.}\left(P\right)=2.2339-0.00183P+4.60195\times {10}^{-5} P^2$$

(6)

The linear term in each polynomial corresponds to the elastic response, indicating the compressibility along a given axis, while the quadratic term captures anharmonic effects at higher pressures, arising from nonlinear atomic interactions, electron-cloud repulsion, and deviations from Hookean behavior. Changes in the c/a ratio quantify the anisotropic mechanical response, which is crucial for predicting phase stability, pressure-induced transitions, and modifications in the electronic structure. These polynomial fits provide a quantitative framework for understanding the interplay between crystal symmetry, bond strength, and lattice deformation under external pressure, offering fundamental insights into the thermomechanical behavior of In₃Sc.

3.4. Elastic Properties and Mechanical Stability

The mechanical stability of crystalline solids is fundamentally linked to their elastic constants C_ij and elastic compliance constants S_ij, which describe the lattice’s response to small deformations. According to Born (1954) [45], the lattice is mechanically stable if the strain energy is positive for any infinitesimal distortion. Compliance constants, being inverses of C_ij, offer additional insight into the magnitude of strain produced under applied stress: lower S_ij values correspond to stiffer, less deformable lattices.

For cubic crystals (SG 221 and SG 225), mechanical stability is assessed using the Born criteria [46]:

$$c_{11}- c_{12} > 0,c_{11}+2c_{12}>0,c_{44}>0$$

(7)

These conditions physically correspond to resistance to shear along [110], volumetric compression, and tetragonal shear.

Table 3. The calculated elastic constants in GPa (Cᵢ_j) at 0 GPa for the various phases investigated.

Phases	Space Group	C11	C12	C13	C33	C44	C66	Stability
AuCu3	221	113.8 a	40.08 a			33.25 a		Stable
		92.36 b	39.99 b			18.62 b
Al3Ti	13	109.06 a	52.64 a	35.45 a	114.90 a	37.20 a	57.47 a	Stable
Ni3Sn	194	87.39 a	47.73 a	52.76 a	76.11 a	22.61 a	19.83 a	Stable
BiF3	225	22.16 a	64.65 a			11.72 a		Unstable

^a This work, ^b ref. [39].

shows that SG 221 (AuCu₃) satisfies all three conditions with C₁₁ = 113.83 GPa, C₁₂ = 40.083, and C₄₄ = 33.25 GPa. Our calculated elastic constants C₁₁, C₁₂, and C₄₄ are systematically higher than those reported in theoretical work [46], with the largest discrepancy in C₄₄ (+79%). Both sets of values fulfill the Born stability criteria, confirming mechanical stability in agreement with Ref. [39]. However, our results predict a larger bulk and shear modulus and a Zener anisotropy closer to unity, indicating a stiffer and more isotropic elastic response than published in Ref. [39]. The positive difference C₁₁ − C₁₂ = 73.75 GPa confirms strong shear resistance, while C₄₄ ensures stability under tetragonal distortions. The corresponding compliance constants S₁₁ = 0.01076 GPa⁻¹ and S₁₂ = −0.0028 GPa⁻¹ (

Table 4. Calculated Elastic Compliance Constants (Sᵢⱼ, in GPa⁻¹) at 0 GPa for Various Crystal Structures of In₃Sc.

Structure (Space Group)	S11	S12	S13	S33	S44	S66
SG 221 cubic	0.01076	−0.0028			0.03008
SG 139 Tetragonal	0.01244	0.00529	−0.0022		0.01006	0.174
SG 194 Hexagonal	0.02067	−0.00454	0.01118	0.02864	0.04422	0.05043
SG 225 cubic	0.01349	0.01005			0.08532

) indicate low strain per unit stress, confirming a stiff and mechanically stable lattice.

In contrast, SG 225 (BiF₃) violates the first criterion (C₁₁ − C₁₂ = −42.49 GPa), indicating mechanical instability. Its compliance constants (S₁₁ = 0.01349, S₁₂ = 0.01005 GPa⁻¹) are comparatively high, showing that even small stresses lead to large strains, consistent with the observed lattice instability.

Tetragonal crystals (SG 139) require additional criteria for mechanical stability [45]:

$$c_{11}> 0, c_{33}> 0, c_{44}>0, c_{66}> 0, \left(c_{11}-c_{12}\right)>0, \left(c_{11}+c_{33}-2c_{13}\right)>0$$

$$\mathrm{And} \left\{2(c_{11}+c_{12}){+c}_{33}+4c_{13}\right\}>0$$

(8)

As shown in Table 3, SG 139 (Al₃Ti) satisfies all these conditions with C₁₁ = 109. GPa, C₁₂ = 52.64 GPa, C₁₃ = 35.45 GPa, C₃₃ = 114.90, C₄₄ = 37.20 GPa, and C₆₆ = 57.47 GPa. High C66 indicates strong basal-plane shear resistance, reflecting the anisotropic bonding network in the tetragonal structure. The compliance constants S₁₁ = 0.01244, S₁₂ = −0.00529, and S₃₃ = 0.01006 GPa⁻¹ (Table 4) suggest moderate anisotropy, with slightly higher compliance along the c-axis compared to the basal plane. Hexagonal (SG 194) lattices also require shear and axial constraints for stability [46]:

$$c_{11}> 0, c_{33}> 0, c_{44}>0, c_{66}> 0, \left(c_{11}-c_{12}\right)>0, \left(c_{11}+c_{33}-2c_{13}\right)>0$$

$$\mathrm{And} \left\{2(c_{11}+c_{12}){+c}_{33}+4c_{13}\right\}>0$$

(9)

Table 3 shows that SG 194 Ni₃Sc (Ni₃Sn) satisfies all criteria with C₁₁ = 87.39 GPa, C₁₂ = 47.73 GPa, C₁₃ = 52.76 GPa, C₃₃ = 76.11 GPa, C₄₄ = 22.61 GPa, and C₆₆ = 19.83 GPa. Lower values of C44 and C66 indicate moderate shear resistance, characteristic of ductile layered structures. Compliance constants S₁₁ = 0.02067, S₁₂ = −0.00454, and S₃₃ = 0.02864 GPa⁻¹ (Table 4) confirm higher compliance along the c-axis, consistent with the structural anisotropy of hexagonal crystals.

3.5. Mechanical Properties and Elastic Moduli

The elastic properties also link directly to other macroscopic mechanical characteristics. For example, the bulk modulus (B) describes the resistance to uniform compression, while the shear modulus (G) reflects the resistance to shape change at constant volume. The ratio B/G is often used to infer ductility or brittleness following Pugh’s criterion [47]: values greater than 1.75 indicate ductile behavior, while smaller values correspond to brittleness. The Young’s modulus (E) can be derived from B and G as E = 9BG/(3B + G) [48], which quantifies the stiffness of the material under tensile loading. The Poisson’s ratio (ν) is obtained from B and G as ν = (3B − 2G)/(6B + 2G) [48], describing the transverse strain response to axial loading. Additionally, the longitudinal P-wave modulus, P = B + 3/4G [49], links the elastic constants to wave propagation, relevant in geophysical and high-pressure studies.

Table 5. Bulk modulus (B), Shear Modulus (G), Young Modulus (E) in GPa, and Poisson’ Ratio (υ), P-wave modulus (P) in GPa, and B/G Using Voigt, Reuss, and Voigt–Reuss–Hill average approximations.

Structure (SG)	Scheme	B	G	E	υ	P	B/G
AuCu3 (221)	Voigt Reuss Average	64.660 64.660 64.660 57.45 [39]	34.698 34.609 34.654 21.35 [39]	88.300 88.107 88.204 56.99 [39]	0.272 0.273 0.273 0.335 [39]	110.924 110.805 110.865	1.863 1.868 1.866 2.691 [39]
Al3Ti (139)	Voigt Reuss Average	64.454 64.339 64.397	40.333 38.258 39.295	100.115 95.787 97.951	0.241 0.252 0.246	118.231 115.349 116.790	1.598 1.682 1.639
Ni3Sn (194)	Voigt Reuss Average	61.931 61.817 61.874	19.521 18.653 19.087	52.996 50.844 51.922	0.357 0.361 0.360	87.959 86.688 87.323	3.173 3.314 3.240
BiF3 (225)	Voigt Reuss Average	50.474 50.474 50.474	−1.477 30.864 14.693	−4.476 76.914 36.219	0.515 0.246 0.380	48.505 91.626 70.065	3.146 1.635 2.526

presents the calculated bulk modulus (B), shear modulus (G), Young’s modulus (E), Poisson’s ratio (ν), P-wave modulus (P), and the B/G ratio using Voigt, Reuss, and Hill (average) approximations [50]. These parameters are crucial for understanding the intrinsic resistance of the studied phases to external mechanical deformation.

Beyond the Pugh’s ratio, the ductility and brittleness of cubic, hexagonal, and tetragonal crystals can also be effectively evaluated using the Cauchy pressure (CP), which provides a complementary and physically meaningful insight into the nature of interatomic bonding. The Cauchy pressure is defined as C₁₂ − C₄₄ for cubic structures [51,52], and C₁₃ − C₄₄ and C₁₂ − C₆₆ for hexagonal and tetragonal structures [53,54,55], respectively. A positive Cauchy pressure indicates metallic bonding and ductile behavior, whereas a negative value suggests directional covalent bonding and hence brittleness. For the cubic AuCu₃ (SG 221) structure, C₁₂ − C₄₄ = +6.83 GPa, indicating a positive Cauchy pressure and, consequently, a ductile nature. Similarly, the hexagonal Ni₃Sn (SG 194) phase yields C₁₃ − C₄₄ = +30.15 GPa and C₁₂ − C₆₆ = +27.90 GPa, both positive, reaffirming its metallic bonding and ductility. The cubic BiF₃ (SG 225) compound also exhibits a positive Cauchy pressure of C₁₂ − C₄₄ = +52.93 GPa, further confirming its ductile behavior despite its lower overall stiffness. In contrast, the tetragonal Al₃Ti (SG 139) structure presents negative Cauchy pressures, C₁₃ − C₄₄ = −1.75 GPa and C₁₂ − C₆₆ = −4.83 GPa, indicating directional covalent bonding and thus brittleness. These Cauchy pressure results are in excellent agreement with the Pugh’s ratio (B/G) values, where phases with B/G > 1.75 (such as AuCu₃, Ni₃Sn, and BiF₃) exhibit ductility, while Al₃Ti, with B/G < 1.75, remains brittle. The strong consistency between Cauchy pressure and Pugh’s ratio demonstrates the robustness of the present mechanical analysis and provides reliable insight into the bonding and deformation characteristics of the investigated In₃Sc compounds.

In the cubic system (SG 221), the bulk modulus (B) remains consistent across Voigt, Reuss, and Hill approximations [47] with a value of 64.660 GPa, reflecting strong isotropic resistance to compression. The shear modulus (G) is calculated as 34.654 GPa on average, showing a good resistance to shape change under applied stress. Young’s modulus (E) is given as 88.204 GPa, indicating a relatively high stiffness of the phase against uniaxial deformation. The Poisson’s ratio (ν) of 0.273 is typical of materials with mixed ionic and metallic bonding, which implies that both central and angular forces play a role in its bonding characteristics. The P-wave modulus (P), averaging 110.865 GPa, further indicates robustness of elastic wave propagation along longitudinal directions. Importantly, the B/G ratio of 1.866 is greater than the critical threshold of 1.75, signifying that this cubic phase should exhibit ductile mechanical behavior according to Pugh’s criterion. For the tetragonal structure (SG 139), the bulk modulus (B) averages to 64.397 GPa, similar to the cubic case, which suggests comparable volumetric resistance. However, the shear modulus (G) is slightly higher at 39.295 GPa, reflecting enhanced rigidity against shear deformation compared to the cubic phase. Young’s modulus (E) reaches 97.951 GPa, indicating greater stiffness under uniaxial strain, consistent with the increased shear modulus. The Poisson’s ratio (ν) averages to 0.246, a lower value than that of the cubic system, implying stronger covalent-like bonding contributions in this phase. The P-wave modulus (P) averages at 116.790 GPa, which is the highest among the systems studied, signifying superior longitudinal wave propagation properties. The B/G ratio is 1.639, which is below the ductility threshold, suggesting that the tetragonal phase tends toward brittle behavior despite its relatively high stiffness.

In the hexagonal phase (SG 194), the bulk modulus is slightly lower than the cubic and tetragonal phases, with an average value of 61.874 GPa. More significantly, the shear modulus (G) is drastically reduced to 19.087 GPa, indicating poor resistance to shear deformations. This reduction is also reflected in the relatively low Young’s modulus (E) of 51.922 GPa, highlighting the softness and reduced stiffness of this phase compared to the cubic and tetragonal structures. The Poisson’s ratio (ν) is much higher, averaging 0.360, which suggests a bonding environment dominated by central forces and strong compressibility in the lateral directions. The P-wave modulus (P) is calculated at 87.323 GPa, lower than both cubic and tetragonal phases, consistent with the reduced stiffness. The B/G ratio is extremely high at 3.24, far above the ductility threshold, indicating a very ductile mechanical nature. However, such high ductility is often accompanied by weak shear rigidity, which limits structural stability under shear loads.

The cubic system with space group 225 exhibits unusual behavior. While the bulk modulus (B) is moderate at 50.474 GPa, the Voigt shear modulus (G) takes a negative value (−1.477 GPa), leading to a negative Young’s modulus (E = −4.476 GPa). This indicates mechanical instability within the Voigt framework, as negative shear and Young’s moduli are unphysical. However, the Reuss and Hill approximations correct this anomaly, giving positive values: G = 30.864 GPa (Reuss) and 14.693 GPa (Hill), with corresponding Young’s moduli of 76.914 GPa and 36.219 GPa, respectively. The Poisson’s ratio also varies significantly: 0.515 in Voigt (indicative of near-incompressibility), 0.246 in Reuss (normal covalent-ionic bonding range), and 0.380 in Hill (intermediate). The P-wave modulus ranges between 48.505 and 91.626 GPa, averaging 70.065 GPa, again reflecting intermediate mechanical stiffness. The B/G ratio is high (3.435 in Hill average), which suggests ductility; nevertheless, the presence of negative elastic constants in the Voigt approximation signals potential elastic instability and raises doubts about the reliability of this phase.

Fracture toughness (K_IC) is a key mechanical parameter that quantifies a material’s ability to resist crack initiation and propagation, thus providing a direct measure of structural integrity and failure tolerance. For intermetallic compounds, where brittleness is a common limitation, evaluating K_IC offers crucial insight into their potential for structural and high-performance applications. While parameters such as the bulk modulus (B), shear modulus (G), and Pugh’s ratio (B/G) can indirectly describe ductility, fracture toughness serves as a more comprehensive indicator of a material’s capacity to absorb and dissipate energy under stress. However, it is important to mention that this property cannot be obtained directly using only the elasticity of the material, since the fracture toughness depends on the energy required to break the bonds at the crack tip, which can involve plastic deformation and other mechanisms not accounted for by the elastic constants.

In this study, the fracture toughness of the investigated In₃Sc-based compounds was estimated using the empirical model proposed by Niu et al. [56,57,58], defined as

$$K_{IC}={\left(V_0\right)}^{1/6}\sqrt{EG}$$

(10)

where $V_0$ is the equilibrium atomic volume, E is the Young’s modulus, and G is the shear modulus. This model effectively links the elastic behavior to fracture resistance, allowing accurate estimation of K_IC from first-principles data.

Using the calculated elastic parameters, the obtained fracture toughness values for the considered structures follow the order Al₃Ti (SG 139) > AuCu₃ (SG 221) > Ni₃Sn (SG 194) > BiF₃ (SG 225), corresponding approximately to 7.2, 6.8, 5.5, and 4.1 $MPa·m^{1/2}$, respectively. The relatively high K_IC value for Al₃Ti reflects its superior resistance to crack propagation, consistent with its high shear and Young’s moduli. Similarly, AuCu₃ exhibits significant fracture toughness, indicating good ductility and metallic bonding characteristics as supported by its positive Cauchy pressure. In contrast, Ni₃Sn and particularly BiF₃ display lower K_IC values, signifying greater brittleness and a tendency toward crack propagation under mechanical stress.

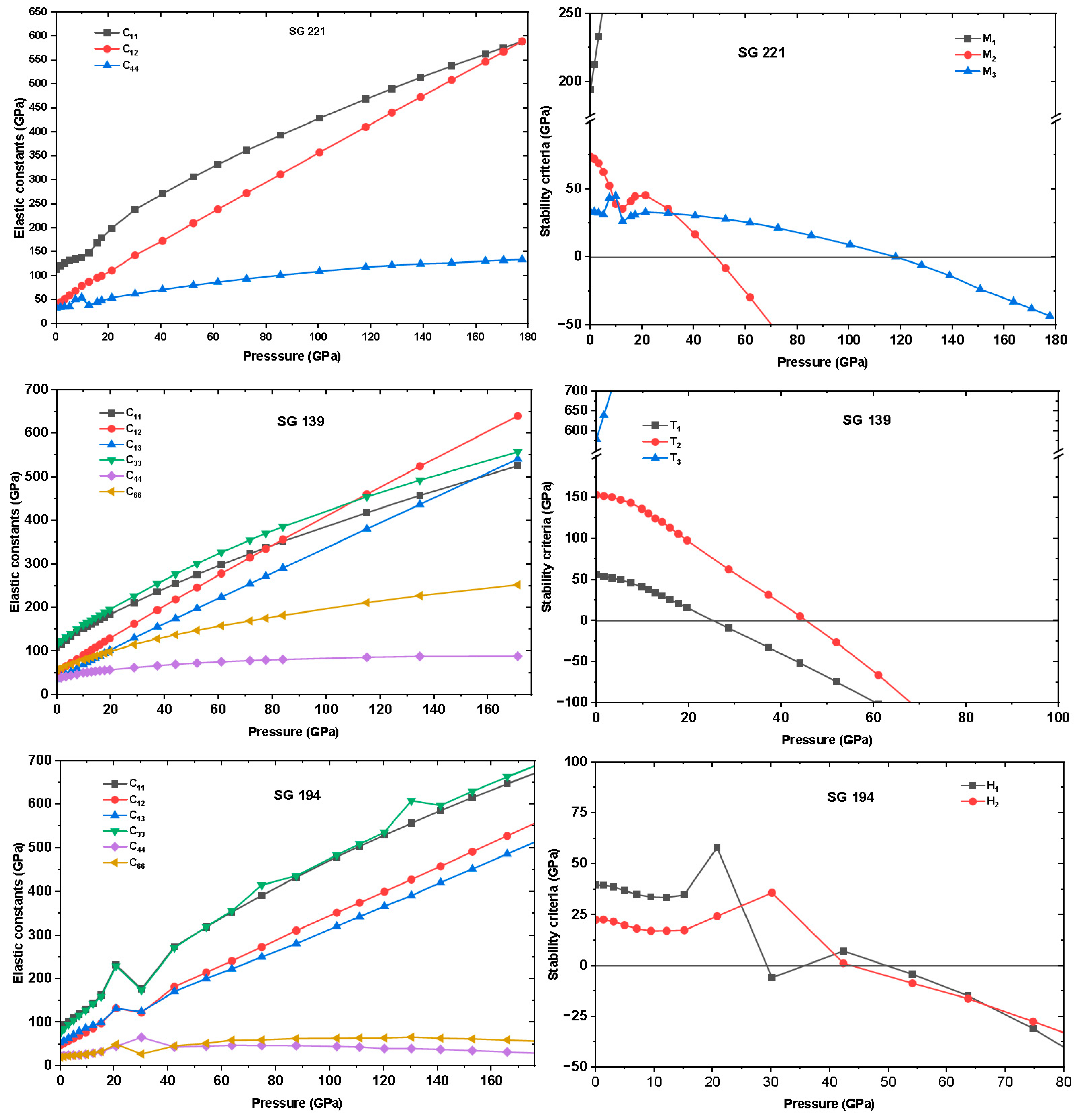
3.6. Elastic Constants and Mechanical Stability Under Pressure

Figure 4 presents the pressure dependence of the elastic constants and stability criteria for cubic, tetragonal, and hexagonal In₃Sc. In the cubic phase, the elastic constants C₁₁, C₁₂, and C₄₄ exhibit the expected monotonic stiffening with pressure. Both C₁₁ and C₁₂ increase steadily, reflecting enhanced resistance to longitudinal compression and interatomic bond shortening under hydrostatic loading. Similarly, C₄₄, associated with shear on {100} planes, remains positive and rises with pressure, suggesting robust shear rigidity at moderate compression. However, mechanical stability is not governed by these raw values but by their pressure-corrected forms: ${\tilde{C}}_{11}=C_{11}-P$, ${\tilde{C}}_{12}=C_{12}+P$, and ${\tilde{C}}_{44}=C_{44}-P$.

The cubic Born stability conditions are:

$$M_1={\tilde{C}}_{11}^P+2{\tilde{C}}_{12}^P>0,M_2= {\tilde{C}}_{11}^P-{\tilde{C}}_{12}^P>0, M_3={\tilde{C}}_{44}^P>0$$

(11)

Up to ~50 GPa, all criteria are satisfied, ensuring elastic stability. Beyond ~52 GPa, however, the M₂ criterion becomes negative despite the continued increase in C₁₁ and C₁₂. This shear-driven instability arises because the difference between longitudinal and transverse responses narrows, preventing the lattice from sustaining shear along ⟨110⟩ directions. Physically, this reflects a competition between bond-stretching and bond-bending forces: while bonds resist further compression, their ability to withstand shear collapses. Consequently, the cubic phase is stable only up to ≈49.09 GPa, beyond which it transforms into a lower-symmetry structure, likely tetragonal.

In the tetragonal phase, the response to compression is anisotropic due to inequivalent axial directions. Both C₁₁ and C₃₃ increase with pressure, though at different rates, revealing stronger stiffening in the basal plane than along the c-axis. The shear constants C₄₄ and C₆₆ remain positive and grow moderately, maintaining finite shear resistance in both axial and basal modes. The corresponding Born criteria are:

$$T_1={\tilde{C}}_{11}^P-{\tilde{C}}_{12}^P>0,T_2={\tilde{C}}_{11}^P+{\tilde{C}}_{33}^P-2{\tilde{C}}_{13}^P>0,$$

$$T_3=2{\tilde{C}}_{11}^P+{\tilde{C}}_{33}^P+2{\tilde{C}}_{12}^P+4{\tilde{C}}_{13}^P>0,$$

(12)

together with, ${\tilde{C}}_{\alpha \alpha }^P>0$ (α = 1, 3, 4, 6). At very low pressure, the T₂ condition is violated, indicating weak coupling between in-plane and out-of-plane compressions. As pressure increases, interlayer bonding strengthens, and above ~25.25 GPa, all stability criteria are fulfilled. This pressure-induced stabilization implies that the tetragonal distortion, initially unfavorable at low density, becomes energetically preferred once orbital overlap along the ccc-axis is enhanced. The wide stability range above this threshold suggests that the tetragonal structure acts as a pressure-stabilized intermediate between cubic and hexagonal phases.

The hexagonal phase shows a distinct elastic evolution governed by its directional bonding. The basal-plane stiffness (C₁₁, C₁₂) increases rapidly with compression, while the axial constant C₃₃ rises more moderately, highlighting strong anisotropy between in-plane and out-of-plane responses. The shear modulus C₄₄ remains positive throughout, confirming sustained rigidity against shear on prismatic planes. The Born criteria for hexagonal crystals are:

$$H_1={\tilde{C}}_{11}-\left|{\tilde{C}}_{12}\right|>0, {H_2=\tilde{C}}_{33}\left({\tilde{C}}_{11}+{\tilde{C}}_{12}\right)-2{{\tilde{C}}_{13}}^2>0, {H_3=\tilde{C}}_{44}>0$$

$${\tilde{C}}_{\partial \partial }=C_{\partial \partial }-P(\partial =1, 3, 4) \mathrm{and}{\tilde{C}}_{1\partial }=C_{1\partial }+P(\partial =2, 3)$$

(13)

At low pressure (0–20 GPa), these criteria are satisfied, indicating that the layered network retains both axial and basal rigidity. However, near ~29.09 GPa, H₁ and H₂ simultaneously collapse due to the softening of C₆₆ and excessive axial–basal coupling through C₁₃, which signals a shear-driven instability of the basal planes coupled with axial strain. The persistent violation of the stability conditions suggests that the hexagonal lattice is not a true high-pressure host but instead a metastable configuration prone to collapse or transform once the critical shear-softening threshold is crossed.

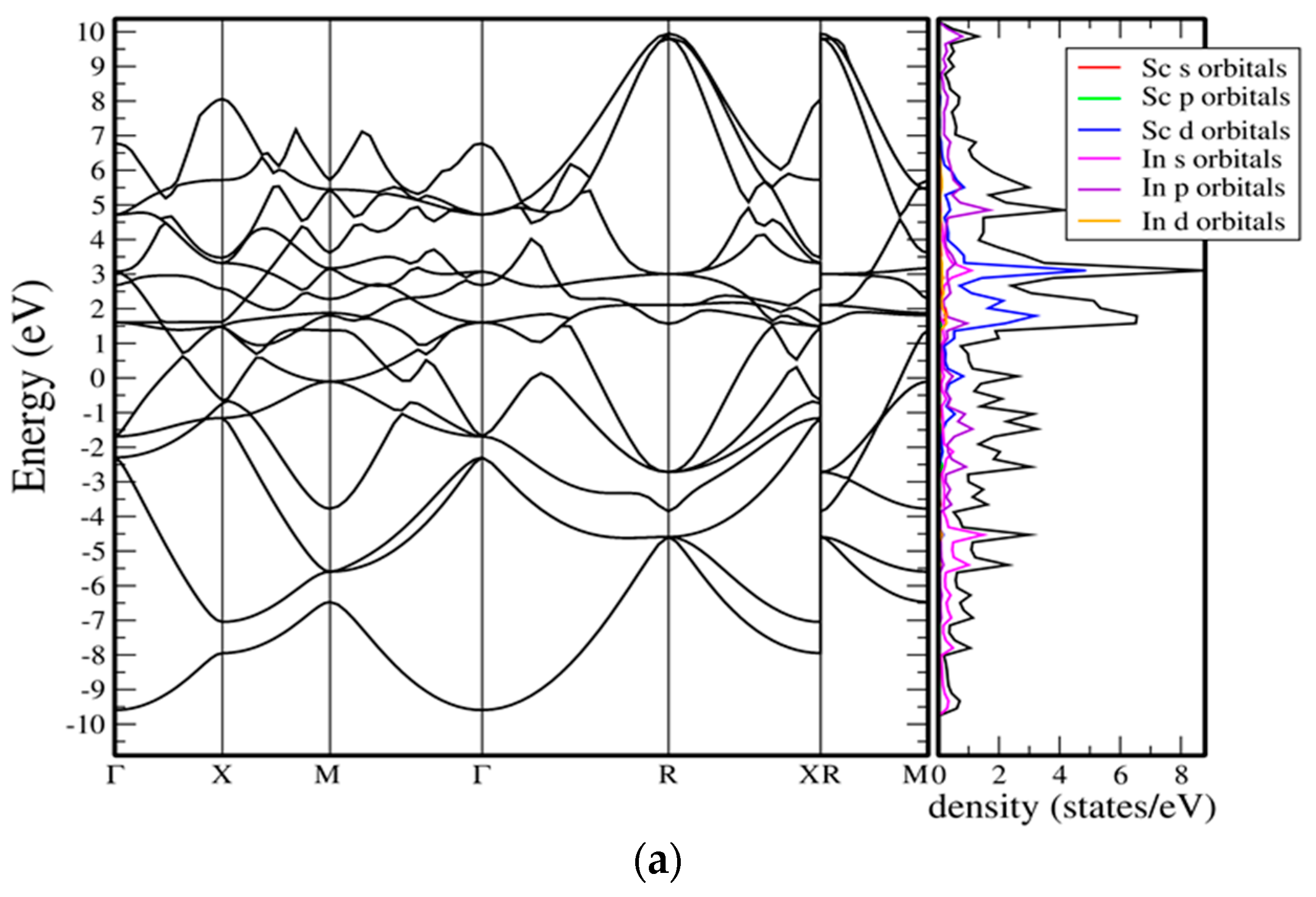
3.7. Electronic Band Structures and Density of States of Cubic, Tetragonal, and Hexagonal In₃Sc

As shown in (Figure 5a), the cubic Pm$\overline{3}$m phase of In₃Sc exhibits a metallic band structure, characterized by multiple dispersive bands crossing the Fermi level along the high-symmetry directions. The conduction and valence bands overlap significantly, with no evidence of a gap, confirming metallicity. Near the Fermi level, the density of states (DOS) is dominated by hybridized In-5p and Sc-3d states. The Sc-d orbitals contribute sharp peaks in the vicinity of the Fermi level, reflecting relatively localized character, while the In-p orbitals form broader features that provide dispersive conduction channels. At lower energies (−5 to −8 eV), deeper In-s states are present, giving rise to pronounced DOS peaks well below the Fermi level. This orbital hybridization results in anisotropic conduction pathways, with the high DOS at E_F suggesting good metallic conductivity. The cubic symmetry ensures isotropic electronic dispersion, but the concentration of Sc-d states at the Fermi level may also predispose the phase to electron–phonon coupling effects, a factor relevant for mechanical softening and possible superconductivity.

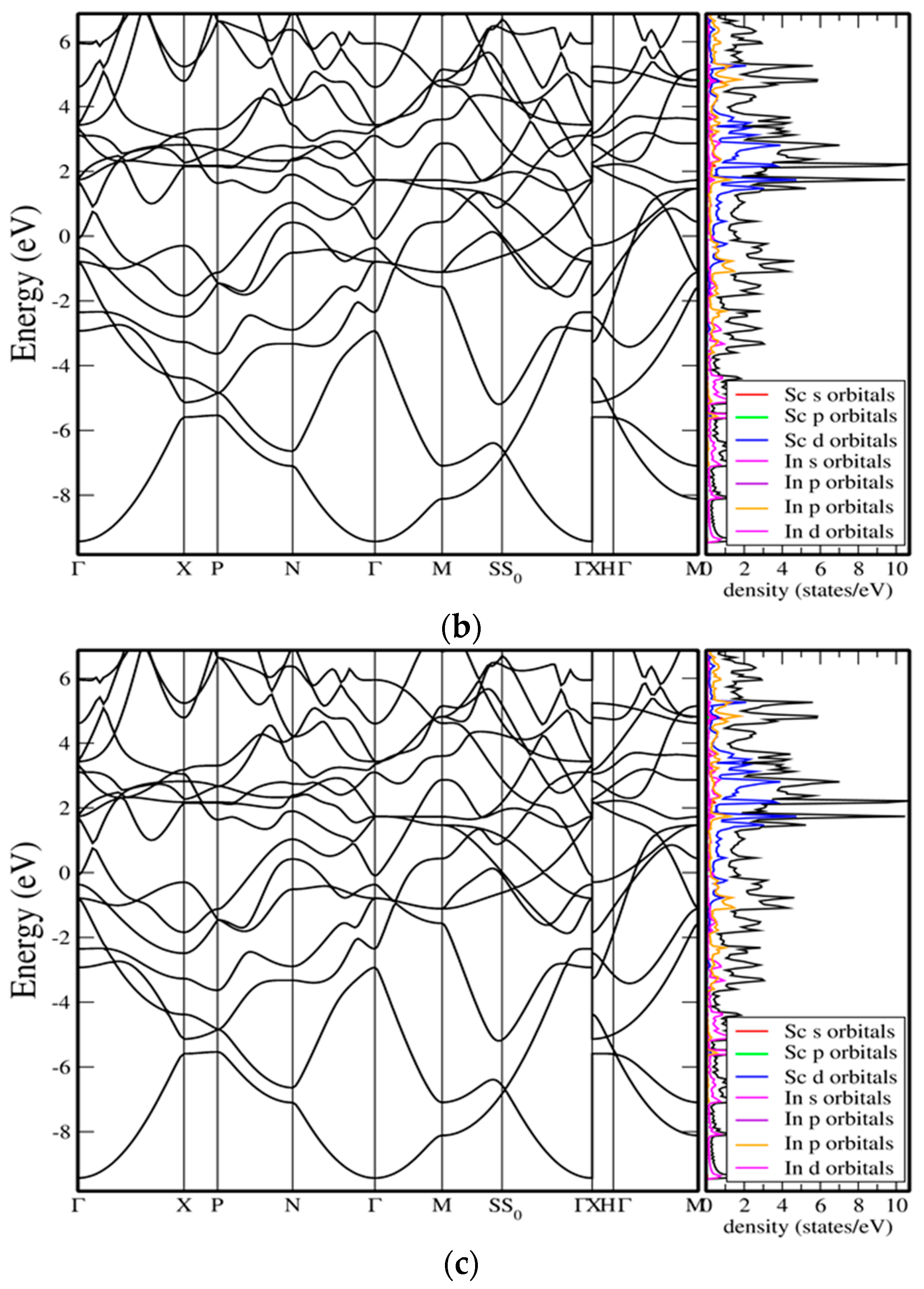
The electronic features of the tetragonal polymorph are illustrated in Figure 5b. The phase preserves the metallic character of In₃Sc but introduces notable anisotropy into its electronic structure due to the inequivalence of in-plane and out-of-plane bonding. The band structure shows several bands crossing the Fermi level, but with reduced dispersion along the c-axis compared to the basal plane, indicating a lower carrier mobility in the out-of-plane direction. The DOS reveals that Sc-d states remain the dominant contribution near E_F, but the splitting of degeneracies compared to the cubic case results in a slightly reduced density at the Fermi level. This subtle decrease suggests that the tetragonal distortion partially lifts band overlap and redistributes electronic states across a broader energy window. In addition, the In-p orbitals continue to hybridize strongly with Sc-d states, producing broad features in the valence region and ensuring conduction remains metallic. From a physical standpoint, the tetragonal band structure indicates that while both cubic and tetragonal phases are nearly degenerate in enthalpy, the tetragonal polymorph may display direction-dependent transport properties, with enhanced in-plane conductivity relative to the c-axis. This anisotropy aligns with the structural distortion observed under pressure and points toward a pressure-stabilized metallic phase with anisotropic electronic behavior.

The band structure and DOS of the hexagonal phase are displayed in Figure 5c. This phase shows the most distinct electronic features among the three polymorphs. Bands near the Fermi level are less dispersive than in the cubic or tetragonal phases, reflecting reduced electronic mobility and a stronger localization of carriers. The DOS confirms metallic behavior, with contributions at E_F arising predominantly from Sc-d orbitals. In this case, however, the hybridization with In-p orbitals is weaker and more anisotropic. A clear separation of orbital contributions is visible: In-s and In-p states dominate the deeper valence region, while Sc-d states cluster near the Fermi level. This orbital distribution leads to a narrower bandwidth and more localized conduction channels, consistent with the layered atomic arrangement of the hexagonal structure. Importantly, the DOS at E_F is lower than in both the cubic and tetragonal phases, implying that while metallicity persists, the phase may exhibit reduced electrical conductivity and weaker electron–phonon coupling. Physically, this behavior suggests that the hexagonal polymorph, although mechanically stable only over limited pressure ranges, is electronically less favorable for high carrier transport but may be stabilized by directional bonding that favors anisotropic conduction within the basal planes.

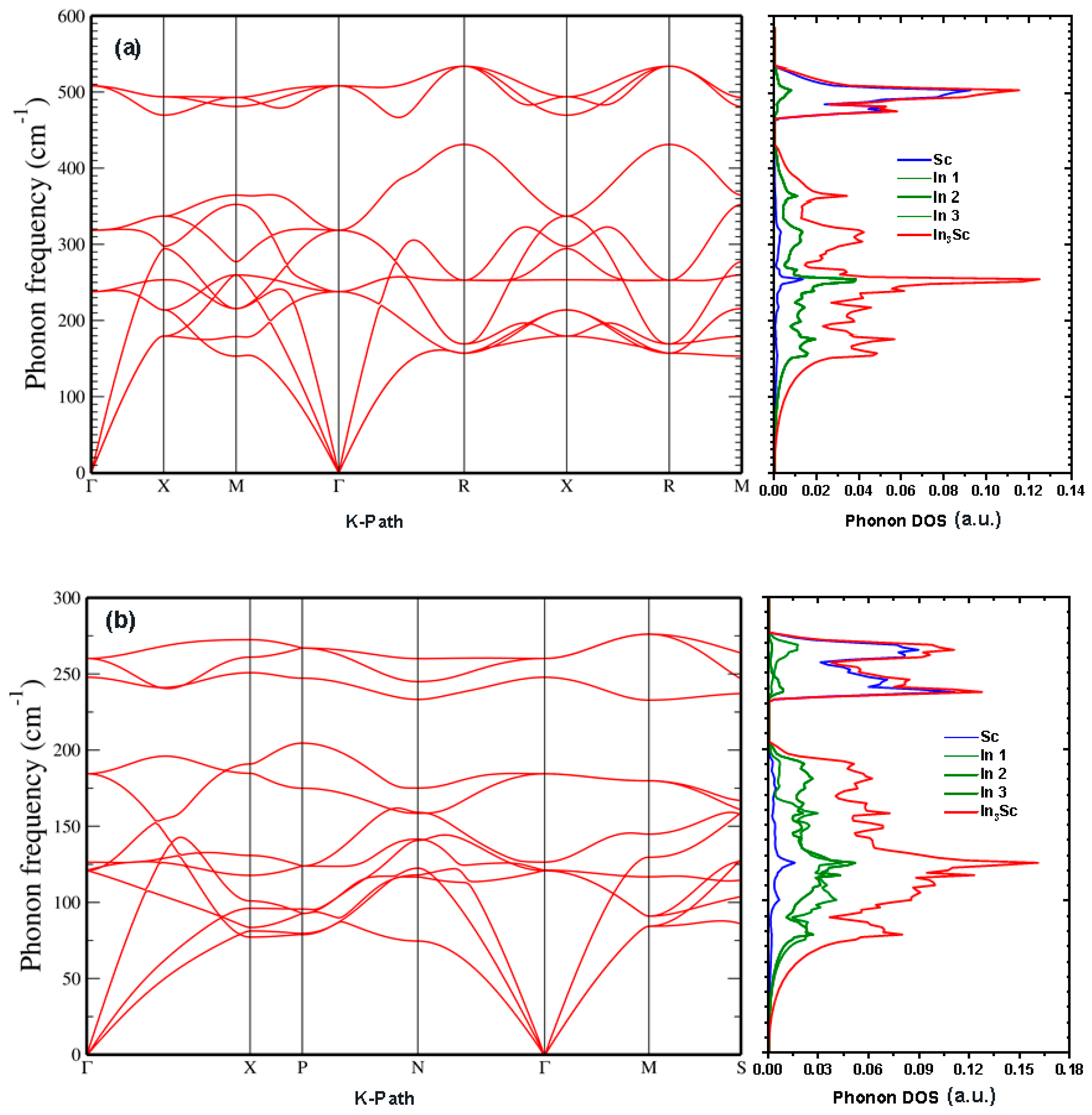
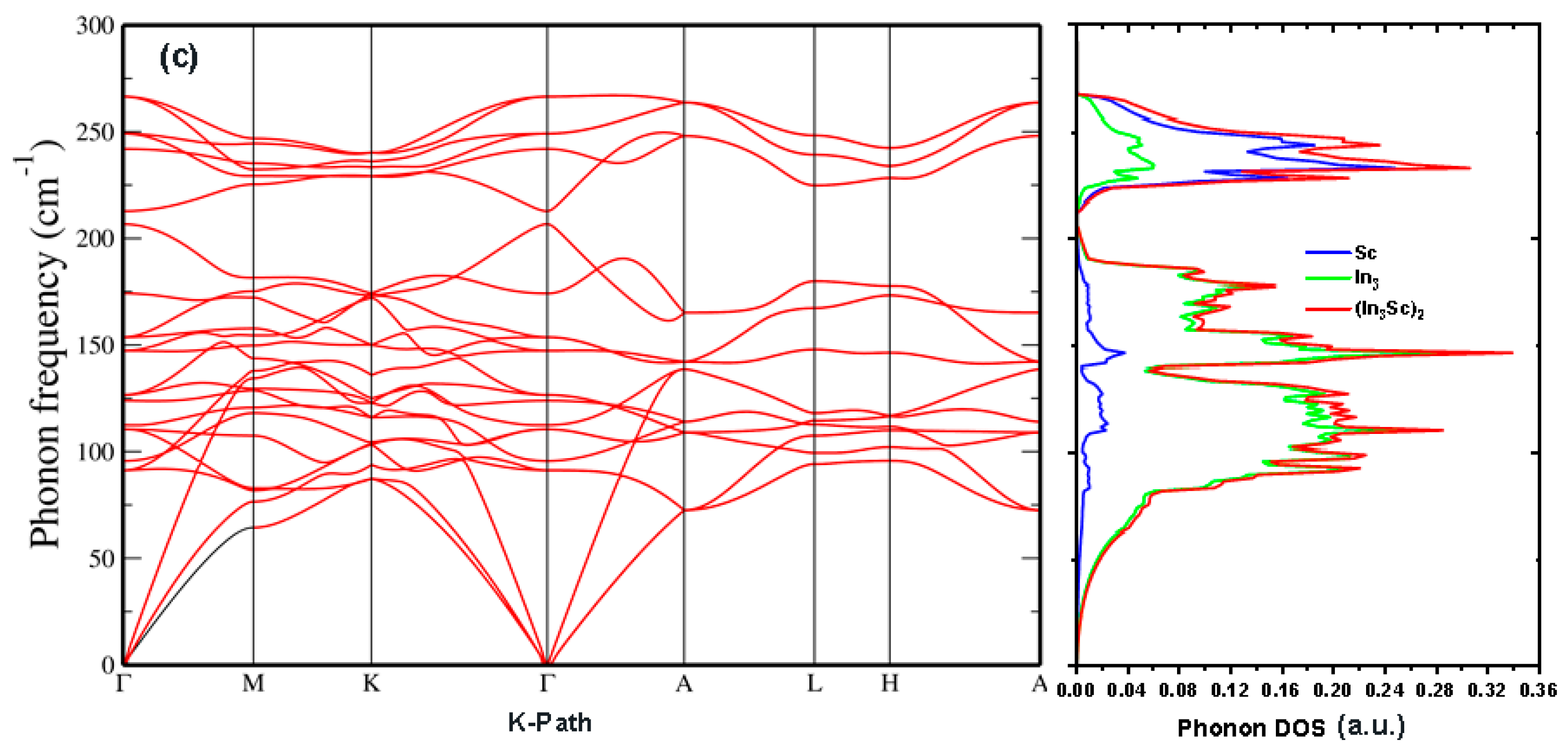
3.8. Phonon Stability and Pressure Evolution

Figure 6a–c presents the phonon spectra for cubic (SG 221), tetragonal (SG 139), and hexagonal (SG 194) phases of In₃Sc at high pressure, while (Figure 7) and (

Table 6. Phonon frequencies and their pressure evolution for the AuCu₃-type (cubic, SG 221) structure of In₃Sc.

Modes	Frequency (ω0 in cm−1)	dω/dp [cm−1·GPa−1]	d2ω/dp2 [cm−1·GPa−2]	Grüneisen Parameter (γ)
T2u	96.700 89.462 [46]	1.43508	−0.0079	0.9074
T1u	126.580 104.639 [46]	1.86806	−0.00465	0.9024
T1u	204.846 181.826 [46]	3.07214	−0.00807	0.9170

,

Table 7. Phonon frequencies and their pressure evolution for the Al₃Ti-type (tetragonal, SG 139) structure of In₃Sc.

Modes	Frequency (ω0 in cm−1)	dω/dp [cm−1·GPa−1]	d2ω/dp2 [cm−1·GPa−1] × 10−3	Grüneisen Parameter (γ)
Eu	87.306	1.861	−8.69	1.329
B1g	89.806	1.642	−7.4	1.141
A2u	86.819	2.270	−11.39	1.631
Eg	138.496	2.539	−11.04	1.4
A2u	180.954	3.837	−17.96	1.322
Eu	196.616	3.6467	−17.38	1.157

and

Table 8. Phonon frequencies and their pressure evolution for the Ni₃Sn-type (hexagonal, SG 194) structure of In₃Sc.

Modes	Frequency (ω0 in cm−1)	dω/dp [cm−1·GPa−1]	d2ω/dp2[cm−1·GPa−2] × 10−3	Grüneisen Parameter (γ)
Infrared modes
E1u	117.575	1.58349	−3.28	0.820
A2u	161.903	2.79616	6.9	1.052
E1u	196.631	2.85516	−3.35	0.884
Silent modes
B2g	76.010	1.790	−4.28	1.434
A2g	76.535	0.914	−2.74	0.727
B2u	98.542	1.625	−3.37	0.823
E2u	122.481	1.106	−3.81	0.807
B1u	135.017	2.106	−5.06	0.950
B2g	186.626	2.972	−6.92	0.970
Raman modes
E2g	72.545	0.895	−2.26	0.752
E1g	86.723	1.132	−2.86	0.795
E2g	100.330	1.330	−3.33	0.807
A1g	159.935	2.263	−5.17	0.862
E2g	211.158	3.021	−7.71	0.871

) quantify the pressure evolution of individual phonon modes. A consistent feature across all phases is the absence of imaginary frequencies in the calculated dispersions, demonstrating that each structure is dynamically stable at very high compression (177.5 GPa for cubic, 17.7 GPa for tetragonal, and 16.9 GPa for hexagonal). Phonon gaps in the AuCu₃- and TiAl₃-type structures of In3Sc result from In and Sc mass differences and stronger ionicity, which split vibrational modes. In contrast, the Ni₃Sn-type structure, which has a different coordination number and weaker ionicity, exhibits a dispersion with a small gap.

In the cubic phase (SG 221), (Table 6) shows that infrared-active T₂u and T₁u modes stiffen linearly with pressure (dω/dp = 1.4–3.1 cm⁻¹/GPa, γ ≈ 0.9). Figure 7 confirms this trend, with all optic branches shifting to higher frequencies under compression. Interestingly, the Born criteria analysis indicated a shear-driven instability at ~52 GPa (violation of M2), yet the phonon spectrum at 177.5 GPa (Figure 6a) remains fully stable. This apparent discrepancy reflects the different sensitivities of elastic versus phonon probes: Born criteria test long-wavelength shear compliance, whereas phonon calculations assess harmonic stability across the entire Brillouin zone. The re-hardening of optic modes at very high compression suggests that short-range repulsion and orbital overlap restore lattice rigidity beyond the softening window, leading to re-entrant dynamical stability.

The tetragonal phase (SG 139) exhibits the strongest phonon hardening with pressure. As shown in Table 7, A₂u and Eu modes have large pressure slopes (up to 3.8 cm⁻¹/GPa) and high Grüneisen parameters (γ ≈ 1.3–1.6), indicating strong anharmonic sensitivity to compression. Figure 6b confirms the absence of imaginary phonons at 17.7 GPa, while (Figure 7) shows steady stiffening across all Raman- and IR-active branches. Physically, this reflects the anisotropic bonding of the tetragonal lattice: in-plane and out-of-plane vibrations stiffen at different rates, but both remain dynamically stable. Together with the elastic results, these phonon spectra confirm that the tetragonal phase is a robust high-pressure polymorph stabilized by enhanced orbital overlap along the c-axis.

The hexagonal phase (SG194) shows a more complex vibrational response. Table 8 reveals that Raman-active E₂g and A₁g modes have moderate slopes (dω/dp ≈ 0.9–2.3 cm⁻¹/GPa), while some silent modes, such as B₂g, exhibit stronger pressure dependence (≈3.0 cm⁻¹/GPa). Grüneisen parameters span a broad range (0.72–1.43), reflecting a mixture of stiff and relatively soft vibrational channels. Elastic stability analysis predicted a collapse of H₁ and H₂ around 30 GPa due to basal-plane shear softening. However, the phonon dispersion at 16.9 GPa (Figure 6c) shows no imaginary frequencies, and (Figure 7) confirms that all branches stiffen under pressure. This indicates that the hexagonal lattice undergoes a softening–recovery cycle: shear instabilities emerge in an intermediate window but are suppressed at extreme compression by strong short-range interactions. Thus, the hexagonal phase is dynamically stable at high pressure, though more pressure-sensitive than the tetragonal form.

The present study provides a comprehensive assessment of the polymorphic forms of In₃Sc, elucidating their potential structural and technological applications. The AuCu₃-type cubic phase (Pm$\overline{3}$m) exhibits high stability, isotropic compressibility, positive Cauchy pressure, and significant ductility (B/G > 1.75), indicating suitability for mechanically robust and electrically conductive applications, such as interconnects and contacts. The tetragonal Al₃Ti-type phase, despite slight brittleness (negative Cauchy pressure, B/G < 1.75), demonstrates elevated fracture toughness and high shear and Young’s moduli, rendering it appropriate for load-bearing components requiring resistance to crack propagation. The hexagonal Ni₃Sn-type phase features anisotropic compressibility, moderate ductility, and layered conduction pathways, suggesting applicability in pressure-sensitive electronics or components with direction-dependent transport properties. The BiF₃-type cubic phase, although mechanically softer, retains high ductility and metallic character, potentially serving in low-stress, high-conductivity environments or as a precursor for pressure-induced phase transformations. Furthermore, pressure-dependent analyses indicate that specific polymorphs can be stabilized or tuned, enabling controlled modulation of electronic and mechanical behavior. Collectively, these findings underscore the versatility of In₃Sc and provide a foundation for the design of phases with tailored mechanical, electronic, and functional properties.

4. Conclusions

In conclusion, this investigation provides a comprehensive assessment of the structural, mechanical, vibrational, and electronic properties of In₃Sc across four prototype phases—Cu₃Au (Pm$\overline{3}$m), Al₃Ti (I4/mmm), Ni₃Sn (P6₃/mmc), and BiF₃ (Fm$\overline{3}$m)—under varying hydrostatic pressures. The energy–volume and enthalpy–pressure analyses demonstrate that the cubic Cu₃Au-type phase is the ground-state configuration at ambient conditions, with the tetragonal Al₃Ti-type phase nearly degenerate in energy, indicating possible coexistence or pressure-induced transformation pathways.

Elastic constant calculations reveal the pressure ranges of mechanical stability, with the cubic phase stable up to ~50 GPa before shear-driven instabilities emerge, the tetragonal phase stabilized above ~25 GPa by enhanced interlayer bonding, and the hexagonal phase displaying pressure-sensitive anisotropy with eventual shear softening.

Phonon dispersion analyses confirm the dynamical stability of the cubic, tetragonal, and hexagonal phases at high pressure, even beyond the elastic instability thresholds, highlighting the nontrivial role of lattice dynamics in stabilizing these polymorphs. The evolution of Raman-, infrared-, and silent-active modes further elucidates the interplay between symmetry, pressure, and vibrational behavior, consistent with positive Grüneisen parameters and pressure-induced phonon stiffening. Finally, the electronic band structures and DOS calculations show that all phases retain metallic character, with Sc-3d and In-5p hybridization dominating near the Fermi level, but with marked differences in anisotropy and carrier localization, especially in the tetragonal and hexagonal structures. Taken together, these results establish In₃Sc as a highly versatile compound with competing polymorphs whose relative stability and physical properties are strongly pressure-dependent, offering valuable insights into phase competition, elastic softening, and electronic anisotropy in rare-earth intermetallics.