Crystal Plasticity Modeling of Mechanical Anisotropy for TiAl Alloy Under Uniaxial and Biaxial Loading
Abstract
1. Introduction
2. Constitutive Model
2.1. Finite Strain Crystal Plasticity Theory
2.2. Linear Transformation-Based Anisotropic Yield Criterion
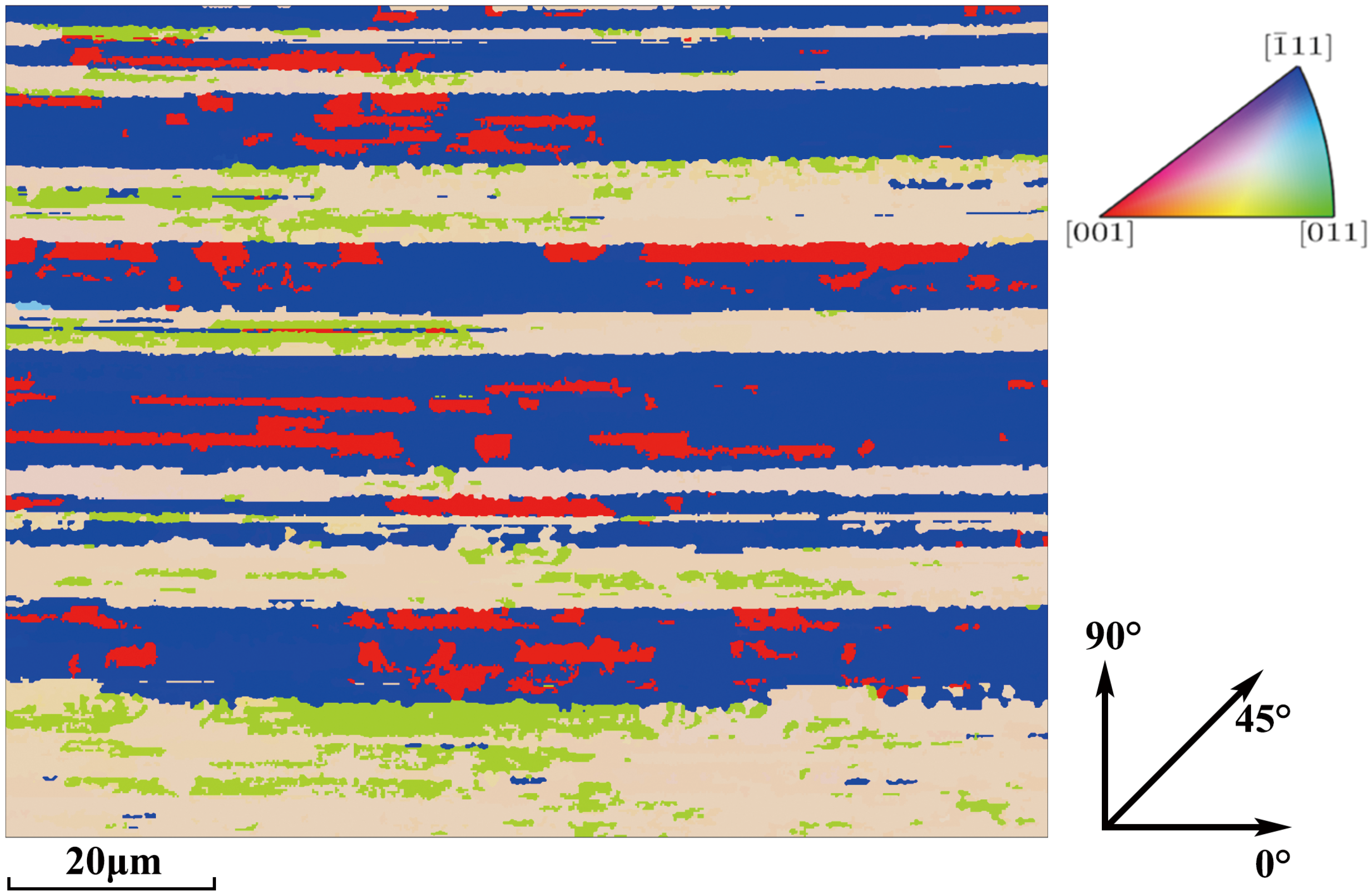
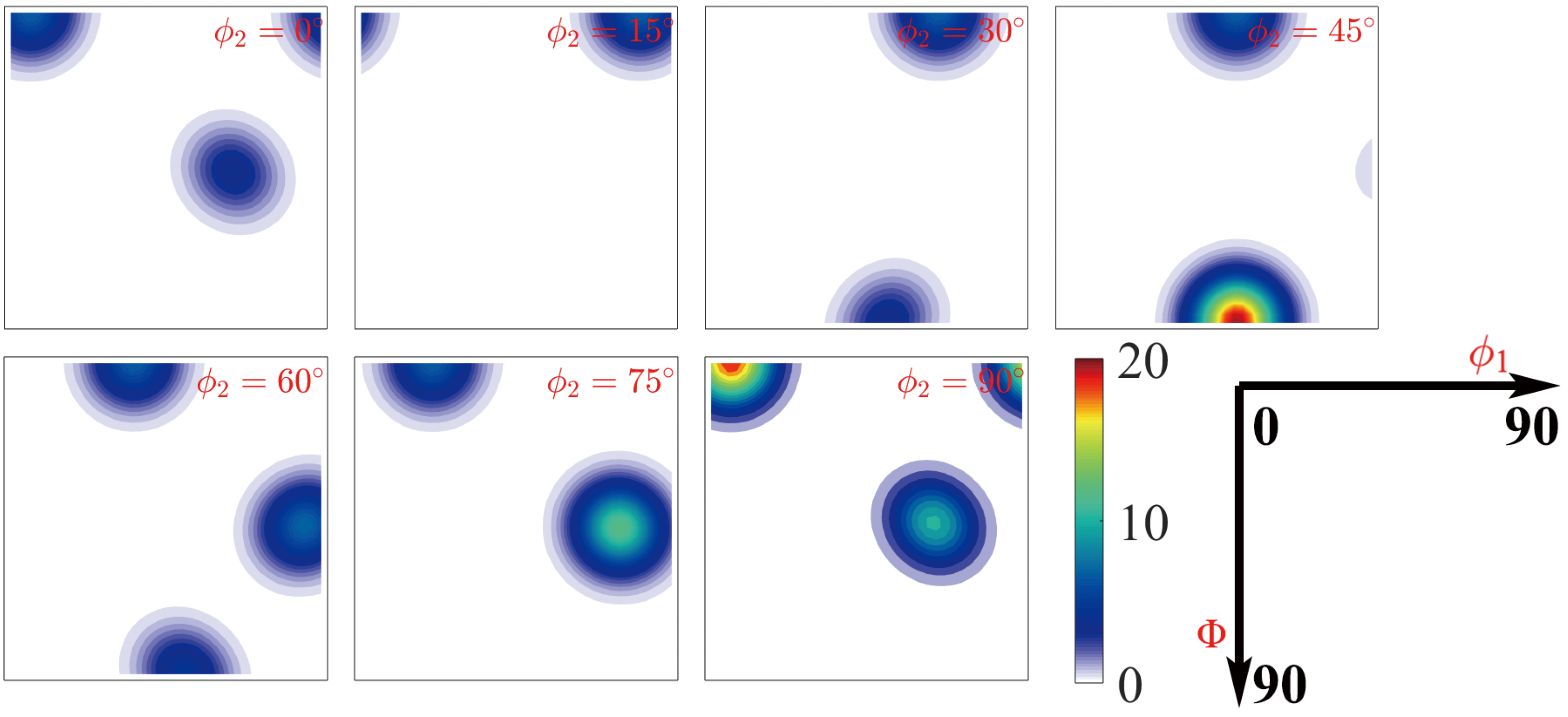
3. Microstructure of TiAl Alloy
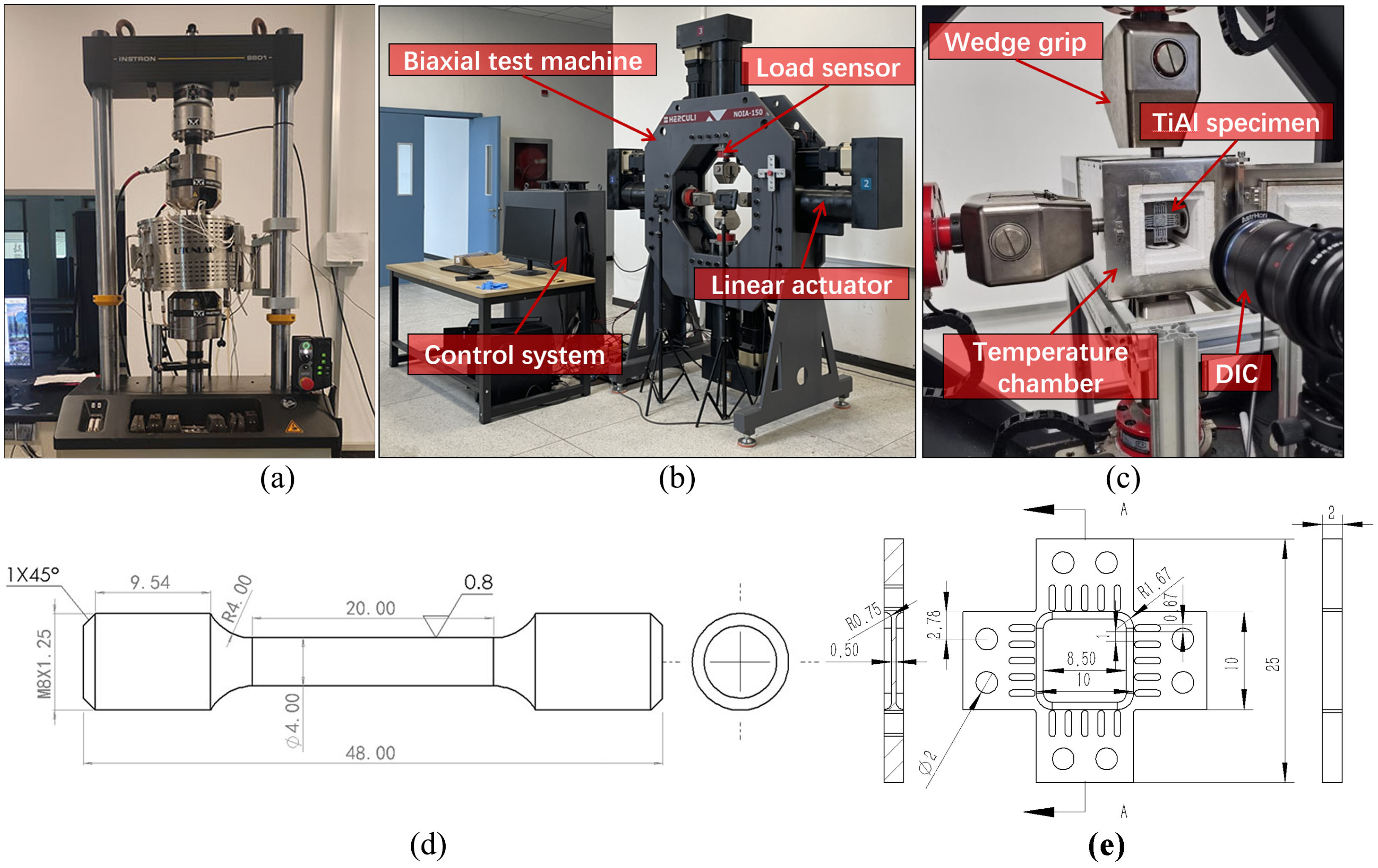
4. Experimental Uniaxial and Biaxial Test of TiAl Alloy
5. Results and Discussion
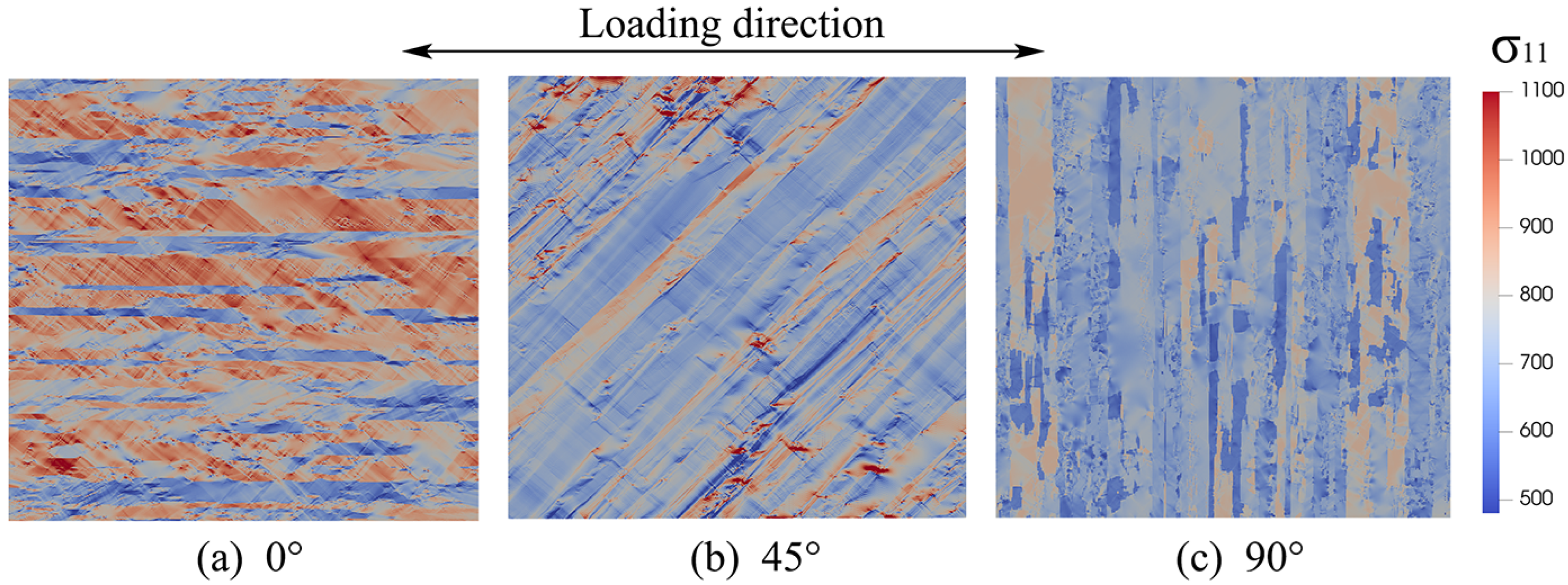
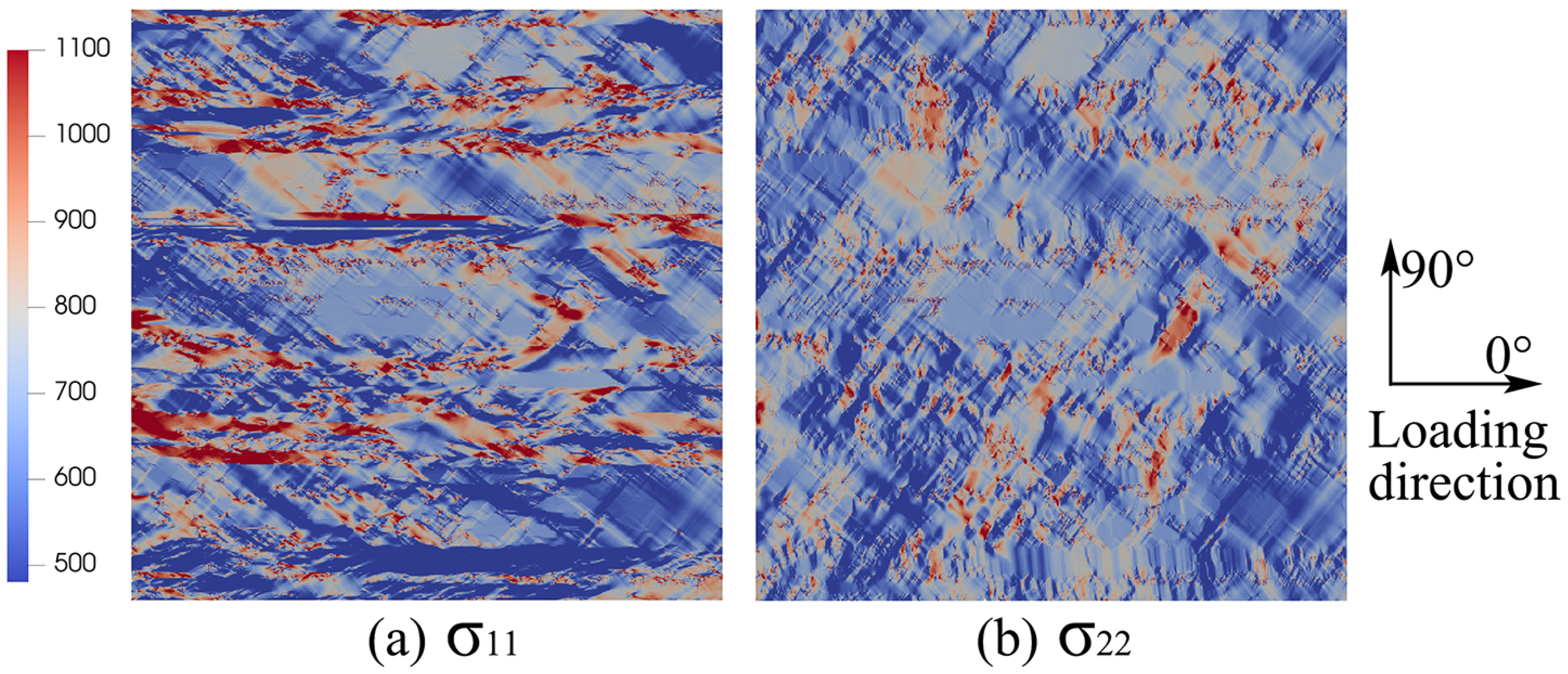
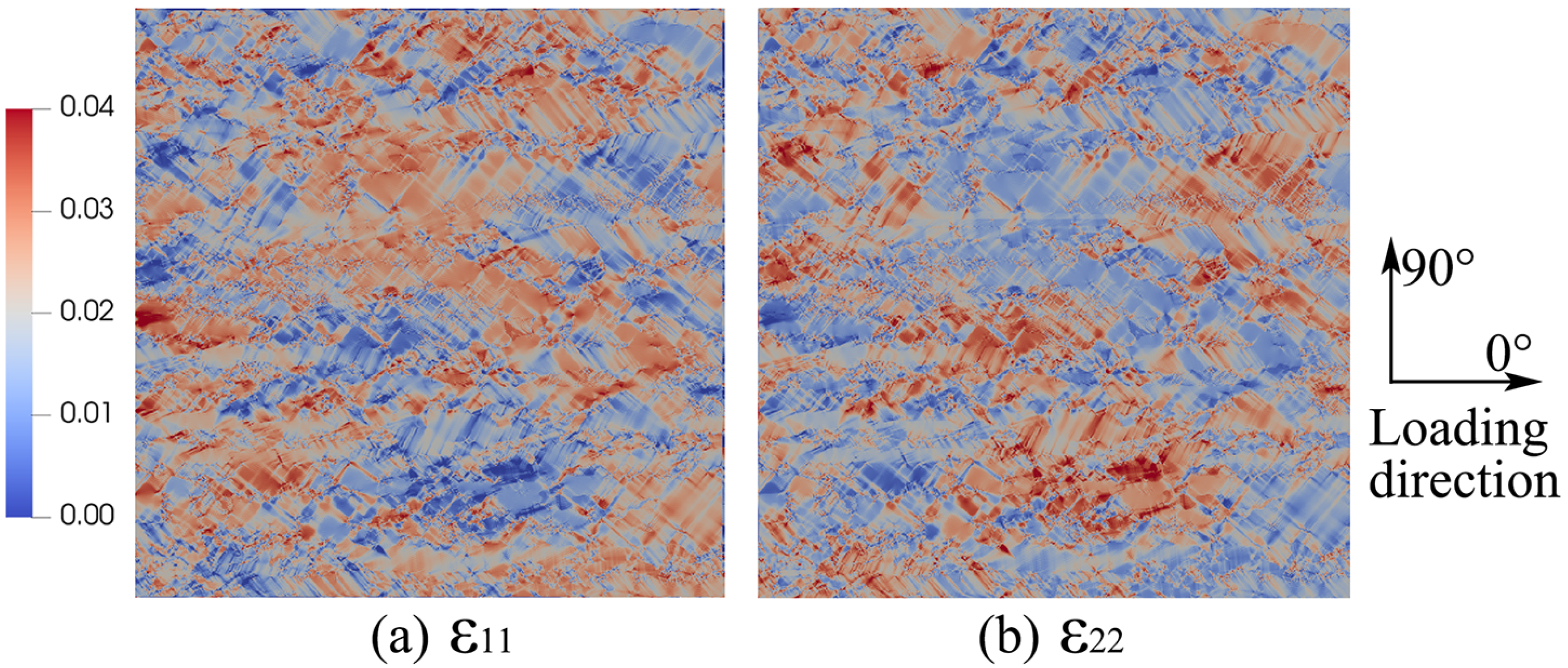
5.1. Full-Field CP Modeling in Various Stress States
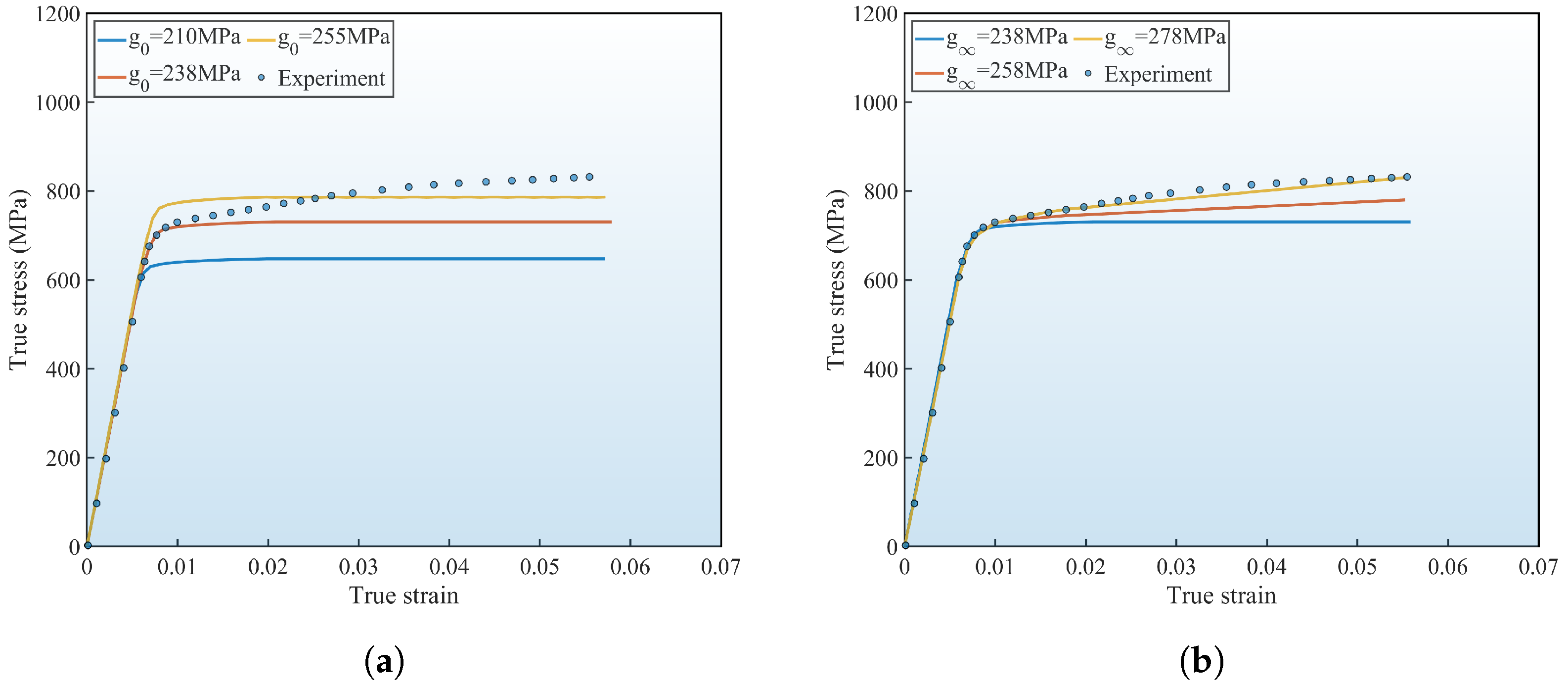
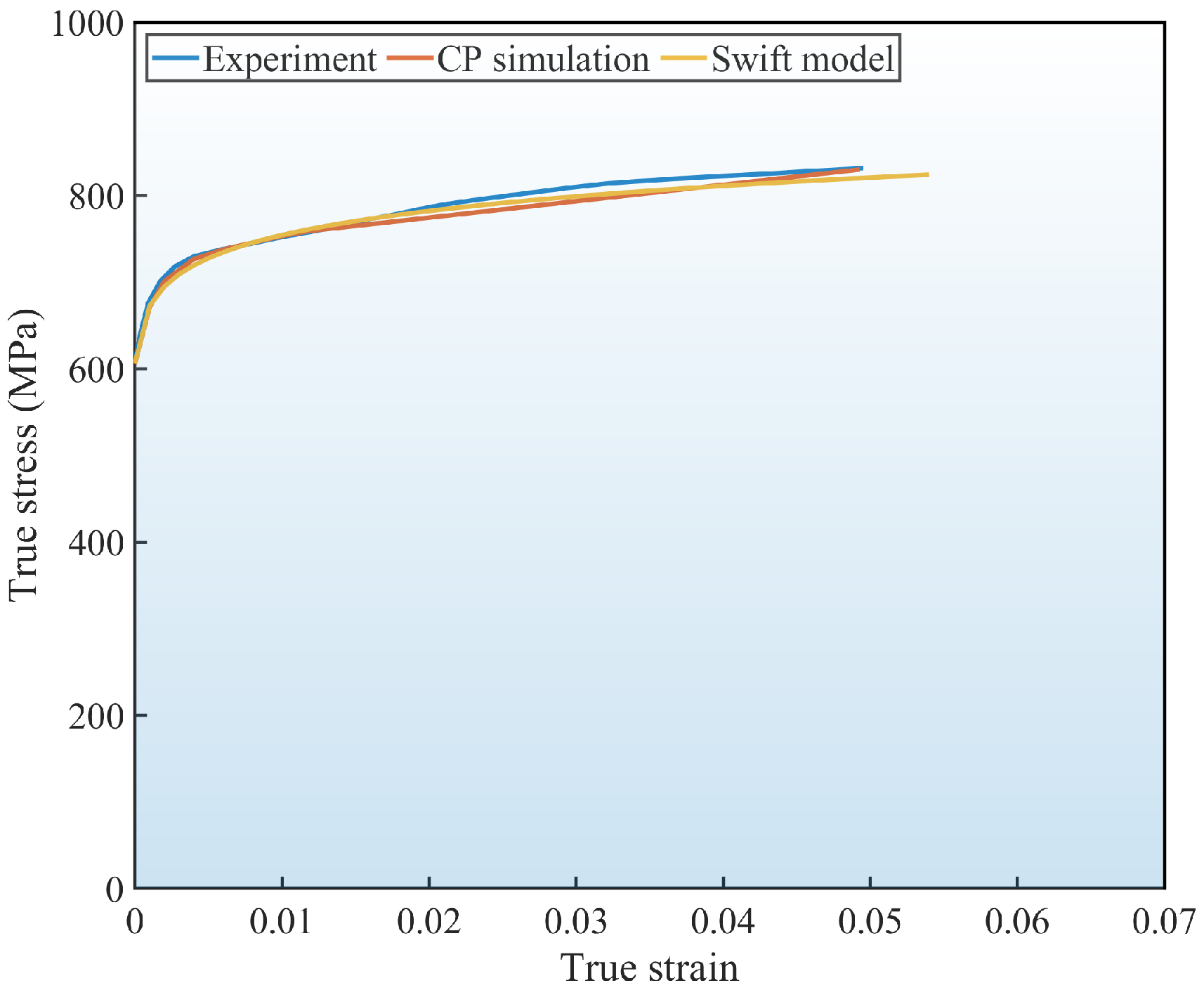
5.2. Calibration of Anisotropic Constitutive Model
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tetsui, T. Identifying low-cost, machinable, impact-resistant TiAl alloys suitable for last-stage turbine blades of jet engines. Intermetallics 2024, 168, 108263. [Google Scholar] [CrossRef]
- Han, D.; Pan, Y.; Niu, Y.; Chen, Y.; Qi, Z.; Pan, X.; Zheng, X.; Chen, G. Isothermal oxidation resistance and microstructure evolution of VPS-TiAlCrY coating on TiAl single crystals at 1100–1200 °C. Corros. Sci. 2022, 208, 110664. [Google Scholar] [CrossRef]
- Zheng, M.; Dai, X.; Qu, D.; Lu, Q.; Chen, W.; Wei, X.; Luo, D.; Zhu, Z. Impact of phase/grain boundary on tensile properties and dynamic deformation mechanisms of duplex fully lamellar TiAl polycrystalline. J. Alloys Compd. 2025, 1039, 183111. [Google Scholar] [CrossRef]
- Tang, J.; Cheng, X.; Sun, Y.; Zhang, Y.; Liu, B.; Zhu, Y. Microstructure and mechanical properties of TC11-TiAl three-dimensional heterogeneous material fabricated by laser directed energy deposition. Mater. Lett. 2025, 402, 139342. [Google Scholar] [CrossRef]
- Wei, Y.; Miao, B.; Shu, S.; Yang, H.; Zhong, X.; Dong, B.; Chen, L.; Qiu, F.; Jiang, Q. Development and future of TiAl composites – microstructural characteristics and high-temperature service performance. J. Mater. Res. Technol. 2025, 38, 651–673. [Google Scholar] [CrossRef]
- Nath, P.; Bar, H.N.; Bhattacharjee, A.; Sen, I. Designing of novel microstructure and its impact on the improved service temperature mechanical performance of 2nd and 3rd generation advanced intermetallic TiAl alloys. Mater. Sci. Eng. A 2024, 893, 146108. [Google Scholar] [CrossRef]
- Zhu, Y.; Yi, M.; Guo, W. Pseudo-twin boundary improves flow stress and cyclic stability of TiAl single crystal. Int. J. Plast. 2024, 179, 104021. [Google Scholar] [CrossRef]
- Tetsui, T.; Lee, Y.Y.; Vaubois, T.; Sallot, P. Effects of Composition on Melt Fillability and Impact Resistance of TiAl Alloys for Thin-Blade Turbine Wheels: Laboratory Predictions and Product Verification. Metals 2025, 15, 474. [Google Scholar] [CrossRef]
- Han, D.; Tong, Z.; Pan, X.; Jin, Z.; Sun, T.; Shen, Y.; Niu, Y. Oxidation and thermal shock resistance of TiAlCrY/YSZ thermal barrier coating on single-crystal TiAl alloys. J. Mater. Res. Technol. 2025, 35, 4859–4869. [Google Scholar] [CrossRef]
- Hao, J.; Qian, K.; Li, X.; Xue, P.; Shu, L.; Chen, B.; Liu, K. Thermomechanical characterization and conventional rolling of a novel b-solidifying y-TiAl alloy with excellent comprehensive properties. J. Mater. Res. Technol. 2023, 26, 18. [Google Scholar] [CrossRef]
- Huang, D.; Tan, Q.; Zhou, Y.; Yin, Y.; Wang, F.; Wu, T.; Yang, X.; Fan, Z.; Liu, Y.; Zhang, J.; et al. The significant impact of grain refiner on γ-TiAl intermetallic fabricated by laser-based additive manufacturing. Addit. Manuf. 2021, 46, 102172. [Google Scholar] [CrossRef]
- Wang, Y.; Li, S.; Ma, T.; Wang, X.; Li, Q.; Wang, Y.; Fang, H.; Chen, R. In-situ synthesized Ti5Si3-Ti2AlC reinforced TiAl composite with enhanced tribological properties. Intermetallics 2025, 185, 108880. [Google Scholar] [CrossRef]
- Sun, Y.; Chen, F.; Qian, S.; Wang, N.; Ding, J.; Chang, H.; Chen, X.; Zhou, L. Microstructure evolution mechanism of Fe microalloying high Nb–TiAl alloy fabricated by HIP. J. Mater. Res. Technol. 2025, 36, 1273–1282. [Google Scholar] [CrossRef]
- Kwak, S.; Kim, J.; Ding, H.; Xu, X.; Chen, R.; Guo, J.; Fu, H. Machine learning prediction of the mechanical properties of γ-TiAl alloys produced using random forest regression model. J. Mater. Res. Technol. 2022, 18, 520–530. [Google Scholar] [CrossRef]
- Chen, G.; Peng, Y.; Zheng, G.; Qi, Z.; Wang, M.; Yu, H.; Dong, C.; Liu, C.T. Polysynthetic twinned TiAl single crystals for high-temperature applications. Nat. Mater. 2016, 15, 876–881. [Google Scholar] [CrossRef] [PubMed]
- Genc, O.; Unal, R. Development of gamma titanium aluminide (γ-TiAl) alloys: A review. J. Alloys Compd. 2022, 929, 167262. [Google Scholar] [CrossRef]
- Chen, Y.; Cao, Y.; Qi, Z.; Chen, G. Increasing high-temperature fatigue resistance of polysynthetic twinned TiAl single crystal by plastic strain delocalization. J. Mater. Sci. Technol. 2021, 93, 53–59. [Google Scholar] [CrossRef]
- Liu, S.; Ding, H.; Chen, R.; Guo, J.; Fu, H. Substantial 〈101] superlattice dislocations and nanotwins achieved without deformation in a casting Cr-rich TiAl-based alloy after a normalizing treatment. Mater. Lett. 2025, 398, 138937. [Google Scholar] [CrossRef]
- Chen, Z.; Sun, M.; Liu, H.; Nie, X.; Wang, M.; Zhao, C.; Li, L.; Pan, J.; Li, N. Vibration-enhanced hot workability of TiAl alloy induced by the motion of 1/2 < 112] superdislocations. Acta Mater. 2025, 296, 121191. [Google Scholar] [CrossRef]
- Xiang, H.; Guo, W. Synergistic effects of twin boundary and phase boundary for enhancing ultimate strength and ductility of lamellar TiAl single crystals. Int. J. Plast. 2022, 150, 103197. [Google Scholar] [CrossRef]
- Wen, Y.; Jin, C.; Yu, Y.; Zeng, X.; Lai, Z.; Xiong, K.; Liu, L. A Theoretical Study of Ordinary Dislocations and Order Twinning in y-TiAl at Finite Temperatures. Metals 2025, 15, 495. [Google Scholar] [CrossRef]
- Liu, W.; Huang, J.; Pang, Y.; Zhu, K.; Li, S.; Ma, J. Multi-scale modelling of evolving plastic anisotropy during Al-alloy sheet forming. Int. J. Mech. Sci. 2023, 247, 108168. [Google Scholar] [CrossRef]
- Liu, J.; Wang, Z.; Li, P.; Zhang, Z.; Zhao, C.; Zhao, Y.; Zhang, Y.; Liang, Y.; Lin, J. Fabrication of high strength TiAl alloy with nano-lamellar and ultra-fine-grained microstructure by selective electron beam melting. J. Mater. Res. Technol. 2025, 35, 7156–7166. [Google Scholar] [CrossRef]
- Zhang, X.; Tang, B.; Wei, B.; Chen, X.; Dai, J.; Pan, X.; Li, J. A new developed Re-containing β-solidified TiAl alloy with superior strength and plasticity at 800 °C. Mater. Charact. 2025, 227, 115314. [Google Scholar] [CrossRef]
- Liu, W.; Liu, J.; Li, X.; Huang, J.; Chen, Y.; Li, Y.; Ma, J.; Cui, H. Anisotropic elastoplasticity and fracture of SCFR-PEEK composites in complex biaxial loading: Experiments and modelling. Compos. Sci. Technol. 2024, 251, 110569. [Google Scholar] [CrossRef]
- Liu, W.; Li, X.; Liu, M.; Cui, H.; Huang, J.; Pang, Y.; Ma, J. Virtual laboratory enabled constitutive modelling of dual phase steels. Int. J. Plast. 2024, 175, 103930. [Google Scholar] [CrossRef]
- Li, R.; Song, X.; Duan, Z.; Hao, Z.; Yang, Y.; Han, Y.; Ran, X.; Liu, Y. Improving the high-temperature ductility of γ-TiAl matrix composites by incorporation of AlCoCrFeNi high entropy alloy particles. J. Alloys Compd. 2025, 1012, 178515. [Google Scholar] [CrossRef]
- Zheng, M.; Zhao, H.; Liu, C.; Wu, J.; Kang, X.; Pu, Z. Simultaneously optimization of microstructure and high-temperature tensile property for TiAl-based composites through Nb step milling and sintering. J. Alloys Compd. 2025, 1020, 179388. [Google Scholar] [CrossRef]
- Brotzu, A.; Felli, F.; Marra, F.; Pilone, D.; Pulci, G. Mechanical properties of a TiAl-based alloy at room and high temperatures. Mater. Sci. Technol. 2018, 34, 1847–1853. [Google Scholar] [CrossRef]
- Barlat, F.; Aretz, H.; Yoon, J.; Karabin, M.; Brem, J.; Dick, R. Linear transfomation-based anisotropic yield functions. Int. J. Plast. 2005, 21, 1009–1039. [Google Scholar] [CrossRef]
- Liu, W.; Huang, J.; Liu, J.; Wu, X.; Zhang, K.; Huang, A. Experimental and crystal plasticity modelling study on the crack initiation in micro-texture regions of Ti-6Al-4V during high cycle fatigue tests. Int. J. Fatigue 2021, 148, 106203. [Google Scholar] [CrossRef]
- Roters, F.; Diehl, M.; Shanthraj, P.; Eisenlohr, P.; Reuber, C.; Wong, S.; Maiti, T.; Ebrahimi, A.; Hochrainer, T.; Fabritius, H.O.; et al. DAMASK—The Düsseldorf Advanced Material Simulation Kit for modeling multi-physics crystal plasticity, thermal, and damage phenomena from the single crystal up to the component scale. Comput. Mater. Sci. 2019, 158, 420–478. [Google Scholar] [CrossRef]





| m | a | q | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 135 GPa | 78 GPa | 40 GPa | 0.001 s−1 | 1180 MPa | 238 MPa | 273 MPa | 0.02 | 2.0 | 1.4 |
| E (GPa) | (MPa) | n | ||
|---|---|---|---|---|
| 138 | 0.33 | 960.94 | 0.00016 | 0.0528 |
| 1.203214 | 0.946614 | 0.742104 | 1.000489 | 0.688325 | −0.555611 | 0.903064 | −4.301936 | 0.1405193 |
| 0.750400 | 0.268975 | 0.113808 | −0.434232 | 1.302895 | 1.496341 | 1.320048 | 4.045338 | 0.046845 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, W.; Zhao, C.; Leng, K.; Jiang, K.; Meng, W.; Ding, B.; Meng, Q.; Liu, W. Crystal Plasticity Modeling of Mechanical Anisotropy for TiAl Alloy Under Uniaxial and Biaxial Loading. Crystals 2025, 15, 943. https://doi.org/10.3390/cryst15110943
Peng W, Zhao C, Leng K, Jiang K, Meng W, Ding B, Meng Q, Liu W. Crystal Plasticity Modeling of Mechanical Anisotropy for TiAl Alloy Under Uniaxial and Biaxial Loading. Crystals. 2025; 15(11):943. https://doi.org/10.3390/cryst15110943
Chicago/Turabian StylePeng, Wenya, Chunling Zhao, Kun Leng, Kanghe Jiang, Weihua Meng, Bin Ding, Qinghu Meng, and Wencheng Liu. 2025. "Crystal Plasticity Modeling of Mechanical Anisotropy for TiAl Alloy Under Uniaxial and Biaxial Loading" Crystals 15, no. 11: 943. https://doi.org/10.3390/cryst15110943
APA StylePeng, W., Zhao, C., Leng, K., Jiang, K., Meng, W., Ding, B., Meng, Q., & Liu, W. (2025). Crystal Plasticity Modeling of Mechanical Anisotropy for TiAl Alloy Under Uniaxial and Biaxial Loading. Crystals, 15(11), 943. https://doi.org/10.3390/cryst15110943





