Thermal Stress Effects on Band Structures in Elastic Metamaterial Lattices for Low-Frequency Vibration Control in Space Antennas

Abstract

This paper theoretically and numerically investigates temperature-dependent band structures in elastic metamaterial lattices using a plane wave expansion method incorporating thermal effects. We first analyze a one-dimensional (1D) elastic metamaterials beam, demonstrating that band frequencies decrease with rising temperature and increase with cooling. Then, the method is extended to square and rectangular 2D lattices, where temperature variations show remarkable influence on individual bands; while all bands shift to higher frequencies monotonically with cooling, their rates of change diminish asymptotically as they approach characteristic limiting values. Band structure predictions are validated against frequency response simulations of finite-structure. We further characterize temperature dependence of bands and bandgap widths, and quantify thermal sensitivity for the first four bands. These findings establish passive, robust thermal tuning strategies for ultralow frequency vibration suppression, offering new design routes for space-deployed lattice structures.

1. Introduction

Space antennas are trending to larger sizes, lighter mass, and greater structural flexibility [1,2]. Lattice-based designs are widely adopted in aerospace applications due to their low weight, modularity, and high stability [3]. However, these structures often suffer from low natural frequencies, closely spaced modes, and lower damping, making them sensitive to low-frequency vibrations (lower than 20 Hz) under both external and internal disturbances [3,4,5]. Such vibrations are difficult to suppress and can degrade the performance of precision instruments, interfere with spacecraft attitude control, and, in severe cases, lead to structural instability.

Thermal effects are among the primary vibration sources in orbit. As spacecraft repeatedly pass through sunlight and shadow, structures experience rapid and uneven temperature changes, leading to thermal expansion and contraction. Due to mechanical constraints, these thermal deformations induce internal stress [6,7,8], which can drive transient thermal shock in extreme conditions. Addressing these issues requires both accurate modeling and effective vibration control. On one hand, thermoelastic dynamic models are essential to predict temperature-dependent stress distributions and deformation, enabling designers to evaluate vibration risks during thermal transients. On the other hand, various control strategies—ranging from active methods using piezoelectric actuators [9,10,11,12] to passive isolators and dampers [13,14,15] and hybrid active–passive systems [16,17]—have been proposed. Yet, conventional approaches often struggle to suppress low-frequency vibrations efficiently or require continuous energy input [18].

Metamaterials have extensive applications in various fields, such as altering the thermal conductivity of materials [19] and suppressing vibrations. Elastic metamaterials (EMs) offer a promising alternative for passive vibration attenuation. These periodic structures can block wave propagation within specific frequency ranges, known as bandgaps [20,21,22,23,24,25]. Bandgaps arise through either Bragg scattering, effective at wavelengths comparable to the lattice scale, or local resonance, which enables suppression at much lower frequencies. By tuning geometric and material parameters, metamaterials can be designed to attenuate vibrations within targeted frequency ranges. Recent advances demonstrate EMs’ potential in vibration control [26,27,28,29], yet their performance in thermal environments—ubiquitous in space—remains less explored.

There are two primary mechanisms for how thermal effects alter band structures. First, temperature-dependent material properties lead to changes in stiffness and density, shifting the locations of bandgaps. Research on quartz-based [30], ferroelectric ceramic/epoxy composites [31,32,33,34,35] and shellular metamaterials [36] have shown that even moderate temperature variations can significantly alter bandgap frequencies. Second, thermal stress arising from non-uniform temperature fields can significantly affect vibrations and waves propagation. These stresses are typically evaluated by solving the heat conduction equation to obtain the transient temperature field, followed by thermoelastic analysis to determine the resulting internal stress. Such stress will reduce the structural stiffness, shifting the origin bandgaps [37,38,39,40,41,42,43,44].

Despite these advances, the effect of thermal stress on band structures in EM lattices for low-frequency vibration control remains unexplored, limiting their application in space antennas. Here, we present a combined theoretical and numerical study of how thermal stress affects the band structures of two-dimensional (2D) EM lattices under space-relevant conditions. We first develop a temperature-dependent plane wave expansion method (PWEM) to predict band diagrams under thermal loading. The PWEM is an effective approach for calculating the band structure of phononic crystals, which has been developed for elastic metamaterials in the form of beams, half-spaces, and plates (thin and thick) to support the propagation of bending waves, torsional waves, dilatational waves, surface waves, flexural waves, and generalized Lamb waves [45,46,47,48]. To validate this method, we apply it to a 1D EM beam and find excellent agreement between PWEM results and frequency responses. We then extend the framework to 2D square and rectangular lattices, specifically modeling the tensile stress induced by decreasing temperature. Comparison with finite element frequency scans confirms the model’s accuracy across lattice geometries. Finally, we analyze the temperature sensitivity of the band structures and identify the lowest branch as the most responsive to temperature. These results establish a foundation for designing low frequency vibration suppression schemes in space deployed antenna structures with thermal stress.

2. Geometries and Materials

In space antennas, there are various types of lattices. Here, we investigate three EM geometries: a 1D beam, a 2D square lattice, and a 2D rectangular lattice. The 1D beam unit cell [Figure 1a] is a rectangular segment split into two materials, which repeat axially to form the beam. The unit cell is shown in Figure 1d, which has a lattice constant of 40 cm, with a thickness and width of 1 cm. The material on the left spanning 25 cm is Aluminum, while the material on the right spanning 15 cm is Silicone Rubber. The Aluminum and Silicone Rubber components are marked in red and blue, respectively. Its first Brillouin zone is shown in Figure 1g. Detailed material properties and geometric parameters are provided in

Table 1. Material properties.

	Aluminum	Silicone Rubber
Mass density $\rho$ [kg/m3]	2799	1300
Young’s modulus $E$ [N/m2]	7.21 × 1010	1.18 × 105
Poisson ratio $\nu$	0.3	0.468
Coefficient of thermal expansion $\alpha$ [K−1]	21.7 × 10−6	250 × 10−6

.

The 2D square lattice uses a cruciform unit cell [Figure 1b] in which the central and upper left arms share one material, and the lower right arm a second. Figure 1e illustrates the material composition and geometric characteristics of the unit cell. The lattice constant is $a=20 \mathrm{c}\mathrm{m}$, with thickness and width denoted by $H=1 \mathrm{c}\mathrm{m}$, $l=9.5 \mathrm{c}\mathrm{m}$, and $d=1 \mathrm{c}\mathrm{m}$, respectively. Periodically arranging the unit cell along the x- and y-directions yields the lattice, with the first Brillouin zone depicted in Figure 1h.

Finally, the rectangular lattice [Figure 1c] employs a single cell of red and blue regions that repeat to form the array. As shown in Figure 1f, a rectangle with a length of $a=20 \mathrm{c}\mathrm{m}$ and a width of $b=15 \mathrm{c}\mathrm{m}$ and a cross-section of $d\times H=1 \mathrm{c}\mathrm{m}\times 1 \mathrm{c}\mathrm{m}$ for each beam. Take $l=9.5 \mathrm{c}\mathrm{m}$, $p=7 \mathrm{c}\mathrm{m}$. Its first Brillouin zone is displayed in Figure 1f.

3. One-Dimensional EM Beam

This section investigates how thermal stress affects 1D EM beams. Using PWEM, we model these systems by simplifying thermal stress into an equivalent axial force. The governing vibration equation for a functionally graded Euler–Bernoulli beam under axial loading is [49]

$$-A(x){\displaystyle \frac{{\mathsf{\partial }}^{2}u(x,t)}{\mathsf{\partial }{t}^2}}={\displaystyle \frac{{\mathsf{\partial }}^2}{\mathsf{\partial }{x}^2}}\left[B(x){\displaystyle \frac{{\mathsf{\partial }}^{2}u(x,t)}{\mathsf{\partial }{x}^2}}\right]-T(x){\displaystyle \frac{{\mathsf{\partial }}^{2}u(x,t)}{\mathsf{\partial }{x}^2}}$$

(1)

where $u(x,t)$ is the transverse displacement of the beam, and $x$ and $t$ represent the coordinate and time, respectively. $A(x)=\rho (x)S(x)$, $B(x)=E(x)I(x)$, $T(x)=\alpha E(x)S(x)\Delta T$ is a function of position coordinate, uniformly recorded as material parameters $g(x)$. $\rho (x)$ is material density, $S(x)$ is the cross-sectional area, $E(x)$ is the elastic modulus, $I(x)$ is the moment of inertia of the section, $\alpha$ is the coefficient of thermal expansion, and $\Delta T$ is the change in temperature.

According to the periodicity of Euler beams in EMs and the Floquet–Bloch theorem, the displacement of beams can be expressed as [50]

$$u(x,t)=e^{i(kx-\omega t)}{u}_k(x)$$

(2)

in which $k$ is the wave vector, $i=\sqrt{-1}$, $\omega$ is frequency, and $u_k(x)$ is a function with the same spatial periodicity as the material parameters; it can be expanded by Fourier series as

$$u_k(x)={\displaystyle \sum _{G^{\prime }}{e}^{i{G}^{\prime }x}}{u}_k(G^{\prime })$$

(3)

where $G$ is the reciprocal lattice vector.

Combining Equations (2) and (3) gives

$$u(x,t)={\displaystyle \sum _{G^{\prime }}{e}^{i[(k+G^{\prime })x-\omega t]}}{u}_k(G^{\prime })$$

(4)

The material parameters $g(x)$ can also be expanded in Fourier series as

$$g(x)={\displaystyle \sum _G{e}^{iGx}}g(G)$$

(5)

According to Fourier series theory, we can get

$$g(G)={\displaystyle \frac{1}{a}}{\displaystyle {\int }_{-\frac{a}{2}}^{-\frac{a_1}{2}}{m}_B}{e}^{-iGx}dx+{\displaystyle \frac{1}{a}}{\displaystyle {\int }_{\frac{a_1}{2}}^{\frac{a}{2}}{m}_A}{e}^{-iGx}dx+{\displaystyle \frac{1}{a}}{\displaystyle {\int }_{\frac{a_1}{2}}^{\frac{a}{2}}{m}_B}{e}^{-iGx}dx$$

(6)

By using Euler’s formula and the relation between positive lattice vector and inverse lattice vector, we can simplify Equation (6) and get

$$g(G)=\left\{\begin{array}{ll}f{g}_A+(1-f)g_B\hfill & G=0\hfill \\ f(g_A-g_B){\displaystyle \frac{\sin (G{a}_1/2)}{G{a}_1/2}}\hfill & G\ne 0\hfill \end{array}\right.$$

(7)

Substituting Equation (7) into Equation (1) yields:

$${\omega }^{2}A(G^{″}-G^{\prime })u_k(G^{\prime })=B(G^{″}-G^{\prime }){(k+G^{\prime })}^2{(k+G^{″})}^2{u}_k(G^{\prime })-T(G^{″}-G^{\prime }){(k+G^{\prime })}^2{u}_k(G^{\prime })$$

(8)

Equation (8) can be simplified as

$${\omega }^2{A}_{0}u=B_{0}u$$

(9)

We use 101 plane waves to compute the band structure, as shown in Figure 2a. To validate effectiveness of the method, we model the 1D elastic metamaterial beam in COMSOL Multiphysics 6.2 (Burlington, Massachusetts, USA), and obtain the band structure via the finite element method (FEM) [red dashed lines in Figure 2a]. The PWEM predicts band gaps at 0.30–0.75 Hz (first), 1.78–5.46 Hz (second), and 6.51–14.37 Hz (third). The FEM results show band gaps at 0.33–0.77 Hz (first), 1.85–5.31 Hz (second), and 6.40–13.32 Hz (third). The differences between our method and the FEM fall within acceptable margins of error, demonstrating strong consistency especially in the lower bands.

Next, we solved the characteristic equation under thermal gradients of $\Delta T=5 \mathrm{K}$, $\Delta T=-5 \mathrm{K}$, and $\Delta T=-10 \mathrm{K}$, obtaining the band structures in Figure 2b–d. At $\Delta T=5 \mathrm{K}$, thermal stress-induced buckling eliminates the first band entirely. Consequently, the first band gap spans 0–0.56 Hz (starting from zero frequency), widening by 0.11 Hz relative to the unstressed case. The second and third gaps shift to 1.55–5.31 Hz and 6.26–14.08 Hz, respectively. Under cooling ($\Delta T=-5 \mathrm{K}$), gaps emerge at 0.48–0.91 Hz (first), 1.99–5.70 Hz (second), and 6.76–14.66 Hz (third). At $\Delta T=-10 \mathrm{K}$, gaps further shift to 0.63–1.07 Hz (first), 2.18–5.93 Hz (second), and 6.99–14.94 Hz (third), with the first gap narrowing by 0.01 Hz and the second widening by 0.07 Hz. These modifications confirm that thermal stress actively tunes the band structure of 1D EM beams.

4. Two-Dimensional EM Lattice

As demonstrated in Section 3, compressive thermal stress induces structural instability at elevated temperatures, eliminating the first propagation band. Therefore, this section focuses on the band structure evolution of 2D EM lattices during cooling.

4.1. Two-Dimensional Square EM Lattice

This section investigates the impact of thermal stress on square 2D EM lattices. The differential equation of vibration for a 2D EM lattice is

$$\begin{array}{cc}A{\displaystyle \frac{{\mathsf{\partial }}^{2}w(\mathit{r},t)}{\mathsf{\partial }{t}^2}}& =D{\displaystyle \frac{{\mathsf{\partial }}^{4}w(\mathit{r},t)}{\mathsf{\partial }{x}^4}}+B{\displaystyle \frac{{\mathsf{\partial }}^{4}w(\mathit{r},t)}{\mathsf{\partial }{x}^2\mathsf{\partial }{y}^2}}+2\Gamma {\displaystyle \frac{{\mathsf{\partial }}^{4}w(\mathit{r},t)}{\mathsf{\partial }{x}^2\mathsf{\partial }{y}^2}}\\ & +D{\displaystyle \frac{{\mathsf{\partial }}^{2}w(\mathit{r},t)}{\mathsf{\partial }{y}^4}}+B{\displaystyle \frac{{\mathsf{\partial }}^{4}w(\mathit{r},t)}{\mathsf{\partial }{y}^2\mathsf{\partial }{x}^2}}\hfill \\ & -T_x{\displaystyle \frac{{\mathsf{\partial }}^{2}w(\mathit{r},t)}{\mathsf{\partial }{x}^2}}-T_y{\displaystyle \frac{{\mathsf{\partial }}^{2}w(\mathit{r},t)}{\mathsf{\partial }{y}^2}}\hfill \end{array}$$

(10)

in which $w(\mathit{r},t)$ denotes the out-of-plane displacement. The position vector is $\mathit{r}=x\mathit{i}+y\mathit{j}$. The elastic parameters are $A=\rho H$, $D=E{H}^3/[12(1-{\nu }^2)]$, $B=D\nu$, and $\Gamma =D(1-\nu )$. $T_x=T_y=\alpha ES\Delta T$ are axial forces in the $x$ and $y$ direction, respectively, which are related to the thermal expansion coefficient ${\alpha }_A, {\alpha }_B$ of the two materials and temperature change $\Delta T$. $H$ is the thickness of the model.

In the 2D lattice, the displacement can be expressed as [47]

$$w(\mathit{r},t)=e^{i(k\cdot \mathit{r}-\omega t)}{w}_k(\mathit{r})$$

(11)

in which $\mathit{k}$ is the wave vector of the first Brillouin zone, $\omega$ is frequency, and $w_k(\mathit{r})$ is a function with the same spatial periodicity as the material parameters; it can be expanded by Fourier series as

$$w_k(\mathit{r})={\displaystyle \sum _{{\mathit{G}}^{\prime }}{e}^{i{\mathit{G}}^{\prime }\mathit{r}}}{w}_k({\mathit{G}}^{\prime })$$

(12)

where $\mathit{G}$ is the reciprocal lattice vector.

Combining Equations (11) and (12) gives

$$w(\mathit{r},t)={\displaystyle \sum _{{\mathit{G}}^{\prime }}{e}^{i[(\mathbf{k}+{\mathit{G}}^{\prime })\cdot \mathit{r}-\omega t]}}{w}_k({\mathit{G}}^{\prime })$$

(13)

We employ PWEM to analyze 2D EMs arranged on a square lattice, which requires expressing the spatially varying material parameters as a Fourier series, with each coefficient set by the underlying lattice geometry. Accordingly, the structural function takes the form

$$P(\mathit{G})={\displaystyle \frac{1}{S}}{\displaystyle {\iint }_A{e}^{-i\mathbf{G}\cdot \mathbf{r}}}d\mathit{r}$$

(14)

Placing the origin of the coordinate at the center of the unit cell, we partition the domain into two regions—each occupied by one of the constituent materials—and integrate the structural function over these areas. In two dimensions, this can be reduced to

$$P(\mathit{G})={\displaystyle \frac{1}{S}}{\displaystyle {\iint }_A{e}^{-i(G_{x}x+G_{y}y)}}dxdy$$

(15)

After simplification, the structure function of the two regions can be obtained as

$$P_{S1}(G)=\left\{\begin{array}{ll}{\displaystyle \frac{i}{G_y{a}^2}}\left[(e^{-i{G}_{y}d}-e^{i{G}_{y}d})+2d(e^{-i{G}_y(d+l)}-e^{i{G}_{y}d})\right]\hfill & G_x=0\hfill \\ {\displaystyle \frac{i}{G_x{a}^2}}\left[2d(e^{i{G}_{x}d}-e^{i{G}_x(d+l)})+(2d+l)(e^{-i{G}_{x}d}-e^{i{G}_{x}d})\right]\hfill & G_y=0\hfill \\ \begin{array}{l}{\displaystyle \frac{-1}{G_x{G}_y{a}^2}}[(e^{i{G}_{x}d}-e^{i{G}_x(d+l)})(e^{-i{G}_{y}d}-e^{i{G}_{y}d})+\\ \hfill (e^{-i{G}_{x}d}-e^{i{G}_{x}d})(e^{-i{G}_y(d+l)}-e^{i{G}_{y}d})]\end{array}\hfill & G_x\ne 0 \mathrm{and}{G}_y\ne 0\hfill \end{array}\right.$$

(16)

$$P_{S2}(G)=\left\{\begin{array}{ll}{\displaystyle \frac{i}{G_y{a}^2}}\left[2d(e^{i{G}_{y}d}-e^{i{G}_y(d+l)})+l(e^{-i{G}_{y}d}-e^{i{G}_{y}d})\right]\hfill & G_x=0\hfill \\ {\displaystyle \frac{i}{G_x{a}^2}}\left[l(e^{-i{G}_{x}d}-e^{i{G}_{x}d})+2d(e^{-i{G}_x(d+l)}-e^{-i{G}_{x}d})\right]\hfill & G_y=0\hfill \\ \begin{array}{l}{\displaystyle \frac{-1}{G_x{G}_y{a}^2}}[(e^{-i{G}_{x}d}-e^{i{G}_{x}d})(e^{i{G}_{y}d}-e^{i{G}_y(d+l)})+\\ \hfill (e^{-i{G}_x(d+l)}-e^{-i{G}_{x}d})(e^{-i{G}_{y}d}-e^{i{G}_{y}d})]\end{array}\hfill & G_x\ne 0 \mathrm{and} G_y\ne 0\hfill \end{array}\right.$$

(17)

For an EM lattice, the material properties of the vacuum boundary can be regarded as 0. Therefore, the Fourier expansions of the materials can be written as

$$f_S(\mathit{G})=\left\{\begin{array}{ll}{F}_{SA}{f}_{SA}+F_{SB}{f}_{SB}\hfill & \mathit{G}=0\hfill \\ P_{S1}(\mathit{G})f_{SA}+P_{S2}(\mathit{G})f_{SB}\hfill & \mathit{G}\ne 0\hfill \end{array}\right.$$

(18)

where $F_{SA}=[4(dl+d^2)]/a^2$ and $F_{SB}=4dl/a^2$ are the proportions of the two materials. $f_{SA}$ and $f_{SB}$ are material properties. $P_{S1}(G)$ and $P_{S2}(G)$ are structural functions of the two materials.

Using Floquet–Bloch’s theorem and Fourier expansion, and substituting Equations (13) and (18) into Equation (10), we obtain

$$\begin{array}{cc}{\omega }^2{\displaystyle \sum _{{\mathit{G}}^{\prime }}{\mathit{A}}_{(\mathit{G}\prime \prime -{\mathit{G}}^{\prime })}}\mathit{w}({\mathit{G}}^{\prime })& ={\displaystyle \sum _{{\mathit{G}}^{\prime }}{(\mathit{k}+{\mathit{G}}^{\prime })}_x^2}{(\mathit{k}+\mathit{G}\prime \prime )}_x^2{\mathit{D}}_{(\mathit{G}\prime \prime -{\mathit{G}}^{\prime })}\mathit{w}({\mathit{G}}^{\prime })\hfill \\ & +{\displaystyle \sum _{{\mathit{G}}^{\prime }}{(\mathit{k}+{\mathit{G}}^{\prime })}_y^2}{(\mathit{k}+\mathit{G}\prime \prime )}_x^2{\mathit{B}}_{(\mathit{G}\prime \prime -{\mathit{G}}^{\prime })}\mathit{w}({\mathit{G}}^{\prime })\hfill \\ & +2{\displaystyle \sum _{{\mathit{G}}^{\prime }}{(\mathit{k}+{\mathit{G}}^{\prime })}_x}{(\mathit{k}+{\mathit{G}}^{\prime })}_y{(\mathit{k}+\mathit{G}\prime \prime )}_x{(\mathit{k}+\mathit{G}\prime \prime )}_y{\Gamma }_{(\mathit{G}\prime \prime -{\mathit{G}}^{\prime })}\mathit{w}({\mathit{G}}^{\prime })\hfill \\ & +{\displaystyle \sum _{{\mathit{G}}^{\prime }}{(\mathit{k}+{\mathit{G}}^{\prime })}_y^2}{(\mathit{k}+\mathit{G}\prime \prime )}_y^2{\mathit{D}}_{(\mathit{G}\prime \prime -{\mathit{G}}^{\prime })}\mathit{w}({\mathit{G}}^{\prime })\hfill \\ & +{\displaystyle \sum _{{\mathit{G}}^{\prime }}{(\mathit{k}+{\mathit{G}}^{\prime })}_x^2}{(\mathit{k}+\mathit{G}\prime \prime )}_y^2{\mathit{B}}_{(\mathit{G}\prime \prime -{\mathit{G}}^{\prime })}\mathit{w}({\mathit{G}}^{\prime })\hfill \\ & -{\displaystyle \sum _{{\mathit{G}}^{\prime }}{\displaystyle \sum _{\mathit{G}\prime \prime }{(\mathit{k}+{\mathit{G}}^{\prime })}_x^2{{\mathit{T}}_x}_{(\mathit{G}\prime \prime -{\mathit{G}}^{\prime })}}}\mathit{w}({\mathit{G}}^{\prime })-{\displaystyle \sum _{{\mathit{G}}^{\prime }}{\displaystyle \sum _{\mathit{G}\prime \prime }{(\mathit{k}+{\mathit{G}}^{\prime })}_y^2{{\mathit{T}}_y}_{(\mathit{G}\prime \prime -{\mathit{G}}^{\prime })}}}\mathit{w}({\mathit{G}}^{\prime })\hfill \end{array}$$

(19)

Equation (19) can be simplified as

$${\omega }^2{\mathit{A}}_1\mathit{w}={\mathit{B}}_1\mathit{w}$$

(20)

We computed the band structure using 2601 plane waves, determining eigenvalues at each wave vector to obtain the blue curve in Figure 3a. For validation, we simulated the EM lattice in COMSOL, generating the corresponding red dashed curve. The PWEM results show band gaps at 1.84–2.13 Hz (first) and 6.40–15.23 Hz (second), while the FEM results exhibit gaps at 1.43–1.74 Hz (first) and 5.53–11.46 Hz (second). We note a little discrepancy between PWEM and FEM results in the fourth band. This arises because the thin-plate assumption in the governing equation cannot accurately model higher-frequency vibrational modes. However, the excellent consistency of the first three bands between PWEM and FEM results confirms methodological efficiency in a 2D EM lattice.

We then set $\Delta T=-2\mathrm{K}$, $\Delta T=-5\mathrm{K}$, and $\Delta T=-10\mathrm{K}$, respectively, to further investigate the influence of temperature variation on the band structure evolution of the 2D square EM lattice. When $\Delta T=-2\mathrm{K}$ [Figure 3b], the first band gap ranges from 2.48 to 9.13 Hz, and the second band gap ranges from 10.38 to 10.68 Hz. Compared to the band gaps at $\Delta T=0\mathrm{K}$, the first gap is significantly expanded, whereas the second gap is notably reduced. At this temperature difference, the first gap remains between the first and second bands, while the second gap now occurs between the second and third bands. This shift arises because the first band undergoes limited change, while the second and third bands exhibit substantial modifications, leading to the opening of a band gap between the second and third bands and the closure of the gap previously existing between the third and fourth bands. Figure 3c indicates that at $\Delta T=-5\mathrm{K}$, the first band gap, located between the first and second bands, spans 2.49–12.05 Hz. The second band gap, now reappearing between the third and fourth bands, spans 15.86–19.19 Hz. This phenomenon occurs because the subsequent decrease in temperature causes the second and fourth bands to shift upwards more significantly than the third band, resulting in the closure of the band gap between the second and third bands and the re-opening of a band gap between the third and fourth bands. Finally, Figure 3d demonstrates that for $\Delta T=-10\mathrm{K}$, the first band gap (between the first and second bands) covers 2.49–13.28 Hz, and the second band gap (between the third and fourth bands) extends from 15.86 to 24.90 Hz. As the temperature decreases further, the first three bands experience a slight upward shift, whereas the fourth band shifts considerably more. Consequently, compared to the case at $\Delta T=-5\mathrm{K}$, the first band gap changes by only approximately 1 Hz, while the second band gap expands by about 6 Hz. Thus, thermal stress dynamically reconfigures both propagation bands and band gaps in EM lattices as temperature decreases. Our results demonstrate precise, stress-induced band engineering—from low-frequency gap widening to higher-frequency gap transitions—enabling active control of wave propagation in metamaterial systems.

4.2. Two-Dimensional Rectangular EM Lattice

Now, we investigate the effect of thermal stress on 2D rectangular EM lattices, which is another case in space antennas. The research method is almost the same as that of a square EM lattice. We give the structure function of an EM with rectangular grating directly as

$$P_{R1}(\mathit{G})=\left\{\begin{array}{ll}{\displaystyle \frac{i}{ab{G}_y}}\left[l\left(e^{-i{G}_{y}d}-e^{i{G}_{y}d}\right)+2d\left(e^{-i{G}_y(d+p)}-e^{i{G}_{y}d}\right)\right]\hfill & G_x=0\hfill \\ {\displaystyle \frac{i}{ab{G}_x}}\left[2d\left(e^{i{G}_{x}d}-e^{i{G}_x(d+l)}\right)+(2d+p)\left(e^{-i{G}_{x}d}-e^{i{G}_{x}d}\right)\right]\hfill & G_y=0\hfill \\ -{\displaystyle \frac{1}{ab{G}_x{G}_y}}\left[\begin{array}{l}\left(e^{-i{G}_{x}d}-e^{i{G}_{x}d}\right)\left(e^{i{G}_{y}d}-e^{i{G}_y(d+l)}\right)+\\ \left(e^{-i{G}_y(d+p)}-e^{i{G}_{y}d}\right)\left(e^{-i{G}_{x}d}-e^{i{G}_{x}d}\right)\end{array}\right]\hfill & G_x\ne 0 \mathrm{and} G_y\ne 0\hfill \end{array}\right.$$

(21)

$$P_{R2}(\mathit{G})=\left\{\begin{array}{ll}{\displaystyle \frac{i}{ab{G}_y}}\left[2d\left(e^{i{G}_{y}d}-e^{i{G}_y(d+p)}\right)+p\left(e^{-i{G}_{y}d}-e^{i{G}_{y}d}\right)\right]\hfill & G_x=0\hfill \\ {\displaystyle \frac{i}{ab{G}_x}}\left[p\left(e^{-i{G}_{x}d}-e^{i{G}_{x}d}\right)+2d\left(e^{-i{G}_x(d+l)}-e^{-i{G}_{x}d}\right)\right]\hfill & G_y=0\hfill \\ -{\displaystyle \frac{1}{ab{G}_x{G}_y}}\left[\begin{array}{l}\left(e^{-i{G}_{x}d}-e^{i{G}_{x}d}\right)\left(e^{i{G}_{y}d}-e^{i{G}_y(d+l)}\right)+\\ \left(e^{-i{G}_y(d+p)}-e^{i{G}_{y}d}\right)\left(e^{-i{G}_{x}d}-e^{i{G}_{x}d}\right)\end{array}\right]\hfill & G_x\ne 0 \mathrm{and} G_y\ne 0\hfill \end{array}\right.$$

(22)

For rectangular EM lattices,

$$f_R(\mathit{G})=\left\{\begin{array}{ll}{F}_{RA}{f}_{RA}+F_{RB}{f}_{RB}\hfill & \mathit{G}=0\hfill \\ P_{R1}(\mathit{G})f_{RA}+P_{R2}(\mathit{G})f_{RB}\hfill & \mathit{G}\ne 0\hfill \end{array}\right.$$

(23)

where $F_{RA}={\displaystyle \frac{2dl+4d^2+2dp}{ab}}$, and $F_{RB}={\displaystyle \frac{2dl+2dp}{ab}}$; $f_{RA}$ and $f_{RB}$ are material parameters, and $P_{R1}(\mathit{G})$ and $P_{R2}(\mathit{G})$ are structural functions of the two materials.

Substituting Equations (21)–(23) into Equation (10) yields

$$\begin{array}{cc}{\omega }^2{\displaystyle \sum _{{\mathit{G}}^{\prime }}{\mathit{A}}_{(\mathit{G}\prime \prime -{\mathit{G}}^{\prime })}}\mathit{w}({\mathit{G}}^{\prime })& ={\displaystyle \sum _{{\mathit{G}}^{\prime }}{(\mathit{k}+{\mathit{G}}^{\prime })}_x^2}{(\mathit{k}+\mathit{G}\prime \prime )}_x^2{\mathit{D}}_{(\mathit{G}\prime \prime -{\mathit{G}}^{\prime })}\mathit{w}({\mathit{G}}^{\prime })\hfill \\ & +{\displaystyle \sum _{{\mathit{G}}^{\prime }}{(\mathit{k}+{\mathit{G}}^{\prime })}_y^2}{(\mathit{k}+\mathit{G}\prime \prime )}_x^2{\mathit{B}}_{(\mathit{G}\prime \prime -{\mathit{G}}^{\prime })}\mathit{w}({\mathit{G}}^{\prime })\hfill \\ & +2{\displaystyle \sum _{{\mathit{G}}^{\prime }}{(\mathit{k}+{\mathit{G}}^{\prime })}_x}{(\mathit{k}+{\mathit{G}}^{\prime })}_y{(\mathit{k}+\mathit{G}\prime \prime )}_x{(\mathit{k}+\mathit{G}\prime \prime )}_y{\mathit{\Gamma }}_{(\mathit{G}\prime \prime -{\mathit{G}}^{\prime })}\mathit{w}({\mathit{G}}^{\prime })\hfill \\ & +{\displaystyle \sum _{{\mathit{G}}^{\prime }}{(\mathit{k}+{\mathit{G}}^{\prime })}_y^2}{(\mathit{k}+\mathit{G}\prime \prime )}_y^2{\mathit{D}}_{(\mathit{G}\prime \prime -{\mathit{G}}^{\prime })}\mathit{w}({\mathit{G}}^{\prime })\hfill \\ & +{\displaystyle \sum _{{\mathit{G}}^{\prime }}{(\mathit{k}+{\mathit{G}}^{\prime })}_x^2}{(\mathit{k}+\mathit{G}\prime \prime )}_y^2{\mathit{B}}_{(\mathit{G}\prime \prime -{\mathit{G}}^{\prime })}\mathit{w}({\mathit{G}}^{\prime })\hfill \\ & -{\displaystyle \sum _{{\mathit{G}}^{\prime }}{\displaystyle \sum _{\mathit{G}\prime \prime }{(\mathit{k}+{\mathit{G}}^{\prime })}_x^2{{\mathit{T}}_x}_{(\mathit{G}\prime \prime -{\mathit{G}}^{\prime })}}}\mathit{w}({\mathit{G}}^{\prime })-{\displaystyle \sum _{{\mathit{G}}^{\prime }}{\displaystyle \sum _{\mathit{G}\prime \prime }{(\mathit{k}+{\mathit{G}}^{\prime })}_y^2{{\mathit{T}}_y}_{(\mathit{G}\prime \prime -{\mathit{G}}^{\prime })}}}\mathit{w}({\mathit{G}}^{\prime })\hfill \end{array}$$

(24)

Equation (24) can be simplified as

$${\omega }^2{\mathit{A}}_2\mathit{w}={\mathit{B}}_2\mathit{w}$$

(25)

We set $\Delta T=0 \mathrm{K}$, $\Delta T=-2 \mathrm{K}$, $\Delta T=-5 \mathrm{K}$, and $\Delta T=-10 \mathrm{K}$ to investigate the influence of temperature variation on the band structure evolution of the 2D rectangular EM lattice. Figure 4a reveals that for $\Delta T=0 \mathrm{K}$, the first four bands of the rectangular EM lattice exhibit no gaps. The consistency of the first three bands between the PWEM and FEM results confirms the methodological efficiency in 2D EM lattices. Figure 4b indicates that at $\Delta T=-2 \mathrm{K}$, the first band gap, located between the first and second energy bands, spans a frequency range of 3.68–7.65 Hz. Concurrently, a second band gap emerges between the second and third energy bands, covering the range of 7.91–9.76 Hz. As temperature decreases, the first three energy bands undergo upward shifts. Due to the fact that the first band experiences only a minor upward shift while the second and third bands shift substantially, band gaps open between the first–second and second–third bands. Figure 4c shows that at $\Delta T=-5 \mathrm{K}$, the positions of the first and second band gaps remain unchanged, with their respective ranges being 3.70–7.80 Hz and 7.95–12.11 Hz. Both band gaps exhibit increased width; however, the range of the first gap undergoes minimal change, while the range of the second gap expands significantly. This disparity arises because the first and second bands show negligible change, whereas the third band undergoes a substantial modification. Finally, Figure 4d demonstrates that for $\Delta T=-10 \mathrm{K}$, the positions of the first and second band gaps remain stable, with ranges of 3.71–7.81 Hz and 7.95–12.66 Hz, respectively. Both band gaps exhibit minimal changes in their width and range.

In the 2D EM lattice, all four bands shift monotonically with temperature: as temperature rises (with compression thermal stress), band frequencies uniformly decrease; as temperature falls (with tension thermal stress), they uniformly increase. However, this shift exhibits a saturation effect and depends on band order. With large negative temperature difference, each band will asymptotically approach an upper limit, so further cooling produces ever-diminishing frequency changes. Importantly, low-order bands respond more remarkably to temperature changes and therefore reach their asymptotes sooner than higher order bands. As a result, continued cooling widens the band gap; the lower bound stabilizes, while the upper bound—set by a higher-order band—continues to rise. Once both band frequencies have plateaued, the band gap width itself becomes essentially temperature-invariant.

5. Method Verification

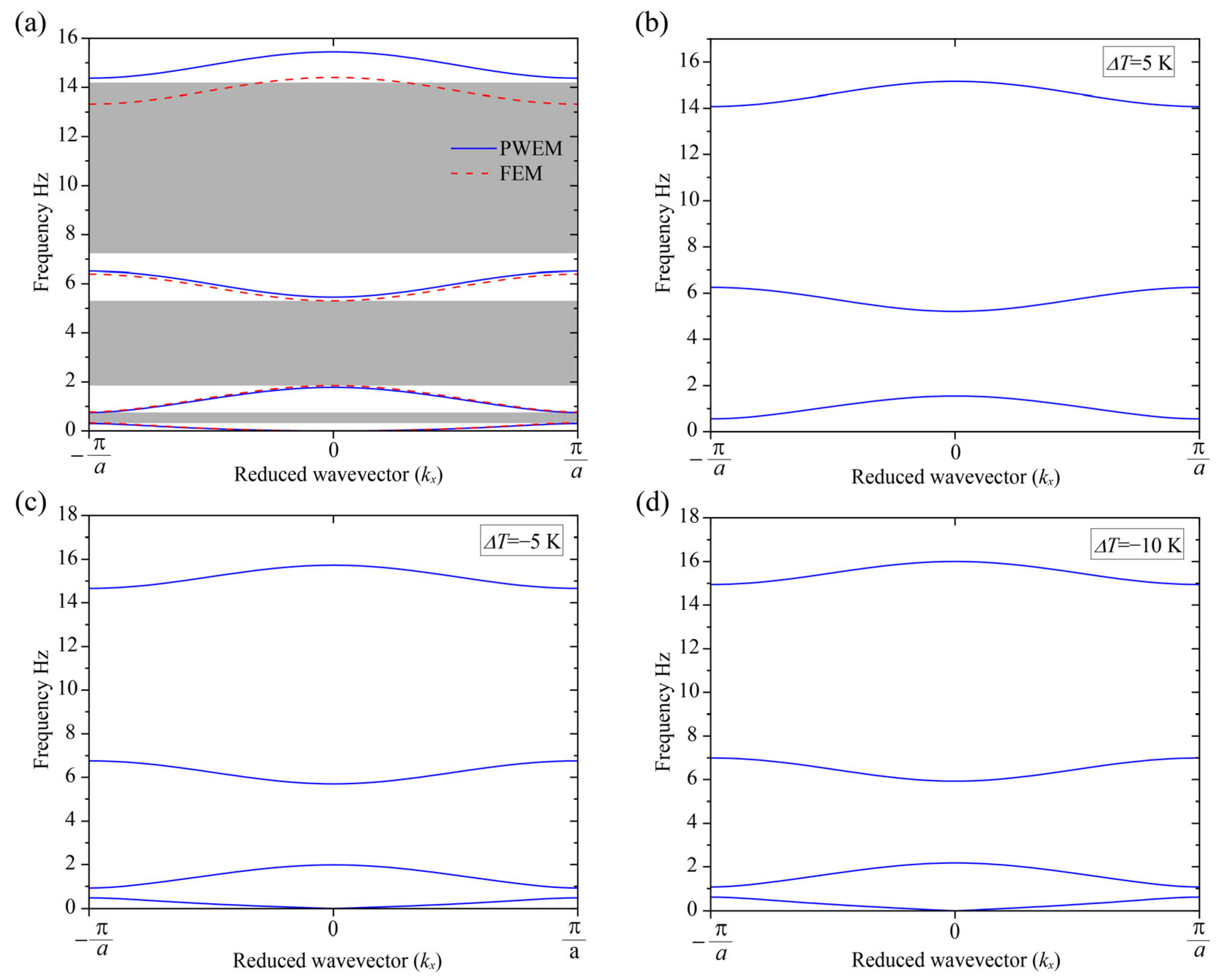
5.1. One-Dimensional EM Beam

To verify the calculated results of the band structure of 1D beam Ems in a thermal environment, we establish a finite periodic model in Comsol Multiphysics. Under fixed boundary conditions, the beam consists of 12 × 1 elements. A point excitation is applied at the right end of the beam. Another two points shown in Figure 5a are used to detect the displacement responses. As shown in Figure 5b, when $\Delta T=5 \mathrm{K}$, the first and second band gap ranges on the transmission curve are 1.6–4.6 Hz and 5.6–12.1 Hz, respectively. These ranges exhibit good agreement with the theoretical predictions of the first two band gaps of 1.55–5.31 Hz and 6.26–14.08 Hz. Figure 5c reveals that under $\Delta T=-5 \mathrm{K}$, the first two gap ranges on the transmission curve are 1.8–5.0 Hz and 5.8–12.4 Hz, respectively. These results align well with the theoretical results of 1.99–5.70 Hz and 6.76–14.66 Hz. Additionally, Figure 5d ($\Delta T=10 \mathrm{K}$) indicates band gap ranges of 2.0–5.0 Hz and 6.1–11.6 Hz, which show small deviations from the theoretical ranges of 1.34–5.01 Hz and 6.05–13.84 Hz. Finally, as shown in Figure 5e for $\Delta T=-10 \mathrm{K}$, the first two gap ranges are observed as 2.1–5.6 Hz and 6.1–12.6 Hz. These compare favorably with the theoretical values of 2.18–5.93 Hz and 6.99–14.94 Hz. All these results demonstrate that we can effectively compute the band structures of 1D EM beams incorporating thermal stress.

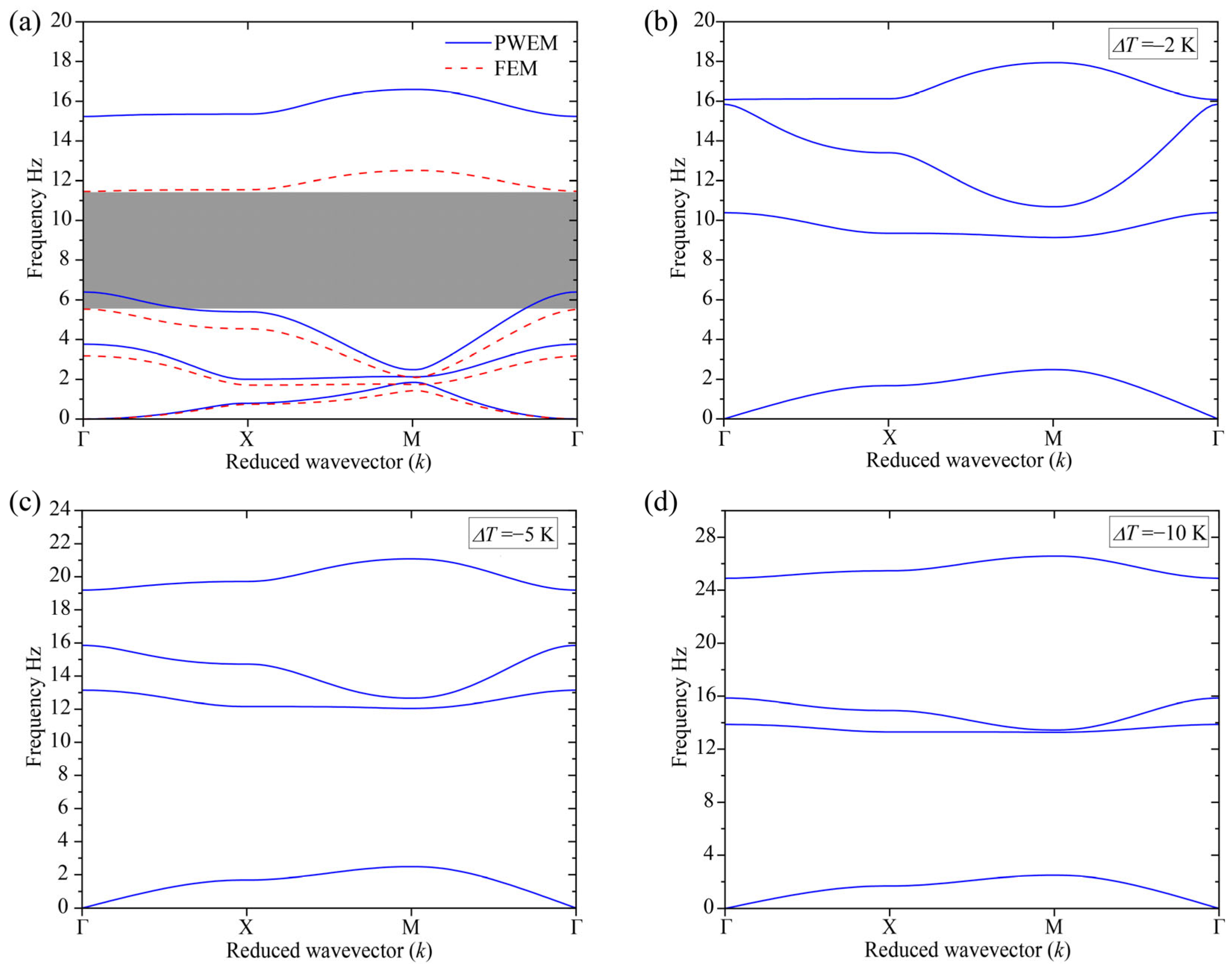
5.2. Two-Dimensional EM Lattice

Now we examine the effectiveness of the proposed PWEM in 2D EM lattices with thermal stress. A square cross model consisting of 12 × 12 cells is constructed, and fixed boundary conditions are imposed. As shown in Figure 6a, a point load is applied to the model at the corner. Displacement responses are measured at two specified points on the model. Frequency response curves are obtained by frequency domain prestress analysis using Comsol Multiphysics. We computed the transmission curves for the 2D square EM lattice under various thermal differentials of $\Delta T=0 \mathrm{K}$, $\Delta T=-2 \mathrm{K}$, $\Delta T=-5 \mathrm{K}$, and $\Delta T=-10 \mathrm{K}$. Figure 6b ($\Delta T=0 \mathrm{K}$) reveals a band gap range of 6.1–14.5 Hz on the transmission curve, which aligns closely with the PWEM determined range of 6.4–15.23 Hz. Figure 6c ($\Delta T=-2 \mathrm{K}$) shows a band gap range of 3.1–14.3 Hz on the transmission curve, which matches well with our calculated results. Moreover, as illustrated in Figure 6d ($\Delta T=-5 \mathrm{K}$), the band gap range on the transmission curve is 3.8–15.0 Hz. While a more noticeable discrepancy is observed in the upper bound compared to our calculated range of 2.49–12.05 Hz, the agreement remains acceptable. Finally, Figure 6e ($\Delta T=-10 \mathrm{K}$) indicates a band gap of 5.9–18.9 Hz, which agrees well with the theoretical results of 6.40–15.23 Hz.

Similar validation for rectangular lattices (Figure 7) demonstrates comparable accuracy: no gap emerges at $\Delta T=0 \mathrm{K}$ (as predicted); $\Delta T=-2 \mathrm{K}$ shows a 4.3–14.1 Hz gap matching calculations; $\Delta T=-5 \mathrm{K}$ yields a single broad gap (5.1–16.2 Hz) merging two adjacent theoretical gaps (3.7–7.8 Hz and 7.95–12.11 Hz) due to their <0.15 Hz separation; $\Delta T=-10 \mathrm{K}$ exhibits 7.1–17.0 Hz encompassing predicted gaps (3.7–7.81 Hz and 7.95–12.66 Hz). Minor discrepancies fall within experimental limits, confirming PWEM’s reliability for rectangular lattices under thermal stress. All these results collectively demonstrate the PWEM to effectively compute the band structures of 2D square EM lattices incorporating thermal stress.

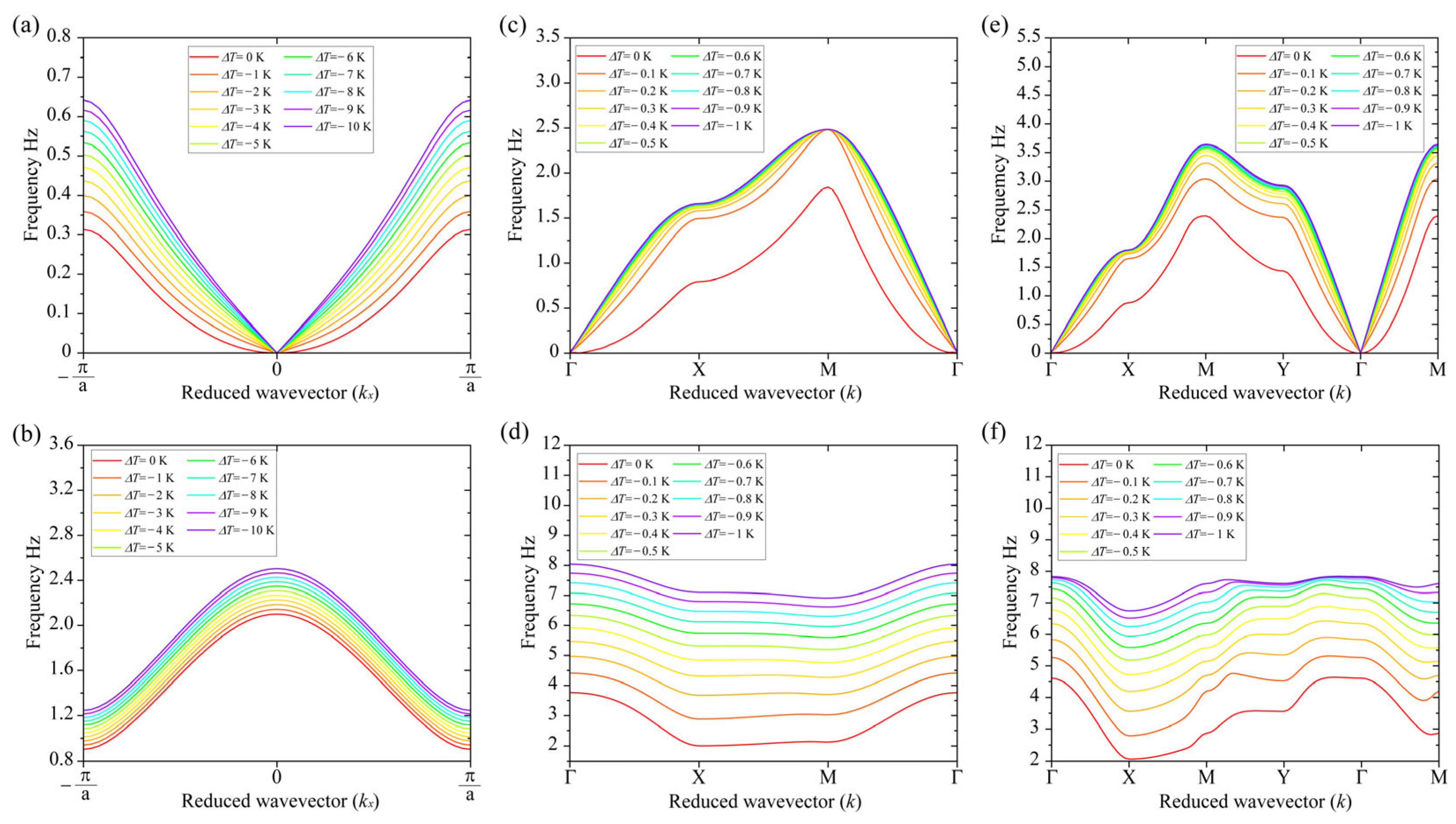
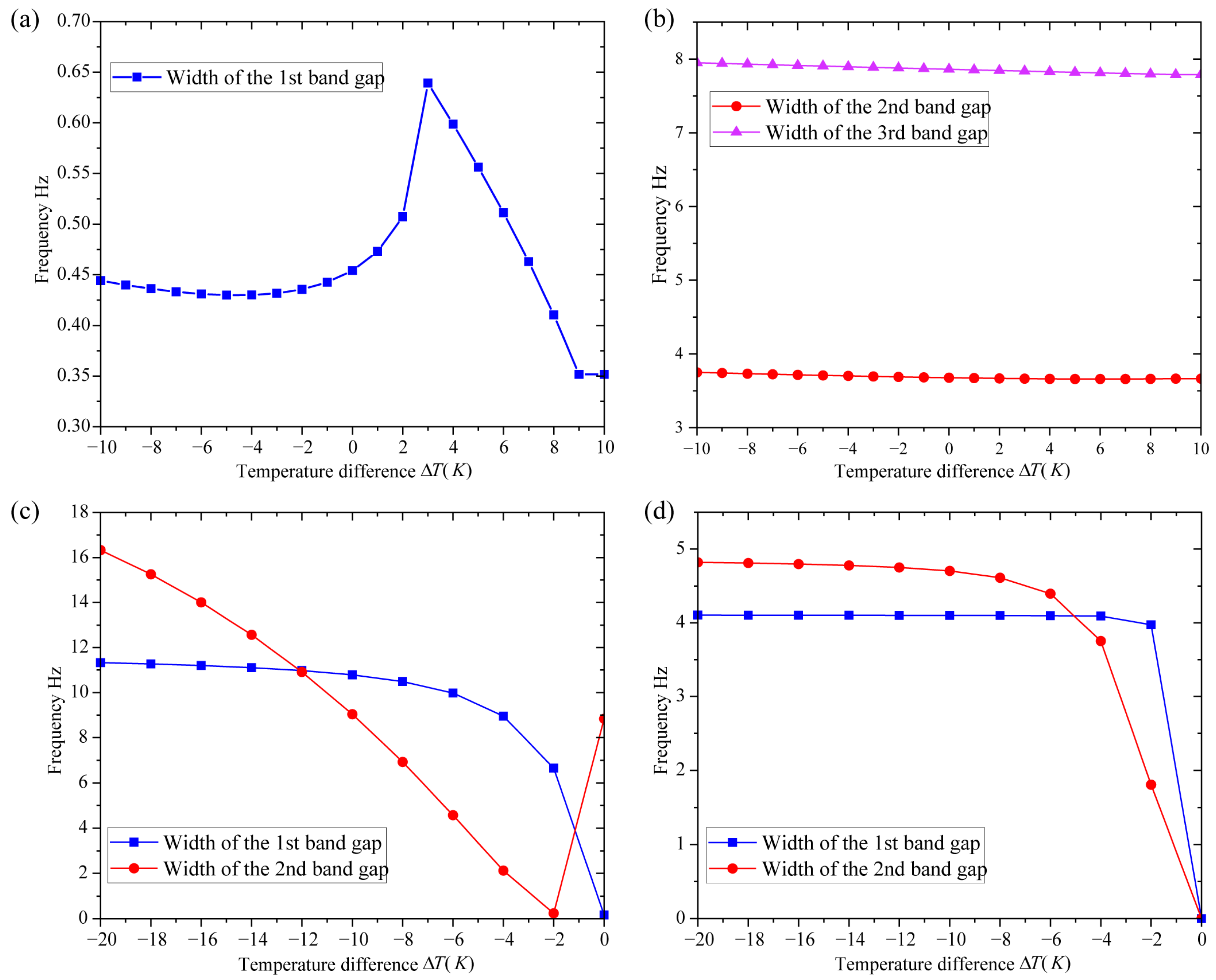
6. Bands and Band Gap Variations Versus Temperature Differences

6.1. Band Variations of EM Lattices

To explore the evolution of the band structure, we analyzed how the first two bands of the three EM lattices respond to decreasing temperature. Figure 8a,b show the variation of the first and second bands of the 1D beam EM as the temperature decreases from $-10 \mathrm{K}$ to $0 \mathrm{K}$ with an interval of $1 \mathrm{K}$. In Figure 8a, the spacing between adjacent bands narrows progressively with cooling, indicating that the effect of temperature on the first band diminishes as the temperature drops. In contrast, Figure 8b shows that the second band shifts upward with cooling, but the trend is less pronounced, confirming that the first band is more sensitive to temperature changes than the second.

Figure 8c,d present the band evolution of the 2D square EM lattice as the temperature decreases from $-1 \mathrm{K}$ to $0 \mathrm{K}$ with an interval of $0.1 \mathrm{K}$. Similar to the 1D case, the first band (Figure 8c) shows a gradual narrowing of the gap with decreasing temperature, revealing a nonlinear sensitivity to thermal changes. The second band (Figure 8d) follows the same trend but with a weaker response, again highlighting the dominant influence of temperature on the first band.

Figure 8e,f illustrate the 2D rectangular EM lattice with the temperature decreasing from $-1 \mathrm{K}$ to $0 \mathrm{K}$ with an interval of $0.1 \mathrm{K}$. Its first band (Figure 8e) exhibits the same behavior observed in the square lattice: as the temperature decreases, the spacing between adjacent bands narrows. The second band (Figure 8f) shows a similar but less pronounced upward shift, consistent with the behavior of the other lattices.

Across all three EM configurations, the first band consistently exhibits greater sensitivity to temperature variation than the second band. This universal trend indicates that temperature primarily affects the lowest-frequency modes, while higher bands respond more weakly to thermal changes.

6.2. Bandwidth Variations of EM Lattices

Furthermore, to understand how thermal stress affects the band gap at various temperature differences, we investigate the band gaps of the 1D EM beams and 2D EM lattices. Figure 9a illustrates the variation of the first band gap width with temperature for a 1D EM beam. As temperature increases, when $0<\Delta T<3 \mathrm{K}$, both the first and second energy bands decrease in frequency. However, due to the greater sensitivity of the first band to temperature changes compared to the second, the magnitude of the decrease is larger for the first band than for the second. Consequently, the width of the first band gap increases. When $3 \mathrm{K}<\Delta T<9 \mathrm{K}$, the first band has reached its minimum value. As temperature continues to increase, the second energy band continues to decrease, leading to a reduction in the width of the first band gap. For $\Delta T>9 \mathrm{K}$, the second band reaches its limiting value. These observations confirm that band gap tuning via thermal loading is governed by the relative saturation behaviors of the constitutive bands.

As temperature decreases, when $-5 \mathrm{K}<\Delta T<0 \mathrm{K}$, both the first and second energy bands increase in frequency. However, the increasing rate is greater for the first energy band than the second, resulting in a decrease in the width of the first band gap. When $-10 \mathrm{K}<\Delta T<-5 \mathrm{K}$, the first band reaches its limiting value, while the second energy band continues to increase. This causes the width of the first band gap to continuously increase.

In addition, Figure 9b depicts the variations in the widths of the second and third band gaps for the 1D beam EM. The change of these two band gaps shows a linear modification when temperature changes.

Figure 9c illustrates the variation in the widths of the first and second band gaps for 2D square EM lattices. As temperature decreases, both the first and second bands move upward in frequency. However, the first band rapidly reaches its limiting value, while the second band continues to rise but with a progressively diminishing rate of increase. Consequently, as temperature decreases, the width of the first gap gradually increases.

For the second band gap formed by the third and fourth bands, when $-2 \mathrm{K}<\Delta T<0 \mathrm{K}$, a decrease in temperature causes both the bands to rise. However, the third band increases at a faster rate than the fourth band, resulting in a decrease in the width of the second band gap. With decreasing temperature, when $-20 \mathrm{K}<\Delta T<-2 \mathrm{K}$, the rate of increase of the third band becomes slower than that of the fourth band. Thus, the width of the second gap increases, but the rate of this increase also diminishes gradually.

Figure 9d depicts the variation in the widths of the first and second band gaps for a 2D rectangular EM lattice. It is shown that both band gap widths follow a similar trend: as temperature decreases, the gap width initially increases significantly before stabilizing. Due to the higher sensitivity of the first energy band in the rectangular lattice EM compared to its counterpart in the square lattice, the band bounds defining the first gap reach their limiting values more rapidly. Therefore, even with further temperature decreases, the width of the first band gap remains essentially constant. The width of the second gap also exhibits an initial increase followed by stabilization.

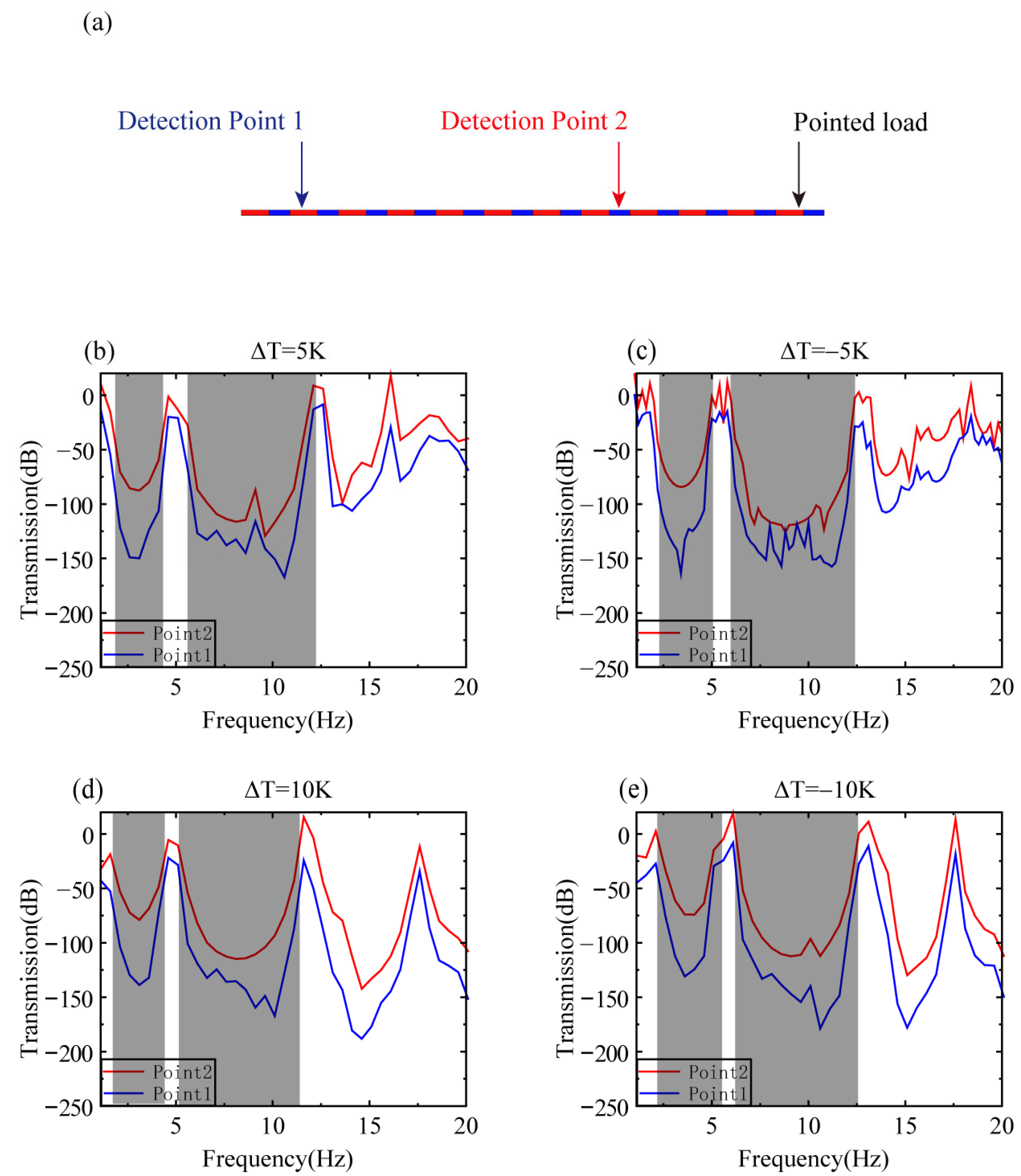
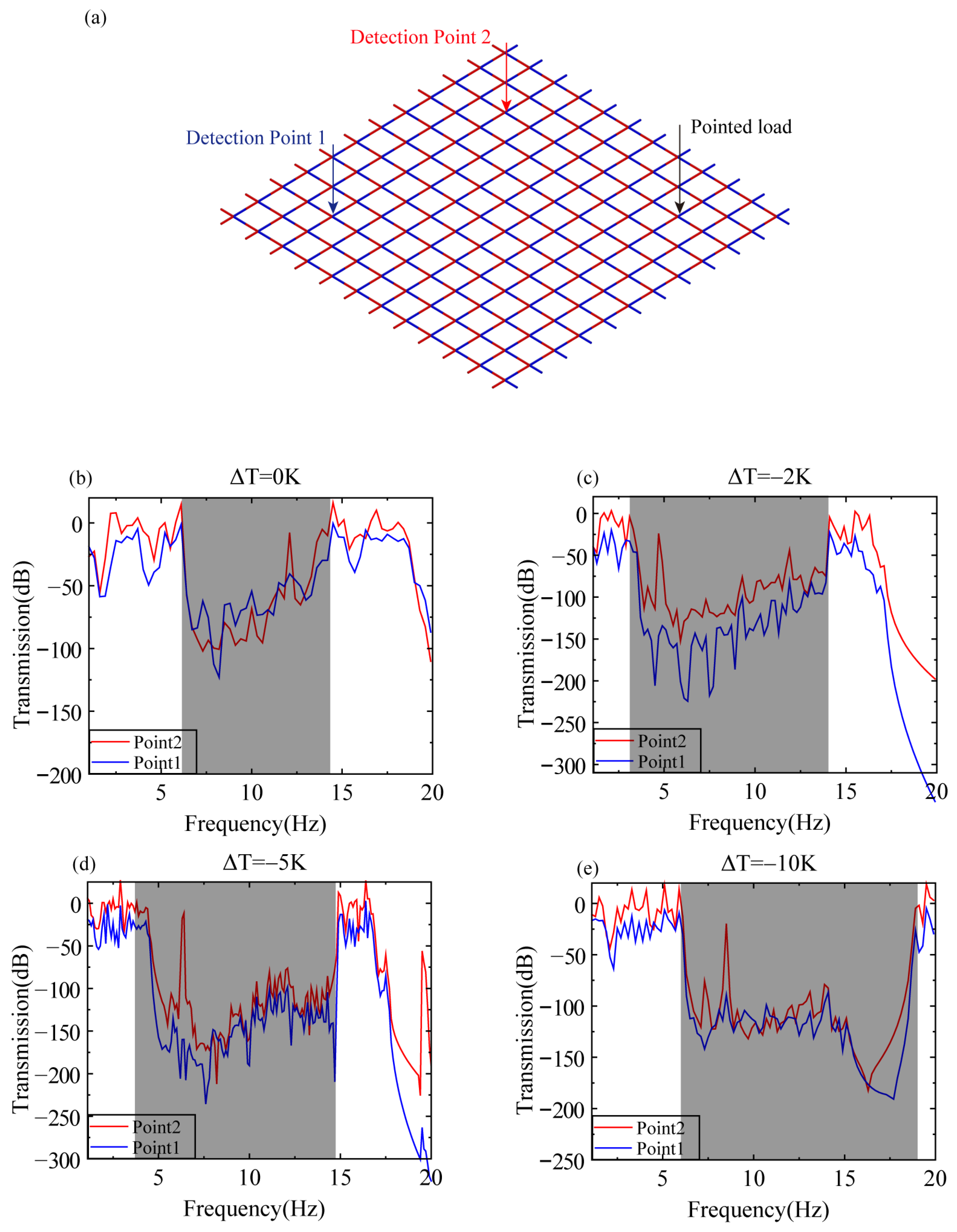
7. Sensitivity Analysis of Band Structure to Temperature Difference

Our analysis reveals nonlinear temperature dependence in band structures across all three EM systems. To quantify this relationship, we perform sensitivity analysis on the first three bands. Adapted from structural parameter optimization methods [39,50], this approach evaluates band frequency sensitivity to temperature variations. The foundation for this analysis stems from the reduced vibration equation for 1D metamaterial beams under plane wave expansion [Equation (9)]:

$${\omega }^2{\mathit{A}}_0\mathit{u}={\mathit{B}}_0\mathit{u}$$

(26)

The derivative of $\Delta T$ on both sides gives

$$2\omega {\displaystyle \frac{\mathsf{\partial }w}{\mathsf{\partial }\Delta T}}{\mathit{A}}_0\mathit{u}+{\omega }^2{\displaystyle \frac{\mathsf{\partial }{\mathit{A}}_0}{\mathsf{\partial }\Delta T}}\mathit{u}+{\omega }^2{\mathit{A}}_0{\displaystyle \frac{\mathsf{\partial }\mathit{u}}{\mathsf{\partial }\Delta T}}={\displaystyle \frac{\mathsf{\partial }{\mathit{B}}_0}{\mathsf{\partial }\Delta T}}\mathit{u}+{\mathit{B}}_0{\displaystyle \frac{\mathsf{\partial }\mathit{u}}{\mathsf{\partial }\Delta T}}$$

(27)

Since ${\mathbf{A}}_0$ does not contain $\Delta T$, therefore

$${\displaystyle \frac{\mathsf{\partial }{\mathit{A}}_0}{\mathsf{\partial }\Delta T}}=0$$

(28)

Substituting Equation (28) into Equation (27) gives

$$2\omega {\displaystyle \frac{\mathsf{\partial }w}{\mathsf{\partial }\Delta T}}{\mathit{A}}_0\mathit{u}+{\omega }^2{\mathit{A}}_0{\displaystyle \frac{\mathsf{\partial }\mathit{u}}{\mathsf{\partial }\Delta T}}={\displaystyle \frac{\mathsf{\partial }{\mathit{B}}_0}{\mathsf{\partial }\Delta T}}\mathit{u}+{\mathit{B}}_0{\displaystyle \frac{\mathsf{\partial }\mathit{u}}{\mathsf{\partial }\Delta T}}$$

(29)

Multiplying both sides of Equation (26) by $u^{\mathrm{T}}$ simultaneously, we obtain

$$2\omega {\displaystyle \frac{\mathsf{\partial }w}{\mathsf{\partial }\Delta T}}{\mathit{u}}^{\mathrm{T}}{\mathit{A}}_0\mathit{u}+{\omega }^2{\mathit{u}}^{\mathrm{T}}{\mathit{A}}_0{\displaystyle \frac{\mathsf{\partial }\mathit{u}}{\mathsf{\partial }\Delta T}}={\mathit{u}}^{\mathrm{T}}{\displaystyle \frac{\mathsf{\partial }{\mathit{B}}_0}{\mathsf{\partial }\Delta T}}\mathit{u}+{\mathit{u}}^{\mathrm{T}}{\mathit{B}}_0{\displaystyle \frac{\mathsf{\partial }\mathit{u}}{\mathsf{\partial }\Delta T}}$$

(30)

The following can be obtained from Equation (26):

$${\omega }^2{\mathit{u}}^{\mathrm{T}}{\mathit{A}}_0{\displaystyle \frac{\mathsf{\partial }\mathit{u}}{\mathsf{\partial }\Delta T}}={\mathit{u}}^{\mathrm{T}}{\mathit{B}}_0{\displaystyle \frac{\mathsf{\partial }\mathit{u}}{\mathsf{\partial }\Delta T}}$$

(31)

The relationship between angular frequency $\omega$ and frequency $f$ is

$$\omega =2\pi f$$

(32)

By substituting Equations (31) and (32) into Equation (30), we can obtain the sensitivity of a 1D EM beam:

$${\displaystyle \frac{\mathsf{\partial }f}{\mathsf{\partial }\Delta T}}={\displaystyle \frac{1}{8{\pi }^{2}f}}{\mathit{u}}^{\mathrm{T}}{\displaystyle \frac{\mathsf{\partial }{\mathit{B}}_0}{\mathsf{\partial }\Delta T}}\mathit{u}$$

(33)

Similarly, by performing the same calculation on Equations (20) and (25), we can obtain the sensitivity expressions for 2D square and rectangular EM lattices:

$${\displaystyle \frac{\mathsf{\partial }f}{\mathsf{\partial }\Delta T}}={\displaystyle \frac{1}{8{\pi }^{2}f}}{\mathit{w}}^{\mathrm{T}}{\displaystyle \frac{\mathsf{\partial }{\mathit{B}}_1}{\mathsf{\partial }\Delta T}}\mathit{w}$$

(34)

$${\displaystyle \frac{\mathsf{\partial }f}{\mathsf{\partial }\Delta T}}={\displaystyle \frac{1}{8{\pi }^{2}f}}{\mathit{w}}^{\mathrm{T}}{\displaystyle \frac{\mathsf{\partial }{\mathit{B}}_2}{\mathsf{\partial }\Delta T}}\mathit{w}$$

(35)

Figure 10a shows temperature sensitivity of the first four bands in 1D EM beams. Band 1 exhibits significantly higher sensitivity than bands 2–4, indicating greater thermal responsiveness. A pronounced sensitivity peak occurs at the Brillouin zone center (Γ-point), confirming localized thermal tuning at this critical wavevector. Higher bands (2–4) show smooth, low-magnitude sensitivity profiles without distinct peaks, indicating uniform but minimal thermal response across the wavevector domain.

Figure 10b,c present sensitivity distributions for 2D square lattices, which show consistent band-order dependence: Band 1 dominates thermal response in both systems with sharp Γ-point sensitivity peaks. Higher bands (2–4) maintain uniformly low sensitivity without localized features, confirming their limited thermal responsiveness throughout the Brillouin zone.

Figure 10d shows the sensitivity of the 2D rectangular EM lattice. Its first and second energy bands exhibit relatively low sensitivity, while the third and fourth energy bands display alternating high and low sensitivity in different intervals. Although this differs from the sensitivity response of 2D square lattices, the variation in its energy bands also has limitations.

8. Conclusions

In summary, we have developed and applied a temperature-dependent PWEM to predict and engineer the band structures of 1D and 2D Ems under thermal stress. By incorporating thermal stress effects into the Floquet–Bloch framework, our approach captures the nonlinear, asymptotic band shifts observed in 1D beams and in square and rectangular 2D lattices. Excellent agreement with transmission curves validates the method’s accuracy across geometries and temperature differentials. Sensitivity analysis further reveals that the lowest band governs thermal tuning: it exhibits both the largest absolute shifts and strong localization at Γ-point, whereas higher-order bands respond weakly and uniformly. This band-order-dependent saturation behavior shows a robust strategy for thermally reconfigurable band gap control, enabling low-frequency vibration suppression. These findings lay the groundwork for passive vibration isolation systems in temperature-varying environments such as deployable space antennas. In this paper, the uniform temperature field is adopted, and the influence of the distribution of the transient temperature field on the band gap of elastic metamaterials is not considered [51]. Future work will focus on experimental demonstration of thermal band gap tuning and on extending the theory to 3D lattice architectures, transient thermal fields [51], and even nonlinear vibration mitigation [52].