Effect of Initial Solid Solution Microstructure on the Hot Deformation Behavior of Mg-Er-Sm-Zn-Zr Alloy
Abstract
1. Introduction
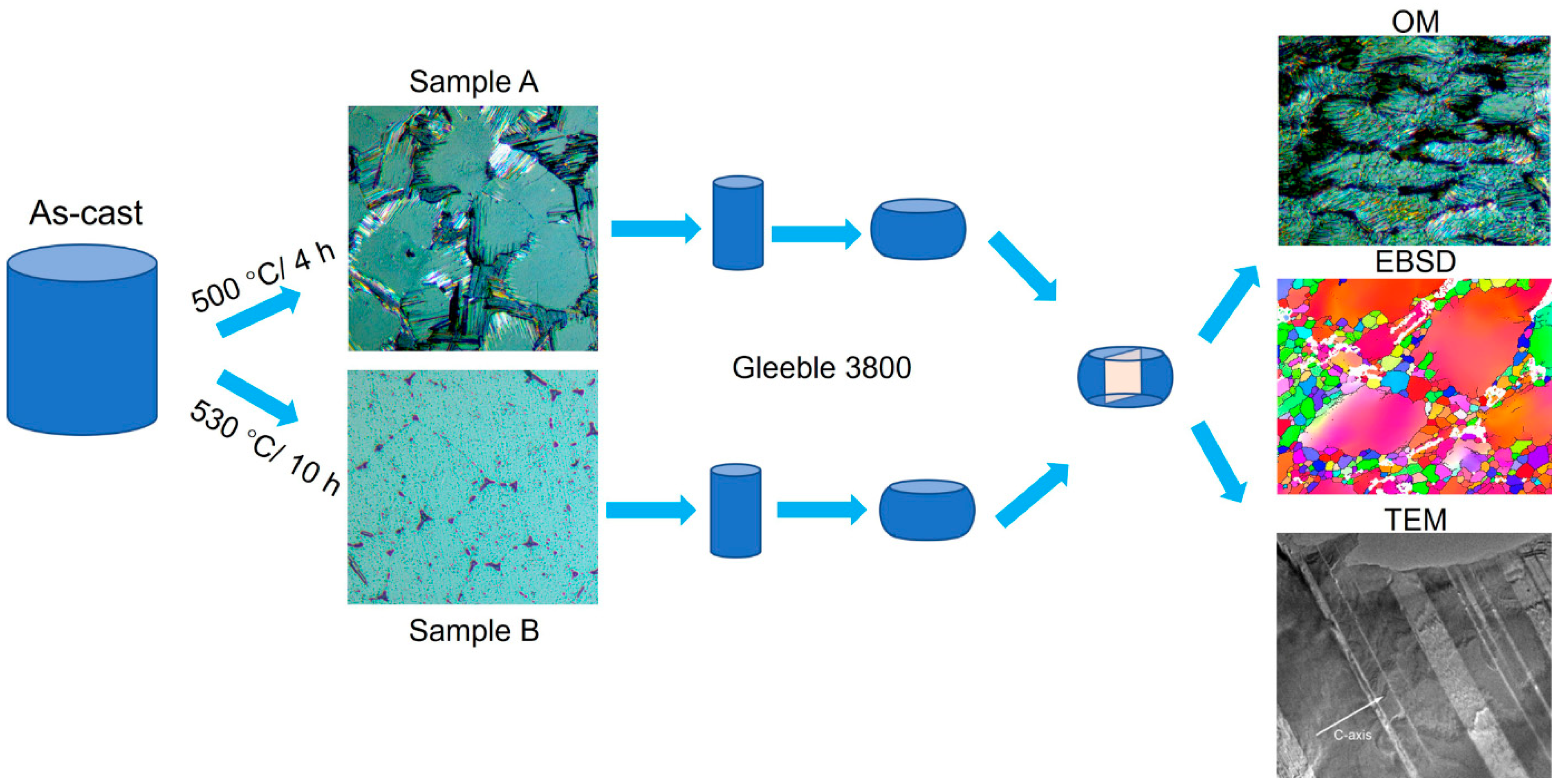
2. Materials and Methods
3. Results and Discussion
3.1. Initial Microstructures
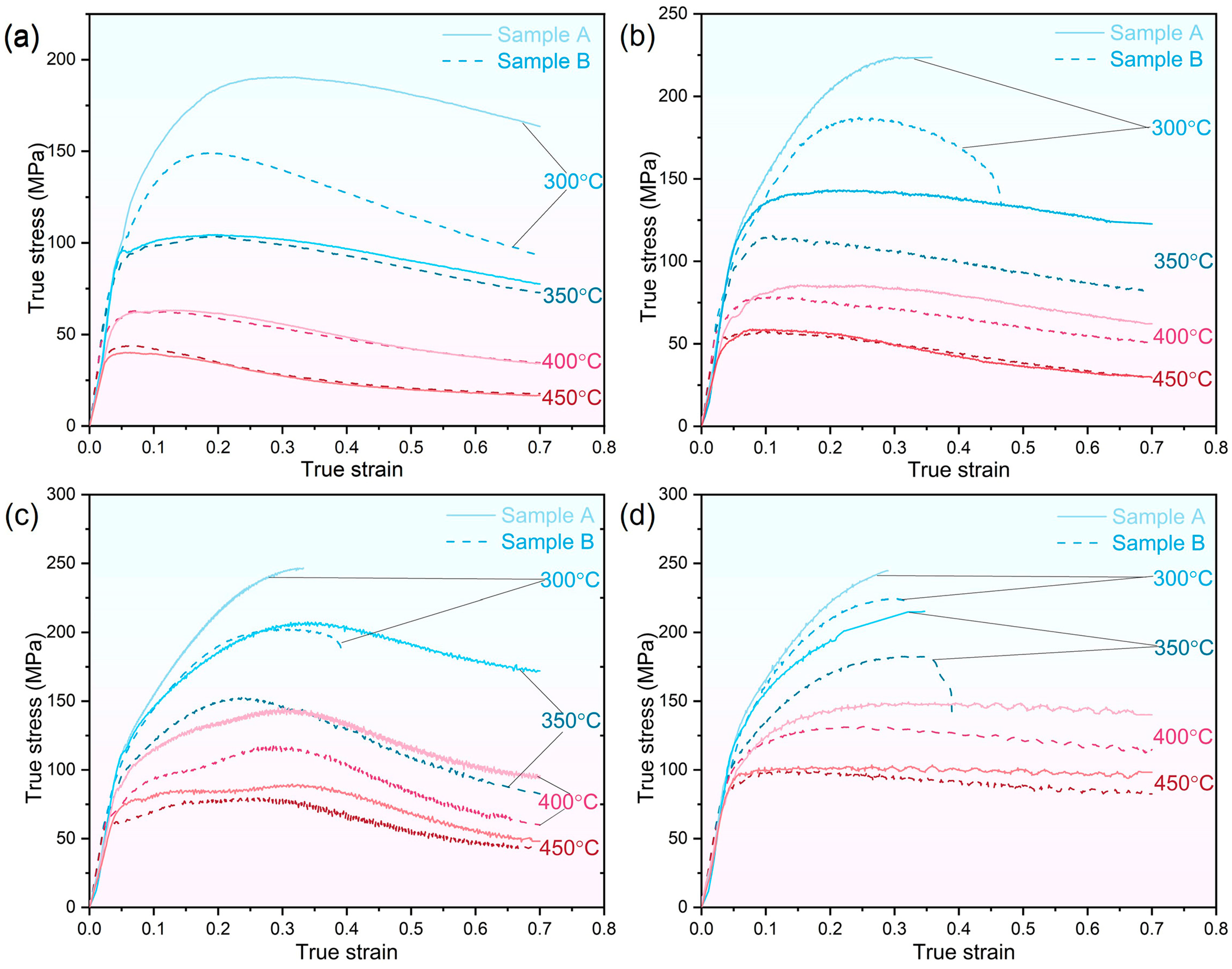
3.2. Flow Stress
3.2.1. Work Hardening and Dynamic Softening
3.2.2. Effect of Initial Microstructures on Flow Stress
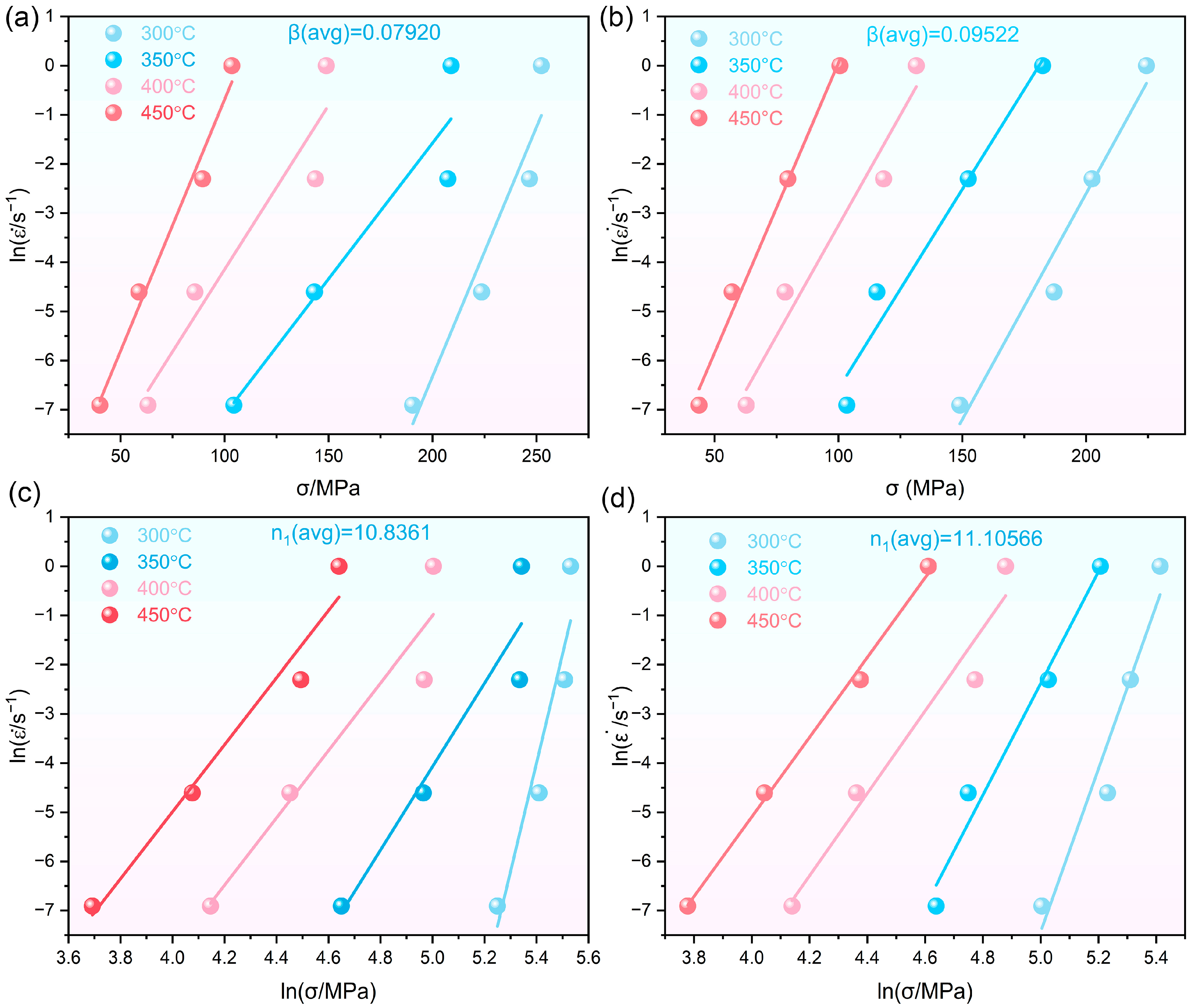
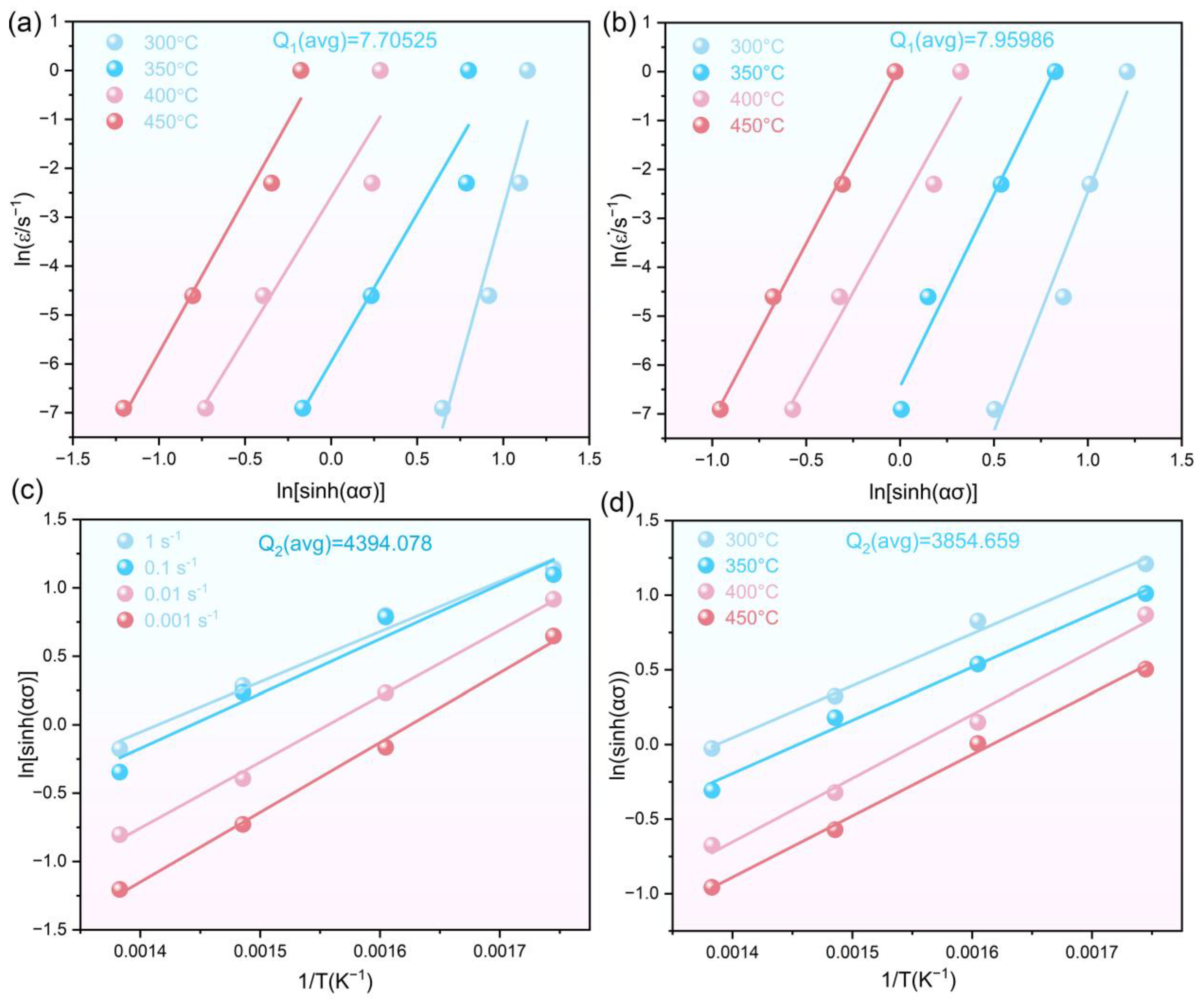
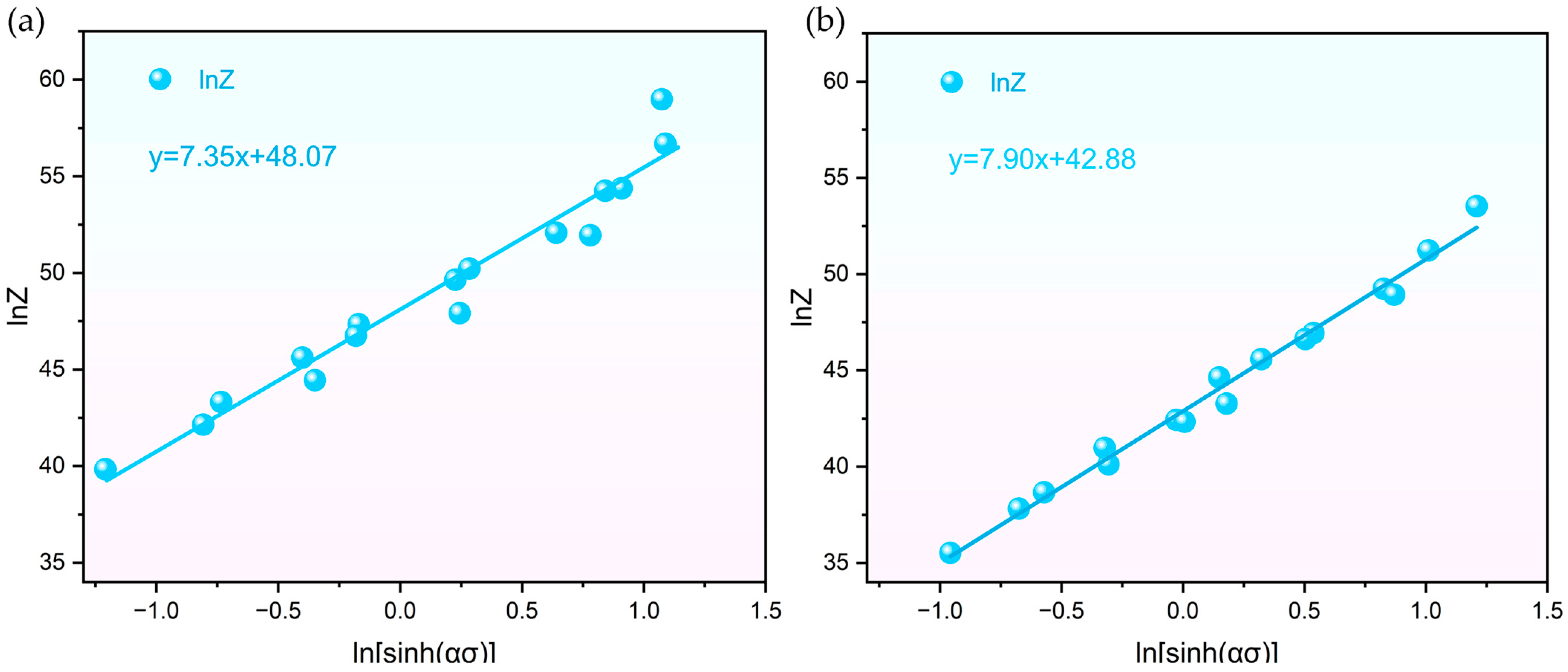
3.3. Constitutive Equation
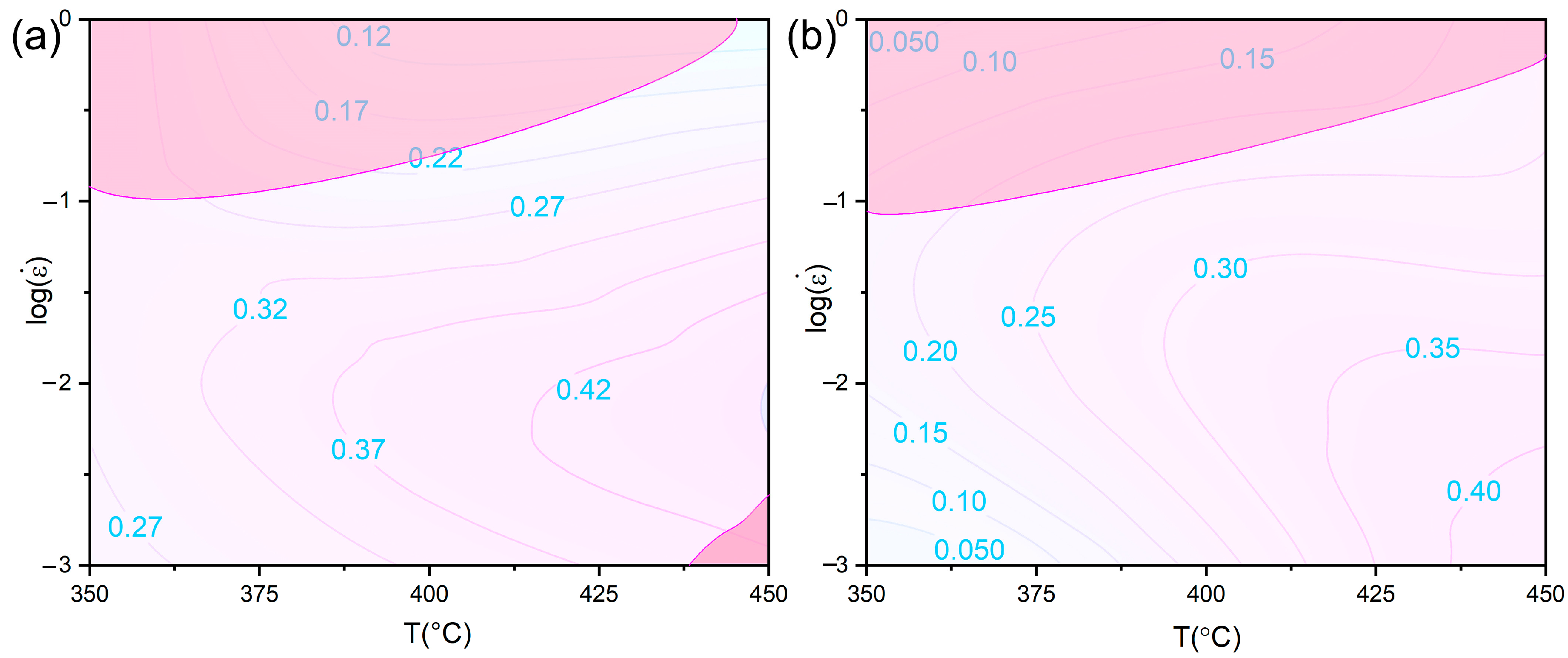
3.4. Processing Maps
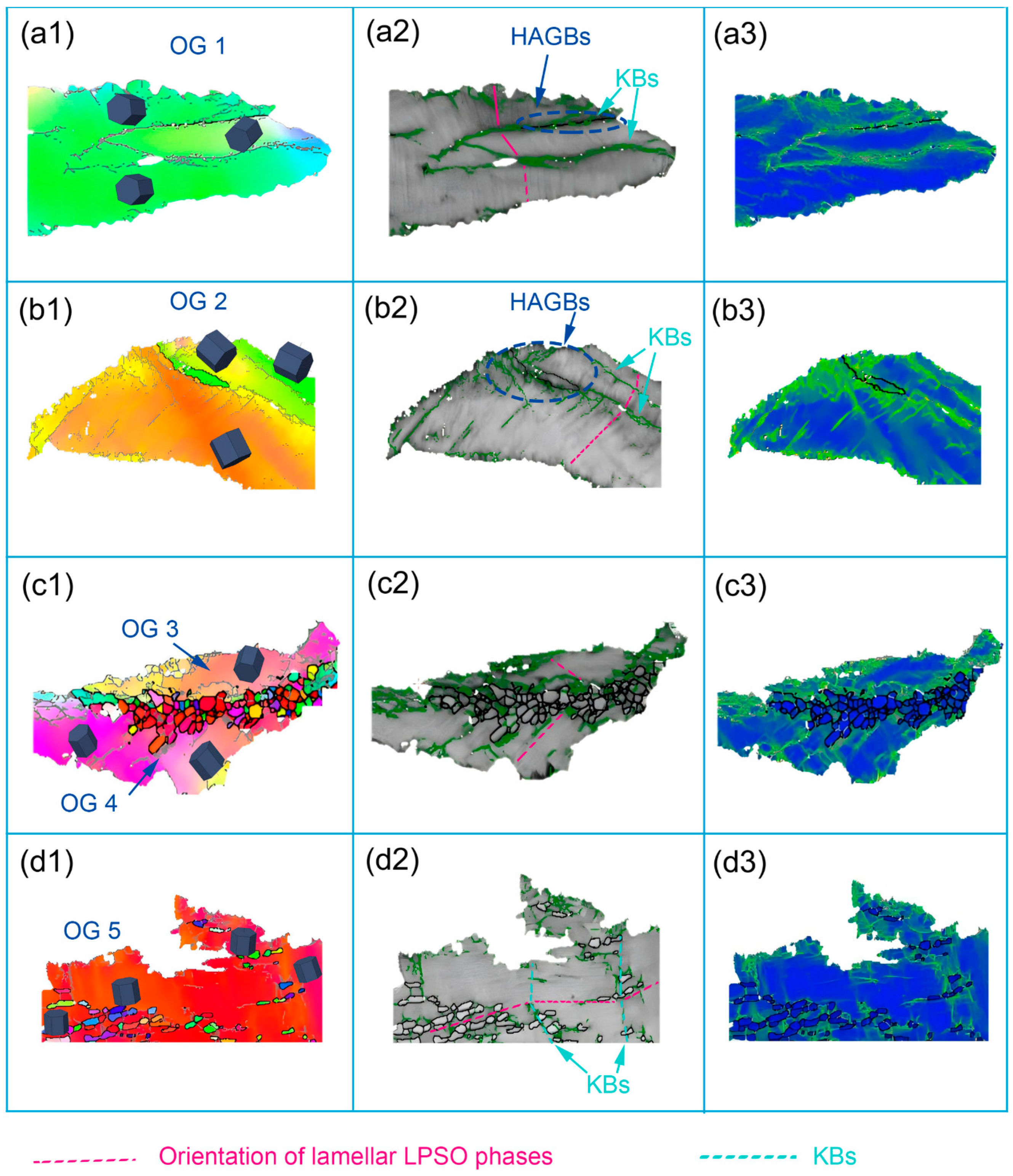
3.5. Microstructures
3.5.1. Dynamic Precipitation of LPSO Phases
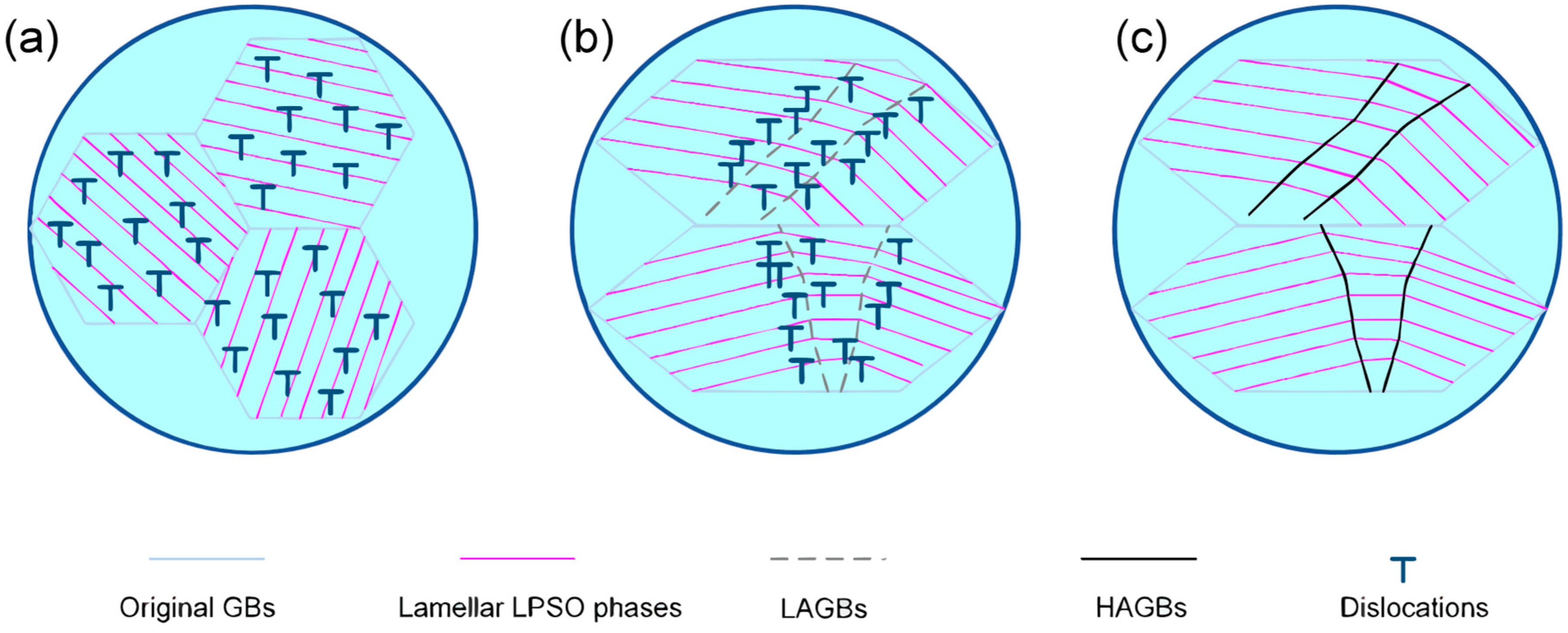
3.5.2. Discontinuous and Continuous DRX
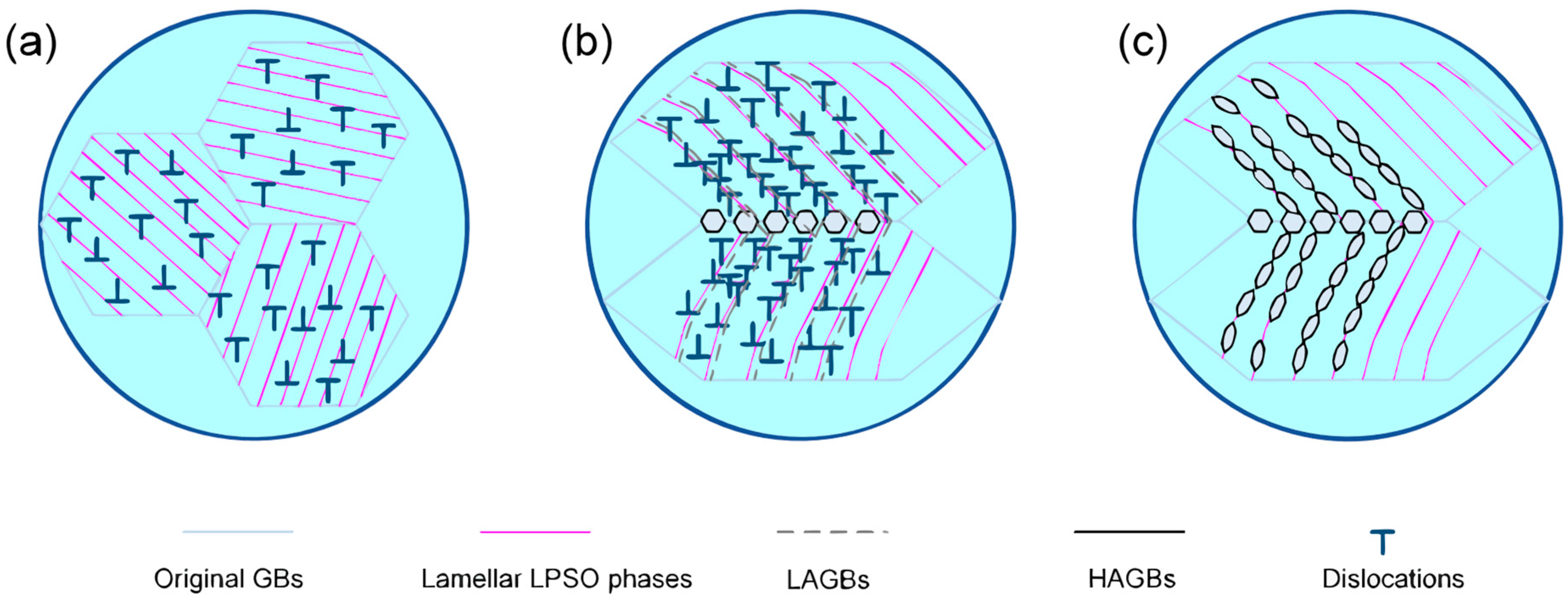
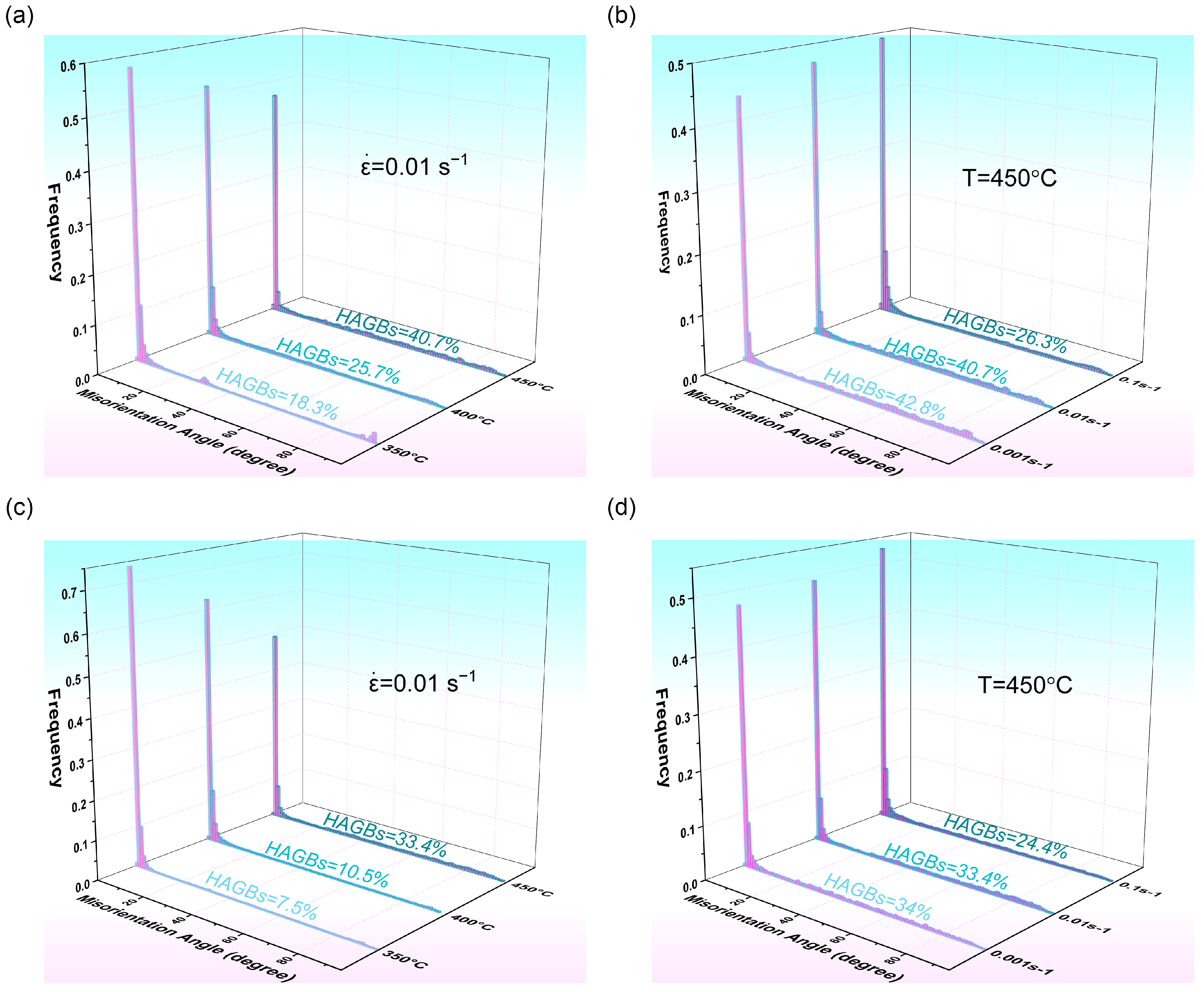
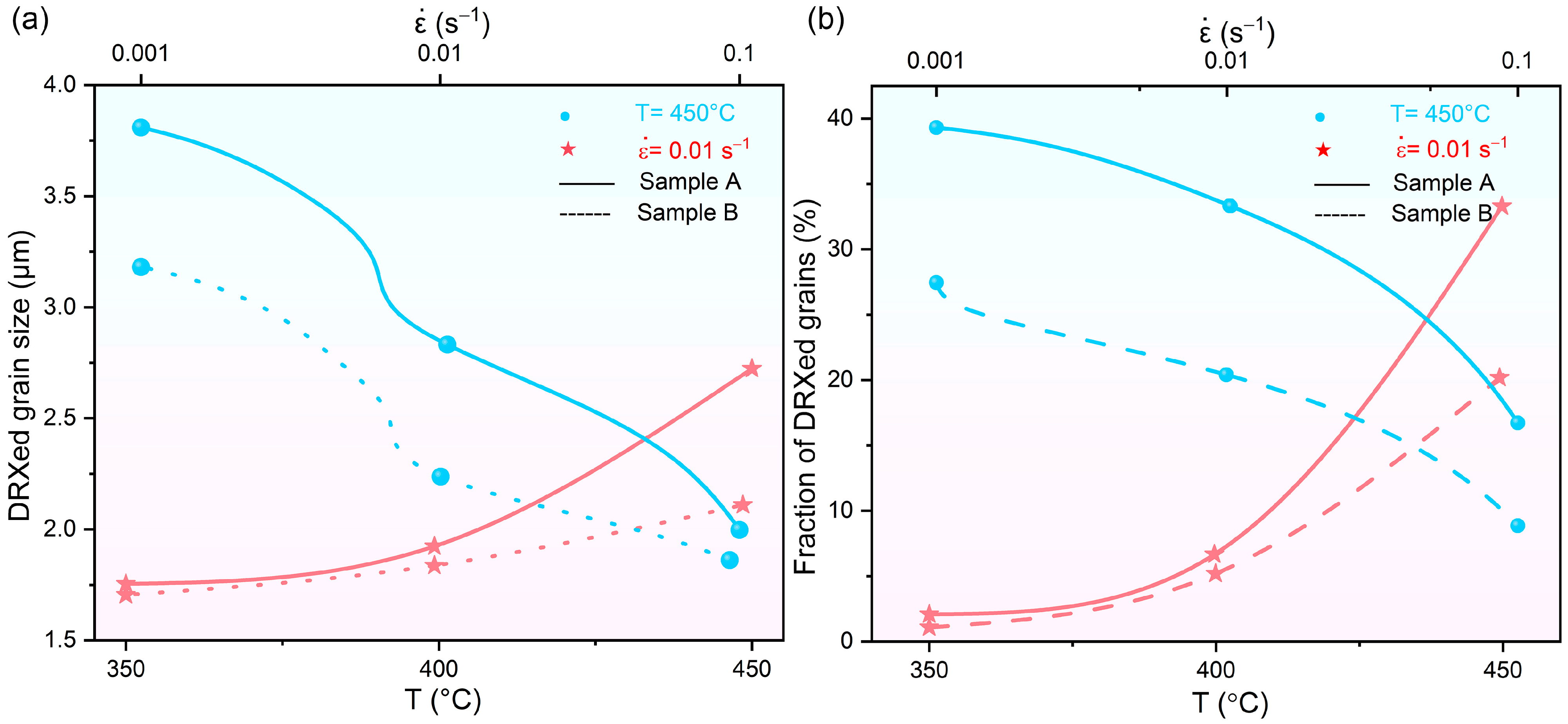
3.5.3. DRXed Grain Sizes and Frequencies
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| LPSO | Long-period stacking order |
| DRX | Dynamic recrystallization |
| Mg | Magnesium |
| RE | rare earth |
| UTS | ultimate tensile strength |
| YS | yield stress |
| DMM | dynamic material model |
| PSN | particle-stimulated nucleation |
| SFs | stacking faults |
| SAED | selected area electron diffraction |
| IPF | inverse pole diagram |
| GBs | grain boundaries |
| DDRX | discontinuous dynamic recrystallization |
| CDRX | continuous dynamic recrystallization |
| KBs | kink bands |
| MSBs | microshear bands |
| LAGBs | low-angle grain boundaries |
| HAGBs | high-angle grain boundaries |
| SFE | stacking fault energy |
References
- Pan, F.; Yang, M.; Chen, X. A Review on Casting Magnesium Alloys: Modification of Commercial Alloys and Development of New Alloys. J. Mater. Sci. Technol. 2016, 32, 1211–1221. [Google Scholar] [CrossRef]
- Song, J.; She, J.; Chen, D.; Pan, F. Latest research advances on magnesium and magnesium alloys worldwide. J. Magnes. Alloys 2020, 8, 1–41. [Google Scholar] [CrossRef]
- Han, T.; Wang, L.; Lu, Y.; Lu, L.; Tiyyagura, H.R. Effect of Tensile Direction on Corrosion Behavior of AZ31 Magnesium Alloy Rolled Sheets. J. Mater. Eng. Perform. 2023, 33, 9194–9213. [Google Scholar] [CrossRef]
- Luo, Q.; Guo, Y.; Liu, B.; Feng, Y.; Zhang, J.; Li, Q.; Chou, K. Thermodynamics and kinetics of phase transformation in rare earth–magnesium alloys: A critical review. J. Mater. Sci. Technol. 2020, 44, 17190. [Google Scholar] [CrossRef]
- Liu, J.; Bian, D.; Zheng, Y.; Chu, X.; Lin, Y.; Wang, M.; Lin, Z.; Li, M.; Zhang, Y.; Guan, S. Comparative in vitro study on binary Mg-RE (Sc, Y, La, Ce, Pr, Nd, Sm, Eu, Gd, Tb, Dy, Ho, Er, Tm, Yb and Lu) alloy systems. Acta Biomater. 2020, 102, 508–528. [Google Scholar] [CrossRef]
- Rokhlin, L.L.; Dobatkina, T.V.; Nikitina, N.I. Constitution and Properties of the Ternary Magnesium Alloys Containing Two Rare-Earth Metals of Different Subgroups. Mater. Sci. Forum 2003, 419–422, 291–296. [Google Scholar] [CrossRef]
- Xia, X.; Sun, W.; Luo, A.A.; Stone, D.S. Precipitation evolution and hardening in Mg-Sm-Zn-Zr alloys. Acta Mater. 2016, 111, 335–347. [Google Scholar] [CrossRef]
- Rokhlin, L.L.; Dobatkina, T.V.; Tarytina, I.E.; Luk’yanova, E.A.; Ovchinnikova, O.A. Effect of Samarium on the Strength Properties of Mg–Y–Gd–Zr Alloys. Russ. Metall. (Met.) 2021, 2021, 267–271. [Google Scholar] [CrossRef]
- Nie, J.F.; Zhu, Y.M.; Morton, A.J. On the Structure, Transformation and Deformation of Long-Period Stacking Ordered Phases in Mg-Y-Zn Alloys. Metall. Mater. Trans. A 2014, 45A, 3338–3348. [Google Scholar] [CrossRef]
- Li, B.; Guan, K.; Yang, Q.; Niu, X.; Zhang, D.; Lv, S.; Meng, F.; Huang, Y.; Hort, N.; Meng, J. Microstructures and mechanical properties of a hot-extruded Mg−8Gd−3Yb−1.2Zn−0.5Zr (wt.%) alloy. J. Alloys Compd. 2019, 776, 666–678. [Google Scholar] [CrossRef]
- Liu, K.; Rokhlin, L.L.; Elkin, F.M.; Tang, D.; Meng, J. Effect of ageing treatment on the microstructures and mechanical properties of the extruded Mg–7Y–4Gd–1.5Zn–0.4Zr alloy. Mater. Sci. Eng. A 2010, 527, 828–834. [Google Scholar] [CrossRef]
- Zhou, J.; Yang, H.; Jiang, B.; He, C.; Dong, Z.; Liu, L.; Luo, X.; Liu, Y.; Huang, D.; Xu, J.; et al. Clarifying the deformation modes and strengthening mechanisms of Mg-11Gd-5Y-2Zn-0.7Zr with outstanding high-temperature mechanical properties. Mater. Sci. Eng. A 2023, 866, 1446–1483. [Google Scholar] [CrossRef]
- Liu, L.; Ding, H. Study of the plastic flow behaviors of AZ91 magnesium alloy during thermomechanical processes. J. Alloys Compd. 2009, 484, 949–956. [Google Scholar] [CrossRef]
- Li, Z.-J.; Wang, J.-G.; Yan, R.-F.; Chen, Z.-Y.; Ni, T.-Y.; Dong, Z.-Q.; Lu, T.-S. Effect of Ce addition on hot deformation behavior and microstructure evolution of AZ80 magnesium alloy. J. Mater. Res. Technol. 2022, 16, 1339–1352. [Google Scholar] [CrossRef]
- Qin, Y.-J.; Pan, Q.-L.; He, Y.-B.; Li, W.-B.; Liu, X.-Y.; Fan, X. Modeling of flow stress for magnesium alloy during hot deformation. Mater. Sci. Eng. A 2010, 527, 2790–2797. [Google Scholar] [CrossRef]
- Prasad, Y.V.R.K.; Gegel, H.L.; Doraivelu, S.M.; Malas, J.C.; Morgan, J.T.; Lark, K.A.; Barker, D.R. Modeling of dynamic material behavior in hot deformation: Forging of Ti-6242. Metall. Mater. Trans. A 1984, 15, 1883–1892. [Google Scholar] [CrossRef]
- Chen, T.; Chen, Z.; Shao, J.; Wang, R.; Mao, L.; Liu, C. The role of long period stacking ordered phase in dynamic recrystallization of a Mg–Zn–Y alloy during hot compression. J. Alloys Compd. 2020, 818, 1528–1541. [Google Scholar] [CrossRef]
- Hu, L.; Wang, J.; Zheng, P.; Lu, L.; Zhang, Y.; Zhang, L.; Tan, J.; Li, R.; Shen, H.; Zhang, J. Hot deformation and dynamic recrystallization of Mg-Gd-Y-Zn-Zr alloy containing high volume fraction 18R-LPSO phase. J. Alloys Compd. 2024, 1003, 175718. [Google Scholar] [CrossRef]
- Zhao, D.; Zhao, C.; Chen, X.; Huang, Y.; Hort, N.; Gavras, S.; Pan, F. Compressive deformation of as-extruded LPSO-containing Mg alloys at different temperatures. J. Mater. Res. Technol. 2022, 16, 944–959. [Google Scholar] [CrossRef]
- Bi, G.L.; Wang, Y.; Jiang, J.; Gu, J.; Li, Y.; Chen, T.; Ma, Y. Microstructure and mechanical properties of extruded Mg-Y-Zn (Ni) alloys. J. Alloys Compd. 2021, 881, 160577. [Google Scholar] [CrossRef]
- Zheng, J.; Chen, Z.; Yan, Z.; Zhang, Z.; Wang, Q.; Xue, Y. Preparation of ultra-high strength Mg-Gd-Y-Zn-Zr alloy by pre-ageing treatment prior to extrusion. J. Alloys Compd. 2022, 894, 162490. [Google Scholar] [CrossRef]
- Jeong, H.T.; Kim, W.J. The hot compressive deformation behavior of cast Mg-Gd-Y-Zn-Zr alloys with and without LPSO phase in their initial microstructures. J. Magnes. Alloys 2022, 10, 2901–2917. [Google Scholar] [CrossRef]
- Jia, J.; Zhang, H.; Meng, M.; Yang, X.; Zhang, X.; Zhang, Z. Strain-induced heterogeneous bimodal microstructure behavior of Mg-Gd-Y-Zn-Zr alloy containing LPSO phase during hot compression. J. Mater. Res. Technol. 2023, 27, 4264–4277. [Google Scholar] [CrossRef]
- Zhao, L.; Hao, J.; Liu, C.; Gui, H.; Zhang, J.; Wang, H.; Cheng, W. Hot compression behavior of Mg-Zn-Y-Mn-Ti magnesium alloy enhanced by lamellar LPSO phase and spherical W phase. J. Mater. Res. Technol. 2023, 25, 4784–4798. [Google Scholar] [CrossRef]
- Zhang, D.; Tan, Z.; Huo, Q.; Xiao, Z.; Fang, Z.; Yang, X. Dynamic recrystallization behaviors of Mg-Gd-Y-Zn-Zr alloy with different morphologies and distributions of LPSO phases. Mater. Sci. Eng. A 2017, 715, 389–403. [Google Scholar] [CrossRef]
- Zhou, X.-J.; Liu, C.-M.; Gao, Y.-H.; Jiang, S.-N.; Han, X.-Z.; Chen, Z.-Y. Evolution of LPSO Phases and Their Effect on Dynamic Recrystallization in a Mg-Gd-Y-Zn-Zr Alloy. Metall. Mater. Trans. A 2017, 48A, 3060–3072. [Google Scholar] [CrossRef]
- Xu, C.; Nakata, T.; Qiao, X.; Zheng, M.; Wu, K.; Kamado, S. Effect of LPSO and SFs on microstructure evolution and mechanical properties of Mg-Gd-Y-Zn-Zr alloy. Sci. Rep. 2017, 7, 4084–4089. [Google Scholar] [CrossRef]
- Zhang, S.; Yuan, G.Y.; Lu, C.; Ding, W.J. The relationship between (Mg,Zn) sub(3)RE phase and 14H-LPSO phase in Mg-Gd-Y-Zn-Zr alloys solidified at different cooling rates. J. Alloys Compd. 2011, 509, 3515–3521. [Google Scholar] [CrossRef]
- Yuan, M.; Zheng, Z.Q. Effects of heat treatment on microstructure and mechanical properties of Mg-2.6Sm- 1.3Gd-0.6Zn-0.5Zr alloy. Mater. Sci. Technol. MST A Publ. Inst. Met. 2014, 30, 261–267. [Google Scholar] [CrossRef]
- Li, B.B.; Shi, G.L.; Zhang, K.; Wang, K.K.; Li, X.G.; Li, Y.J.; Ma, M.L.; Yuan, J.W. Hot deformation behavior and processing map of Mg-12Gd-1MM-0.6Zr magnesium alloy. IOP Conf. Ser. Mater. Sci. Eng. 2020, 770, 012097. [Google Scholar] [CrossRef]
- Poliak, E.I.; Jonas, J.J. Critical Strain for Dynamic Recrystallization in Variable Strain Rate Hot Deformation. ISIJ Int. 2003, 43, 692–700. [Google Scholar] [CrossRef]
- Zhou, S.; Deng, K.; Li, J.; Nie, K.; Xu, F.; Zhou, H.; Fan, J. Hot deformation behavior and workability characteristics of bimodal size SiCp/AZ91 magnesium matrix composite with processing map. Mater. Des. 2014, 64, 177–184. [Google Scholar] [CrossRef]
- Tahreen, N.; Zhang, D.F.; Pan, F.S.; Jiang, X.Q.; Li, C.; Li, D.Y.; Chen, D. Characterization of hot deformation behavior of an extruded Mg–Zn–Mn–Y alloy containing LPSO phase. J. Alloys Compd. 2015, 644, 814–823. [Google Scholar] [CrossRef]
- Li, L.; Qi, F.; Wang, Q.; Hou, C.; Zhao, N.; Yang, Y.; Chai, S.; Ouyang, X. Hot deformation behavior of Mg95.21Zn1.44Y2.86Mn0.49 alloy containing LPSO phase. Mater. Charact. 2020, 169, 110649. [Google Scholar] [CrossRef]
- Wen, Y.; Guan, B.; Xin, Y.; Liu, C.; Wu, P.; Huang, G.; Liu, Q. Solute atom mediated Hall-Petch relations for magnesium binary alloys. Scr. Mater. 2022, 210, 114451. [Google Scholar] [CrossRef]
- Yu, H.; Xin, Y.; Wang, M.; Liu, Q. Hall-Petch relationship in Mg alloys:A review. J. Mater. Sci. Technol. 2018, 34, 248–256. [Google Scholar] [CrossRef]
- Luo, S.; Wang, N.; Wang, Y.; Chen, J.; Qin, H.; Kong, S.; Bai, T.; Lu, W.; Xiao, L.; Ma, X.; et al. Texture, microstructure and mechanical properties of an extruded Mg-10Gd-1Zn-0.4Zr alloy: Role of microstructure prior to extrusion. Mater. Sci. Eng. A 2022, 849, 143476. [Google Scholar] [CrossRef]
- Hagihara, K.; Yamasaki, M.; Kawamura, Y.; Nakano, T. Strengthening of Mg-based long-period stacking ordered (LPSO) phase with deformation kink bands. Mater. Sci. Eng. A 2019, 763, 138163. [Google Scholar] [CrossRef]
- Sellars, C.; Tegart, W. Hot Workability. Int. Mater. Rev. 1972, 17, 1–24. [Google Scholar] [CrossRef]
- Xu, W.; Jin, X.; Shan, D.; Chai, B. Study on the effect of solution treatment on hot deformation behavior and workability of Mg-7Gd-5Y-0.6Zn-0.8Zr magnesium alloy. J. Alloys Compd. 2017, 720, 309–323. [Google Scholar] [CrossRef]
- Zhang, Z.; Yan, Z.; Du, Y.; Zhang, G.; Zhu, J.; Ren, L.; Wang, Y. Hot Deformation Behavior of Homogenized Mg-13.5Gd-3.2Y-2.3Zn-0.5Zr Alloy via Hot Compression Tests. Materials 2018, 11, 2282. [Google Scholar] [CrossRef]
- Oñorbe, E.; Garcés, G.; Pérez, P.; Cabezas, S.; Klaus, M.; Genzel, C.; Frutos, E.; Adeva, P. The evolution of internal strain in Mg–Y–Zn alloys with a long period stacking ordered structure. Scr. Mater. 2011, 65, 719–722. [Google Scholar] [CrossRef]
- Li, B.; Teng, B.; Xu, W. Hot Deformation Characterization of Homogenized Mg-Gd-Y-Zn-Zr Alloy During Isothermal Compression(Article). J. Miner. Met. Mater. Soc. 2019, 71, 4059–4070. [Google Scholar] [CrossRef]
- Xue, Z.; Luo, W.; Zhao, Z.; Ren, Y. Thermal compression, processing maps and microstructural evolution of as-cast Mg-Gd-Y-Zn-Zr alloy with long period stacking ordered phase(Article). Mater. Res. Express 2020, 7, 056512. [Google Scholar] [CrossRef]
- Pang, H.; Li, Q.; Chen, X.; Chen, P.; Li, X.; Tan, J. Hot deformation behavior and microstructure evolution of Mg-Gd-Y(-Sm)-Zr alloys. J. Alloys Compd. 2022, 920, 165937. [Google Scholar] [CrossRef]
- Zener, C.; Hollomon, J.H. Effect of Strain Rate Upon Plastic Flow of Steel. J. Appl. Phys. 1944, 15, 22–32. [Google Scholar] [CrossRef]
- Dong, Y.Y.; Zhang, C.; Lu, X.; Wang, C.; Zhao, G. Constitutive equations and flow behavior of an as-extruded AZ31 magnesium alloy under large strain condition. J. Mater. Eng. Perform. 2016, 25, 2267–2281. [Google Scholar] [CrossRef]
- Cai, J.; Wang, K.; Han, Y. A Comparative Study on Johnson Cook, Modified Zerilli-Armstrong and Arrhenius-Type Constitutive Models to Predict High-Temperature Flow Behavior of Ti-6Al-4V Alloy in alpha plus beta Phase. High Temp. Mater. Process. 2016, 35, 297–307. [Google Scholar] [CrossRef]
- Prasad, Y.V.R.K.; Seshacharyulu, T. Modelling of hot deformation for microstructural control. Int. Mater. Rev. 1998, 43, 243–258. [Google Scholar] [CrossRef]
- Srinivasan, N.; Prasad, Y.V.R.K. Microstructural control in hot working of IN-718 superalloy using processing map. Metall. Mater. Trans. A 1994, 25, 2275–2284. [Google Scholar] [CrossRef]
- Xin, J.; Zhang, L.; Ge, G.; Lin, J. Characterization of microstructure evolution in β-γ TiAl alloy containing high content of Niobium using constitutive equation and power dissipation map. Mater. Des. 2016, 107, 406–415. [Google Scholar] [CrossRef]
- Prasad, Y.; Rao, K. Processing maps for hot deformation of rolled AZ31 magnesium alloy plate: Anisotropy of hot workability. Mater. Sci. Eng. A 2008, 487, 316–327. [Google Scholar] [CrossRef]
- Kaibyshev, R.; Gottstein, G.; Galiyev, A. Correlation of plastic deformation and dynamic recrystallization in magnesium alloy ZK60. Acta Mater. 2001, 49, 1199–1207. [Google Scholar] [CrossRef]
- Su, N.; Deng, Q.; Wu, Y.; Peng, L.; Yang, K.; Chen, Q. Deformation-induced dissolution of long-period stacking ordered structures and its re-precipitation in a Mg-Gd-Zn-Mn alloy. Mater. Charact. 2020, 171, 110756. [Google Scholar] [CrossRef]
- Zhao, X.; Yang, Z.; Zhang, J.; Liang, M.; Wang, L. Formation and transformation of metastable LPSO building blocks clusters in Mg-Gd-Y-Zn-Zr alloys by spinodal decomposition and heterogeneous nucleation. J. Magnes. Alloys 2024, 12, 673–686. [Google Scholar] [CrossRef]
- Huang, K.; Logé, R.E. A review of dynamic recrystallization phenomena in metallic materials. Mater. Des. 2016, 111, 548–574. [Google Scholar] [CrossRef]
- Zhou, X.J.; Liu, C.M.; Gao, Y.H.; Jiang, S.N.; Chen, Z.Y. Improved workability and ductility of the Mg-Gd-Y-Zn-Zr alloy via enhanced kinking and dynamic recrystallization. J. Alloys Compd. 2018, 749, 878–886. [Google Scholar] [CrossRef]
- Yu, J.; Zhang, Z.; Wang, Q.; Yin, X.; Cui, J.; Qi, H. Dynamic recrystallization behavior of magnesium alloys with LPSO during hot deformation. J. Alloys Compd. 2017, 704, 382–389. [Google Scholar] [CrossRef]
- Li, K.; Chen, Z.; Chen, T.; Shao, J.; Wang, R.; Liu, C. Hot deformation and dynamic recrystallization behaviors of Mg-Gd-Zn alloy with LPSO phases. J. Alloys Compd. 2019, 792, 894–906. [Google Scholar] [CrossRef]
- Zhang, J.; Yi, Y.; Huang, S.; Mao, X.; He, H.; Tang, J.; Guo, W.; Dong, F. Dynamic recrystallization mechanisms of 2195 aluminum alloy during medium/high temperature compression deformation. Mater. Sci. Eng. A 2021, 804, 140650. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, J.; Xu, C.; Zong, X.; Zhu, W.; Ma, Q. Precipitation behaviors of 14H LPSO lamellae in Mg96Gd3Zn0.5Ni0.5 alloys during severe plastic deformation. J. Mater. Sci. 2017, 52, 13271–13283. [Google Scholar] [CrossRef]
- Xiao, J.; Chen, Z.; Shao, J.; Chen, T.; Lin, X.; Liu, C. Evolution of long-period stacking ordered phases and their effect on recrystallization in extruded Mg-Gd-Y-Zn-Zr alloy during annealing. Mater. Charact. 2020, 167, 110515. [Google Scholar] [CrossRef]






| Element | Er | Sm | Zn | Zr | Mg |
|---|---|---|---|---|---|
| Composition (wt.%) | 9.235 | 4.856 | 2.223 | 0.5940 | Bal. |
| Alloy Composition (wt.%) | Deformation Temperature Range (K) | Strain Rate Range (s−1) | Activation Energy (Q, kJ/mol) |
|---|---|---|---|
| Pure Mg [41,43,44] | 623~773 | 0.001~1 | 135 |
| Mg-13.5Gd-3.2Y-2.3Zn-0.5Zr [41] | 623~773 | 0.001~1 | 263.17 |
| Mg-13Gd-4Y-2Zn-0.6Zr [43] | 673~748 | 0.001~1 | 276.21 |
| Mg-7.5Gd-2.5Y-1.5Zn-0.5Zr [44] | 623~723 | 0.001~1 | 234.6 |
| Mg-6Gd-3Y-0.5Zr [45] | 623~773 | 0.003~1 | 206.17 |
| Mg-6Gd-3Y-3Sm-0.5Zr [45] | 623~773 | 0.003~1 | 263.07 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shao, G.; Cai, Z.; Che, C.; Cheng, L.; Shi, M.; Han, T.; Liang, X.; Zhang, H. Effect of Initial Solid Solution Microstructure on the Hot Deformation Behavior of Mg-Er-Sm-Zn-Zr Alloy. Crystals 2025, 15, 855. https://doi.org/10.3390/cryst15100855
Shao G, Cai Z, Che C, Cheng L, Shi M, Han T, Liang X, Zhang H. Effect of Initial Solid Solution Microstructure on the Hot Deformation Behavior of Mg-Er-Sm-Zn-Zr Alloy. Crystals. 2025; 15(10):855. https://doi.org/10.3390/cryst15100855
Chicago/Turabian StyleShao, Guiyang, Zhongyi Cai, Chaojie Che, Liren Cheng, Minqiang Shi, Tingzhuang Han, Xiaobo Liang, and Hongjie Zhang. 2025. "Effect of Initial Solid Solution Microstructure on the Hot Deformation Behavior of Mg-Er-Sm-Zn-Zr Alloy" Crystals 15, no. 10: 855. https://doi.org/10.3390/cryst15100855
APA StyleShao, G., Cai, Z., Che, C., Cheng, L., Shi, M., Han, T., Liang, X., & Zhang, H. (2025). Effect of Initial Solid Solution Microstructure on the Hot Deformation Behavior of Mg-Er-Sm-Zn-Zr Alloy. Crystals, 15(10), 855. https://doi.org/10.3390/cryst15100855






