Crystal Morphology Prediction Models and Regulating Methods
Abstract
1. Introduction
2. Crystal Growth Models & Prediction
2.1. Gibbs–Curie–Wulff Principle
2.2. BFDH Model
2.3. AE & MAE Model
2.4. The Occupancy Model
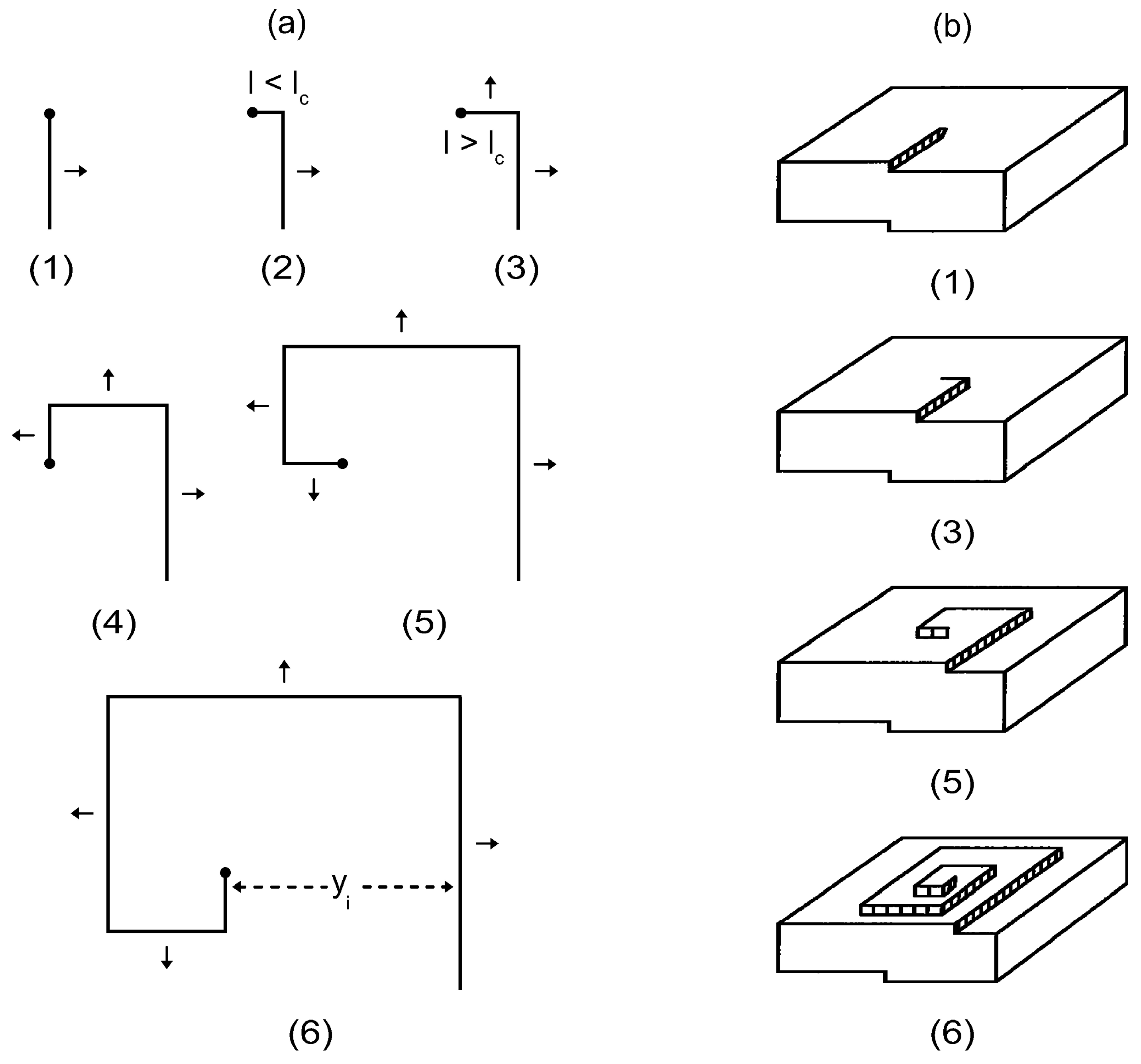
2.5. Spiral Crystal Growth Model
2.6. Molecular Simulation
3. Methods of Modification
3.1. Temperature
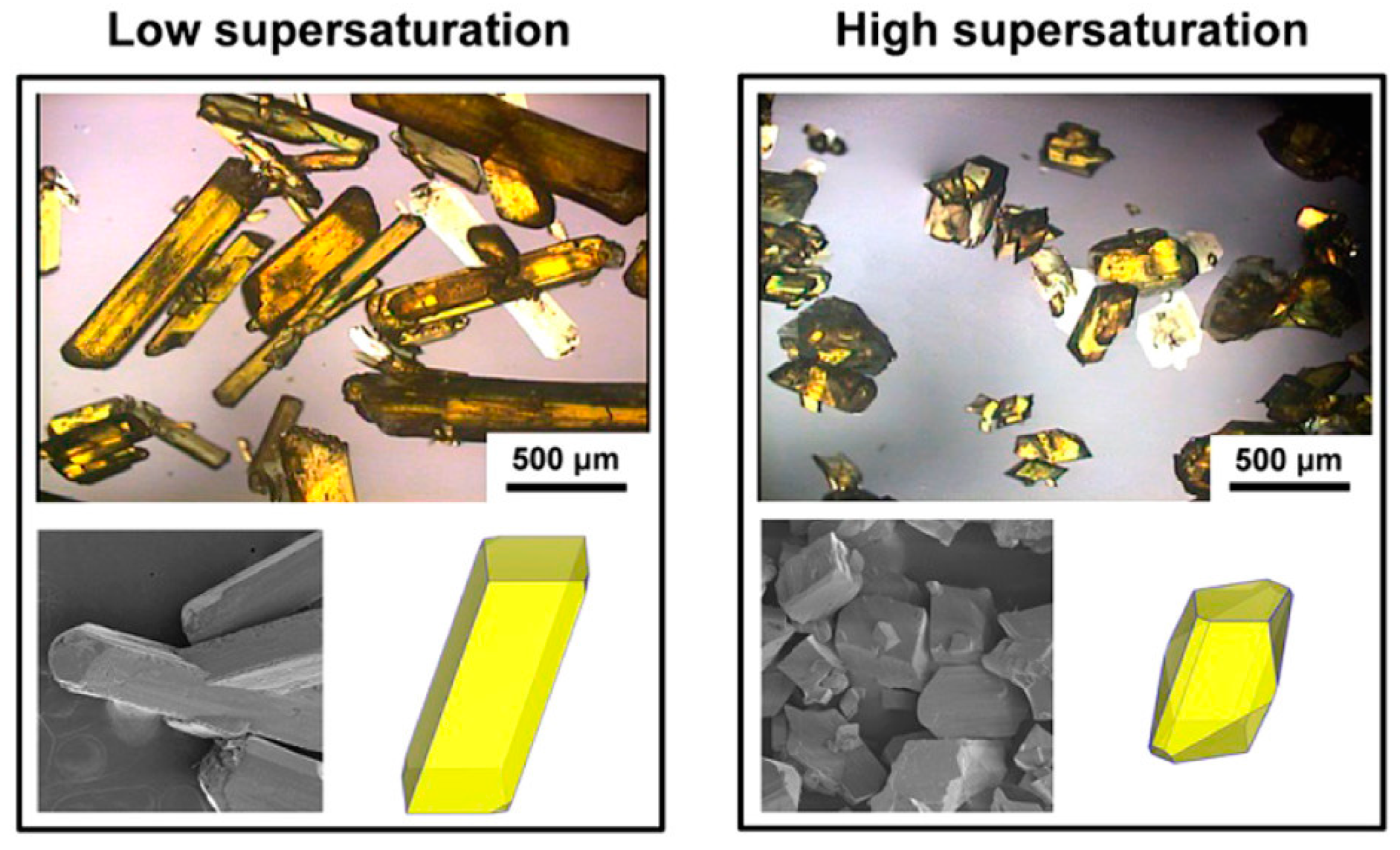
3.2. Supersaturation
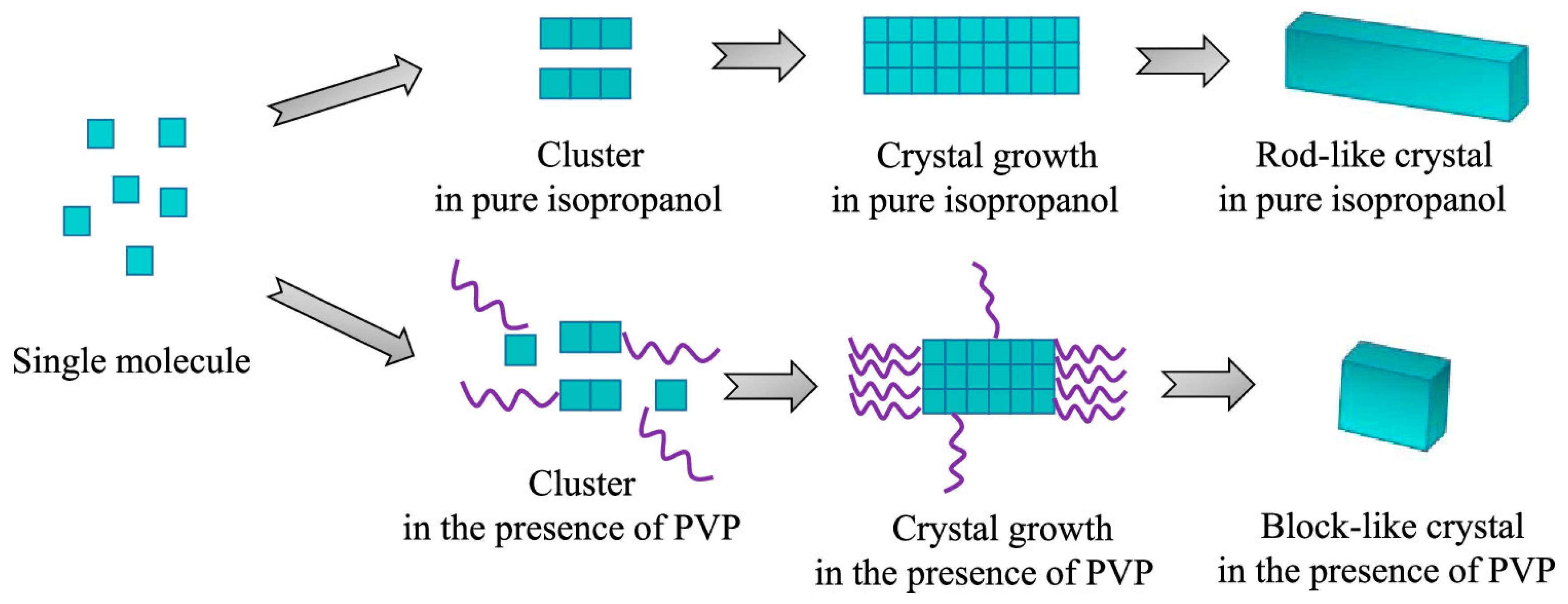
3.3. Foreign Molecules
3.4. Solvents
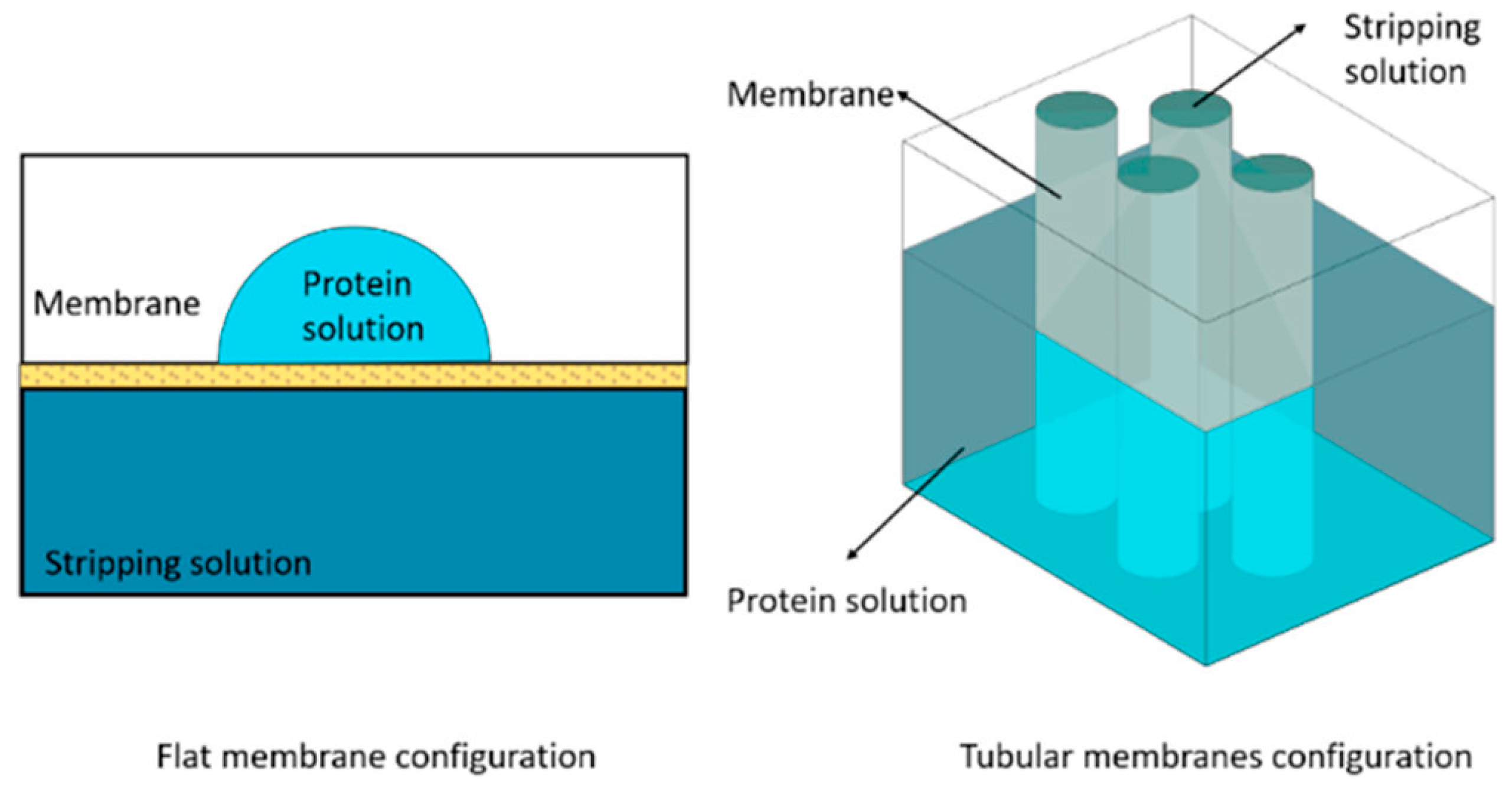
3.5. Membrane Assistance
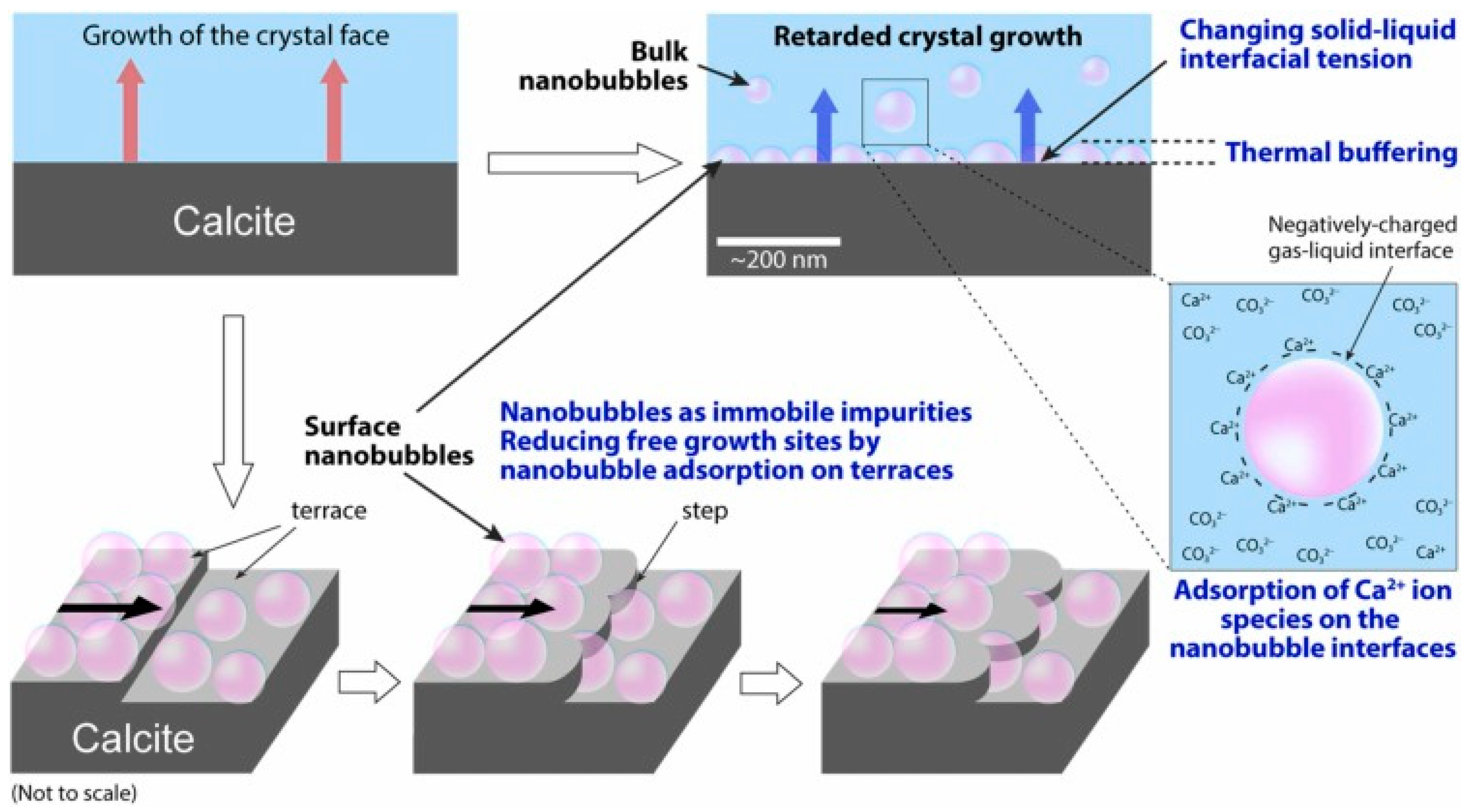
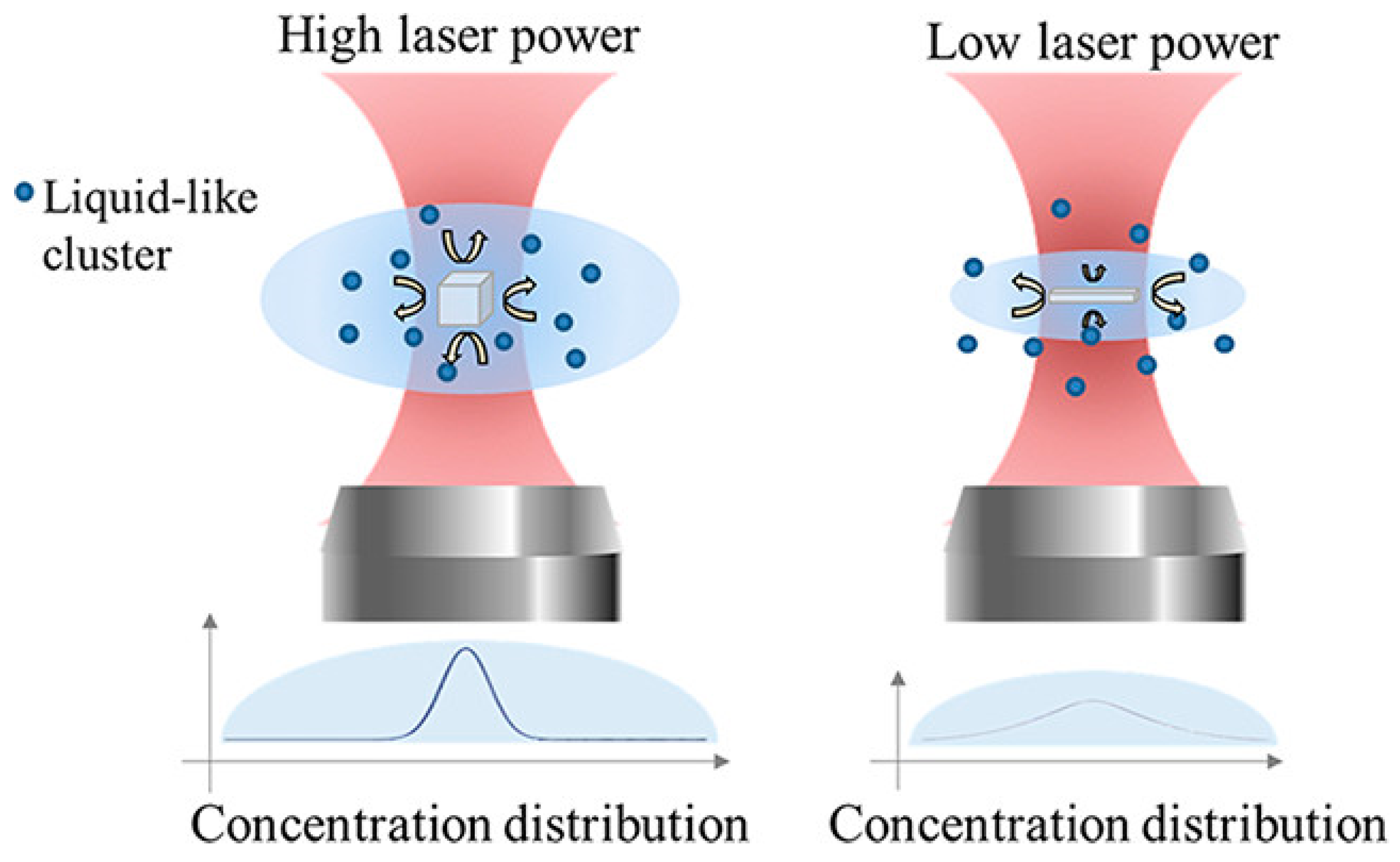
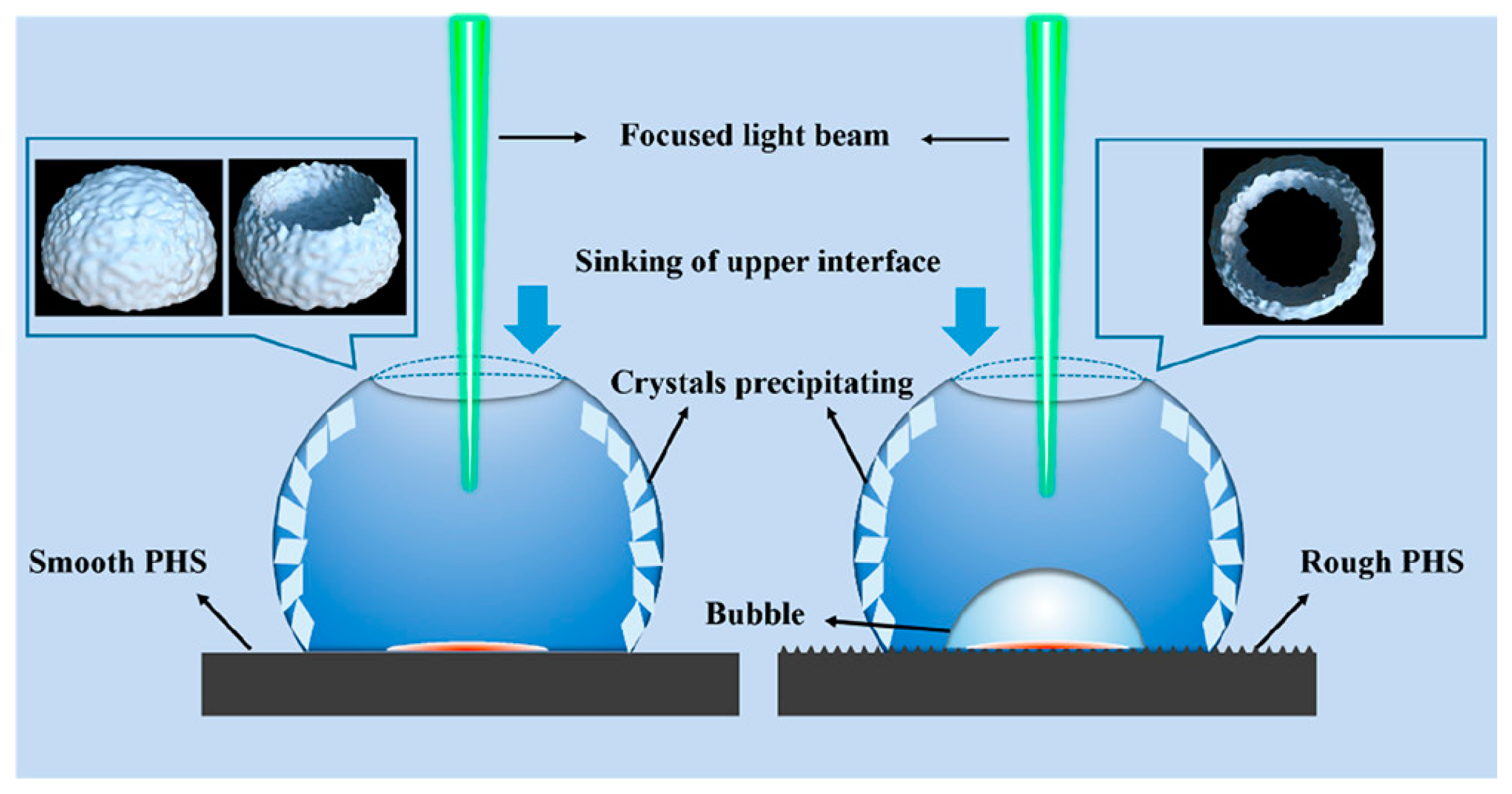
3.6. External Physical Fields
3.7. Ball Milling
4. Summary and Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kou, Y.; Song, X.; Guo, K.; Cheng, Z.; Wang, Y. Characterization, Thermolysis, and Energetic Properties of an MTNP/PETN Eutectic Prepared via the Solvent/Anti-Solvent Method. Propellants Explos. Pyrotech. 2021, 46, 299–308. [Google Scholar] [CrossRef]
- Shekunov, B.Y.; York, P. Crystallization processes in pharmaceutical technology and drug delivery design. J. Cryst. Growth 2000, 211, 122–136. [Google Scholar] [CrossRef]
- Guo, C.; Wang, Y.; Xie, J.; Zhu, B.; Qi, M.-H.; Hong, M.; Ren, G.-B. Novel Salts of the Atypical Antipsychotic Drug Lurasidone with Improved Solubility and Bioavailability. Cryst. Growth Des. 2022, 23, 326–332. [Google Scholar] [CrossRef]
- Cheng, X.; Huang, X.; Hao, Y.; Wang, B.; Sun, C.; Shu, J.; Hao, H. Unveiling the Role of Additives in Modifying Crystallization Behaviors of 4-(Hydroxymethyl) Benzoic Acid. Ind. Eng. Chem. Res. 2022, 61, 7193–7203. [Google Scholar] [CrossRef]
- Cheng, X.; Huang, X.; Zheng, Z.; Dong, Y.; Wang, T.; Hao, H. Toward Understanding the Growth of Cefradine in Aqueous Solution. Cryst. Growth Des. 2021, 21, 1993–2004. [Google Scholar] [CrossRef]
- Tanguy, D.; Marchal, P.A.H. Relations between the properties of particles and their process of manufacture. Chem. Eng. Res. Des. 1996, 74, 715–722. [Google Scholar]
- Variankaval, N.; Cote, A.S.; Doherty, M.F. From form to function: Crystallization of active pharmaceutical ingredients. AIChE J. 2008, 54, 1682–1688. [Google Scholar] [CrossRef]
- Miller, J.K.; Mares, J.O.; Gunduz, I.E.; Son, S.F.; Rhoads, J.F. The impact of crystal morphology on the thermal responses of ultrasonically-excited energetic materials. J. Appl. Phys. 2016, 119, 024903. [Google Scholar] [CrossRef]
- Jiao, F.; Xiong, Y.; Li, H.; Zhang, C. Alleviating the energy & safety contradiction to construct new low sensitivity and highly energetic materials through crystal engineering. CrystEngComm 2018, 20, 1757–1768. [Google Scholar] [CrossRef]
- Song, L.; Zhao, F.-Q.; Xu, S.-Y.; Ju, X.-H.; Ye, C.-C. Crystal Morphology Prediction and Anisotropic Evolution of 1,1-Diamino-2,2-dinitroethylene (FOX-7) by Temperature Tuning. Sci. Rep. 2020, 10, 2317. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, X.; Du, W.; Huang, Y.-h.; Guo, M.-x.; Li, Y.; Zhang, Z.-x.; Hou, B.-h.; Yin, Q.-x. Effects of solvent and supersaturation on crystal morphology of cefaclor dihydrate: A combined experimental and computer simulation study. CrystEngComm 2016, 18, 9085–9094. [Google Scholar] [CrossRef]
- Li, J.-J.; Doherty, M.F. Steady State Morphologies of Paracetamol Crystal from Different Solvents. Cryst. Growth Des. 2017, 17, 659–670. [Google Scholar] [CrossRef]
- Simone, E.; Klapwijk, A.R.; Wilson, C.C.; Nagy, Z.K. Investigation of the Evolution of Crystal Size and Shape during Temperature Cycling and in the Presence of a Polymeric Additive Using Combined Process Analytical Technologies. Cryst. Growth Des. 2017, 17, 1695–1706. [Google Scholar] [CrossRef] [PubMed]
- Cheng, X.; Li, F.; Luo, L.; Ding, Z.; Zeng, L.; Mao, Y.; Huang, X.; Hao, H. On the selection of wetting liquid for spherical agglomeration of cefotaxime sodium. Powder Technol. 2020, 363, 593–601. [Google Scholar] [CrossRef]
- Zhang, S.; Zhou, L.; Yang, W.; Xie, C.; Wang, Z.; Hou, B.; Hao, H.; Zhou, L.; Bao, Y.; Yin, Q. An Investigation into the Morphology Evolution of Ethyl Vanillin with the Presence of a Polymer Additive. Cryst. Growth Des. 2020, 20, 1609–1617. [Google Scholar] [CrossRef]
- Salvalaglio, M.; Vetter, T.; Giberti, F.; Mazzotti, M.; Parrinello, M. Uncovering molecular details of urea crystal growth in the presence of additives. J. Am. Chem. Soc. 2012, 134, 17221–17233. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Tilbury, C.J.; Kim, S.H.; Doherty, M.F. A design aid for crystal growth engineering. Prog. Mater. Sci. 2016, 82, 1–38. [Google Scholar] [CrossRef]
- Docherty, R.; Clydesdale, G.; Roberts, K.J.; Bennema, P. Application of Bravais-Friedel-Donnay-Harker, attachment energy and Ising models to predicting and understanding the morphology of molecular crystals. J. Phys. D Appl. Phys. 1991, 24, 89. [Google Scholar] [CrossRef]
- Cheng, Y.; She, C.; Qiao, M.; Jin, S.; Chen, S.; Li, L.; Chen, K. Molecular dynamics simulation on the crystal morphology of β-HMX affected by binary and ternary solvent systems. J. Cryst. Growth 2022, 598, 126874. [Google Scholar] [CrossRef]
- Trampuž, M.; Teslić, D.; Likozar, B. Crystal-size distribution-based dynamic process modelling, optimization, and scaling for seeded batch cooling crystallization of Active Pharmaceutical Ingredients (API). Chem. Eng. Res. Des. 2021, 165, 254–269. [Google Scholar] [CrossRef]
- Jiang, F.; Yang, L.; Zhou, D.; He, G.; Zhou, J.; Wang, F.; Chen, Z.-G. First-principles atomistic Wulff constructions for an equilibrium rutile TiO2 shape modeling. Appl. Surf. Sci. 2018, 436, 989–994. [Google Scholar] [CrossRef]
- Pisarek, J.; Malinska, M. Structure and Morphology of Indole Analogue Crystals. ACS Omega 2020, 5, 17141–17151. [Google Scholar] [CrossRef] [PubMed]
- Bravais, A. Études cristallographiques, première partie: Du cristal considéré comme un simple assemblage de points. Présenté à lʼAcadémie des sciences 1849, 26, 168. [Google Scholar]
- Friedel, G. Études sur la loi de Bravais. Bull. Soc. Fr. Minér. 1907, 9, 326. [Google Scholar] [CrossRef]
- Donnay, J.D.H.; Harker, D. A new law of crystal morphology extending the Law of Bravais. Am. Mineral. 1937, 22, 446–467. [Google Scholar]
- Frank, F.C. Introductory Lecture; John Wiley & Sons: Hoboken, NJ, USA, 1958. [Google Scholar]
- Bade, I.; Verma, V.; Rosbottom, I.; Heng, J.Y.Y. Crystal regeneration—A unique growth phenomenon observed in organic crystals post breakage. Mater. Horiz. 2023, 10, 1425–1430. [Google Scholar] [CrossRef] [PubMed]
- Ouasri, A.; Lambarki, F.; Fakherddine, R.; Aatiq, A.; Rhandour, A. Structural characterisation, BFDH morphology, DSC, infrared and Raman studies of the disordered tetramethylammonium nonachlorodibismuthate [(CH3)4N]3Bi2Cl9. Polyhedron 2024, 251, 116875. [Google Scholar] [CrossRef]
- Hartman, P.; Bennema, P. The attachment energy as a habit controlling factor: I. Theoretical considerations. J. Cryst. Growth 1980, 49, 145–156. [Google Scholar] [CrossRef]
- Song, L.; Lv, S.; Guo, H.; Cui, Y.; Zhang, X.; Zhang, S.; Tian, Y.; Yang, C. Crystal morphology regulation of pronamide through solvent selection: Prediction and implementation. J. Chem. Thermodyn. 2022, 169, 106743. [Google Scholar] [CrossRef]
- Ge, M.; Chen, K.; Li, L.; Huang, L.; Ning, L.; Liu, Q. The effect of solvents on the morphology of NTO crystal by molecular dynamics. J. Phys. Conf. Ser. 2022, 2285, 012034. [Google Scholar] [CrossRef]
- Keller, K.W. I. Sunagawa (Ed.) Morphology of crystals. Part A. Terra Scientific Publ. Co., Tokyo and D. Reidel Publ. Co., Dordrecht 1987, pp. XXI + 365, 188 figs., 4 tables. Price Dfl. 220.00. ISBN 90-277-2507-1. Cryst. Res. Technol. 1989, 24, 20. [Google Scholar] [CrossRef]
- Liu, Y.; Niu, S.; Lai, W.; Yu, T.; Ma, Y.; Gao, H.; Zhao, F.; Ge, Z. Crystal morphology prediction of energetic materials grown from solution: Insights into the accurate calculation of attachment energies. CrystEngComm 2019, 21, 4910–4917. [Google Scholar] [CrossRef]
- Duan, X.; Wei, C.; Liu, Y.; Pei, C. A molecular dynamics simulation of solvent effects on the crystal morphology of HMX. J. Hazard. Mater. 2010, 174, 175–180. [Google Scholar] [CrossRef] [PubMed]
- Mao, J.-s.; Wang, B.-g.; He, J.-c.; Yang, C.-s.; Fu, J.-b.; Chen, Y.-f. Prediction of morphology of CL-20/TFAZ cocrystal crystals in binary solvents based on modified attachment energy model. J. Cryst. Growth 2024, 637–638, 127718. [Google Scholar] [CrossRef]
- Zhang, C.; Ji, C.; Li, H.; Zhou, Y.; Xu, J.; Xu, R.; Li, J.; Luo, Y. Occupancy Model for Predicting the Crystal Morphologies Influenced by Solvents and Temperature, and Its Application to Nitroamine Explosives. Cryst. Growth Des. 2012, 13, 282–290. [Google Scholar] [CrossRef]
- Liu, N.; Zhou, C.; Wu, Z.; Lu, X.; Wang, B.; Wang, W. Theoretical study on crystal morphologies of 1,1-diamino-2,2-dinitroethene in solvents: Modified attachment energy model and occupancy model. J. Mol. Graph. Model. 2018, 85, 262–269. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.; Huang, S.; Zhu, W. Solvent effects on the crystal morphology of β-HMXstudied bymodified attachment energy and occupancy models. J. Cryst. Growth 2022, 585, 126605. [Google Scholar] [CrossRef]
- Budewski, E.; Bostanoff, W.; Witanoff, T.; Stoinoff, Z.; Kotzewa, A.; Kaischew, R. Keimbildungserscheinungen an versetzungsfreien (100)-flächen von silbereinkristallen. Electrochim. Acta 1966, 11, 1697–1707. [Google Scholar] [CrossRef]
- Burton, W.K.; Cabrera, N.; Frank, F.C. The Growth of Crystals and the Equilibrium Structure of their Surfaces. Philos. Trans. R. Soc. Lond. 1951, 243, 299–358. [Google Scholar]
- Mazal, T.; Doherty, M.F. Modeling Impurity-Mediated Crystal Growth and Morphologies of Centrosymmetric Molecules. Cryst. Growth Des. 2022, 23, 369–379. [Google Scholar] [CrossRef]
- Lovette, M.A.; Browning, A.R.; Griffin, D.W.; Sizemore, J.P.; Snyder, R.C.; Doherty, M.F. Crystal Shape Engineering. Ind. Eng. Chem. Res. 2008, 47, 9812–9833. [Google Scholar] [CrossRef]
- Shim, H.-M.; Koo, K.-K. Crystal Morphology Prediction of Hexahydro-1,3,5-trinitro-1,3,5-triazine by the Spiral Growth Model. Cryst. Growth Des. 2014, 14, 1802–1810. [Google Scholar] [CrossRef]
- Tilbury, C.J.; Doherty, M.F. Modeling layered crystal growth at increasing supersaturation by connecting growth regimes. AIChE J. 2017, 63, 1338–1352. [Google Scholar] [CrossRef]
- Martins, P.M.; Rocha, F. Characterization of crystal growth using a spiral nucleation model. Surf. Sci. 2007, 601, 3400–3408. [Google Scholar] [CrossRef]
- Li, L.; Ji, X.; Cheng, X.; Li, D.; Wang, T.; Huang, X.; Wang, N.; Yin, Q.; Hao, H. Effect of the solvent on the morphology of sulfamerazine crystals and its molecular mechanism. CrystEngComm 2022, 24, 5497–5506. [Google Scholar] [CrossRef]
- Cote, A.; Erdemir, D.; Girard, K.P.; Green, D.A.; Lovette, M.A.; Sirota, E.; Nere, N.K. Perspectives on the Current State, Challenges, and Opportunities in Pharmaceutical Crystallization Process Development. Cryst. Growth Des. 2020, 20, 7568–7581. [Google Scholar] [CrossRef]
- Piana, S.; Reyhani, M.; Gale, J.D. Simulating micrometre-scale crystal growth from solution. Nature 2005, 438, 70–73. [Google Scholar] [CrossRef] [PubMed]
- Shim, H.-M.; Kim, H.-S.; Koo, K.-K. Molecular Modeling on Supersaturation-Dependent Growth Habit of 1,1-Diamino-2,2-dinitroethylene. Cryst. Growth Des. 2015, 15, 1833–1842. [Google Scholar] [CrossRef]
- Mao, X.; Song, X.; Lu, G.; Sun, Y.; Xu, Y.; Yu, J. Control of Crystal Morphology and Size of Calcium Sulfate Whiskers in Aqueous HCl Solutions by Additives: Experimental and Molecular Dynamics Simulation Studies. Ind. Eng. Chem. Res. 2015, 54, 4781–4787. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, X.; Li, M.; Zhou, X.; Zhang, Z.-Q.; Gong, J.; Li, H.; Zhang, Q. Uncovering the Morphological Regulation Mechanism of Low Sensitivity and Highly Energetic Materials in Solvents: Changing Crystal Morphology Induced by Hydrogen Bonding. Cryst. Growth Des. 2022, 22, 5935–5946. [Google Scholar] [CrossRef]
- Berkovitch-Yellin, Z.; Van Mil, J.; Addadi, L.; Idelson, M.; Lahav, M.; Leiserowitz, L. Crystal morphology engineering by “tailor-made” inhibitors; a new probe to fine intermolecular interactions. J. Am. Chem. Soc. 1985, 107, 3111–3122. [Google Scholar] [CrossRef]
- Matsuura, R.; Horii, S.; Alavi, S.; Ohmura, R. Diversity in Crystal Growth Dynamics and Crystal Morphology of Structure-H Hydrate. Cryst. Growth Des. 2019, 19, 6398–6404. [Google Scholar] [CrossRef]
- Zhao, W.; Li, B.; Liu, S.; Deng, Y.; Zhang, R.; Jiang, Y. Kinetic study of complicated anti-solvent and cooling crystallization of disodium 5′-ribonucleotide. Particuology 2023, 73, 103–112. [Google Scholar] [CrossRef]
- Patchigolla, K.; Wilkinson, D. Characterization of Organic and Inorganic Chemicals Formed by Batch-Cooling Crystallization: Shape and Size. Ind. Eng. Chem. Res. 2008, 47, 804–812. [Google Scholar] [CrossRef]
- Doki, N.; Seki, H.; Takano, K.; Asatani, H.; Yokota, M.; Kubota, N. Process Control of Seeded Batch Cooling Crystallization of the Metastable α-Form Glycine Using an in-Situ ATR-FTIR Spectrometer and an in-Situ FBRM Particle Counter. Cryst. Growth Des. 2004, 4, 949. [Google Scholar] [CrossRef]
- Zhang, S.; Jia, N.; Zhang, L.; Hou, H.; Su, M. Dynamic evolution investigation on crystal size and morphology of sodium sulfate based on a combination of ultrasonic and image on-line testing. J. Cryst. Growth 2024, 625, 127450. [Google Scholar] [CrossRef]
- Jiang, M.; Zhu, X.; Molaro, M.C.; Rasche, M.L.; Zhang, H.; Chadwick, K.; Raimondo, D.M.; Kim, K.-K.K.; Zhou, L.; Zhu, Z.; et al. Modification of Crystal Shape through Deep Temperature Cycling. Ind. Eng. Chem. Res. 2014, 53, 5325–5336. [Google Scholar] [CrossRef]
- Kim, Y.; Kawajiri, Y.; Rousseau, R.W.; Grover, M.A. Modeling of Nucleation, Growth, and Dissolution of Paracetamol in Ethanol Solution for Unseeded Batch Cooling Crystallization with Temperature-Cycling Strategy. Ind. Eng. Chem. Res. 2023, 62, 2866–2881. [Google Scholar] [CrossRef]
- Poornachary, S.K.; Chia, V.D.; Yani, Y.; Han, G.; Chow, P.S.; Tan, R.B.H. Anisotropic Crystal Growth Inhibition by Polymeric Additives: Impact on Modulation of Naproxen Crystal Shape and Size. Cryst. Growth Des. 2017, 17, 4844–4854. [Google Scholar] [CrossRef]
- Zhu, Y.; Lu, M.; Gao, F.; Zhou, C.; Jia, C.; Wang, J. Role of Tailor-Made Additives in Crystallization from Solution: A Review. Ind. Eng. Chem. Res. 2023, 62, 4800–4816. [Google Scholar] [CrossRef]
- McPherson, A.; Nguyen, C.; Cudney, R.; Larson, S.B. The Role of Small Molecule Additives and Chemical Modification in Protein Crystallization. Cryst. Growth Des. 2011, 11, 1469–1474. [Google Scholar] [CrossRef]
- Kothari, R.; Winter, H.H.; Watkins, J.J. Rheological Study of Order-to-Disorder Transitions and Phase Behavior of Block Copolymer–Surfactant Complexes Containing Hydrogen-Bonded Small Molecule Additives. Macromolecules 2014, 47, 8048–8055. [Google Scholar] [CrossRef]
- Shtukenberg, A.G.; Ward, M.D.; Kahr, B. Crystal Growth with Macromolecular Additives. Chem. Rev. 2017, 117, 14042–14090. [Google Scholar] [CrossRef] [PubMed]
- Baruah, A.; Pathak, A.K.; Ojha, K. Study on the Thermal Stability of Viscoelastic Surfactant-Based Fluids Bearing Lamellar Structures. Ind. Eng. Chem. Res. 2015, 54, 7640–7649. [Google Scholar] [CrossRef]
- Tegladza, I.D.; Lin, G.; Liu, C.; Gu, X. Control of crystal nucleation, size and morphology using micro−/nanobubbles as green additives—A review. Sep. Purif. Technol. 2023, 311, 123232. [Google Scholar] [CrossRef]
- Addadi, L.; Berkovitch-Yellin, Z.; Weissbuch, I.; van Mil, J.; Shimon, L.J.W.; Lahav, M.; Leiserowitz, L. Growth and Dissolution of Organic Crystals with “Tailor-Made” Inhibitors—Implications in Stereochemistry and Materials Science. Angew. Chem. Int. Ed. Engl. 1985, 24, 466–485. [Google Scholar] [CrossRef]
- Kaskiewicz, P.L.; Rosbottom, I.; Hammond, R.B.; Warren, N.J.; Morton, C.; Dowding, P.J.; George, N.; Roberts, K.J. Understanding and Designing Tailor-Made Additives for Controlling Nucleation: Case Study of p-Aminobenzoic Acid Crystallizing from Ethanolic Solutions. Cryst. Growth Des. 2021, 21, 1946–1958. [Google Scholar] [CrossRef]
- Yu, S.; Wang, Z.; Ma, Y.; Xue, F. Effect of natural polymer additives on crystal form and morphology of clozapine anhydrate and monohydrate. J. Mol. Liq. 2022, 364, 119985. [Google Scholar] [CrossRef]
- Liu, Q.; Lin, G.; Zhou, J.; Huang, L.; Liu, C. Hydrogen-bond mediated and concentrate-dependent NaHCO3 crystal morphology in NaHCO3–Na2CO3 aqueous solution: Experiments and computer simulations. Chin. J. Chem. Eng. 2023, 55, 49–58. [Google Scholar] [CrossRef]
- Madeja, B.; Avaro, J.; Van Driessche, A.E.S.; Rückel, M.; Wagner, E.; Cölfen, H.; Kellermeier, M. Tuning the growth morphology of gypsum crystals by polymers. Cem. Concr. Res. 2023, 164, 107049. [Google Scholar] [CrossRef]
- Wang, C.; Gao, L.; Liu, M.; Xia, S.; Han, Y. Self-crystallization behavior of paraffin and the mechanism study of SiO2 nanoparticles affecting paraffin crystallization. Chem. Eng. J. 2023, 452, 139287. [Google Scholar] [CrossRef]
- Wang, Y.; Xue, F.; Yu, S.; Cheng, Y.; Yin, M.; Du, S.; Gong, J. Insight into the morphology and crystal growth of DL-methionine in aqueous solution with presence of cellulose polymers. J. Mol. Liq. 2021, 343, 116967. [Google Scholar] [CrossRef]
- Hatcher, L.E.; Li, W.; Payne, P.; Benyahia, B.; Rielly, C.D.; Wilson, C.C. Tuning Morphology in Active Pharmaceutical Ingredients: Controlling the Crystal Habit of Lovastatin through Solvent Choice and Non-Size-Matched Polymer Additives. Cryst. Growth Des. 2020, 20, 5854–5862. [Google Scholar] [CrossRef]
- Rosencrantz, R.R.; Rahimi, K.; Kuehne, A.J.C. Morphology Control in Poly(9,9-di-n-octyl-2,7-fluorene) Spherulite Particles Prepared via Dispersion Polymerization. J. Phys. Chem. B 2014, 118, 6324–6328. [Google Scholar] [CrossRef] [PubMed]
- Sun, Z.; Zhou, L. Clathrate hydrate formation and crystal growth with additives. J. Mol. Liq. 2022, 358, 119220. [Google Scholar] [CrossRef]
- Mitarai, M.; Kishimoto, M.; Suh, D.; Ohmura, R. Surfactant Effects on the Crystal Growth of Clathrate Hydrate at the Interface of Water and Hydrophobic-Guest Liquid. Cryst. Growth Des. 2015, 15, 812–821. [Google Scholar] [CrossRef]
- Wu, H.; Wang, J.; Liu, Q.; Zong, S.; Tian, B.; Huang, X.; Wang, T.; Yin, Q.; Hao, H. Influences and the Mechanism of Additives on Intensifying Nucleation and Growth of p-Methylacetanilide. Cryst. Growth Des. 2020, 20, 973–983. [Google Scholar] [CrossRef]
- Yin, H.; Ge, H.; Chen, Z.; Yuan, S. Growth behavior of β form DL-methionine crystal in the presence of inorganic acids and bases additives: A combination of experiments and molecular dynamics simulation study. J. Cryst. Growth 2022, 587, 126636. [Google Scholar] [CrossRef]
- Han, D.; Yu, B.; Liu, Y.; Du, S.; Rohani, S.; Zhang, T.; Liu, S.; Shi, P.; Wang, H.; Zhou, L.; et al. Effects of Additives on the Morphology of Thiamine Nitrate: The Great Difference of Two Kinds of Similar Additives. Cryst. Growth Des. 2018, 18, 775–785. [Google Scholar] [CrossRef]
- Nahi, O.; Kulak, A.N.; Broad, A.; Xu, Y.; OʼShaughnessy, C.; Cayre, O.J.; Day, S.J.; Darkins, R.; Meldrum, F.C. Solvent-Mediated Enhancement of Additive-Controlled Crystallization. Cryst. Growth Des. 2021, 21, 7104–7115. [Google Scholar] [CrossRef]
- Mutabingwa, T.K. Artemisinin-based combination therapies (ACTs): Best hope for malaria treatment but inaccessible to the needy! Acta Trop. 2005, 95, 305–315. [Google Scholar] [CrossRef] [PubMed]
- Chou, T.C. Theoretical basis, experimental design, and computerized simulation of synergism and antagonism in drug combination studies. Pharmacol. Rev. 2006, 58, 621–681. [Google Scholar] [CrossRef] [PubMed]
- Ma, W.; Lutsko, J.F.; Rimer, J.D.; Vekilov, P.G. Antagonistic cooperativity between crystal growth modifiers. Nature 2020, 577, 497–501. [Google Scholar] [CrossRef] [PubMed]
- Truong, T.; Palmer, M.; Bansal, N.; Bhandari, B. Effect of dissolved carbon dioxide on the sonocrystallisation and physical properties of anhydrous milk fat. Int. Dairy J. 2019, 93, 45–56. [Google Scholar] [CrossRef]
- Zhou, S.; Marcelino, K.R.; Wongkiew, S.; Sun, L.; Guo, W.; Khanal, S.K.; Lu, H. Untapped Potential: Applying Microbubble and Nanobubble Technology in Water and Wastewater Treatment and Ecological Restoration. ACS EST Eng. 2022, 2, 1558–1573. [Google Scholar] [CrossRef]
- Tagomori, K.; Kioka, A.; Nakagawa, M.; Ueda, A.; Sato, K.; Yonezu, K.; Anzai, S. Air nanobubbles retard calcite crystal growth. Colloids Surf. A Physicochem. Eng. Asp. 2022, 648, 129319. [Google Scholar] [CrossRef]
- Kleetz, T.; Scheel, R.; Schembecker, G.; Wohlgemuth, K. Cooling Crystallization: Does Gassing Compete with Seeding? Cryst. Growth Des. 2018, 18, 4906–4910. [Google Scholar] [CrossRef]
- Jiang, L.; Chen, W.; Zhou, L.; Xu, L.; He, F.; Heng, J.Y.Y.; Shehzad, H.; Ouyang, J. Uncovering crystal growth and regeneration mechanism to control crystal morphology: The case study of aceclofenac. Sep. Purif. Technol. 2024, 347, 127577. [Google Scholar] [CrossRef]
- Jiang, M.; Ni, X.-W. Effects of solvents and impurity on crystallization kinetics and crystal properties in a reactive crystallization of paracetamol. J. Cryst. Growth 2019, 523, 125150. [Google Scholar] [CrossRef]
- Chen, G.; Chen, C.; Xia, M.; Lei, W.; Wang, F.; Gong, X. A study of the solvent effect on the crystal morphology of hexogen by means of molecular dynamics simulations. RSC Adv. 2015, 5, 25581–25589. [Google Scholar] [CrossRef]
- Cui, P.; Yin, Q.; Zhang, S.; Cheng, X.; Dai, J.; Zhang, Z.; Zhou, L.; Xie, C. The effect of solvents on crystal morphology of sucralose: Experiments and molecular dynamics simulation studies. J. Cryst. Growth 2020, 532, 125398. [Google Scholar] [CrossRef]
- Cao, Z.; Wu, Y.; Zhu, L.; Li, Y.; Li, T.; Ren, B. Exploring the solvent effect on risperidone (form I) crystal morphology: A combination of molecular dynamics simulation and experimental study. J. Mol. Liq. 2023, 376, 121358. [Google Scholar] [CrossRef]
- Guo, Q.; Zhang, S. A theoretical investigation into the effect of solvent on crystal morphology of 1-methyl-3,4,5-trinitro-1H-pyrazole (MTNP). J. Cryst. Growth 2023, 601, 126952. [Google Scholar] [CrossRef]
- Zhao, Y.; Su, G.; Liu, G.; Wei, H.; Dang, L. Effect of modification of binary solvent molecules on ε-CL-20 crystal morphology: A molecular dynamics study. CrystEngComm 2021, 23, 3524–3536. [Google Scholar] [CrossRef]
- Sun, Y.; Tilbury, C.J.; Reutzel-Edens, S.M.; Bhardwaj, R.M.; Li, J.; Doherty, M.F. Modeling Olanzapine Solution Growth Morphologies. Cryst. Growth Des. 2018, 18, 905–911. [Google Scholar] [CrossRef]
- Neugebauer, P.; Cardona, J.; Besenhard, M.O.; Peter, A.; Gruber-Woelfler, H.; Tachtatzis, C.; Cleary, A.; Andonovic, I.; Sefcik, J.; Khinast, J.G. Crystal Shape Modification via Cycles of Growth and Dissolution in a Tubular Crystallizer. Cryst. Growth Des. 2018, 18, 4403–4415. [Google Scholar] [CrossRef]
- Pawar, N.; Agrawal, S.; Methekar, R. Modeling, Simulation, and Influence of Operational Parameters on Crystal Size and Morphology in Semibatch Antisolvent Crystallization of α-Lactose Monohydrate. Cryst. Growth Des. 2018, 18, 4511–4521. [Google Scholar] [CrossRef]
- Badens, E.; Masmoudi, Y.; Mouahid, A.; Crampon, C. Current situation and perspectives in drug formulation by using supercritical fluid technology. J. Supercrit. Fluids 2018, 134, 274–283. [Google Scholar] [CrossRef]
- Crampon, C.; Detoisien, T.; Itani, L.; Nicolas, F.; Myotte, E.; Badens, E. Novel crystal morphology for sodium bicarbonate obtained by using the supercritical anti-solvent process. Powder Technol. 2023, 418, 118313. [Google Scholar] [CrossRef]
- Field, C.N.; Hamley, P.A.; Webster, J.M.; Gregory, D.H.; Titman, J.J.; Poliakoff, M. Precipitation of Solvent-Free C60(CO2)0.95 from Conventional Solvents: A New Antisolvent Approach to Controlled Crystal Growth Using Supercritical Carbon Dioxide. J. Am. Chem. Soc. 2000, 122, 2480–2488. [Google Scholar] [CrossRef]
- Singha, D.; Sahu, D.K.; Sahu, K. Anomalous Spectral Modulation of 4-Aminophthalimide inside Acetonitrile/AOT/n-Heptane Microemulsion: New Insights on Reverse Micelle to Bicontinuous Microemulsion Transition. J. Phys. Chem. B 2018, 122, 6966–6974. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.; Wang, J.; Wu, H.; Zong, S.; Huang, X.; Wang, T.; Hao, H. Manipulating of Crystal Morphology and Polymorph by Crystallization in Microemulsions. Ind. Eng. Chem. Res. 2020, 59, 13024–13032. [Google Scholar] [CrossRef]
- Chen, C.; Nicholson, C.E.; Ramsey, H.E.; Cooper, S.J. Nonclassical Crystallization of Dipicolinic Acid in Microemulsions. Cryst. Growth Des. 2015, 15, 1060–1066. [Google Scholar] [CrossRef]
- Polino, M.; Portugal, C.A.M.; Di Profio, G.; Coelhoso, I.M.; Crespo, J.G. Protein Crystallization by Membrane-Assisted Technology. Cryst. Growth Des. 2019, 19, 4871–4883. [Google Scholar] [CrossRef]
- Jiang, X.; Niu, Y.; Du, S.; He, G. Membrane crystallization: Engineering the crystallization via microscale interfacial technology. Chem. Eng. Res. Des. 2022, 178, 454–465. [Google Scholar] [CrossRef]
- Jiang, X.; Li, G.; Lu, D.; Xiao, W.; Ruan, X.; Li, X.; He, G. Hybrid Control Mechanism of Crystal Morphology Modification for Ternary Solution Treatment via Membrane Assisted Crystallization. Cryst. Growth Des. 2017, 18, 934–943. [Google Scholar] [CrossRef]
- Ye, W.; Lin, J.; Shen, J.; Luis, P.; Van der Bruggen, B. Membrane Crystallization of Sodium Carbonate for Carbon Dioxide Recovery: Effect of Impurities on the Crystal Morphology. Cryst. Growth Des. 2013, 13, 2362–2372. [Google Scholar] [CrossRef]
- Liu, F.; Hashim, N.A.; Liu, Y.; Abed, M.R.M.; Li, K. Progress in the production and modification of PVDF membranes. J. Membr. Sci. 2011, 375, 1–27. [Google Scholar] [CrossRef]
- Zhang, X.; Koirala, R.; Pramanik, B.; Fan, L.; Date, A.; Jegatheesan, V. Challenges and advancements in membrane distillation crystallization for industrial applications. Environ. Res. 2023, 234, 116577. [Google Scholar] [CrossRef]
- Xiao, W.; He, Z.; Shao, G.; Li, P.; Ruan, X.; Yan, X.; Wu, X.; Li, X.; He, G.; Jiang, X. Membrane-Assisted Cooling Crystallization for Interfacial Nucleation Induction and Self-Seeding Control. Ind. Eng. Chem. Res. 2021, 61, 765–776. [Google Scholar] [CrossRef]
- De Poel, W.; Münninghoff, J.A.W.; Elemans, J.A.A.W.; van Enckevort, W.J.P.; Rowan, A.E.; Vlieg, E. Surfaces with Controllable Topography and Chemistry Used as a Template for Protein Crystallization. Cryst. Growth Des. 2018, 18, 763–769. [Google Scholar] [CrossRef] [PubMed]
- Majidi Salehi, S.; Manjua, A.C.; Belviso, B.D.; Portugal, C.A.M.; Coelhoso, I.M.; Mirabelli, V.; Fontananova, E.; Caliandro, R.; Crespo, J.G.; Curcio, E.; et al. Hydrogel Composite Membranes Incorporating Iron Oxide Nanoparticles as Topographical Designers for Controlled Heteronucleation of Proteins. Cryst. Growth Des. 2018, 18, 3317–3327. [Google Scholar] [CrossRef]
- Jeon, T.; Jin, H.M.; Lee, S.H.; Lee, J.M.; Park, H.I.; Kim, M.K.; Lee, K.J.; Shin, B.; Kim, S.O. Laser Crystallization of Organic-Inorganic Hybrid Perovskite Solar Cells. ACS Nano 2016, 10, 7907–7914. [Google Scholar] [CrossRef] [PubMed]
- Liao, Z.; Wynne, K. A Metastable Amorphous Intermediate Is Responsible for Laser-Induced Nucleation of Glycine. J. Am. Chem. Soc. 2022, 144, 6727–6733. [Google Scholar] [CrossRef] [PubMed]
- McAnany, S.D.; Veenhuizen, K.; Nolan, D.A.; Aitken, B.G.; Dierolf, V.; Jain, H. Challenges of Laser-Induced Single-Crystal Growth in Glass: Incongruent Matrix Composition and Laser Scanning Rate. Cryst. Growth Des. 2019, 19, 4489–4497. [Google Scholar] [CrossRef]
- Esqueda-Barron, Y.; Perez Del Pino, A.; Lebiere, P.G.; Musheghyan-Avetisyan, A.; Bertran-Serra, E.; Gyorgy, E.; Logofatu, C. Boost of Charge Storage Performance of Graphene Nanowall Electrodes by Laser-Induced Crystallization of Metal Oxide Nanostructures. ACS Appl. Mater. Interfaces 2021, 13, 17957–17970. [Google Scholar] [CrossRef]
- Iefuji, N.; Murai, R.; Maruyama, M.; Takahashi, Y.; Sugiyama, S.; Adachi, H.; Matsumura, H.; Murakami, S.; Inoue, T.; Mori, Y.; et al. Laser-induced nucleation in protein crystallization: Local increase in protein concentration induced by femtosecond laser irradiation. J. Cryst. Growth 2011, 318, 741–744. [Google Scholar] [CrossRef]
- Cheng, A.-C.; Masuhara, H.; Sugiyama, T. Evolving Crystal Morphology of Potassium Chloride Controlled by Optical Trapping. J. Phys. Chem. C 2020, 124, 6913–6921. [Google Scholar] [CrossRef]
- Bodeau, W.; Otoge, K.; Yeh, W.; Kobayashi, N.P. Laser-Induced Crystallization of Copper Oxide Thin Films: A Comparison between Gaussian and Chevron Beam Profiles. ACS Appl. Mater. Interfaces 2022, 14, 49919–49927. [Google Scholar] [CrossRef]
- Li, H.; Chen, R.; Zhu, X.; Ye, D.; Yang, Y.; Li, W.; Li, D.; Liao, Q. Light Controlled 3D Crystal Morphology for Droplet Evaporative Crystallization on Photosensitive Hydrophobic Substrate. J. Phys. Chem. Lett. 2022, 13, 5910–5917. [Google Scholar] [CrossRef]
- Jancik, J.; Jancik Prochazkova, A.; Scharber, M.C.; Kovalenko, A.; Másilko, J.; Sariciftci, N.S.; Weiter, M.; Krajcovic, J. Microwave-Assisted Preparation of Organo-Lead Halide Perovskite Single Crystals. Cryst. Growth Des. 2020, 20, 1388–1393. [Google Scholar] [CrossRef] [PubMed]
- Radacsi, N.; Horst, J.H.t.; Stefanidis, G.D. Microwave-Assisted Evaporative Crystallization of Niflumic Acid for Particle Size Reduction. Cryst. Growth Des. 2013, 13, 4186–4189. [Google Scholar] [CrossRef]
- Alabanza, A.M.; Aslan, K. Metal-Assisted and Microwave-Accelerated Evaporative Crystallization: Application to l-Alanine. Cryst. Growth Des. 2011, 11, 4300–4304. [Google Scholar] [CrossRef] [PubMed]
- Mauge-Lewis, K.; Mojibola, A.; Toth, E.A.; Mohammed, M.; Seifu, D.; Aslan, K. Metal-Assisted and Microwave-Accelerated Evaporative Crystallization: Proof-of-Principle Application to Proteins. Cryst. Growth Des. 2015, 15, 3212–3219. [Google Scholar] [CrossRef]
- Pinard, M.A.; Aslan, K. Metal-Assisted and Microwave-Accelerated Evaporative Crystallization. Cryst. Growth Des. 2010, 10, 4706–4709. [Google Scholar] [CrossRef]
- Richards, W.T.; Loomis, A.L. THE CHEMICAL EFFECTS OF HIGH FREQUENCY SOUND WAVES I. A PRELIMINARY SURVEY. J. Am. Chem. Soc. 1927, 49, 3086–3100. [Google Scholar] [CrossRef]
- Gao, Y.; Meng, Z. Crystallization of lipids and lipid emulsions treated by power ultrasound: A review. Crit. Rev. Food Sci. Nutr. 2022, 64, 1882–1893. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Wang, J.; Bao, Y.; Guo, Z.; Zhang, M. Rapid sonocrystallization in the salting-out process. J. Cryst. Growth 2003, 247, 192–198. [Google Scholar] [CrossRef]
- Bhangu, S.; Ashokkumar, M.; Lee, J. Ultrasound Assisted Crystallization of Paracetamol: Crystal Size Distribution and Polymorph Control. Cryst. Growth Des. 2016, 16, 1934–1941. [Google Scholar] [CrossRef]
- Jordens, J.; Gielen, B.; Xiouras, C.; Hussain, M.N.; Stefanidis, G.D.; Thomassen, L.C.J.; Braeken, L.; Van Gerven, T. Sonocrystallisation: Observations, theories and guidelines. Chem. Eng. Process.—Process Intensif. 2019, 139, 130–154. [Google Scholar] [CrossRef]
- Awari, H.D.; Sabnis, S.S.; Gogate, P.R. Improved Crystallization of Ampicillin Trihydrate Based on the Use of Ultrasound. Ind. Eng. Chem. Res. 2022, 61, 2538–2547. [Google Scholar] [CrossRef]
- Ramisetty, K.A.; Rasmuson, Å.C. Controlling the Product Crystal Size Distribution by Strategic Application of Ultrasonication. Cryst. Growth Des. 2018, 18, 1697–1709. [Google Scholar] [CrossRef]
- Schieber, M. The effects of high magnetic fields on the isothermal dissolution and growth rates of Fe(NH4)2(SO4)2 · 6H2O and KAl(SO4)2 · 12H2O seed crystals. J. Cryst. Growth 1967, 1, 131–138. [Google Scholar] [CrossRef]
- Zhao, Y.; Hou, B.; Liu, C.J.; Ji, X.; Huang, Y.; Sui, J.; Liu, D.; Wang, N.; Hao, H. Mechanistic Study on the Effect of Magnetic Field on the Crystallization of Organic Small Molecules. Ind. Eng. Chem. Res. 2021, 60, 15741–15751. [Google Scholar] [CrossRef]
- Wakayama, N.I. Effects of a Strong Magnetic Field on Protein Crystal Growth. Cryst. Growth Des. 2003, 3, 17–24. [Google Scholar] [CrossRef]
- Wakayama, N.; Ataka, M.; Abe, H. Effects of a Magnetic Field Gradient on the Crystallization of Hen Lysozyme. J. Cryst. Growth 1997, 178, 653–656. [Google Scholar] [CrossRef]
- Potticary, J.; Hall, C.L.; Guo, R.; Price, S.L.; Hall, S.R. On the Application of Strong Magnetic Fields during Organic Crystal Growth. Cryst. Growth Des. 2021, 21, 6254–6265. [Google Scholar] [CrossRef]
- Milojevic, M.M.; Vucetic, B.M.; Maksimovic, B.Z.; Klisuric, O.R.; Mitrovic, M.M.; Zekic, A.A. Influence of a Static Magnetic Field on the ⟨100⟩ Growth Rates of Sodium Chlorate Crystals from Aqueous Solution. ACS Omega 2022, 7, 47701–47708. [Google Scholar] [CrossRef] [PubMed]
- Belenguer, A.M.; Lampronti, G.I.; Cruz-Cabeza, A.J.; Hunter, C.A.; Sanders, J.K.M. Solvation and surface effects on polymorph stabilities at the nanoscale. Chem. Sci. 2016, 7, 6617–6627. [Google Scholar] [CrossRef]
- Hammadi, Z.; Veesler, S. New approaches on crystallization under electric fields. Prog. Biophys. Mol. Biol. 2009, 101, 38–44. [Google Scholar] [CrossRef]
- Wakamatsu, T. Method and apparatus for characterization of electric field-induced aggregation in pre-crystalline protein solutions. Rev. Sci. Instrum. 2015, 86, 015112. [Google Scholar] [CrossRef] [PubMed]
- Hou, D. Ac field enhanced protein crystallization. Appl. Phys. Lett.—APPL PHYS LETT 2008, 92, 223902. [Google Scholar] [CrossRef]
- Li, F.; Lakerveld, R. Influence of Alternating Electric Fields on Protein Crystallization in Microfluidic Devices with Patterned Electrodes in a Parallel-Plate Configuration. Cryst. Growth Des. 2017, 17, 3062–3070. [Google Scholar] [CrossRef]
- Li, F.; Lakerveld, R. Electric-Field-Assisted Protein Crystallization in Continuous Flow. Cryst. Growth Des. 2018, 18, 2964–2971. [Google Scholar] [CrossRef]
- Yang, H.K.; Jeong, J.H. Synthesis, Crystal Growth, and Photoluminescence Properties of YAG:Eu3+ Phosphors by High-Energy Ball Milling and Solid-State Reaction. J. Phys. Chem. C 2010, 114, 226–230. [Google Scholar] [CrossRef]
- Li, Y.; Liu, Y.; Huang, J.; Mei, Y. Improved length of calcium sulfate crystal seeds and whiskers via ball milling and hydration treatment. Chin. J. Chem. Eng. 2024. [Google Scholar] [CrossRef]
- Ahmad, S.I.; Hamoudi, H.; Ponraj, J.; Youssef, K.M. In-situ growth of single-crystal plasmonic aluminum–lithium-graphene nanosheets with a hexagonal platelet-like morphology using ball-milling. Carbon. 2021, 178, 657–665. [Google Scholar] [CrossRef]
- Xiao, Y.; Jin, T.; Geng, X.; Zhu, X. Azilsartan-nicotinamide cocrystal: Preparation, characterization and in vitro/vivo evaluation. Eur. J. Pharm. Sci. 2022, 176, 106241. [Google Scholar] [CrossRef]
- Liu, Y.; Ma, Y.; Yu, C.; Gao, Y.; Li, K.; Tong, L.; Chen, M.; Gong, J. Spherical agglomeration of high melting point drugs in water at low temperature by developing a two-step oiling-out mechanism and the design strategy. Green. Chem. 2022, 24, 5779–5791. [Google Scholar] [CrossRef]






| Time | Theory/Model | Presenter |
|---|---|---|
| 1866 | Laws of Bravais | Bravais |
| 1878 | Gibbs–Wulff principle | Gibbs and Wulff |
| 1901 | Gibbs–Curie–Wulff principle | Gibbs, Curie, and Wulff |
| 1927 | Layer Growth theory | Kossel and Stranski |
| 1937 | BFDH | Bravais, Friedel, Donnay, and Harker |
| 1951 | BCF | Burton, Cabrera, and Frank |
| 1952 | Periodic Bond Chain theory | Hartman and Perdok |
| 1952 | BPS | Burton, Prim, and Slichter |
| 1955 | Hartman–Perdok theory | Hartman and Perdok |
| 1959 | Rough Interface model | Jackson |
| 1966 | Dispersion Interface model | Temkin |
| 1966 | 2D nucleation model | Budevsky and Bostanov |
| Types | Classic Examples | Advantages | Ref. |
|---|---|---|---|
| Tailor-made additives | Amino acids and inorganic salts. | Easy operation, small amount, allowing for careful design | [61] |
| Small-molecule additives | Coenzymes, inhibitors, metal ions and prosthetic groups. | Versatility, directionality, and stability | [62,63] |
| Large-molecule additives | Polymers, peptides and proteins. | Safe and have no impact on crystal structures | [64] |
| Surfactant | Sodium dodecyl sulfate, AES | Significant effect on hydrate crystallization | [65] |
| Micro-/nanobubbles | O2, CO2 and N2. | Low cost, no pollution | [66] |
| Types | Most Commonly Used Process | Scope of Application |
|---|---|---|
| Precipitation solvent | Rapid Expansion of a Supercritical Solution (RESS) process | Solutes having a solubility higher than about 10−3 g·g−1 of SCF |
| Precipitation anti-solvent | Supercritical Anti-Solvent (SAS) process | Polar drug molecule |
| Dispersing agent | Particles from Gas Saturated Solutions (PGSS) process | Polymers in which CO2 is sorbed in significant quantities |
| Types | Advantages | Ref. |
|---|---|---|
| Polypropylene (PP) | High porosity and hydrophobicity | [107] |
| Polyvinylidene fluoride (PVDF) | High permeable flux, microporous structure, and hydrophobicity | [109] |
| Polytetrafluoroethylene (PTFE) | High mechanical strength, thermal stability, chemical resistance, and high hydrophobicity | [110] |
| Polyethersulfone (PES) | High alternative surface area | [111] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Y.; Song, W.; Yang, J.; Ji, X.; Wang, N.; Huang, X.; Wang, T.; Hao, H. Crystal Morphology Prediction Models and Regulating Methods. Crystals 2024, 14, 484. https://doi.org/10.3390/cryst14060484
Gao Y, Song W, Yang J, Ji X, Wang N, Huang X, Wang T, Hao H. Crystal Morphology Prediction Models and Regulating Methods. Crystals. 2024; 14(6):484. https://doi.org/10.3390/cryst14060484
Chicago/Turabian StyleGao, Yuan, Wenxi Song, Jinyue Yang, Xiongtao Ji, Na Wang, Xin Huang, Ting Wang, and Hongxun Hao. 2024. "Crystal Morphology Prediction Models and Regulating Methods" Crystals 14, no. 6: 484. https://doi.org/10.3390/cryst14060484
APA StyleGao, Y., Song, W., Yang, J., Ji, X., Wang, N., Huang, X., Wang, T., & Hao, H. (2024). Crystal Morphology Prediction Models and Regulating Methods. Crystals, 14(6), 484. https://doi.org/10.3390/cryst14060484









