Next Article in Journal
Magnesium-Substituted Brushite Cement: Physical and Mechanical Properties
Previous Article in Journal
Hybrid Joining of Dissimilar Thin Metallic Sheets—Mechanical Joining and Adhesive Bonding
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Crystals
Volume 14
Issue 3
10.3390/cryst14030221
crystals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

High-Pressure Phases of Boron Pnictides BX (X = As, Sb, Bi) with Quartz Topology from First Principles

by
Vladimir L. Solozhenko
1,* and
Samir F. Matar
2
1
LSPM–CNRS, Université Sorbonne Paris Nord, 93430 Villetaneuse, France
2
Lebanese German University (LGU), Jounieh P.O. Box 206, Lebanon
*
Author to whom correspondence should be addressed.
Crystals 2024, 14(3), 221; https://doi.org/10.3390/cryst14030221
Submission received: 11 February 2024 / Revised: 20 February 2024 / Accepted: 22 February 2024 / Published: 25 February 2024
Browse Figures
Versions Notes

Abstract

:
The superdense hexagonal boron pnictides BX (X = As, Sb, Bi), whose structures are formed by distorted tetrahedra and characterized by a quartz-derived (qtz) topology, have been predicted from first principles as potential high-pressure phases. From full geometry structure relaxation and ground state energy calculations based on quantum density functional theory (DFT), qtz BX was found to be mechanically (elastic constants) and dynamically (phonons) stable. From the energy–volume equations of state, at high but experimentally accessible pressures, qtz boron pnictides were found to be more energetically favorable than corresponding cubic zinc–blende phases with diamond-like (dia) topology. According to the electronic band structures, the zinc–blende BX have larger band gaps than the qtz phases, which can be attributed to the higher covalence of the latter. A metallic behavior is only observed for qtz BBi, which is related to the dynamic instability as it follows from the phonon band structure.

1. Introduction

The III–V compound semiconductors provide the material basis for a number of well-established technologies and new classes of advanced high-temperature, high-power, and high-frequency electronic/optoelectronic devices such as high-electron-mobility heterostructures, light-emitting diodes, diode lasers, electro-optic modulators, photodetectors, frequency-mixing modules, etc. [1].
Among the AIII–BV semiconductors, boron monopnictides are interesting because of their unique behavior due to the small size of the boron atom and the absence of p-electrons. The most studied compounds in this group are boron nitride (BN) and boron phosphide (BP). Boron arsenide (BAs) is much less studied experimentally (see recent review [2] and references therein), while BSb and BBi have not yet been synthesized and have been studied only by theoretical methods [3,4,5,6,7].
Theoretical studies of BAs at high pressure have so far been mainly limited to the consideration of the phase with rocksalt structure [5,7,8,9,10,11,12,13,14]. Wentzcovitch et al. [8] have studied the relative stability of different BAs phases using the total-energy pseudopotential technique and reported structural transition from the fourfold coordinated zinc–blende (zb) phase to sixfold coordinated rocksalt (rs) phase at 110 GPa. According to other works [9,10,11,12,13,14], the transition pressure varies from 93 GPa [13] to 134 GPa [9]. However, this transition has never been observed experimentally; on the contrary, it was found that BAs underwent a collapse from the zinc–blende phase to an amorphous state at pressures above 125 GPa [15]. As for the hypothetical high-pressure phases with β-Sn and CsCl structure, they were found to be less energetically favorable than the rocksalt phase of BAs [8].
Phase diagrams of the B-Sb [16] and B-Bi [17] systems at ambient pressure have a similar topology, characterized by the absence of binary compounds and the presence of noninvariant reactions of decomposition of the liquid phase into β-rhombohedral boron and a vapor phase. Therefore, zinc–blende BSb and BBi, which have been claimed to be the ground-state phases [3,4,5,6,7], are hypothetical. The same is true for their high-pressure transitions to corresponding rocksalt phases.
The structures of the currently known zinc–blende boron pnictides (BN, BP, and BAs) have dia topology (as cubic diamond) [18], which is characterized by the spatial arrangement of BN4, BP4, or BAs4 perfect (angle ∠109.47°) sp3-like corner-sharing tetrahedra in three-dimensional 3D nets. Recently, we discovered significant structural densification of zinc–blende BN and BP by adopting a quartz-derived structure (qtz topology) characterized by distorted corner-sharing BN4 and BP4 tetrahedra [19,20].
In this context, the present work extends our investigation to boron pnictides with heavier elements (As, Sb, and Bi). As in previous works [19,20], the studies are based on quantum mechanics calculations of the ground-state energy structures and derived properties in the framework of the density functional theory (DFT) [21,22]. It is shown that BX phases (X = As, Sb, Bi) with qtz topology are cohesive and stable both mechanically (elastic constants and their combinations) and dynamically (phonon band structures). It should be noted, however, that there is a small dynamical instability of qtz BX in the case of the heaviest pnictogen, bismuth. The respective equations of state (EOS) have been determined for all phases, and the transition pressures from zb-BX to the corresponding high-pressure qtz structures have been estimated. The electronic band structures show a reduction in the band gaps in the proposed qtz phases compared to zb-BX, with metallization observed in the case of qtz BBi. Finally, the thermodynamic properties (heat capacity and entropy) of the new phases have been calculated and compared with the available experimental data.

2. Computational Methodology

The identification of the ground state structures corresponding to the energy minima and the prediction of their mechanical and dynamical properties were carried out by DFT-based calculations using the Vienna Ab initio Simulation Package (VASP) code [23,24] and the projector augmented wave (PAW) method [24,25] for the atomic potentials. DFT exchange-correlation (XC) effects were considered using the generalized gradient functional approximation (GGA) [26]. Preliminary calculations with the original DFT-XC local density approximation (LDA) [27] resulted in underestimated lattice constants of zb-BX at ambient pressure and were subsequently abandoned. The atoms were relaxed to the ground state structures using the conjugate gradient algorithm, according to Press et al. [28]. The Blöchl tetrahedron method [29] with corrections according to the Methfessel and Paxton scheme [30] was used for geometry optimization and energy calculations, respectively. Brillouin-zone integrals were approximated by a special k-point sampling, according to Monkhorst and Pack [31]. Structural parameters were optimized until atomic forces were below 0.02 eV/Å and all stress components were <0.003 eV/Å3. The calculations were converged at an energy cutoff of 400 eV for the plane-wave basis set in terms of the k-point integration in the reciprocal space from kx(6) × ky(6) × kz(6) up to kx(12) × ky(12) × kz(12) for zb-BX and kx(6) × ky(6) × kz(4) up to kx(12) × ky(12) × kz(8) for qtz BX to obtain a final convergence and relaxation to zero strains. In the post-processing of the ground state electronic structures, the charge density projections were operated on the lattice sites.
The mechanical stability was evaluated from the elastic constants calculations. The analysis of the elastic tensors was carried out using the ELATE software [32], which provides the bulk (B), shear (G), and Young’s (E) moduli along different averaging methods; the Voigt approach [33] was chosen here. Vickers hardness (HV) from elastic properties was evaluated using the empirical Mazhnik–Oganov [34] and Chen–Niu [35] models. The hardness was also estimated using the thermodynamic model, which is based on thermodynamic properties and crystal structure [36], and the Lyakhov–Oganov approach [37], which considers the topology of the crystal structure, the strength of covalent bonds, the degree of ionicity, and directionality. The fracture toughness (KIc) was evaluated within the Mazhnik–Oganov model [34].
The dynamic stabilities of the considered boron pnictides were confirmed by the positive values of phonon frequencies. The corresponding phonon band structures were obtained according to Togo and Tanaka [38]. Thermodynamic properties (heat capacity at constant volume CV and entropy S) were calculated from the phonon frequencies using the statistical thermodynamics on a high-precision sampling mesh in the Brillouin zone [39].
The electronic band structures were obtained using the all-electron DFT-based ASW method [40] and the GGA XC functional [26]. The VESTA (Visualization for Electronic and Structural Analysis) software [41] was used to visualize the crystal structures and charge densities.

3. Results and Discussion

3.1. Crystal Chemistry

The preliminary computations consisted of calculating the structures of zb-BX to reproduce the experimental [42] and theoretical [43] findings. Table 1 shows the calculated and available experimental lattice constants a of zb-BAs, which are in good agreement. The zinc–blende structure is shown in Figure 1 in ball-and-stick and tetrahedral representations (Figure 1b). The latter shows that the tetrahedra are regular as in diamond, presenting the sp3-like ∠109.47° angle as mentioned above, with only B–As bonds. The observation is relevant in that the qtz topology is characterized by distorted tetrahedra.
Recently, we reported a novel qtz C6 belonging to space group P6522 (No. 179) with a single six-fold Wyckoff position [44] (Figure 1a). To consider binary compounds, it was necessary to change the space group to P6222 (No. 180), with a splitting into two three-fold Wyckoff positions. The results of the unconstrained geometry optimizations are shown in Table 1. A comparison of zb-BX (X = As, Sb, Bi) shows a systematic decrease in volume as per formula unit (FU), which suggests densification. However, the shortest interatomic distance is systematically larger in qtz BX than in zb-BX, accompanied by the presence of distorted tetrahedra with angles smaller and larger than the ideal angle of 109.47° (Figure 1c). The total energy per FU is lower (higher in absolute value) in qtz BX than in zb-BX. This observation is expected from the fact that zb-BX phases are the ground state structures with ΔE/F, largest for X = As versus X = Bi. These results, which show denser qtz BX phases with smaller volumes and higher energies than those for zb-BX, suggest that qtz BX are potential high-pressure phases, as will be shown below.
In terms of chemical behavior, with the χ symbol denoting Pauling electronegativity, χB = 2.04 on the one hand, and χAs = 2.19, χSb = 2.05, and χBi = 2.02 on the other. Based on Δχ, BAs can be considered ionocovalent with Δχ(BAs) = 0.15, while the other two boron pnictides characterized by Δχ(BSb) = 0.01 and Δχ(BBi) = 0.02 should be considered covalent.

3.2. Mechanical Properties

The mechanical behavior of boron pnictides has been analyzed by calculating the elastic properties by performing finite distortions of the lattice. The calculated sets of elastic constants Cij (i and j correspond to directions) for zinc–blende and qtz phases are given in Table 2. All Cij values are positive, indicating mechanically stable phases. qtz pnictides have systematically larger C11, C33, and C66 values than corresponding zinc–blende polymorphs due to the smaller volumes per formula unit. Along the BAs–BSb–BBi series, there is a tendency for the Cij values of zinc–blende and qtz phases to decrease due to the increase in atomic radii: r(As) = 1.2 Å; r(Sb) = 1.4 Å; r(Bi) = 1.5 Å, and consequently to increase cell volume and compressibility.
The bulk (BV), shear (GV), and Young’s (EV) moduli were then obtained by Voigt averaging [33] the elastic constants using ELATE software [32]. The last three columns of Table 2 show the elastic moduli with values that follow the trends observed for Cij.
It should be noted that the bulk modulus of zb-BAs calculated from the elastic constants (134 GPa) is ~10% smaller than the experimental values obtained by synchrotron X-ray diffraction study (148(6) GPa [15]) and picosecond interferometry (148(9) GPa [45]). On the other hand, the B0 value of 146 GPa calculated in the framework of the thermodynamic model [36] is in perfect agreement with the experimental data. For this reason, the bulk modulus values obtained using the thermodynamic model (see Table 3) should also be preferred for all other pnictides.
The Vickers hardness (HV) values of all considered boron pnictides, calculated using four contemporary models [34,35,36,37], are summarized in Table 3. For zb-Bas, all models except the empirical Chen–Niu model give hardness values that are in good agreement with the experimental value of 22(3) GPa [46]. For BSb and BBi, there is a significant divergence of HV values calculated by different models (see Table 3), and the nature of these divergences indicates that, in this case, all models except the thermodynamic one [36] can be considered unreliable. Previously, we observed a similar situation for the superhard phases of the B-C-N system [47]. Based on the hardness values calculated using the thermodynamic model, we can conclude that in the BAs–BSb–BBi series, the Vickers hardness decreases from 24 to 15 GPa, with practically no differences observed between zinc–blende and qtz polymorphs. In any case, all considered boron pnictides are hard phases with Vickers hardness exceeding that of cemented tungsten carbide, the conventional hard material.
The fracture toughness of zb-BAs evaluated within the Mazhnik–Oganov model [34], KIc = 1.4 MPa·m½, agrees well with the experimental value of 1.2 MPa·m½ [46], indicating that cubic boron arsenide (as well as qtz polymorph) is more brittle than cubic BN (2.8 MPa·m½ [48]) and cubic BP (1.8 MPa·m½ [49]). Hypothetical boron antimonide and boron bismuthate (both zinc–blende and qtz polymorphs) were found to be even more brittle (see Table 3).

3.3. Equations of State and Possible High-Pressure Phase Transitions

When considering different structures of crystalline solids, comparative energy trends can be determined from their equations of state (EOS). This was achieved based on a series of calculations of total energy as a function of volume for the zinc–blende and qtz BX phases. The resulting E(V) curves, shown in Figure 2, were fitted to the third-order Birch equations of state [50]:
E(V) = E0(V0) + (9/8)∙V0B0[([(V0)/V])⅔ − 1]2 + (9/16)∙B0(B′ − 4)V0[([(V0)/V])⅔ − 1]3,
where E0, V0, B0, and B‘ are the equilibrium energy, volume, bulk modulus, and its first pressure derivative, respectively. The calculated values for the static properties, the transition pressures, and reduced volumes are summarized in Table 4.
In the case of boron arsenide (Figure 2a), the intersection of E(V) curves of zinc–blende and qtz phases is observed at V/FU = 19.0 Å, which for zb-BAs is equivalent to a reduced volume of 0.697. The corresponding pressure can be calculated from the Murnaghan equation [51].
p = B0/B0′ [(V0)/V])B0′ – 1],
using the experimental values of B0, B0′, and V0 (Table 4), and is equal to 117 GPa. Thus, it can be assumed that the pressure-induced phase transition from zb-BAs to qtz BAs can occur at pressures not lower than 117 GPa, which is consistent with the experimental data on the absence of room-temperature phase transitions of zb-BAs up to 125 GPa [15].
For two other boron pnictides, the intersections of the E(V) curves of zb-BX and qtz BX are observed at V/V0 = 0.724 for zb-BSb (Figure 2b) and V/V0 = 0.763 for zb-BBi (Figure 2c). The corresponding pressures, 71 GPa and 51 GPa, were estimated using the most reliable B0 values calculated in the framework of the thermodynamic model (Table 4), while B0’ values were fixed at 4.
Thus, with increasing pnictogen atomic number, a drastic decrease in the zb-to-qtz transition pressure is observed from 144 GPa for BP [20] down to 51 GPa for BBi.

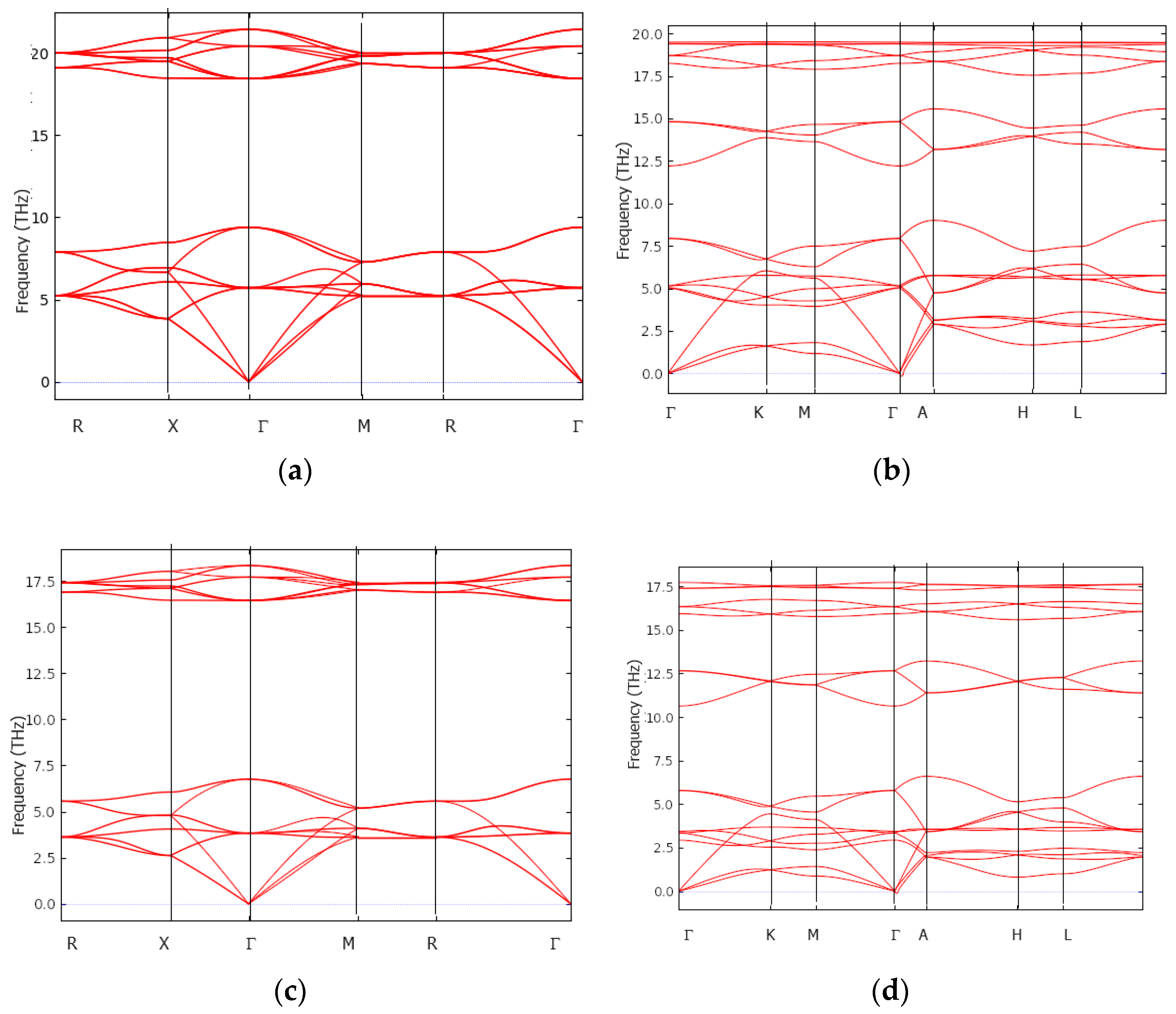
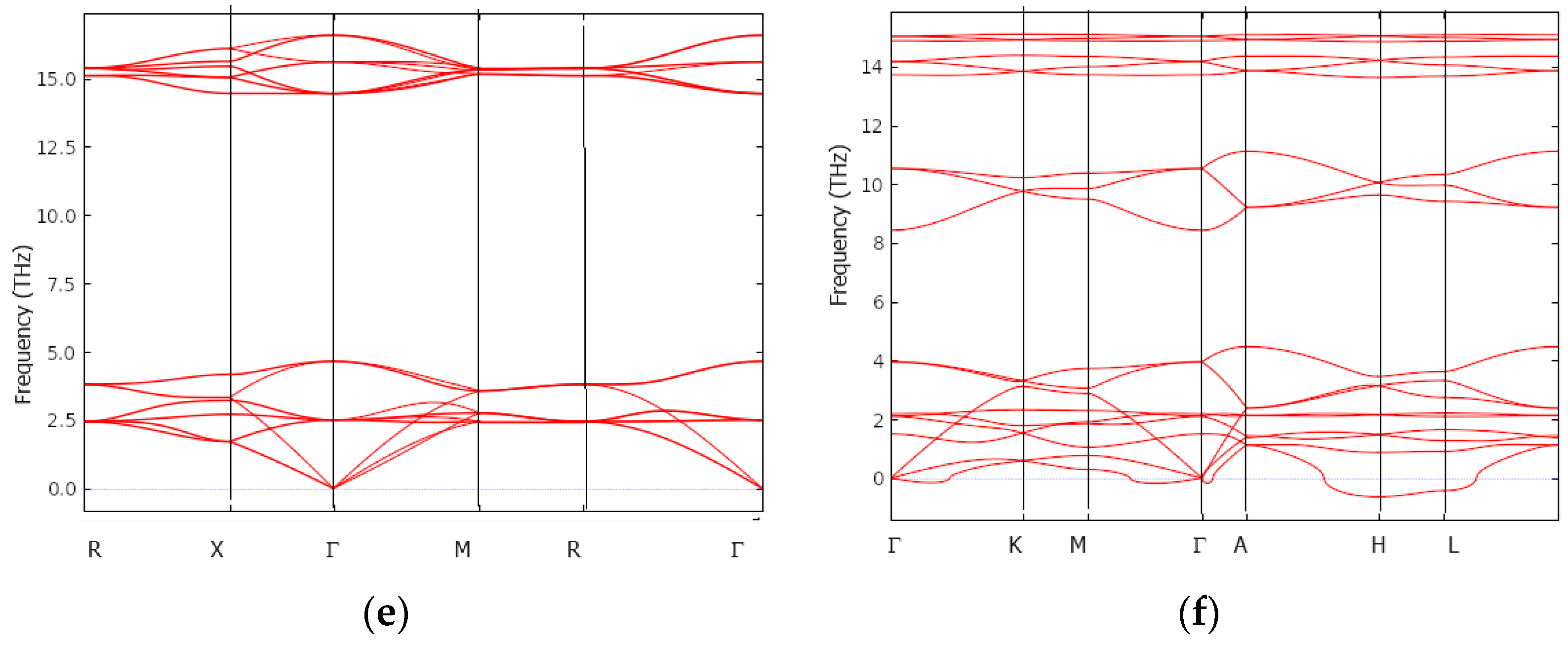
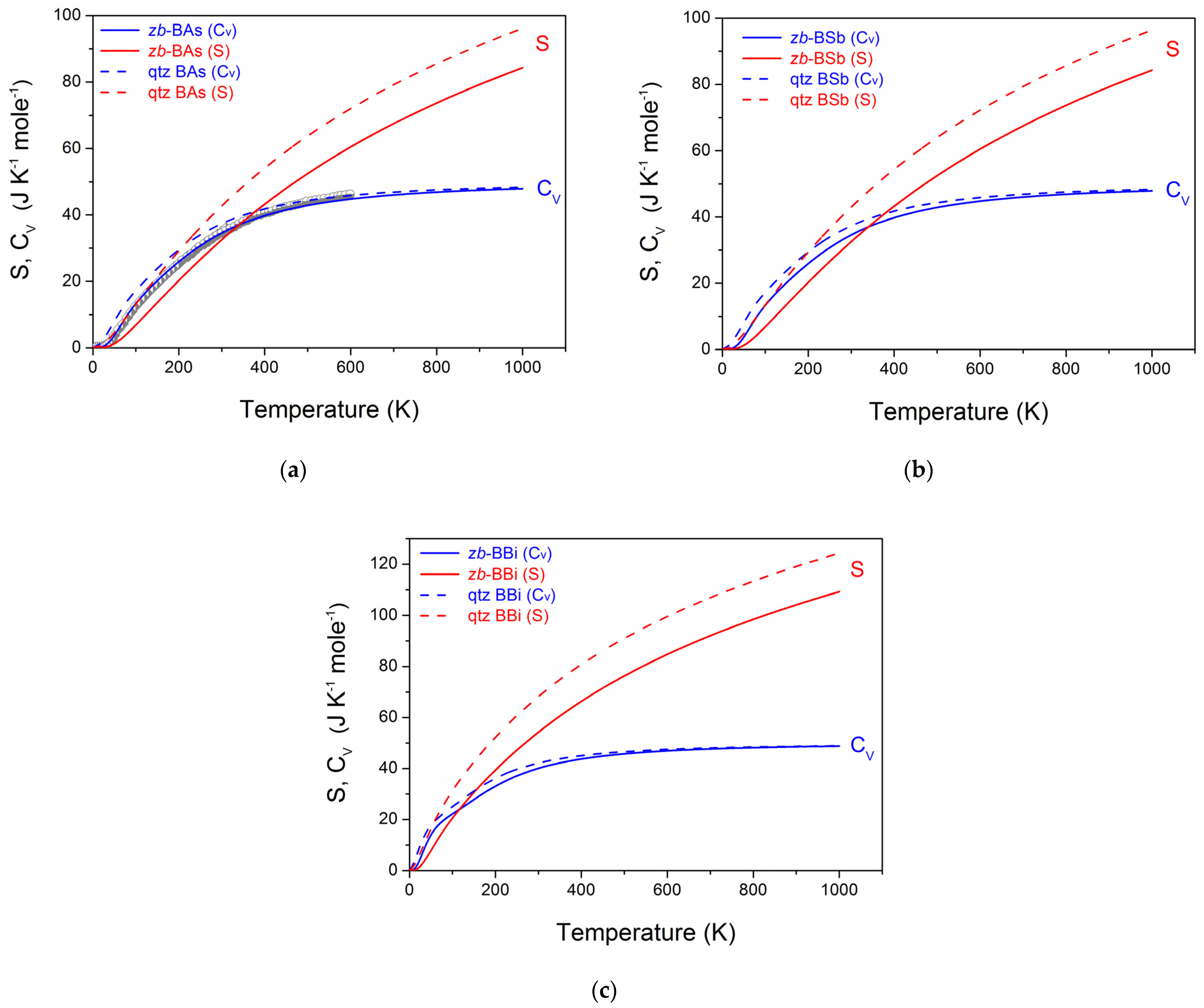
3.4. Dynamic and Thermodynamic Properties from the Phonons

To verify the dynamical stability of the predicted phases, their phonon properties were studied. The phonon band structures (red lines) obtained according to the protocol presented in Section 2 are shown in Figure 3. The horizontal direction corresponds to the main directions of the hexagonal Brillouin zone, while the vertical direction shows the frequencies ω, given in terahertz (THz). The absence of negative frequencies indicates dynamically stable phases. The band structure includes 3N bands with 3N-3 optical modes found at higher energies than three acoustic modes starting from zero energy (ω = 0) at the Γ point, the center of the Brillouin zone, up to a few terahertz. They correspond to the lattice rigid translation modes of the crystal (two transverse and one longitudinal). Five panels in Figure 3a–e show all positive frequency values, while for qtz BBi (Figure 3f), acoustic negative phonon curves are observed along most of the Brillouin zone directions. zb-BBi, however, shows no such negative phonons. This indicates an instability of the longitudinal acoustic mode in qtz BBi, which may result from drastic changes in the electronic structure as described below.
The thermodynamic properties of the boron pnictides were calculated from the phonon frequencies using the statistical thermodynamic approach [39] on a high-precision sampling mesh in the Brillouin zone. The temperature dependencies of heat capacity at constant volume (Cv) and entropy (S) of zinc–blende and qtz BAs are shown in Figure 4a in comparison with experimental Cp data for zb-BAs [2,52]. The observed excellent agreement between the calculated and experimental data indicates the validity of the method used to estimate the thermodynamic properties for the case of boron pnictides. For all three compounds, the heat capacity and entropy of qtz BX phases are slightly higher than those of zb-BX (Figure 4), which is expected for structures containing distorted corner-sharing tetrahedra compared to the ideal zinc–blende structure.

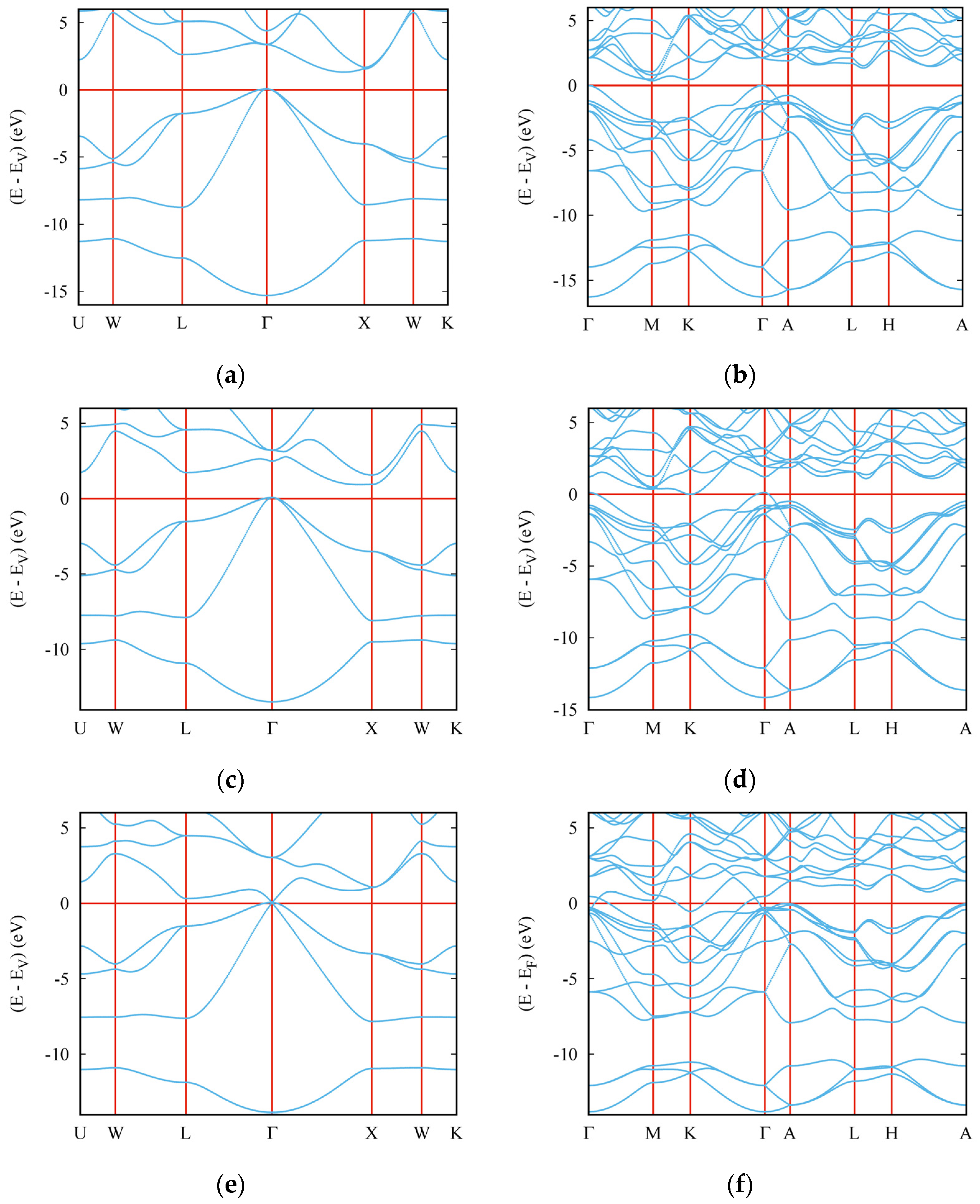
3.5. Electronic Band Structures

Using the crystal parameters in Table 1, the electronic band structures were calculated using the all-electrons DFT-based augmented spherical method (ASW) [40] with the GGA exchange-correlation XC functional, as in the VASP calculations above. The results are shown in Figure 5. The bands (blue lines) develop along the main directions of the respective Brillouin zones, i.e., cubic for zb-BX and hexagonal for qtz BX. In all panels, except for Figure 5f corresponding to qtz BBi, the zero energy along the vertical axis is considered with respect to EV at the top of the filled valence band (VB), separated from the empty conduction band (CB) by a small band gap. For all three boron pnictides, the zinc–blende phases have larger band gaps compared to the qtz phases. The smaller magnitudes for the latter result from the smaller volumes per formula unit, leading to an increased covalence. Within the same structure, going from BAs to BSb and then to BBi, the covalent character of the phase increases, as shown above with the Pauling electronegativity values χ and their differences Δχ for the considered boron pnictides. As a result, the energy gap within the zinc–blende BX series decreases. The same is observed for high-pressure qtz BX, but the pressure has already reduced the band gap of all these phases, and finally, there is a total closing of the band gap in qtz BBi, which behaves as a metal with the energy reference at the Fermi level EF. The transition from semiconducting zb-BBi to metallic qtz BBi can be proposed to explain the dynamic instability observed from the phonons.

4. Conclusions

Based on crystal chemistry and density functional theory calculations, superdense hexagonal (P6422) boron pnictides BX (X = As, Sb, Bi) with quartz-derived topology were predicted as possible high-pressure phases. The new hexagonal qtz BX phases were found to be cohesive, with higher energies than the cubic zinc-blende (F-43m) polymorphs, but they tend to predominate at low volumes (high pressures). The transition pressures calculated from the corresponding energy-volume E(V) equations of state are 117 GPa (BAs), 71 GPa (BSb), and 51 GPa (BBi). In addition to mechanical stability from elastic constants, the qtz BX phases are also dynamically stable, as indicated by the phonon band structures. The heat capacities of the qtz phases calculated from the phonon frequencies were found to be slightly higher than those of the corresponding zinc–blende phases, which is quite expected for structures containing distorted corner-sharing tetrahedra. From the analysis of the electronic band structures, it was found that all zinc-blende boron pnictides had larger band gaps than the corresponding qtz phases, which can be attributed to an increased covalence due to the higher density of the latter. A special feature observed for metallic qtz BBi is related to the dynamic instability observed from the phonon band structure.

Author Contributions

Conceptualization, V.L.S. and S.F.M.; methodology, V.L.S. and S.F.M.; investigation, V.L.S. and S.F.M.; formal analysis, V.L.S. and S.F.M.; data curation, V.L.S. and S.F.M.; visualization, V.L.S. and S.F.M.; validation, V.L.S. and S.F.M.; resources, S.F.M.; writing—original draft preparation, S.F.M.; writing—review and editing, V.L.S. All authors have read and agreed to the published version of this manuscript.

Funding

This research received no external funding.

Data Availability Statement

The data presented in this study are available on reasonable request.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Vurgaftman, I.; Meyer, J.R.; Ram-Mohan, L.R. Band parameters for III–V compound semiconductors and their alloys. Appl. Phys. Rev. 2001, 89, 5815–5875. [Google Scholar] [CrossRef]
  2. Kang, J.S.; Li, M.; Wu, H.; Nguyen, H.; Hua, Y. Basic physical properties of cubic boron arsenide. Appl. Phys. Lett. 2019, 115, 122103. [Google Scholar] [CrossRef]
  3. Ferhat, M.; Bouhafs, B.; Zaoui, A.; Aourag, H. First-principles study of structural and electronic properties of BSb. J. Phys. Condens. Matter 1998, 10, 7995. [Google Scholar] [CrossRef]
  4. Zaoui, A.; Ferhat, M. High-pressure structural phase transition of BSb. Phys. Stat. Sol. (b) 2001, 225, 15–19. [Google Scholar] [CrossRef]
  5. Ustundag, M.; Aslan, M.; Yalcin, B.G. The first-principles study on physical properties and phase stability of Boron-V (BN, BP, BAs, BSb and BBi) compounds. Comput. Mater. Sci. 2014, 81, 471–477. [Google Scholar] [CrossRef]
  6. Bioud, N.; Sun, X.-W.; Daoud, S.; Song, T.; Liu, Z.-J. Structural stability and thermodynamic properties of BSb under high pressure and temperature. Mater. Res. Exp. 2018, 5, 085904. [Google Scholar] [CrossRef]
  7. Mujica, A.; Rubio, A.; Munoz, A.; Needs, R.J. High-pressure phases of group-IV, III–V, and II–VI compounds. Rev. Mod. Phys. 2003, 75, 863–912. [Google Scholar] [CrossRef]
  8. Wentzcovitch, R.M.; Cohen, M.L.; Lam, P.K. Theoretical study of BN, BP, and BAs at high pressures. Phys. Rev. B 1987, 36, 6058–6068. [Google Scholar] [CrossRef]
  9. Cui, S.; Feng, W.; Hua, H.; Feng, Z.; Wang, Y. First-principles study of zinc-blende to rocksalt phase transition in BP and BAs. Comput. Mater. Sci. 2009, 44, 1386–1389. [Google Scholar] [CrossRef]
  10. Lu, B.; Linghu, R.-F.; Yi, Y.; Yang, X.-D. Characterisation of the high-pressure structural transition and elastic properties in boron arsenic. Chin. Phys. B 2010, 19, 076201. [Google Scholar]
  11. Varshney, D.; Joshi, G.; Varshney, M.; Shriya, S. Pressure induced mechanical properties of boron based pnictides. Solid State Sci. 2010, 12, 864–872. [Google Scholar] [CrossRef]
  12. Talati, M.; Jha, P.K. Structural phase transition in boron compounds at high pressure. Int. J. Mod. Phys. B 2010, 24, 1235–1244. [Google Scholar] [CrossRef]
  13. Sarwan, M.; Bhardwaj, P.; Singh, S. Zinc-blende to rock-salt structural phase transition of BP and BAs under high pressure. Chem. Phys. 2013, 426, 1–8. [Google Scholar] [CrossRef]
  14. Daoud, S.; Bioud, N.; Bouarissa, N. Structural phase transition, elastic and thermal properties of boron arsenide: Pressure-induced effects. Mater. Sci. Semicond. Process. 2015, 31, 124–130. [Google Scholar] [CrossRef]
  15. Greene, R.G.; Luo, H.; Ruoff, A.L.; Trail, S.S.; DiSalvo, F.J. Pressure induced metastable amorphization of BAs: Evidence for a kinetically frustrated phase transformation. Phys. Rev. Lett. 1994, 73, 2476–2479. [Google Scholar] [CrossRef] [PubMed]
  16. Okamoto, H. BSb (BoronAntimony). J. Phase Equil. 1991, 125, 391–393. [Google Scholar] [CrossRef]
  17. Okamoto, H. B-Bi (Boron-Bismuth). J. Phase Equil. 1991, 125, 391. [Google Scholar] [CrossRef]
  18. Alexandrov, E.V.; Blatov, V.A.; Kochetkov, A.V.; Proserpio, D.M. Underlying nets in three-periodic coordination polymers: Topology, taxonomy and prediction from a computer-aided analysis of the Cambridge Structural Database. Cryst. Eng. Comm. 2011, 13, 3947–3958. [Google Scholar] [CrossRef]
  19. Matar, S.F.; Solozhenko, V.L. Ultrahigh-density superhard hexagonal BN and SiC with quartz topology from crystal chemistry and first principles. Crystals 2023, 13, 1498. [Google Scholar] [CrossRef]
  20. Solozhenko, V.L.; Matar, S.F. Superdense hexagonal BP and AlP with quartz topology: Crystal chemistry and DFT study. Crystals 2023, 13, 1622. [Google Scholar] [CrossRef]
  21. Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. B 1964, 136, 864–871. [Google Scholar] [CrossRef]
  22. Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. A 1965, 140, 1133–1138. [Google Scholar] [CrossRef]
  23. Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
  24. Kresse, G.; Joubert, J. From ultrasoft pseudopotentials to the projector augmented wave. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
  25. Blöchl, P.E. Projector augmented wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed]
  26. Perdew, J.; Burke, K.; Ernzerhof, M. The Generalized Gradient Approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
  27. Ceperley, D.M.; Alder, B.J. Ground state of the electron gas by a stochastic method. Phys. Rev. Lett. 1980, 45, 566–569. [Google Scholar] [CrossRef]
  28. Press, W.H.; Flannery, B.P.; Teukolsky, S.A.; Vetterling, W.T. Numerical Recipes, 2nd ed.; Cambridge University Press: New York, NY, USA, 1986. [Google Scholar]
  29. Blöchl, P.; Jepsen, O.; Anderson, O. Improved tetrahedron method for Brillouin-zone integrations. Phys. Rev. B 1994, 49, 16223–16233. [Google Scholar] [CrossRef] [PubMed]
  30. Methfessel, M.; Paxton, A.T. High-precision sampling for Brillouin-zone integration in metals. Phys. Rev. B 1989, 40, 3616–3621. [Google Scholar] [CrossRef] [PubMed]
  31. Monkhorst, H.J.; Pack, J.D. Special k-points for Brillouin Zone integration. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
  32. Gaillac, R.; Pullumbi, P.; Coudert, F.X. ELATE: An open-source online application for analysis and visualization of elastic tensors. J. Phys. Condens. Matter 2016, 28, 275201. [Google Scholar] [CrossRef]
  33. Voigt, W. Über die Beziehung zwischen den beiden Elasticitätsconstanten isotroper Körper. Annal. Phys. 1889, 274, 573–587. [Google Scholar] [CrossRef]
  34. Mazhnik, E.; Oganov, A.R. A model of hardness and fracture toughness of solids. J. Appl. Phys. 2019, 126, 125109. [Google Scholar] [CrossRef]
  35. Chen, X.Q.; Niu, H.; Li, D.; Li, Y. Modeling hardness of polycrystalline materials and bulk metallic glasses. Intermetallics 2011, 19, 1275–1281. [Google Scholar] [CrossRef]
  36. Mukhanov, V.A.; Kurakevych, O.O.; Solozhenko, V.L. The interrelation between hardness and compressibility of substances and their structure and thermodynamic properties. J. Superhard Mater. 2008, 30, 368–378. [Google Scholar] [CrossRef]
  37. Lyakhov, A.O.; Oganov, A.R. Evolutionary search for superhard materials: Methodology and applications to forms of carbon and TiO2. Phys. Rev. B 2011, 84, 092103. [Google Scholar] [CrossRef]
  38. Togo, A.; Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 2015, 108, 1–5. [Google Scholar] [CrossRef]
  39. Dove, M.T. Introduction to Lattice Dynamics; Cambridge University Press: New York, NY, USA, 1993. [Google Scholar]
  40. Eyert, V. Basic notions and applications of the augmented spherical wave method. Int. J. Quantum Chem. 2000, 77, 1007–1031. [Google Scholar] [CrossRef]
  41. Momma, K.; Izumi, F. VESTA3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
  42. Eliseev, A.A.; Babitsyuna, A.A.; Medvedeva, Z.S. X-ray investigation of the arsenic-boron system. Russ. J. Inorg. Chem. 1964, 9, 633–636. [Google Scholar]
  43. Schowalter, M.; Rosenauer, A.; Volz, K. Parameters for temperature dependence of mean-square displacements for B-, Bi- and Tl-containing binary III-V compounds. Acta Crystallogr. A 2012, 68, 319–323. [Google Scholar] [CrossRef]
  44. Matar, S.F.; Solozhenko, V.L. First principles search for novel ultrahard high-density carbon allotropes: Hexagonal C6, C9 and C12. J. Superhard Mater. 2023, 45, 239–248. [Google Scholar] [CrossRef]
  45. Mahat, S.; Li, S.; Wu, H.; Koirala, P.; Lv, B.; Cahill, D.G. Elastic constants of cubic boron phosphide and boron arsenide. Phys. Rev. Mater. 2021, 5, 033606. [Google Scholar] [CrossRef]
  46. Tian, F.; Luo, K.; Xie, C.; Liu, B.; Liang, X.; Wang, L.; Gamage, G.A.; Sun, H.; Ziyaee, H.; Sun, J.; et al. Mechanical properties of boron arsenide single crystal. Appl. Phys. Lett. 2019, 114, 131903. [Google Scholar] [CrossRef]
  47. Solozhenko, V.L.; Matar, S.F. Prediction of novel ultrahard phases in the B–C–N system from first principles: Progress and problems. Materials 2023, 16, 886. [Google Scholar] [CrossRef]
  48. Brookes, C.A. The mechanical properties of cubic boron nitride. Proc. Int. Conf. Sci. Hard Mater. 1986, 207–220. [Google Scholar]
  49. Solozhenko, V.L.; Bushlya, V. Mechanical properties of boron phosphides. J. Superhard Mater. 2019, 41, 84–89. [Google Scholar] [CrossRef]
  50. Birch, F. Finite strain isotherm and velocities for single-crystal and polycrystalline NaCl at high pressures and 300 K. J. Geophys. Res. 1978, 83, 1257–1268. [Google Scholar] [CrossRef]
  51. Murnaghan, F.D. The compressibility of media under extreme pressures. Proc. Nation. Acad. Sci. USA 1944, 30, 244–247. [Google Scholar] [CrossRef] [PubMed]
  52. Koshchenko, V.I.; Demidenko, A.F.; Grinberg, Y.K.; Yachmenev, V.E. Specific-heats and thermodynamic functions of BP, BAs and B6As at 5-310 K. Izv. Akad. Nauk SSSR Neorg. Mater. 1981, 17, 1965–1968. (In Russian) [Google Scholar]
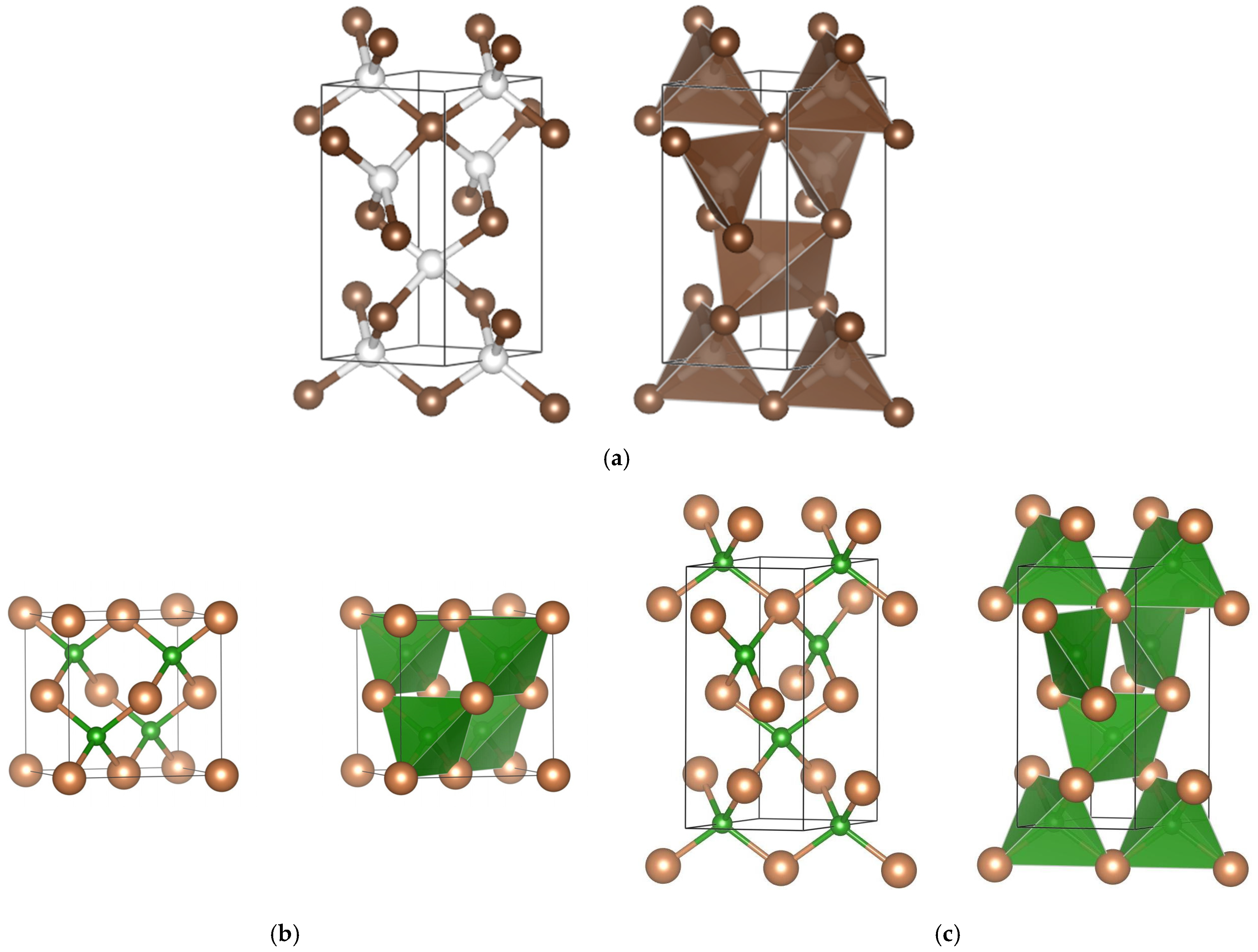
Crystals 14 00221 g001
Figure 1. Ball-and-stick and tetrahedral representations of the template qtz C6 (space group P6222) [44] (a), in which two carbon substructures C1 (3c) (white spheres) and C2 (3d) (brown spheres) allow for accommodation of two different types of atomic constituents to form hexagonal (qtz) structure of boron pnictides BX (X = As, Sb, Bi) (c). Cubic (zinc–blende) BX structure (b) is shown for comparison. Green and brick spheres correspond to B and X atoms, respectively.
Figure 1. Ball-and-stick and tetrahedral representations of the template qtz C6 (space group P6222) [44] (a), in which two carbon substructures C1 (3c) (white spheres) and C2 (3d) (brown spheres) allow for accommodation of two different types of atomic constituents to form hexagonal (qtz) structure of boron pnictides BX (X = As, Sb, Bi) (c). Cubic (zinc–blende) BX structure (b) is shown for comparison. Green and brick spheres correspond to B and X atoms, respectively.
Crystals 14 00221 g001
Crystals 14 00221 g002
Figure 2. Calculated total energy per formula unit as a function of volume for zinc–blende and qtz boron pnictides: BAs (a); BSb (b); and BBi (c).
Figure 2. Calculated total energy per formula unit as a function of volume for zinc–blende and qtz boron pnictides: BAs (a); BSb (b); and BBi (c).
Crystals 14 00221 g002
Crystals 14 00221 g003aCrystals 14 00221 g003b
Figure 3. Phonon band structures of zb-BAs (a); qtz BAs (b); zb-BSb (c); qtz BSb (d); zb-BBi (e), and qtz BBi (f).
Figure 3. Phonon band structures of zb-BAs (a); qtz BAs (b); zb-BSb (c); qtz BSb (d); zb-BBi (e), and qtz BBi (f).
Crystals 14 00221 g003aCrystals 14 00221 g003b
Crystals 14 00221 g004
Figure 4. Heat capacity at constant volume (CV) and entropy (S) of zinc–blende and qtz boron pnictides as functions of temperature: BAs (a); BSb (b); and BBi (c). Experimental heat capacity data for zb-BAs [2,52] are shown as gray symbols.
Figure 4. Heat capacity at constant volume (CV) and entropy (S) of zinc–blende and qtz boron pnictides as functions of temperature: BAs (a); BSb (b); and BBi (c). Experimental heat capacity data for zb-BAs [2,52] are shown as gray symbols.
Crystals 14 00221 g004
Crystals 14 00221 g005
Figure 5. Electronic band structures of zb-BAs (a); qtz BAs (b); zb-BSb (c); qtz BSb (d); zb-BBi (e); and qtz BBi (f).
Figure 5. Electronic band structures of zb-BAs (a); qtz BAs (b); zb-BSb (c); qtz BSb (d); zb-BBi (e); and qtz BBi (f).
Crystals 14 00221 g005
Table 1. Crystal structure parameters of BX (X = As, Sb, Bi) polymorphs.
Table 1. Crystal structure parameters of BX (X = As, Sb, Bi) polymorphs.
zb-BAs (Z = 4)
F-43m (No. 216)		qtz BAs (Z = 3)
P6422 (No. 181)		zb-BSb (Z = 4)
F-43m (No. 216)		qtz BSb (Z = 3)
P6422 (No. 181)		zb-BBi (Z = 4)
F-43m (No. 216)		qtz BBi (Z = 3)
P6422 (No. 181)
a, Å4.813 (4.777 [42])3.4615.279 (5.267 [43])3.7655.536 (5.528 [43])3.944
c, Å–7.486–8.289–8.79252
Vcell, Å3111.5177.66146.97101.78169.65118.46
V/FU, Å327.8825.89
ΔV/FU = 1.99		36.7433.93
ΔV/FU = 2.81		42.4139.49
ΔV/FU = 2.92
Shortest bond, Å2.082.132.292.332.402.45
Angle (deg.)109.47108.42/90.74109.47108.41/90.74109.47106.76/91.93
Atomic positionsB (4c) ¼, ¼, ¼
As (4a) 0, 0, 0		B (3c) ½, 0, 0
As (3d) ½, 0, ½		B (4c) ¼, ¼, ¼
Sb (4a) 0, 0, 0		B (3c) ½, 0, 0
Sb (3d) ½, 0, ½		B (4c) ¼, ¼, ¼
Bi (4a) 0, 0, 0		B (3c) ½, 0, 0
Bi (3d) ½, 0, ½
Etotal, eV
Etotal/FU, eV		−45.47
−11.37		−31.44
−10.48
ΔE/FU = −0.89 eV		−40.14
−10.03		−28.01
−9.34
ΔE/FU = −0.69 eV		−35.69
−8.92		−25.06
−8.35
ΔE/FU = −0.57 eV
Table 2. Elastic constants Cij of BX polymorphs. Bulk (BV), shear (GV), and Young’s (EV) moduli calculated by the Voight averaging. All values are in GPa.
Table 2. Elastic constants Cij of BX polymorphs. Bulk (BV), shear (GV), and Young’s (EV) moduli calculated by the Voight averaging. All values are in GPa.
C11C12C13C33C44C66BVGVEV
zb-BAs2686767 268146146134128291
qtz BAs32338 57307143160140146324
zb-BSb182585818297 979983195
qtz BSb21431572239111410598223
zb-BBi124393912467676757134
qtz BBi135493915243727557137
Table 3. Mechanical properties of BX polymorphs: Vickers hardness (HV), bulk modulus (B), shear modulus (GV), Young’s modulus (EV), Poisson’s ratio (ν), and fracture toughness (KIc).
Table 3. Mechanical properties of BX polymorphs: Vickers hardness (HV), bulk modulus (B), shear modulus (GV), Young’s modulus (EV), Poisson’s ratio (ν), and fracture toughness (KIc).
HVBGVEVν **KIc‡
T *LO †MO ‡CN §B0 *BV
GPa MPa·m½
zb-BAs #216242222291461341282910.1381.4
qtz BAs #180252227361541401463240.1131.2
zb-BSb #2161816121910799831950.1731.0
qtz BSb #1801991624116105982230.1491.0
zb-BBi #21614128158667571340.1690.6
qtz BBi #1801577129275571370.1970.6
* Thermodynamic model [36]; † Lyakhov–Oganov model [37]; ‡ Mazhnik–Oganov model [34]; § Chen–Niu model [35]; ** ν values calculated using isotropic approximation.
Table 4. Calculated properties of BX polymorphs: bulk moduli (B0); total energies (E0) and equilibrium volumes (V0) per formula unit; zb-to-qtz transition pressures (ptr); and corresponding reduced volumes (Vtr/V0).
Table 4. Calculated properties of BX polymorphs: bulk moduli (B0); total energies (E0) and equilibrium volumes (V0) per formula unit; zb-to-qtz transition pressures (ptr); and corresponding reduced volumes (Vtr/V0).
BAsBSbBBi
zbqtzzbqtzzbqtz
B0 (GPa)146 *1541071168692
E0/FU (eV)−11.37−10.45−10.06−9.32−8.92−8.34
V0/FU (Å3)27.88 †25.8936.7433.9342.4139.47
Vtr/V00.6970.7240.763
ptr (GPa)1177151
* Experimental values: B0 = 148(6) GPa and B′ = 3.9(3) [15]; B0 = 148(9) GPa [45]. † Experimental value: V0/FU = 27.26 Å3 [42].
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Solozhenko, V.L.; Matar, S.F. High-Pressure Phases of Boron Pnictides BX (X = As, Sb, Bi) with Quartz Topology from First Principles. Crystals 2024, 14, 221. https://doi.org/10.3390/cryst14030221

AMA Style

Solozhenko VL, Matar SF. High-Pressure Phases of Boron Pnictides BX (X = As, Sb, Bi) with Quartz Topology from First Principles. Crystals. 2024; 14(3):221. https://doi.org/10.3390/cryst14030221

Chicago/Turabian Style

Solozhenko, Vladimir L., and Samir F. Matar. 2024. "High-Pressure Phases of Boron Pnictides BX (X = As, Sb, Bi) with Quartz Topology from First Principles" Crystals 14, no. 3: 221. https://doi.org/10.3390/cryst14030221

APA Style

Solozhenko, V. L., & Matar, S. F. (2024). High-Pressure Phases of Boron Pnictides BX (X = As, Sb, Bi) with Quartz Topology from First Principles. Crystals, 14(3), 221. https://doi.org/10.3390/cryst14030221

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop