Abstract
A method for full Stokes polarization imaging based on broadband liquid crystal polarization grating (LCPG) is presented. Firstly, the properties of the LCPG-based polarization detection module, which consists of a phase retarder and a broadband polarization grating in series, were investigated by means of Stokes calculus. The relationship between the polarization state of the incidence and the efficiencies of the diffractions was derived. Then, the azimuth parameters of the polarization detection module were optimized by using an equally weighted variance (EWV) evaluation criterion. Finally, the detection of the linearly and arbitrarily polarized laser beam and a linearly polarized broadband object were experimentally verified. The proposed method provides the design of polarization imaging systems based on LCPGs and has the advantages of compact structure, and broad wavelength coverage, therefore offering potential applications for image polarization information acquisition.
1. Introduction
Polarimetric imaging, which can measure the state of polarization (SOP) of two-dimensional (2D) scenes, yields comparable performance to that of classical intensity imaging [,,]. Recently, there is a wide variety of applications for imaging polarimeters, including remote sensing [,,], sky navigation [,,], and biomedical detection [,]. Thus, the development of polarization imaging technology for the acquisition of the polarization characteristics of detected targets is currently a hot topic in optical sensing. Generally, a polarimeter uses a polarizer or wave plate to decode the polarization parameters from the intensity values of the light field [,]. To overcome the bulky volume or mechanical instability of traditional structures, there are various schematics of imaging polarimeters for different applications using complex polarization elements such as scattering materials [], micro-polarizer array [], Savart plates [], liquid crystal modulators [,], gradient refractive index (GRIN) lens [], etc. Among these, high-quality polarization grating (PG) with strong polarization sensitivity and low incoherent scattering is a promising candidate. Techniques using polarized diffraction grating as a method of polarization measurement have been studied. A modified Sagnac interferometer was developed by using a pair of identical PGs to replace the Savart plate for a compact design []. The detection of the light’s polarization state by using crossed polarization gratings or merged vector gratings was reported [,,]. A reported imaging spectropolarimeter provided the ability to provide snapshot spectral polarization measurements on a single detector with polarization grating [,]. However, the above methods suffer from either sophisticated calibration or low spatial definition.
In this paper, we promote an approach that combines a high-quality LCPG and a phase retarder to construct linear and full Stokes polarization imaging. The broadband LCPG was prepared using our previously published interference-free and single-exposure method. The linear Stokes polarization detection and full Stokes polarization detection are demonstrated separately. The presented method has the advantages of high robustness, low cost, and simple optical design.
2. Principle
The basic schematic for polarization detection is depicted in Figure 1. It is a quite simple principle, and the basic module is compact and consists of a phase retarder and a broadband polarization grating in series. The phase retarder is placed so that the fast axis has an angle of relative to the x-axis. The phase delay of the phase retarder is . In this section, we establish a quantitative link between the transmission matrix of the polarization detection module and the polarization-dependent intensity distribution to map the polarization information to an intensity distribution.
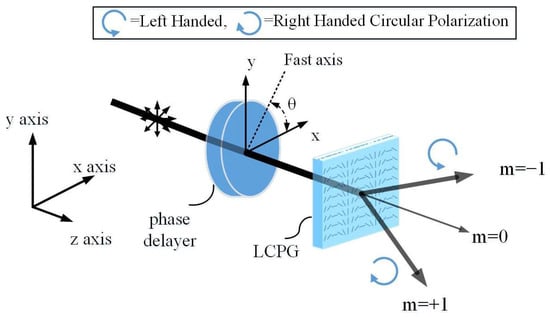
Figure 1.
Schematic diagram of LCPG-based polarization detection module.
The PG employed here has a cycloidal distribution of birefringence, which is realized by photo-aligned liquid crystal (LC) polymers [,,]. It acts as a thin-film polarization-dependent beam splitter, which separates the left-/right-handed circular polarization component of the incident light into ±1 diffraction orders. The ±1 orders exhibit orthogonal circular polarization states, and the diffraction efficiency can be described as follows []:
where Q is the factor determined by the LCPG structure, and S3 is the normalized Stokes parameter corresponding to the ellipticity of the incident light. It needs to be emphasized that factor Q is firstly determined by the azimuthal pattern of the aligned LC directors. When the surface alignment satisfies the continuous distribution of the cycloidal pattern, it forms a birefringent grating with LC directors following the surface alignment, which is called the single-wavelength PG. In this case, factor Q equals 1 at a certain wavelength, which is called the half-wave condition (∆nd = λ/2). In addition, when a multi-layer, twisted structure (shown in Figure 2a) is introduced by adding chiral doping, the high-efficient range is broadened from a single wavelength to a wide spectral band. Our results in Figure 2b show high diffraction efficiency (>93%) in the most visible wavelengths (e.g., 450–800 nm). As for the polarization of diffractive beams, the ellipticity |S3| of ±1 diffraction orders shows that the diffractive beams are perfectly circular-polarized even when the efficiency is away from the peak value.
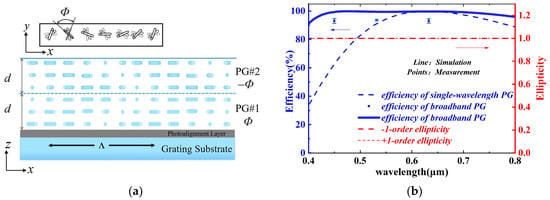
Figure 2.
Structure and properties of broadband PG: (a) LC director view of broadband PG with two chiral layers; (b) diffraction efficiency and ellipticity of broadband PG in visible range.
There are several notable aspects of broadband PG to be applied for polarization detections. Firstly, the ±1-order efficiencies are highly sensitive to incident polarization, which is the basis of PG to be applied in polarization detections. Secondly, the efficiency of the polarization-dependent ±1 orders exhibits a high and unchanged value over a relatively wide spectral range. Thus, the intensity fluctuation due to chromatic reason is minimized, although chromatic aberration still exists. Thirdly, the 0th order maintains the incident polarization, and the efficiency of the 0th order can be designed as a non-zero value. It provides the possibility for original image monitoring or other applications.
In a recent work [], we illustrated a method for generating a cycloidal pattern of liquid crystal molecules by interference-free and single exposure. Here, the method and principles of multi-layer twisting were applied to manufacture broadband LCPGs. In particular, we utilized sulfonic azo-dye SD1 (DIC. Tokyo, Japan) as the photoalignment layer material. A birefringent prism and a quarter waveplate (QWP) were used to manipulate the polarization of the exposed beam (shown in Figure 3a), and the surface alignment pattern was recorded in the SD1 layer. After exposure, the LC films were spun onto the SD1-coated substrate, the polarization orientation pattern was transferred to the LC molecules, and the PG was formed through UV curing. The first PG layer was composed of polymerizable liquid crystal material UCL-P100 (DIC. Tokyo, Japan), doped with a small amount (0.18 wt.%) of chiral molecule S811 (Merck, left-handed). A thickness of d ≈ 1.7 μm was selected to meet the half-wave condition, and the twist Φ = +70°occurred simultaneously. The second PG layer consisted of UCL-P100 doped with chiral molecule R811 (0.18 wt.%, Merck, right-handed), resulting in the same LC layer thickness and an opposite twist angle of Φ = −70°. With two antisymmetric chiral layers, the approximate polarization separation and phase delay could be achieved in the wide band of visible light based on the principle of phase compensation []. The manufactured broadband LCPG sample is shown in Figure 3b, with an effective area of about 4πcm2.
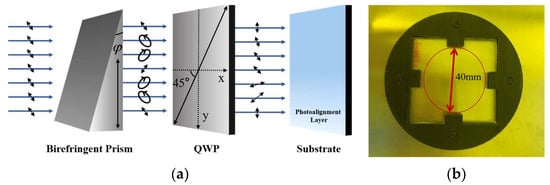
Figure 3.
(a) Schematics of generation of exposure beam with continuously changing polarization state using birefringent prism and QWP []; (b) photograph of manufactured broadband LCPG.
The Mueller matrix MPG of the LCPG is the sum of 0th and ±1st orders, which are written with absorption and scattering neglected as follows:
with
For the arbitrarily polarized state of the incident light, the Stokes vector can be derived after passing through the polarization detection module composed of phase retarder and broadband PG as
where Mretarder is the Muller matrix of phase retarder. Here, let us assume that the incident wavelength falls in the high-efficiency range of broadband PG (Q = 1). Therefore, by solving the Stokes vectors, the theoretical efficiencies are given by
The diffractive ±1 orders are complementary. The sum equals 1 assuming Q = 1. For more general cases with Q ≠ 1, the intensity ratio γ of +1 or −1 order over the sum of diffractive orders depends only on incident polarization.
Thus far, the theoretical model has been established in Equations (8) and (9), which can encode the polarization information of incidence into the intensity distribution of diffractive ±1 orders.
3. Linear Stokes Detection
Given that the incident light is linearly polarized, the linear components S1 and S2 of the Stokes vector need to be solved. Mathematically, to solve the two parameters S1 and S2, two equations are required. Thus, according to Equation (8) or Equation (9), it is necessary to perform the intensity ratio γ measurements twice. corresponding to two phase-retardance conditions, for instance, (θ1, δ1) and (θ2, δ2). In this case, it is simplified as a linear equation with two variables:
where the coefficients are , , and .
Thus, the linear Stokes parameters S1 and S2 can be easily solved. To make the above linear equation solvable, the coefficients must satisfy , which is further simplified as .
From the above mathematical derivation, we can draw the conclusion that it is not possible to solve the polarization of incidence with a fixed direction of fast axis θ and varied retardance δ1 and δ2. In other words, to obtain the direction of the incident linear polarization, it is necessary to modulate the fast axis of the retarder. As for the implementation of polarimetry, it can be either a division-of-time or division-of-amplitude type. A cascaded structure, which is typical for the division-of-amplitude type, using 0 order as the input of the next stage is reported and verified for fiber communication applications []. However, the intensity distribution among the cascaded stages needs to be delicately designed. As explained in the following sections, for the purpose of the principal-of-operation verification, we used a rotatable QWP to achieve the modulation of fast axis θ for imaging acquisition.
3.1. Optimal Design of Polarization Detection System
For a practical polarization measurement system, the signal-to-noise ratio (SNR) is one of the most critical parameters. The noise suppression effect is closely related to the design of the measurement matrix [,]. Therefore, to obtain higher-quality polarization measurement results, it is extremely necessary to optimize the angle parameters of the measurement matrix.
According to Equation (5), by using a QWP, the middle part of the Muller matrix of the polarization detection module can be indicated as
The EWV criterion is adopted to evaluate the noise propagation performance in the process of the optimization of polarization measurement structures [,]. The minimum sum of the estimated variance of each component of the Stokes vector is taken as the objective function of the optimization problem. It is supposed that the distribution of noise is in accord with the Gaussian additional noise (GAN) interference with noise variance σ2; thus, the EWV value estimated by the Stokes vector can be calculated from Equation (12):
When or is satisfied, the EWV is the minimum, which is consistent with the result shown in Figure 4. Therefore, the fast axis azimuth angles of 0° and 45° were selected to perform the linear polarization detection.
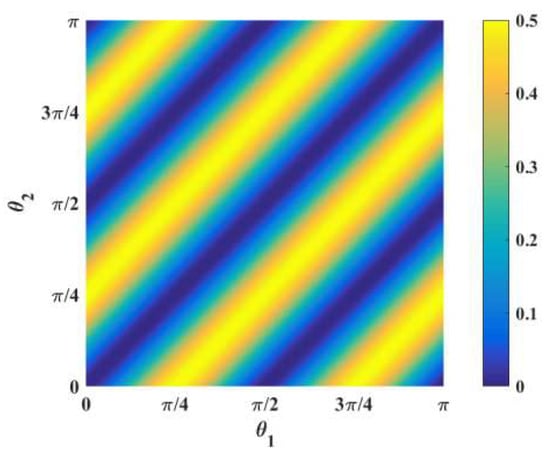
Figure 4.
Relationship between σ2/EWV and fast axis azimuth angles (θ1, θ2) of QWP.
3.2. Linear Stokes Parameter Reconstruction
To verify the proposed method, we built a setup for linear Stokes parameter detection using a linearly polarized laser as the incidence. As shown in Figure 5a, the measurement setup was composed of a laser light source, a polarizer, a QWP, an LCPG, and an optical power meter (PM16-140, Thorlabs Inc. Newton, NJ, USA). Briefly, 532 nm and 632.8 nm lasers were used as the light source. The rotation of the polarizer was controlled by the stepping motor (K10CR1/M, Thorlabs Inc. Newton, NJ, USA). The LCPG was fabricated according to the method previously proposed by our laboratory []. Its diffraction pattern and texture are shown in Figure 5b. Additionally, the diffraction efficiency was more than 93% at 532 nm and 632.8 nm, and the measured period using a microscope image was 158 μm.
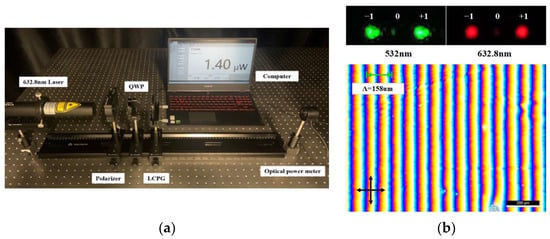
Figure 5.
(a) Linear polarized light detection experimental device; (b) diffraction patterns of polarization grating and textures of LCPG observed under polarized microscope with black arrows showing polarizer and analyzer direction.
The polarization parameter was acquired by rotating the QWP. Specifically, the intensity of the ±1st order diffracted beams was obtained by rotating the waveplate, and then the Stokes linear polarization parameters, the degree of linear polarization (DoLP), and the angle of polarization (AoP) were calculated according to Equation (10) []:
The linearly polarized light with different polarization directions α was generated as the detection target by rotating the polarizer, and the beam diffraction intensity could be collected under the different fast axis angles of the QWP. The root-mean-squared error was calculated between the actual measured data and the theoretical values as approximately 0.4% for γ±1, and the specific experimental results are demonstrated in Figure 6 and Table 1.
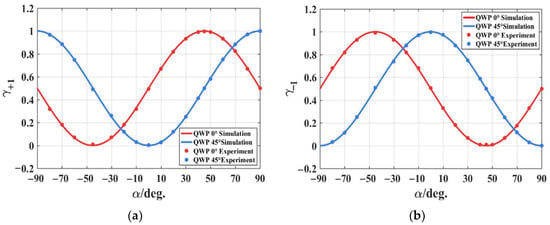
Figure 6.
Plots of (a) γ+1 and (b) γ−1 as a function of the direction α of linearly polarized incidence. the theoretical values are represented by solid curves, while the experimental measurements are represented by dots mark.

Table 1.
Experimental data of linear polarization detection.
Furthermore, we also detected the linear polarization of the broadband image scene, and the experimental device is illustrated in Figure 7. Firstly, the object (Figure 8a) was placed in front of the detection device, and we adjusted the fast axis of the polarizer to −45°. Hence, the polarization information of the image was modulated to a uniform −45° linear polarization state. Then, we changed the QWP to 0° (Figure 8b) and 45° (Figure 8c), respectively, and took pictures with a camera (acA 1600-60gm, Basler Arensberg, Germany). After being diffracted by the LCPG, the incidence was divided into +1st- and −1st-order images (Ignore 0th). Using the principle, the intensity of the diffracted beam was all concentrated in the −1st order when the QWP was 0°, while the emitted +1st and −1st order diffraction efficiency was the same for the QWP at 45°. In addition, the number of pixels occupied by the 0-order image, shown in Figure 8b, was 37 rows × 94 columns, and the −1-order diffraction image was 43 rows × 94 columns. The inconsistency in the number of rows is caused by grating dispersion, and the smaller the grating period, the more pronounced the dispersion, and the more unfavorable it is for polarization solving. In imaging detection, it is necessary to ensure that the distance between the target and the QWP (object distance) is large enough to realize the separation of all the levels of diffraction images, which will not affect the compactness between the QWP and the camera in the system.

Figure 7.
Polarization imaging experiment based on linearly polarized light.

Figure 8.
(a) Raw image; polarization image of QWP at (b) 0° and (c) 45°.
Figure 9 depicts the two-dimensional polarization information of the selected target area. The average values of S1, S2, AoP and DoLP were 0.004 ± 0.026, −0.970 ± 0.036, −44.872° ± 0.761°, and 0.971 ± 0.019, respectively. Furthermore, the experimental results show that the proposed method could effectively measure the polarization characteristics of the object.

Figure 9.
The polarization parameters calculated using the broadband object.
4. Full Stokes Detection
The circular polarization information S3 of the object reveals the comprehensive features of the object in addition to its linear components. The LCPGs divide the left-handed and right-handed circular polarization components into ±1 diffraction orders (refer to Equation (2) for details). Therefore, S3 measurement can be performed by directly placing the LCPG in front of the camera and collecting the resulting images. Thus, the full Stokes polarization detection was performed by adding an additional measurement step when the QWP was removed.
Hence, the degree of circular polarization (DoCP) can also be solved by using Equation (15) [].
Full Stokes Parameter Reconstruction
To verify the full Stokes polarization detection method, a full Stokes parameter detection setup was built by taking a laser beam as the light source, as shown in Figure 10. The 632.8 nm laser, polarizer, and QWP1 constituted a polarization generation module. Specifically, the light transmission axis direction of the polarizer was horizontally fixed (i.e., β = 0), and the polarized light with different ellipticities was generated by rotating QWP1 as the incidence to be detected. Then, the diffracted beams modulated by QWP2 and the LCPG were received by the optical power meter, and the polarization state of the incident light wave was solved according to the light intensity.
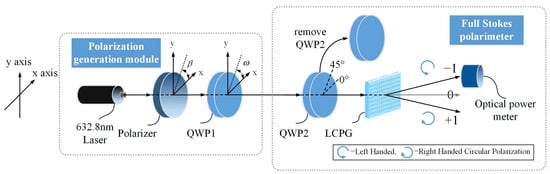
Figure 10.
Configuration diagrams of full Stokes polarization detection.
When the fast axis angle of QWP2 was 0°, 45°, and the QWP2 was removed, the light intensity data of ±1 orders were collected, respectively, and then the polarization state of the incident light was calculated. In addition, the results of the detected polarization state are shown in Figure 11a,b. The standard deviations in figures are marked by an error bar. The deviation between the experimental and theoretical values of the polarization characteristic parameters was small, indicating that the full Stokes polarization detection method designed in this paper can achieve full polarization detection.
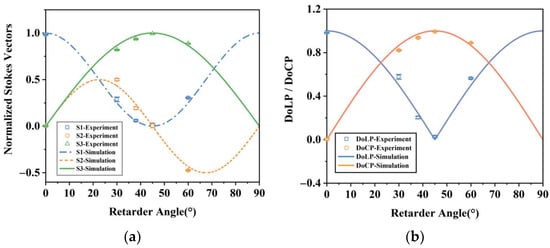
Figure 11.
Plots of (a) the experimental and simulation values of S1, S2, S3, and (b) DoLP and DoCP parameters as a function of the fast axis orientation of QWP1 at 632.8 nm measured by the full Stokes polarization detection method.
5. Conclusions
This research put forward two polarization detection methods based on the LCPG: linear polarization detection and full Stokes polarization detection. When combined with a quarter waveplate, the visible broadband polarization grating can be used to solve the full Stokes parameters. The intensity ratio between +1 and −1 orders was adopted instead of the efficiencies when considering the more general cases, for instance, 0-order leakage or thickness mismatch. Additionally, the phase modulation of the incidence in front of the LCPG for measuring polarization parameters was summarized. Using the LCPG for polarization detection is expected to overcome any limitations in physical size and complexity. In addition, due to its simple configuration, it can be easily integrated into existing systems and has the potential to be widely used in optoelectronic systems such as optical memory devices and optical information processing.
Author Contributions
Investigation, Y.X. and H.Z. (Hao Zhang); methodology, Y.X.; software, Y.X.; validation, Y.X.; formal analysis, Y.X.; resources, H.Z. (Huijie Zhao); writing—original draft preparation, Y.X.; writing—review and editing, Q.G. and Y.X.; supervision, Q.G.; project administration, Q.G.; funding acquisition, Q.G. and H.Z. (Huijie Zhao). All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (NSFC); (No. 61875004, No. 62075202).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rubin, N.A.; D’Aversa, G.; Chevalier, P.; Shi, Z.; Chen, W.T.; Capasso, F. Matrix Fourier Optics Enables a Compact full-Stokes Polarization Camera. Science 2019, 365, 43. [Google Scholar] [CrossRef] [PubMed]
- Basiri, A.; Chen, X.; Bai, J.; Amrollahi, P.; Carpenter, J.; Holman, Z.; Wang, C.; Yao, Y. Nature-inspired chiral metasurfaces for circular polarization detection and full-Stokes polarimetric measurements. Light Sci. Appl. 2019, 8, 78. [Google Scholar] [CrossRef] [PubMed]
- Dai, M.; Wang, C.; Qiang, B.; Wang, F.; Ye, M.; Han, S.; Luo, Y.; Wang, Q.J. On-chip mid-infrared photothermoelectric detectors for full-Stokes detection. Nat. Commun. 2022, 13, 4560. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.; Yu, Y.; Liu, W.; Zhang, X. Fully integrated CMOS-compatible polarization analyzer. Nanophotonics 2019, 8, 467–474. [Google Scholar] [CrossRef]
- Hou, W.; Li, Z.; Wang, J.; Xu, X.; Goloub, P.; Qie, L. Improving Remote Sensing of Aerosol Microphysical Properties by Near-Infrared Polarimetric Measurements Over Vegetated Land: Information Content Analysis. J. Geophys. Res. Atmos. 2018, 123, 2215–2243. [Google Scholar] [CrossRef]
- Asgarimehr, M.; Hoseini, M.; Semmling, M.; Ramatschi, M.; Camps, A.; Nahavandchi, H.; Haas, R.; Wickert, J. Remote sensing of precipitation using reflected GNSS signals: Response analysis of polarimetric observations. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–12. [Google Scholar] [CrossRef]
- Horváth, G.; Barta, A.; Gál, J.; Suhai, B.; Haiman, O. Ground-based full-sky imaging polarimetry of rapidly changing skies and its use for polarimetric cloud detection. Appl. Opt. 2002, 41, 543–559. [Google Scholar] [CrossRef]
- Zhao, H.; Xu, W.; Zhang, Y.; Li, X.; Zhang, H.; Xuan, J.; Jia, B. Polarization patterns under different sky conditions and a navigation method based on the symmetry of the AOP map of skylight. Opt. Express 2018, 26, 28589. [Google Scholar] [CrossRef]
- Li, Q.; Hu, Y.; Hao, Q.; Cao, J.; Cheng, Y.; Dong, L.; Huang, X. Skylight polarization patterns under urban obscurations and a navigation method adapted to urban environments. Opt. Express 2021, 29, 42090. [Google Scholar] [CrossRef]
- He, C.; He, H.; Chang, J.; Chen, B.; Ma, H.; Booth, M.J. Polarisation optics for biomedical and clinical applications: A review. Light Sci. Appl. 2021, 10, 194. [Google Scholar] [CrossRef]
- Kuzyk, A.; Schreiber, R.; Fan, Z.; Pardatscher, G.; Roller, E.; Högele, A.; Simmel, F.C.; Govorov, A.O.; Liedl, T. DNA-based self-assembly of chiral plasmonic nanostructures with tailored optical response. Nature 2012, 483, 311–314. [Google Scholar] [CrossRef] [PubMed]
- Myhre, G.; Hsu, W.L.; Peinado, A.; LaCasse, C.; Brock, N.; Chipman, R.A.; Pau, S. Liquid crystal polymer full-stokes division of focal plane polarimeter. Opt. Express 2012, 20, 27393–27409. [Google Scholar] [CrossRef] [PubMed]
- Gruev, V.; Perkins, R.; York, T. CCD polarization imaging sensor with aluminum nanowire optical filters. Opt. Express 2010, 18, 19087–19094. [Google Scholar] [CrossRef] [PubMed]
- Töppel, F.; Aiello, A.; Marquardt, C.; Giacobino, E.; Leuchs, G. Classical entanglement in polarization metrology. New J. Phys. 2014, 16, 73019–73021. [Google Scholar] [CrossRef]
- York, T.; Marinov, R.; Gruev, V. 260 frames-per-second 648x488 resolution division-of-focal-plane polarimeter with structural dynamics and tracking applications. Opt. Express 2016, 24, 8243–8252. [Google Scholar] [CrossRef]
- Luo, H.; Oka, K.; DeHoog, E.; Kudenov, M.; Schiewgerling, J.; Dereniak, E.L. Compact and miniature snapshot imaging polarimeter. Appl. Opt. 2008, 47, 4413–4417. [Google Scholar] [CrossRef]
- López-Morales, G.; Sánchez-López, M.; Lizana, Á.; Moreno, I.; Campos, J. Mueller Matrix Polarimetric Imaging Analysis of Optical Components for the Generation of Cylindrical Vector Beams. Crystals 2020, 10, 1155. [Google Scholar] [CrossRef]
- Chang, J.; Zeng, N.; He, H.; He, Y.; Ma, H. Single-shot spatially modulated Stokes polarimeter based on a GRIN lens. Opt. Lett. 2014, 39, 2656–2659. [Google Scholar] [CrossRef]
- Kudenov, M.W.; Escuti, M.J.; Dereniak, E.L.; Oka, K. White-light channeled imaging polarimeter using broadband polarization gratings. Appl. Opt. 2011, 50, 2283–2293. [Google Scholar] [CrossRef]
- Sasaki, T.; Hatayama, A.; Emoto, A.; Ono, H.; Kawatsuki, N. Simple detection of light polarization by using crossed polarization gratings. J. Appl. Phys. 2006, 100, 63502. [Google Scholar] [CrossRef]
- Sasaki, T.; Wada, T.; Noda, K.; Kawatsuki, N.; Ono, H. Merged vector gratings recorded in a photocrosslinkable polymer liquid crystal film for polarimetry. J. Appl. Phys. 2014, 115, 23110. [Google Scholar] [CrossRef]
- Noda, K.; Momosaki, R.; Matsubara, J.; Sakamoto, M.; Sasaki, T.; Kawatsuki, N.; Goto, K.; Ono, H. Polarization imaging using an anisotropic diffraction grating and liquid crystal retarders. Appl. Opt. 2018, 57, 8870–8875. [Google Scholar] [CrossRef]
- Escuti, M.J.; Oh, C.; Sánchez, C.; Bastiaansen, C.; Broer, D.J. Simplified spectropolarimetry using reactive mesogen polarization gratings. Imaging Spectrom. XI SPIE 2006, 6302, 21–31. [Google Scholar]
- Kim, J.; Escuti, M.J. Snapshot imaging spectropolarimeter utilizing polarization gratings. Imaging Spectrom. XIII SPIE 2008, 7086, 29–38. [Google Scholar]
- Lin, T.; Xie, J.; Zhou, Y.; Zhou, Y.; Yuan, Y.; Fan, F.; Wen, S. Recent Advances in Photoalignment Liquid Crystal Polarization Gratings and their Applications. Crystals 2021, 11, 900. [Google Scholar] [CrossRef]
- Chen, D.; Zhao, H.; Yan, K.; Xu, D.; Guo, Q.; Sun, L.; Wu, F.; Chigrinov, V.G.; Kwok, H. Interference-free and single exposure to generate continuous cycloidal alignment for large-area liquid crystal devices. Opt. Express 2019, 27, 29332. [Google Scholar] [CrossRef]
- Zhang, S.; Chen, W.; Yu, Y.; Wang, Q.; Mu, Q.; Li, S.; Chen, J. Twisting Structures in Liquid Crystal Polarization Gratings and Lenses. Crystals 2021, 11, 243. [Google Scholar] [CrossRef]
- Gao, B.; Beeckman, J.; Neyts, K. Design and Realization of a Compact Efficient Beam Combiner, Based on Liquid Crystal Pancharatnam–Berry Phase Gratings. Crystals 2021, 11, 220. [Google Scholar] [CrossRef]
- Mu, T.; Chen, Z.; Zhang, C.; Liang, R. Optimal design and performance metric of broadband full-Stokes polarimeters with immunity to Poisson and Gaussian noise. Opt. Express 2016, 24, 29691. [Google Scholar] [CrossRef]
- Letnes, P.A.; Nerbo, I.S.; Aas, L.M.; Ellingsen, P.G.; Kildemo, M. Fast and optimal broad-band Stokes/Mueller polarimeter design by the use of a genetic algorithm. Opt. Express 2010, 18, 23095–23103. [Google Scholar] [CrossRef]
- Sabatke, D.S.; Descour, M.R.; Dereniak, E.L.; Sweatt, W.C.; Kemme, S.A.; Phipps, G.S. Optimization of retardance for a complete Stokes polarimeter. Opt. Lett. 2000, 25, 802–804. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Hu, H.; Goudail, F.; Liu, T. Fundamental precision limits of full Stokes polarimeters based on DoFP polarization cameras for an arbitrary number of acquisitions. Opt. Express 2019, 27, 31261. [Google Scholar] [CrossRef] [PubMed]
- Goldstein, D.H. Polarized Light, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).