Design of Porous Shape Memory Alloys with Small Mechanical Hysteresis

Abstract

The mechanical hysteresis loop behavior always limits the applicability of shape memory alloys (SMAs) in mechanical devices requiring high sensitivity, durability and energy conversion efficiency. In this study, through experiments and finite element simulations, we systematically investigated the effects of porosity and pore distribution on the mechanical hysteresis behavior of porous Ti_49.2Ni_50.8 SMAs. Inspired by atomic crystal structures, some porous SMAs with ordered void distributions were investigated to compare them with SMAs with random pore distributions. Our results show that the hysteresis reduces with increasing porosity in porous SMAs. The designed BCC-type ordered porous SMAs possess a narrower hysteresis loop with less energy dissipation at the same porosity. The gradual and homogenous martensitic-phase transformations are responsible for this characteristic. The present work provides an effective way to design porous SMAs with narrow hysteresis, which is promising in applications for mechanical sensors or actuators.

1. Introduction

Shape memory alloy (SMA) is one kind of advanced intelligent functional material, which has received extensive attention due to its two closely related and unique properties: shape memory effect (SME) and superelasticity (SE) [1,2,3,4,5]. When the alloy undergoes a certain degree of plastic deformation at a temperature lower than the martensitic phase-transformation temperature, it can be heated to restore its original shape before deformation. This unique phenomenon is called the shape memory effect. When the alloy is subjected to plastic-like recoverable deformation (nonlinear elastic deformation) under a stress above the phase-transformation temperature, it undergoes a stress-induced martensitic transformation (SIMT) and can be restored to its original shape before deformation by directly releasing the stress. Since the deformation can bear the recoverable strain several times or even dozens of times larger than the normal metal, it is called superelasticity [6]. Due to the above two functional features, shape memory alloys can realize the mutual conversion between thermal energy and mechanical energy, or between mechanical energy and mechanical energy. Consequently, these unique properties make them attractive for many applications, such as sensors, actuators and micro-electromechanical systems (MEMS) [7,8,9,10].

Superelasticity is desirable in applications of stress/strain driving devices and mechanical sensors based on SMAs [6,10]. However, due to the inherent properties of the first-order martensitic phase transformation, the stress–strain curves of SMAs always display the mechanical hysteresis effect, in which the unloading path does not overlap the initial loading path. It generates the energy dissipation for SMAs during the superelastic cycling, resulting from the energy conversion from mechanical to thermal energy [11]. In addition, the stress-induced martensitic phase transformation leads to the non-linear stress–strain behavior. Thus, the mechanical hysteresis in martensitic transformation limits the usefulness of SMAs in mechanical devices that require high sensitivity, high durability and high energy efficiency [12,13].

To broaden the application of SMAs, it is highly desirable to optimize the SMAs for achieving near-linear stress–strain correlation and small (narrow) mechanical hysteresis [14,15,16,17]. Recently, porous SMAs have attracted much attention because of their light-weight structures and tunable functional properties. Some porous SMAs with ordered structures have been prepared by additive manufacturing or the space-holder technique [18,19,20,21,22]. Among them, finite element simulations always play critical roles in structural optimization and revealing the internal mechanism [20,21,22]. The porous SMAs can be regarded as special composite materials combining the real SMA with the particular constituent material’s “voids” together [23]. In principle, as the structural defects, the voids/pores will give rise to the structural inhomogeneity of SMA, thereby leading to the martensitic phase transformation of SMA change from one-step uniform transformation to multi-step non-uniform transformation. As a result, the porous SMA could weaken the hysteresis and reduce the energy dissipation. The design of SMAs with defects could be an effective strategy to modulate their related superelasticity behavior [17].

In this study, we selected TiNi as one prototypical SMA to investigate the effect of porous structure on mechanical hysteresis. First, using experiments, the hysteresis loop of Ti_49.2Ni_50.8 was measured in ambient conditions. Then, by finite element simulations, the models and the corresponding parameters for realizing superelasticity were established based on experimental results. After that, the effects of porosity and distribution on hysteresis behavior were investigated systematically. The results indicate that SMAs with BCC-distributed pores have the smallest (narrowest) hysteresis loops; others had random or other types of ordered distributions. The transformation from austenite to martensite in BCC-type porous SMAs is homogeneous and mild, which is the underlying mechanism for realizing small mechanical hysteresis in porous SMAs.

2. Methodology

In the experiments, the NiTi alloy was selected as the prototypical SMA. The samples were purchased from SaiTe Metal Materials Development Company with slight Ni-rich composition, i.e., Ti_49.2Ni_50.8. The as-received samples were sealed in evacuated quartz tubes with an Ar atmosphere and solution treated at 1173 K for 24 h, followed by water quenching. The samples were cut to a dog-bone shape with a 5 × 35 mm stretch section. The MTS tensile machine equipped with Nyilas extensometer strain was used to measure the superelastic behavior at a rate of 1 mm/min at room temperature.

For the finite-element method simulations, a phenomenological constitutive model, which was proposed by Auricchio and Taylor, was employed to investigate the mechanical responses of SMAs [24,25]. In this model, the corresponding stress–strain curve consists of a purely linear elastic range and a transformation platform range, which can reveal the nonlinear superelastic behavior that occurs during the reversible transformation from austenite to martensite and from martensite to austenite. To capture the microstructure of the random porous SMA with various porosity, the representative volume element (RVE) and random sequential adsorption algorithm approaches were used to build the models [26,27]. In porous SMAs, the pores were simplified into spherical voids with a diameter d = 500 µm and embedded in an RVE with a length of L. The value of L was selected to be 6d, which can satisfy the requirement of convergence. In addition, inspired by crystal structures, several porous RVEs with ordered pores distribution were created. In RVEs of porous SMAs, the elastic properties of the pores were assigned to negligible stiffness [28,29]. The key parameters used to simulate the superelastic behavior of the Ti_49.2Ni_50.8 SMA sample are summarized in

Table 1. Material parameters of a dense SMA constitutive model.

Material Parameter	Value
Martensite elastic modulus $E_{\mathrm{M}}$ (MPa)	43,708
Austenite elastic modulus $E_{\mathrm{A}}$ (MPa)	29,400
Starting stress for austenite to martensite transformation ${\sigma }_L^S$ (MPa)	334
Finishing stress for austenite to martensite transformation ${\sigma }_L^E$ (MPa)	454
Starting stress for martensite to austenite transformation ${\sigma }_U^S$ (MPa)	214
Finishing stress for martensite to austenite transformation ${\sigma }_U^E$ (MPa)	115
Transformation strain ${\epsilon }_{\mathrm{L}}$	0.0372

. All the models in our simulations were finely meshed, and calculations were implemented by the CalculiX finite element program [30]. About 40,000 three-dimension linear elements were produced for each RVE. The mesh grids in the opposite boundary surfaces were the same, so as to apply the periodic boundary conditions and static tensile load (along the x-axis direction), ensuring the accuracy of simulations [31,32]. In this analysis, the stress–strain relations of the models can be calculated using a volume average approach as follows:

$$\overline{\sigma }=\frac{{{\displaystyle \sum }}_{i=1}^j{v}_i{\sigma }_i}{V}$$

(1)

where $\overline{\sigma }$ is the average stress of the sample; $j$ and $V$ are the number and volume of elements in the model; $v_i$ and ${\sigma }_i$ are the volume and the corresponding stress of the element $i$, respectively. The expression for average strain $\overline{\epsilon }$ has similar form.

3. Results and Discussion

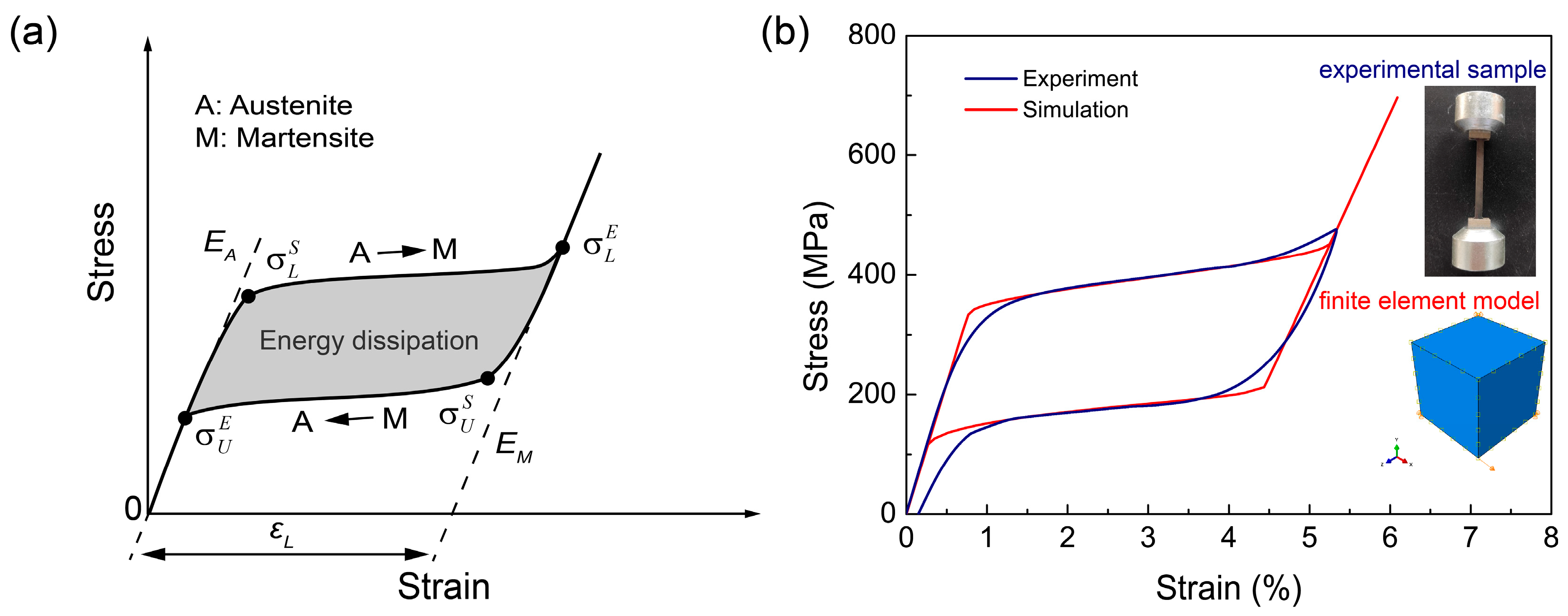
3.1. Experiment and Simulation for Bulk SMA

In a typical superelastic curve, as shown in Figure 1a, the SMA specimen presents itself in an austenite phase, which behaves linearly elastically with an elastic modulus $E_{\mathrm{A}}$. Upon loading, this austenite phase transforms into a martensite phase. The transformation is triggered by stress at the starting stress ${\sigma }_L^S$ and produces a substantial amount of strain (transformation strain ${\epsilon }_L$). With further loading, the SIMT is finished at the finishing stress ${\sigma }_L^E$, and then the specimen presents a martensite elastic deformation with modulus $E_{\mathrm{M}}$. Upon unloading, the transformation is reversible, and there are two critical stresses, i.e., the starting stress for martensite-to-austenite transformation ${\sigma }_U^S$, and the finishing stress for martensite-to-austenite transformation ${\sigma }_U^E$. The stress levels at which such reversible transformation occurs are smaller than those required to produce the original transformation, resulting in some energy dissipation and a hysteresis loop.

In Figure 1b, the blue curve presents the experimental result of a Ti_49.2Ni_50.8 sample. The external stress was applied for the dog-bone shaped sample (inset of Figure 1b) to measure the stress–strain curve at room temperature. It is clear that good superelastic behavior occurs, as the typical non-linear recoverable hysteresis loop can be observed. The critical stress inducing a phase transformation from austenite to martensite is about 330 MPa. The mechanical dissipation energy was measured by the area of the hysteresis, which was about 9.27 ${\mathrm{MJ}/\mathrm{m}}^3$. The red curve in Figure 1b is the superelastic curve obtained from the finite element simulation. The curve is in good agreement with the actual measured data (blue curve). Meanwhile, the dissipation energy of the simulation result was estimated to be ~9 ${\mathrm{MJ}/\mathrm{m}}^3$, which is very close to the experimental result. These demonstrate the validity of our simulation strategy.

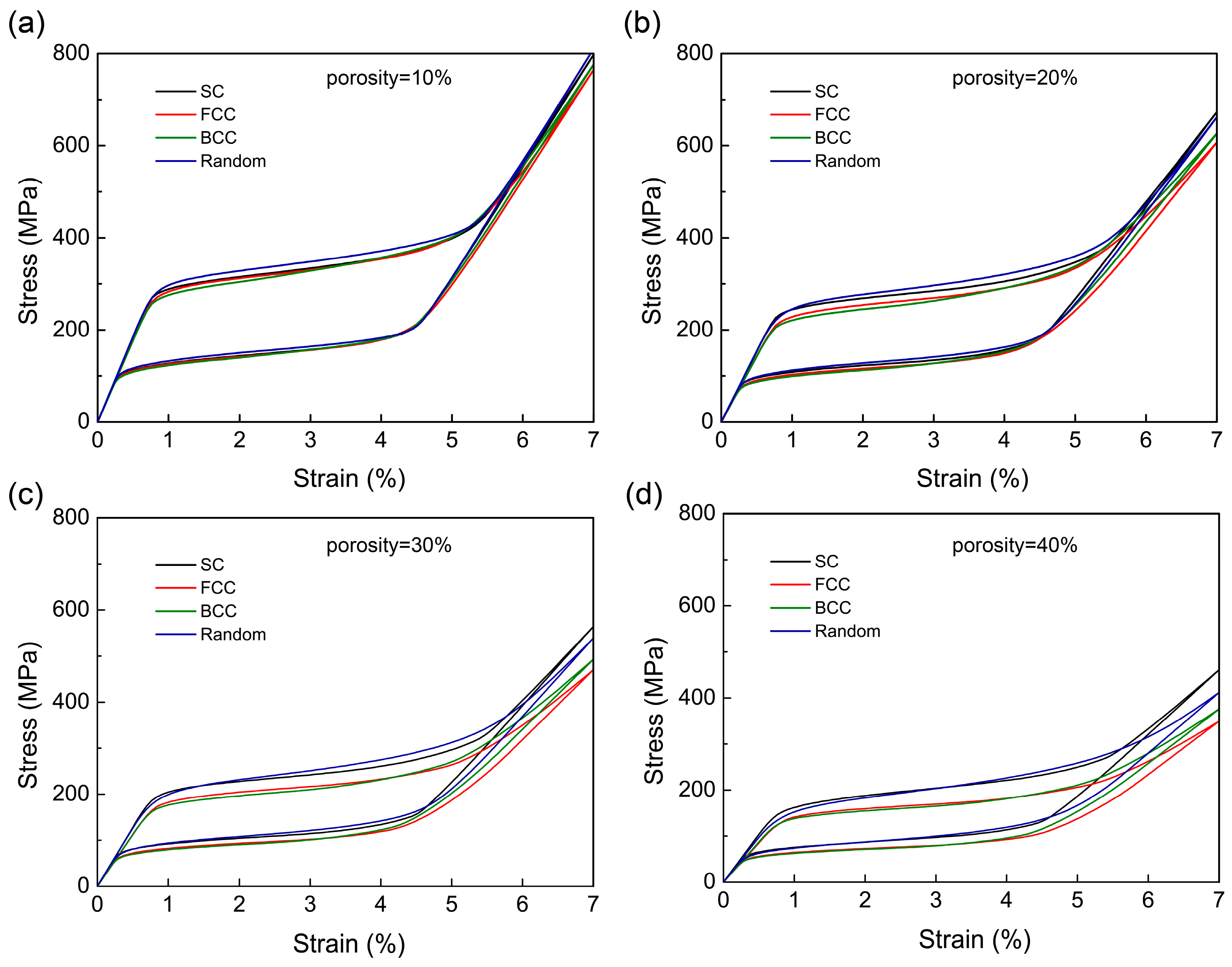
3.2. Effect of Porosity on Hysteresis Loops of the Random Porous SMAs

In conventional porous SMAs, the pores are randomly distributed. Thus, the porosity of porous SMAs becomes a critical factor for affecting their mechanical responses. Figure 2a shows the RVEs of randomly porous Ti_49.2Ni_50.8 SMAs with porosity ranging from 10% to 40%. The corresponding simulated mechanical responses are shown in Figure 2b. It is obvious that the porosity has a significant effect on the superelastic properties of SMAs. As the porosity increases, the mechanical properties of porous SMAs decrease significantly, including the elastic modulus of austenite and martensite, starting and finishing stress for martensitic phase transformation and reverse martensitic phase transformation. Therefore, the hysteresis loop of the porous SMA with randomly distributed pores decreases as the porosity increases. When the porosity reaches 40% (blue line), its energy dissipation is reduced to ~5.5 ${\mathrm{MJ}/\mathrm{m}}^3$.

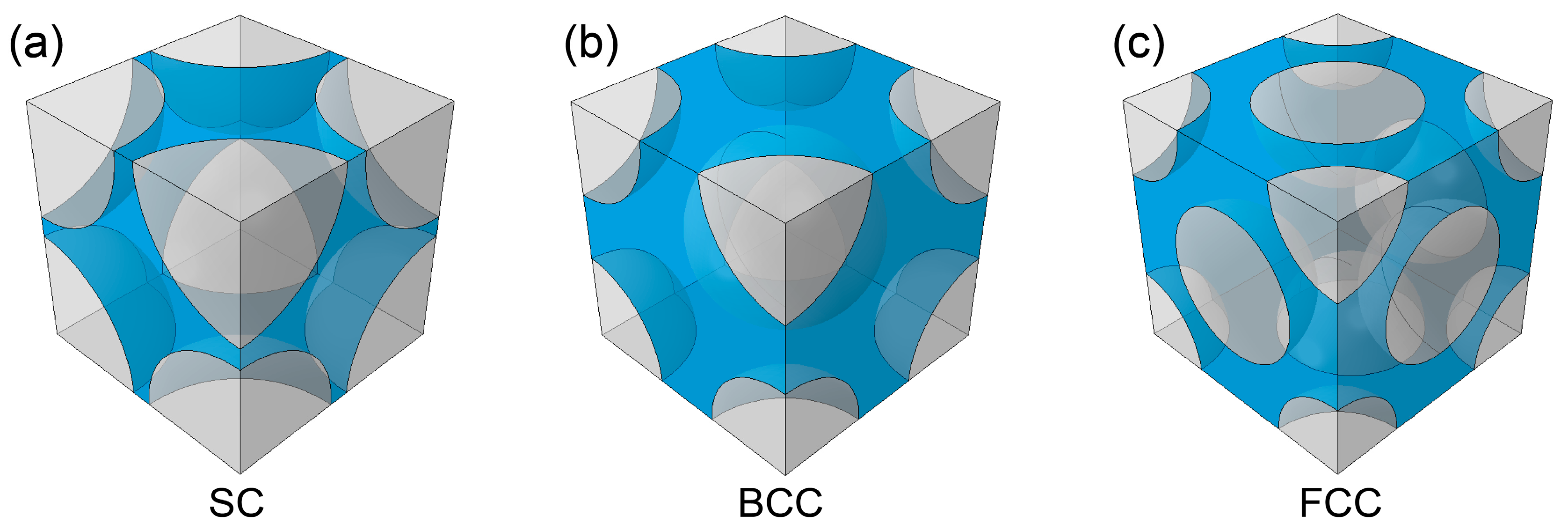
3.3. Microstructure Design of Porous SMAs to Achieve Narrow Hysteresis

For porous materials, the design of the porous structure is expected to enable the structural material to obtain new functional properties [33,34,35,36], which implies that the hysteresis loops of the porous SMAs could be modulated through the design of pore distributions. Inspired by atomic crystal structures, we proposed several porous SMA models with simple cubic (SC), body-centered cubic (BCC) and face-centered cubic (FCC) ordered porous distributions with varied porosity ranging from 10% to 40%. Figure 3 shows the engineered porous microstructures with a porosity of 40%.

Figure 4a–c show the calculated superelastic curves of the designed ordered porous Ti_49.2Ni_50.8 SMAs with porosity ranging from 10% to 40%. When the porosity of the porous SMA is lower (Figure 4a,b), all the porous SMAs show similar mechanical responses, which can be regarded as typical nonlinear superelastic behavior. In Figure 4c,d, when the porous SMA has a relatively higher porosity, the BCC and FCC-type porous SMAs have significantly lower starting stress and ending stress during phase transformation from austenite to martensite, leading to a lower-stress platform than the other structures during phase transformation. During the reverse phase transformation, due to the release of the superelastic strain, the difference in the stress platform between the ordered porous structure and other structures becomes not obvious.

Figure 5 shows the dissipation energies of different porous Ti_49.2Ni_50.8 SMAs. The dissipation energy decreases with increasing porosity. When the porosity of the BCC structure increases from 10% to 40%, its hysteresis loop area decreases by almost 100%. Moreover, the random-type porous SMAs exhibited the highest damping performance, whereas the porous SMAs with BCC porous structures had the smallest hysteresis loop areas at the same porosity. This can be attributed to the lower-stress platform and smaller transformation strain in the BCC-stacking pores SMAs according to Figure 4.

3.4. Martensitic Transformation Behavior of Porous SMAs during the Loading Processes

In SMAs, the superelastic behavior is caused by SIMT. The non-uniform internal stress in porous SMAs, in principle, results in the gradual/continuous martensitic transformation instead of abrupt/sharp martensitic transformation [37,38,39]. Figure 6 demonstrates the evolution of the martensite transformation within the porous Ti_49.2Ni_50.8 SMAs during tensile loading along the x-axis direction. The red and purple regimes represent austenite-martensite mixed phases and pure martensite phases, respectively. The Mises stress below ${\sigma }_L^S$ represents pure austenite. When the external strain achieves ~1%, the local internal stress around the pores within porous SMA structures exceeds the starting stress of martensitic transformation, resulting in the nucleation and growth of the martensitic phases (Figure 6(a1–d1)).

We notice that the region of SIMT in the BCC porous structure was more homogeneous than in other structures. In contrast, the evolution of the martensite phase caused by external stress in the random porous structure was seriously inhomogeneous, indicating a serious stress concentration between adjacent holes, thereby deteriorating the tensile performance of the porous structure. When the strain increases to ~5% (Figure 6(a2–d2)), most areas of the porous structure undergo a martensitic transformation, but the degree of transformation in each part varies with the degree of stress concentration. For the BCC structure, the phase transformation from pure austenite to pure martensite is a more homogeneous and gentle process (Figure 6(a1,a2)). The pure austenite phases still exist within some regions of the BCC structure (Figure 6(a2)). In contrast, for the random porous structure, most of the regions retain austenite and martensite phases’ coexistence (Figure 6(d2)), which leads to a higher stress plateau in the corresponding stress–strain curve.

For a deeper analysis of the stress-induced phase transformation occurring in the bulk and porous SMA with various porosity levels and structures, we performed a comparative analysis of the second derivative of the mechanical responses. Although the overall stress–strain curves of the porous Ni_49.2Ti_50.8 SMAs look smooth, the nucleation and evolution of martensite phases in a porous structure are “jerky”. Figure 7 shows the jerky spectrum of ${\left(d\sigma /d\epsilon \right)}^{″}$ at the stage of local initiation and propagation of the martensite phase in some typical porous models, i.e., a bulk SMA (Figure 7a), a random porous SMA with 10% porosity (Figure 7b), a random porous SMA with 40% porosity porosity (Figure 7c) and a BCC porous SMA with 40% porosity (Figure 7d).

For the bulk Ti_49.2Ni_50.8 SMA, as shown in Figure 7a, the single violent jerk at the strain of 0.75% means an abrupt martensitic transformation, which is classical martensite transformation behavior. For a porous Ni_49.2Ti_50.8 SMA with a porosity of 10%, local stress concentration occurs around the defective pores/voids, triggering local martensitic transformations at first. As the external load increases, the stress values in more and more areas exceed the critical stress of SIMT, leading to a gradual martensitic phase transition. As a result, many tiny fluctuations occur within the statistics of stress–strain curves (Figure 7b). In Figure 7c, more pores (40% porosity) lead to more local regions exhibiting non-uniform stress concentrations. The martensitic transformation behavior transforms from a discontinuous manner to a gradual manner due to the multi-step nucleation, resulting in many more fluctuations in the stress–strain curves. For the BCC porous SMA (Figure 7d), the phase transformation behavior is still multi-step nucleation, but it is more intense at the high level of porosity (40%). It can be attributed to the fact that in a BCC porous SMA, the phase transformation behavior is more homogeneous than in a random porous SMA (as shown in Figure 6(a1)). The combination of the defective pores and their ordered distribution gives rise to the compromise of gradual martensitic phase transition and homogeneous stress/strain distribution, obtaining the superelastic behavior with a narrow hysteresis loop.

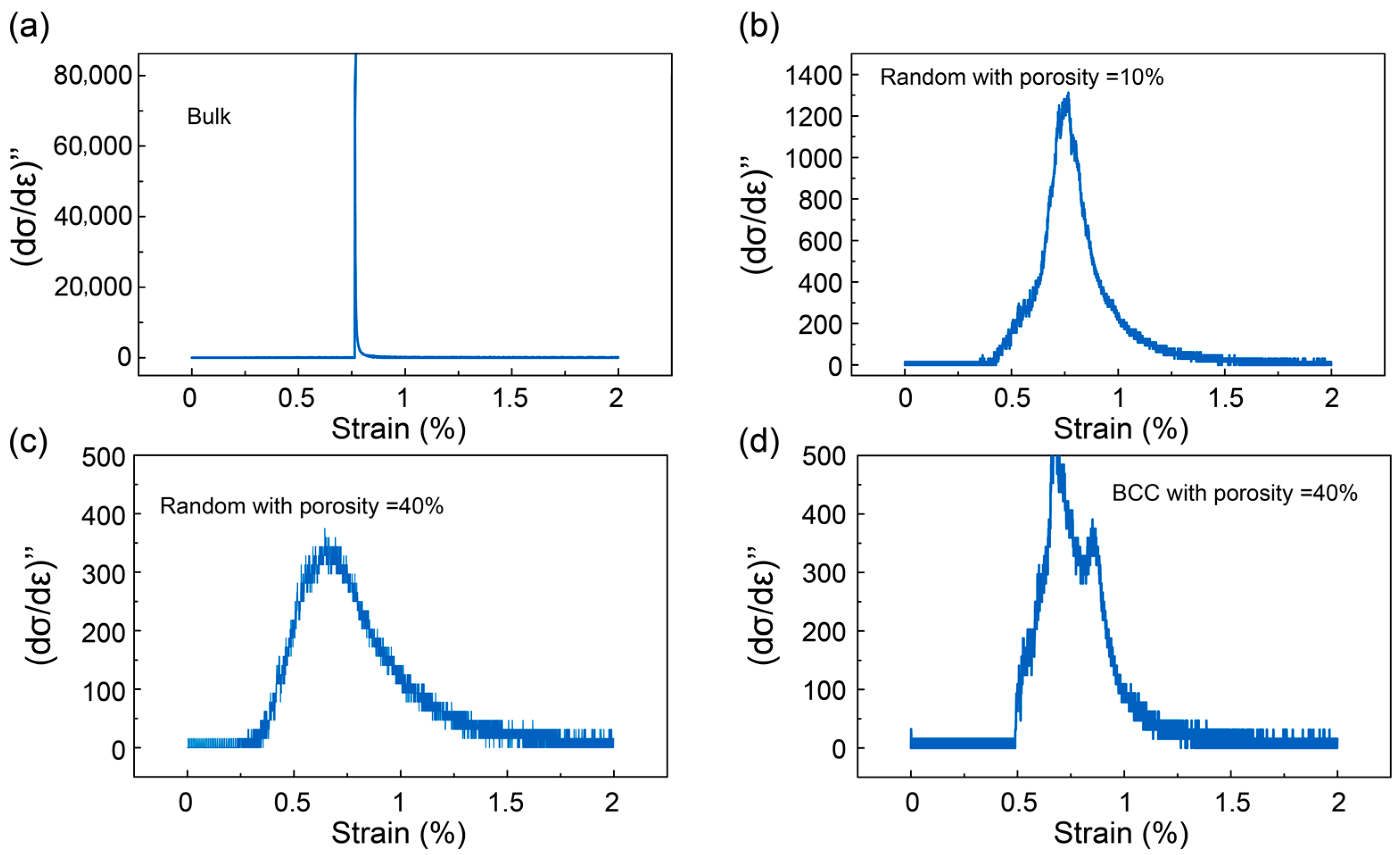
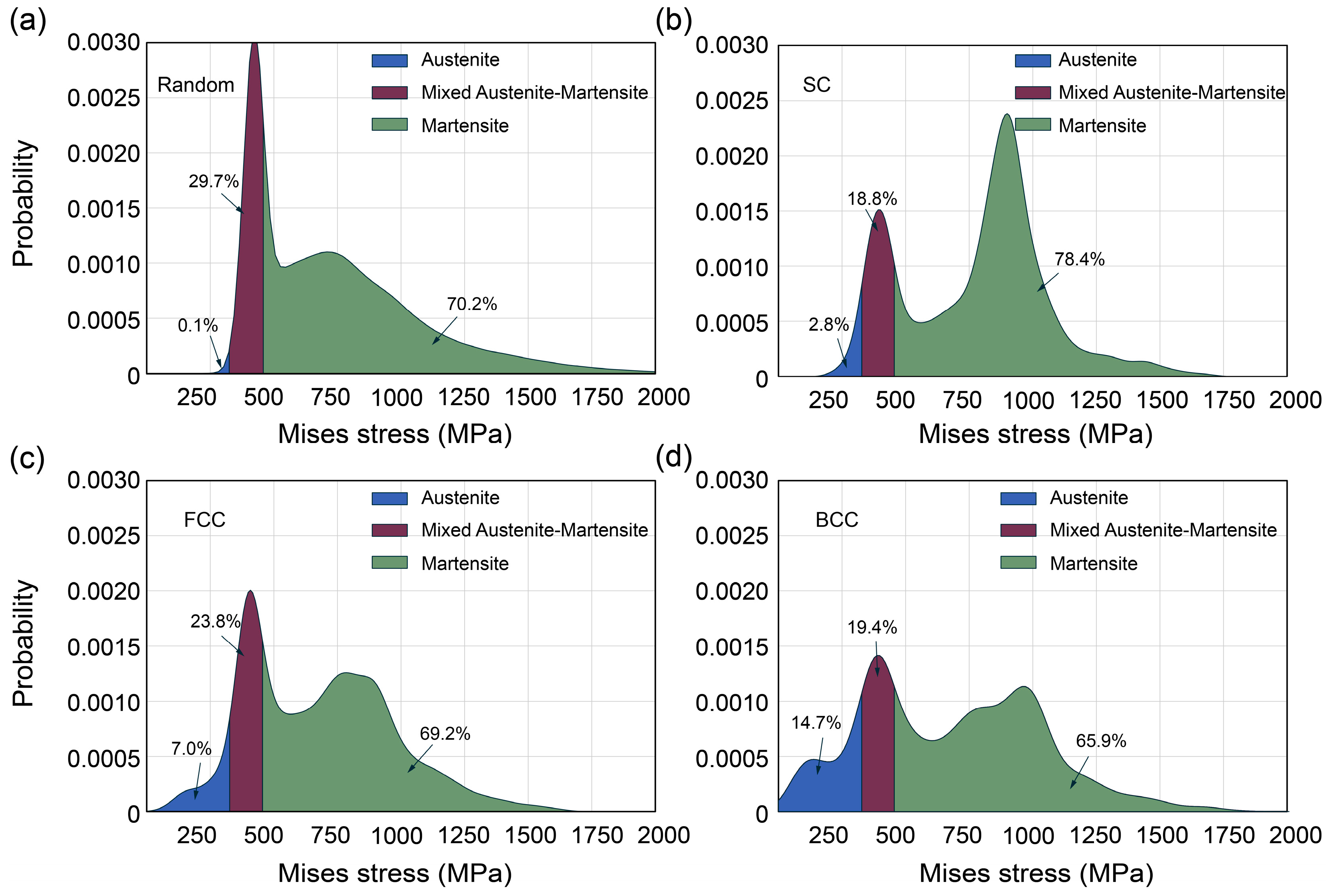
3.5. Probability Statistics and Stress Analysis in Random and BCC-Type Porous SMAs

To analyze the underlying mechanisms of the effects on the hysteresis loop, we performed a statistical analysis to reveal the phase transformation states in random porous and ordered porous Ti_49.2Ni_50.8 SMAs with 40% porosity. Figure 8 shows the probability density function diagram of the equivalent local stress at a 7% external strain. The blue range represents the pure austenite phase; the wine-red range represents the austenite–martensite mixed phase; and the green range represents the martensite phase.

As shown in Figure 8a, when the external strain reaches 7%, there is almost no austenite phase in the random porous SMA. The fraction of austenite–martensite coexistence is much higher than in the ordered porous SMAs, indicating a serious stress concentration within the random porous SMA. On the contrary, for the ordered porous SMAs (Figure 8b–d), there is a certain amount of austenite phase, and the stress concentration is significantly reduced. The distribution of phase states is more uniform in the BCC-type porous SMAs. This indicates that the martensite phase transformation occurs more continuously and is smoother for BCC-type porous SMAs. It is noted that even if the external strain reaches 7%, there is still a certain amount of austenite phase in this structure (14.7%). The elastic deformation of martensite is beneficial to small hysteresis because it involves no energy dissipation. In addition, the gentler distribution of phase states in the BCC-type porous SMAs leads to a low-stress plateau. Both reasons are helpful for BCC-type porous SMAs to exhibit high efficiency of energy conversion, and thus well-controlled hysteresis behavior.

4. Conclusions

Although the present work is based on the ideal elastic-superelastic model, our work theoretically provides an effective strategy for designing porous SMAs for real applications, such as accurate sensors and actuators with minimal energy damping. From the results obtained in the present work, the following conclusions can be drawn:

(1)

The mechanical hysteresis loops of SMAs can be effectively modulated by introducing porous structures. Higher porosity helps the SMAs achieve a smaller hysteresis loop area, indicating less energy dissipation.

(2)

The lowest damping performance can be obtained when the pores are distributed in a BCC-type fashion. This characteristic can be attributed to the gradual martensitic-phase-transformation behavior caused by inhomogeneous local stress in porous SMAs.

(3)

In BCC-type porous SMAs, the phase transformations occur more homogeneously, and the stress concentration can be effectively avoided compared to a random porous structure.