Stability and Rupture of Liquid Crystal Bridges under Microgravity
Abstract
1. Introduction
2. Setup and Materials
3. Results
3.1. Stability Limits
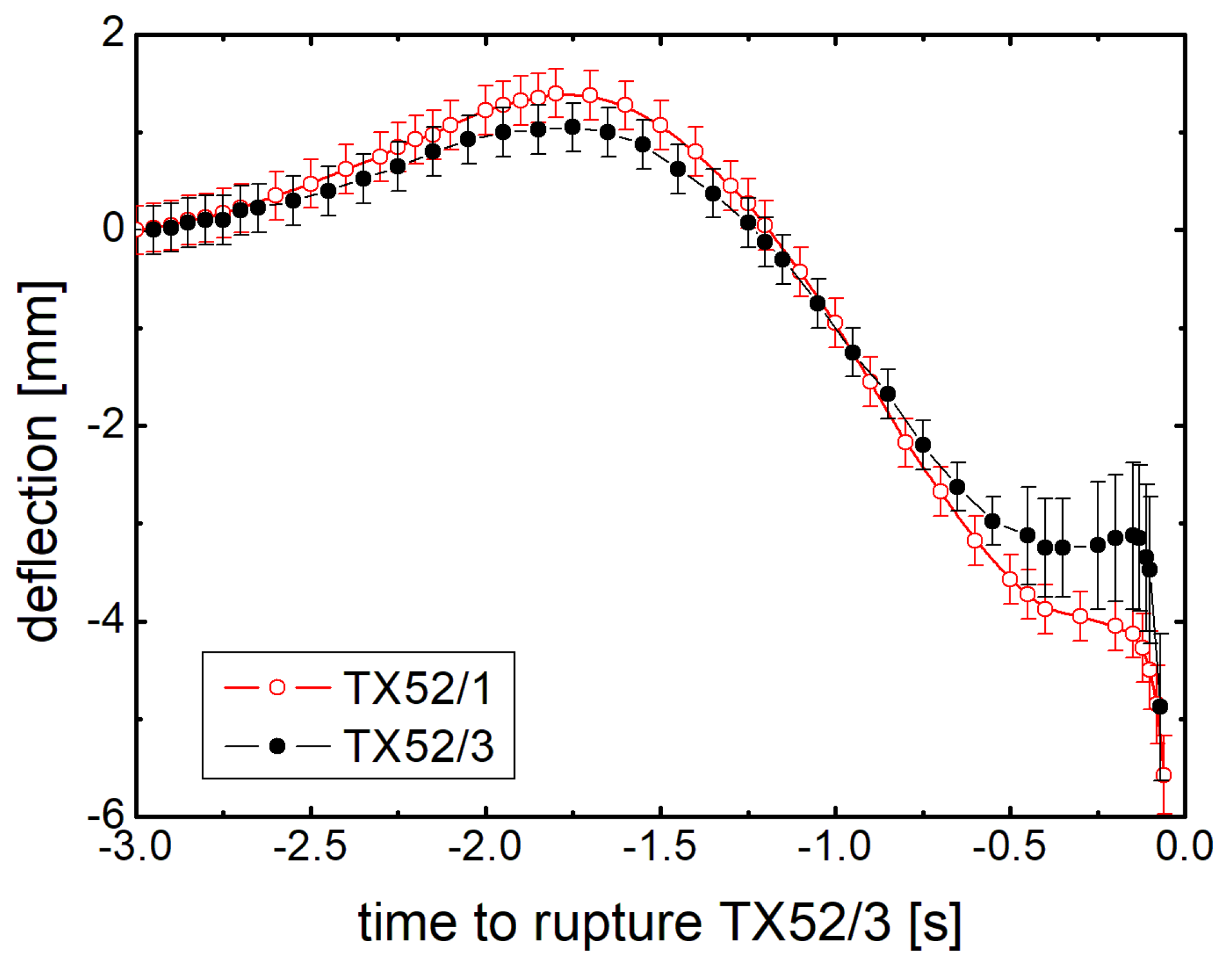
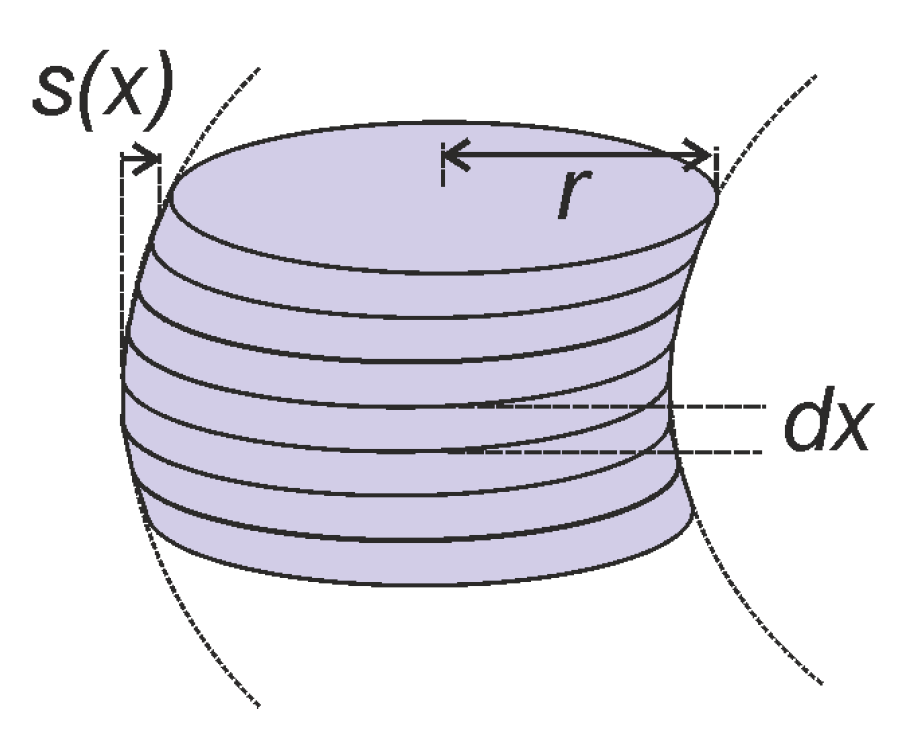
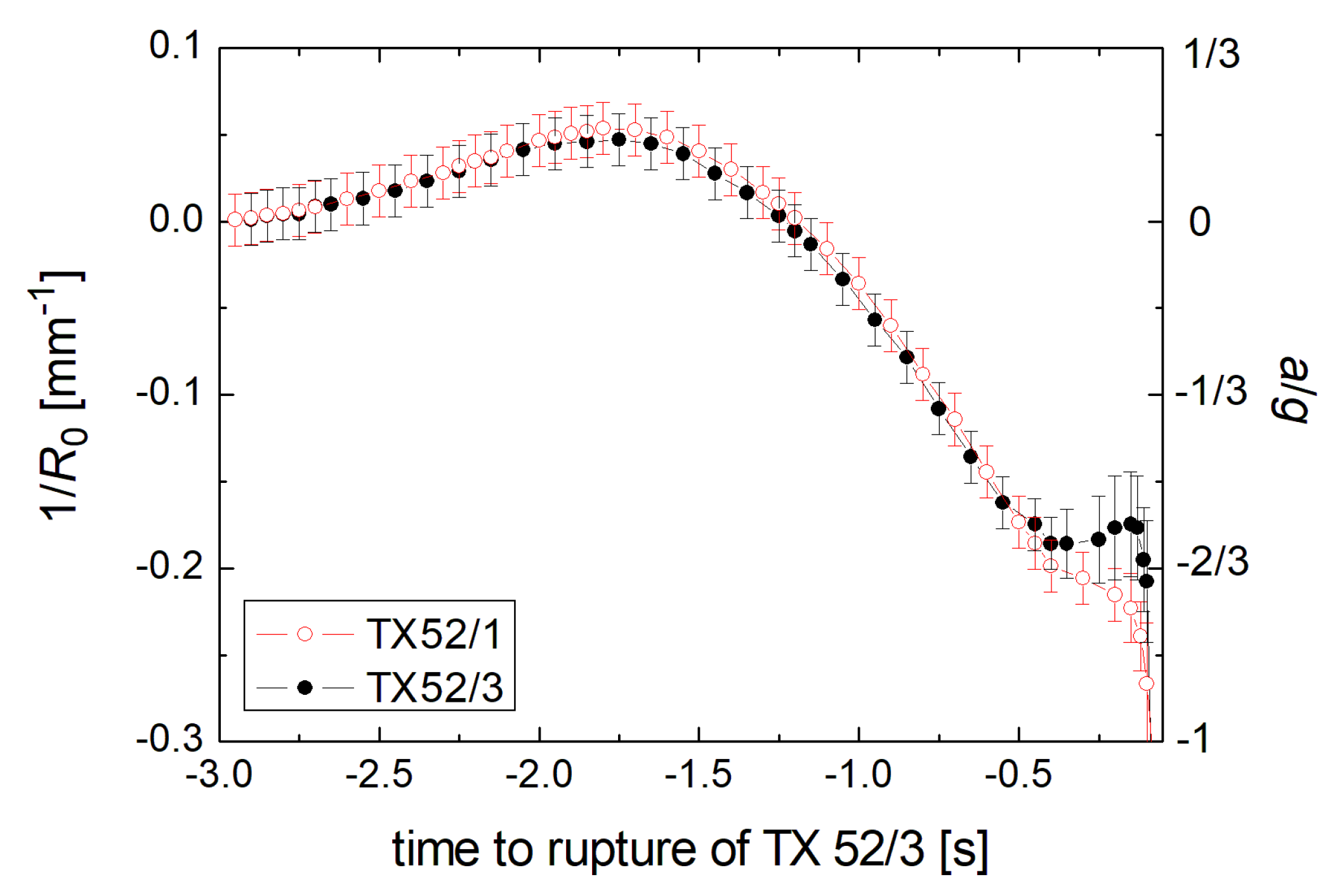
3.2. Bending under Lateral Acceleration
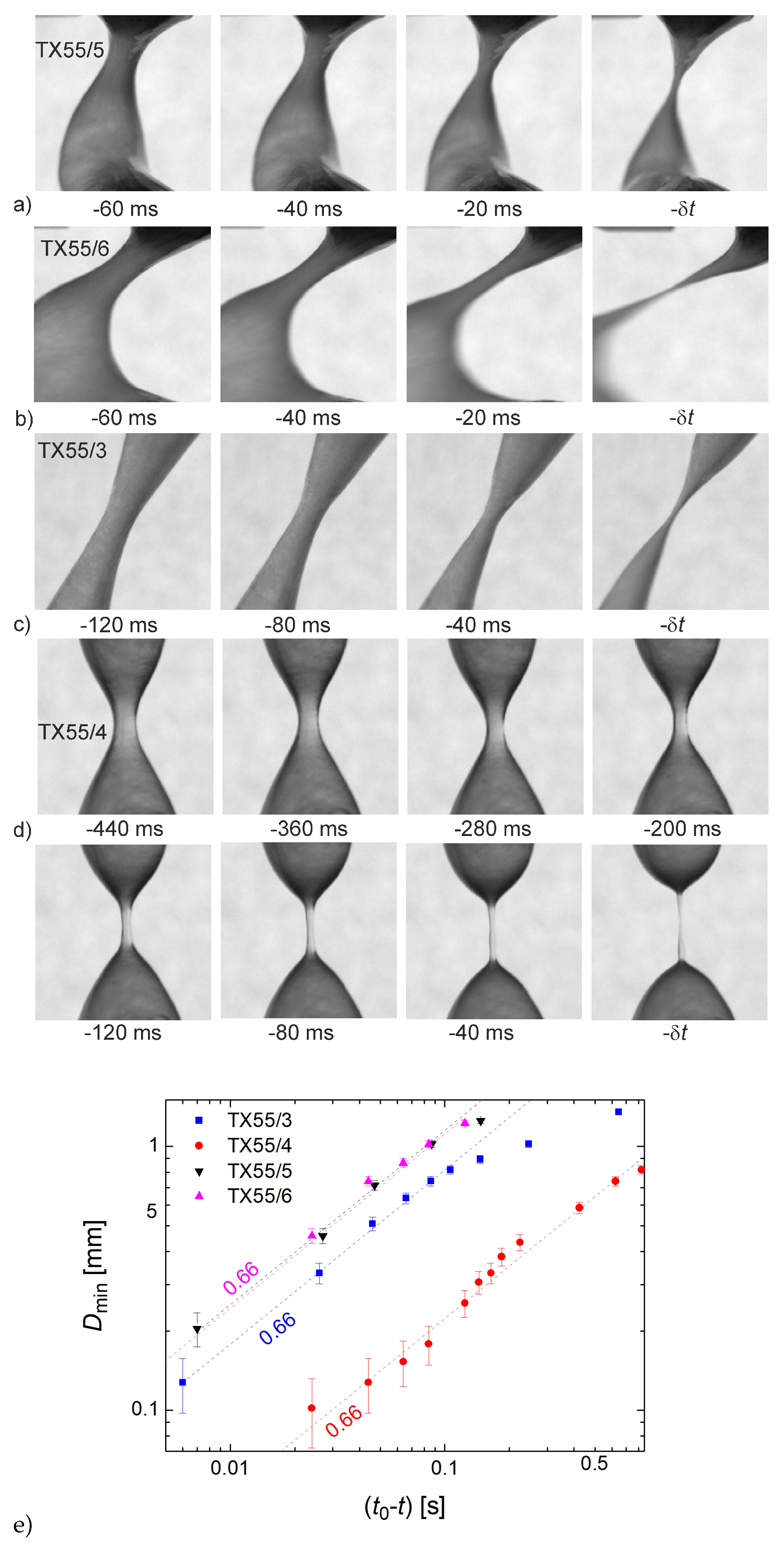
3.3. Rupture Dynamics
4. Summary and Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A

| Experiment | Material | Phase | at Breakup |
|---|---|---|---|
| TX55/G1 | ST02890 | SmA | 1.14 |
| TX55/G2 | ST02890 | SmA | 1.51 |
| TX55/G3 | ST00554 | SmC | 2.33 |
| TX55/G4 | ST00552 | SmA | 2.35 |
| TX55/G5 | ST00554 | SmC | 1.81 |
| TX55/G6 | ST00552 | SmA | 1.845 |
References
- Plateau, J. Statique Expérimentale et Théorique des Liquides Soumis aux Seules Forces Moléculaires; Gauthier-Villars: Paris, France, 1873; Volume II, Chapter XI; p. 293. [Google Scholar]
- Savart, F. Mémoire sur la constitution des veines liquides lancés par des orifices circulaires en mince paroi. Ann. Chim. Phys. Paris 1833, LIII, 337. [Google Scholar]
- Lord Rayleigh, On the instability of jets. Proc. Lond. Math. Soc. 1878, 1, 4–13.
- Lord Rayleigh, On the Stability, or Instability, of certain Fluid Motions. Proc. Lond. Math. Soc. 1879, 1, 57–72.
- Tjahjadi, M.; Stone, H.A.; Ottino, J.M. Satellite and subsatellite formation in capillary breakup. J. Fluid Mech. 1992, 243, 297. [Google Scholar] [CrossRef]
- Gier, S.; Wagner, C. Visualization of the flow profile inside a thinning filament during capillary breakup of a polymer solution via particle image velocimetry and particle tracking velocimetry. Phys. Fluids 2012, 24, 53102. [Google Scholar] [CrossRef]
- Montanero, J.M.; Ponce-Torres, A. Review on the Dynamics of Isothermal Liquid Bridges. Appl. Mech. Rev. 2020, 72, 10803. [Google Scholar] [CrossRef]
- Schulkes, R.M.S.M. Nonlinear dynamics of liquid columns: A comparative study. Phys. Fluids A 1993, 5, 2121. [Google Scholar] [CrossRef]
- Li, Y.; Sprittles, J.E. Capillary breakup of a liquid bridge: Identifying regimes and transitions. J. Fluid Mech. 2016, 797, 22. [Google Scholar] [CrossRef]
- Meseguer, J. The influence of axial microgravity on the breakage of axisymmetric slender liquid bridges. J. Cryst. Growth 1983, 62, 557–586. [Google Scholar] [CrossRef]
- Meseguer, J. The breaking of axisymmetric slender liquid bridges. J. Fluid Mech. 1983, 130, 123–151. [Google Scholar] [CrossRef]
- Meseguer, J.; Bezdenejnykh, N.A.; Perales, J.M.; de Francisco, P.R. Theoretical and experimental analysis of stability limits of non-axisymmetrical liquid bridges under microgravity conditions. Microgravity Sci. Techn. 1995, 8, 2–9. [Google Scholar]
- Meseguer, J.; Slobozhanin, L.A.; Perales, J.M. A review on the stability of liquid bridges. Adv. Space Res. 1995, 16, 5. [Google Scholar] [CrossRef]
- Meseguer, J.; Mayo, L.A.; Llorente, J.C.; Fernandez, A. Experiments with liquid bridges in simulated microgravity. J. Cryst. Growth 1985, 73, 609–621. [Google Scholar] [CrossRef]
- Resnick, A.; Alexander, J. Plateau tank apparatus for the study of liquid bridges. Rev. Sci. Instrum. 1997, 68, 1495–1500. [Google Scholar] [CrossRef][Green Version]
- Mahajan, M.P.; Tsige, M.; Taylor, P.L.; Rosenblatt, C. Liquid crystal bridges. Liq. Cryst. 1999, 26, 443–448. [Google Scholar] [CrossRef]
- Mahajan, M.P.; Tsige, M.; Taylor, P.L.; Rosenblatt, C. Stability of liquid crystalline bridges. Phys. Fluids 1999, 11, 491. [Google Scholar] [CrossRef]
- Meseguer, J.; Sanz-Andrés, A.; Pérez-Grande, I.; Pindado, S.; Franchini, S.; Alonso, G. Surface tension and microgravity. Eur. J. Phys. 2014, 34, 55010. [Google Scholar] [CrossRef]
- Langbein, D. Oscillations of finite liquid columns. Microgravity Sci. Techn. 1992, 5, 73–85. [Google Scholar] [CrossRef]
- Langbein, D.; Falk, F.; Großbach, R. Oscillations of liquid columns under microgravity. Adv. Space Res. 1995, 16, 23. [Google Scholar] [CrossRef]
- Martínez, I.; Perales, J.M.; Meseguer, J. Response of a liquid bridge to an acceleration varying sinusoidally with time. Lect. Notes Phys. 1996, 464, 271–282. [Google Scholar]
- Martínez, I. Deformaciones de una columna líquida frente a cargas cuasi-estáticas en un cohete de sondeo. Ing. Aeronaut. Astronaut. 1996, 344, 17–30. [Google Scholar]
- DiLisi, G.; Dempsey, R.; Rarick, R.; Rosenblatt, C. Using parabolic flights to examine quantitatively the stability of liquid bridges under varying total body force. Microgravity Sci. Tech. 2015, 27, 145–153. [Google Scholar] [CrossRef]
- Mahajan, M.P.; Tsige, M.; Zhang, S.; Alexander, J.I.D.; Taylor, P.L.; Rosenblatt, C. Collapse dynamics of liquid bridges investigated by time-varying magnetic levitation. Phys. Rev. Lett. 2000, 84, 338. [Google Scholar] [CrossRef]
- Cheong, A.G.; Rey, A.D.; Mather, P.T. Capillary instabilities in thin nematic liquid crystalline fibers. Phys. Rev. E 2001, 64, 41701. [Google Scholar] [CrossRef]
- Jákli, A.; Krüerke, D.; Nair, G.G. Liquid crystal fibers of bent-core molecules. Phys. Rev. E 2003, 67, 51702. [Google Scholar] [CrossRef]
- Stannarius, R.; Nemeş, A.; Eremin, A. Plucking a liquid chord: Mechanical response of a liquid filament. Phys. Rev. E 2005, 72, 20702. [Google Scholar] [CrossRef]
- Eremin, A.; Nemeş, A.; Stannarius, R.; Schulz, M.; Nadasi, H.; Weissflog, W. Structure and mechanical properties of liquid crystalline filaments. Phys. Rev. E 2005, 71, 31705. [Google Scholar] [CrossRef]
- Nemeş, A.; Eremin, A.; Stannarius, R.; Schulz, M.; Weissflog, W. Structure characterization of free standing filaments drawn in the liquid crystal state. Phys. Chem. Chem. Phys. 2006, 8, 469. [Google Scholar] [CrossRef]
- Bailey, C.; Gartland Jr., E.C.; Jákli, A. Structure and stability of bent core liquid crystal fibers. Phys. Rev. E 2007, 75, 31701. [Google Scholar] [CrossRef]
- Bailey, C.; Murphy, M.; Eremin, A.; Weissflog, W.; Jákli, A. Bundles of fluid fibers formed by bent-core molecules. Phys. Rev. E 2010, 81, 31708. [Google Scholar] [CrossRef]
- Baumann, P.; Phillips, D. Analysis and stability of bent-core liquid crystal fibers. Discret. Contin. Dyn. Syst. 2012, 17, 1707. [Google Scholar]
- Morys, M.; Trittel, T.; Eremin, A.; Murphy, P.; Stannarius, R. Tension of freely suspended fluid filaments. Phys. Rev. E 2012, 86, 040501(R). [Google Scholar] [CrossRef] [PubMed]
- Salili, S.M.; Ostapenko, T.; Kress, O.; Bailey, C.; Weissflog, W.; Harth, K.; Eremin, A.; Stannarius, R.; Jákli, A. Rupture and Recoil of Bent-Core Liquid Crystal Filaments. Soft Matter 2016, 12, 4725. [Google Scholar] [CrossRef] [PubMed]
- van Winkle, D.H.; Clark, N.A. Freely Suspended Strands of Tilted Columnar Liquid-Crystal Phases: One-Dimensional Nematics with Orientational Jumps. Phys. Rev. Lett. 1982, 48, 1407. [Google Scholar] [CrossRef]
- Ostapenko, T.; Weyland, M.; Eremin, A.; Lehmann, M.; Stannarius, R. Filaments formed in the hexagonal columnar liquid crystal phase of star-shaped oligobenzoates. Liq. Cryst. 2013, 40, 345. [Google Scholar] [CrossRef]
- Pratibha, R.; Madhusudana, N.V. Cylindrical growth of smectic A liquid crystals from the isotropic phase in some binary mixtures. J. Phys. II Fr. 1991, 2, 383–400. [Google Scholar] [CrossRef]
- Naito, H.; Okuda, M.; Zhong-can, O.Y. Pattern formation and instability of smectic-A filaments grown from an isotropic phase. Phys. Rev. E 1997, 55, 1655. [Google Scholar] [CrossRef]
- E, W.; Palffy-Muhoray, P. Dynamics of Filaments during the Isotropic-Smectic A Phase Transition. J. Nonlinear Sci. 1999, 9, 417–437. [Google Scholar] [CrossRef]
- Todorokihara, M.; Iwata, Y.; Naito, H. Periodic buckling of smectic-A tubular filaments in an isotropic phase. Phys. Rev. E 2004, 70, 21701. [Google Scholar] [CrossRef]
- Eggers, J.; Villermaux, E. Physics of liquid jets. Rep. Prog. Phys. 2008, 71, 36601. [Google Scholar] [CrossRef]
- Keller, J.B.; Miksis, M.J. Surface Tension Driven Flows. SIAM J. Appl. Math. 1983, 43, 268–277. [Google Scholar] [CrossRef]
- Brenner, M.P.; Eggers, J.; Joseph, K.; Nagel, S.R.; Shi, X.D. Breakdown of scaling in droplet fission at high Reynolds number. Phys. Fluids 1997, 9, 1573. [Google Scholar] [CrossRef]
- Chen, A.U.; Notz, P.K.; Basaran, O.A. Computational and Experimental Analysis of Pinch-Off and Scaling. Phys. Rev. Lett. 2002, 88, 174501. [Google Scholar] [CrossRef]
- Verhoeff, A.A.; Lekkerkerker, H.N.W. Droplet snap-off in fluids with nematic liquid crystalline ordering. New J. Phys. 2012, 14, 23010. [Google Scholar] [CrossRef]
- Porter, D.; Savage, J.R.; Cohen, I.; Spicer, P.; Caggioni, M. Temperature dependence of droplet breakup in 8CB and 5CB liquid crystals. Phys. Rev. E 2012, 85, 41701. [Google Scholar] [CrossRef]
- Savage, J.R.; Caggioni, M.; Spicer, P.T.; Cohen, I. Partial universality: Pinch-off dynamics in fluids with smectic liquid crystalline order. Soft Matter 2010, 6, 892. [Google Scholar] [CrossRef]
- Dolganov, P.V.; Zverev, A.S.; Baklanova, D.; Dolganov, V.K. Dynamics of capillary coalescence and breakup: Quasi-two-dimensional nematic and isotropic droplets. Phys. Rev. E 2021, 104, 014702. [Google Scholar] [CrossRef]
- Dolganov, P.V.; Zverev, A.S.; Baklanova, D.; Dolganov, V.K. Quasi-two-dimensional coalescence of nematic and isotropic droplets and Rayleigh-Plateau instability in flat optical cells. Soft Matter 2022, 18, 126. [Google Scholar] [CrossRef]
- Zhang, C.; Diorio, N.; Radhika, S.; Sadashiva, B.K.; Sprunt, S.N.; Jákli, A. Two distinct modulated layer structures of an asymmetric bent-shape smectic liquid crystal. Liq. Cryst. 2012, 39, 1149–1157. [Google Scholar] [CrossRef]
- Bezdenejnykh, N.A.; Meseguer, J. Stability limits of minimum volume and breaking of axisymmetric liquid bridges between unequal disks. Microgravity Sci. Techn. 1991, 4, 235. [Google Scholar]
- Schüring, H.; Thieme, C.; Stannarius, R. Surface tensions of smectic liquid crystals. Liq. Cryst. 2001, 28, 241. [Google Scholar] [CrossRef]








| Experiment | Material | Temperature (°C) | Phase | Modus |
|---|---|---|---|---|
| TX52/1 | ST00552 | 44 | SmC | ↑ |
| TX52/2 | ST02890 | 44 | SmA | ↑ |
| TX52/3 | ST00552 | 52 | SmA | ↑ |
| TX52/4 | ST02890 | 52 | Iso | ↑ |
| TX52/5 | ST00552 | 60 | Nem | ↑ |
| TX52/6 | ST04524 | 60 | M2 | ↑ |
| TX55/1 | ST02890 | 46.5→ 53 | SmA→Iso | ↑ |
| TX55/2 | ST02890 | 46.5→ 53 | SmA→Iso | ↑ |
| TX55/3 | ST00554 | 53 | SmC | ↑ |
| TX55/4 | ST00552 | 53 | SmA | ↑ |
| TX55/5 | ST00554 | 53 | SmC | |
| TX55/6 | ST00552 | 53 | SmA |
| Sample | Chemical Formula and Phase Sequence |
|---|---|
| ST00552 | 2-(4-n-Hexyloxyphenyl)-5-n-octylpyrimidine |
| Cr 27.5 SmC 44.5 SmA 57.5 Nem 65 Iso | |
| ST00554 | 2-(4-n-Decyloxyphenyl)-5-n-octylpyrimidine |
| Cr 32 SmC 59.5 SmA 65.5 Nem 69.5 I | |
| ST02890 | 4-n-Nonyl-biphenyl-4-carbonitrile, 9 CB |
| Cr 42 SmA 47.5 Nem 49.5 Iso | |
| ST04524 | 2,3,6,7,10,11-Hexakis[dodecyloxy]triphenylene |
| Cr 55 M1 58 M2 63 Iso |
| Experiment | Material | Phase | Result |
|---|---|---|---|
| TX52/1 | ST00552 | SmC | Stable until re-entry at |
| TX52/2 | ST02890 | SmA | Wetted hull: breakup at |
| TX52/3 | ST00552 | SmA | Stable until re-entry at |
| TX52/4 | ST02890 | Iso | Asymmetric: breakup at |
| TX52/5 | ST005520 | Nem | Wetted hull: breakup at |
| TX52/6 | ST04524 | M2 | Stable even after re-entry |
| TX55/1 | ST02890 | Nem | Breakup after melting at |
| TX55/2 | ST02890 | Nem | Breakup after melting at |
| TX55/3 | ST00554 | SmC | Stable until re-entry at |
| TX55/4 | ST00552 | SmA | Air bubbles: breakup at |
| TX55/5 | ST00554 | SmC | Stable until re-entry at |
| TX55/6 | ST00552 | SmA | Stable until re-entry at |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trittel, T.; Klopp, C.; Harth, K.; Stannarius, R. Stability and Rupture of Liquid Crystal Bridges under Microgravity. Crystals 2022, 12, 1092. https://doi.org/10.3390/cryst12081092
Trittel T, Klopp C, Harth K, Stannarius R. Stability and Rupture of Liquid Crystal Bridges under Microgravity. Crystals. 2022; 12(8):1092. https://doi.org/10.3390/cryst12081092
Chicago/Turabian StyleTrittel, Torsten, Christoph Klopp, Kirsten Harth, and Ralf Stannarius. 2022. "Stability and Rupture of Liquid Crystal Bridges under Microgravity" Crystals 12, no. 8: 1092. https://doi.org/10.3390/cryst12081092
APA StyleTrittel, T., Klopp, C., Harth, K., & Stannarius, R. (2022). Stability and Rupture of Liquid Crystal Bridges under Microgravity. Crystals, 12(8), 1092. https://doi.org/10.3390/cryst12081092






