Abstract
Ferroelectric materials manifest unique dielectric, ferroelastic, and piezoelectric properties. A targeted design of ferroelectrics at the nanoscale is not only of fundamental appeal but holds the highest potential for applications. Compared to two-dimensional nanostructures such as thin films and superlattices, one-dimensional ferroelectric nanowires are investigated to a much lesser extent. Here, we reveal a variety of the topological polarization states, particularly the vortex and helical chiral phases, in loaded ferroelectric nanowires, which enable us to complete the strain–temperature phase diagram of the one-dimensional ferroelectrics. These phases are of prime importance for optoelectronics and quantum communication technologies.
1. Introduction
Ferroelectrics are being turned into a leading material in modern electronics [1,2] owing to their exceedingly broad range of applications enabling innovative devices, such as memory and logical units, tunnel junctions, field-effect transistors, non-volatile ferroelectric random access memory, nano-electromechanical systems, energy-harvesting devices, advanced sensors and photocatalysis systems. A remarkable feature of ferroelectrics is that, in the course of the occurring dimensional downscaling of devices, they not only enable the superdensely packed circuits but also come up with new functionalities related to the emergence of topological polarization states and specific surface-induced electrodynamics [3,4,5]. The two-dimensional and quasi-two-dimensional ferroelectric thin films and superlattices harboring a variety of topological excitations such as soft domains [6], vortices [7], skyrmions [8], and merons [9] are now understood reasonably well. At the same time, cognizance surrounding the properties of topological excitations in their lower-dimensional relatives, zero-dimensional nanodots, is much less extensive, although similar excitations—vortices [10,11,12,13,14], skyrmions [15,16], and hopfions [17]—have been predicted. Furthermore, while the fabrication methods of one-dimensional nanorods, nanotubes, and nanowires have achieved considerable progress [18,19,20,21,22,23], the topological dynamics in these one-dimensional nanostructures remain even more puzzling.
The past progress in this study of ferroelectric one-dimensional nanostructures has been mostly dealing with general issues of the thermodynamic properties of the uniform polarization states [24,25,26,27]. The importance of “new physics” related to the emergence of unconventional topological vortex states was also realized [28], but only a few studies considered the systematics of their appearance [29,30,31]. In particular, the important practical aspects of operations with the different topological states remain underexplored.
Here, we investigated the emergent topological phase states in a strained ferroelectric nanowire arising due to the electrostatic confinement of polarization and demonstrate the ways of manipulating and switching these states by the load applied to the ends of the nanowire.
Here, we advance the existing Ginzburg–Landau–Devonshire (GLD) approach, via creating a synergistic technique harnessing the analytical treatment, the phase-field numerical calculations, and the atomistic simulations. A simultaneous use of these components not only enables new revelations but, most importantly, brings in strong reliability to derived results. These results show how new topological phases form in a confined strained nanoscale wire. We consider a nanowire made of PbTiO (PTO), taking the latter as an exemplary ferroelectric material. We construct the strain–temperature phase diagram of the system and reveal the three qualitatively different polar phases: the vortex state (v phase) with polarization swirling around the nanowire c axis; the helical state (h phase), with the polarization screwing along the c axis; and the uniform polarization state extending along the c axis (c phase). Each state has unique physical properties for applications. In particular, the h phase hosts the spontaneously broken polarization chirality, easily tunable by the applied strain and temperature. This property of tunable chirality is of prime importance for optoelectronics and quantum communication technologies and does not have natural analogs.
2. Materials and Methods
2.1. Functional
A general approach to the description of ferroelectrics is based on the Ginzburg–Landau–Devonshire (GLD) functional, , which in the case of a free-standing sample is the Gibbs thermodynamic potential of the system. The corresponding free-energy density, , harnesses the ferroelectric, elastic, and electrostatic components, written in terms of the polarization vector, , stress tensor, , and electric field (where is an electrostatic potential), respectively. For the pseudo-cubic perovskite crystal, free energy density takes the form [32]:
where the first brackets correspond to the uniform polarization energy [32], written in a form as in [33]; the next term accounts for the energy, related to the polarization gradient [34]; the stress-polarization coupling is described by the third term [32]; the fourth term represents the elastic energy contribution; and the coupling of polarization with the electric field and the electrostatic energy are given by the last two terms [35]. Indices take the values (or ), and the summation over repeated indices is assumed. For PTO with pseudo-cubic symmetry, the coefficients in free energy density (1) take standard values [36] (with cubic symmetry permutations) with Cm N K, °C (Curie temperature), Cm N, Cm N, Cm N, Cm N, and C m N. The components of the stress-polarization coupling tensor, , are Cm, Cm, and Cm. The components of the elastic compliance tensor, m, m, and m are calculated as the inverse of the elastic tensor, . The gradient energy coefficients are Cm N, , and Cm N [34]. The constant is the vacuum permittivity, and [37] is the background dielectric constant due to nonpolar ions.
The free energy density defined by Equation (1) written in terms of elastic stresses is ordinarily used for the description of the bulk free-standing systems. When discussing nanosystems confined in certain directions, it becomes more suitable to use the displacements corresponding to the confined degrees of freedom as driving parameters rather than stress variables. To that end, we go over to the strains, as to variables conjugated to the stresses, , and perform the Legendre transformation to replace part of the stresses by corresponding strains. As a result, we arrive at the mixed description in terms of both stress and strain variables, the choice depending on the particular geometry of the system and the property to be described.
2.2. Phase-Field Simulations
Phase-field simulations of the PTO nanowires are performed with the help of the FEniCS software package [38]. The evolution of the polarization vector field to its equilibrium fashion is governed by the relaxation equation:
where the energy density is taken as a function of electric potential and the strain tensor , obtained from the stress-dependent energy given by Equation (1) by the Legendre transformation [39]. Equation (2) is closed by the Poisson equation which takes into account electrostatic effects:
and by the linear equation of elasticity:
The value of the parameter is taken equal to one, as it is not crucial for the static case. The approximation of the time derivative on the left hand side of Equation (2) is accomplished by BDF2 variable-time stepper [40]. The system of nonlinear partial differential equations given by Equation (2) is solved by Newton’s method. Linear Equations (3) and (4) are solved using the iterative generalized minimum residual method (GMRES) [41,42]. The computational space is represented by the cylindrical volume, partitioned into tetrahedrons by the 3D mesh generator gmsh [43]. All variables , , and are periodically constrained in the z direction in addition to the assumed quasi-periodicity of the displacement along the cylinder axis, . Here, h is the cylinder height and is the applied strain. The procedure of calculation of the phase diagram is as follows. Let each point (T,) of the system be initially at the paraelectric phase with a random distribution of with components. Other initial states are the c phase with uniformly oriented polarization along the cylinder axis and the vortex v phase in which polarization rotates circularly around the cylinder axis. Then, let the system evolve with time and then choose for each point the state with the minimum energy defined by Equation (1).
2.3. Atomistic Simulations
Complementing the phenomenological approach, atomic-level descriptions are useful to model the microscopic behavior of ferroelectrics. Models based on interatomic potentials are computationally efficient for the simulation of finite-temperature properties in systems with a large number of atoms. In particular, a shell model approach with parameters fitted to first-principle results has been extensively used to study ferroelectric oxides [44,45,46]. In the shell model, atoms are thought to consist of an ion core coupled to an “electronic” shell in order to include its electronic polarization. The core and shell of an atom interact with each other as well as with the cores and shells of other ions via electrostatic interactions. The description also includes short-range interactions which are normally restricted to act between shells only [47]. The potential energy, V, is then a function of the positions of cores and shell, and is expressed as
where represents the contribution of the interatomic core–shell coupling, contains the long-range electrostatic interactions among cores and shells of different atoms, and accounts for the contributions of short-range interactions between shells. For the PTO model used here, cores and shells interact through an anharmonic spring , where w is the core–shell separation within an ion. Two different types of short-range potentials are considered: a Rydberg potential, is used for the Pb–Ti, Pb–O and Ti–O pairs, and a Buckingham potential, , is used for O–O interactions. Coefficients , , a, b, c and are the shell model fitting parameters. The multi-scale model with 23 independent parameters was originally developed to study bulk properties of PTO [48], and it was then successfully used to describe the behavior of surfaces, interfaces, and nanoparticles without including any additional coefficients [11,49,50].
The PTO wires are constructed from elementary perovskite unit-cells centered on Ti atoms with axes along pseudocubic directions (x, y and z axes lie along the [100], [010], and [001] directions, respectively). In addition, we consider that all surface faces consist of PbO planes. Molecular dynamics simulations with the atomistic model are carried out using the DL-POLY package [51] in a box with periodic boundary conditions. The nanowires extend along the z axis and they are surrounded by enough empty space to avoid any possible interaction between periodic replicas. Runs are performed by employing a constant volume and temperature (NVT) algorithm. The time step is set to 0.2 fs, which provides enough accuracy for the integration of the shell coordinates. The runs are made at temperature intervals of 50 C. Each MD run consists of at least 100,000 time steps for data collection after 50,000 time steps for thermalization.
In contrast to the GLD functional, the atomistic description does not contain polarization as an explicit variable, and its value needs to be estimated from the positions of cores and shells. The local polarization is defined as the dipole moment per unit volume of a perovskite cell centered at the Ti atom, , where v is the volume of the cell, and denote the charge and the position of the i-th particle, respectively, and is a weight factor equal to the number of cells to which the particle belongs.
3. Results
As an exemplary system, we employed the ferroelectric nanowire of the radius nm and observed topologically different polarization textures for different strains and temperatures. Figure 1 summarizes the observed results as a -T phase diagram that exhibits the domains of existence of every discovered phase. The driving strain, , is calculated as the elongation of the lattice parameter of the nanowire c with respect to the relaxed bulk value as . The pairs of the cross-cut cylinders around the diagram exhibit the polarization structure in the observed phases. The left cylinder of each pair displays the polarization texture obtained from the phase field simulations visualized as the vector field, while the right cylinders show the results of the atomistic simulations visualized as polarization field lines. The red and blue lines in the phase diagram show the phase boundaries found from the phase-field and atomistic simulations, respectively. The high-temperature paraelectric phase is marked as the p phase in the phase diagram.
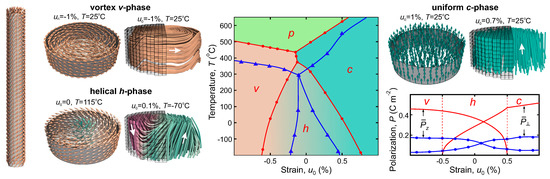
Figure 1.
Emergent phases of strained ferroelectric nanowires. In the center of the figure is the strain–temperature phase diagram comprising the results of the simulations. The red lines are the guides-for-the-eye which connect the data-points and depict the phase transition lines separating distinct ferroelectric phases obtained by phase-field simulations: the vortex phase (v), helical phase (h), uniform phase (c), as well as the paraelectric phase (p). The blue lines show interfaces between the same phases obtained by atomistic simulations. The structures of the observed phases are exemplified by drawings around the phase diagram showing the cross-sectional cylinders of the nanowire. The left picture of each panel represents the polarization vector field obtained from phase-field simulations and the right picture shows the polarization field lines obtained from the atomistic simulations, respectively; the cells in the atomic simulations results sketch the atomic lattices. The teal, fuchsia, and terracotta represent the up, down, and plane directions of the polarization vector, respectively. The exemplary values of the parameters used in simulations are indicated at the tops of the panels. The total view of the nanowire hosting the h phase is shown on the left. The bottom-right corner demonstrates the ways of identification of the phases from the characteristic features of the plot of the averages , and as functions of the strain . Again, the red lines depict the results of the phase field simulations at C, and the blue lines stand for atomistic simulations at C, respectively.
The vortex v phase arising at large compressing strains, harbors the closed field lines turning around the nanowire axis and lying in the plane perpendicular to this axis. The uniform c phase, arising at large tensile strains is the homogeneous phase when polarization is directed along the nanowire axis. Finally, the helical h phase is a new phase revealed by the phase-field simulations and arising when polarization exercises screw rotation around the nanowire axis. This phase exists at small strains and mediates the continuous transformation from a to c phases by changing the incline of the polarization vector with respect to the nanowire axis. The total view of the nanowire with the h phase is shown in Figure 1 on the left. In atomistic simulations, the h phase looks less regular, exhibiting a sort of propensity to history-dependent chaotic behavior. This may result from the surface or bulk-lattice pinning of polarization leading to the formation of the extra variety of the metastable states. Notably, as follows from the phase-field simulations, the second-order v–h and h–c transition lines join at high-temperatures, to form the line of the direct v–c first-order transition along the short segment hitting the critical temperature line. Unfortunately, the precision of the atomistic simulation remains insufficient to test the thermodynamics in the region of the contact of the v, h, and c phases close to the critical temperature.
The low-right panel in Figure 1 demonstrates the practical way of the phase identification by plotting the average polarizations along and perpendicular the nanowire axis, , and as function of at given T. The regions where , , , and , correspond to the v, h, and c phase, respectively. This method gives satisfactory precision for the phase-field simulations (red curves) but is of more qualitative character in case the atomistic simulation (blue curves).
As follows from Figure 1, the phase diagram obtained from the atomistic simulation is shifted with respect to the phase-field phase diagram to lower temperatures, and the corresponding characteristic values of polarization are smaller. The transition temperatures and polarization produced by the atomistic simulations are indeed underestimated with respect to those resulting from the phase-field simulations (and experimental results). This discrepancy is a consequence of the smaller equilibrium volume of the model and is related to the LDA database used to fit model parameters. It is well known that the volume and volume-dependent properties are underestimated when using the LDA approximation for the exchange-correlation functional in first-principle calculations which, in turn, lead to the significant underestimation of the polarization and transition temperatures. In bulk, for instance, the model gives a tetragonal ground state with the lattice parameter Å, a tetragonal distortion = 1.043, and the spontaneous polarization C m, while the experimental data are Å, = 1.065, and C m, respectively. The underestimation of the static structural properties is translated via the adjusted model to the finite temperature behavior. Molecular dynamics simulations showed the cubic–tetragonal transition at 180 C, which is of approximately 300 C lower than the experimental value. Nevertheless, the qualitative temperature behavior of lattice parameters and polarization is correctly reproduced [48].
4. Discussion
Now we are in a position to incorporate our results into a general context of the existing research addressing the emergence of new polarization phases, homogeneous and inhomogeneous ones, in nanostructured ferroelectrics. A glorious avenue of exploring the properties of 2D and quasi-2D nanoscale ferroelectric heterostructures was paved by the seminal work of Pertsev, Zembilgotov, and Tagantsev [52], who constructed the phenomenological thermodynamic theory of strained ferroelectric films with uniform polarization and derived the strain–temperature phase diagram of the system. The applied mechanical in-plane strains were considered as the constraints for the partial Legendre transformations. Although the approach of [52] suffered from oversimplifications due to neglecting the depolarization effects and instabilities related to the emergence of ferroelectric and ferroelastic domains, it provided a gold standard for the initial approach to the consideration of the numerous nonuniform states discovered in ferroelectric 2D structures: complex networks of interplay of domains with and domain walls [53], periodic arrays of stripe soft polarization domains [35], having the texture of oppositely rotating vortices [7], or the double-periodic structure of cylindrical domains [54], having the textures of bubble skyrmions [8].
Here, we adapt the approach of [52] to 1D systems to gain, first of all, a general insight into the appearance of topological states in ferroelectric nanowires. We assume that the load applied to the ends of the nanowire results in the fixed strain along the nanowire (so that for stretching, and for compression). We further assume the absence of the off-diagonal strains, which implies . At the same time, the nanowire is supposed to be free to expand in the transversal x and y directions, while still being subject to the surface-applied pressure, p. This external pressure originates from either contact with the embedding material or from the Laplace pressure, , induced by the surface tension in the case of the cylinder sample [24,25]. Both cases result in the uniform in-plane compression stress .
The application of the partial Legendre transformations with the described constraints gives the effective free energy density as Equation (6), that is similar to the thermodynamic potential obtained in [52] but with the differently renormalized coefficients denoted by asterisks:
The analytical expressions for the renormalized coefficients and their numerical values for PTO are given in Table 1.

Table 1.
Analytical expressions and numerical values (for PTO) of coefficients in free energy density .
Figure 2a presents the strain–temperature phase diagram (depicted by black lines) of the strained nanowires obtained as a result of minimization of the effective free energy density (6). The phase diagram contains an a phase with the transversal to the wire polarization, (or equivalently the b phase with ) and the c phase in parallel to the wire polarization, ; we assume here that the external pressure is absent, . Naturally, on the phase diagram, the negative (compressive) strain favors the a phase whereas the positive (tensile) strain favors the c phase.
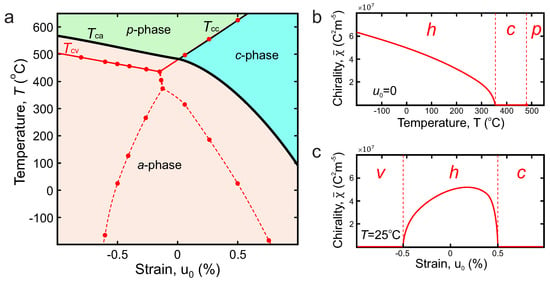
Figure 2.
Phases of the strained nanowire. (a) Calculated thermodynamic phase diagram of the uniform phases in the nanowire. The phase boundaries between the paraelectric p phase and uniformly polarized ferroelectric a phase and c phase when the depolarization effects of the surface bound charges that are neglected are shown in black. The thick lines correspond to the discontinuous first-order transitions and the thin line to the continuous second-order transition. The phase diagram, obtained from the phase-field simulations, that replicates the diagram shown in Figure 1 is shown by red lines. The dashed red lines are the guides-for-the-eye connecting the data-points. The solid red lines correspond to the analytical results for critical temperatures, and , fitting the data points; (b) chirality density of the nanowire as function of temperature at given strain; and (c) chirality density of the nanowire as a function of the strain at a given temperature. The plots shown in (b,c) panels demonstrate a distinction between the chiral h phase and other non-chiral ferroelectric phases, the uniform c phase and vortex v phase.
Similar to the strained film [52], the behavior of the transition temperature of the ferroelectric nanowire, is depicted by the curve combining and dependencies on the applied strain, , having a cusp at (at ), see Figure 2a. Here, and are the Curie temperatures of the a and c phases, respectively; their dependence on and p, provided by conditions and , is given in Table 2. The specific feature of the ferroelectric phase transition to the a phase is that it is the transition of the weak first order, because the fourth-order coefficients , are negative but very small in magnitude. We neglect the small discontinuity of this transition here. In the nonlinear region, below , the a phase occupies the substantial part of the diagram, including the clamped nanowire region with . The c phase appears mostly at the large tensile strains and at high temperatures. The transition between the a and c phases occurs in a discontinuous way.

Table 2.
Critical temperatures (C).
The preceding consideration, however, gives only a general structure of the phase diagram since it does not account for the electrostatic energy of the depolarization field induced by the surface bound charges arising at the surface points of polarization termination. Accordingly, the aforementioned phase diagram of the uniform ferroelectric phases is valid in the absence of depolarization effects, for instance, when the nanowire is submerged in the conducting media and the free conducting carriers screen the depolarization charges. Accounting for the electrostatic effects in the absence of screening modifies the emergent phases, making them nonuniform. The breakdown of the uniformity is caused by the necessity to reduce the value of the depolarization energy, ideally to zero, hence to avoid appearance of bound charges inducing the depolarization fields. Mathematically, this requirement implies that the system always prefers polarization textures with divergenceless polarization lines tangent to the lateral nanowire surface. The observed vortex v phase is one of such realized possibilities. The comparison of the uniform phase diagram with the results of our phase field simulations (shown by solid red lines in Figure 1, also replicated in Figure 2a by the red dashed lines) demonstrates that the nonuniform v phase forms from the uniform a phase, when the polarization vectors transversal to the wire swirl into the vortex to avoid the formation of bound charges at the lateral surface. The gradient energy, however, makes the v phase less favorable than the uniform a phase in case of screening. This reduces the critical temperature of the v phase and shifts its phase boundaries to the smaller strains with respect to the c phase which is evidently not affected by depolarization effects.
Importantly, the critical temperature of the vortex phase, , can be analytically calculated by linearizing the GLD equations, obtained from the variation of the functional (1). The corresponding linearized equation in cylindrical coordinates for the axisymmetric polarization distribution assumes the form:
which, taking the variational free boundary conditions , defines the critical temperature and yields the corresponding vortex solution below [29] as
where is the first-order Bessel function, is the first zero of the derivative , and nm is the coherence length. The amplitude coefficient C is found by solving the nonlinear equations. Taking into account that on the -T diagram, according to Equation (8), the critical temperature of the v phase shifts down with respect to the screened a phase. We obtain that the cusp in the strain dependence of the total critical temperature of the system, also shifts down and to the left, to lower strains, with respect to the case of the uniform (screened) system. Shown by the solid red line in Figure 2a, this dependence perfectly coincides with the results of the phase-field simulations.
Another new phase, emerging from the strained ferroelectric nanowire is the helical h phase in which the polarization is inclined with respect to the nanowire axis and rotates around this axis. This phase, appearing at small strains, extends deep into the nonlinear region lying between the c and v phases and mediates the continuous transition between them by the gradual inclining of the rotating polarization vector from the direction parallel to the nanowire to the transversal to the nanowire direction. This helical phase is a state analogous to other topological states with non-zero helicity harboring skyrmions [15,16], coreless vortices [56], merons [9], and hopfions [17].
The importance of this phase is that it realizes a polarization state possessing a chiral asymmetry, a fundamental property of matter describing the systems distinguishable from their mirror images. The dependence of the quantitative characteristic of polarization chirality, the chirality density [17], on the strain and temperature is shown in Figure 2b,c, respectively, by the red lines. It is non-zero for the h phase and zero for the c and v phases, clearly indicating the region of the existence of the helical phase.
5. Conclusions
The theoretical investigation of a one-dimensional strained PbTiO nano-wire undertaken herein allowed to reveal and model the emerging topological states in the ferroelectric as functions of strain and temperature. Two simulation techniques have been exercised and compared: the phase-field simulations employing the GLD functional and the atomistic simulations. Compressive and tensile strains were simulated at the upper and lower boundaries of the nano-wire along the axis. The strain–temperature phase diagram showing the different phases was produced and compared to the phase diagram that came from the simple free energy minimization procedure and which appeared more similar to the bulk phase diagram. Furthermore, the proposed novel methods enabled the discovery of two novel phases related to the considered depolarization effects, the vortex phase, having the polarization perpendicular to the wire axis, and the h phase, which mediates between the v phase and the uniform and previously known c phase.
As we demonstrated, the nanoscale confinement of a ferroelectric forming the strained nanowire stabilizes emerging topological states brings functionalities that do not exist in bulk materials. Nanowires supporting vortices and helical phase are of special interest for applications since these topological excitations are well controlled and manipulated by electric fields. This may promote and trigger giant piezo- and ferroelectric responses. Remarkably, we revealed that ferroelectric topological excitations in nanowires are controllable not only by electric fields, but are well tunable by the temperature and lattice strain. The possibility of switching between these states paves the way for using ferroelectric nanowires as base units for the multi-level logic ferroelectric devices [2,33,57], and neuromorphic computing circuits [1].
On top of that, chirality, a new functionality of confined ferroelectrics, has recently received explosive interest [16,17,58,59]. The newly discovered polarization chirality of nanowires, including its unprecedented tunability by the strains and temperature, opens a broad spectrum of fascinating directions promising to revolutionize different technological fields ranging from plasmonic and photonics relevant for quantum optoelectronic communications to chemical, pharmaceutical, and biomedical applications.
Author Contributions
Conceptualization, I.A.L.; methodology, I.A.L., V.M.V., S.K., M.S., Y.A.T. and L.B.; software, F.D.R., M.S., M.A.P. and Y.A.T.; validation, A.G.R., A.S., S.K. and V.M.V.; investigation, L.B., M.A.P., F.D.R., S.K. and A.S.; writing—original draft preparation, V.M.V., S.K., I.A.L. and A.G.R.; writing—review and editing, V.M.V., S.K. and I.A.L.; project administration, I.A.L., V.M.V., M.S. and A.G.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was financially supported by the European Union H2020-MSCA-RISE ENGIMA and MELON actions. S.K. acknowledges the support from the Alexander von Humboldt Foundation. The work of V.M.V. was supported by Terra Quantum AG and, in part, by the Fulbright Foundation. F.D.R. and M.S. acknowledge the support from CONICET (No. PUE-IFIR 2017-2022 N0076).
Data Availability Statement
Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Oh, S.; Hwang, H.; Yoo, I.K. Ferroelectric materials for neuromorphic computing. APL Mater. 2019, 7, 091109. [Google Scholar] [CrossRef] [Green Version]
- Mikolajick, T.; Schroeder, U.; Slesazeck, S. The Past, the Present, and the Future of Ferroelectric Memories. IEEE Trans. Electron. Devices 2020, 67, 1434–1443. [Google Scholar] [CrossRef]
- Das, S.; Hong, Z.; McCarter, M.; Shafer, P.; Shao, Y.T.; Muller, D.A.; Martin, L.W.; Ramesh, R. A new era in ferroelectrics. APL Mater. 2020, 8, 120902. [Google Scholar] [CrossRef]
- Chen, S.; Yuan, S.; Hou, Z.; Tang, Y.; Zhang, J.; Wang, T.; Li, K.; Zhao, W.; Liu, X.; Chen, L.; et al. Recent progress on topological structures in ferroic thin films and heterostructures. Adv. Mater. 2021, 33, 2000857. [Google Scholar] [CrossRef] [PubMed]
- Tian, G.; Yang, W.; Gao, X.; Liu, J.M. Emerging phenomena from exotic ferroelectric topological states. APL Mater. 2021, 9, 020907. [Google Scholar] [CrossRef]
- Stephanovich, V.A.; Luk’yanchuk, I.A.; Karkut, M.G. Domain-enhanced interlayer coupling in ferroelectric/paraelectric superlattices. Phys. Rev. Lett. 2005, 94, 047601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yadav, A.; Nelson, C.; Hsu, S.; Hong, Z.; Clarkson, J.; Schleputz, C.; Damodaran, A.; Shafer, P.; Arenholz, E.; Dedon, L.; et al. Observation of polar vortices in oxide superlattices. Nature 2016, 530, 198–201. [Google Scholar] [CrossRef]
- Das, S.; Tang, Y.; Hong, Z.; Gonçalves, M.; McCarter, M.; Klewe, C.; Nguyen, K.; Gómez-Ortiz, F.; Shafer, P.; Arenholz, E.; et al. Observation of room-temperature polar skyrmions. Nature 2019, 568, 368–372. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Y.; Feng, Y.; Zhu, Y.; Tang, Y.; Yang, L.; Zou, M.; Geng, W.; Han, M.; Guo, X.; Wu, B.; et al. Polar meron lattice in strained oxide ferroelectrics. Nat. Mater. 2020, 19, 881–886. [Google Scholar] [CrossRef]
- Naumov, I.; Bratkovsky, A.M. Unusual polarization patterns in flat epitaxial ferroelectric nanoparticles. Phys. Rev. Lett. 2008, 101, 107601. [Google Scholar] [CrossRef] [Green Version]
- Stachiotti, M.G.; Sepliarsky, M. Toroidal ferroelectricity in PbTiO3 nanoparticles. Phys. Rev. Lett. 2011, 106, 137601. [Google Scholar] [CrossRef] [Green Version]
- Mangeri, J.; Espinal, Y.; Jokisaari, A.; Alpay, S.P.; Nakhmanson, S.; Heinonen, O. Topological phase transformations and intrinsic size effects in ferroelectric nanoparticles. Nanoscale 2017, 9, 1616–1624. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kondovych, S.; Pavlenko, M.; Tikhonov, Y.; Razumnaya, A.; Lukyanchuk, I. Vortex states in a ferroelectric cylinder. arXiv 2021, arXiv:2112.10129. [Google Scholar]
- Di Rino, F.; Sepliarsky, M.; Stachiotti, M.G. Topology of the polarization field in PbTiO3 nanoparticles of different shapes by atomic-level simulations. J. Appl. Phys. 2020, 127, 144101. [Google Scholar] [CrossRef]
- Nahas, Y.; Prokhorenko, S.; Louis, L.; Gui, Z.; Kornev, I.; Bellaiche, L. Discovery of stable skyrmionic state in ferroelectric nanocomposites. Nat. Commun. 2015, 6, 8542. [Google Scholar] [CrossRef] [PubMed]
- Tikhonov, Y.; Kondovych, S.; Mangeri, J.; Pavlenko, M.; Baudry, L.; Sené, A.; Galda, A.; Nakhmanson, S.; Heinonen, O.; Razumnaya, A.; et al. Controllable skyrmion chirality in ferroelectrics. Sci. Rep. 2020, 10, 8657. [Google Scholar] [CrossRef]
- Luk’yanchuk, I.; Tikhonov, Y.; Razumnaya, A.; Vinokur, V. Hopfions emerge in ferroelectrics. Nat. Commun. 2020, 11, 2433. [Google Scholar] [CrossRef]
- Alexe, M.; Hesse, D.; Schmidt, V.; Senz, S.; Fan, H.J.; Zacharias, M.; Gösele, U. Ferroelectric nanotubes fabricated using nanowires as positive templates. Appl. Phys. Lett. 2006, 89, 172907. [Google Scholar] [CrossRef]
- Rørvik, P.M.; Grande, T.; Einarsrud, M.A. One-dimensional nanostructures of ferroelectric perovskites. Adv. Mater. 2011, 23, 4007–4034. [Google Scholar] [CrossRef]
- Varghese, J.; Whatmore, R.W.; Holmes, J.D. Ferroelectric nanoparticles, wires and tubes: Synthesis, characterisation and applications. J. Mater. Chem. C 2013, 1, 2618–2638. [Google Scholar] [CrossRef] [Green Version]
- Polking, M.J.; Alivisatos, A.P.; Ramesh, R. Synthesis, physics, and applications of ferroelectric nanomaterials. MRS Commun. 2015, 5, 27–44. [Google Scholar] [CrossRef]
- Liang, L.; Kang, X.; Sang, Y.; Liu, H. One-dimensional ferroelectric nanostructures: Synthesis, properties, and applications. Adv. Sci. 2016, 3, 1500358. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xia, W.; Lu, Y.; Zhu, X. Preparation Methods of Perovskite-Type Oxide Materials. In Revolution of Perovskite; Springer: Berlin/Heidelberg, Germany, 2020; pp. 61–93. [Google Scholar] [CrossRef]
- Morozovska, A.N.; Eliseev, E.A.; Glinchuk, M.D. Ferroelectricity enhancement in confined nanorods: Direct variational method. Phys. Rev. B 2006, 73, 214106. [Google Scholar] [CrossRef]
- Morozovska, A.N.; Glinchuk, M.D.; Eliseev, E.A. Phase transitions induced by confinement of ferroic nanoparticles. Phys. Rev. B 2007, 76, 014102. [Google Scholar] [CrossRef] [Green Version]
- Ma, W. Surface tension and Curie temperature in ferroelectric nanowires and nanodots. Appl. Phys. A 2009, 96, 915–920. [Google Scholar] [CrossRef]
- Wang, J.; Tagantsev, A.K.; Setter, N. Effective-surface-energy approach for size effects in ferroics. Phys. Rev. B 2015, 91, 125432. [Google Scholar] [CrossRef]
- Naumov, I.I.; Bellaiche, L.; Fu, H. Unusual phase transitions in ferroelectric nanodisks and nanorods. Nature 2004, 432, 737. [Google Scholar] [CrossRef]
- Lahoche, L.; Luk’yanchuk, I.; Pascoli, G. Stability of vortex phases in ferroelectric easy-plane nano-cylinders. Integr. Ferroelectr. 2008, 99, 60–66. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Yang, B.; Cao, W.; Fohtung, E.; Lookman, T. Enhanced Energy Storage with Polar Vortices in Ferroelectric Nanocomposites. Phys. Rev. Appl. 2017, 8, 034014. [Google Scholar] [CrossRef]
- Morozovska, A.N.; Hertel, R.; Cherifi-Hertel, S.; Reshetnyak, V.Y.; Eliseev, E.A.; Evans, D.R. Chiral polarization textures induced by the flexoelectric effect in ferroelectric nanocylinders. Phys. Rev. B 2021, 104, 054118. [Google Scholar] [CrossRef]
- Haun, M.J.; Furman, E.; Jang, S.; McKinstry, H.; Cross, L. Thermodynamic theory of PbTiO3. J. Appl. Phys. 1987, 62, 3331–3338. [Google Scholar] [CrossRef]
- Baudry, L.; Lukyanchuk, I.; Vinokur, V.M. Ferroelectric symmetry-protected multibit memory cell. Sci. Rep. 2017, 7, 42196. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, J.; Shi, S.Q.; Chen, L.Q.; Li, Y.; Zhang, T.Y. Phase-field simulations of ferroelectric/ferroelastic polarization switching. Acta Mater. 2004, 52, 749–764. [Google Scholar] [CrossRef]
- Luk’yanchuk, I.A.; Lahoche, L.; Sené, A. Universal properties of ferroelectric domains. Phys. Rev. Lett. 2009, 102, 147601. [Google Scholar] [CrossRef]
- Chen, L.Q. Landau Free-Energy Coefficients. In Physics of Ferroelectrics: A Modern Perspective; Rabe, K.M., Dawber, M., Lichtensteiger, C., Ahn, C.H., Triscone, J.M., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 363–369. [Google Scholar]
- Mokrý, P.; Sluka, T. Identification of defect distribution at ferroelectric domain walls from evolution of nonlinear dielectric response during the aging process. Phys. Rev. B 2016, 93, 064114. [Google Scholar] [CrossRef] [Green Version]
- Logg, A.; Mardal, K.A.; Wells, G.N. (Eds.) Automated Solution of Differential Equations by the Finite Element Method. Volume 84: Lecture Notes in Computational Science and Engineering; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar] [CrossRef]
- Devonshire, A.F. XCVI. Theory of barium titanate: Part I. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1949, 40, 1040–1063. [Google Scholar] [CrossRef]
- Janelli, A.; Fazio, R. Adaptive stiff solvers at low accuracy and complexity. J. Comput. Appl. Math. 2006, 191, 246. [Google Scholar] [CrossRef] [Green Version]
- Balay, S.; Abhyankar, S.; Adams, M.F.; Benson, S.; Brown, J.; Brune, P.; Buschelman, K.; Constantinescu, E.; Dalcin, L.; Dener, A.; et al. PETSc Web Page. 2021. Available online: https://petsc.org/ (accessed on 3 March 2022).
- Balay, S.; Abhyankar, S.; Adams, M.F.; Benson, S.; Brown, J.; Brune, P.; Buschelman, K.; Constantinescu, E.; Dalcin, L.; Dener, A.; et al. PETSc/TAO Users Manual; Technical Report ANL-21/39; Revision 3.16; Argonne National Laboratory: Lemont, IL, USA, 2021. [Google Scholar]
- Geuzaine, C.; Remacle, J.F. Gmsh: A three-dimensional finite element mesh generator with built-in pre- and post-processing facilities. Int. J. Numer. Methods Eng. 2009, 79, 1039–1331. [Google Scholar] [CrossRef]
- Tinte, S.; Stachiotti, M.G.; Phillpot, S.R.; Sepliarsky, M.; Wolf, D.; Migoni, R.L. Ferroelectric properties of BaxSr1−xTiO3 solid solutions obtained by molecular dynamics simulation. J. Phys. Condens. Matter 2004, 16, 3495–3506. [Google Scholar] [CrossRef]
- Sepliarsky, M.; Cohen, R.E. First-principles based atomistic modeling of phase stability in PMN–xPT. J. Phys. Condens. Matter 2011, 23, 435902. [Google Scholar] [CrossRef] [Green Version]
- Machado, R.; Di Loreto, A.; Frattini, A.; Sepliarsky, M.; Stachiotti, M. Site occupancy effects of Mg impurities in BaTiO3. J. Alloys Compd. 2019, 809, 151847. [Google Scholar] [CrossRef]
- Dick, B.G.; Overhauser, A.W. Theory of the Dielectric Constants of Alkali Halide Crystals. Phys. Rev. 1958, 112, 90–103. [Google Scholar] [CrossRef]
- Sepliarsky, M.; Wu, Z.; Asthagiri, A.; Cohen, R. Atomistic model potential for PbTiO3 and PMN by fitting first principles results. Ferroelectrics 2004, 301, 55–59. [Google Scholar] [CrossRef]
- Sepliarsky, M.; Asthagiri, A.; Phillpot, S.; Stachiotti, M.; Migoni, R. Atomic-level simulation of ferroelectricity in oxide materials. Curr. Opin. Solid State Mater. Sci. 2005, 9, 107–113. [Google Scholar] [CrossRef]
- Sepliarsky, M.; Stachiotti, M.G.; Migoni, R.L. Interface Effects in Ferroelectric PbTiO3 Ultrathin Films on a Paraelectric Substrate. Phys. Rev. Lett. 2006, 96, 137603. [Google Scholar] [CrossRef] [Green Version]
- Todorov, I.T.; Smith, W.; Trachenko, K.; Dove, M.T. DL_POLY_3: New dimensions in molecular dynamics simulations via massive parallelism. J. Mater. Chem. 2006, 16, 1911–1918. [Google Scholar] [CrossRef] [Green Version]
- Pertsev, N.A.; Zembilgotov, A.G.; Tagantsev, A.K. Effect of Mechanical Boundary Conditions on Phase Diagrams of Epitaxial Ferroelectric Thin Films. Phys. Rev. Lett. 1998, 80, 1988–1991. [Google Scholar] [CrossRef]
- Tagantsev, A.K.; Cross, L.E.; Fousek, J. Domains in Ferroic Crystals and Thin Films; Springer: Berlin/Heidelberg, Germany, 2010; Volume 13. [Google Scholar]
- Hooton, J.A.; Merz, W.J. Etch Patterns and Ferroelectric Domains in BaTiO3 Single Crystals. Phys. Rev. 1955, 98, 409. [Google Scholar] [CrossRef]
- Hlinka, J.; Marton, P. Phenomenological model of a 90° domain wall in BaTiO3-type ferroelectrics. Phys. Rev. B 2006, 74, 104104. [Google Scholar] [CrossRef]
- Baudry, L.; Sené, A.; Luk’yanchuk, I.A.; Lahoche, L.; Scott, J.F. Polarization vortex domains induced by switching electric field in ferroelectric films with circular electrodes. Phys. Rev. B 2014, 90, 024102. [Google Scholar] [CrossRef] [Green Version]
- Martelli, P.W.; Mefire, S.M.; Luk’yanchuk, I.A. Multidomain switching in the ferroelectric nanodots. Europhys. Lett. 2015, 111, 50001. [Google Scholar] [CrossRef] [Green Version]
- Chen, P.; Tan, C.; Jiang, Z.; Gao, P.; Sun, Y.; Li, X.; Zhu, R.; Liao, L.; Hou, X.; Wang, L.; et al. Manipulation of polar vortex chirality in oxide superlattices. arXiv 2021, arXiv:2104.12310. [Google Scholar]
- Behera, P.; May, M.A.; Gómez-Ortiz, F.; Susarla, S.; Das, S.; Nelson, C.T.; Caretta, L.; Hsu, S.L.; McCarter, M.R.; Savitzky, B.H.; et al. Electric field control of chirality. Sci. Adv. 2022, 8, eabj8030. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
