Microstructure-Based Fatigue Modeling with Residual Stresses: Effect of Inclusion Shape on Very High Cycle Fatigue Life
Abstract
:1. Introduction
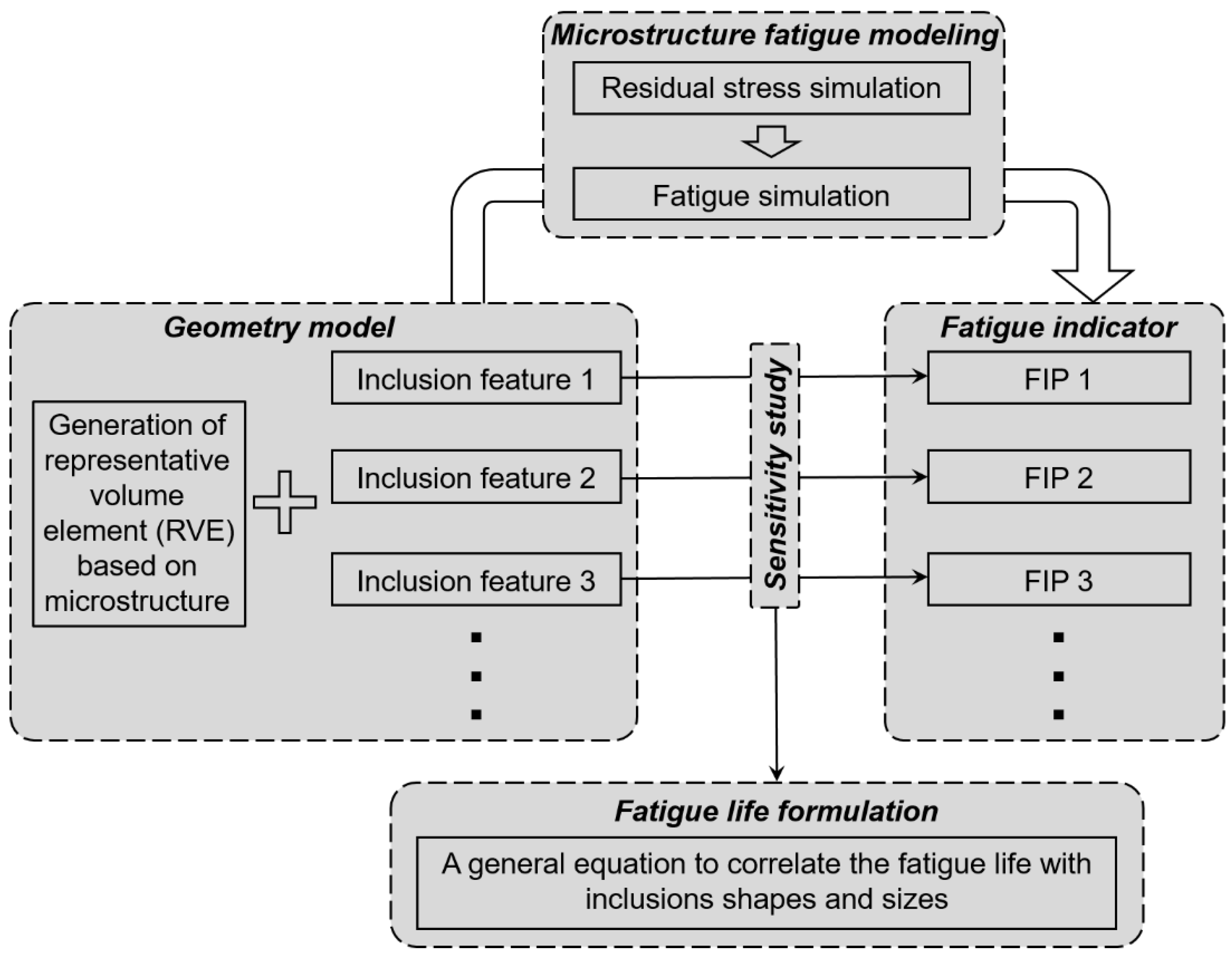
2. Modeling Strategy
2.1. Reconstruction of Microstructure
2.2. Digitalization of Inclusions
2.3. Residual Stress Simulation
2.4. Crystal Plasticity Model and Parameter Calibration
2.5. Fatigue Indicator Parameter and Fatigue Simulation
3. Results and Discussion
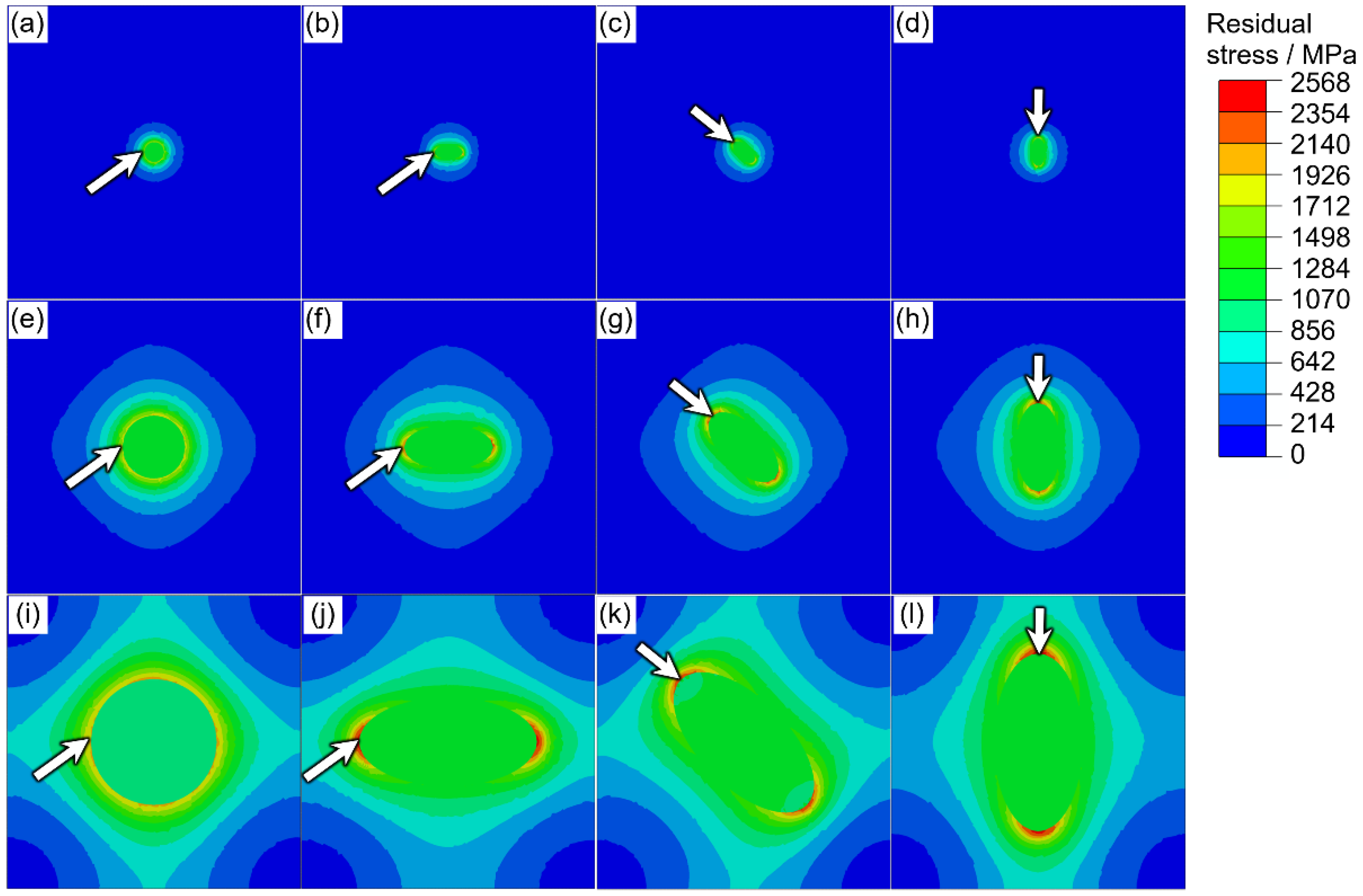
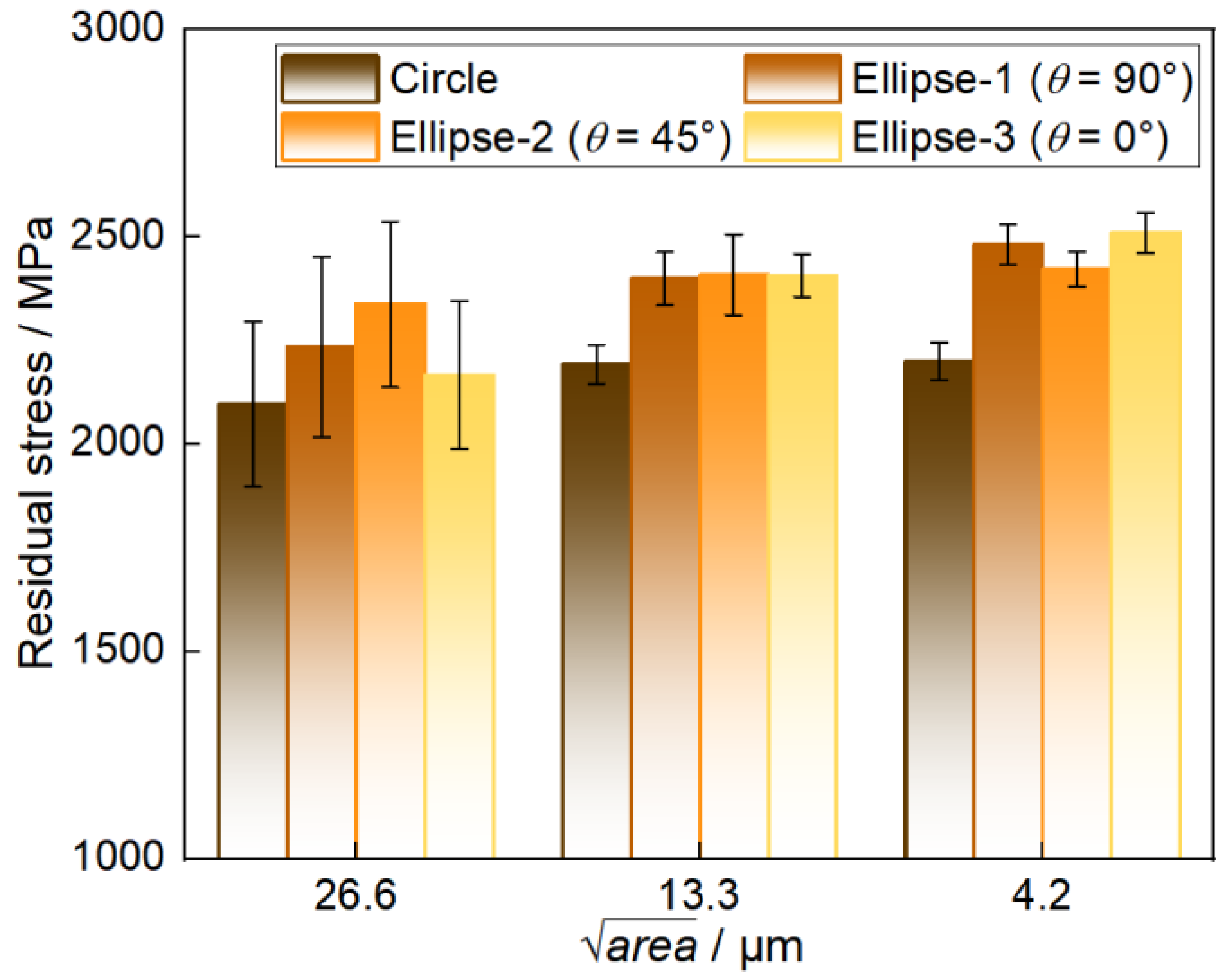
3.1. Residual Stress Distribution with Different Inclusions
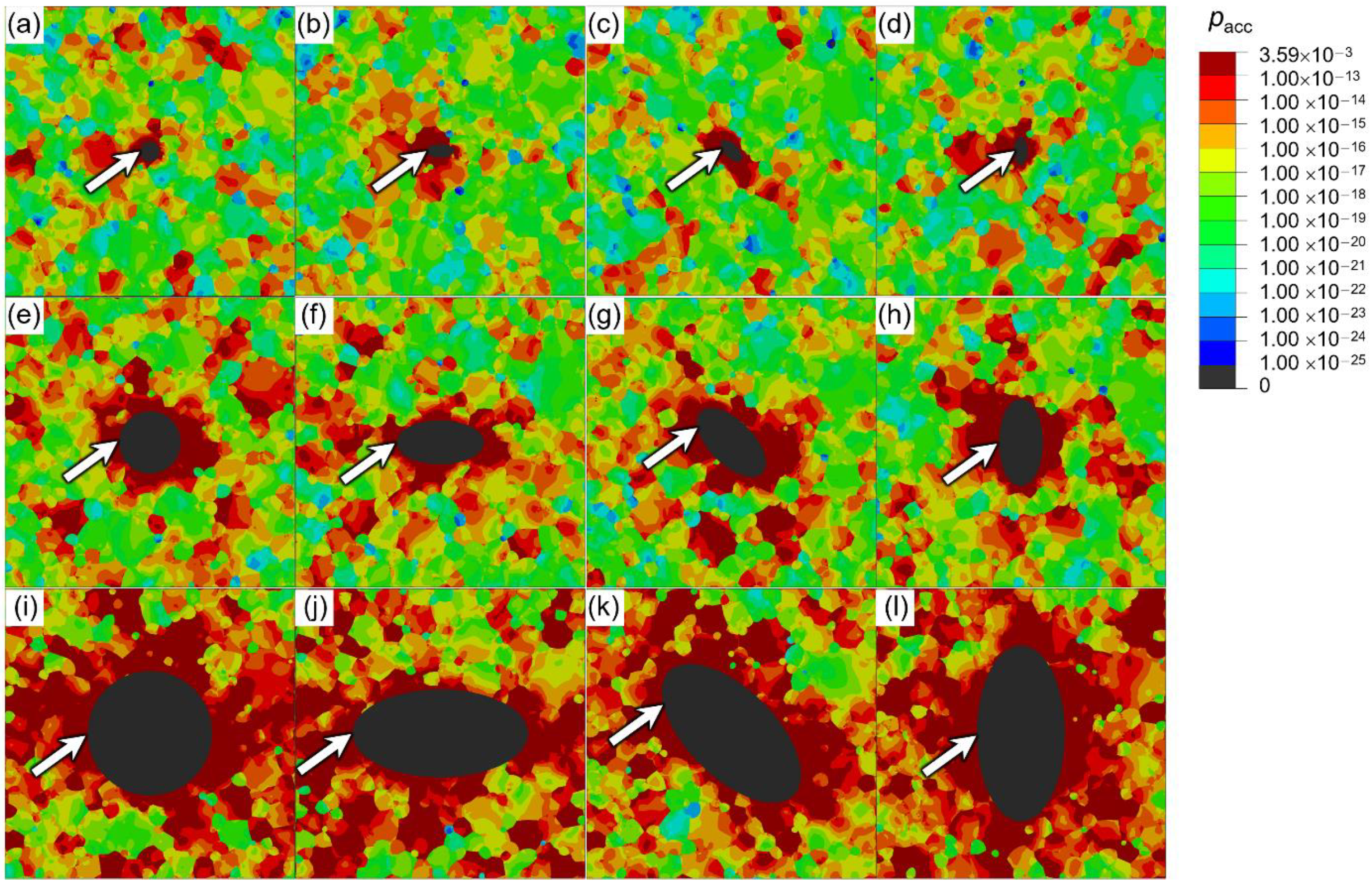
3.2. Fatigue Crack Initiation Site Prediction
3.3. Fatigue Life Prediction
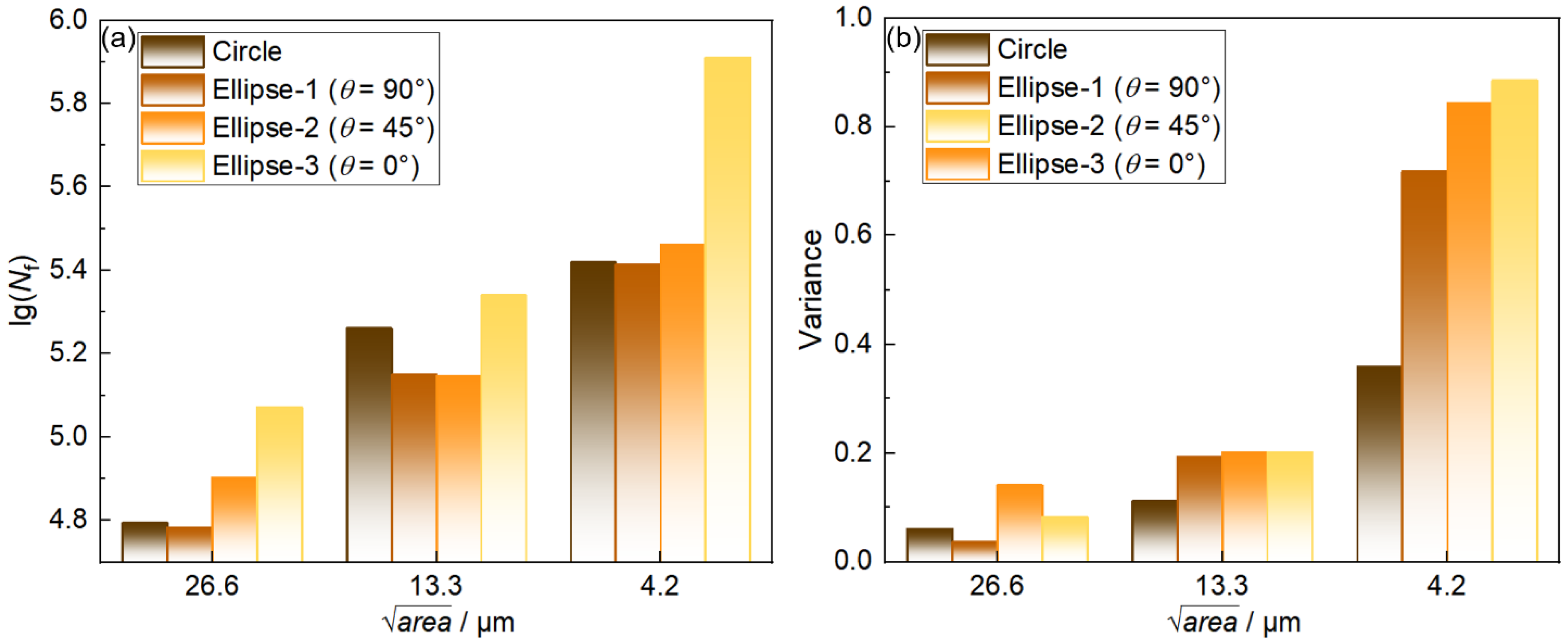
3.3.1. Results of Fatigue Life Prediction with Microstructure Modeling
3.3.2. Inclusion Parameters Unifying and the Formulation of Fatigue Life concerning Inclusion Parameters
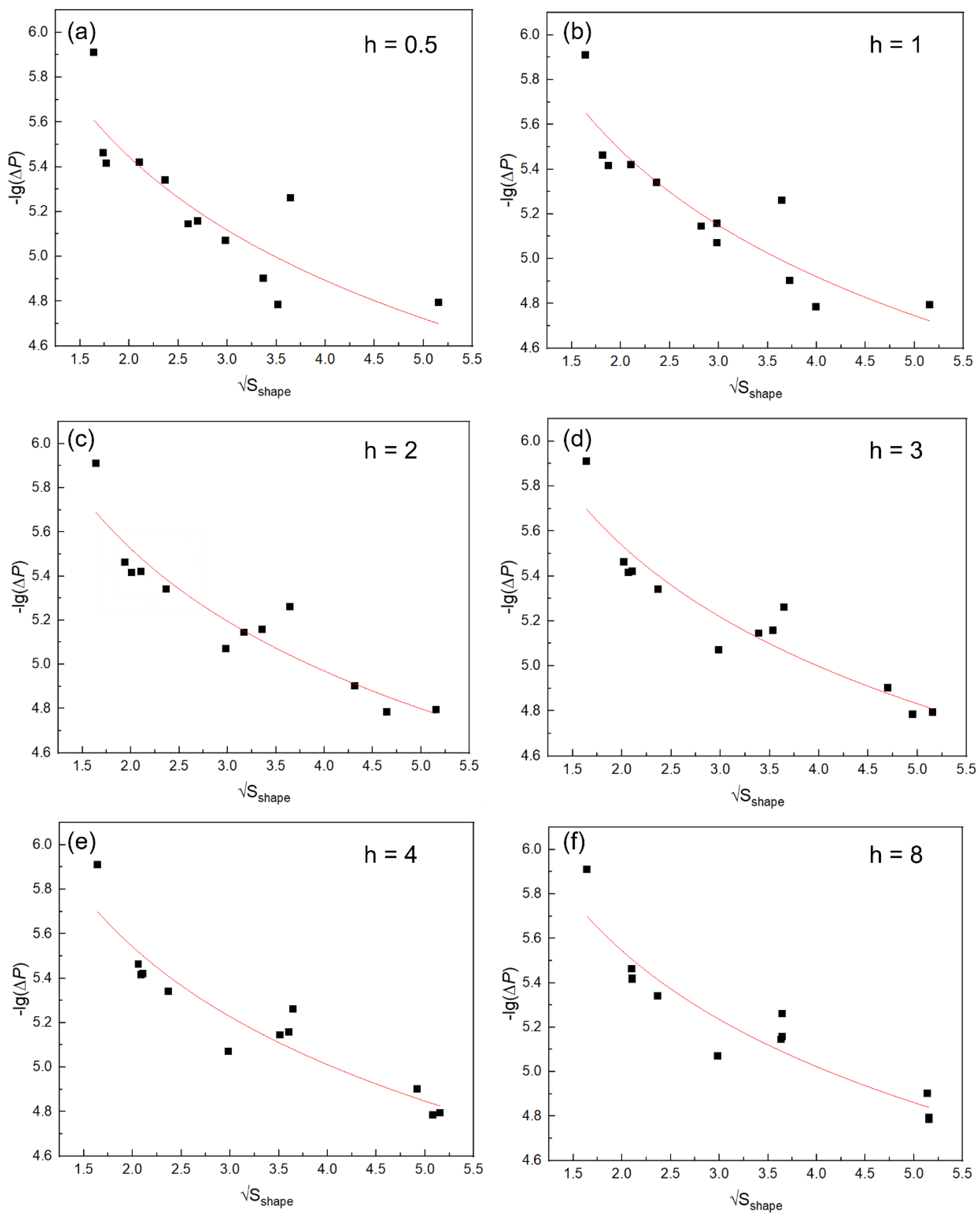
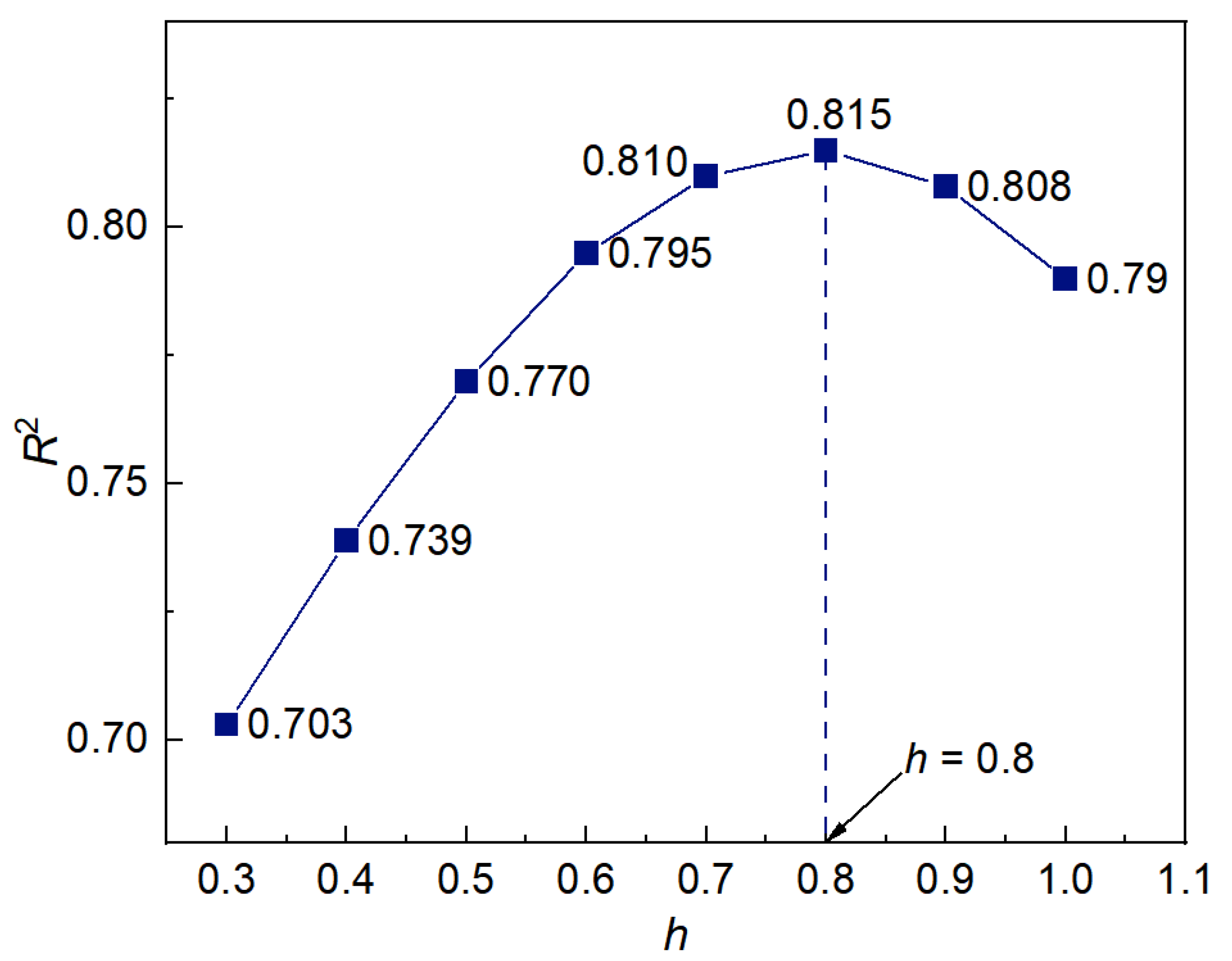
3.3.3. Validation of the Formulation of Fatigue Life concerning Inclusion Parameters
4. Conclusions
- (1)
- In this study, the effect of the shape features of inclusions on fatigue life is systematically investigated via a microstructure-based modeling approach. Based on the findings, an analytical formulation to correlate the fatigue life with the size and shape features of inclusions is proposed. This formulation extends the former fatigue equation to shape parameters (aspect ratio, A, and tilting angle, θ).
- (2)
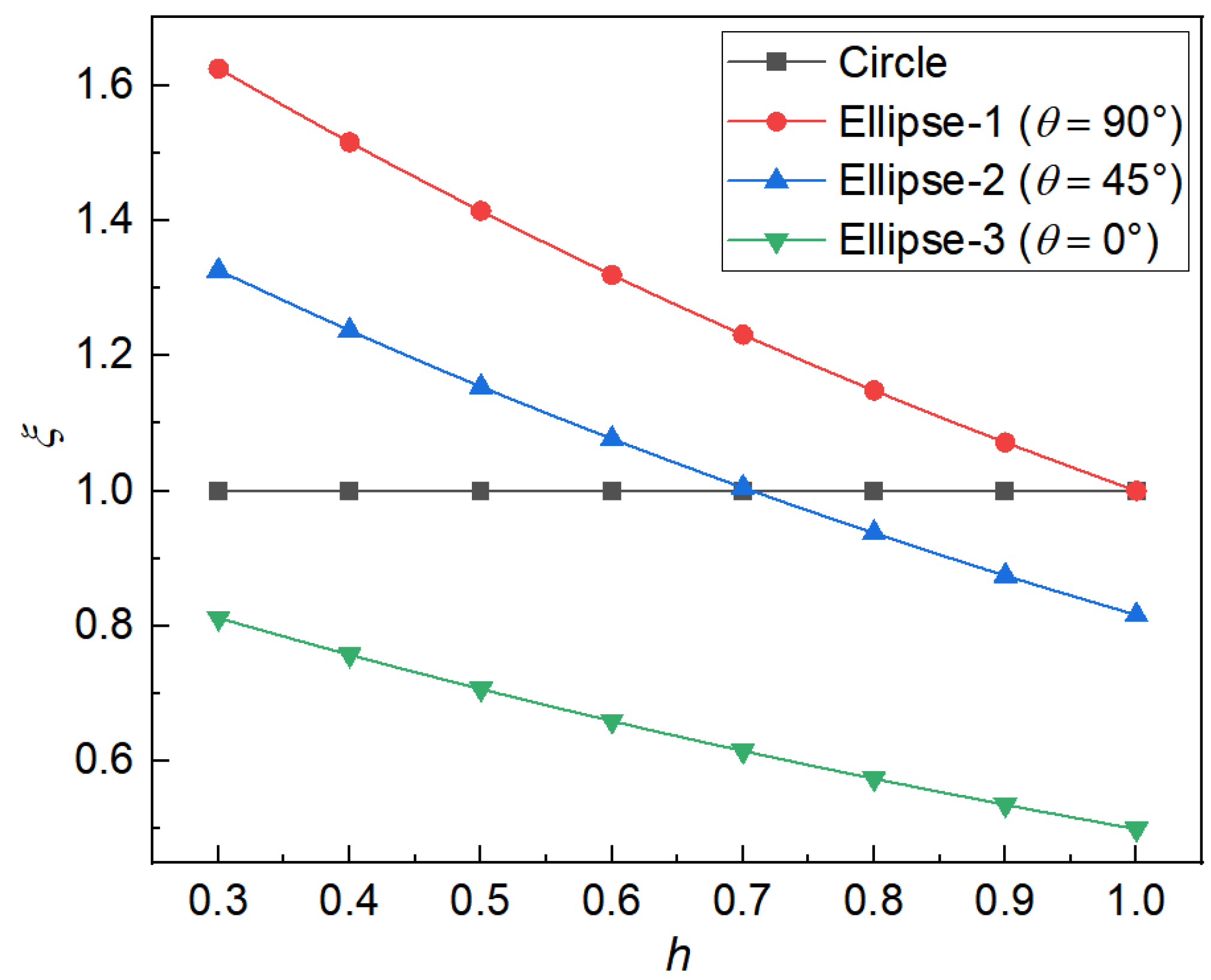
- To describe the inclusion shape, a new parameter, , which unifies the aspect ratio and tilting angle of the inclusion, is introduced. This parameter, , shows its representativeness in both the geometrical and physical sides. This new parameter and inclusion area jointly determine the equivalent inclusion area, which was adopted in the formulation of fatigue life as a single variable.
- (3)
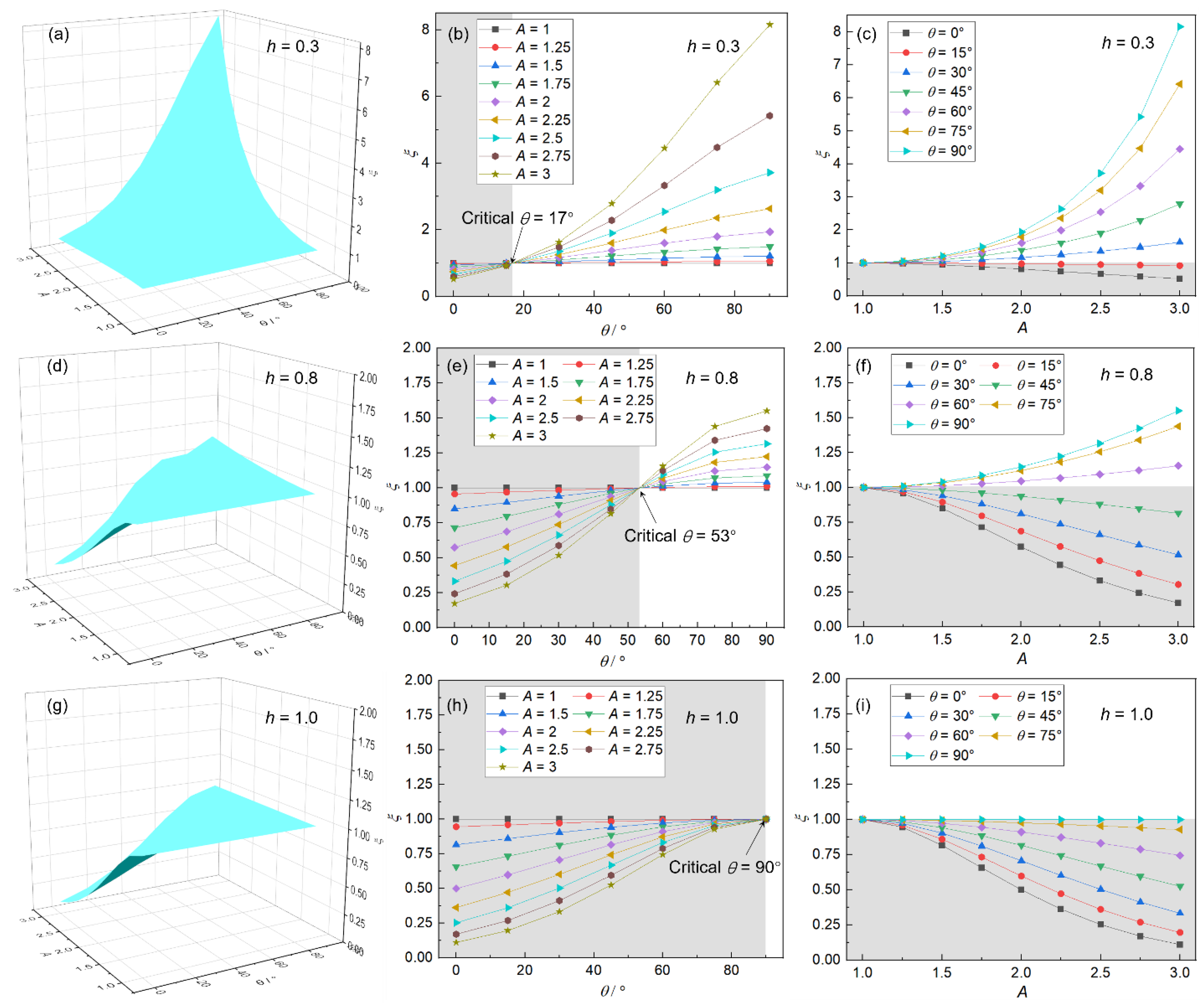
- A critical θ is also offered. When θ > 53°, the effect of inclusion on the fatigue property will increase when A increases; when θ < 53°, the effect of inclusion on the fatigue property will decrease when A increases.
- (4)
- For smaller inclusions, the value of the maximum residual stress around the inclusion is affected by the microstructure of the steel matrix around the inclusion more seriously compared with the inclusion features itself; meanwhile, for larger inclusions, the inclusion shape is more important in residual stress analysis.
- (5)
- The predicted fatigue life in this study concerning the inclusion depends on the square root of the equivalent inclusion area to the −1/26th power.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, Y.; Yang, Z.; Li, S.; Liu, Y.; Chen, S.; Hui, W.; Weng, Y. Effect of Hydrogen on Fatigue Strength of High-Strength Steels in the VHCF Regime. Adv. Eng. Mater. 2009, 11, 561–567. [Google Scholar] [CrossRef]
- Li, S.X.; Weng, Y.Q.; Hui, W.J.; Yang, Z.G. Very High Cycle Fatigue Properties of High Strength Steels-Effects of Nonmetallic Inclusions; Metallurgical Industry Press: Beijing, China, 2010. [Google Scholar]
- Gu, C.; Liu, W.-Q.; Lian, J.-h.; Bao, Y.-P. In-depth analysis of the fatigue mechanism induced by inclusions for high-strength bearing steels. Int. J. Miner. Metall. Mater. 2021, 28, 826–834. [Google Scholar] [CrossRef]
- Xiao, W.; Bao, Y.-p.; Gu, C.; Wang, M.; Liu, Y.; Huang, Y.-s.; Sun, G.-T. Ultrahigh cycle fatigue fracture mechanism of high-quality bearing steel obtained through different deoxidation methods. Int. J. Miner. Metall. Mater. 2021, 28, 804–815. [Google Scholar] [CrossRef]
- Gu, C.; Lian, J.; Bao, Y.; Münstermann, S. Microstructure-based fatigue modelling with residual stresses: Prediction of the microcrack initiation around inclusions. Mater. Sci. Eng. A 2019, 751, 133–141. [Google Scholar] [CrossRef]
- Gu, C.; Lian, J.; Bao, Y.; Xie, Q.; Münstermann, S. Microstructure based fatigue modelling with residual stresses: Prediction of the fatigue life for various inclusion sizes. Int. J. Fatigue 2019, 129, 105158. [Google Scholar] [CrossRef]
- Murakami, Y.; Yokoyama, N.; Nagata, J. Mechanism of fatigue failure in ultralong life regime. Fatigue Fract. Eng. Mater. Struct. 2002, 25, 735–746. [Google Scholar] [CrossRef]
- Murakami, Y.; Nomoto, T.; Ueda, T.; Murakami, Y. On the mechanism of fatigue failure in the superlong life regime (N > 107 cycles). Part II: A fractographic investigation. Fatigue Fract. Eng. Mater. Struct. 2000, 23, 903–910. [Google Scholar] [CrossRef]
- Murakami, Y.; Nomoto, T.; Ueda, T.; Murakami, Y. On the mechanism of fatigue failure in the superlong life regime (N > 107 cycles). Part I: Influence of hydrogen trapped by inclusions. Fatigue Fract. Eng. Mater. Struct. 2000, 23, 893–902. [Google Scholar] [CrossRef]
- Murakami, Y. Metal Fatigue: Effects of Small Defects and Nonmetallic Inclusions; Elsevier: London, UK, 2002. [Google Scholar]
- Fu, H.; Rydel, J.J.; Gola, A.M.; Yu, F.; Geng, K.; Lau, C.; Luo, H.; Rivera-Díaz-del-Castillo, P.E.J. The relationship between 100Cr6 steelmaking, inclusion microstructure and rolling contact fatigue performance. Int. J. Fatigue 2019, 129, 104899. [Google Scholar] [CrossRef]
- Gu, C.; Wang, M.; Bao, Y.; Wang, F.; Lian, J. Quantitative analysis of inclusion engineering on the fatigue property improvement of bearing steel. Metals 2019, 9, 476. [Google Scholar] [CrossRef] [Green Version]
- Karr, U.; Schuller, R.; Fitzka, M.; Schönbauer, B.; Tran, D.; Pennings, B.; Mayer, H. Influence of inclusion type on the very high cycle fatigue properties of 18Ni maraging steel. J. Mater. Sci. 2017, 52, 5954–5967. [Google Scholar] [CrossRef]
- Naragani, D.; Sangid, M.D.; Shade, P.A.; Schuren, J.C.; Sharma, H.; Park, J.-S.; Kenesei, P.; Bernier, J.V.; Turner, T.J.; Parr, I. Investigation of fatigue crack initiation from a non-metallic inclusion via high energy x-ray diffraction microscopy. Acta Mater. 2017, 137, 71–84. [Google Scholar] [CrossRef]
- Dunne, F.; Wilkinson, A.; Allen, R. Experimental and computational studies of low cycle fatigue crack nucleation in a polycrystal. Int. J. Plast. 2007, 23, 273–295. [Google Scholar] [CrossRef]
- McDowell, D.; Dunne, F. Microstructure-sensitive computational modeling of fatigue crack formation. Int. J. Fatigue 2010, 32, 1521–1542. [Google Scholar] [CrossRef]
- Lin, L.; Zeng, J.-Q. Consideration of green intelligent steel processes and narrow window stability control technology on steel quality. Int. J. Miner. Metall. Mater. 2021, 28, 1264–1273. [Google Scholar] [CrossRef]
- Wang, L.; Song, B.; Yang, Z.-B.; Cui, X.-K.; Liu, Z.; Cheng, W.-S.; Mao, J.-H. Effects of Mg and La on the evolution of inclusions and microstructure in Ca-Ti treated steel. Int. J. Miner. Metall. Mater. 2021, 28, 1940–1948. [Google Scholar] [CrossRef]
- Chu, J.; Bao, Y.; Li, X.; Gao, F.; Wang, M. Characterization of oxidation behavior of Mn fumes generated in the vacuum treatment of melting Mn steels. Steel Res. Int. 2021, 92, 2000333. [Google Scholar] [CrossRef]
- Xing, L.; Guo, J.; Li, X.; Zhang, Z.; Wang, M.; Bao, Y.; Zeng, F.; Chen, B. Control of TiN precipitation behavior in titanium-containing micro-alloyed steel. Mater. Today Commun. 2020, 25, 101292. [Google Scholar] [CrossRef]
- Gillner, K.; Henrich, M.; Münstermann, S. Numerical study of inclusion parameters and their influence on fatigue lifetime. Int. J. Fatigue 2018, 111, 70–80. [Google Scholar] [CrossRef]
- Gu, C.; Lian, J.; Bao, Y.; Xiao, W.; Münstermann, S. Numerical study of the effect of inclusions on the residual stress distribution in high-strength martensitic steels during cooling. Appl. Sci. 2019, 9, 455. [Google Scholar] [CrossRef] [Green Version]
- Lian, J.; Yang, H.; Vajragupta, N.; Münstermann, S.; Bleck, W. A method to quantitatively upscale the damage initiation of dual-phase steels under various stress states from microscale to macroscale. Comput. Mater. Sci. 2014, 94, 245–257. [Google Scholar] [CrossRef]
- Ma, Y.; Cui, Y. Study of the effect of sulfur contents on fracture toughness of railway wheel steels for high speed train. Acta Met. Sin 2011, 47, 978–983. [Google Scholar]
- Brooksbank, D.; Andrews, K.W. Tessellated stresses associated with some inclusions in steel. J. Iron Steel Inst. 1969, 207, 474–483. [Google Scholar]
- Brooksbank, D.; Andrews, K. Thermal expansion of some inclusions found in steels and relation to tessellated stresses. J. Iron Steel Inst. 1968, 206, 595–599. [Google Scholar]
- Roters, F.; Eisenlohr, P.; Hantcherli, L.; Tjahjanto, D.D.; Bieler, T.R.; Raabe, D. Overview of constitutive laws, kinematics, homogenization and multiscale methods in crystal plasticity finite-element modeling: Theory, experiments, applications. Acta Mater. 2010, 58, 1152–1211. [Google Scholar] [CrossRef]
- Xie, Q.; Van Bael, A.; An, Y.G.; Lian, J.; Sidor, J.J. Effects of the isotropic and anisotropic hardening within each grain on the evolution of the flow stress, the r-value and the deformation texture of tensile tests for AA6016 sheets. Mater. Sci. Eng. A 2018, 721, 154–164. [Google Scholar] [CrossRef]
- Xie, Q.; Lian, J.; Sidor, J.J.; Sun, F.; Yan, X.; Chen, C.; Liu, T.; Chen, W.; Yang, P.; An, K.; et al. Crystallographic orientation and spatially resolved damage in a dispersion-hardened Al alloy. Acta Mater. 2020, 193, 138–150. [Google Scholar] [CrossRef]
- Xie, Q.; Li, R.; Wang, Y.D.; Su, R.; Lian, J.; Ren, Y.; Zheng, W.; Zhou, X.; Wang, Y. The in-depth residual strain heterogeneities due to an indentation and a laser shock peening for Ti-6Al-4V titanium alloy. Mater. Sci. Eng. A 2018, 714, 140–145. [Google Scholar] [CrossRef]
- Gillner, K.; Münstermann, S. Numerically predicted high cycle fatigue properties through representative volume elements of the microstructure. Int. J. Fatigue 2017, 105, 219–234. [Google Scholar] [CrossRef]
- Sharaf, M.; Kucharczyk, P.; Vajragupta, N.; Münstermann, S.; Hartmaier, A.; Bleck, W. Modeling the microstructure influence on fatigue life variability in structural steels. Comput. Mater. Sci. 2014, 94, 258–272. [Google Scholar] [CrossRef]
- Dahl, W. Grundlagen des festigkeits- und bruchverhaltens. Materialwiss. Werkst. 1976, 7, 123–124. [Google Scholar]
- Mughrabi, H. Microstructural fatigue mechanisms: Cyclic slip irreversibility, crack initiation, non-linear elastic damage analysis. Int. J. Fatigue 2013, 57, 2–8. [Google Scholar] [CrossRef]
- Mughrabi, H. Dislocations in Fatigue. In Dislocations and Properties of Real Materials; The Institute of Metals: London, UK, 1984; pp. 244–262. [Google Scholar]
- Mughrabi, H. Cyclic slip irreversibility and fatigue life: A microstructure-based analysis. Acta Mater. 2013, 61, 1197–1203. [Google Scholar] [CrossRef]
- Manonukul, A.; Dunne, F.P.E. High- and low-cycle fatigue crack initiation using polycrystal plasticity. Proc. R. Soc. A Math. Phys. Eng. Sci. 2004, 460, 1881–1903. [Google Scholar] [CrossRef]
- Cheong, K.-S.; Busso, E.P. Effects of lattice misorientations on strain heterogeneities in FCC polycrystals. J. Mech. Phys. Solids 2006, 54, 671–689. [Google Scholar] [CrossRef]
- Boeff, M.; Hassan, H.U.; Hartmaier, A. Micromechanical modeling of fatigue crack initiation in polycrystals. J. Mater. Res. 2017, 32, 4375–4386. [Google Scholar] [CrossRef] [Green Version]
- Furuya, Y.; Hirukawa, H.; Kimura, T.; Hayaishi, M. Gigacycle fatigue properties of high-strength steels according to inclusion and ODA sizes. Metall. Mater. Trans. A 2007, 38, 1722–1730. [Google Scholar] [CrossRef]



| Inclusion Shape | Circle | Ellipse-1 | Ellipse-2 | Ellipse-3 |
|---|---|---|---|---|
| Geometry sketches of inclusions |  |  |  |  |
| Parameters | A = 1 θ: unconstrained | A = 2 θ = 90° | A = 2 θ = 45° | A = 2 θ = 0° |
| Material | Coefficient of Linear Expansion, α (10−6·°C) | Young’s Modulus, E (GPa) | Poisson’s Ratio, v |
|---|---|---|---|
| Calcium Aluminate | 5.0 | 113 | 0.23 |
| Steel Matrix | 23.0 | 206 | 0.30 |
| Constitutive Equation | |
| γa—slip rate along the slip system α; —initial slip rate; —resolved shear stress along a slip system α; —backstress on slip system α; —critical resolved shear stress on slip system α; 1/m—strain rate sensitivity factor. | |
| Calculation of Shear Stress | |
| na—normal to the slip plane; ma—slip direction; S—second Piola–Kirchhoff stress tensor. | |
| Isotropic Hardening Law | |
| —initial resolved shear stress; —latent hardening parameter; , ,—hardening parameter; —plastic slip increment of each slip system β. | |
| Kinematic Hardening | |
| G1, G2—kinematic hardening constant; —backstress tensor of slip system α. |
| C11: 193.9 GPa | C12: 94.6 GPa | C44: 92.2 GPa | γ0: 0.01 |
| 1/m: 100 | τ0: 645 MPa | G1: 100,000 MPa | G2: 2000 |
| h0: 1000 MPa | a: 1.1 |
| Circle | Ellipse-1 | Ellipse-2 | Ellipse-3 | |
|---|---|---|---|---|
| Geometry sketches of inclusions |  |  |  |  |
| A | 1 | 2 | 2 | 2 |
| θ | / | 90° | 45° | 0° |
| A − 1 | 0 | 1 | 1 | 1 |
| sinθ | / | 1 | /2 | 0 |
| sinθ × (A − 1) | 0 | 1 | /2 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, C.; Lian, J.; Lv, Z.; Bao, Y. Microstructure-Based Fatigue Modeling with Residual Stresses: Effect of Inclusion Shape on Very High Cycle Fatigue Life. Crystals 2022, 12, 200. https://doi.org/10.3390/cryst12020200
Gu C, Lian J, Lv Z, Bao Y. Microstructure-Based Fatigue Modeling with Residual Stresses: Effect of Inclusion Shape on Very High Cycle Fatigue Life. Crystals. 2022; 12(2):200. https://doi.org/10.3390/cryst12020200
Chicago/Turabian StyleGu, Chao, Junhe Lian, Ziyu Lv, and Yanping Bao. 2022. "Microstructure-Based Fatigue Modeling with Residual Stresses: Effect of Inclusion Shape on Very High Cycle Fatigue Life" Crystals 12, no. 2: 200. https://doi.org/10.3390/cryst12020200
APA StyleGu, C., Lian, J., Lv, Z., & Bao, Y. (2022). Microstructure-Based Fatigue Modeling with Residual Stresses: Effect of Inclusion Shape on Very High Cycle Fatigue Life. Crystals, 12(2), 200. https://doi.org/10.3390/cryst12020200






