A Theoretical Modeling of Adaptive Mixed CNT Bundles for High-Speed VLSI Interconnect Design
Abstract
:1. Introduction
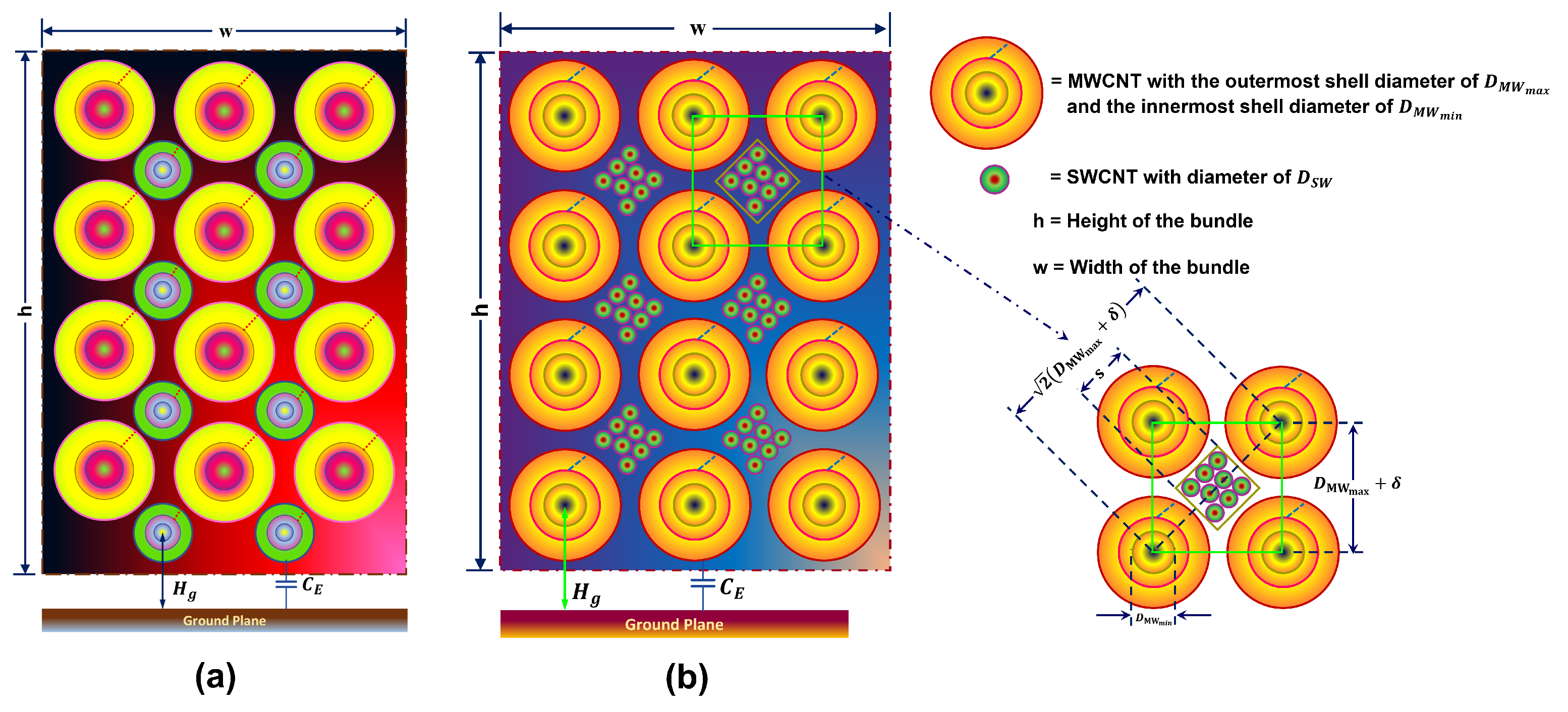
2. Modified Mixed CNT Bundle Configuration
3. Improved Mathematical Models
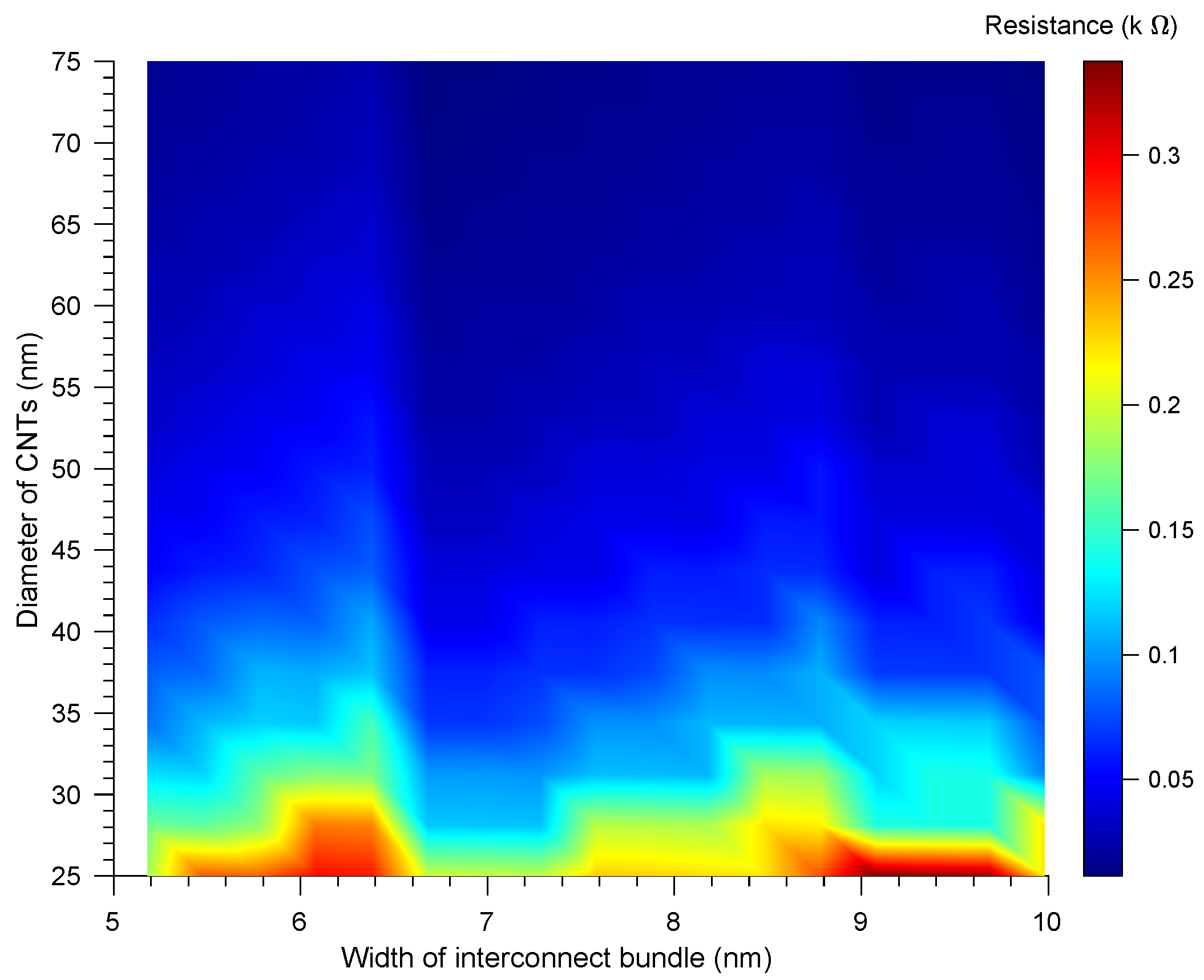
3.1. Resistance in Mixed CNT Bundle
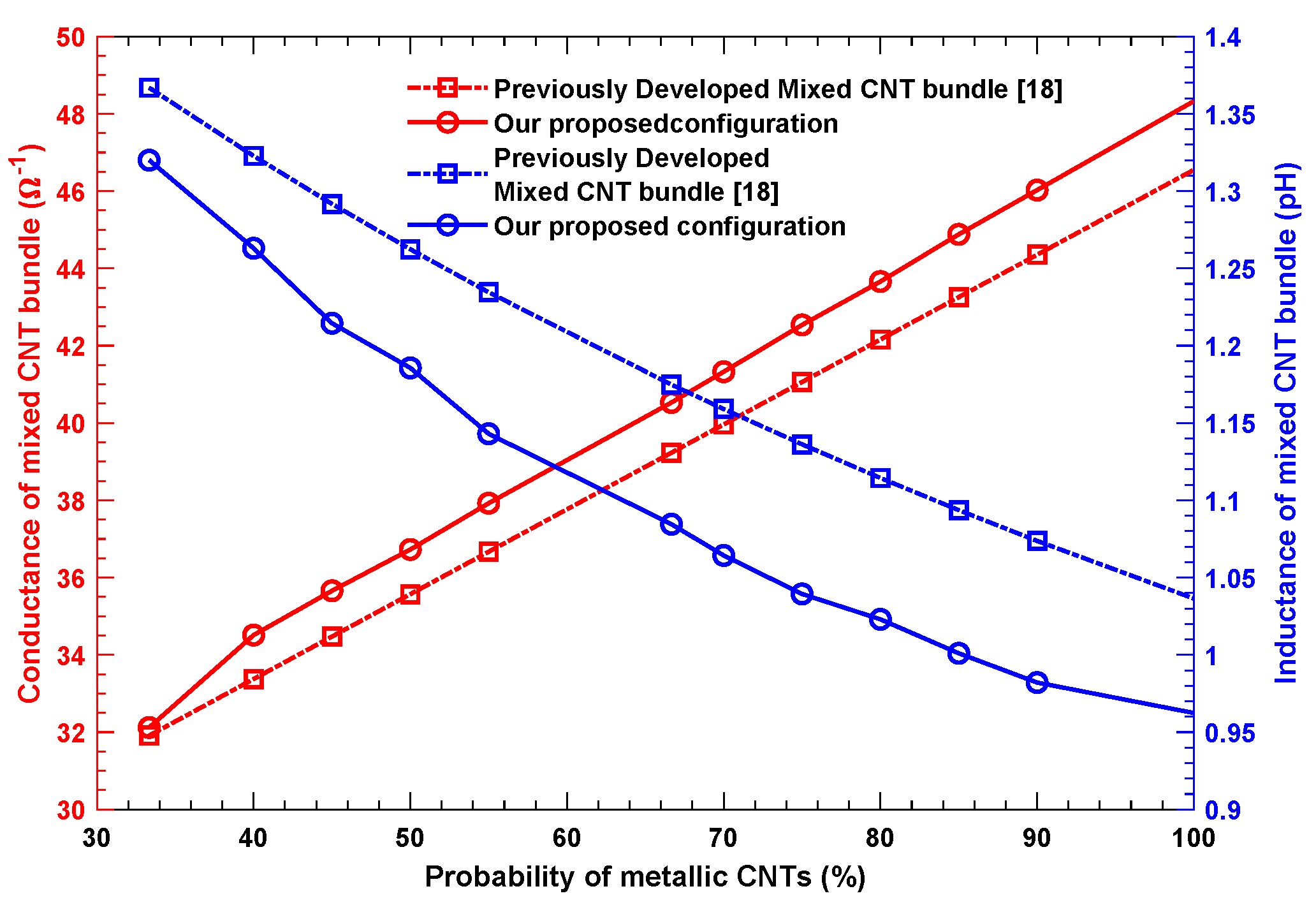
3.2. Inductance in Mixed CNT Bundle
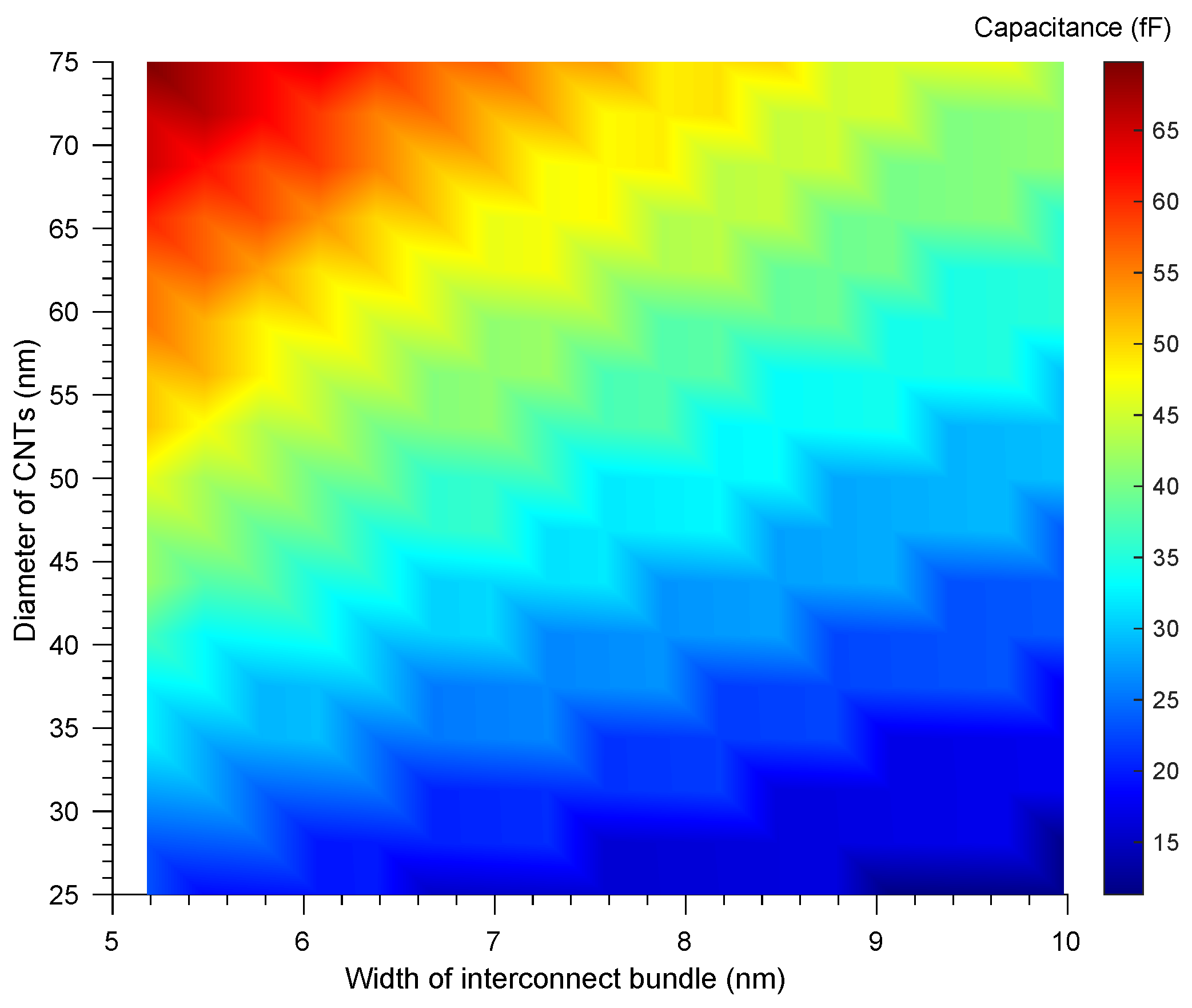
3.3. Capacitance in Mixed CNT Bundle
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, H.; Yin, W.Y.; Banerjee, K.; Mao, J.F. Circuit modeling and performance analysis of multi-walled carbon nanotube interconnects. IEEE Trans. Electron Devices 2008, 55, 1328–1337. [Google Scholar] [CrossRef] [Green Version]
- Kabir, M.S. Controlled Growth of a Nanostructure on a Substrate, and Electron Emission Devices Based on the Same. U.S. Patent 7,977,761, 12 July 2011. [Google Scholar]
- Liew, K.; Wong, C.; He, X.; Tan, M. Thermal stability of single and multi-walled carbon nanotubes. Phys. Rev. B 2005, 71, 075424. [Google Scholar] [CrossRef]
- Kaushik, B.K.; Majumder, M.K. Carbon Nanotube Based VLSI Interconnects: Analysis and Design; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Pu, S.; Yin, W.; Mao, J.; Liu, Q.H. Crosstalk Prediction of Single- and Double-Walled Carbon-Nanotube (SWCNT/DWCNT) Bundle Interconnects. IEEE Trans. Electron Devices 2009, 56, 560–568. [Google Scholar] [CrossRef]
- Subash, S.; Kolar, J.; Chowdhury, M.H. A new spatially rearranged bundle of mixed carbon nanotubes as VLSI interconnection. IEEE Trans. Nanotechnol. 2011, 12, 3–12. [Google Scholar] [CrossRef]
- Kim, S.; Kulkarni, D.D.; Rykaczewski, K.; Henry, M.; Tsukruk, V.V.; Fedorov, A.G. Fabrication of an ultralow-resistance ohmic contact to MWCNT–metal interconnect using graphitic carbon by electron beam-induced deposition (EBID). IEEE Trans. Nanotechnol. 2012, 11, 1223–1230. [Google Scholar] [CrossRef]
- Amin, A.B.; Ullah, M.S. Mathematical Framework of Tetramorphic MWCNT Configuration for VLSI Interconnect. IEEE Trans. Nanotechnol. 2020, 19, 749–759. [Google Scholar] [CrossRef]
- Majumder, M.K.; Kaushik, B.K.; Manhas, S.K. Analysis of delay and dynamic crosstalk in bundled carbon nanotube interconnects. IEEE Trans. Electromagn. Compat. 2014, 56, 1666–1673. [Google Scholar] [CrossRef]
- Rai, M.K.; Garg, H.; Kaushik, B. Temperature-dependent modeling and crosstalk analysis in mixed carbon nanotube bundle interconnects. J. Electron. Mater. 2017, 46, 5324–5337. [Google Scholar] [CrossRef]
- Sharma, M.; Rai, M.K.; Khanna, R. Temperature-dependent crosstalk and frequency spectrum analyses in adjacent interconnects of a mixed CNT bundle. J. Comput. Electron. 2020, 19, 177–190. [Google Scholar] [CrossRef]
- Sandha, K.S.; Thakur, A. Comparative Analysis of Mixed CNTs and MWCNTs as VLSI Interconnects for Deep Sub-micron Technology Nodes. J. Electron. Mater. 2019, 48, 2543–2554. [Google Scholar] [CrossRef]
- Kahng, A.B.; Muddu, S. An analytical delay model for RLC interconnects. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 1997, 16, 1507–1514. [Google Scholar] [CrossRef] [Green Version]
- Ullah, M.S.; Chowdhury, M.H. Analytical models of high-speed RLC interconnect delay for complex and real poles. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2017, 25, 1831–1841. [Google Scholar] [CrossRef]
- Sanaullah, M.; Chowdhury, M.H. Analysis of RLC interconnect delay model using second order approximation. In Proceedings of the 2014 IEEE International Symposium on Circuits and Systems (ISCAS), Melbourne, VIC, Australia, 1–5 June 2014; pp. 2756–2759. [Google Scholar] [CrossRef]
- Sanaullah, M.; Chowdhury, M.H. A new real pole delay model for RLC interconnect using second order approximation. In Proceedings of the 2014 IEEE 57th International Midwest Symposium on Circuits and Systems (MWSCAS), College Station, TX, USA, 3–6 August 2014; pp. 238–241. [Google Scholar] [CrossRef]
- Amin, A.B.; Ullah, M.S. Performance Analysis of Squarely Packed Dimorphic MWCNT Bundle for High Speed VLSI Interconnect. In Proceedings of the 2020 IEEE Canadian Conference on Electrical and Computer Engineering (CCECE), London, ON, Canada, 30 August–2 September 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Subash, S.; Chowdhury, M.H. Mixed carbon nanotube bundles for interconnect applications. Int. J. Electron. 2009, 96, 657–671. [Google Scholar] [CrossRef]
- Li, H.; Lu, W.; Li, J.; Bai, X.; Gu, C. Multichannel ballistic transport in multiwall carbon nanotubes. Phys. Rev. Lett. 2005, 95, 086601. [Google Scholar] [CrossRef] [Green Version]
- Naeemi, A.; Meindl, J.D. Compact physical models for multiwall carbon-nanotube interconnects. IEEE Electron Device Lett. 2006, 27, 338–340. [Google Scholar] [CrossRef]
- Amin, A.B.; Ullah, M.S. Performance Analysis of Squarely Packed Polymorphic SWCNT Interconnect. In Proceedings of the 2019 IEEE 10th Annual Ubiquitous Computing, Electronics Mobile Communication Conference (UEMCON), New York, NY, USA, 10–12 October 2019; pp. 1199–1203. [Google Scholar] [CrossRef]
- Naeemi, A.; Meindl, J.D. Physical modeling of temperature coefficient of resistance for single-and multi-wall carbon nanotube interconnects. IEEE Electron Device Lett. 2007, 28, 135–138. [Google Scholar] [CrossRef]
- Das, D.; Rahaman, H. Analysis of crosstalk in single-and multiwall carbon nanotube interconnects and its impact on gate oxide reliability. IEEE Trans. Nanotechnol. 2011, 10, 1362–1370. [Google Scholar] [CrossRef]
- Majumder, M.K.; Das, P.K.; Kaushik, B.K. Delay and crosstalk reliability issues in mixed MWCNT bundle interconnects. Microelectron. Reliab. 2014, 54, 2570–2577. [Google Scholar] [CrossRef]
- Srivastava, N.; Li, H.; Kreupl, F.; Banerjee, K. On the applicability of single-walled carbon nanotubes as VLSI interconnects. IEEE Trans. Nanotechnol. 2009, 8, 542–559. [Google Scholar] [CrossRef]
- Sahoo, M.; Ghosal, P.; Rahaman, H. Modeling and analysis of crosstalk induced effects in multiwalled carbon nanotube bundle interconnects: An ABCD parameter-based approach. IEEE Trans. Nanotechnol. 2015, 14, 259–274. [Google Scholar] [CrossRef]
- Sarto, M.S.; Tamburrano, A. Single-conductor transmission-line model of multiwall carbon nanotubes. IEEE Trans. Nanotechnol. 2009, 9, 82–92. [Google Scholar] [CrossRef]
- Banerjee, K.; Srivastava, N. Are carbon nanotubes the future of VLSI interconnections? In Proceedings of the 43rd annual Design Automation Conference, San Francisco, CA, USA, 24–28 July 2006; pp. 809–814. [Google Scholar]

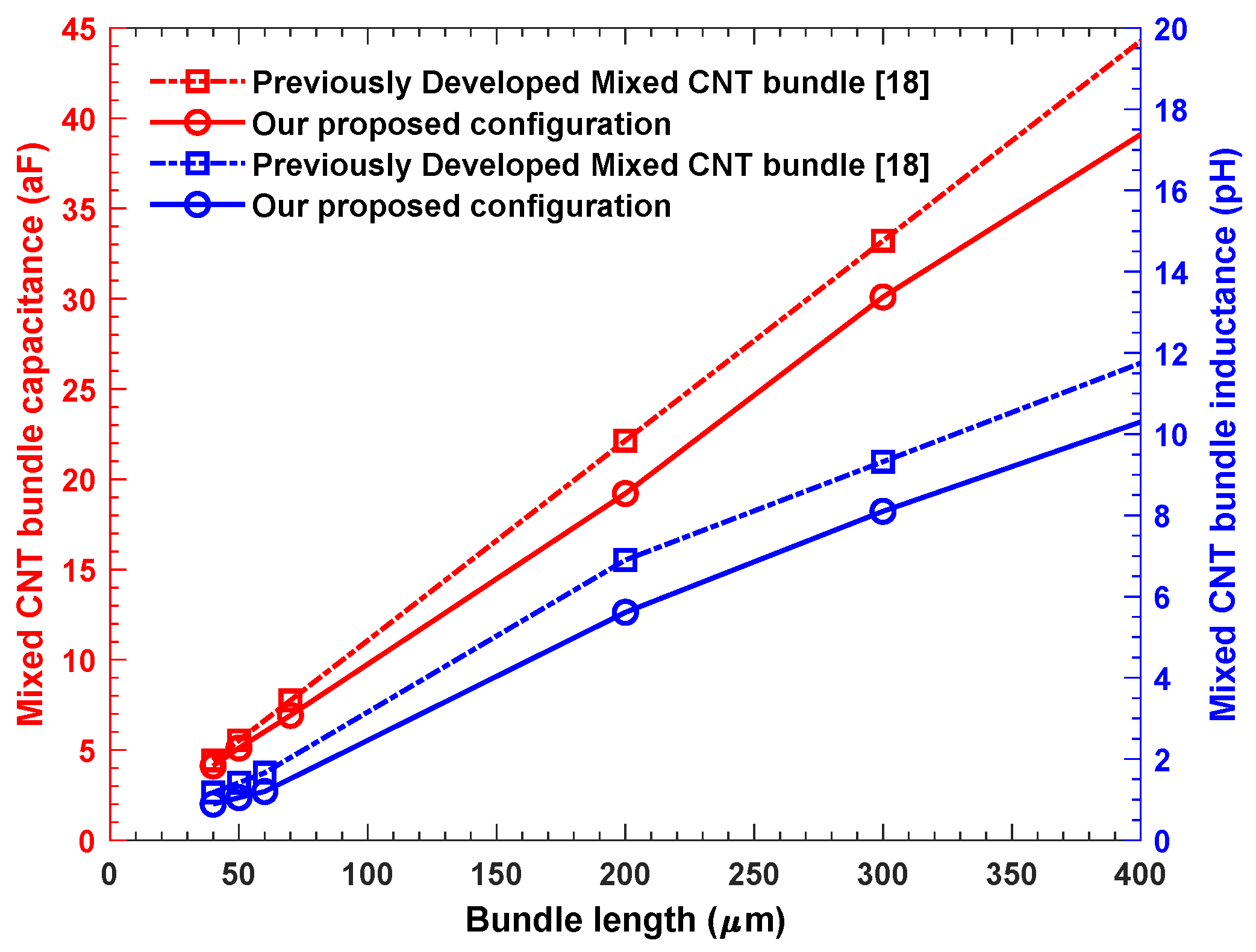
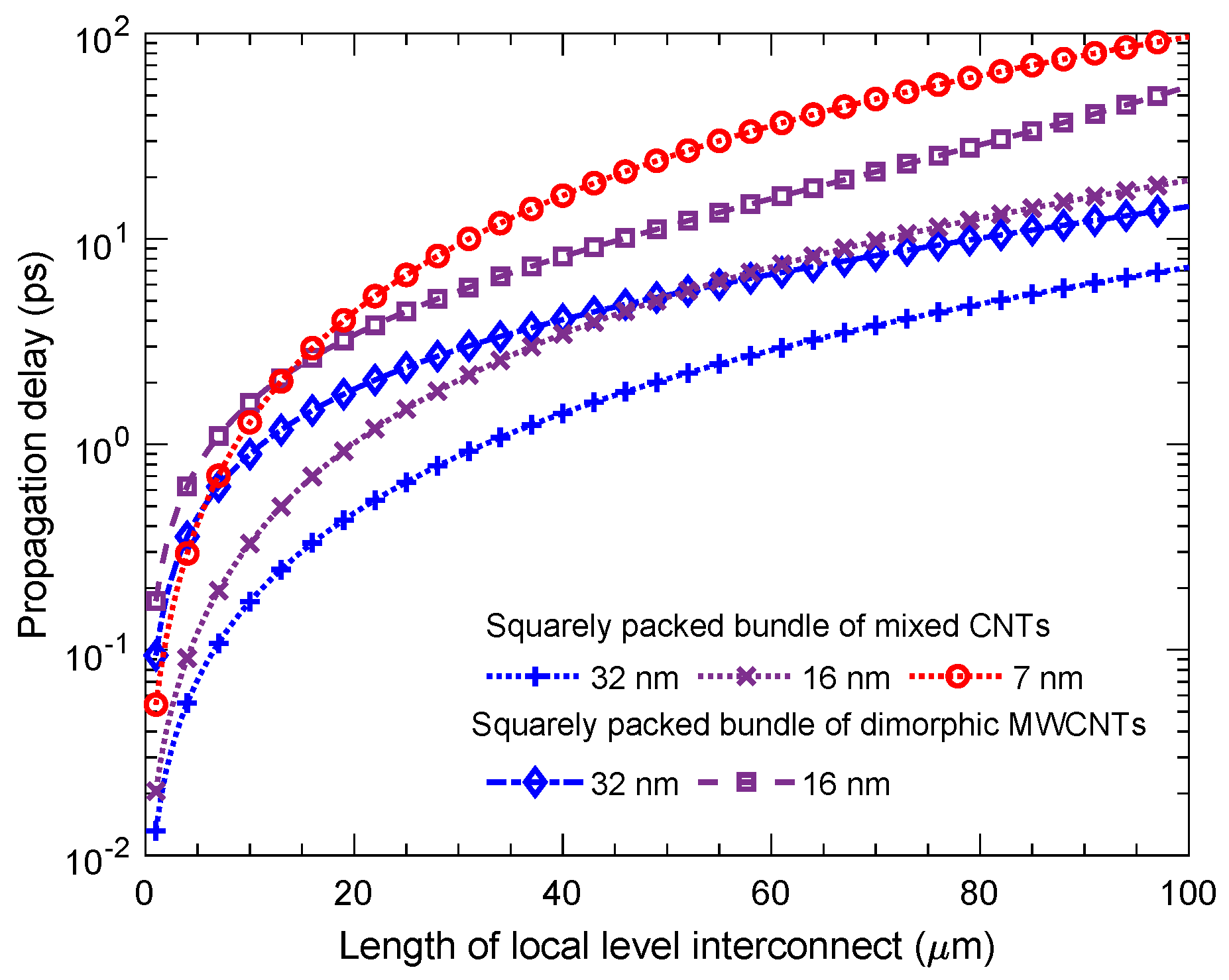
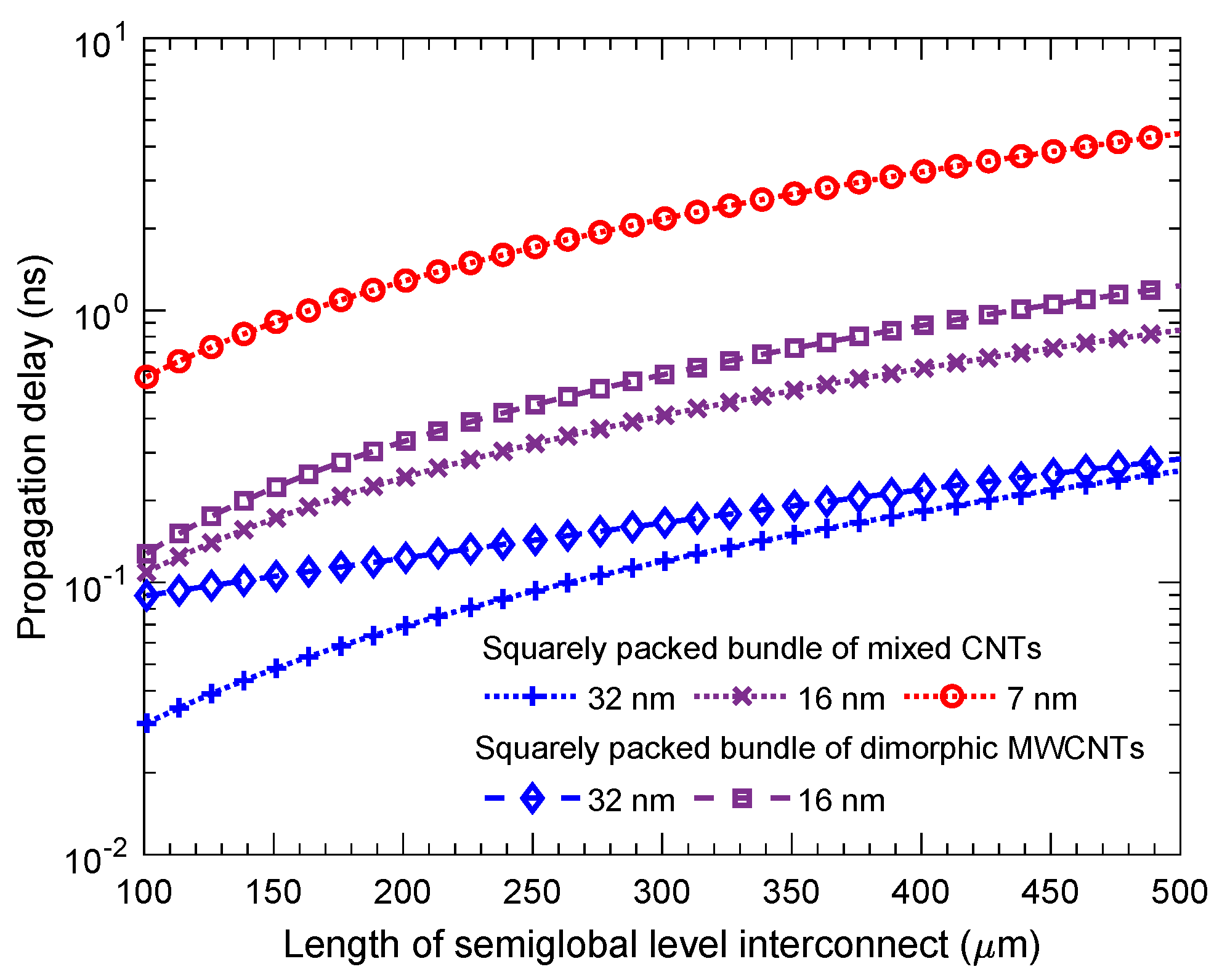
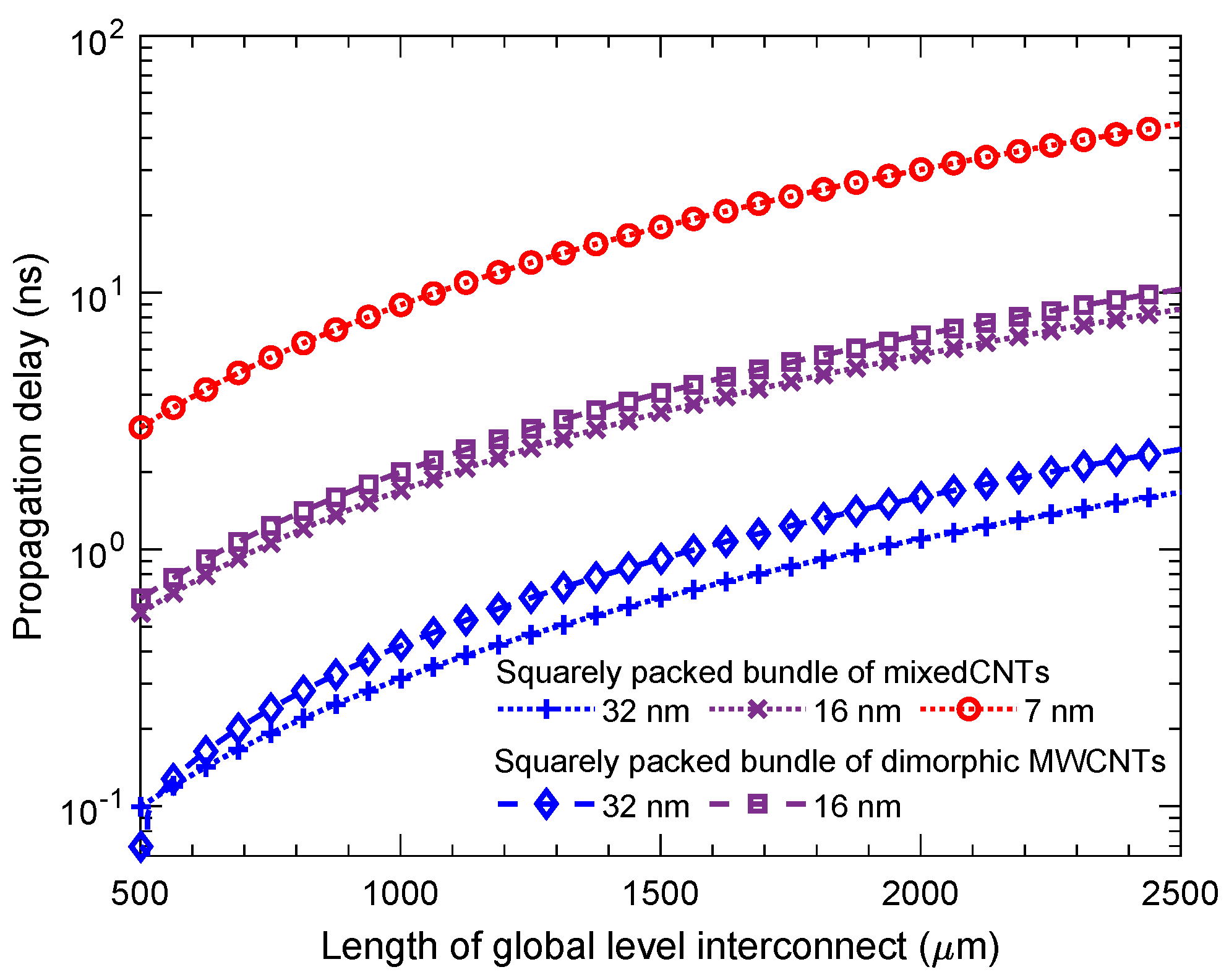
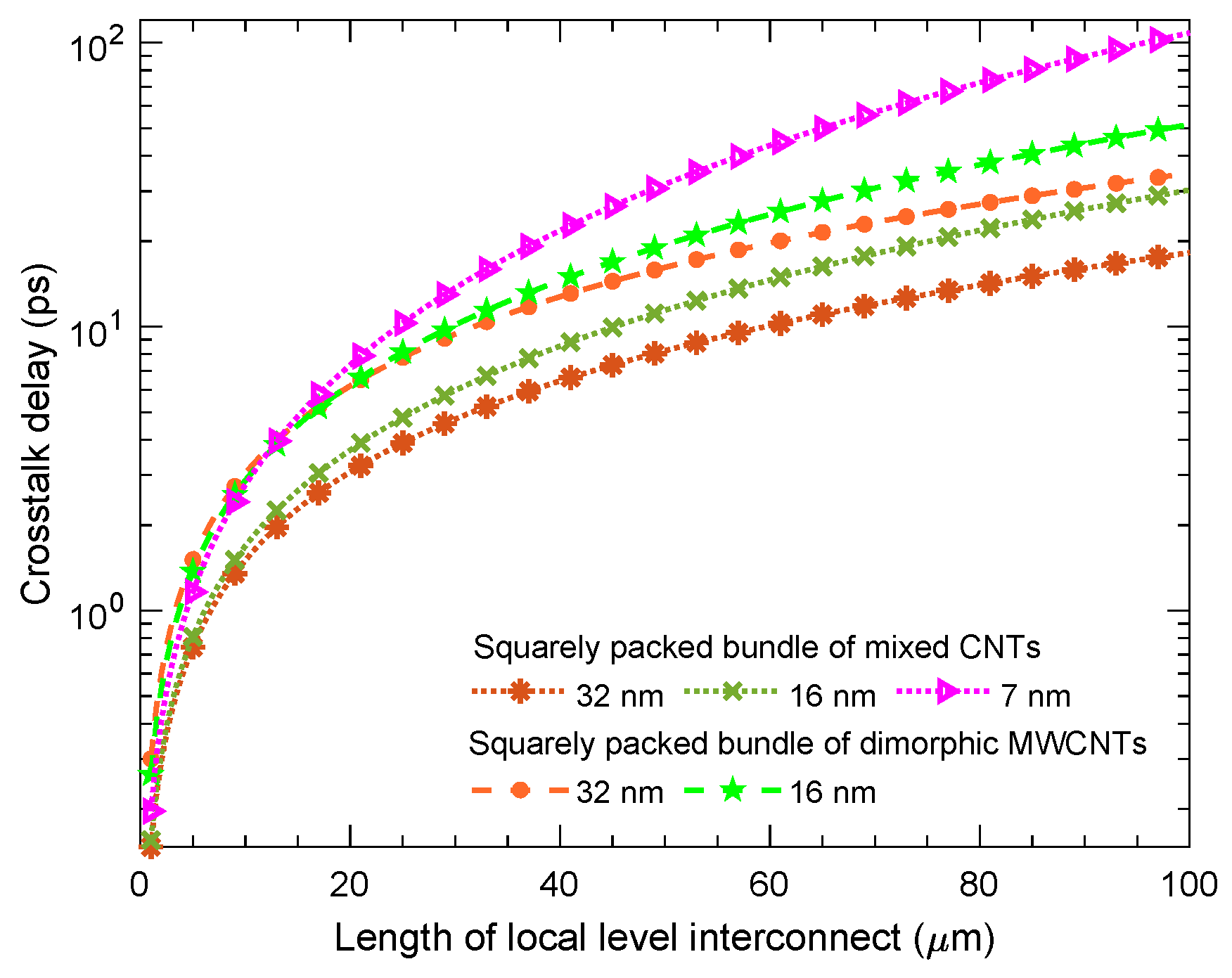
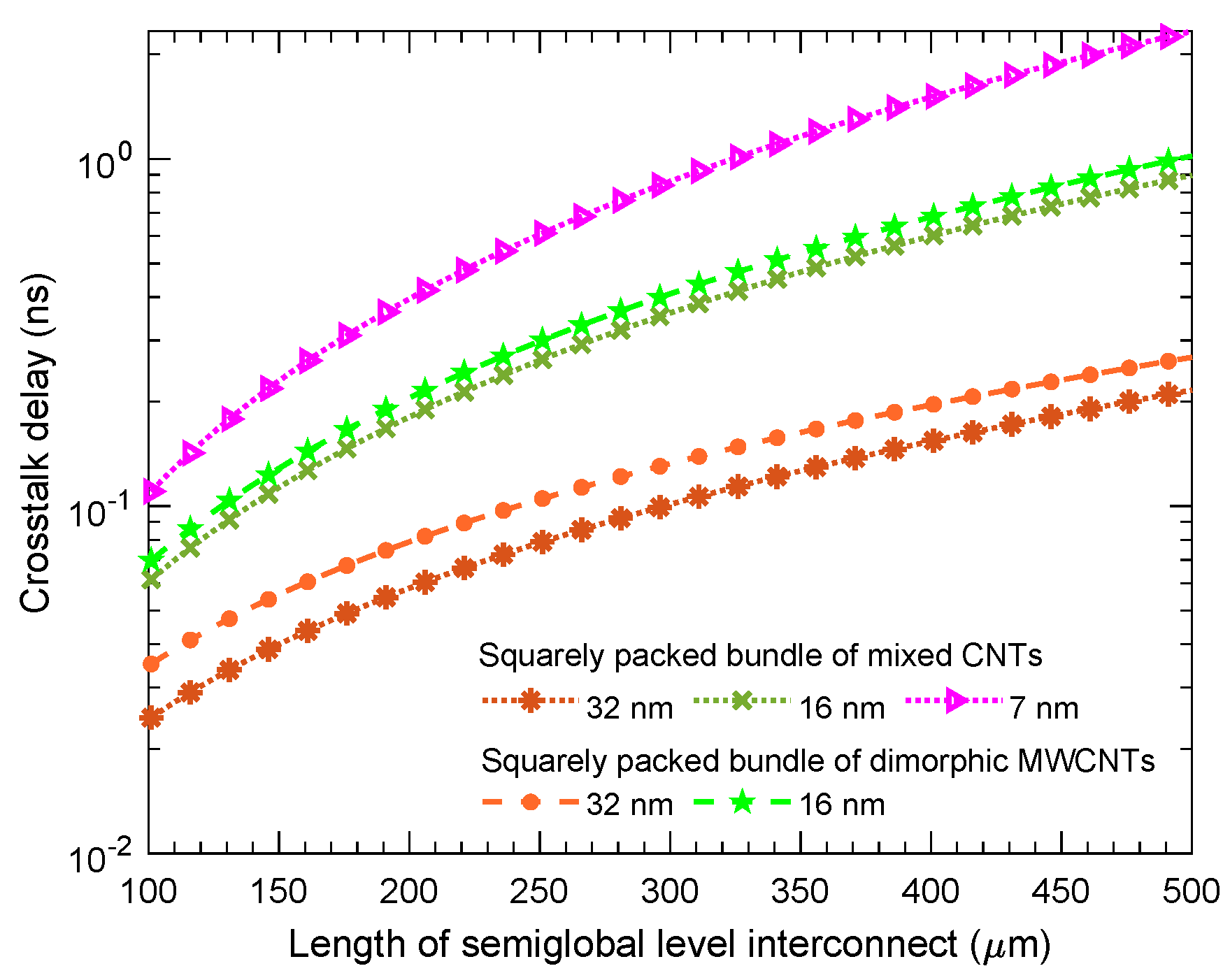
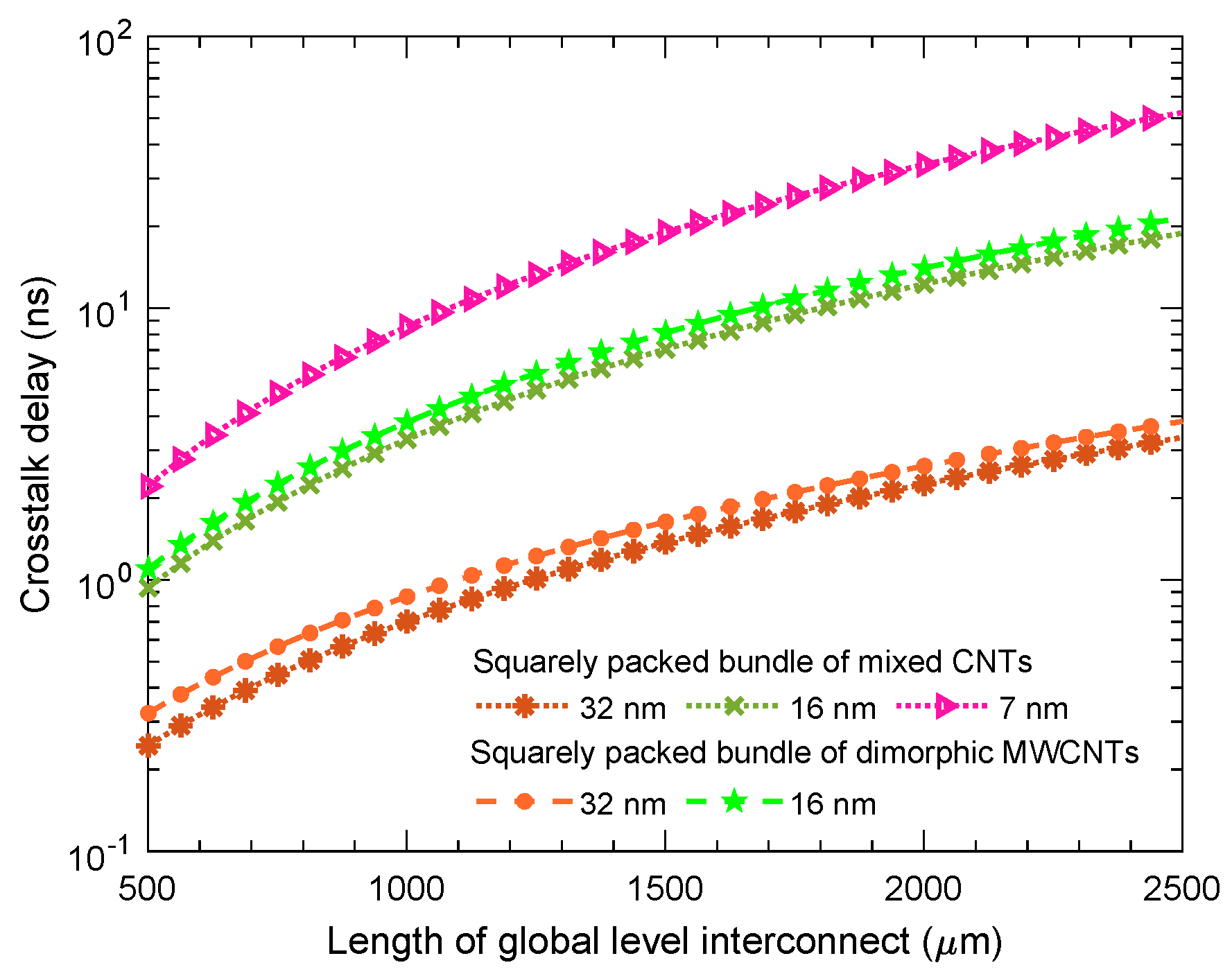
| Interconnect Length (m) | Technology Node (nm) | Squarely Packed Dimorphic | Squarely Packed Mixed | ||||||
|---|---|---|---|---|---|---|---|---|---|
(nm) | (nm) | (nm) | (nm) | ||||||
| Local (0–100) | 32 | 10 | 32 | 4.31 | 21 | 10 | 21 | 1 | 96 |
| 16 | 8.5 | 8 | 3.72 | 3 | 8.5 | 8 | 1 | 15 | |
| 7 | - | - | - | - | 4.5 | 3 | 1 | 8 | |
| Semiglobal (101–500) | 32 | 10 | 32 | 4.31 | 21 | 10 | 21 | 1 | 96 |
| 16 | 8.5 | 8 | 3.72 | 3 | 8.5 | 8 | 1 | 15 | |
| 7 | - | - | - | - | 4.5 | 3 | 1 | 8 | |
| Global (501–2500) | 32 | 10 | 48 | 4.31 | 33 | 10 | 33 | 1 | 160 |
| 16 | 8.5 | 14 | 3.72 | 6 | 8.5 | 12 | 1 | 25 | |
| 7 | - | - | - | - | 4.5 | 12 | 1 | 5 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amin, A.B.; Shakil, S.M.; Ullah, M.S. A Theoretical Modeling of Adaptive Mixed CNT Bundles for High-Speed VLSI Interconnect Design. Crystals 2022, 12, 186. https://doi.org/10.3390/cryst12020186
Amin AB, Shakil SM, Ullah MS. A Theoretical Modeling of Adaptive Mixed CNT Bundles for High-Speed VLSI Interconnect Design. Crystals. 2022; 12(2):186. https://doi.org/10.3390/cryst12020186
Chicago/Turabian StyleAmin, Abu Bony, Syed Muhammad Shakil, and Muhammad Sana Ullah. 2022. "A Theoretical Modeling of Adaptive Mixed CNT Bundles for High-Speed VLSI Interconnect Design" Crystals 12, no. 2: 186. https://doi.org/10.3390/cryst12020186
APA StyleAmin, A. B., Shakil, S. M., & Ullah, M. S. (2022). A Theoretical Modeling of Adaptive Mixed CNT Bundles for High-Speed VLSI Interconnect Design. Crystals, 12(2), 186. https://doi.org/10.3390/cryst12020186








