1. Introduction
Rare-earth tritellurides (RTe
) are layered materials that have been widely studied due to the numerous quantum states they exhibit, including charge density waves, magnetic ordering, and superconductivity. In particular, scientists have been interested in the charge density wave (CDW) states of RTe
and how CDW states interact and coexist with other quantum states [
1]. While other materials exhibit all these quantum states, heightened interest in RTe
stems from the fact that their properties can be tuned through the application of pressure [
2], varying the rare-earth ion, and intercalation of guest atoms [
3] or molecules [
4] in the gaps between Te layers. These gaps are referred to as Van der Waals (VdW) gaps because the layers are weakly bound together with Van der Waals forces [
5], similar to graphite. In this work, we report first-principles calculations of the magnetic and optical properties of some representative rare-earth tritellurides (ErTe
and SmTe
) and ditellurides (ErTe
and SmTe
).
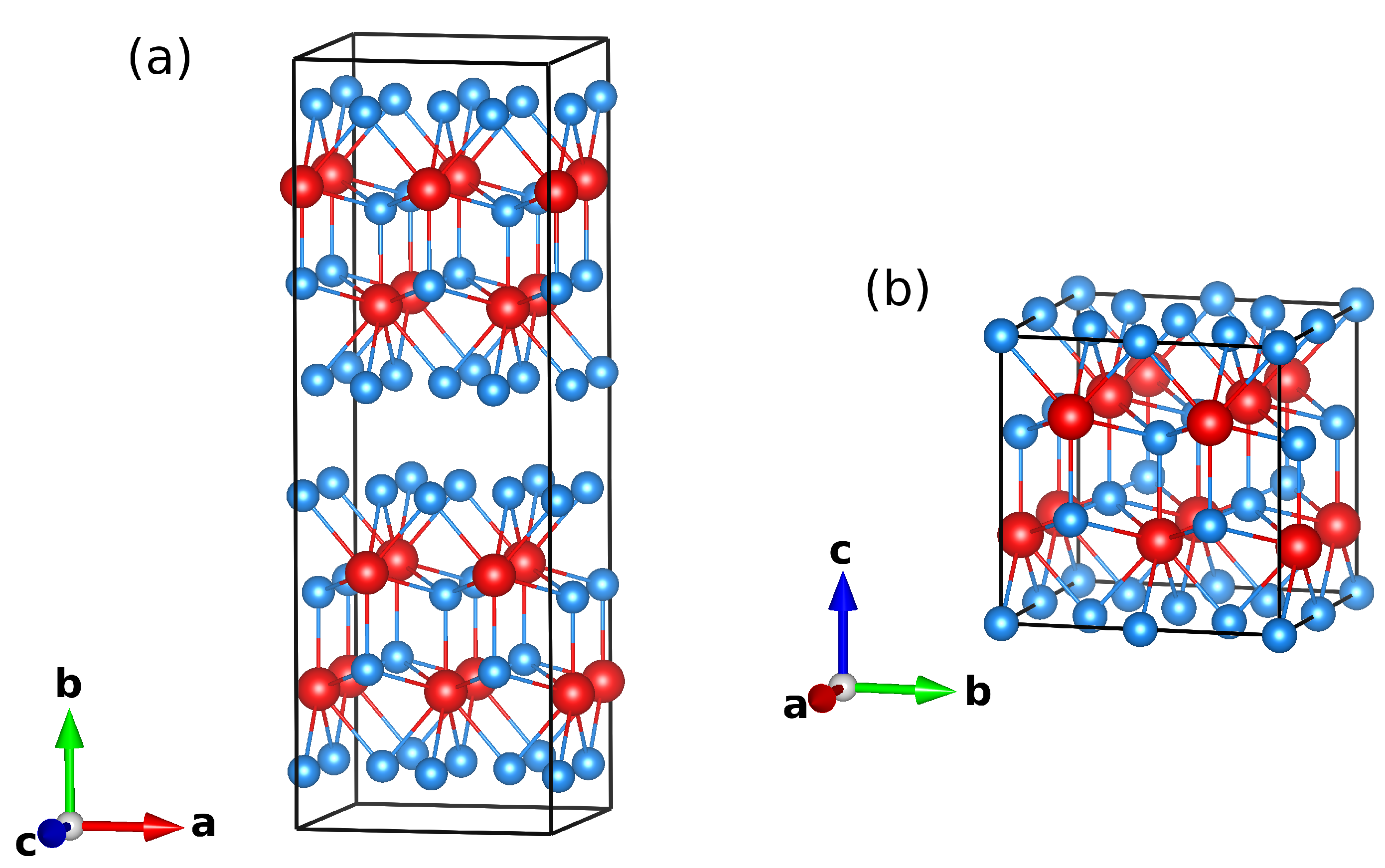
RTe
(space group 63: Cmcm) has a weakly orthorhombic structure [
6], meaning two lattice parameters are nearly equal (a ≈ c ≠ b, where b is perpendicular to the layers), with double layers of square Te sheets (sometimes referred to as tellurene). The VdW gap occurs in the space between the two Te layers, which make up the double layer. These Te double layers alternate with double layers of rare-earth telluride (RTe). These two RTe layers can also be viewed as four square layers of a single atom type. From lowest to highest (see
Figure 1a), these layers are RE, Te, Te, and RE. However, the distance between the first and second (or third and fourth) layer is very small, typically less than 1 Å, so they are conventionally viewed as a single puckered layer [
7]. In these puckered layers, one RE lies at the center of four nearest neighbor Te ions. As can be seen in
Figure 1a, the unit cell of RTe
has two blocks. The first block consists of an RTe double-layer sandwiched between two Te layers, while the second block is obtained from the first by a translation with the vector
.
A closely related group of materials are the tetragonal rare-earth ditellurides (RTe
). RTe
(see
Figure 1b) also contains RTe double layers with a structure similar to that in RTe
, but these alternate with single layers of square Te, so that there is no VdW gap [
8]. In RTe
, the long axis, perpendicular to the layers, is conventionally taken as c, while in RTe
it is b.
Conduction of electrons in RTe
occurs mainly in the square Te layers of rare-earth tellurides, while the puckered RTe layers do not significantly contribute to the conductivity [
9]. This motivated a 2d tight-binding model of the electronic band structure, incorporating the
and
orbitals of Te [
10,
11]. The Fermi surface produced by this model is very similar to that measured using angle-resolved photoemission spectroscopy (measured for R = La, Ce, Sm, Gd, Tb, and Dy) [
12] and those calculated for LaTe
using density functional theory (DFT) [
13]. This same tight-binding model has also been applied to RTe
[
14], giving somewhat reasonable agreement with ARPES measurements in LaTe
and CeTe
[
15]. Some evidence that this model may be appropriate was provided when resistivity measurements showed that CeTe
was metallic in the plane of the layers and semiconducting perpendicular to the layers [
16].
Most rare-earth atoms have unpaired, highly localized 4f electrons, indicating that crystals containing them are likely to have a ferromagnetic or antiferromagnetic ground state. Antiferromagnetism (AFM) occurs when the spins of the magnetic atoms in a material exhibit a regular pattern, but the total magnetic moment adds up to zero, even within a very small volume of the crystal. Unlike ferromagnetism, AFM can lead to several possible arrangements of spin. The long range magnetic orders of RTe
were investigated by Ru et al. [
17] using magnetic susceptibility and specific heat measurements above 1.8 K for various RTe
compounds. All RTe
compounds, except those with R = La, Pr, Er, and Tm, were found to exhibit AFM below a maximum Neel temperature (the temperature at which an AFM transition takes place) of about 11 K. La is nonmagnetic, while previous work suggests PrTe
has a singlet ground state [
18]. The remaining structures, ErTe
and TmTe
, may have an AFM ground state with a Neel temperature below 1.8 K. AFM states have also been observed for GdTe
below 9.8 K [
19] and CeTe
below 4 K [
20], while PrTe
and LaTe
again were found to be nonmagnetic. The magnetic and electronic properties of GdTe
have also been investigated using the VASP DFT code, which confirmed an AFM ground state [
21]. The electronic band structures of LaTe
and NdTe
have been calculated [
22] using the Quantum Espresso DFT code, while those of YTe
were calculated [
3] with VASP. Both VASP [
23] and Quantum Espresso [
24] use plane waves to expand the wave function of valence electrons, and a pseudopotential to represent the interaction of the valence electrons with core electrons.
Rare-earth tellurides are uniaxial anisotropic materials, meaning symmetry is broken along one of the crystal axes. The interactions of these materials with light depend on the direction of the incident light. This causes the dielectric constant to become a dielectric tensor. Since rare-earth telluride crystals are either tetragonal (RTe
) or almost tetragonal (RTe
), the dielectric tensor can be fully described by two components, namely
and
, where the principal axis is assumed to be along the z-direction. The dielectric function depends on the frequency of incoming light; the dispersion equation relating the dielectric function components, frequency of light, and wave vectors for uniaxial materials is:
where
, and
are the wave vector components along the
x-,
y-, and
z-axes, respectively. For many materials, this equation implies ellipsoidal surfaces of constant frequency in k-space. However, if one of the dielectric function components,
or
, is negative while the other component is positive, the isofrequency surfaces become hyperboloids, which are unbounded surfaces in k-space. This means that, in theory, the wave vector can become arbitrarily large in these materials [
25]. This has led to research in a number of exciting applications, such as sub-diffraction-limit imaging [
26], spontaneous emission engineering [
27], and thermal emission engineering [
28].
To understand this phenomenon and its application to RTe, we must ask under what circumstances does a material become hyperbolic? A critical feature of a metal is that its dielectric function is negative for some range of frequencies. So the requirement that either
or
become negative implies that the material must act as a metal in one or two directions, but as a dielectric in the other one or two. One way to accomplish this is by stacking an alternating sequence of metal and dielectric layers. The layers should have a thickness much smaller than the wavelengths of light under consideration, so that the composite material (known as metamaterial) is approximately homogeneous. In this configuration, the material is metallic in the plane of the layers, but not perpendicular to it. This is referred to as a multilayer hyperbolic metamaterial (HMM). Since the material is metallic in two directions, it produces a hyperboloid of one sheet in k-space, referred to as a type 1 HMM. Another option is to take conducting nanowires and insulate them from each other by embedding them in dielectric [
29]. Clearly, this makes the material metallic only in the direction along the nanowires. This produces a hyperboloid of two sheets in k-space, which makes it a type 2 HMM (see
Figure 2).
Not all hyperbolic materials need to be engineered in this way. It turns out that there are a number of naturally-occurring materials that meet the requirements for hyperbolic dispersion, including graphite, cuprates, ruthenates, bismuth, sapphire, and hexagonal boron nitride [
30]. Graphite, for instance, is a layered material that is known to be able to conduct electrons within the plane of its graphene sheets, but this conduction cannot occur between the layers, because the electrons cannot easily jump across the VdW gap. These are exactly the conditions required for hyperbolic dispersion, and in fact, graphite is hyperbolic for a small range of frequencies in the ultraviolet regime [
31]. Cuprates are known to conduct electrons within their copper oxide planes, but not between the planes and, therefore, not in the direction perpendicular to these planes, making them give hyperbolic dispersion [
32]. Most of the naturally-occurring hyperbolic materials exhibit hyperbolic behavior in the infrared region [
33]. The layered structure of rare-earth tellurides, with conducting tellurium layers separated by nonconducting layers, makes them possible candidates for displaying optical hyperbolic behavior.
The optical properties of RTe
(with R = La, Ce, Nd, Sm, Gd, Tb, Dy) and RTe
(with R = La, Ce) have been investigated through reflectivity measurements by Sacchetti and Lavagnini [
9,
34,
35,
36]. These measurements were primarily concerned with investigating the CDW phase and its dependence on pressure. For this reason, only the interactions with incident light perpendicular to the plane of the layers were studied, and the full, two-component, frequency-dependent dielectric tensor remains unknown.
By calculating the total energy of ferromagnetic (FM) and various possible AFM spin configurations, we find that the ground states, in all four compounds, exhibit an antiferromagnetic order. We also performed optical properties calculations, which predict that all four compounds show hyperbolic behavior in a frequency range extending from the infrared into the visible region.
2. Methods
Both the electronic and optical properties were calculated using Wien2k, an all-electron, full-potential, linearized, augmented plane wave DFT code [
37]. Wien2k approximates the electronic wave function using a “muffin-tin” method, in which space is divided into two regions. One region consists of the inside of non-overlapping spheres surrounding the nuclei, while the other is the interstitial region between the spheres. Within the spheres, the wave function is expanded in spherical harmonics up to
. In the interstitial region, the wave function is expanded in terms of plane waves up to a maximum wave vector
, which is chosen so that
, where
is the smallest muffin-tin radius in the unit cell. The electron density is Fourier expanded in the interstitial region with a wave vector cutoff of
, where
is the Bohr radius. Inside the spheres, it is expanded in a product of radial functions and lattice harmonics with
. The electronic exchange and correlation were treated using the generalized gradient approximation (GGA) and Perdew–Burke–Ernzerhof (PBE) exchange–correlation functionals [
38]. In the self-consistent field calculations, integration over the Brillouin zone is replaced by a summation over a mesh of 1800 k-points within the Brillouin zone, and convergence is achieved with a tolerance of
Ry in energy and
in charge. In carrying out the DFT calculations on RTe
and RTe
(R = Sm, Er), we used the experimental values of the lattice constants and atomic position coordinates. The lattice parameters are given in
Table 1.
Because of the strong localization of electrons in the 4f orbitals of rare-earth atoms, we add an onsite Coulomb repulsion term, known as a Hubbard U term. Thus, we carry out what is known as a DFT+U calculation of the electronic and optical properties of the rare-earth tellurides. The U values are usually several electron-volts, depending on the type of ion, the localized orbitals, and the chemical environment. In our calculations, we have chosen U = 7 eV for both the samarium and erbium atoms. This is consistent with prior DFT calculations and the generally accepted U values for rare-earth atoms [
21,
40,
41,
42].
The dielectric function, absorption, optical conduction, and related quantities, collectively called the optical properties, describe the interaction of a material with light. These interactions are caused by scattering from one state to another by the perturbing potential of light. Scattering can occur within a band (if the band is partially filled) or between filled bands and partially filled or empty bands. Scattering within a band is approximated using the Drude model of free electrons with damping. The damping is characterized by the Drude term,
, which varies by material, and may vary depending on direction in anisotropic materials. The intraband contribution to the dielectric function is
Here,
is the plasma frequency, which, in cgs units, is given by
, where
n is the free electron density and
m is the effective mass of the electron [
43]. It should be noted that in anisotropic materials, such as the rare-earth tellurides studied here, the effective mass is a tensor rather than a scalar; this implies that
is also a tensor. In the calculations reported in this work, we used a value for
corresponding to an energy of 0.1 eV.
Interband scattering contributes to the permittivity for both metals and dielectrics. In this case, the energy of a photon is absorbed, causing an electron to jump from a valence band to a conduction band. One important consideration is that the photon wave vector is typically much smaller than the width of the Brillouin zone, so that in a transition, the electron wave vector is approximately unchanged. The interband contribution to the imaginary part of the permittivity is given by [
44]:
Here,
is the Fermi distribution function,
is the
component of the momentum operator,
n and
are band indices, and
is a Dirac delta function. The optical matrix elements
are related to the probability amplitude for a transition from band
to band
n. This matrix element leaves the wave vector unchanged since the photon momentum is relatively small. Scattering can only occur from an occupied state to an empty one, which is taken into account by the Fermi functions. Finally, conservation of energy demands that the final energy is equal to the initial energy plus the photon energy, which is guaranteed by the delta function. Knowing the imaginary part of permittivity, the real part may be calculated using the Kramers–Kronig relations. The real and imaginary parts of permittivity are then used to calculate all other optical properties.
Because accurate calculation of the dielectric function requires many more points in the Brillouin zone, a denser mesh of k-points is used. Since rare-earth atoms are heavy, we ran these calculations with the spin-orbit coupling contribution added for each material.
3. Results and Discussion
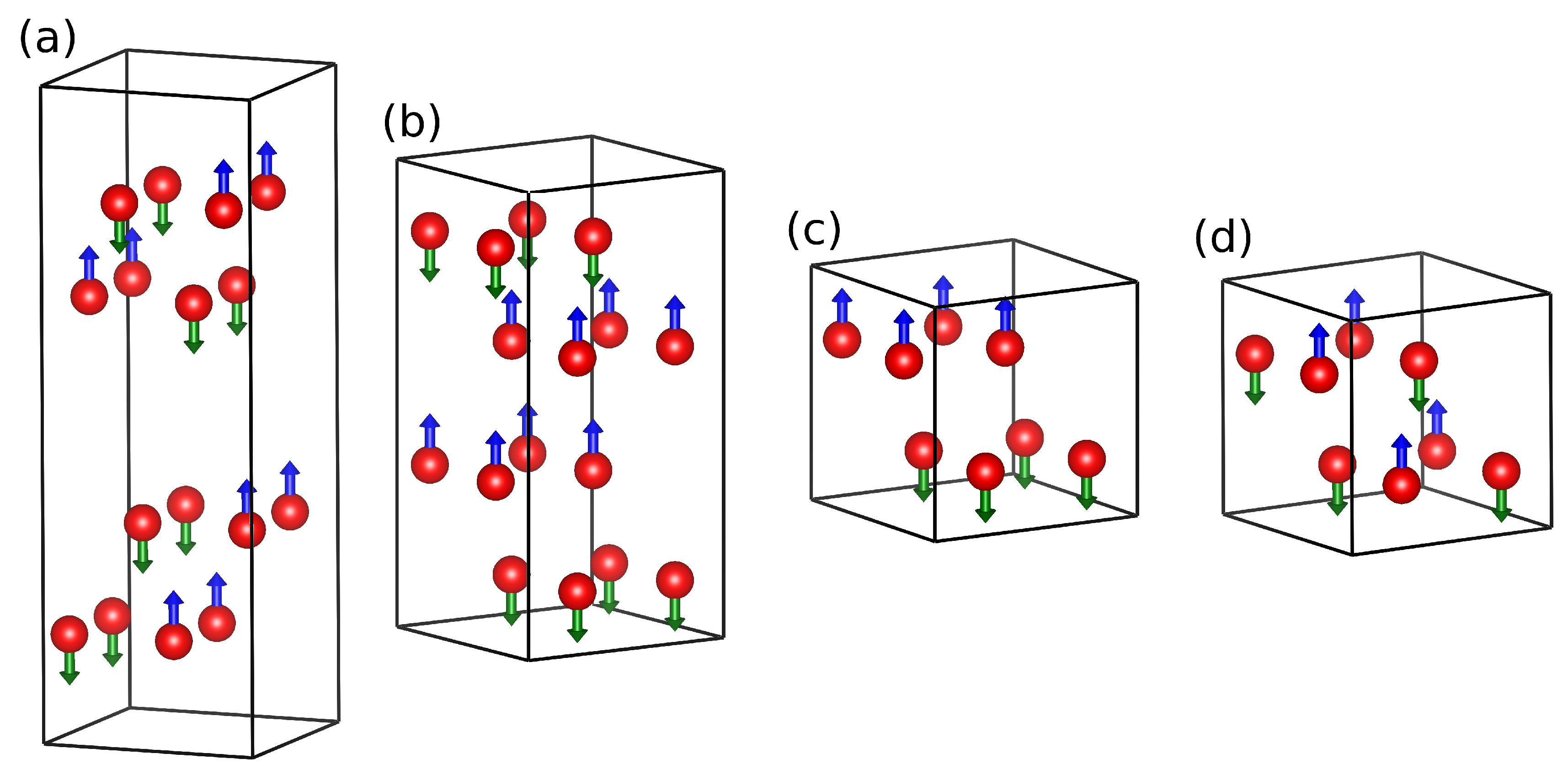
For each material, we calculated the energy of the nonmagnetic, ferromagnetic, and several AFM spin arrangements in order to find the ground state. In the ABAB interlayer AFM configuration, each layer of rare-earth atoms is all spin up or down, with spin direction alternating each layer. ABBA interlayer AFM also has each layer all spin up or down, but alternates spin direction every other layer; i.e., in this arrangement, two adjacent rare-earth layers with one spin direction are followed by two adjacent rare-earth layers with the opposite spin direction. In intralayer AFM, each layer is separately antiferromagnetic. In the stripe configuration, the spins in a row of atoms along a lattice vector are aligned, but the spin direction alternates each row (See
Figure 3). In the case of RTe
, we calculated the energies of ABAB interlayer, intralayer, and stripes along both of the two shorter lattice vectors (
a and
c). For RTe
, we calculated the total energy for the ABAB interlayer, ABBA interlayer, and intralayer AFM configurations. Stripe AFM only applies to RTe
because the two shorter lattice vectors are slightly different in length, making it possible to break the symmetry along these directions. ABBA interlayer does not apply to RTe
because the distance between RTe double layers is large, making the interactions between atoms in one double layer with those in the adjacent double layer very weak.
The calculated total energies of the various configurations are presented in
Table 2. As the table shows, the ground state is predicted to be antiferromagnetic for each of the four compounds: SmTe
, SmTe
, ErTe
, and ErTe
. As we noted in the introduction, SmTe
was indeed found to be antiferromagnetic at very low temperatures, while ErTe
did not undergo an AFM transition above 1.8 K. Our results, however, suggest that ErTe
should have an AFM ground state at sufficiently low temperatures. Similarly, we predict that SmTe
and ErTe
should also be antiferromagnetic at low temperatures. SmTe
and ErTe
were found to have the lowest energy in the AFM stripe configuration, with both compounds favoring stripes along the
a-axis, which has the slightly shorter in-plane lattice parameter. Previous DFT calculations of the possible AFM states of GdTe
also found the ground state to be stripe AFM, though the stripe axis was not specified [
21]. The ground states of SmTe
and ErTe
exhibited intralayer AFM. In some cases, the energy difference between the ground state and first excited state magnetic configuration was very small, on the order of meV, suggesting that these configurations may be quite unstable. The magnetic moments of Sm in both SmTe
and SmTe
were calculated to be approximately 3
, where
is the Bohr magneton, while the moments of Er in ErTe
and ErTe
were about 5.3
.
We have calculated the band structure for the ground state configuration (stripe AFM) of ErTe
, shown in
Figure 4. The bands along the
Y direction, corresponding to the axis perpendicular to the layers, are notably flat. Since the electron effective mass is related to the curvature of the band, this implies a very large effective mass for the electrons along this direction, indicating that conduction along this direction is very poor, which is in good agreement with experimental observations [
11]. Since
is inversely proportional to the electron effective mass, and assuming the
z-axis is perpendicular to the rare-earth and tellurium layers, this implies that
will be considerably larger than
, as we show later by explicit calculations.
The density of states for ErTe
in the stripe AFM configuration, which we predicted to be the spin state adopted at very low temperatures, is shown in
Figure 5a. In this configuration, the unit cell contains four Er and twelve Te atoms; however, the crystal symmetry dictates that there are eight nonequivalent positions. Thus, each atom occupies a position that is equivalent by symmetry to the position occupied by one other atom. Hence, two Er atoms occupy two positions equivalent by symmetry, and one of these atoms is denoted Er1. The other two Er atoms also occupy another two symmetry equivalent positions, and one of these atoms is denoted Er2. A similar situation holds for the 12 Te atoms, where we identify six nonequivalent positions. In
Figure 5a we plot the total density of states for stripe AFM ErTe
, along with the partial density derived from the two nonequivalent Er atoms and one of the Te atoms. The plot reveals that states derived from Te orbitals dominate at the Fermi level, indicating that they are the main drivers of electronic conduction. This agrees with theoretical work by DiMasi et al. [
11], but is in contrast with a previous calculation of the density of states for NdTe
[
22]. That calculation, using Quantum Espresso, found the density of states for the 4f electrons of Nd to be much larger than that of Te at the Fermi level. They theorized that this was due to hybridization between Nd 4f and Te 5p orbitals. It could be that this disparity is due to differences between the two materials. However, the different result may also be due to the fundamental differences between Wien2k and Quantum Espresso. Wien2k is an all-electron, full potential DFT code, while Quantum Espresso treats core electrons approximately using a pseudopotential.
On the other hand, the density of states for ErTe
(
Figure 5b) shows a somewhat larger contribution from Er than Te at the Fermi level. It seems likely that this is because the quasi-2d character of RTe
is reduced compared with RTe
due to having one fewer Te layer separating the RTe layers and to the absence of a VdW gap, across which conduction is extremely difficult. As a result, conduction for RTe
parallel to the layers is up to 3000 times greater than that perpendicular to the layers [
9], while for RTe
, this ratio is between roughly 50 and 100 [
15]. This indicates that the tight binding model in RTE
, using only Te 5p orbitals, is perhaps less accurate than in the RTe
case, though clearly still accurate enough to be useful, given experimental results.
The results in
Figure 5 were obtained without including the effect of spin-orbit coupling. Upon including this effect, the only significant change was a downshift in the energy, by about 0.5 eV, of the two peaks below about −8 eV, and a reduction in their height. We therefore concluded that spin-orbit coupling does not lead to a significant change in the electronic properties of these materials. This is consistent with prior RTe DFT calculations, which did not include this interaction and produced results that matched experimental measurements of their electronic properties [
3,
21,
22].
We now consider the optical properties of rare-earth tellurides. As indicated earlier, the dielectric function is the sum of two parts, and . The first part depends on the plasma frequency which, due to the anisotropy of the crystals under study, is a tensor. Taking the axis perpendicular to the layers as the z-axis, we have for the weakly orthorhombic (almost tetragonal) RTe crystals, and for tetragonal RTe crystals. Since we are interested in the optical properties of rare-earth tellurides at room temperature, and since the AFM order sets in only at very low temperatures, we calculate the optical properties of these materials in the non-magnetic phase. Expressed in energy units, the calculated plasma frequencies and are respectively given by 3.11 eV and 0.49 eV for SmTe, 4.95 eV and 1.03 eV for ErTe, 4.98 eV and 1.56 eV for SmTe, and 5.07 eV and 1.60 eV for ErTe. The large difference between the values of and is a consequence of the large anisotropy in these materials.
The calculated real parts of the components
and
of the dielectric functions are shown in
Figure 6, while the corresponding imaginary parts are shown in
Figure 7. The plots show that there are energy ranges where the real parts of
and
have opposite signs; this indicates that in those ranges of the spectrum, the tellurides display hyperbolic dispersion. The imaginary parts were found to be rather large in the hyperbolic range, suggesting that losses would be large if these materials were used in devices. Large losses have been a stumbling block in utilizing hyperbolic materials to their full potential [
45]. However, one of the main reasons rare-earth tellurides have been so widely studied is their high degree of tunability. Perhaps these losses could be greatly reduced by tuning the number of charge carriers, their mobility, or other properties using intercalation, substitution, vacancies, or pressure. In particular, it has been shown that pressure has a large impact on the optical properties of CeTe
, as does varying the rare-earth ion, which can be viewed as applying chemical pressure [
34]. Another study demonstrated the possibility of altering the Fermi surface and band structure of YTe
by intercalating Pd atoms in the VdW gap [
3]. This would certainly affect the optical properties by altering the available interband transitions, while introducing charge carriers would impact the Drude permittivity. Significant Te vacancies would similarly affect the available band transitions and carrier densities. Substitution of Te atoms with Sb in RTe
is another possible tuning method that has been experimentally demonstrated [
14]. Further study is required to determine the exact effects of these modifications on the full dielectric tensor.
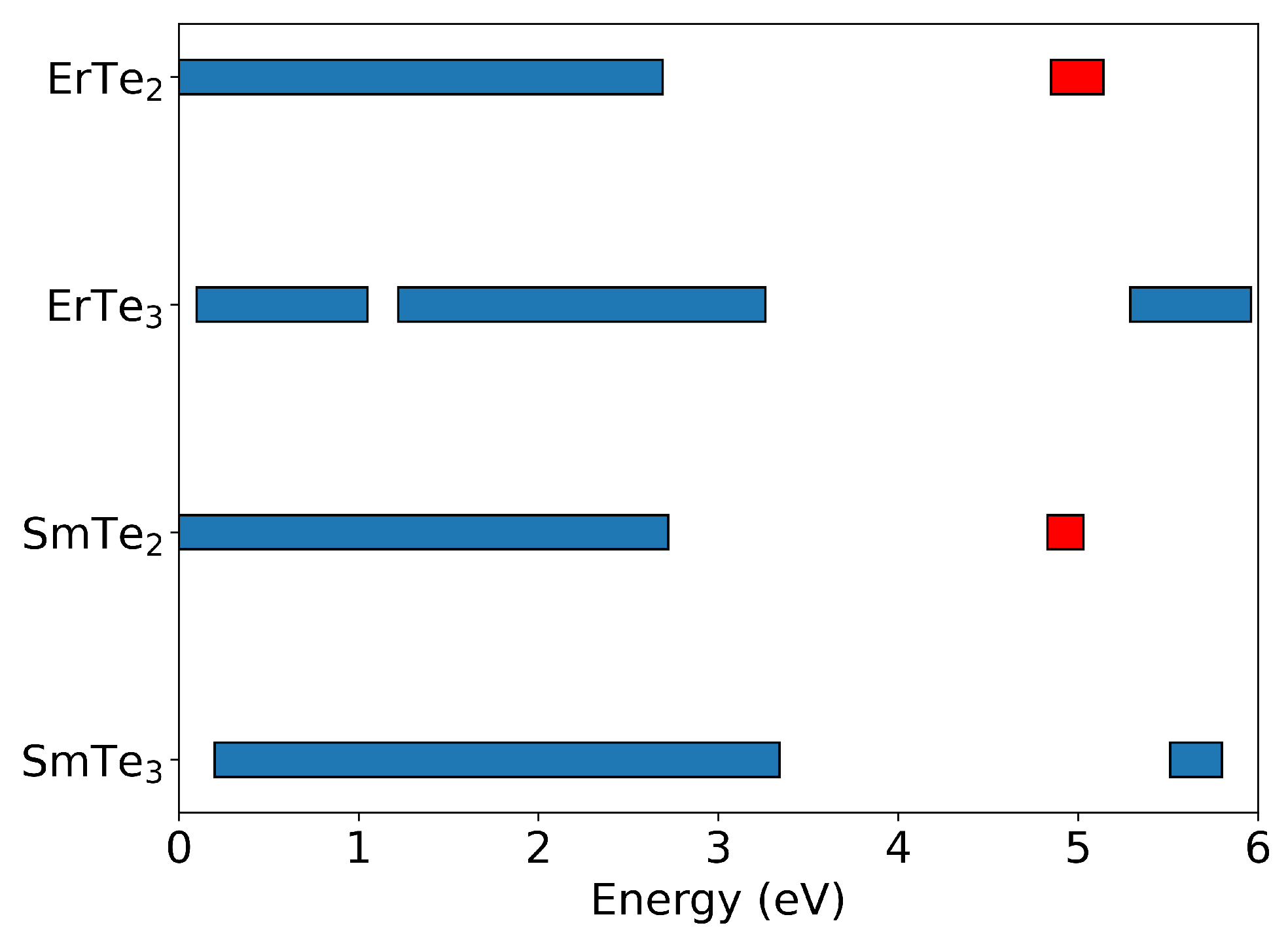
Our calculations predict that all crystals studied in this work (SmTe
, ErTe
, SmTe
, and ErTe
) display hyperbolic dispersion in the infrared to visible frequency ranges, as can be seen in
Figure 8. They all exhibited type 1 hyperbolic behavior for some range of energies. This behavior is a consequence of the large anisotropy attending the electronic properties of these materials, with conductivity in the plane of the layers being much greater than that normal to the layers. For a very limited range of frequencies, however, SmTe
and ErTe
were also found to exhibit type 2 hyperbolic behavior in the ultraviolet. This further demonstrates that metallic behavior perpendicular to the layers is much more possible in RTe
, since electrons are not insulated by a VdW gap.
In conclusion, we have calculated the particular AFM ground states of several rare-earth tellurides, along with their electronic and optical properties, providing deeper insight into how these properties differ between RTe and RTe. We predict that both classes of materials are hyperbolic in the technologically important visible and infrared range, and suggest several feasible methods for altering the optical properties to suit the needs of the experimenter.