Next Article in Journal
Wetting of Refractory Ceramics with High-Manganese and Structural Steel and Description of Interfacial Interaction
Next Article in Special Issue
The Presence of Charge Transfer Defect Complexes in Intermediate Band CuAl1−pFepS2
Previous Article in Journal
Formation of α-Hemihydrate Inside of a Gypsum Crystal during the Dehydration Process
Previous Article in Special Issue
Hydrogen-Induced Order–Disorder Effects in FePd3
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Crystals
Volume 12
Issue 12
10.3390/cryst12121783
crystals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Investigation of Magnetocaloric Properties in the TbCo2-H System

by
Galina Politova
1,2,*,
Irina Tereshina
3,
Ioulia Ovchenkova
3,
Abdu-Rahman Aleroev
3,
Yurii Koshkid’ko
4,
Jacek Ćwik
4 and
Henryk Drulis
4
1
Baikov Institute of Metallurgy and Material Science RAS, Moscow 119991, Russia
2
Institute of Electronics and Telecommunications, Peter the Great St. Petersburg Polytechnic University, Saint Petersburg 195251, Russia
3
Faculty of Physics, Lomonosov Moscow State University, Moscow 119991, Russia
4
Institute of Low Temperature and Structure Research PAS, 50-950 Wroclaw, Poland
*
Author to whom correspondence should be addressed.
Crystals 2022, 12(12), 1783; https://doi.org/10.3390/cryst12121783
Submission received: 8 November 2022 / Revised: 1 December 2022 / Accepted: 3 December 2022 / Published: 8 December 2022
(This article belongs to the Special Issue Intermetallic Compound (Volume II))
Browse Figures
Review Reports Versions Notes

Abstract

:
In this work the magnetocaloric effect in the TbCo2-H system in the region of the Curie temperature was studied both by direct and indirect methods in external magnetic fields up to ~1.4 and 14 T, respectively. We have paid special attention to the magnetic and magnetothermal properties of the TbCo2–H with high hydrogen content. The mechanisms responsible for the change in the Curie temperature were established, and the field and temperature dependences of the magnetocaloric effect were analyzed in detail. In addition, the magnetocaloric properties (including critical parameters) for various systems based on the TbCo2 compound were compared. The main regularities of the change in the MCE value and the Curie temperature depending on the composition are discovered and discussed.

1. Introduction

RCo2 intermetallic compounds with a Laves phase structure demonstrate appreciable magnetocaloric effect (MCE) (quantified as the adiabatic temperature change ΔTad or isothermal entropy change ΔS when exposed to a magnetic field) near the magnetic phase transition, at the Curie temperature (TC) [1,2,3,4,5,6]. It is well known [7], that the Curie temperatures of magnetically ordered rare-earth compounds cover a wide range from ~400 K (GdCo2) to ~4 K (TmCo2). The fact that LuCo2 and YCo2 compounds are merely the enhanced Pauli paramagnets emphasizes the special role of rare-earth ions in the magnetic properties of these compounds.
Among RCo2 compounds, the highest MCE values have been found for compounds exhibiting first-order magnetic phase transitions: at TC = 140 K for DyCo2, at TC = 75 K for HoCo2 and at TC = 32 K for ErCo2 [7]. RCo2-type compounds with heavy rare-earth elements such as Gd or Tb demonstrate second-order transitions (SOTs) at temperatures above 200 K. Although they have lower MCE values, their practical use in magnetic refrigerators is preferable due to the absence of magnetic hysteresis.
Doping of RCo2-type compounds with suitable impurities (strongly or weakly magnetic [8,9,10,11,12,13,14]) can provide control of the Curie temperature and, consequently, the position of the peak in the ΔTad(T) and ΔS(T) dependences, and its magnitude. The patterns of change in the magnitude of the magnetocaloric effect in doped compounds have not been fully disclosed, despite the large number of experimental works available in the literature. An important contribution to the study of magnetothermal phenomena in pseudo-binary compounds of the (R,R’)Co2-type in the region of magnetic phase transitions was made by N.A. de Oliveira [15]. By using theoretical calculations, he confirmed the experimentally observed magnitude of the magnetocaloric effect, for compounds exhibiting phase transitions of both the second and/or first order.
It is known that the analysis of the field dependences of the MCE is of great importance in the study of the magnetocaloric properties of materials. An initial assumption about the field dependence of the MCE was made by Belov K.P. [16]. Based on Landau’s theory of phase transitions, he showed that ΔTad~Hn, where n = 2/3. An attempt to explain the field dependence of ΔSmax for magnetic materials with a second-order phase transition was made by H. Oesterreicher and F. T. Parker. They assumed that in the mean field approximation ΔSmax~Hn, where n = 2/3 [17]. However, experimental results often deviated from this n value. An alternative approach was proposed by Romanov and Silin [18]. Their analysis of the MCE in inhomogeneous magnets was based on Landau’s theory of second-order phase transitions [19]. As a result, rather complicated equations were obtained. A great deal of work comparing theoretical and experimental data on ΔS(H) for various compounds was done by Franco V. et al. [20,21,22].
Among RCo2-type compounds, TbCo2 attracts special attention, since its magnetic ordering temperature is in the ambient temperature range and is ~235 K (~−38 °C) (Curie temperatures vary from 231 to 238 K in various sources [7,8,9,23,24,25,26,27,28,29]). Moreover, such working temperature is important to design magnetic refrigerators for long-term storage of various biomaterials, vaccines and drugs. That is why the study of the magnetocaloric effect in TbCo2-based compounds modified by interstitial or substitutional atoms will not only significantly expand the possibilities of practical use of these materials, but will also allow to collect new experimental data to test existing theoretical models [8,9,11,24,25,26,27,28,29].
Note that only a few works have been devoted to study the effect of interstitial atoms (such as hydrogen), on the magnetic and magnetocaloric properties of the TbCo2 compound [30,31]. Thus, in the work of Mushnikov [30], the magnetic properties of TbCo2Hx samples with x = 0, 0.7, 2, 2.4, 3.9 were obtained and investigated. The magnetic moment at Co atoms and the Curie temperature were found to exhibit an increase at low hydrogen contents, whereas at high hydrogen contents, both magnetic characteristics decrease substantially. MCE was not studied in TbCo2-H system.
It is known [32] that high MCE values for RCo2 compounds with Laves phase structure are obtained only at temperatures below 200 K. That is why new compositions with Tc less than 200 K are of particular interest. The purpose of this work was, first of all, to study and analyze the effect of hydrogen on the Curie temperature and MCE, and to compare the magnetocaloric characteristics of TbCo2Hx hydrides with other substituted TbCo2-based compositions to establish the main patterns of their changes depending on the composition.

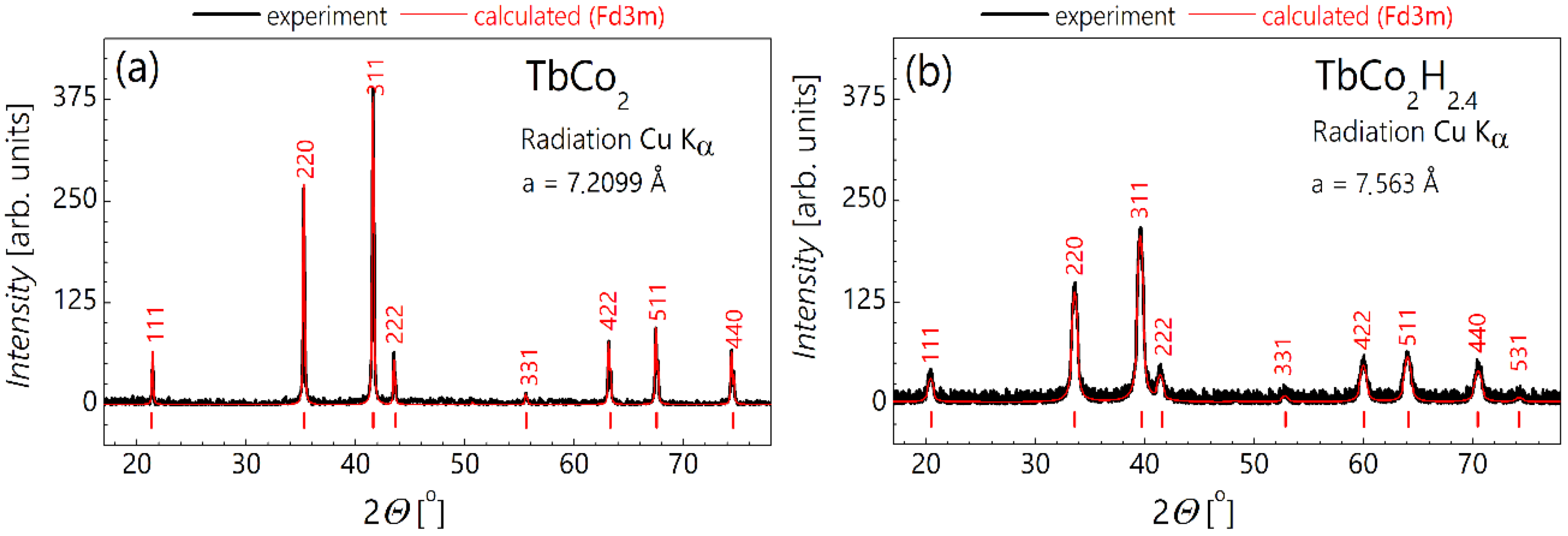
2. Materials and Methods

We obtained TbCo2Hx compounds with x = 0, 0.5, 2.4 (the initial sample and samples with low and high hydrogen content). Details of the synthesis and certification of TbCo2 compounds were described in our previous work [12]. The TbCo2 sample weighing 0.6 g was placed in a 6 cm3 reaction tube of fully automated stainless steel Sievert’s-type volumetric apparatus. Before hydrogen absorption began, the sample was thermally activated under a high vacuum of 10−4 Torr, at 250 °C for 1 h. After cooling the sample to room temperature, the pure (99.999%) hydrogen gas was introduced into the reaction tube under a pressure of about 10 bars and left for 12 h at room temperature. The hydrogen contents were determined by monitoring pressure changes in a system with a known volume before and after the reaction. Pressures were monitored using a Honeywell ST3000 strain gauge. The accuracy of determination of absorbed hydrogen concentration is ±0.02 H atoms per formula unit (H/f.u.). The XRD patterns were recorded at scanning step of 0.02 (at the 2-s exposition) on a Rigaku Ultima IV powder diffractometer with a CuKα radiation. The qualitative and quantitative phase analysis was performed using a program PDXL by Rigaku (Japan) integrated with the international database ICDD.
Field-dependent magnetization measurements (field range 0–14 T) were carried out using a vibration sample magnetometer (VSM) [33]. Magnetization isotherms were obtained in the temperature range 4.2–300 K. The temperature and type of magnetic phase transition were determined by the Belov–Arrott method [34]. The analysis of the magnetocaloric effect was carried out by calculating the change in entropy from magnetization isotherms (indirect method [1]).
Direct measurements of the magnetocaloric effect were performed using a special setup in fields up to 1.35 T in the temperature range 78–310 K. The measurements were carried out by recording the temperature change of the sample during the adiabatic increase in the magnetic field (ΔTad). Adiabaticity was achieved by good thermal insulation of the sample, by placing a copper–constantan thermocouple inside the sample, and by quickly turning on the magnetic field. The temperature changes of the sample were monitored with accuracy better than ±0.01 K. The study of the MCE by the direct method was possible only for samples with x = 0 and 0.5 obtained in the cast state. The sample with x = 2.4 was obtained in the form of a powder (indirect method of MCE estimation was used for it).

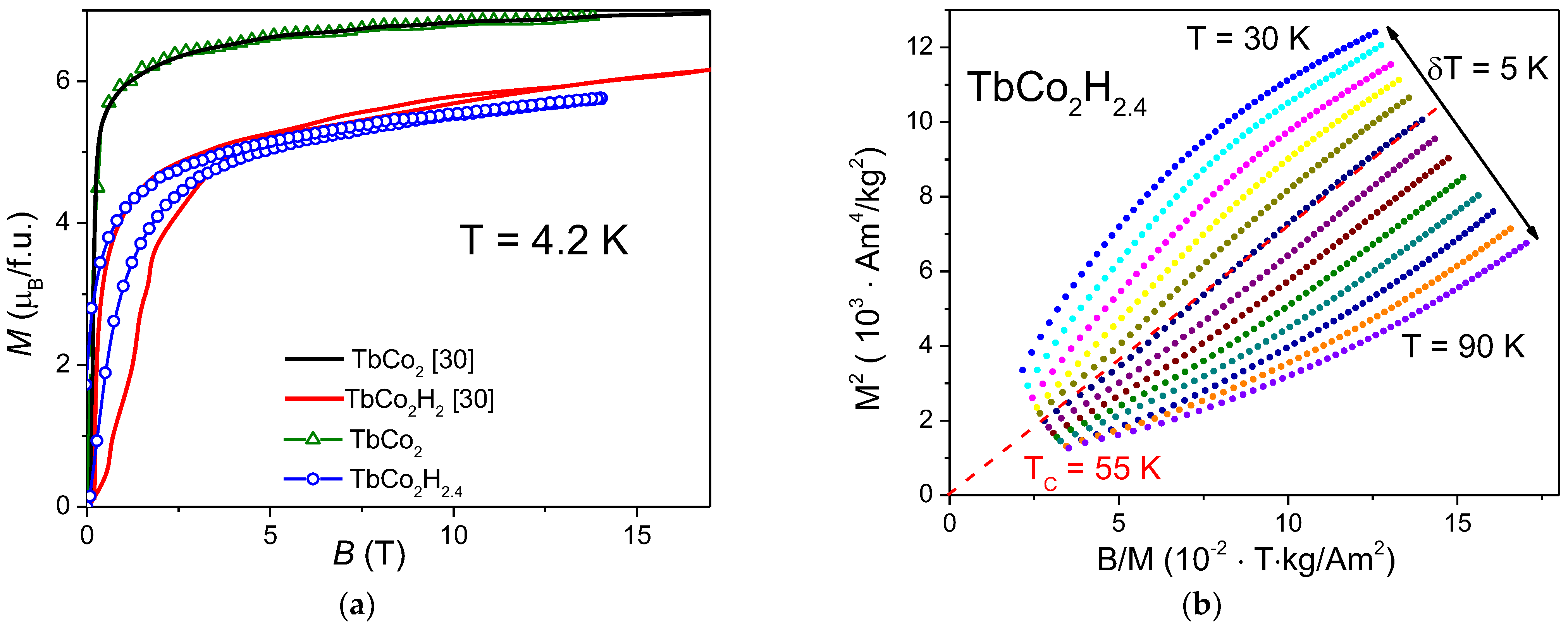
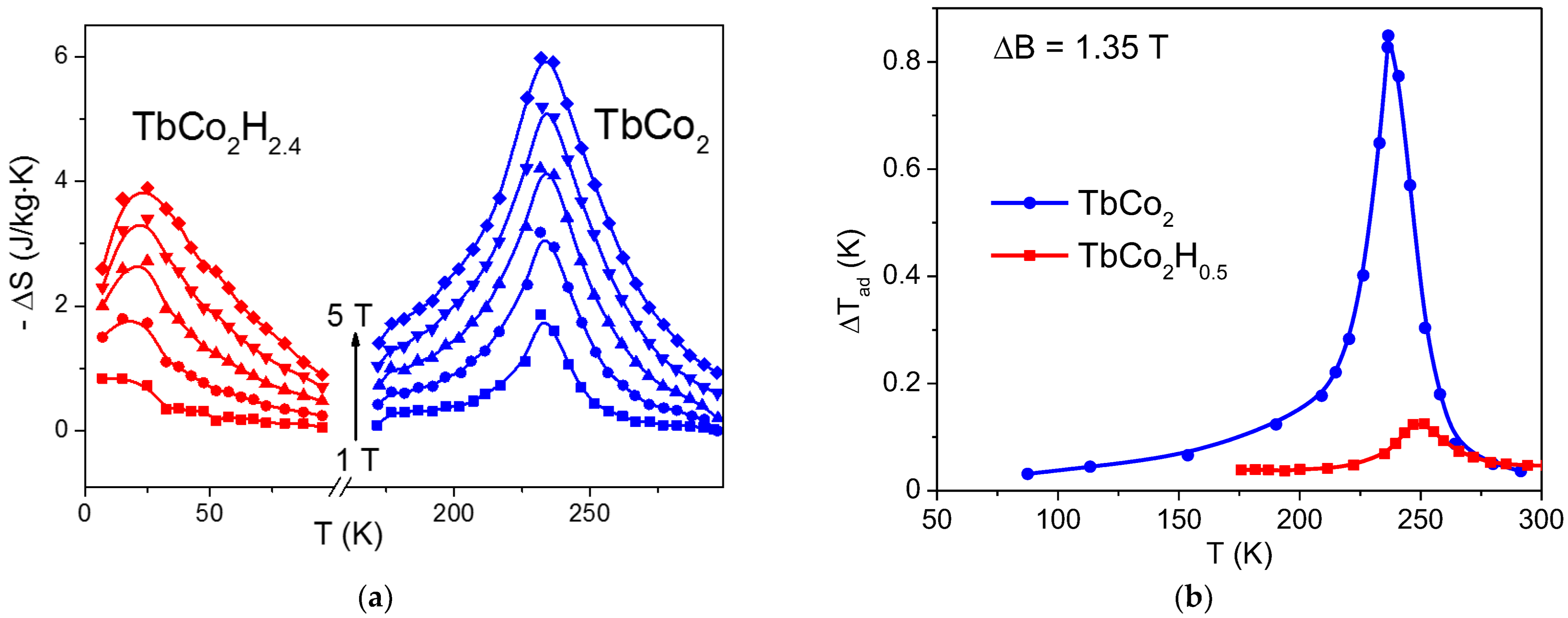
3. Results and Discussion

X-ray diffraction analysis (see Figure 1) showed that in all the obtained TbCo2Hx (x = 0, 0.5, 2.4) compounds, the content of the main phase, which has a cubic structure of the MgCu2 type, is not less than 96%. The parameters of the TbCo2 initial sample are in good agreement with the data in [30]. The increase of the relative unit cell volume ΔV/V varies depending on the hydrogen content, from 0.5% for the TbCo2H0.5 compound to 15% for the TbCo2H2.4.
Figure 2a shows the magnetization isotherms M(B) at T = 4.2 K for the TbCo2 and TbCo2H2.4 hydride in comparison with the known data for the initial composition and for the TbCo2H2 dihydride [30]. It can be seen that the data are in good agreement with each other. The type of magnetic phase transition for TbCo2H2.4 was analyzed in detail by Belov–Arrott plots (M2 versus B/M) and the Banerjee criterion [35], as illustrated in Figure 2b. No negative slope or inflection was found as a characteristic of the first-order magnetic transition, which suggests that the phase transition in the TbCo2H2.4 is of a second-order type. It is known that the initial TbCo2 compound exists on the instability boundary, and the type of its transition can be considered both as the first kind [36] or the second kind [8,9,37]. Therefore, the insertion of interstitial and/or substitution atoms in TbCo2 can easily shift the boundary and make the transition type either first or second. This phenomenon is mainly associated with the instability of the magnetism of the cobalt sublattice, which demonstrates a strong dependence on the crystal lattice parameter a in RCo2 compounds [37].
The Curie temperature of the TbCo2H2.4 hydride was determined to be equal to TC = 55 K. In terms of lattice expansion, the insertion of hydrogen is equivalent to the application of a negative hydrostatic pressure. The change in the Curie temperature in the hydride we considered as a result of a change in the unit cell volume.
The effect of pressure on the Curie temperature (dTc/dp = −9 K/GPa for TbCo2) [38] and compressibility κ ≈ 10−2 GPa−1 [39]) determined from the literature data are shown in Figure 3 by a dashed line. The rate of decrease in Tc with an increase in the volume of the unit cell can be calculated by the formula
dlnTC/dp = −(κ/TC)dTC/dlnV,
where κ = −(dV/V)/p. Hence dTC/dlnV = dTC/(dV/V) = 9 K per 1% change in unit cell volume. To determine the Curie temperatures for the TbCo2-H system, we also used the inflection point technique based on analysis of the behavior of the temperature dependences of the magnetization in the magnetic field [30]. Figure 3 shows that the experimentally determined decrease in Tc is less than that expected in consequence of an increase in the unit cell volume when ΔV/V exceeds 20%. Herewith, when values of ΔV/V are close to 13–15%; the experimental and calculated data practically coincide. This means that the volume effect is the dominant mechanism in the latter case. However, with a further increase in volume, other factors also come into play, the most important of which is a change in the electronic structure of the compound due to the insertion of hydrogen atoms into the crystal lattice of the TbCo2 compound [40,41,42].
The Curie temperature of TbCo2Hx increases at low hydrogen concentrations. It should be noted that hydrogen can occupy two types of tetrahedral interstices in the structure of the C15 Laves phase: positions AB3 (32e) and A2B2 (96g) [43]. According to neutron diffraction data for ErFe2Hx, at low hydrogen concentrations, A2B2 interstices are predominantly filled, while at high hydrogen concentrations, interstices of both types are partially filled [44], which has an additional effect on the functional properties.
The magnitude of the magnetocaloric effect in TbCo2H2.4 was calculated from the experimentally obtained magnetization isotherms M(B) by an indirect method [1]. The temperature dependences of the change in the magnetic part of the entropy in various magnetic fields (from 1 to 14 T) are shown in Figure 4a.
It is clearly seen that the temperature at which the maximum MCE (Tmax) is observed increases with an increase in the external magnetic field. Figure 4b shows the field dependences of the Tmax and the temperature (Tmid) in the middle of the working zone. The working zone is defined as the temperature range at which the values ΔS = 0.5.(ΔSmax) (see inset to Figure 4b). It can be seen that the dependence Tmax (B) demonstrates a linear increase in applied fields, while the dependence Tmid (B) approximates to saturation.
Figure 5a shows a comparison of the MCE values for the TbCo2H2.4 hydride and the TbCo2 sample at various magnetic field changes from 0 to 1, to 2, to 3, to 4, and up to 5 T (the most commonly used ranges of magnetic fields). The MCE values for the initial composition are in good agreement with the literature data [26]. It is clear that the value of the MCE of the hydrogenated sample decreases by a factor of 1.5, whereas the maximum temperature decreases by 200 K.
Figure 5b compares the MCE measured by the direct method for the initial TbCo2 compound and for low-hydrogen content TbCo2H0.5 hydride within the magnetic field change ΔB = 1.35 T. It can be seen that the MCE of the hydrogenated sample is decreased by a factor of 10, while the Curie temperature (at which the maximum of the magnetocaloric effect is observed), on the contrary, is increased (by about 10 K). Such behavior of the Curie temperature and the MCE in hydrides with high (TbCo2H2.4) and low (TbCo2H0.5) hydrogen content may be related to the fact that hydrogen atoms occupy different positions in the MgCu2-type cubic structure [30], but the type of the magnetic phase transition does not change in these cases.
For a detailed analysis of the nature of the magnetic phase transition in TbCo2H2.4 hydride we studied the critical exponents near the Curie temperature TC. According to the scaling hypothesis [45,46] for a second-order phase transition in the TC region, the critical exponents β (associated to spontaneous magnetization), γ (associated to the initial susceptibility), and δ (associated to the magnetization isotherm) are related by:
MS (T) = MS (−ε)β, ε < 0
χ0−1 (T) = (h0/M0)εγ, ε > 0
where ε is the reduced temperature equal to (T – TC)/TC.
At Curie temperature, the exponent δ relates magnetization M and applied magnetic field B by
M(B,TC) = A0(B) 1/δ, ε= 0
where A0 are the critical amplitudes (Kouvel–Fisher method [47]).
According to Equation (4), the value of δ can be obtained by a linear fit to the high field plots ln(M) vs. ln(B) near TC, as shown in the insets in Figure 6a. The δ value obtained for TbCo2H2.4 was compared by us with the data for the TbCo2, as well as for Tb(Co,Fe)2 compositions (see Table 1).
It can be seen that both interstitial and substitutional atoms contribute to a decrease in the critical exponent δ. Moreover, the effect of interstitial atoms (hydrogen) on this indicator is less than the effect of substitution atoms.
According to the scaling hypothesis, the magnitude of the entropy change in the Curie temperature range is related to the magnitude of the external magnetic field by the following relation:
−ΔS (T = TC)~B n
The exponent n is related to the critical exponents β and δ by the following relation [26]:
n = 1 + 1/δ(1 − 1/β)
According to relation (6), we obtain n = 0.76, while a linear approximation of the dependences lnΔS vs. lnB gives us the values n = 0.72 at T = 25 K and n = 1.25 at TC = 55 K (Figure 5b). A similar analysis of the experimental results performed for several families of magnetically soft bulk alloys in the amorphous state [18] shows that the field dependence −ΔS(B) has the following features: at temperatures significantly below TC, n = 1, while at temperatures significantly above TC, n = 2. At a temperature corresponding to the maximum |−ΔSmax|, the value of n is minimal and can approach 2/3. The high-temperature limit for n = 2 is a consequence of the Curie–Weiss law. Since the magnetization has a linear dependence on the field in the high-temperature region, the change in the magnetic part of the entropy also has a quadratic dependence on the field. The low temperature limit can also be explained by simple arguments: at temperatures well below the Curie temperature and in a moderate applied fields the magnetization does not show a strong field dependence [48]. The consequence of this fact is n = 1.
Table 1 contains data on the MCE for the substituted Tb(Co,Fe)2 compositions. It can be seen that with an increase in the Fe content, the MCE value decreases. Note also that a decrease in the MCE in this system is accompanied by a significant increase in the Curie temperature: from 235 (4) K (for TbCo2) to 303 K (for TbCo1.9Fe0.1). The insertion of hydrogen atoms into the crystal lattice of the TbCo2 compound (as in the case of the Tb(Co,Fe)2 system) leads to a significant decrease in the MCE, not only at low (in the TbCo2H0.5), but also at high (in the TbCo2H2.4) hydrogen concentrations. In the TbCo2–H systems, at low concentrations of hydrogen, one can observe a slight increase in TC, however, in TbCo2H2.4 the Curie temperature decreases from 234 K (in TbCo2) to 55 K.
Neither interstitial (hydrogen) nor substitutional (iron) atoms change the type of magnetic phase transition in the TbCo2 compound. This task, as well as the problem of a significant increase in the MCE in TbCo2, can be solved due to substitutions in the rare earth sublattice, namely, the replacement of Tb atoms with Dy, Ho, Er atoms [12,13,32].

4. Conclusions

TbCo2Hx (x = 0, 0.5, and 2.4) with cubic MgCu2-type structure have been successfully synthesized. It has been established that hydrogenation leads to a significant (almost 200 K) decrease in TC at hydrogen concentration of 2.4 at ./f.u when the increase in relative unit cell volume, ΔV/V, is close to 15%, which agrees well with calculations made using compressibility and dTC/dp. This means that the volume effect is dominant in its influence on the Curie temperature. As a consequence of the strong influence of the volume effect on the magnetic properties, the MCE value in hydrides, both with low and high hydrogen content (hydrogen fills different types of tetrahedral interstices in the structure of the C15 Laves phase: namely, positions AB3 (32e) and A2B2 (96g)), decreases through the increase in the distances between magnetically active ions. The type of magnetic phase transition from a magnetically ordered to a disordered state does not change upon hydrogenation.
An analysis of the field dependences of the MCE of the TbCo2H2.4 hydride showed that interstitial atoms contribute to a decrease in the critical index δ and an increase in the indices β and n, similarly to the partial replacement of cobalt atoms by iron atoms in TbCo2 compound.

Author Contributions

Conceptualization, I.T. and J.Ć.; methodology, Y.K., H.D. and I.O.; formal analysis, I.T. and G.P.; investigation, Y.K., J.Ć. and I.O.; resources, G.P., I.T. and A.-R.A.; data curation, I.T.; writing—original draft preparation, G.P.; writing—review and editing, I.T.; visualization, G.P.; supervision, H.D.; project administration, I.T. and J.Ć. All authors have read and agreed to the published version of the manuscript.

Funding

The work is supported by the Russian Science Foundation, pr. No. 22-29-00773. The work of J. Ćwik was supported by the National Science Center, Poland, through the OPUS Program under Grant No. 2019/33/B/ST5/01853.

Data Availability Statement

The main data is contained within the article. The data presented in this study are available on request from the corresponding author.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Tishin, A.M.; Spichkin, Y.I. The Magnetocaloric Effect and Its Applications; Institute of Physics Publishing: Bristol, PA, USA, 2003; p. 476. [Google Scholar]
  2. Kitanovski, A.; Tušek, J.; Tomc, U.; Plaznik, U.; Ožbolt, M.; Poredoš, A. Magnetocaloric Energy Conversion from Theory to Applications; Springer International Publishing: Cham, Switzerland, 2015; p. 456. [Google Scholar]
  3. Duc, N.H.; Kim, A.D.T.; Brommer, P.E. Metamagnetism, giant magnetoresistance and magnetocaloric effects in RCo2-based compounds in the vicinity of the Curie temperature. Phys. B 2002, 319, 1–8. [Google Scholar] [CrossRef]
  4. Gschneidner, K.A.; Pecharsky, V.K., Jr. Magnetocaloric materials. Annu. Rev. Mater. Sci. 2000, 30, 387–429. [Google Scholar] [CrossRef] [Green Version]
  5. Singh, N.K.; Suresh, K.G.; Nigam, A.K.; Malik, S.K.; Coelho, A.A.; Gama, S. Itinerant electron metamagnetism and magnetocaloric effect in RCo2-based Laves phase compounds. J. Magn. Magn. Mater. 2007, 317, 68–79. [Google Scholar] [CrossRef] [Green Version]
  6. Stein, F.; Leineweber, A. Laves phases: A review of their functional and structural applications and an improved fundamental understanding of stability and properties. J. Mater. Sci. 2021, 56, 5321–5427. [Google Scholar] [CrossRef]
  7. Gratz, E.; Markosyan, A.S. Physical properties of RCo2 Laves phases. J. Phys. Condens. Matter. 2001, 13, 385–413. [Google Scholar] [CrossRef]
  8. Zeng, Y.; Tian, F.; Chang, T.; Chen, K.; Yang, S.; Cao, K.; Zhou, C.; Song, X. Large magnetocaloric effect and near-zero thermal hysteresis in the rare earth intermetallic Tb1−xDyxCo2 compounds. J. Phys. Condens. Matter 2017, 29, 055804. [Google Scholar] [CrossRef] [PubMed]
  9. Balli, M.; Fruchart, D.; Gignoux, D. A study of magnetism and magnetocaloric effect in Ho1-xTbxCo2 compounds. J. Magn. Magn. Mater. 2007, 314, 16–20. [Google Scholar] [CrossRef]
  10. Cwik, J.; Palewski, T.; Nenkov, K.; Gutfleisch, O.; Klamut, J. The influence of Er substitution on magnetic and magnetocaloric properties of Dy1-xErxCo2 solid solutions. Intermetallics 2011, 19, 1656–1660. [Google Scholar] [CrossRef]
  11. Zhouv, K.W.; Zhuang, Y.H.; Li, J.Q.; Deng, J.Q.; Zhu, Q.M. Magnetocaloric effects in (Gd1-xTbx)Co2. Solid State Comm. 2006, 137, 275–277. [Google Scholar]
  12. Tereshina, I.S.; Chzhan, V.B.; Tereshina, E.A.; Khmelevskyi, S.; Burkhanov, G.S.; Ilyushin, A.S.; Paukov, M.A.; Havela, L.; Karpenkov, A.Y.; Cwik, J.; et al. Magnetostructural phase transitions and magnetocaloric effect in Tb-Dy-Ho-Co-Al alloys with a Laves phase structure. J. Appl. Phys. 2016, 120, 013901. [Google Scholar] [CrossRef]
  13. Politova, G.A.; Tereshina, I.S.; Cwik, J. Multifunctional phenomena in Tb-Dy-Gd(Ho)-Co(Al) compounds with a Laves phase structure: Magnetostriction and magnetocaloric effect. J. Alloys Compd. 2020, 843, 155887. [Google Scholar] [CrossRef]
  14. Tereshina, I.; Politova, G.; Tereshina, E.; Nikitin, S.; Burkhanov, G.; Chistyakov, O.; Karpenkov, A. Magnetocaloric and magnetoelastic effects in (Tb0.45Dy0.55)1-xErxCo2 multicomponent compounds. J. Phys. Conf. Ser. 2010, 200, 092012. [Google Scholar] [CrossRef]
  15. De Oliveira, N.A.; von Ranke, P.J. Theoretical aspects of the magnetocaloric effect. Phys. Rep. 2010, 489, 89–159. [Google Scholar] [CrossRef]
  16. Belov, K.P. Magnetic Transitions; Consultants Bureau: New York, NY, USA, 1961. [Google Scholar]
  17. Oesterreicher, H.; Parker, F.T. Magnetic cooling near Curie temperatures above 300 K. J. Appl. Phys. 1984, 55, 4334–4338. [Google Scholar] [CrossRef]
  18. Romanov, A.Y.; Silin, V.P. On the magnetocaloric effect in inhomogeneous ferromagnets. Phys. Met. Metallogr. 1997, 83, 111–115. [Google Scholar]
  19. Landau, L.D. Theory of Phase Transformations. II. Zh. Eksp. Teor. Fiz. 1937, 7, 627. (In Russian) [Google Scholar]
  20. Franco, V.; Blázquez, J.; Conde, A. Field dependence of the magnetocaloric effect in materials with a second order phase transition: A master curve for the magnetic entropy change. Appl. Phys. Lett. 2006, 89, 222512. [Google Scholar] [CrossRef]
  21. Franco, V.; Conde, A.; Pecharsky, V.K.; Gschneidner, K.A. Field dependence of the magnetocaloric effect in Gd and (Er1−xDyx)Al2: Does a universal curve exist. EPL 2007, 79, 47009. [Google Scholar] [CrossRef]
  22. Franco, V.; Blázquez, J.S.; Ipus, J.J.; Law, J.Y.; Moreno-Ramírez, L.M.; Conde, A. Magnetocaloric effect: From materials research to refrigeration devices. Prog. Mater. Sci. 2018, 93, 112–232. [Google Scholar] [CrossRef]
  23. Huang, D.; Gao, J.; Lapidus, S.H.; Brown, D.E.; Ren, Y. Exotic hysteresis of ferrimagnetic transition in Laves compound TbCo2. Mater. Res. Lett. 2020, 8, 97–102. [Google Scholar] [CrossRef] [Green Version]
  24. Nikitin, S.A.; Tskhadadze, G.A.; Ovthenkova, I.A.; Zhukova, D.A.; Ivanova, T.I. The Magnetic Phase Transitions and Magnetocaloric Effect in the Ho(Co1-xAlx)2 and Tb(Co1-xAlx)2 Compounds. Solid State Phenom. 2011, 168–169, 119–121. [Google Scholar]
  25. Ovchenkova, I.A.; Tskhadadze, G.A.; Zhukova, D.A.; Ivanova, T.I.; Nikitin, S.A. Magnetocaloric effect in RCo2 compounds. Solid State Phenom. 2012, 190, 339–342. [Google Scholar] [CrossRef]
  26. Janatova, M.; Poltierova, J.; Vejpravova, J.; Javorsky, P.; Prokleska, J.; Svoboda, P.; Danis, S. Effect of Si Substitution and Annealing on Magnetocaloric Properties in TbCo2. Acta Phys. Pol. A 2008, 113, 311–314. [Google Scholar] [CrossRef]
  27. Gerasimov, E.G.; Inishev, A.A.; Terentev, P.B.; Kazantsev, V.A.; Mushnikov, N.V. Magnetostriction and thermal expansion of nonstoichiometric TbCo2Mnx compounds. J. Magn. Magn. Mater. 2021, 523, 167628. [Google Scholar] [CrossRef]
  28. Halder, M.; Yusuf, S.M.; Mukadam, M.D. Magnetocaloric effect and critical behavior near the paramagnetic to ferrimagnetic phase transition temperature in TbCo2−xFex. Phys. Rev. B 2010, 81, 174402. [Google Scholar] [CrossRef] [Green Version]
  29. Fang, C.H. Tuning the magnetic and structural transitions in TbCo2Mnx compounds. Phys. Rev. B 2017, 96, 064425. [Google Scholar] [CrossRef] [Green Version]
  30. Mushnikov, N.V.; Gaviko, V.S.; Goto, T. Magnetic Properties of Hydrides RCo2Hx with R = Gd, Tb, Dy, Ho, and Er. Phys. Met. Metallogr. 2005, 100, 338–348. [Google Scholar]
  31. Tereshina, I.S.; Kaminskaya, T.P.; Chzhan, V.B.; Ovchenkova, Y.A.; Trusheva, A.S.; Viryus, A.A. The Influence of Hydrogenation on the Structure, Magnetic and Magnetocaloric Properties of Tb–Dy–Co Alloys with a Laves Phase Structure. Phys. Solid State 2019, 61, 1169–1175. [Google Scholar] [CrossRef]
  32. Tereshina, I.; Cwik, J.; Tereshina, E.; Politova, G.; Burkhanov, G.; Chzhan, V.; Ilyushin, A.; Miller, M.; Zaleski, A.; Schultz, L.; et al. Multifunctional Phenomena in Rare-Earth Intermetallic Compounds With a Laves Phase Structure: Giant Magnetostriction and Magnetocaloric Effect. IEEE Trans. Magn. 2014, 50, 2504604. [Google Scholar] [CrossRef]
  33. Nizhankovskii, V.I.; Lugansky, L.B. Vibrating sample magnetometer with a step motor. Meas. Sci. Technol. 2007, 18, 1533–1537. [Google Scholar] [CrossRef]
  34. Belov, K.P. Magnetic Transformations; FizMatGiz: Moscow, Russia, 1959; p. 260. [Google Scholar]
  35. Banerjee, S.K. On a generalised approach to first and second order magnetic transitions. Phys. Lett. 1964, 12, 16–17. [Google Scholar] [CrossRef]
  36. Zhou, C.; Chang, T.; Dai, Z.; Chen, Y.; Guo, C.; Matsushita, Y.; Ke, X.; Murtaza, A.; Zhang, Y.; Tian, F.; et al. Unified understanding of the first-order nature of the transition in TbCo2. Phys. Rev. B. 2022, 106, 064409. [Google Scholar] [CrossRef]
  37. Khmelevskyi, S.; Mohn, P. The order of the magnetic phase transitions in RCo2 (R = rare earth) intermetallic compounds. J. Phys. Condens. Matter 2000, 12, 9453–9464. [Google Scholar] [CrossRef]
  38. Burzo, E.; Vlaic, P.; Kozlenko, D.P.; Kichanov, S.E.; Dang, N.T.; Lukin, E.V.; Savenko, B.N. Magnetic properties of TbCo2 compound at high pressures. J. Alloys Compd. 2013, 551, 702–710. [Google Scholar] [CrossRef]
  39. Brouha, M.; Buschow, K.H.J. The pressure dependence of the Curie temperature of rare earth—Cobalt compounds. J. Phys. F Met. Phys. 1973, 3, 2218–2226. [Google Scholar] [CrossRef]
  40. Tereshina, E.A.; Khmelevskyi, S.; Politova, G.; Kaminskaya, T.; Drulis, H.; Tereshina, I.S. Magnetic ordering temperature of nanocrystalline Gd: Enhancement of magnetic interactions via hydrogenation-induced “negative” pressure. Sci. Rep. 2016, 6, 22553. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  41. Tereshina, E.A.; Yoshida, H.; Andreev, A.V.; Tereshina, I.S.; Koyama, K.; Kanomata, T. Magnetism of a Lu2Fe17H Single Crystal under Pressure. J. Phys. Soc. Jpn. 2007, 76 (Suppl. A), 82–83. [Google Scholar] [CrossRef] [Green Version]
  42. Nikitin, S.A.; Tereshina, I.S.; Verbetsky, V.N.; Salamova, A.A.; Skokov, K.P.; Pankratov, N.Y.; Skourski, Y.V.; Tristan, N.V.; Zubenko, V.V.; Telegina, I.V. Magnetostriction and magnetic anisotropy in TbFe11TiHx single crystal. J. Alloys Compd. 2001, 322, 42–44. [Google Scholar] [CrossRef]
  43. Shoemaker, D.P.; Shoemaker, C.B. Concerning atomic sites and capacities for hydrogen absorption in the AB2 Friauf-Laves phases. J. Less-Common Met. 1979, 68, 43–58. [Google Scholar] [CrossRef]
  44. DeSaxce, T.; Berthier, Y.; Fruchart, D. Magnetic and structural properties of the ternary hydrides of ErFe2. J. Less-Common Met. 1985, 107, 35–43. [Google Scholar] [CrossRef]
  45. Stanley, H.E. Introduction to Phase Transitions and Critical Phenomena; Oxford University Press: New York, NY, USA, 1971. [Google Scholar]
  46. Stanley, H.E. Scaling, universality, and renormalization: Three pillars of modern critical phenomena. Rev. Mod. Phys. 1999, 71, 358–366. [Google Scholar] [CrossRef] [Green Version]
  47. Khan, N.; Midya, A.; Mydeen, K.; Mandal, P.; Loidl, A.; Prabhakaran, D. Critical behavior in single-crystalline La0.67 Sr0.33 CoO3. Phys. Rev. B 2010, 82, 064422. [Google Scholar] [CrossRef]
  48. Sokolovskiy, V.V.; Miroshkina, O.N.; Buchelnikov, V.D.; Marchenkov, V.V. Magnetocaloric Effect in Metals and Alloys. Phys. Metals Metallogr. 2022, 123, 315–318. [Google Scholar] [CrossRef]
Crystals 12 01783 g001 550
Figure 1. X-ray diffraction patterns for TbCo2 (a) and its hydride TbCo2H2.4 (b).
Figure 1. X-ray diffraction patterns for TbCo2 (a) and its hydride TbCo2H2.4 (b).
Crystals 12 01783 g001
Crystals 12 01783 g002 550
Figure 2. (a) Field dependence of the magnetization of the initial compound TbCo2 and its hydrides TbCo2H2 and TbCo2H2.4; (b) the Curie temperature determination of the TbCo2H2.4 hydride by the Belov–Arrott method.
Figure 2. (a) Field dependence of the magnetization of the initial compound TbCo2 and its hydrides TbCo2H2 and TbCo2H2.4; (b) the Curie temperature determination of the TbCo2H2.4 hydride by the Belov–Arrott method.
Crystals 12 01783 g002
Crystals 12 01783 g003 550
Figure 3. Curie temperature dependence on the relative increase in unit cell volume ΔV/V for the TbCo2—H system and the expected change in TC (dashed line), determined on the basis of literature data on the effect of hydrostatic pressure on the Curie temperature [30,38,39].
Figure 3. Curie temperature dependence on the relative increase in unit cell volume ΔV/V for the TbCo2—H system and the expected change in TC (dashed line), determined on the basis of literature data on the effect of hydrostatic pressure on the Curie temperature [30,38,39].
Crystals 12 01783 g003
Crystals 12 01783 g004 550
Figure 4. Temperature dependences of the change in the magnetic part of the entropy at various changes in the magnetic field of TbCo2H2.4 (a); field dependences of the maximum temperature −ΔS(Tmax) and the temperature of the middle of the working zone (Tmid) (b).
Figure 4. Temperature dependences of the change in the magnetic part of the entropy at various changes in the magnetic field of TbCo2H2.4 (a); field dependences of the maximum temperature −ΔS(Tmax) and the temperature of the middle of the working zone (Tmid) (b).
Crystals 12 01783 g004
Crystals 12 01783 g005 550
Figure 5. Temperature dependences of the change in the magnetic part of the entropy at various changes in the magnetic field (from 0 to 1–5 T) in the TbCo2H2.4 hydride and the initial composition TbCo2 (a); Temperature dependences of the MCE at ΔB = 1.35 T measured by the direct method of TbCo2H0.5 and the initial composition TbCo2 (b).
Figure 5. Temperature dependences of the change in the magnetic part of the entropy at various changes in the magnetic field (from 0 to 1–5 T) in the TbCo2H2.4 hydride and the initial composition TbCo2 (a); Temperature dependences of the MCE at ΔB = 1.35 T measured by the direct method of TbCo2H0.5 and the initial composition TbCo2 (b).
Crystals 12 01783 g005
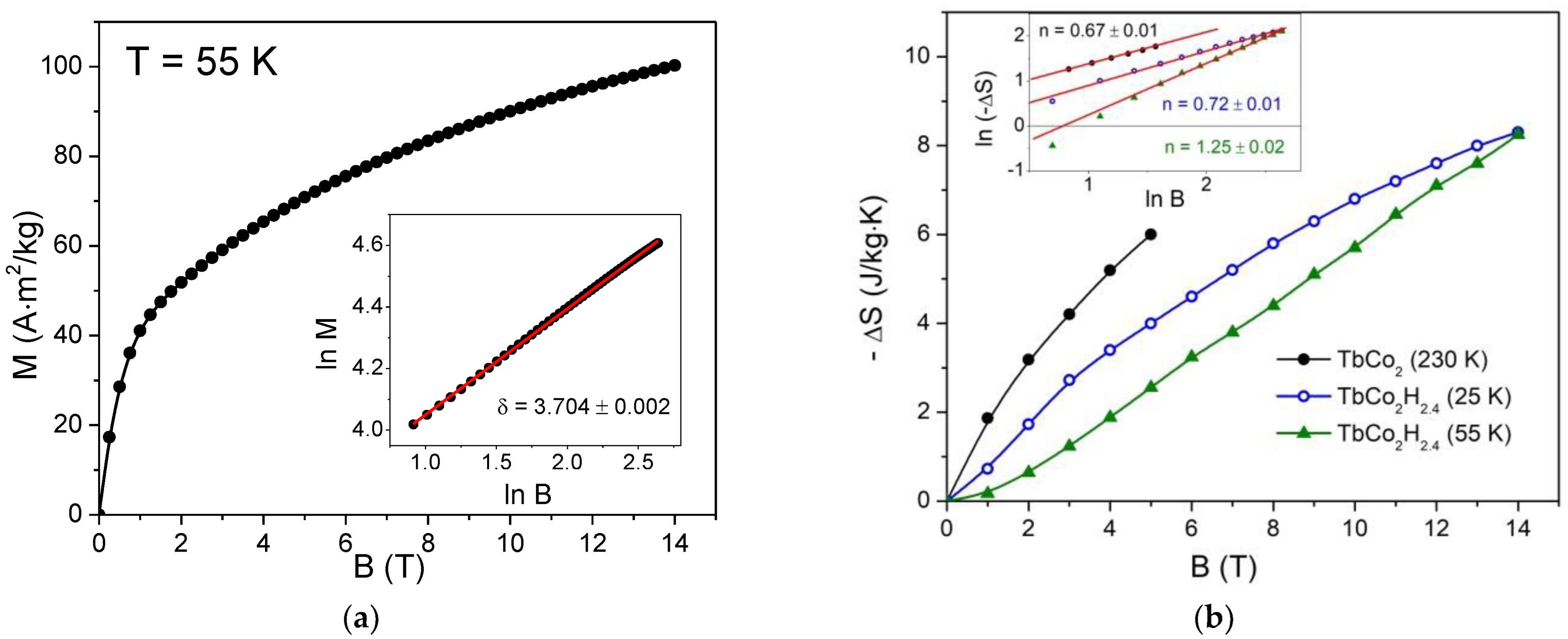
Crystals 12 01783 g006 550
Figure 6. Critical exponent analysis of TbCo2-H for: (a) Critical isotherm of M vs. B of TbCo2H2.4 close to the Curie temperature Tc = 55 K. Inset shows the same on log–log scale and the straight line is the linear fit following Equation (4); the critical exponent δ is obtained from the slope of the linear fit. (b) Critical isotherm of −ΔS vs. B of TbCo2 close to the Curie temperature Tc = 230 K and TbCo2H2.4 close to the temperatures T = 25 and 55 K. Inset shows the same on log–log scale and the straight line is the linear fit following Equation (5); the critical exponent n is obtained from the slope of the linear fit.
Figure 6. Critical exponent analysis of TbCo2-H for: (a) Critical isotherm of M vs. B of TbCo2H2.4 close to the Curie temperature Tc = 55 K. Inset shows the same on log–log scale and the straight line is the linear fit following Equation (4); the critical exponent δ is obtained from the slope of the linear fit. (b) Critical isotherm of −ΔS vs. B of TbCo2 close to the Curie temperature Tc = 230 K and TbCo2H2.4 close to the temperatures T = 25 and 55 K. Inset shows the same on log–log scale and the straight line is the linear fit following Equation (5); the critical exponent n is obtained from the slope of the linear fit.
Crystals 12 01783 g006
Table
Table 1. Critical exponents β, δ and n, Curie temperature TC and maximum change of magnetic entropy |−ΔS| at 0–5 T, for the TbCo2, substituted compounds Tb(Co,Fe)2 and the hydride TbCo2H2.4.
Table 1. Critical exponents β, δ and n, Curie temperature TC and maximum change of magnetic entropy |−ΔS| at 0–5 T, for the TbCo2, substituted compounds Tb(Co,Fe)2 and the hydride TbCo2H2.4.
CompoundsβδnTc−ΔS (0–5 T)Reference
TbCo20.386 (5)4.83 (4)0.67 (1)2346This work
TbCo2--0.67 (1)2356[25]
TbCo20.380 (4)4.85 (3)0.65 (1)2316.9[26]
TbCo1.94Fe0.06---2753.9[25]
TbCo1.9Fe0.10.541 (1)2.75 (4)0.76 (2)3033.7[25]
TbCo2H2.40.53 (3)3.704 (2)0.72 (1)552.5This work
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Politova, G.; Tereshina, I.; Ovchenkova, I.; Aleroev, A.-R.; Koshkid’ko, Y.; Ćwik, J.; Drulis, H. Investigation of Magnetocaloric Properties in the TbCo2-H System. Crystals 2022, 12, 1783. https://doi.org/10.3390/cryst12121783

AMA Style

Politova G, Tereshina I, Ovchenkova I, Aleroev A-R, Koshkid’ko Y, Ćwik J, Drulis H. Investigation of Magnetocaloric Properties in the TbCo2-H System. Crystals. 2022; 12(12):1783. https://doi.org/10.3390/cryst12121783

Chicago/Turabian Style

Politova, Galina, Irina Tereshina, Ioulia Ovchenkova, Abdu-Rahman Aleroev, Yurii Koshkid’ko, Jacek Ćwik, and Henryk Drulis. 2022. "Investigation of Magnetocaloric Properties in the TbCo2-H System" Crystals 12, no. 12: 1783. https://doi.org/10.3390/cryst12121783

APA Style

Politova, G., Tereshina, I., Ovchenkova, I., Aleroev, A.-R., Koshkid’ko, Y., Ćwik, J., & Drulis, H. (2022). Investigation of Magnetocaloric Properties in the TbCo2-H System. Crystals, 12(12), 1783. https://doi.org/10.3390/cryst12121783

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop