Hydrogen-Induced Order–Disorder Effects in FePd₃

Abstract

Binary intermetallic compounds, such as FePd₃, attract interests due to their physical, magnetic and catalytic properties. For a better understanding of their hydrogenation properties, both ordered FePd₃ and disordered Fe_0.25Pd_0.75 are studied by several in situ methods, such as thermal analysis, X-ray powder diffraction and neutron powder diffraction, at moderate hydrogen pressures up to 8.0 MPa. FePd₃ absorbs small amounts of hydrogen at room temperature and follows Sieverts’ law of hydrogen solubility in metals. [Pd₆] octahedral voids are filled up to 4.7(9)% in a statistical manner at 8.00(2) MPa, yielding the hydride FePd₃H_0.047(9). This is accompanied by decreasing long-range order of Fe and Pd atoms (site occupancy factor of Fe at Wyckoff position 1a decreasing from 0.875(3) to 0.794(4)). This trend is also observed during heating, while the ordered magnetic moment decreases up to the Curie temperature of 495(8) K. The temperature dependences of the magnetic moments of iron atoms in FePd₃ under isobaric conditions (p(D₂) = 8.2(2) MPa) are consistent with a 3D Ising or Heisenberg model (critical parameter β = 0.28(5)). The atomic and magnetic order and hydrogen content of FePd₃ show a complex interplay.

1. Introduction

The incorporation of hydrogen is a well-known tool for influencing the structural, electric, magnetic and optic properties of intermetallic compounds [1,2]. The interplay between hydrogen uptake and magnetism is often quite complex. Upon hydrogen uptake, intermetallic compounds may lose ferro-(LaCo₅) or ferrimagnetism (Y₆Mn₂₃) or become ferromagnets (CeNi₃, Hf₂Fe and Th₇Fe₃) [1]. The influence of hydrogen incorporation on the atomic order in crystal structures of intermetallics is also widely studied. In an extreme case, it may lead to amorphous hydrides in a process known as hydrogen-induced amorphization (HIA) [2]. The process involves short-range diffusion of metallic atoms, and the driving force seems to be the different hydrogen occupation sites in crystalline and amorphous states of the alloy. In some cases, such as Laves phases, the latter can be predicted by geometric factors, such as the atomic size ratio of constituting atoms [2]. Obviously, hydrogen uptake, atomic order (crystal structure) and magnetic order (cooperative phenomena) influence each other. In most studies, however, only the interaction between two of these factors is investigated and the third neglected or assumed not to play a role, which might be an oversimplification in some cases. Clearly, more in-depth investigations are needed to reveal the complex interplay between hydrogen uptake, atomic order and magnetic order in intermetallics. In this respect, we studied the crystal and magnetic structure of FePd₃ and its solid solution with hydrogen (also called hydride throughout this text) in detail in order to thoroughly characterize the interesting system FePd₃-H₂ and to reveal the potential cross-links between these factors. In order to obtain a high depth of knowledge, the hydrogenation of FePd₃ was analyzed by time-resolved in situ neutron diffraction, mapping the crystal structure, including hydrogen atom positions and magnetic moments.

FePd₃ has attracted interest as a functional material due to its diverse physical properties. It has a characteristic pressure-induced invar behavior by means of an anomalously low thermal expansion at high applied pressures [3,4,5], and it is ferromagnetic with a Curie temperature of 499 K [6]. A soft ferromagnetic behavior was found in carbon-based materials by encapsulation of FePd₃ [7,8,9]. FePd₃ can be used in electrocatalysis to enhance the cycle stability of hybrid Li–air batteries [10] or as an electrocatalyst to oxidize formic acid [11]. In addition, a higher attraction between 2-methylfuran and hydrogen compared to palladium was found in hydrogenation catalysis [12]. The use of bimetallic catalysts changes the electronic structure at the surface [13] and decreases the Pd-Pd coordination number; this can hinder the formation of unfavorable surface species, thus avoiding unwanted side reactions, e.g., decarbonylation, in the solvent-free hydrodeoxygenation of furan compounds for a Pd-FeO_x/SiO₂ catalyst [14]. Knowledge of the crystal structure is of great importance for catalytic applications, since it has a distinct influence on catalytic properties. The phase diagram of the Fe-Pd system shows a solid solution with a large phase width of about ±10% around an Fe:Pd atomic ratio of 1:3 [15]. 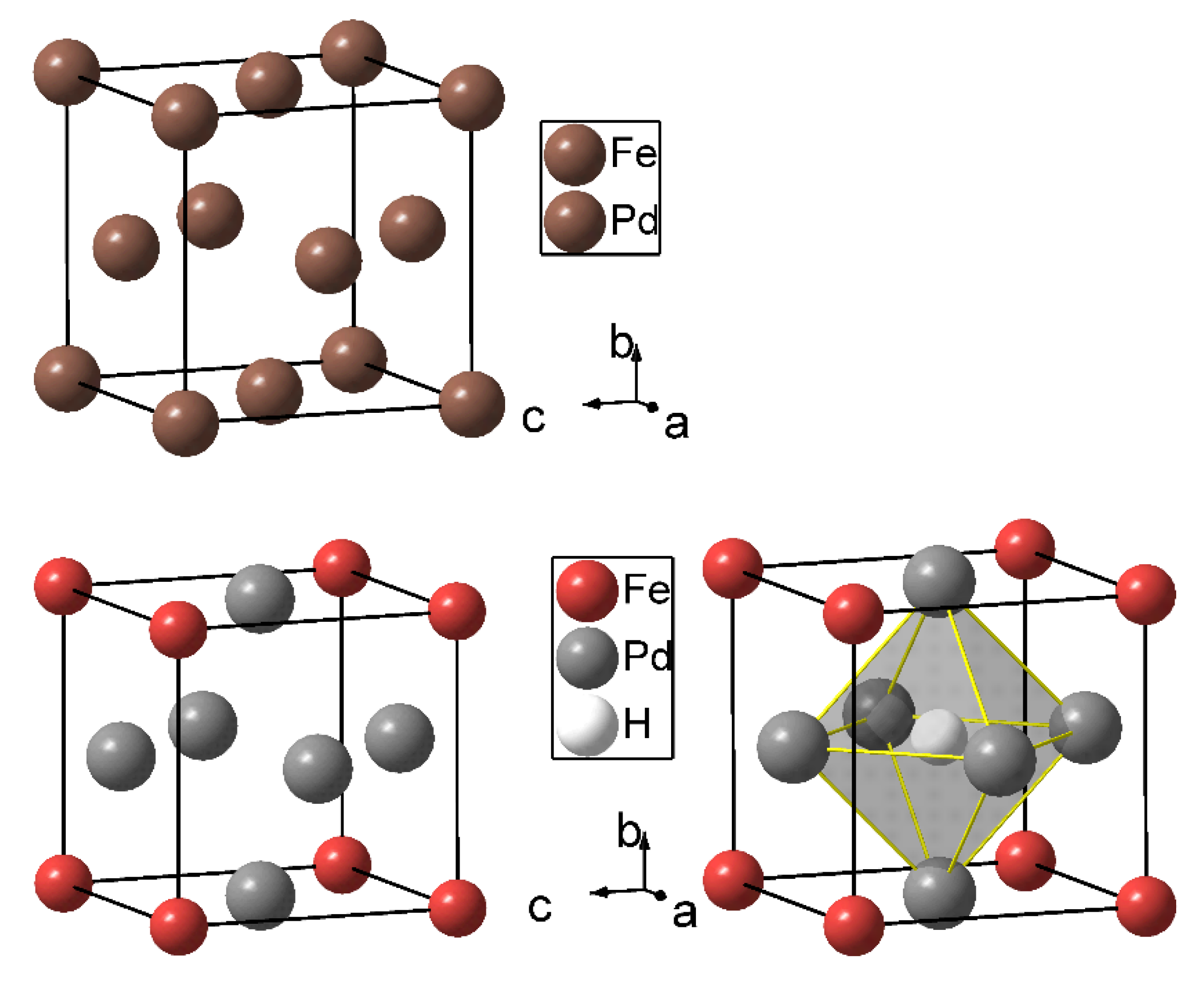In addition to the disordered phase Fe_0.25Pd_0.75 (Cu type, Fm$\overline{3}$m), an ordered phase is known. FePd₃ crystallizes in an ordered variant of a cubic close packing (AuCu₃ type, Pm$\overline{3}$m, Figure 1). The annealing times for the ordering process are long due to similar electronic and geometric properties of the constituting atoms [16]. FePd₃, with a high degree of crystallographic order, shows a higher hydrogen incorporation at high hydrogen pressures compared to (partially) disordered samples [17]. Disordered Fe_0.25Pd_0.75 needs more than two orders of magnitude higher hydrogen pressure to obtain the same electrical resistivity as found in ordered FePd₃ [18]. The position of hydrogen atoms in FePd₃H_x is not known yet.

In this work, we employ in situ studies to show the influence of moderate hydrogen pressures on the order–disorder transition in FePd₃, thus complementing studies of hydrogen absorption of FePd₃ at high hydrogen pressures [17]. In situ neutron powder diffraction, as an established method [19,20], was used to determine the level of atomic disorder, the magnetic moment and the amount of incorporated hydrogen.

2. Materials and Methods

Synthesis and Chemical Analysis: Due to air sensitivity, iron was handled in an argon-filled glove box. Disordered Fe_0.25Pd_0.75 was synthesized from stoichiometric amounts of palladium powder (99.95%, ≤150 μm, Goodfellow) and iron granules (99.98%, 1–2 mm, abcr) in sealed silica glass ampoules under argon atmosphere. The mixture was heated to 1423 K (100 K h⁻¹ heating rate) for 48 h and afterward quenched in air. The ordered compound was synthesized analogously; however, one small crystal of iodine (resublimed, Merck) was added as a mineralizing agent. This mixture was heated to 923 K (100 K h⁻¹ heating rate) for 7 d in a sealed silica ampoule. A further sample was afterward annealed for one month at 773 K. The products were ground in a mortar after cooling.

Iodine was removed by sublimation to the opposite side of the ampoule. Chemical analyses were performed by an EDX INCA SYSTEM from Oxford Instruments, mounted on a Zeiss LEO 1530 scanning electron microscope, with an acceleration voltage of 20 kV and a working distance of 15 mm.

Thermal Analysis: Differential scanning calorimetry (DSC) was performed under hydrogen pressure on a DSC HP 2+ (Mettler Toledo) equipped with a gas pressure chamber. An amount of 20 mg of the powdered sample was put in an aluminum crucible, which was closed with an aluminum lid. This was placed inside the pressure chamber, which was then purged several times with hydrogen gas, before filling to the final hydrogen gas pressure of 5.0 MPa. The sample was heated to 723 K with 10 K min⁻¹, held at this temperature for a minimum of 1 h and cooled to 300 K. Two runs were performed; afterward, the hydrogen pressure was released, the sample removed and structural characterization undertaken by XRPD.

Ex situ X-ray Powder Diffraction (XRPD): X-ray powder diffraction data from flat transmission samples were collected on a G670 diffractometer (Huber, Rimsting, Germany) with Mo-K_α1 radiation (70.926 pm) and from flat reflection samples on a SmartLab powder high-resolution X-ray powder diffractometer (Rigaku, Tokyo, Japan) with a HyPix-3000 two-dimensional semiconductor detector using Co-K_α radiation with parallel beam. The instrumental resolution function and the wavelength distribution were determined using a measurement on an external silicon NIST640d standard sample. The wavelengths were found to be 178.9789(4) pm and 179.3625(4) pm, close to the usual values for Co-K_α1 and Co-K_α2; the difference was caused by optical components of the diffractometer affecting the wavelength distribution.

In situ X-ray Powder Diffraction: In situ X-ray powder diffraction was performed on a SmartLab powder high-resolution X-ray powder diffractometer (Rigaku, Tokyo, Japan) in an Anton Paar XRK 900 reaction chamber (Graz, Austria) with 0.5 MPa hydrogen pressure (H₂, Air Liquide, 99.9%) and Co-K_α radiation with parallel beam on a flat FePd₃ specimen on top of an Al₂O₃ layer.

Ex situ Neutron Powder Diffraction (NPD): Neutron powder diffraction was carried out at the Institute Laue-Langevin in Grenoble, France, with a high-flux diffractometer D20 in high-resolution mode. Powdered samples (≈1 cm⁻³) were held in air-tight vanadium containers with 6 mm inner diameter and were each measured for 15 min. The wavelength λ = 186.80(2) pm was calibrated using an external silicon NIST640b standard sample in a 5 mm vanadium container. Deuterides rather than hydrides were used to avoid the high incoherent scattering of ¹H.

In situ Neutron Powder Diffraction:In situ neutron powder diffraction (NPD) was performed on a high-intensity two-axis diffractometer D20 at the Institute Laue-Langevin (ILL), Grenoble, France. Time-resolved neutron diffraction data were collected under deuterium pressure and heating by two lasers. These in situ experiments were carried out in (leuco-)sapphire single-crystal cells with 6 mm inner diameter connected to a gas supply system. The details are given elsewhere [19,20]. The sample cell was filled with FePd₃ and attached to the gas supply system, which was subsequently evacuated. The reactions were performed under various deuterium pressures (D₂, Air Liquide, 99.8% isotope purity). Data sets were obtained with 2 min time resolution. They are presented with an additional internal raw label (NUMOR), referring to proposal 5-24-613 [21]. For the in situ studies, NUMORs 131613–131859 were used.

Rietveld Refinement: Rietveld refinements [22,23] were performed using FullProf [24] and Topas [25]. Deuterium atoms were located by difference Fourier analysis. Simultaneous refinements of FePd₃ based on XRPD data and neutron powder diffraction data were performed with constrained mixed occupation parameters to reduce correlation with the ordered magnetic moment of the iron atoms. Further details of the crystal structure investigations may be obtained from FIZ Karlsruhe, 76344 Eggenstein-Leopoldshafen, Germany (fax: (+49)7247-808-666; e-mail: crysdata@fiz-karlsruhe.de), on quoting the deposition number CSD-2163436.

3. Results

For reasons of clarity and simplification, partially disordered FePd₃ (typically with between 10% and 20% palladium atoms on iron sites and vice versa, vide infra) is referred to as ordered, and the completely disordered Fe_0.25Pd_0.75, with statistical distribution of iron and palladium atoms as disordered in the following text. The term hydride is used to include all hydrogen isotopes, unless indicated otherwise, e.g., for deuterides used in neutron diffraction experiments. Because of the small amount of dissolved hydrogen (deuterium), these phases may also be seen as solid solutions of hydrogen (deuterium) in FePd₃.

3.1. Synthesis and Chemical Analysis

The intermetallic compound FePd₃ was synthesized from the elements. To facilitate the ordering of the metal atoms, iodine was added as a mineralizing agent. The annealed and quenched samples were gray powders with a metallic luster. Based on chemical analysis, the empirical formulae Fe_0.97(13)Pd_3.03(13) for the ordered and Fe_1.0(2)Pd_3.0(2) for the disordered phase were determined, with values averaged from at least 20 energy dispersive X-ray (EDX) spectra of each. Based on these results, we assign the same sum formula FePd₃ for both the ordered and the disordered phase. We distinguish them by nomenclature, i.e., FePd₃ for the (partially) ordered and Fe_0.25Pd_0.75 for the disordered phase. The products are stable in air. The powder particles align with the magnetic field of a permanent magnet.

3.2. X-ray Diffraction and Thermal Analysis

X-ray diffraction is well suited to tracking down unit cell volume changes due to hydrogen uptake and to distinguishing between iron and palladium atoms, i.e., to investigating the atomic order. X-ray powder diffraction patterns of ordered FePd₃ exhibit anisotropic reflection broadening (Figure A1). Reflections common to both disordered (Cu type, Fm$\overline{3}$m) and ordered (AuCu₃ type, Pm$\overline{3}$m) are sharp (hkl all even or all odd), whereas those extinct by F centering and seen only in the ordered phase are considerably broader (hkl mixed even and odd), e.g., 100 with a half width at full maximum of 0.785°, 111 with 0.188°. This broadening can be attributed to small ordered domains joined by anti-phase boundaries to larger crystallites. This effect is also present in cubic MnPd₃ [26]. In the Rietveld refinement, the anisotropic reflection broadening was modeled by dividing the diffraction data set into two patterns with different regions of the 2θ range—one containing only reflections with hkl all even or all odd, and one containing all the others, i.e., those with hkl mixed even and odd (Figure A1 and

Table A1. Crystal structure parameters of FePd₃ (Pm$\overline{3}$m, a = 385.380(5) pm) based on XRPD data (see Figure A1) at 296(1) K.

Atom	Wyckoff Position	x	y	z	Biso/10−4 pm²	SOF
Fe1	1a	0	0	0	0.18(4)	0.87(2)
Fe2	3c	0	½	½	0.88(1)	(1 − SOF(Fe1))/3
Pd1	1a	0	0	0	Biso(Fe1)	1 − SOF(Fe1)
Pd2	3c	0	½	½	Biso(Fe2)	1 − (1 − SOF(Fe1))/3

). Each of the two patterns was treated independently in terms of profile parameters but constrained in terms of crystal structure parameters and scale factors. The refinement of occupation parameters (site occupation factors, SOF) for the 1a and 3c sites, with a stoichiometric constraint on the sum formula FePd₃, yielded SOF(Fe) = 0.876(2) at Wyckoff position 1a, i.e., about 12% palladium at iron sites (Figure 2 and Figure A1, and

Table 1. Crystal structure parameters of FePd₃ (Pm$\overline{3}$m) based on neutron powder diffraction (a = 385.204(6) pm, μ_Fe = 2.3(2) μ_B; see Figure 2) and XRPD (a = 385.390(3) pm; compare Figure A1) at 296(1) K.

Atom	Wyckoff Position	x	y	z	Biso1/10−4 pm² NPD	Biso2/10−4 pm² XRPD	SOF
Fe1	1a	0	0	0	2.17(8)	0.19(4)	0.876(2)
Fe2	3c	0	½	½	1.11(12)	0.88(4)	(1 − SOF(Fe1))/3
Pd1	1a	0	0	0	Biso1(Fe1)	Biso2(Fe1)	1 − SOF(Fe1)
Pd2	3c	0	½	½	Biso1(Fe2)	Biso2(Fe2)	1 − (1 − SOF(Fe1))/3

and Table A1). The long-time annealed sample yielded SOF(Fe) = 0.99(2) instead, i.e., it was fully ordered (Figure A2 and

Table A2. Crystal structure parameters of FePd₃ (long-time annealed sample, Pm$\overline{3}$m, a = 385.412(4) pm) based on XRPD data (see Figure A2) at 296(1) K.

Atom	Wyckoff Position	x	y	z	Biso/10−4 pm²	SOF  1
Fe1	1a	0	0	0	1.5(2)	0.99(2)
Fe2	3c	0	½	½	1.88(4)	(1 − SOF(Fe1))/3
Pd1	1a	0	0	0	Biso(Fe1)	1 − SOF(Fe1)
Pd2	3c	0	½	½	Biso(Fe2)	1 − (1 − SOF(Fe1))/3

¹ The stoichiometric ratio of Fe to Pd atoms was fixed at 1:3.

).

The thermal analysis (DSC, p_start(H₂) = 5.00(2) MPa, T_max = 723 K) of the FePd₃ phase shows no thermal signal (Figure A3). However, the unit cell increases by 0.08% (a(FePd₃) = 385.330(5) pm, a(FePd₃H_x) = 385.433(3) pm, according to Rietveld analysis of XRPD data), and the disorder increases as well (SOF(Fe, 1a, FePd₃) = 0.909(10), SOF(Fe, 1a, FePd₃H_x) = 0.841(12)) based on X-ray powder diffraction (Mo-K_α1 radiation) before and after DSC (Figure A4).

In situ X-ray diffraction at 0.50(5) MPa hydrogen pressure on the long-time annealed FePd₃ sample shows a decrease in the level of atomic order. After the in situ chamber was flushed with hydrogen to a pressure of 0.50(5) MPa, SOF(Fe) decreased from 0.99(2) to 0.877(2). Furthermore, the cell volume increased by 0.2% (a(FePd₃) = 385.412(4) pm; a(FePd₃H_x) = 385.631(4) pm), indicating hydrogen uptake at room temperature. In the subsequent heating and cooling steps of 50 K to a maximum temperature of 550 K, SOF stays constant, and the lattice parameters change reversibly with temperature (Figure A5 and Figure A6, and

Table A3. Conditions and refined parameters of the Rietveld refinement of FePd₃ (long-time annealed sample, Pm$\overline{3}$m) based on in situ XRPD data (see Figure A5 and Figure A6, and Table A4) using Topas; X-ray absorption modeled with an overall B value of −4 × 10⁻⁴ pm² [25].

Frame	T/K	p/MPa	a/pm	V/106 pm³	Biso(1a)/10−4 pm²	Biso(3c)/10−4 pm²	SOF(Fe, 1a) 1
0	350 (2)	0.50 (5)	385.631 (4)	57.348 (2)	1.9 (2)	2.54 (4)	0.877 (11)
1	400 (2)	0.50 (5)	385.914 (4)	57.474 (2)	1.8 (2)	2.67 (4)	0.898 (11)
2	450 (2)	0.50 (5)	386.211 (5)	57.607 (2)	1.8 (2)	2.76 (5)	0.901 (11)
3	500 (2)	0.50 (5)	386.503 (5)	57.738 (2)	1.9 (2)	2.79 (5)	0.886 (11)
4	550 (2)	0.50 (5)	386.818 (5)	57.879 (2)	2.2 (2)	2.97 (5)	0.885 (11)
5	500 (2)	0.50 (5)	386.506 (5)	57.739 (2)	2.0 (2)	2.80 (5)	0.894 (11)
6	450 (2)	0.50 (5)	386.194 (4)	57.599 (2)	2.2 (2)	2.68 (4)	0.891 (11)
7	400 (2)	0.50 (5)	385.902 (4)	57.469 (2)	1.8 (2)	2.71 (4)	0.893 (11)
8	350 (2)	0.50 (5)	385.632 (4)	57.348 (2)	1.5 (2)	2.54 (4)	0.903 (11)

¹ The stoichiometric ratio of Fe to Pd atoms was fixed at 1:3.

and

Table A4. Residual parameters of the Rietveld refinement of FePd₃ (long-time annealed sample, Pm$\overline{3}$m) based on in situ XRPD data (see Figure A5 and Figure A6, and Table A3) using Topas [25].

Frame	Rp1	Rp2	Rwp1	Rwp2	χ²	RBragg
0	0.155	0.41	0.273	0.51	1.06	5.34
1	0.158	0.41	0.275	0.51	1.08	5.78
2	0.153	0.42	0.266	0.52	0.98	5.7
3	0.154	0.42	0.263	0.52	0.96	5.58
4	0.161	0.42	0.270	0.53	1.02	5.84
5	0.156	0.41	0.268	0.52	1.00	5.74
6	0.150	0.41	0.262	0.52	0.96	5.83
7	0.151	0.42	0.266	0.52	1.00	5.44
8	0.152	0.42	0.265	0.52	1.00	5.38

), indicating that the hydrogen-induced disorder occurs at room temperature and does not proceed further at elevated temperatures.

3.3. Neutron Diffraction

3.3.1. Ex Situ Neutron Diffraction

The disordered Fe_0.25Pd_0.75 sample shows no significant cell volume increase (Figure A7, a_before = 385.12(4) pm, a_after = 385.18(2) pm) when subjected to deuterium gas (p_max(D₂) = 8.3 MPa, T_max = 558 K). Furthermore, no deuterium atoms can be found in the crystal structure (zero occupation at Wyckoff position 4b, ½, ½, ½; analogous to PdH [27]), and the iron and palladium atoms remain disordered. Therefore, we conclude that disordered Fe_0.25Pd_0.75 does not take up hydrogen under the given conditions. This result is in accordance with hydrogenation studies under higher pressures [17].

The neutron diffraction pattern of ordered FePd₃ shows the same anisotropic reflection broadening (Figure 2) as observed with XRPD (vide supra and Figure A1). For modeling in Rietveld refinements, the same strategy of dividing into two patterns as described above for XRPD was used. Each of the patterns was constrained to the respective XRPD pattern in a simultaneous refinement on X-ray and neutron diffraction data. Please note that here, and for the following refinements, the residual values for pattern 2 are quite high because of low intensities and broad reflections (purple line in Figure 2, Figure A1, Figure A2, Figure A4, Figure A7, Figure A8, Figure A9, Figure A10, Figure A11, Figure A12, Figure A13, Figure A14, Figure A15, Figure A16, Figure A17, Figure A18, Figure A19, Figure A20, Figure A21, Figure A22, Figure A23, Figure A24, Figure A25, Figure A26 and Figure A27). Approximately 12% palladium atoms on iron sites were found with a fixed composition of FePd₃ as a constraint (Table 1). The refined value for the magnetic moment of the iron atoms of 2.3(2) μ_B along [001] is in accordance with the literature data (μ_Fe = 2.73(13) μ_B [28]) within two standard uncertainties. Palladium atoms were not included in the magnetic structure, since the refinements did not converge, indicating small μ_Pd values. This is in line with the small magnetic moments of palladium atoms in FePd₃ found earlier (μ_Pd = 0.35 μ_B [29]).

The unit cell volume of ordered FePd₃ expanded by 0.20% upon deuterium uptake (a(FePd₃) = 385.204(3) pm, a(FePd₃D_0.047(9)) = 385.372(2) pm). Deuterium atoms were localized by difference Fourier analysis. For the refinement of deuterium occupation, the magnetic moment of iron was fixed at 2.344 μ_B due to convergence problems. Two possible deuterium sites were tested by Rietveld refinement. The Wyckoff position 3d (0 0 ½) yields a negative deuterium occupation and is thus considered to be empty. The occupation of deuterium in [Pd₆] octahedral voids at Wyckoff position 1b (½ ½ ½) was refined to 0.047(9). We therefore conclude the deuteride to be FePd₃D_0.047(9) with an anti-perovskite type structure (Figure 1).

3.3.2. In Situ Neutron Diffraction

To study the influence of structural order in FePd₃ on hydrogenation properties, in situ neutron powder diffraction on an ordered sample using deuterium in a sapphire single-crystal cell was performed (Figure 3). Deuterium gas pressure was slowly increased up to 8.0 MPa before raising the temperature to about 550 K. After maintaining the temperature for one hour, the cell was cooled to room temperature under deuterium pressure. As seen in the 2D plot, the intensities of reflections with hkl mixed even and odd (e.g., at 2θ = 28°, 40°, 66°, 73°) decrease with increasing temperature. This observation indicates an increasing level of disorder and decreasing ordered magnetic moment. Reflections (2θ = 42.4°; 45.6°; 56.1°) at high temperatures are single-crystal reflections from the sapphire cell that shift into the range of the detector due to thermal expansion.

The Rietveld refinements of selected NUMORs during the isothermal deuterium pressure increase were performed with fixed magnetic moments. Magnetic investigations of isotypic FePd₃B_x show that only the ordered magnetic moment of the immediate boron environment (only Pd atoms) is changed upon boron incorporation [30], while the magnetic moment of the Fe atoms is not affected. Therefore, we consider fixing the magnetic moments of iron atoms to be an appropriate approximation. The refinements during the quasi-isobaric temperature variation were performed with fixed mixed occupancy. This is because in situ XRPD at 0.5 MPa hydrogen pressure showed no significant change, and a simultaneous refinement of the magnetic moment, the hydrogen occupation, and the mixed occupancy of the metal atoms did not converge. The lattice parameter a of FePd₃D_x increases with rising deuterium pressure (Figure 4, left), which is reflected in the increasing deuterium content. At 8 MPa deuterium pressure, the composition FePd₃D_0.047(9) is reached. The disorder increases with deuterium uptake, as seen from the iron occupation at Wyckoff position 1a decreasing from 0.875(3) to 0.794(3). In the heating step (T_max = 539 K) at 8.2(2) MPa deuterium pressure, the lattice parameter a increases almost linearly, and the deuterium content does not change significantly (Figure 4). The ordered magnetic moment decreases with increasing temperature to zero. The data were fitted with a function for a second-order transition based on the Landau theory with the magnetic moment as the order parameter:

$${\mu }_{ord.}=A {\left(\frac{T_C-T}{T_C}\right)}^{\beta }$$

The resulting Curie temperature, T_C, is 495(8) K, and the critical exponent β equals 0.28(5) (Figure 4). The ordered magnetic moments at temperatures above the Curie temperature are not significantly different from zero or are set to zero at the maximum temperature of 539 K. All observed trends are fully reversible during the cooling step.

4. Discussion

The atomic order in FePd₃ can be controlled via the synthesis protocol, most easily by using iodine as a mineralizing agent. Its use allows full atomic order in one month as compared to 91% order in two months [16]. This method is well known for its potential to promote single-crystal growth [31,32], the synthesis of metastable compounds [32] or single-phase ordered compounds with shorter annealing times [31].

The magnetic moment of 2.3(2) μ_B of FePd₃ determined by refinement of neutron diffraction data differs somewhat from the literature values (μ_Fe = 2.73(13) μ_B [28]); however, the difference is less than two combined standard uncertainties. The difference may also be caused by varying disorder in FePd₃, which was not taken into account in early studies [28,33]. The Curie temperature of 495(8) K, determined by a second-order transition fit (Figure 5), is in accordance with the literature (T_c = 499 K [6]). The determined critical exponent of this fit (β = 0.28(5)) is close (less than two standard uncertainties apart) to the expected values of a 3D Ising model (β = 0.325) and a 3D Heisenberg model (β = 0.365) but far from the mean-field model (β = 0.5) [34]. This is in perfect agreement with a short-range interaction as typical for a magnetic exchange. The disparity between this and previous investigations reporting on a Heisenberg magnet with a critical exponent of 0.371 [6] may be explained by the method of determination. The ordered magnetic moment in this study is only refined in the 001 direction, resulting in a bias toward the 3D Ising model. Furthermore, the uncertainties are relatively high due to the correlation of the hydrogen occupation, the mixed occupation and the ordered magnetic moment.

Deuterium occupies exclusively [Pd₆] octahedral voids in a statistical manner with small occupation parameters. The small deuterium contents are in accordance with studies at high gas pressures [17] (Figure 6, left). The Pd-D distances are between 192.644(2) pm and 192.686(2) pm for FePd₃D_0.013(8) and FePd₃D_0.047(9), respectively, and comparable to known hydrides of MPd₃ compounds, such as MnPd₃H_0.61 (190.0 pm ≤ d(Pd-H) ≤ 197.6 pm) [35].

FePd₃ takes up much less hydrogen than, i.e., MgPd₃ [20], MnPd₃ [35,37] or InPd₃ [38]. This is in accordance with a proposed structure map correlating electronegativity and atomic radius of the metal M with the hydrogen content of MPd₃H_x [39]. Iron, with quite a small atomic radius and an electronegativity of 1.6, is predicted to take up small amounts of hydrogen, which is confirmed in this study. Furthermore, the density of states at the Fermi level of FePd₃ (6.2 [40] or 11.1 states eV⁻¹ atom⁻¹ [41]) is remarkably high compared to other MPd₃ compounds crystallizing in the AuCu₃ type, such as MgPd₃ (1.13 states eV⁻¹ atom⁻¹ [42]), MnPd₃ (2.18 [43] or 2.84 states eV⁻¹ atom⁻¹ [44]) and InPd₃ (3.3 states eV⁻¹ atom⁻¹ [45]), which might also have an impact on the hydrogen uptake capacity. At room temperature, the hydrogenation follows Sieverts’ law [36] (Figure 6, right), with low pressure (this work) and high pressure data [17] differing somewhat (Figure 6). The moderate fit and higher error in fit parameters for the high pressure data may be caused by increasing hydrogen–hydrogen interaction in the solid solution and larger differences between fugacity and pressure, the latter of which was used here as an approximation.

To compare the possible hydrogenation of ordered and disordered FePd₃, it is useful to look at the maximum hydrogen content of both structure types. The unit cell of MPd₃ compounds in the AuCu₃ type contains one [Pd₆] and three [M₂Pd₄] octahedral voids. Therefore, the probability of a [Pd₆] octahedral void is 0.25, yielding the formula MPd₃H for a maximum occupation of hydrogen in [Pd₆] sites. For disordered MPd₃ compounds crystallizing in the Cu type, the probability of a [Pd₆] octahedral void is 0.178 (=0.75⁶), assuming a 75% probability of finding a palladium atom at any position in the crystal structure. A maximum hydrogen occupation using only [Pd₆] sites yields the formula MPd₃H_0.712. According to this consideration, the ordered compound may absorb more hydrogen if only [Pd₆] sites are involved. It is well known that hydrogen uptake in disordered FePd₃ is indeed less than that for ordered FePd₃ [17]. In this regard, it is remarkable that the disorder in FePd₃H_x increases with hydrogen uptake despite the statistical decrease in [Pd₆] octahedral sites. Furthermore, the disorder reversibly increases with temperature, with near constant hydrogen content. The preference of [Pd₆] sites for hydrogen atoms can be inferred from many examples of hydrogenation reactions of MPd₃ compounds structurally related to cubic close packing. The thermodynamic driving force for hydrogen-induced rearrangements (from TiAl₃ type or ZrAl₃ type to AuCu₃ type) arises from the preference for Pd-H bonding and, consequently, an increase in the number of [Pd₆] octahedral voids [46]. Furthermore, other interstitial FePd₃ compounds, such as FePd₃B_x, also prefer [Pd₆] octahedral sites for the interstitial atoms [30]. The immediate environment of absorbed hydrogen is responsible for the hydrogen solubility in metals and intermetallic compounds [47]. Under the assumption of a preference of hydrogen atoms for [Pd₆] octahedra, the unexpected increasing disorder upon hydrogenation may be understood in terms of local short-range order of formed HPd₆ octahedra and a lack of long-range crystallographic order.

The findings on the magnetic and structural details of FePd₃ and its hydrides show the complex interplay between hydrogen uptake, atomic and magnetic order in intermetallics. This raises questions on the validity of the assumption of constant atomic order, which is often made for investigations on the effects of hydrogen incorporation on magnetic properties, and calls for further investigations on this fascinating subject.

5. Conclusions

The use of iodine as a mineralizing agent decreases the annealing time and enables higher ordering of metal atoms in the synthesis of FePd₃. At moderate hydrogen pressures (p ≤ 8 MPa), disordered Fe_0.25Pd_0.75 absorbs a negligible amount of hydrogen, and ordered FePd₃ forms the hydride FePd₃H_0.047(9). Hydrogen is incorporated at [Pd₆] octahedral voids, and the hydrogenation follows Sieverts’ law. During heating, the ordered magnetic moment decreases, and FePd₃H_x behaves like a 3D Ising or Heisenberg magnet. Simultaneously, the disorder of the metal atoms increases slightly. All temperature-dependent effects are fully reversible. Hydride formation in FePd₃ influences crystallographic and magnetic order alike. The citation of Carl G. Jung “In all chaos there is a cosmos, in all disorder a secret order” [48] can be understood as order only arising from chaos. In contrast to that, hydrogen seems to enhance the metal diffusion in FePd₃, resulting in long-range disorder arising from local order of the immediate hydrogen environment. This induced metal diffusion and the resulting change in the arrangement of the metal atoms at the surface might raise interest in catalysis.