Multiscale Simulations for Defect-Controlled Processing of Group IV Materials
Abstract
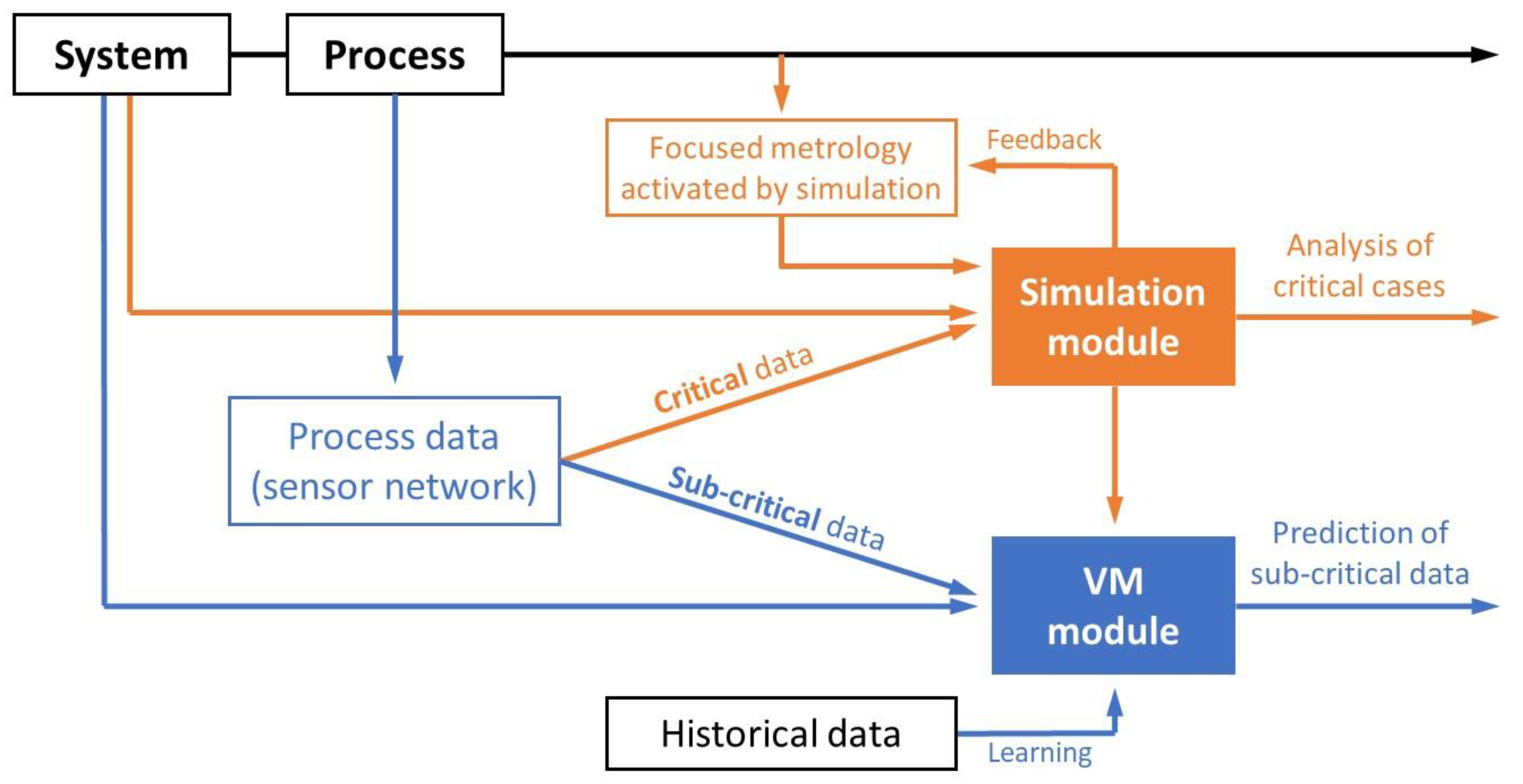
:1. Introduction
2. Methods
3. Results
3.1. Environment Scale Study and Modeling
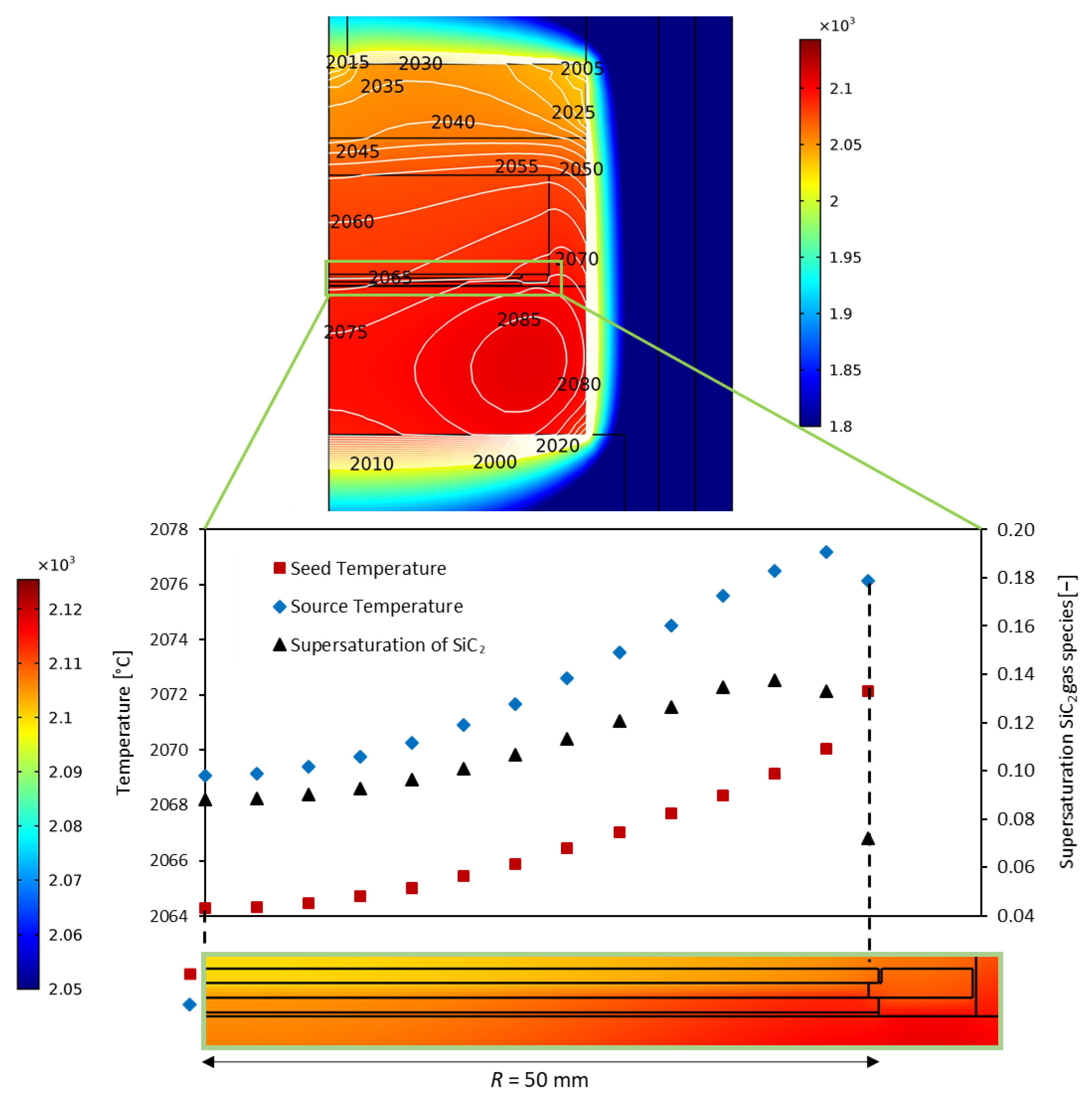
3.1.1. Temperature Field Analysis in PVD Processes of SiC Growth
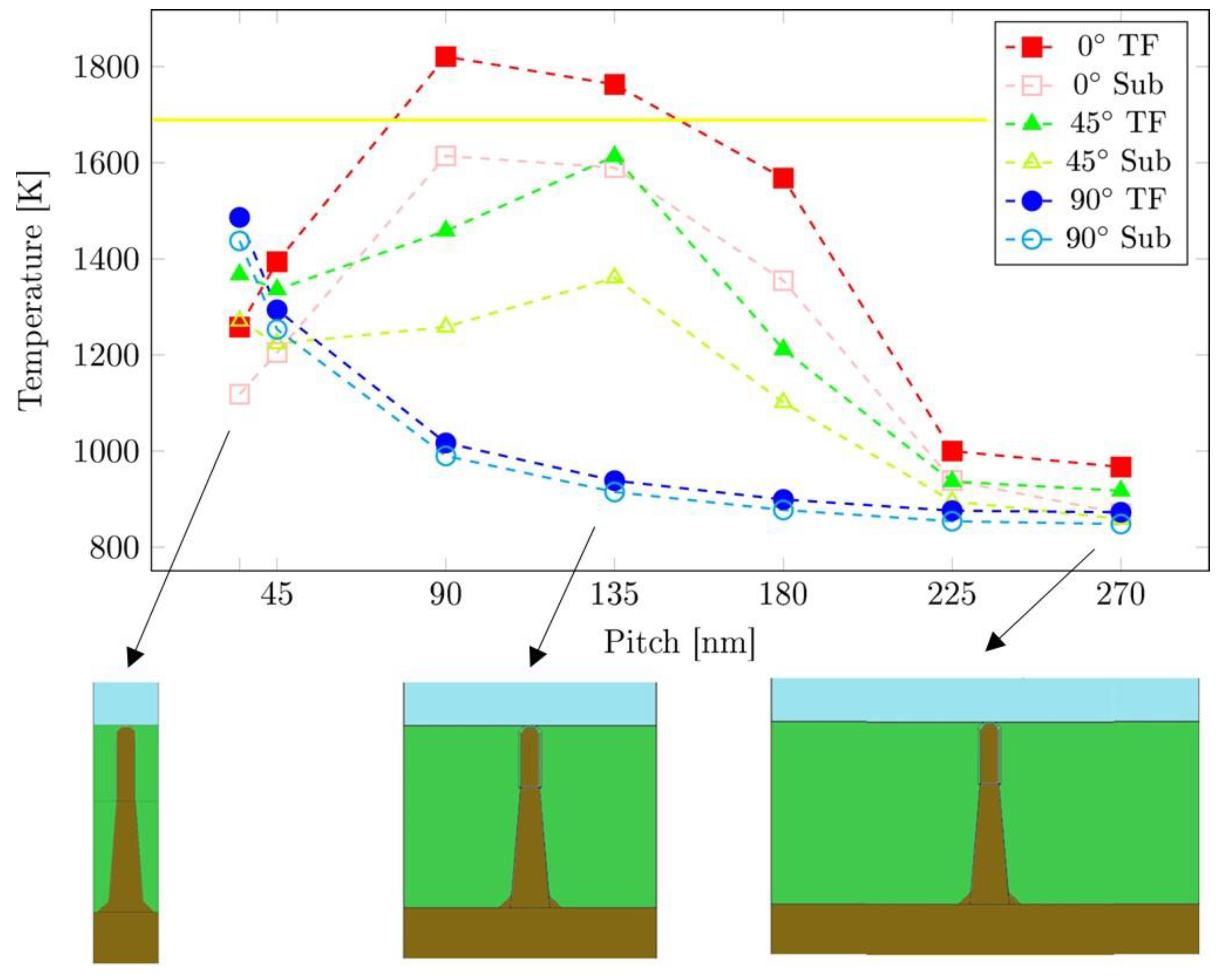
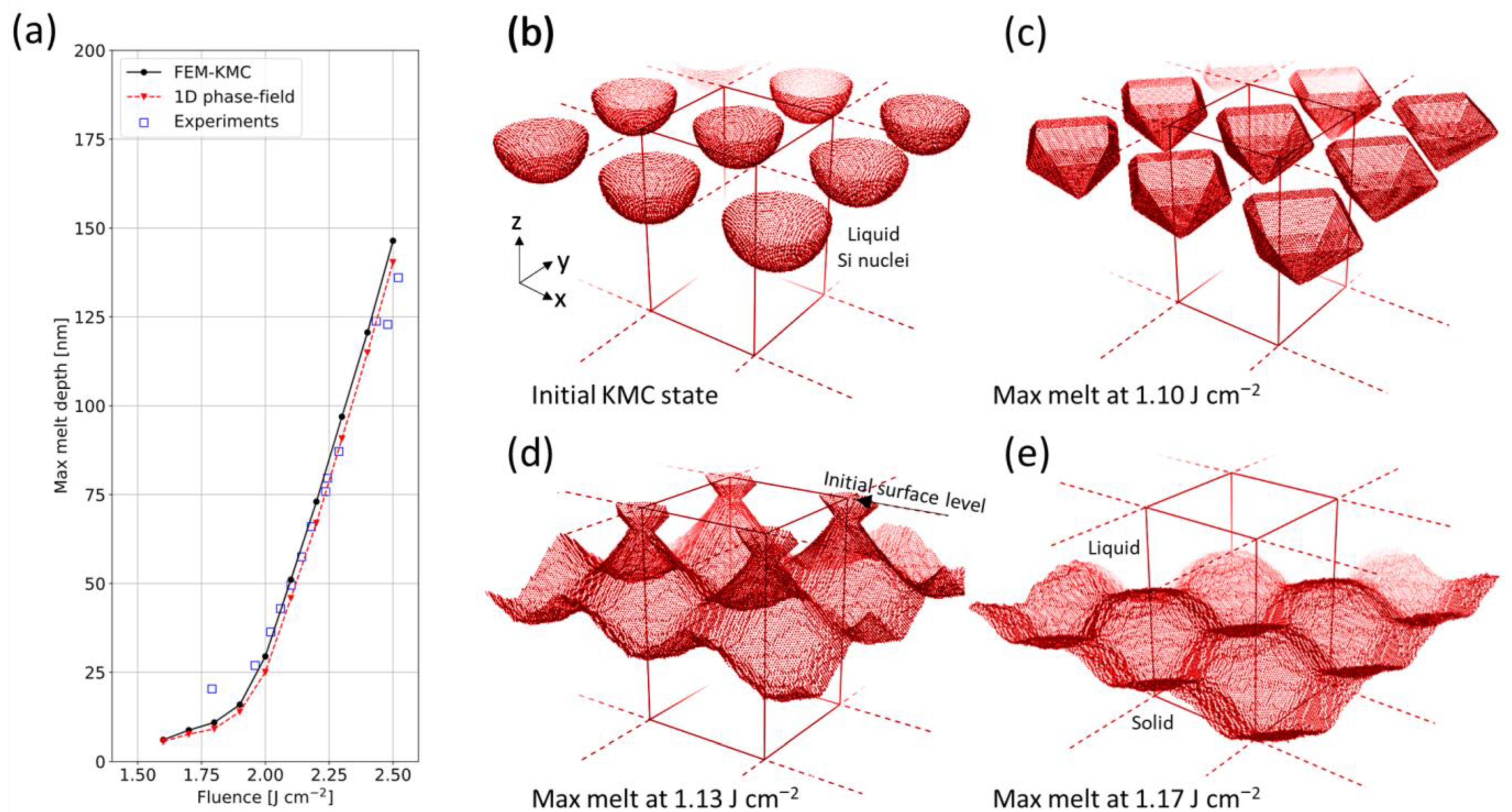
3.1.2. Ultra-Fast Heating of Materials in PLA Processing
3.2. Process Simulation Predictions at the Mesoscale
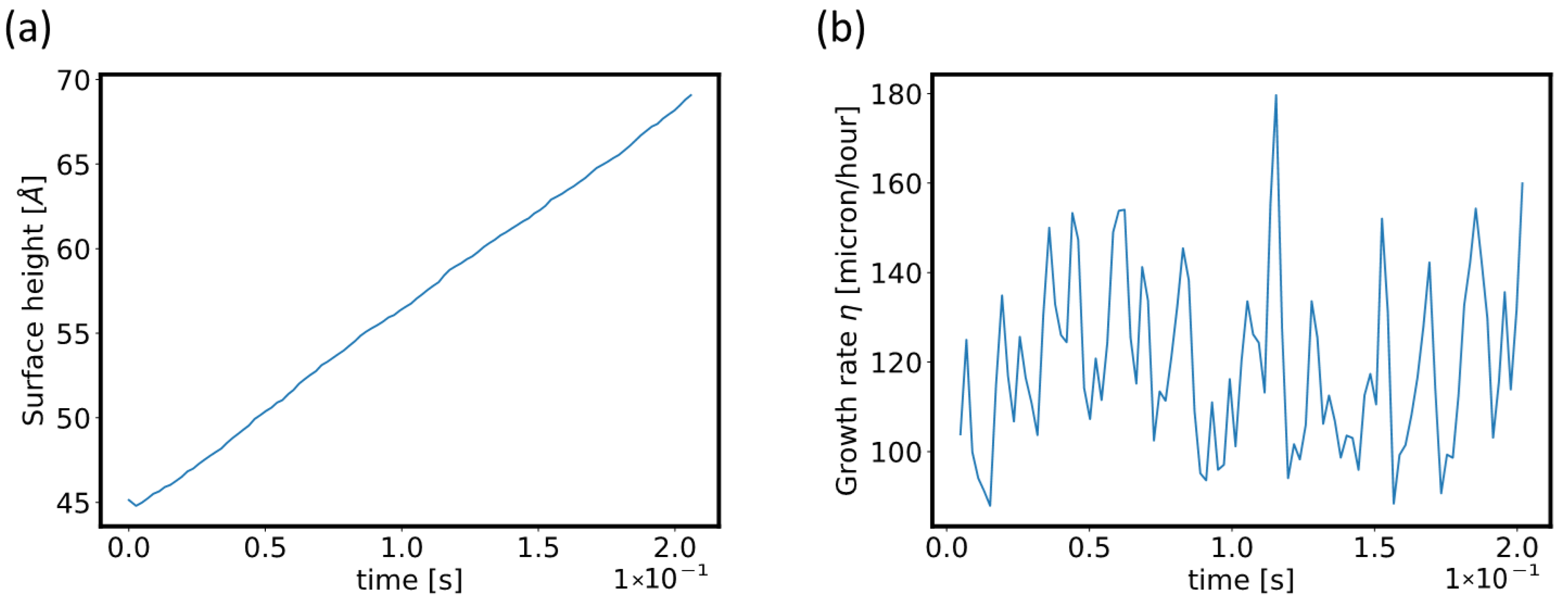
3.2.1. Local Growth Rate Prediction for a 3C-SiC PVT Growth
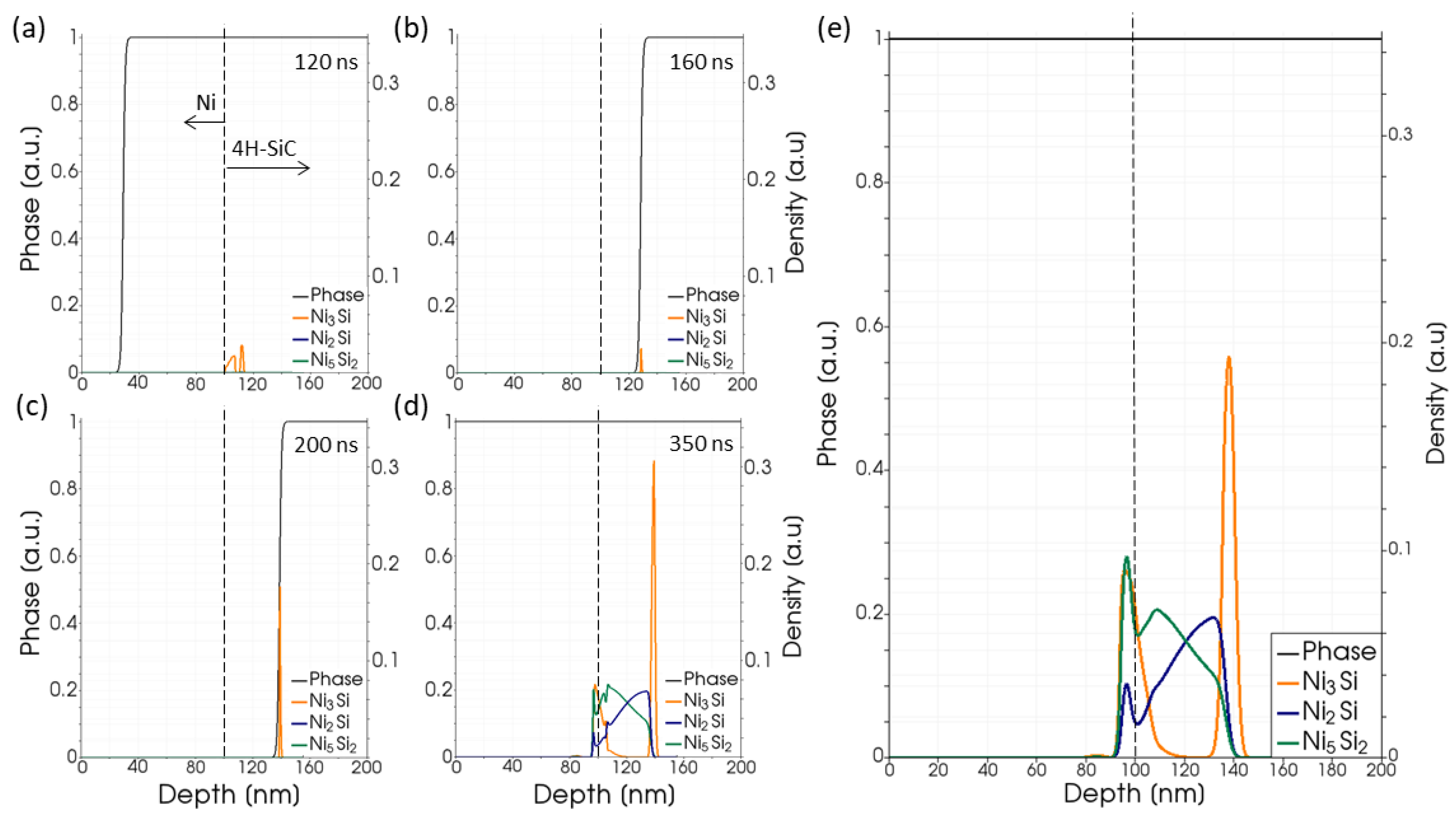
3.2.2. Material Transformations at the Mesoscale in a PLA Process
3.3. Process Simulation Predictions at the Atomic Scale
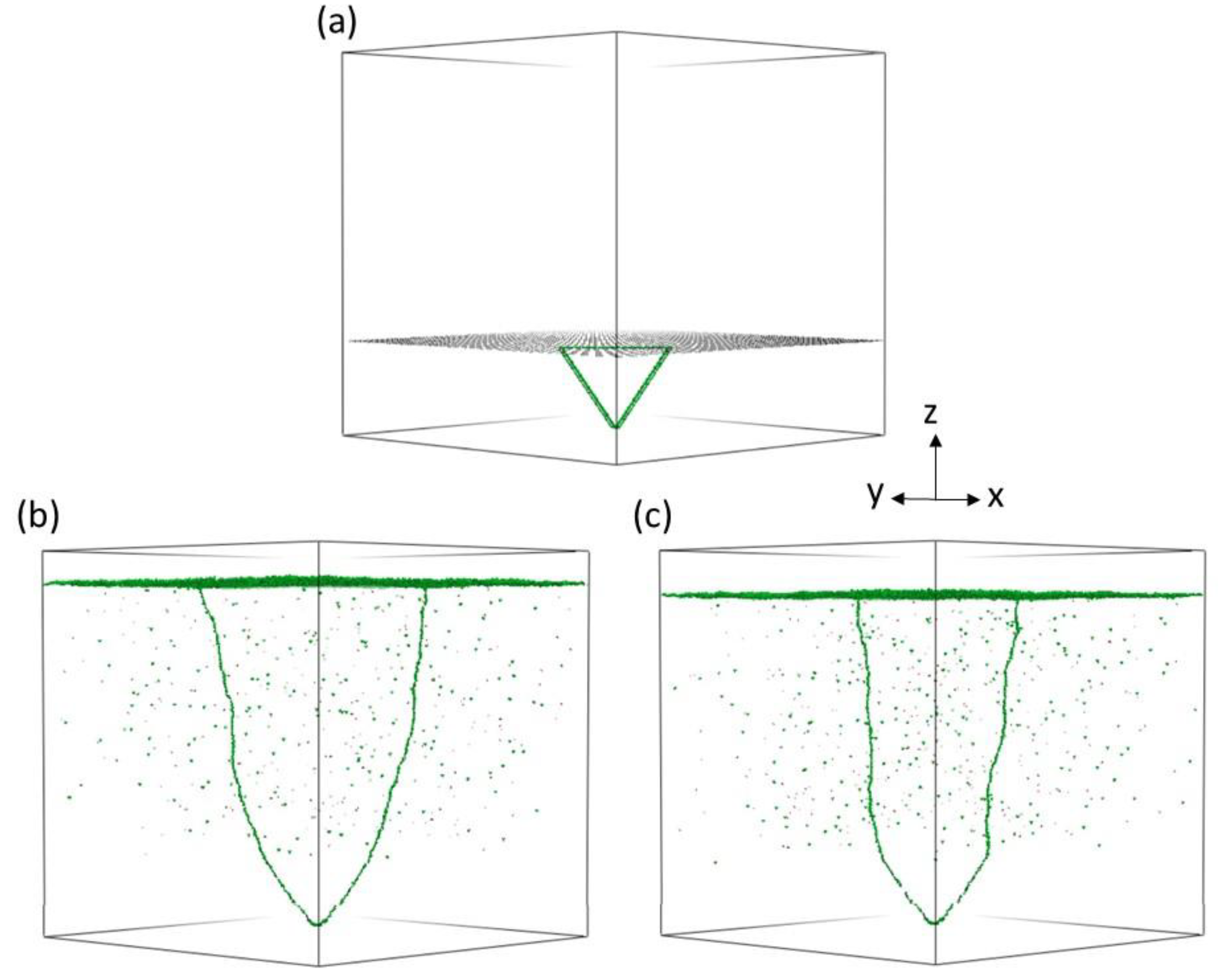
3.3.1. Defect Generation and Evolution in a 3C-SiC PVD Growth
- First, the growth rate of the process is estimated from the experimental gas vapor pressures.
- Consequently, the input file for the simulation of the PVD epitaxial growth within the MulSKIPS code is generated. This contains information on the simulated structure, the energetics of the Monte Carlo events, as well as their frequency pre-factors.
- Then, the MulSKIPS simulation runs in a pre-defined folder.
- At the end of the simulation, analysis of the crystalline quality of the epitaxial-growth substrate and the eventual epitaxial defects takes place.
- Finally, the growth rate is extracted from the KMC MulSKIPS run and can be readily compared to the respective experimental results.
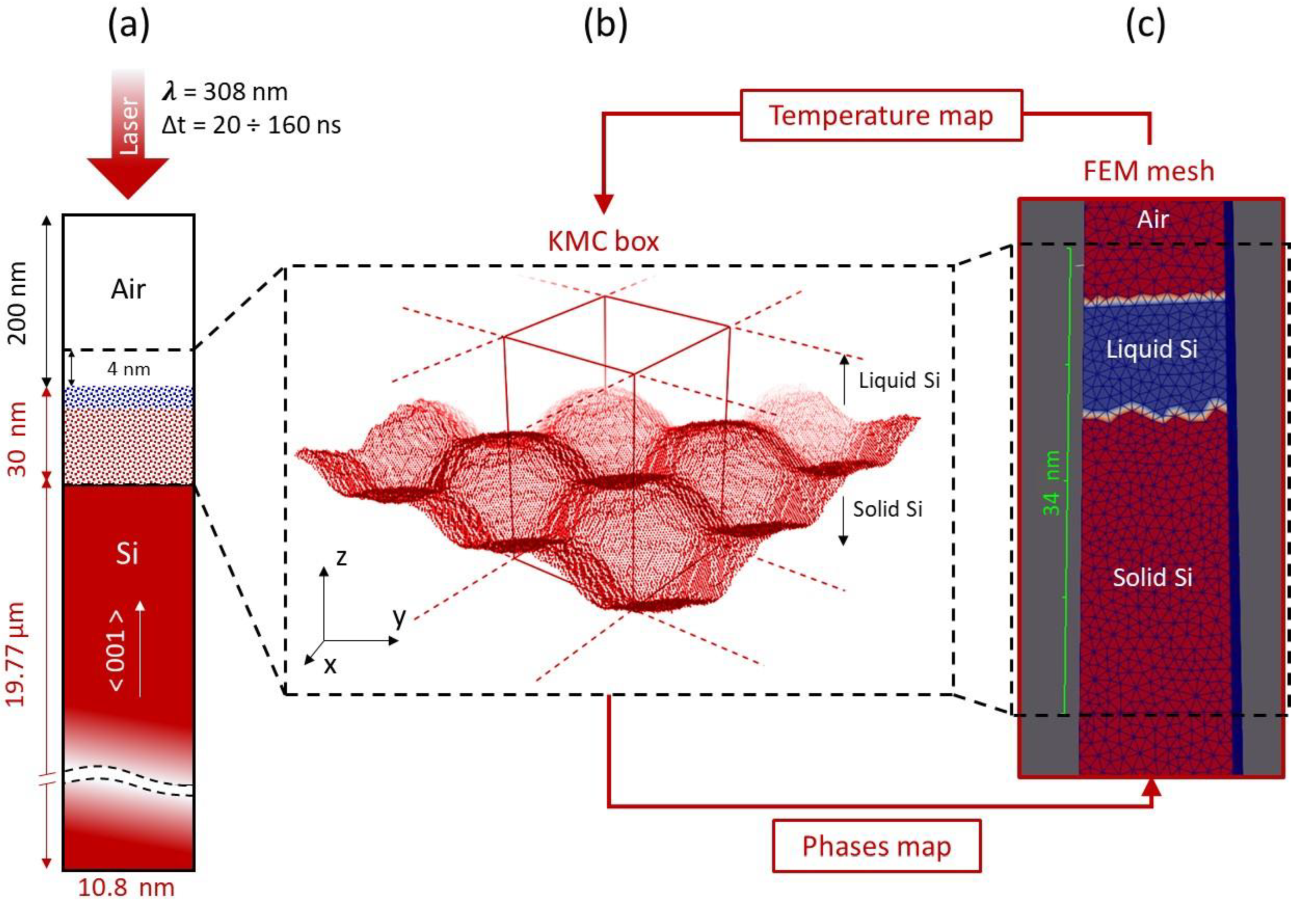
3.3.2. FEM–KMC Modeling of PLA of a Si(001) Surface
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- IBM. What Is a Digital Twin? Available online: https://www.ibm.com/topics/what-is-a-digital-twin (accessed on 20 November 2022).
- Ed Fontes “Digital Twins: Not Just Hype”. Available online: https://www.comsol.com/blogs/digital-twins-not-just-hype/ (accessed on 20 November 2022).
- Deagen, M.E.; Brinson, L.C.; Vaia, R.A.; Schadler, L.S. The materials tetrahedron has a “digital twin”. MRS Bull. 2022, 47, 379–388. [Google Scholar] [CrossRef] [PubMed]
- Marsland, S. Machine Learning; CRC Press: Boca Raton, FL, USA; Taylor & Francis Inc.: Boca Raton, FL, USA, 2014. [Google Scholar]
- Fei, T.; Jiangfeng, C.; Qinglin, Q.; Zhang, M.; Zhang, H.; Fangyuan, S. Digital twin-driven product design, manufacturing and service with big data. Int. J. Adv. Manuf. Technol. 2018, 94, 3563–3576. [Google Scholar]
- Chang, Y.; Kang, Y.; Hsu, C.; Chang, C.-T.; Chan, T.Y. Virtual Metrology Technique for Semiconductor Manufacturing. In Proceedings of the 2006 IEEE International Joint Conference on Neural Network Proceedings, Vancouver, BC, Canada, 16–21 July 2006; pp. 5289–5293. [Google Scholar]
- Kang, P.; Lee, H.-J.; Cho, S.; Kim, D.; Park, J.; Park, C.-K.; Doh, S. A virtual metrology system for semiconductor manufacturing. Exp. Sys. Appl. 2009, 36, 12554. [Google Scholar] [CrossRef]
- Suthar, K.; Shah, D.; Wang, J.; He, Q.P. Next-generation virtual metrology for semiconductor manufacturing: A feature-based framework. Comp. Chem. Eng. 2019, 127, 140. [Google Scholar] [CrossRef]
- Lenz, B.; Barak, B.; Mührwald, J.; Leicht, C.; Lenz, B. Virtual Metrology in Semiconductor Manufacturing by Means of Predictive Machine Learning Models. In Proceedings of the 12th International Conference on Machine Learning and Applications, Miami, FL, USA, 4–7 December 2013; pp. 174–177. [Google Scholar]
- Choi, J.E.; Hong, S.J. Machine learning-based virtual metrology on film thickness in amorphous carbon layer deposition process. Meas. Sens. 2021, 16, 100046. [Google Scholar] [CrossRef]
- Fish, J.; Wagner, G.J.; Keten, S. Mesoscopic and multiscale modelling in materials. Nat. Mater. 2021, 20, 774l. [Google Scholar] [CrossRef]
- Cheimarios, N.; Kokkoris, G.; Boudouvis, A.G. Multiscale modeling in chemical vapor deposition processes: Coupling reactor scale with feature scale computations. Chem. Eng. Sci. 2010, 65, 5018. [Google Scholar] [CrossRef]
- Danielsson, O.; Karlsson, M.; Sukkaew, P.; Pedersen, H.; Ojamae, L. A Systematic Method for Predictive In Silico Chemical Vapor Deposition. J. Phys. Chem. C 2020, 124, 7725. [Google Scholar] [CrossRef] [Green Version]
- Fisicaro, G.; Bongiorno, C.; Deretzis, I.; Giannazzo, F.; La Via, F.; Roccaforte, F.; Zielinski, M.; Zimbone, M.; La Magna, A. Genesis and evolution of extended defects: The role of evolving interface instabilities in cubic SiC. Appl. Phys. Rev. 2020, 7, 021402. [Google Scholar] [CrossRef]
- COMSOL. Available online: https://www.comsol.com/ (accessed on 20 November 2022).
- Steiner, J.; Arzig, A.; Denisov, A.; Wellmann, P. Impact of Varying Parameters on the Temperature Gradients in 100 mm Silicon Carbide Bulk Growth in a Computer Simulation Validated by Experimental Results. Cryst. Res. Technol. 2020, 55, 1900121. [Google Scholar] [CrossRef]
- MulSKIPS. Available online: https://github.com/MulSKIPS/MulSKIPS (accessed on 20 November 2022).
- La Magna, A.; Alberti, A.; Barbagiovanni, E.; Bongiorno, C.; Cascio, M.; Deretzis, I.; La Via, F.; Smecca, E. Simulation of the growth kinetics in group IV compound semiconductors. Phys. Status Solidi A 2019, 216, 1800597. [Google Scholar] [CrossRef]
- FENICS. Available online: https://fenicsproject.org/ (accessed on 20 November 2022).
- Alnæs, M. The fenics project version 1.5. Arch. Numer. Softw. 2015, 3, 9–23. [Google Scholar]
- Calogero, G.; Raciti, D.; Acosta-Alba, P.; Cristiano, F.; Deretzis, I.; Fisicaro, G.; Huet, K.; Kerdilès, S.; Sciuto, A.; La Magna, A. Multiscale modeling of ultrafast melting phenomena. npj Comput. Mater. 2022, 8, 36. [Google Scholar] [CrossRef]
- Paraview. Available online: https://www.paraview.org/ (accessed on 20 November 2022).
- CEA. V_sim. Available online: https://www.mem-lab.fr/en/Pages/L_SIM/Softwares/V_Sim.aspx (accessed on 20 November 2022).
- Gmsh. Available online: https://gmsh.info/ (accessed on 20 November 2022).
- Geuzaine, C.; Remacle, J.-F. Gmsh: A 3-d finite element mesh generator with built-in pre- and post-processing facilities. Int. J. Numer. Methods Eng. 2009, 79, 1309–1331. [Google Scholar] [CrossRef]
- Haidar, Y.; Rhallabi, A.; Pateau, A.; Mokrani, A.; Taher, F.; Roqueta, F.; Boufnichel, M. Simulation of cryogenic silicon etching under SF6/O2/Ar plasma discharge. J. Vac. Sci. Technol. 2016, 34, 061306. [Google Scholar] [CrossRef]
- Pateau, A.; Rhallab, A.; Fernande, M.-C.; Boufnichel, M.; Roqueta, F. Modeling of inductively coupled plasma SF6/O2/Ar plasma discharge: Effect of O2 on the plasma kinetic properties. J. Vac. Sci. Technol. A 2014, 32, 021303. [Google Scholar] [CrossRef]
- La Magna, A.; Fisicaro, G.; Nicotra, G.; Spiege, Y.; Torregrosa, F. Atomic scale Monte Carlo simulations of BF3 plasma immersion ion implantation in Si. Phys. Stat. Sol. C 2014, 11, 109. [Google Scholar]
- La Magna, A.; Alippi, P.; Privitera, V.; Fortunato, G. Role of light scattering in excimer laser annealing of Si. Appl. Phys. Lett. 2005, 86, 161905. [Google Scholar] [CrossRef]
- Escoffery, C.A. Improved Knudsen-Cell Vapor Source for Vacuum Depositions. Rev. Sci. Instrum. 1964, 35, 913. [Google Scholar] [CrossRef]
- Smecca, E.; Valenzano, V.; Valastro, S.; Deretzis, I.; Mannino, G.; Malandrino, G.; Accorsi, G.; Colella, S.; Rizzo, A.; la Magna, A.; et al. Two-step MAPbI3 deposition by low-vacuum proximity-space-effusion for high-efficiency inverted semitransparent perovskite solar cells. J. Mater. Chem. A 2021, 9, 16456. [Google Scholar] [CrossRef]
- Wellmann, P.; Ohtani, N.; Rupp, R. (Eds.) Wide Bandgap Semiconductors for Power Electronics: Materials, Devices, Applications; Wiley-VCH: Weinheim, Germany, 2021; Chapter 5. [Google Scholar]
- Ma, R.H.; Chen, Q.S.; Zhang, H.; Prasad, V.; Balkas, C.M.; Yushin, N.K. Modeling of silicon carbide crystal growth by physical vapor transport method. J. Cryst. Growth 2000, 211, 352–359. [Google Scholar] [CrossRef]
- Avrov, D.; Bakin, A.; Dorozhkin, S.; Rastegaev, V.; Tairov, Y. The analysis of mass transfer in system beta-SiC—Alpha-SiC under silicon carbide sublimation growth. J. Cryst. Growth 1999, 198–199, 1011–1014. [Google Scholar] [CrossRef]
- Rankl, D.; Jokubavicius, V.; Syväjärvi, M.; Wellman, P.J. Quantitative Study of the Role of Supersaturation during Sublimation Growth on the Yield of 50 mm 3C-SiC. Mater. Sci. Forum 2015, 821–823, 77–80. [Google Scholar] [CrossRef]
- Cristiano, F.; La Magna, A. Laser Annealing Processes in Semiconductors Technology: Theory, Modeling, and Applications in Nanoelectronics; Elsevier: Duxford, UK, 2021. [Google Scholar]
- Lombardo, S.F.; Boninelli, S.; Cristiano, F.; Fisicaro, G.; Fortunato, G.; Grimaldi, M.G.; Impellizzeri, M.; Italia, A.; Marino, R.; Milazzo, E.; et al. Laser annealing in Si and Ge: Anomalous physical aspects and modeling approaches. Mat. Sci. Sem. Proc. 2017, 62, 80. [Google Scholar] [CrossRef]
- Cartoixà, X.; Colombo, L.; Rurali, R. Thermal Rectification by Design in Telescopic Si Nanowires. Nano Lett. 2015, 15, 8255. [Google Scholar] [CrossRef]
- Kaiser, J.; Feng, T.; Maassen, J.; Wang, X.; Ruan, X.; Lundstrom, M. Thermal transport at the nanoscale: A Fourier’s law vs. phonon Boltzmann equation study. J. Appl. Phys. 2017, 121, 044302. [Google Scholar] [CrossRef] [Green Version]
- Sciuto, A.; Lombardo, S.F.; Deretzis, I.; Grimaldi, M.G.; Huet, K.; La Magna, A. Phononic transport and simulations of annealing processes in nanometric complex structures. Phys. Rev. Mat. 2020, 4, 056007. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, S.; Wan, S.; Zhang, Y.; Huang, M.; Yi, L. Transient reflectivity measurement of photocarrier dynamics in GaSe thin films. Appl. Phys. B 2017, 123, 86. [Google Scholar] [CrossRef]
- Lombardo, S.F.; Boninelli, S.; Cristiano, F.; Deretzis, I.; Grimaldi, M.G.; Huet, K.; Napolitani, E.; La Magna, A. Phase field model of the nanoscale evolution during the explosive crystallization phenomenon. J. Appl. Phys. 2018, 123, 105105. [Google Scholar] [CrossRef]
- Osano, Y.; Ono, K. An Atomic Scale Model of Multilayer Surface Reactions and the Feature Profile Evolution during Plasma Etching. Jpn. J. Appl. Phys. 2005, 44, 8650. [Google Scholar] [CrossRef]
- Osher, S.; Sethian, J.A. Fronts propagating with curvature-dependent speed: Algorithms based on Hamilton-Jacobi formulations. J. Comp. Phys. 1988, 79, 12. [Google Scholar] [CrossRef] [Green Version]
- La Magna, A.; Garozzo, G. Factors Affecting Profile Evolution in Plasma Etching of SiO2: Modeling and Experimental Verification. J. Electrochem. Soc. 2003, 150, 178. [Google Scholar] [CrossRef]
- Wellmann, P.J. Review of SiC crystal growth technology. Semicond. Sci. Technol. 2018, 33, 103001. [Google Scholar] [CrossRef]
- Cale, T.S.; Mahadev, V. Feature scale transport and reaction during low-pressure deposition processes. Thin Film. 1996, 22, 175–276. [Google Scholar]
- Lilov, S.K. Thermodynamic analysis of the Gas Phase at the Dissociative Evaporation of Silicon Carbide. Cryst. Res. Technol 1993, 28, 503–510. [Google Scholar] [CrossRef]
- Qiu, Y.; Cristiano, F.; Huet, K.; Mazzamuto, F.; Fisicaro, G.; La Magna, A.; Quillec, M.; Cherkashin, N.; Wang, H.; Duguay, S.; et al. Extended Defects Formation in Nanosecond Laser-Annealed Ion Implanted Silicon. Nano Lett. 2014, 14, 1769–1775. [Google Scholar] [CrossRef] [Green Version]
- Cerny, R.; Chab, V.; Prikryl, P. Numerical simulation of the formation of Ni silicides induced by pulsed lasers. Comp. Mat. Sci. 1995, 4, 269. [Google Scholar] [CrossRef]
- Almeida, J.M.P.; Paula, K.T.; Arnold, C.B.; Medonca, C.R. Sub-wavelength self-organization of chalcogenide glass by direct laser writing. Opt. Mat. 2018, 84, 259. [Google Scholar] [CrossRef]
- Stiffler, S.; Evans, P.; Greer, A. Interfacial transport kinetics during the solidification of silicon. Acta Metall. Mater. 1992, 40, 401617. [Google Scholar] [CrossRef]
- Karma, A.; Rappel, W.J. Quantitative phase-field modeling of dendritic growth in two and three dimensions. Phys. Rev. E 1998, 57, 4323. [Google Scholar] [CrossRef] [Green Version]
- Huet, K.; Aubin, J.; Raynal, P.E.; Curvers, B.; Verstraete, A.; Lespinasse, B.; Mazzamuto, A.; Sciuto, S.F.; Lombardo, A.; La Magna, P.; et al. Pulsed laser annealing for advanced technology nodes: Modeling and calibration. Appl. Surf. Sci. 2020, 505, 144470. [Google Scholar] [CrossRef]
- Alberti, A.; La Magna, A.; Cuscunà, M.; Fortunato, G.; Spinella, C.; Privitera, V. Nickel-affected silicon crystallization and silicidation on polyimide by multipulse excimer laser annealing. J. Appl. Phys. 2010, 108, 123511. [Google Scholar] [CrossRef]
- Alberti, A.; La Magna, A. Role of the early stages of Ni-Si interaction on the structural properties of the reaction products. J. Appl. Phys. 2013, 114, 121301. [Google Scholar] [CrossRef]
- Sanzaro, S.; Bongiorno, C.; Badalà, P.; Bassi, A.; Franco, G.; Vasquez, P.; Alberti, A.; La Magna, A. Inter-diffusion, melting and reaction interplay in Ni/4H-SiC under excimer laser annealing. Appl. Surf. Sci. 2021, 539, 148218. [Google Scholar] [CrossRef]
- Sanzaro, S.; Bongiorno, C.; Badalà, P.; Bassi, A.; Deretzis, I.; Enachescu, M.; Franco, G.; Fisicaro, G.; Vasquez, P.; Alberti, A.; et al. Simulations of the Ultra-Fast Kinetics in Ni-Si-C Ternary Systems under Laser Irradiation. Materials 2021, 14, 4769. [Google Scholar] [CrossRef] [PubMed]
- Schöler, M.; La Via, F.; Mauceri, M.; Wellmann, P. Overgrowth of Protrusion Defects during Sublimation Growth of Cubic Silicon Carbide Using Free-Standing Cubic Silicon Carbide Substrates. Cryst. Growth Des. 2021, 21, 4046–4054. [Google Scholar] [CrossRef]
- Sun, Z.; Gupta, M.C. A study of laser-induced surface defects in silicon and impact on electrical properties. J. Appl. Phys. 2018, 124, 223103. [Google Scholar] [CrossRef]
- Bonati, L.; Parrinello, M. Silicon Liquid Structure and Crystal Nucleation from Ab Initio Deep Metadynamics. Phys. Rev. Lett. 2018, 121, 265701. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dagault, L.; Kerdilès, S.; Acosta-Alba, P.; Hartmann, J.-M.; Barnes, J.-P.; Gergaud, P.; Scheid, E.; Cristiano, F. Investigation of recrystallization and stress relaxation in nanosecond laser annealed Si1−xGex/Si epilayers. Appl. Surf. Sci. 2020, 527, 146752. [Google Scholar] [CrossRef]
- Buta, D.; Asta, M.; Hoyt, J.J. Atomistic simulation study of the structure and dynamics of a faceted crystal-melt interface. Phys. Rev. E 2008, 78, 031605. [Google Scholar] [CrossRef]
- Hribernik, K.; Cabri, G.; Mandreoli, F.; Mentzas, G. Autonomous, context-aware, adaptive Digital Twins—State of the art and roadmap. Comput. Ind. 2021, 133, 103508. [Google Scholar] [CrossRef]
- Lovarelli, G.; Calogero, G.; Fiori, G.; Iannaccone, G. Multiscale Pseudoatomistic Quantum Transport Modeling for van der Waals Heterostructures. Phys. Rev. Appl. 2022, 18, 034045. [Google Scholar] [CrossRef]
- Auf der Maur, M.; Penazzi, G.; Romano, G.; Sacconi, F.; Pecchia, A.; Di Carlo, A. The Multiscale Paradigm in Electronic Device Simulation. IEEE Trans. Elec. Dev. 2011, 58, 1425. [Google Scholar] [CrossRef]
- Perno, M.; Hvam, L.; Haug, A. Implementation of digital twins in the process industry: A systematic literature review of enablers and barriers. Comput. Ind. 2022, 134, 103558. [Google Scholar] [CrossRef]


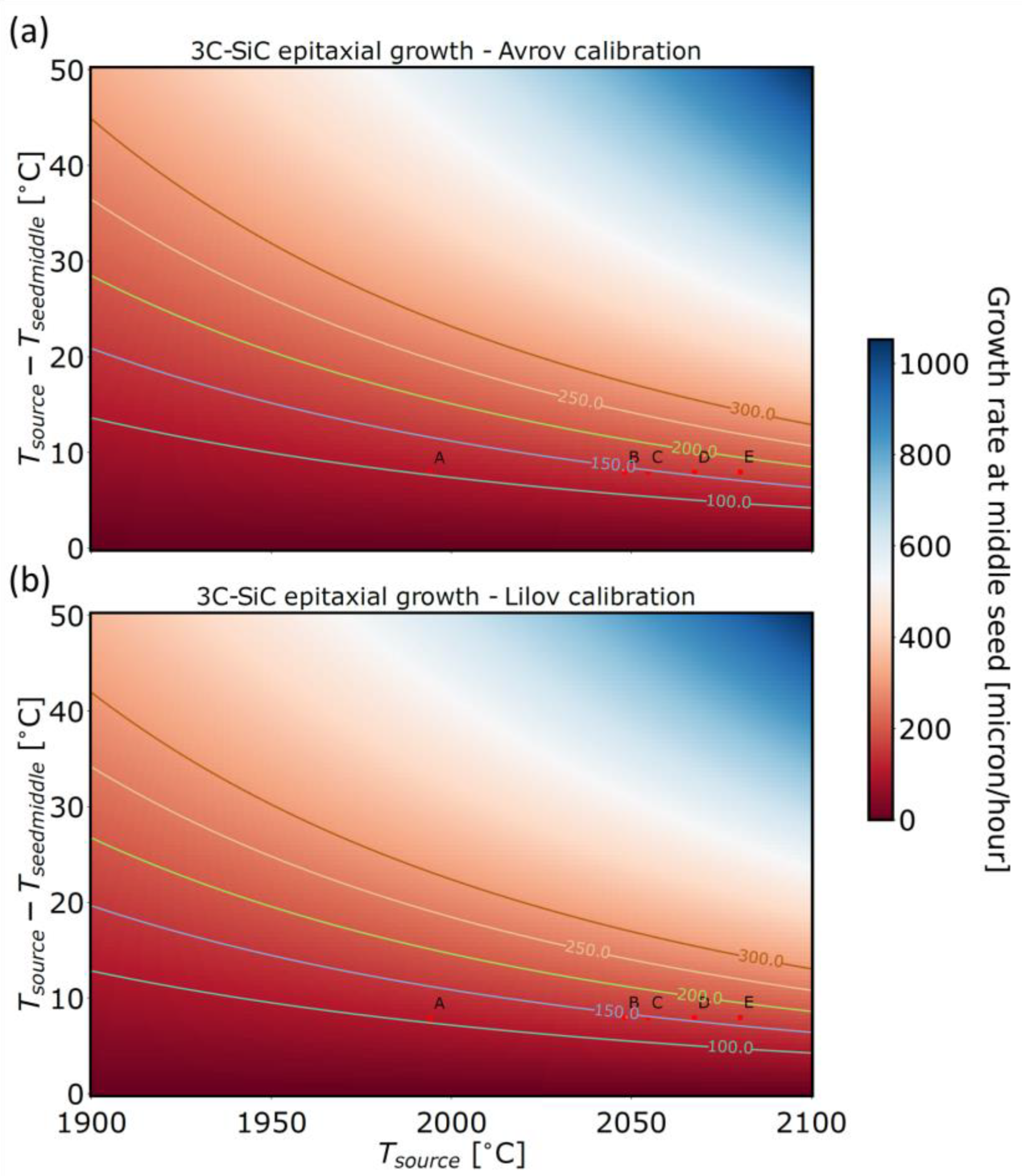

| Growth Rates [μm/Hours] | Sample A | Sample B | Sample C | Sample D | Sample E |
|---|---|---|---|---|---|
| Experimental | 101 | 208 | 230 | 231 | 287 |
| KMC MulSKIPS | 119 | 164 | 170 | 183 | 196 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Calogero, G.; Deretzis, I.; Fisicaro, G.; Kollmuß, M.; La Via, F.; Lombardo, S.F.; Schöler, M.; Wellmann, P.J.; La Magna, A. Multiscale Simulations for Defect-Controlled Processing of Group IV Materials. Crystals 2022, 12, 1701. https://doi.org/10.3390/cryst12121701
Calogero G, Deretzis I, Fisicaro G, Kollmuß M, La Via F, Lombardo SF, Schöler M, Wellmann PJ, La Magna A. Multiscale Simulations for Defect-Controlled Processing of Group IV Materials. Crystals. 2022; 12(12):1701. https://doi.org/10.3390/cryst12121701
Chicago/Turabian StyleCalogero, Gaetano, Ioannis Deretzis, Giuseppe Fisicaro, Manuel Kollmuß, Francesco La Via, Salvatore F. Lombardo, Michael Schöler, Peter J. Wellmann, and Antonino La Magna. 2022. "Multiscale Simulations for Defect-Controlled Processing of Group IV Materials" Crystals 12, no. 12: 1701. https://doi.org/10.3390/cryst12121701
APA StyleCalogero, G., Deretzis, I., Fisicaro, G., Kollmuß, M., La Via, F., Lombardo, S. F., Schöler, M., Wellmann, P. J., & La Magna, A. (2022). Multiscale Simulations for Defect-Controlled Processing of Group IV Materials. Crystals, 12(12), 1701. https://doi.org/10.3390/cryst12121701










