Electron and Hole Mobility of SnO2 from Full-Band Electron–Phonon and Ionized Impurity Scattering Computations
Abstract
1. Introduction
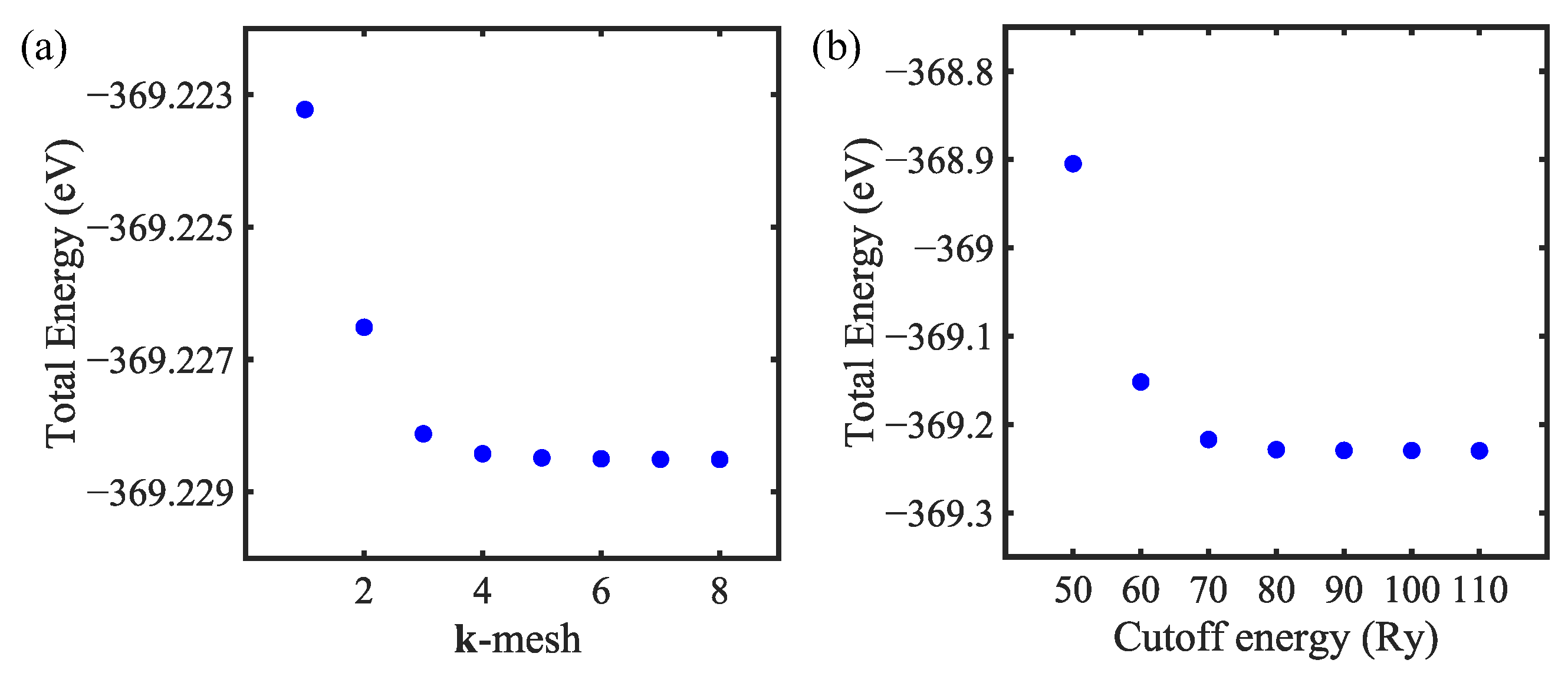
2. Computational Methods
3. Results and Discussions
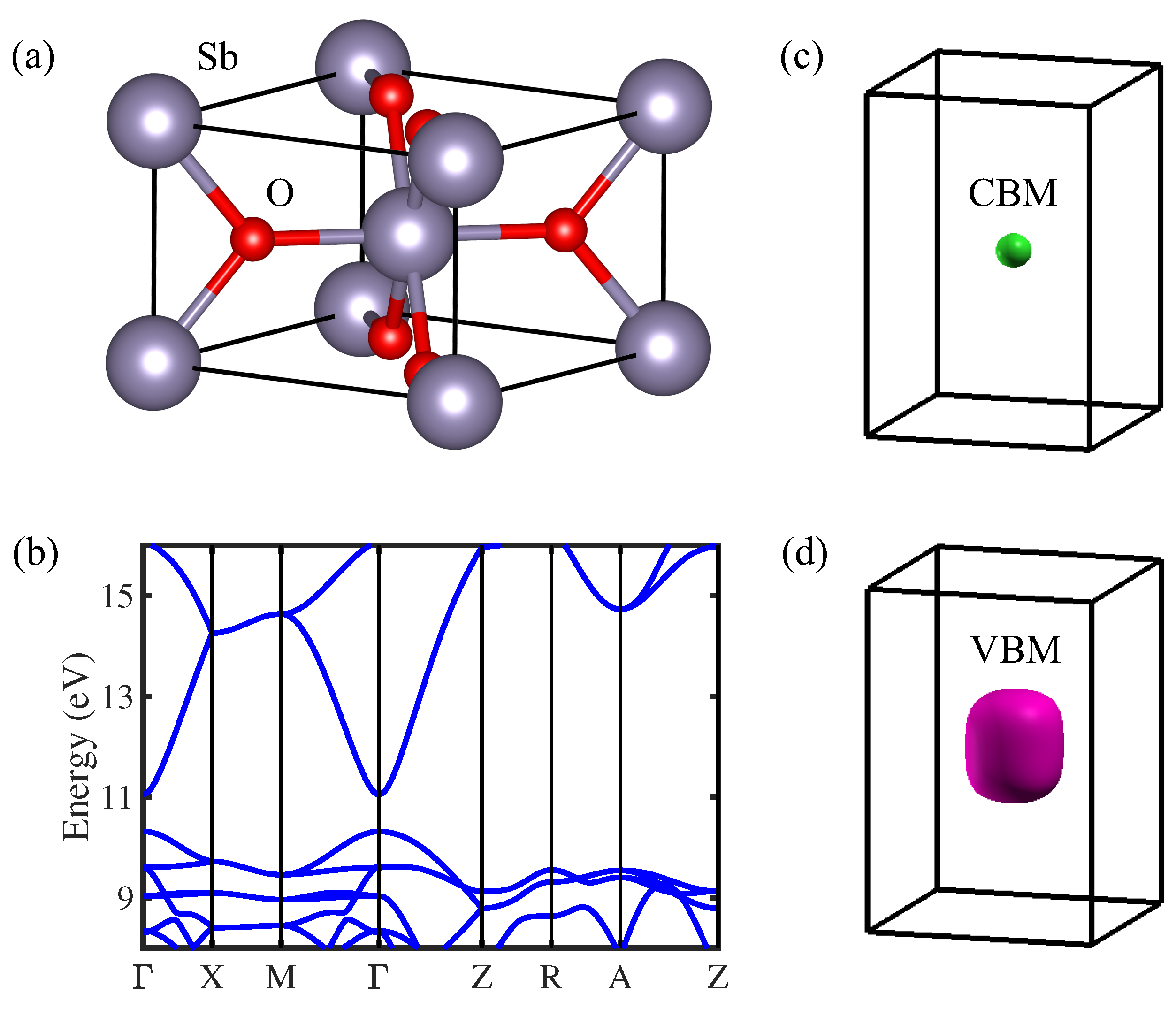
3.1. Effective Mass Extraction Method
3.2. Scattering Rates
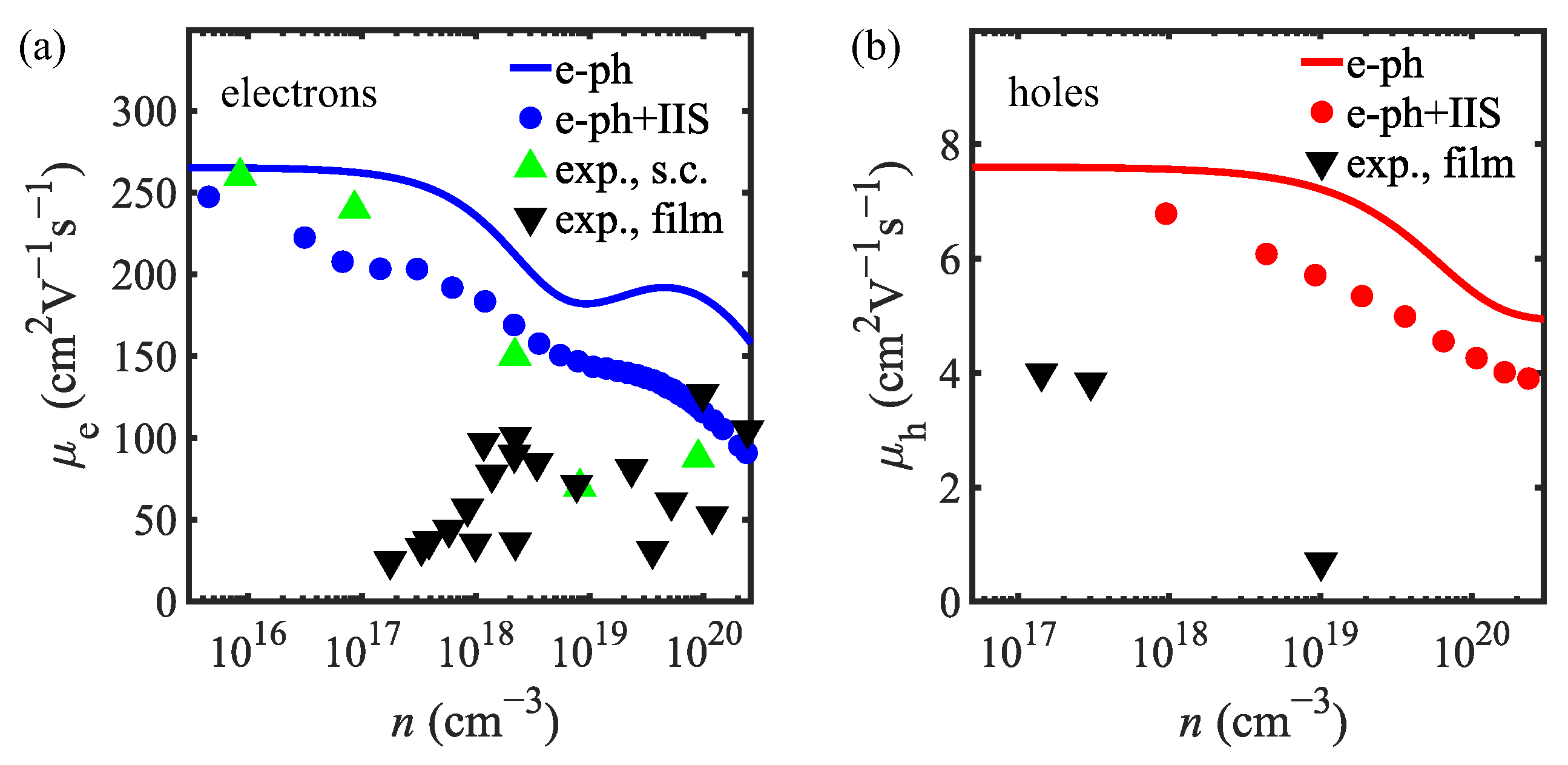
3.3. Mobility Calculations
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sundaram, K.B.; Bhagavat, G.K. Optical absorption studies on tin oxide films. J. Phys. D 1981, 14, 921–925. [Google Scholar] [CrossRef]
- Melsheimer, J.; Ziegler, D. Band gap energy and Urbach tail studies of amorphous, partially crystalline and polycrystalline tin dioxide. Thin Solid Films 1985, 129, 35–47. [Google Scholar] [CrossRef]
- Xiong, L.; Guo, Y.; Wen, J.; Liu, H.; Yang, G.; Qin, P.; Fang, G. Review on the application of SnO2 in perovskite solar cells. Adv. Funct. Mater. 2018, 28, 1802757. [Google Scholar] [CrossRef]
- Chen, J.S.; Lou, X.W. SnO2-based nanomaterials: Synthesis and application in lithium-ion batteries. Small 2013, 9, 1877–1893. [Google Scholar] [CrossRef] [PubMed]
- Das, S.; Jayaraman, V. SnO2: A comprehensive review on structures and gas sensors. Prog. Mater. Sci. 2014, 66, 112–255. [Google Scholar] [CrossRef]
- Staerz, A.; Suzuki, T.; Weimar, U.; Barsan, N. 12-SnO2: The most important base material for semiconducting metal oxide-based materials. In Tin Oxide Materials; Orlandi, M.O., Ed.; Elsevier: Amsterdam, The Netherlands, 2020; pp. 345–377. [Google Scholar]
- Sun, C.; Yang, J.; Xu, M.; Cui, Y.; Ren, W.; Zhang, J.; Zhao, H.; Liang, B. Recent intensification strategies of SnO2-based photocatalysts: A review. Chem. Eng. J. 2022, 427, 131564. [Google Scholar] [CrossRef]
- Chen, X.; Gregory, O.J.; Amani, M. Thin-film thermocouples based on the system In2O3–SnO2. J. Am. Ceram. Soc. 2011, 94, 854–860. [Google Scholar] [CrossRef]
- Morgan, D.F.; Wright, D.A. Electrical properties of single crystals of antimony-doped stannic oxide. Br. J. Appl. Phys. 1966, 17, 337–340. [Google Scholar] [CrossRef]
- Fonstad, C.G.; Rediker, R.H. Electrical properties of high-quality stannic oxide crystals. J. Appl. Phys. 1971, 42, 2911–2918. [Google Scholar] [CrossRef]
- Galazka, Z.; Uecker, R.; Klimm, D.; Irmscher, K.; Pietsch, M.; Schewski, R.; Albrecht, M.; Kwasniewski, A.; Ganschow, S.; Schulz, D.; et al. Growth, characterization, and properties of bulk SnO2 single crystals. Phys. Status Solidi A 2014, 211, 66–73. [Google Scholar] [CrossRef]
- Okude, M.; Ueno, K.; Itoh, S.; Kikuchi, M.; Ohtomo, A.; Kawasaki, M. Effect of in situ annealed SnO2 buffer layer on structural and electrical properties of (0 0 1) SnO2/TiO2 heterostructures. J. Phys. D 2008, 41, 125309. [Google Scholar] [CrossRef]
- Toyosaki, H.; Kawasaki, M.; Tokura, Y. Electrical properties of Ta-doped SnO2 thin films epitaxially grown on TiO2 substrate. Appl. Phys. Lett. 2008, 93, 132109. [Google Scholar] [CrossRef]
- White, M.E.; Bierwagen, O.; Tsai, M.Y.; Speck, J.S. Electron transport properties of antimony doped SnO2 single crystalline thin films grown by plasma-assisted molecular beam epitaxy. J. Appl. Phys. 2009, 106, 093704. [Google Scholar] [CrossRef]
- Mun, H.; Yang, H.; Park, J.; Ju, C.; Char, K. High electron mobility in epitaxial SnO2-x in semiconducting regime. APL Mater. 2015, 3, 076107. [Google Scholar] [CrossRef]
- Fukumoto, M.; Nakao, S.; Shigematsu, K.; Ogawa, D.; Morikawa, K.; Hirose, Y.; Hasegawa, T. High mobility approaching the intrinsic limit in Ta-doped SnO2 films epitaxially grown on TiO2 (001) substrates. Sci. Rep. 2020, 10, 6844. [Google Scholar] [CrossRef] [PubMed]
- Chattopadhyay, D.; Queisser, H.J. Electron scattering by ionized impurities in semiconductors. Rev. Mod. Phys. 1981, 53, 745–768. [Google Scholar] [CrossRef]
- Erginsoy, C. Neutral Impurity Scattering in Semiconductors. Phys. Rev. 1950, 79, 1013–1014. [Google Scholar] [CrossRef]
- Blatter, G.; Greuter, F. Electrical breakdown at semiconductor grain boundaries. Phys. Rev. B 1986, 34, 8555–8572. [Google Scholar] [CrossRef]
- Jaszek, R. Carrier scattering by dislocations in semiconductors. J. Mater. Sci. Mater. 2001, 12, 1–9. [Google Scholar] [CrossRef]
- Li, Z.; Miao, N.; Zhou, J.; Sun, Z.; Liu, Z.; Xu, H. High Thermoelectric performance of few-quintuple Sb2Te3 nanofilms. Nano Energy 2018, 43, 285–290. [Google Scholar] [CrossRef]
- Madsen, G.K.H.; Carrete, J.; Verstraete, M.J. BoltzTraP2, a program for interpolating band structures and calculating semi-classical transport coefficients. Comput. Phys. Commun. 2018, 231, 140–145. [Google Scholar] [CrossRef]
- Li, Z.; Han, S.; Pan, Y.; Miao, N.; Zhou, J.; Xu, H.; Sun, Z. Origin of high thermoelectric performance with a wide range of compositions for BixSb2-xTe3 single quintuple layers. Phys. Chem. Chem. Phys. 2019, 21, 1315–1323. [Google Scholar] [CrossRef]
- Gorai, P.; Stevanović, V.; Toberer, E.S. Computationally guided discovery of thermoelectric materials. Nat. Rev. Mater. 2017, 2, 17053. [Google Scholar] [CrossRef]
- Graziosi, P.; Kumarasinghe, C.; Neophytou, N. Impact of the scattering physics on the power factor of complex thermoelectric materials. J. Appl. Phys. 2019, 126, 155701. [Google Scholar] [CrossRef]
- Li, Z.; Graziosi, P.; Neophytou, N. Deformation potential extraction and computationally efficient mobility calculations in silicon from first principles. Phys. Rev. B 2021, 104, 195201. [Google Scholar] [CrossRef]
- Graziosi, P.; Li, Z.; Neophytou, N. Bipolar conduction asymmetries lead to ultra-high thermoelectric power factor. Appl. Phys. Lett. 2022, 120, 072102. [Google Scholar] [CrossRef]
- Hu, Y.; Hwang, J.; Lee, Y.; Conlin, P.; Schlom, D.G.; Datta, S.; Cho, K. First principles calculations of intrinsic mobilities in tin-based oxide semiconductors SnO, SnO2, and Ta2SnO6. J. Appl. Phys. 2019, 126, 185701. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. Quantum ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Conden. Matter. 2009, 21, 395502. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Hamann, D.R. Optimized norm-conserving Vanderbilt pseudopotentials. Phys. Rev. B 2013, 88, 085117. [Google Scholar] [CrossRef]
- Graziosi, P.; Li, Z.; Neophytou, N. ElecTra code: Full-band electronic transport properties of materials. arXiv 2022, arXiv:2208.00745. [Google Scholar]
- Madelung, O. Semiconductors: Data Handbook; Springer Science & Business Media: New York, NY, USA, 2004. [Google Scholar]
- Stampfl, C.; Mannstadt, W.; Asahi, R.; Freeman, A.J. Electronic structure and physical properties of early transition metal mononitrides: Density-functional theory LDA, GGA, and screened-exchange LDA FLAPW calculations. Phys. Rev. B 2001, 63, 155106. [Google Scholar] [CrossRef]
- El Haj Hassan, F.; Moussawi, S.; Noun, W.; Salameh, C.; Postnikov, A.V. Theoretical calculations of the high-pressure phases of SnO2. Comput. Mater. Sci. 2013, 72, 86–92. [Google Scholar] [CrossRef]
- Perdew, J.P.; Yang, W.; Burke, K.; Yang, Z.; Gross, E.K.U.; Scheffler, M.; Scuseria, G.E.; Henderson, T.M.; Zhang, I.Y.; Ruzsinszky, A.; et al. Understanding band gaps of solids in generalized Kohn-Sham theory. Proc. Natl. Acad. Sci. USA 2017, 114, 2801–2806. [Google Scholar] [CrossRef] [PubMed]
- Heyd, J.; Scuseria, G.E.; Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 2003, 118, 8207–8215. [Google Scholar] [CrossRef]
- Aryasetiawan, F.; Gunnarsson, O. The GW method. Rep. Prog. Phys. 1998, 61, 237–312. [Google Scholar] [CrossRef]
- Anisimov, V.I.; Zaanen, J.; Andersen, O.K. Band theory and Mott insulators: Hubbard U instead of Stoner I. Phys. Rev. B 1991, 44, 943–954. [Google Scholar] [CrossRef]
- Isaacs, E.B.; Wolverton, C. Performance of the strongly constrained and appropriately normed density functional for solid-state materials. Phys. Rev. Mater. 2018, 2, 063801. [Google Scholar] [CrossRef]
- Tran, F.; Blaha, P. Accurate band gaps of semiconductors and insulators with a semilocal exchange-correlation potential. Phys. Rev. Lett. 2009, 102, 226401. [Google Scholar] [CrossRef]
- Neophytou, N.; Kosina, H. Large nnhancement in hole velocity and mobility in p-type [110] and [111] silicon nanowires by cross section scaling: An atomistic analysis. Nano Lett. 2010, 10, 4913–4919. [Google Scholar] [CrossRef]
- Graziosi, P.; Kumarasinghe, C.; Neophytou, N. Material descriptors for the discovery of efficient thermoelectrics. ACS Appl. Energy Mater. 2020, 3, 5913–5926. [Google Scholar] [CrossRef]
- Rahman, A.; Guo, J.; Datta, S.; Lundstrom, M. Theory of ballistic nanotransistors. IEEE Trans. Electron Devices 2003, 50, 1853–1864. [Google Scholar] [CrossRef]
- Lundstrom, M. Fundamentals of Carrier Transport, 2nd ed.; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Neophytou, N. Theory and Simulation Methods for Electronic and Phononic Transport in Thermoelectric Materials; Springer Nature: New York, NY, USA, 2020. [Google Scholar]
- Turkes, P.; Pluntke, C.; Helbig, R. Thermal conductivity of SnO2 single crystals. J. Phys. C Solid State Phys. 1980, 13, 4941–4951. [Google Scholar] [CrossRef]
- Samsonidze, G.; Kozinsky, B. Accelerated screening of thermoelectric materials by first-principles computations of electron–phonon scattering. Adv. Energy Mater. 2018, 8, 1800246. [Google Scholar] [CrossRef]
- Jacoboni, C.; Reggiani, L. The Monte Carlo method for the solution of charge transport in semiconductors with applications to covalent materials. Rev. Mod. Phys. 1983, 55, 645–705. [Google Scholar] [CrossRef]
- Nag, B.R. Electron Transport in Compound Semiconductors; Springer Science & Business Media: New York, NY, USA, 1980; Volume 11. [Google Scholar]
- Matthiessen, A.; Vogt, A.C.C. IV. On the influence of temperature on the electric conducting-power of alloys. Philos. Trans. R. Soc. Lond. 1864, 154, 167–200. [Google Scholar]
- Yu, S.; Zhang, W.; Li, L.; Xu, D.; Dong, H.; Jin, Y. Fabrication of p-type SnO2 films via pulsed laser deposition method by using Sb as dopant. Appl. Surf. Sci. 2013, 286, 417–420. [Google Scholar] [CrossRef]
- Fu, W.; Li, M.; Li, J.; Fang, G.; Ye, P.; E, W.; Xiao, X.; Wei, H.; Liu, B.; Lu, Y.; et al. Achieving p-type conductivity in wide-bandgap SnO2 by a two-step process. Appl. Phys. Lett. 2021, 118, 112102. [Google Scholar] [CrossRef]
- Semancik, S.; Cavicchi, R.E. The growth of thin, epitaxial SnO2 films for gas sensing applications. Thin Solid Films 1991, 206, 81–87. [Google Scholar] [CrossRef]
- Rachut, K.; Körber, C.; Brötz, J.; Klein, A. Growth and surface properties of epitaxial SnO2. Phys. Status Solid A 2014, 211, 1997–2004. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Graziosi, P.; Neophytou, N. Electron and Hole Mobility of SnO2 from Full-Band Electron–Phonon and Ionized Impurity Scattering Computations. Crystals 2022, 12, 1591. https://doi.org/10.3390/cryst12111591
Li Z, Graziosi P, Neophytou N. Electron and Hole Mobility of SnO2 from Full-Band Electron–Phonon and Ionized Impurity Scattering Computations. Crystals. 2022; 12(11):1591. https://doi.org/10.3390/cryst12111591
Chicago/Turabian StyleLi, Zhen, Patrizio Graziosi, and Neophytos Neophytou. 2022. "Electron and Hole Mobility of SnO2 from Full-Band Electron–Phonon and Ionized Impurity Scattering Computations" Crystals 12, no. 11: 1591. https://doi.org/10.3390/cryst12111591
APA StyleLi, Z., Graziosi, P., & Neophytou, N. (2022). Electron and Hole Mobility of SnO2 from Full-Band Electron–Phonon and Ionized Impurity Scattering Computations. Crystals, 12(11), 1591. https://doi.org/10.3390/cryst12111591








