Abstract
Charge-transfer salts based on bis(ethylenedioxy)tetrathiafulvalene (BEDO-TTF or BO for short) provide a stable two-dimensional (2D) metallic state, while the electrical resistance often shows an upturn at low temperatures below ~10 K. Such 2D weak carrier localization was first recognized for BO salts in the Langmuir–Blodgett films fabricated with fatty acids; however, it has not been characterized in charge-transfer solid crystals. In this paper, we discuss the carrier localization of two crystalline BO charge-transfer salts with or without magnetic ions at low temperatures through the analysis of the weak negative magnetoresistance. The phase coherence lengths deduced with temperature dependence are largely dominated by the electron–electron scattering mechanism. These results indicate that the resistivity upturn at low temperatures is caused by the 2D weak localization. Disorders causing elastic scattering within the metallic domains, such as those of terminal ethylene groups, should be suppressed to prevent the localization.
1. Introduction
Since the 1970s, molecular conductors with tetrathiafulvalene (TTF) derivatives have attracted attention for their rich variety of electronic phenomena such as metal–insulator transitions and superconductivity [1,2]. Bis(ethylenedithio)-substituted derivative BEDT-TTF (or ET for short) is especially well known for the production of a variety of superconductors (more than 40 kinds). Additionally, the bis(ethylenedioxy)-substituted derivative, BEDO-TTF (or BO for short, Figure 1a), in which the sulfur atoms in the outer six-membered ring of ET are replaced by oxygen atoms, has also attracted attention as a building molecule. This donor molecule shows the strong tendency to create complexes of two-dimensional (2D) layers due to the self-aggregation ability caused by the intermolecular π–π interactions, along with the C–H···O hydrogen bonding [2,3]. While most of the BO salts exhibit metallic conduction, only a few examples are reported to show superconductivity [4,5], in contrast to the ET complexes.
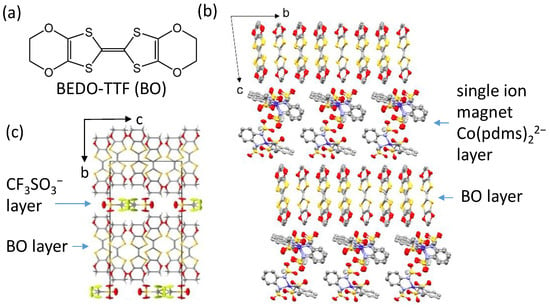
Figure 1.
(a) The chemical structure of the donor molecule BEDO-TTF or BO, i.e., bis(ethylenedioxy)tetrathiafulvalene). Crystal structures of (b) β″-(BO)3[Co(pdms)2](CH3CN)(H2O)2 and (c) κ-(BO)2CF3SO3 viewed along a-axis. Each atom is colored as: gray, C; white, H; blue, N; green, F; navy, Co; red, O; yellow, S.
Applying this peculiarity, metallic Langmuir–Blodgett (LB) films were fabricated by mixing BO with fatty acids for potential applications in molecular electronics [4,5,6]. Self-organization provided a stable 2D BO layer which was sandwiched by the layers composed of fatty acids such as stearic [6,7] or arachidic [8] acid. Although the LB films exhibited room-temperature conductivity as high as 100 S cm−1, the electrical resistance increased at low temperatures. Two-dimensional weak localization has been proposed as the origin of the behavior. The characteristic negative magnetoresistance (MR) under the magnetic field applied perpendicularly to the 2D layer was observed owing to the destruction of the constructive interference between waves along a closed loop in opposite senses with equal probabilities [9,10].
On the other hand, the carrier localization in crystalline charge-transfer salts at low temperatures [11] has not been mentioned much so far in BO complexes, although resistance upturn at low temperatures has often been found with [12] or without [3,13] magnetic ions. Clarification on the origin of the resistivity upturn at low temperatures is important to explore electronic phase transition, such as metal–insulator transition and/or superconductivity in charge-transfer solid crystals, whether they stem from magnetic interaction or not.
In this paper, we will discuss two crystalline BO salts with and without magnetic ions to explore the resistance upturn phenomena in single crystals, β″-(BO)3[Co(pdms)2](CH3CN)(H2O)2 (abbreviated hereafter as β″-BO3) [14], where H2pdms = 1,2-bis(methanesulfonamido)benzene, and κ-(BO)2CF3SO3 (abbreviated hereafter as κ-BO2) [15]. The crystal structures of the two materials are shown in Figure 1b,c, respectively, consisting of 2D layers of BO molecules.
β″-BO3 has a 1/3 band filling with the β″-type molecular arrangement, according to the classification for ET salts, showing a metallic state down to 15 K [14]. This salt was synthesized in order to develop the possible interaction between the conduction electron and single ion magnet, exhibiting typical frequency dependence of ac magnetic susceptibility due to the bistable spin state of Co2+. This is a sister compound of β″-(BO)4[Co(pdms)2]·3H2O, (abbreviated hereafter as β″-BO4), which was grown using the same molecules but with a different solvent, which exhibited ferromagnetic interaction at low temperatures between BO and Co(pdms)2 ions [16]. The MR of β″-BO4 cannot be understood by the weak localization model, showing contribution from the π–d interaction [16]. On the other hand, the π–d interaction with the BO layer in the β″-BO3 was considered to be weak in view of the band structure calculation [14].
κ-BO2 has a 1/4 band filling with the κ-type molecular arrangement according to the classification for ET salts. This is a BO analogue salt of the ET salt with the same structure, κ-(ET)2CF3SO3 [17], which is a Mott insulator at ambient pressure but shows metallic behavior by applying a pressure above 1 GPa, and the superconducting transition occurs at 4.8 K under 1.1 GPa [18]. Although semiconducting behavior is observed from room temperature in the first report of κ-BO2 [15], here, a metallic conduction was observed down to around 10 K, below which electrical resistance increases. The change in the resistive behavior may be ascribed to the effect of grease (weak pressurization on crystals by cooling) and slow cooling in the present study.
In terms of common features, the low-temperature MR measurements showed that both β″-BO3 and κ-BO2 salts have a negative MR, similar to those observed in LB films. Here, we analyze the negative MR of the two different types of BO salt with the 2D weak localization model. The phase coherence lengths are deduced with temperature dependence largely dominated by the electron–electron scattering mechanism. These values are comparable to those of other type of materials, such as LB films and polymer poly(ethylenedioxythiophene):polystyrene sulfonate (PEDOT:PSS), implying a common origin of the inelastic scattering. These results indicate that the resistivity upturn at low temperatures is caused by the 2D weak localization, which confirms the 2D nature of the conduction layer made of BO molecules. Disorders causing elastic scattering within the metallic domains, such as those of terminal ethylene groups, should be suppressed to prevent the localization.
2. Materials and Methods
The single crystals were prepared by galvanostatic electrooxidation according to the literature [14,15]. The electrical resistivity was measured with the four-probe method by attaching annealed platinum wires on sample surfaces with carbon paste. We measured three samples for β″-BO3 (#1, #2, #3) and κ-BO2 (#1, #3 for intralayer direction and #2 for interlayer direction). For intralayer measurement, the current was applied along b-axis for β″-BO3 and along c-axis for κ-BO2. For κ-BO2, interlayer resistivity was also measured for the sample #2 along b-axis direction; however, β″-BO3 crystals were too thin to measure the interlayer resistivity reliably.
Electrical resistivity from room temperature to 2 K and MR under magnetic fields up to 9 T were measured using physical property measurement system, QUANTUM DESIGN, with a cooling rate of 0.2–0.3 K/min. A low measurement current of 10 μA was used to suppress self-heating. The sample was coated with Apiezon N grease to suppress the discontinuous jumping of resistance which has been often observed in charge-transfer complexes, possibly caused by microcracking [1]. A gentle pressure of 0.03 GPa was applied to the sample after being wrapped in Apiezon N grease and cooled down to low temperature [19]. The sample was rotated in the magnetic field to adjust the sample position using a horizontal rotator when the magnetic field was perpendicular and parallel to the 2D layer.
3. Results
Figure 2a shows the temperature dependence of the intralayer resistivity along the b-axis of β″-BO3 down to 2 K. The resistivity decreased at ambient pressure down to 10~15 K, below which it began to increase, as shown in Figure 2b [14]. Figure 2c shows the plot of the intralayer conductivity in the lnT scale. In the temperature range of the resistivity increase, the conductivity followed the lnT dependence asymptotically.
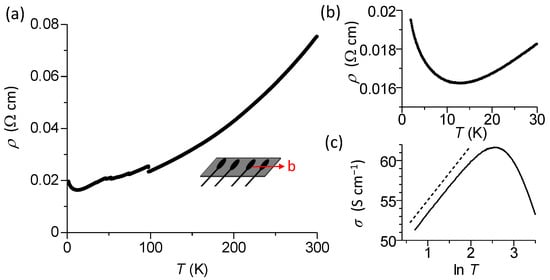
Figure 2.
(a) The temperature (T) dependence of intralayer (b-axis) resistivity (ρ) of β″-BO3 (sample #1). (b) Intralayer resistivity in the low temperature region. (c) Intralayer conductivity as a function of lnT. The broken line represents the relationship of σ ∝ lnT.
To investigate the origin of the low-temperature upturn of the resistivity, the angle dependence of MR was investigated in a magnetic field (B) oriented perpendicular (θ = 90°) and parallel (θ = 0°) with respect to the 2D layer. MR is defined by the increase of resistivity by the magnetic field: MR (%) = [ρ(B, T) − ρ(0, T)]/ρ(0, T) × 100%, where ρ is the resistivity. Figure 3a shows the MR of β″-BO3 at 2 K for θ = 0° and 90°. Positive MR of metals was observed for the high field region above 4 T for both magnetic field directions; however, clear negative MR was observed up to 4 T only when the magnetic field was applied perpendicular to the 2D layer (θ = 90°). No negative MR was observed when the magnetic field was applied parallel to the 2D layer (θ = 0°). This behavior is typical for the weak negative MR caused by weak localization within the 2D conducting layer [9,10], as was observed for the LB films. The MR can be understood without considering any contribution from the magnetic anion layers, in sharp contrast to the case of β″-BO4 salt [16]. As shown in Figure 3b, the negative MR at θ = 90° was observed up to ~15 K, where the lnT dependence in the temperature dependence of resistivity disappeared and turned to show a metallic behavior.
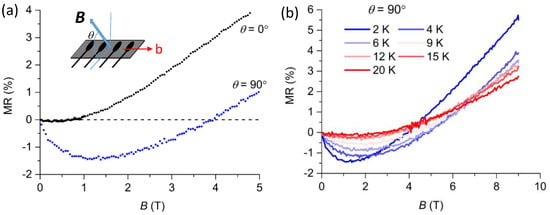
Figure 3.
(a) The MR (current along b-axis) of β″-BO3 (sample #1) at 2 K under magnetic field B parallel (θ = 0°) and perpendicular (θ = 90°) to the 2D layer. Clear negative MR was observed when θ = 90°. (b) The MR for the perpendicular field in the temperature range of 2–20 K.
Figure 4a shows the temperature dependence of the electrical conductivity of κ-BO2 in the direction parallel (sample #1, along c-axis) and perpendicular (sample #2, along b-axis) to the 2D layer. From room temperature down to ~10 K, the electrical resistivities decreased; however, the intralayer resistivity increased below 10 K, as shown in Figure 4b. Figure 4c shows the plot of the intralayer conductivity of the sample #1 in the lnT scale; the conductivity follows the lnT dependence asymptotically below 8 K, similar to β″-BO3. The interlayer resistivity (sample #2) also increased at low temperatures but very weakly below 4 K. The anisotropy of electrical conductivity reached 1 × 105, which is high compared to its ET counterpart, κ-(ET)2CF3SO3 [18], implying the strong 2D nature of the conduction in κ-BO2.
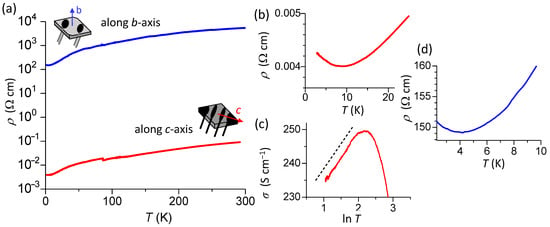
Figure 4.
(a) The temperature (T) dependence of the electrical resistivity (ρ) of κ-BO2 in the direction parallel (sample #1, along c-axis) and perpendicular (sample #2, along b-axis) to the 2D layer. (b) Intralayer resistivity of the sample #1 in the low temperature region. (c) Intralayer conductivity of the sample #1 as a function of lnT. The broken line represents the relationship of σ ∝ lnT. (d) Interlayer resistivity of sample #2 in the low temperature region.
Figure 5a shows the MR of κ-BO2 under magnetic fields parallel and perpendicular to the 2D layer. The negative MR for κ-BO2 was obvious at B < 2 T only under the perpendicular field, similar to β″-BO3. Figure 5b shows the MR of κ-BO2 at different temperatures (2–10 K) under the perpendicular field. The negative MR diminished at 10 K.
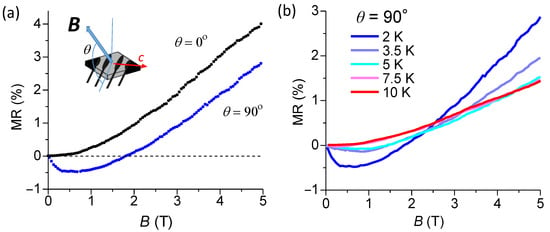
Figure 5.
(a) The MR (current along c-axis) of κ-BO2 (sample #1) at 2 K under magnetic field B parallel (θ = 0°) and perpendicular (θ = 90°) to the 2D layer. Clear negative MR was observed when θ = 90°. (b) The MR for the perpendicular field in the temperature range of 2–10 K.
4. Discussion
For both BO salt crystals, the intralayer resistivity increased asymptotically with lnT at low temperatures. Negative MR was observed under a magnetic field perpendicular to the 2D layer. Under the magnetic field parallel to the 2D layer, there manifested no negative MR, but only positive MR. These features are characteristic of 2D weak localization [9,10]. The elastic scatterings of electrons by disorders or imperfections occur several times within a metallic domain in which phase coherence of the wavefunction is preserved. Then, a closed loop can be formed within the metallic domain and the constructive interference between waves in opposite senses with equal probabilities causes the carrier localization [9,10].
To further investigate whether the negative MR showed weak 2D localization, the changes in MR with respect to temperature and magnetic field were examined. The time-reversal, symmetry-breaking perturbations, such as magnetic field, applied perpendicular to the closed loop destroyed the interference and, thus, suppressed the localization to cause the negative MR. The negative MR is formulated as the increase in the electrical conductivity σ due to the magnetic field (magnetoconductance, MC) based on the Hikami–Larkin–Nagaoka (HLN) expression [10]:
where A1, A2, Bi and α are fitting parameters. ψ is a digamma function. The first term represents the contribution from the 2D localization. The second term represents the negative MC (i.e., positive MR) of a metal which increases when the magnetic field increased. The exponent of α is in the range 1~2. The strength of the negative MR can be scaled with the ratio of A1 and A2. The characteristic magnetic field Bi is associated with the phase coherence length λ, in which the phase coherence of the carrier wavefunction is preserved between each inelastic scattering:
where ℏ is the reduced Planck constant and e is the elementary charge.
We show typical examples of the fitting of MC under the perpendicular magnetic field with respect to Equation (1) in the supplementary materials, Figures S1–S3 for β″-BO3 and Figures S4 and S5 for κ-BO2. Corresponding fitting parameters are given in Tables S1–S5 in the supplementary materials, respectively. For β″-BO3, the curves are fitted to Equation (1) up to 6 T because the fitting to the metallic MC A2Bα with single exponent α up to 9 T is rather inappropriate and the exponent α seems to change to a smaller value above ~6 T, especially at the lowest temperature of 2 K.
Figure 6 shows the temperature dependence of λ deduced by the analysis in terms of Equations (1) and (2) on a logarithmic scale in the temperature range where the negative MR was observed for β″-BO3 and κ-BO2, together with those found for LB films [6,7,8]. The intralayer coherence length was far larger than the conducting 2D layer thickness of 1.5~2.0 nm, indicating the 2D nature of the conduction. The coherence length increased with lowering temperature. The temperature dependence of the phase coherence length λ followed the relation λ∝T−p/2, in which p ~ 1 and p ~ 2 were associated with the situations in which phase-breaking inelastic scatterings occurred due to electron–electron [20] and electron–phonon [21,22] interactions, respectively. In the present case of the BO solids and LB films [6,7,8], the exponent was rather close to p ~ 1. The mechanism of the inelastic scattering in these BO solids and LB films may be understood mainly as the electron–electron interactions.
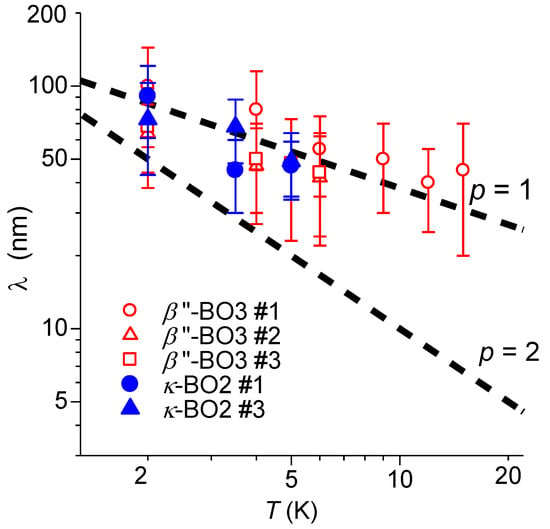
Figure 6.
Temperature dependence of the phase coherence length λ for β″-BO3 (sample #1, #2, #3), κ-BO2 (sample #1, #3). The broken lines represent the temperature dependence following λ∝T−p/2 with p = 1 or p = 2.
The result indicates that the negative MR for the crystalline BO salts is well understood in terms of the weak 2D localization model, as in the case of the LB films reported previously [6,7,8]. The observation of the weak 2D localization is also shared by the recent report for polymer PEDOT:PSS, which shows high crystallinity and a 2D nature with a similar range of phase coherence length [23]. PEDOT also has terminal ethylene groups at the end of EDOT moiety, which may cause elastic scattering similar to the BO cases.
5. Conclusions
We have studied the low-temperature carrier localization of the charge-transfer salts of BO. The resistivity upturn in the two BO salt crystals can be ascribed to the 2D weak localization with the observation of the negative MR. The present study implies that the 2D weak localization was universally observed in BO charge-transfer salts, regardless of the BO packing and band filling. The electron–electron interaction is considered to be the dominant mechanism for the inelastic scattering. The phenomena demonstrate the formation of the robust 2D metallic state in the BO salts. However, the carrier localization may mask the possible electronic transition such as superconductivity of BO salts. Disorders causing elastic scattering within the metallic domains, such as those of terminal ethylene groups, should be suppressed to prevent the localization.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/cryst12010023/s1, Figure S1: A typical fitting result for the magnetoconductance of β″-BO3 #1 along the weak 2D localization model under the perpendicular magnetic field. Figure S2: A typical fitting result for the magnetoconductance of β″-BO3 #2 along the weak 2D localization model under the perpendicular magnetic field. Figure S3: A typical fitting result for the magnetoconductance of β″-BO3 #3 along the weak 2D localization model under the perpendicular magnetic field. Figure S4: A typical fitting result for the magnetoconductance of κ-BO2 #1 along the weak 2D localization model under the perpendicular magnetic field. Figure S5: A typical fitting result for the magnetoconductance of κ-BO2 #3 along the weak 2D localization model under the perpendicular magnetic field. Table S1: Parameters obtained by the fitting shown in Figure S1. Table S2: Parameters obtained by the fitting shown in Figure S2. Table S3: Parameters obtained by the fitting shown in Figure S3. Table S4: Parameters obtained by the fitting shown in Figure S4. Table S5: Parameters obtained by the fitting shown in Figure S5.
Author Contributions
BO molecule synthesis, M.I., A.O. and H.Y.; β″-BO3 crystals preparation, Y.S. and M.Y.; κ-BO2 crystals preparation, Y.Y. and G.S.; measurements and analysis, H.I., M.M., S.K., S.K.Y. and T.T.; manuscript preparation, H.I. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by JSPS KAKENHI (grant nos. 19K22127, 20H05867, 20H05664, 20H05862, 20K05448 and 21K04865) and JST CREST (grant no. JPMJCR17I5). M.Y. acknowledges the support by the 111 project (B18030) from China.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are available from H.I. upon request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ishiguro, T.; Yamaji, K.; Saito, G. Organic Superconductors, 2nd ed.; Springer: Berlin, Germany, 1998. [Google Scholar]
- Yamada, J.; Sugimoto, T. TTF Chemistry; Kodansha & Springer: Tokyo, Japan, 2004. [Google Scholar]
- Horiuchi, S.; Yamochi, H.; Saito, G.; Sakaguchi, K.; Kusunoki, M. Nature and Origin of Stable Metallic State in Organic Charge-Transfer Complexes of Bis(ethylenedioxy)tetrathiafulvalene. J. Am. Chem. Soc. 1996, 118, 8604–8622. [Google Scholar] [CrossRef]
- Beno, M.A.; Wang, H.H.; Kini, A.M.; Carlson, K.D.; Geiser, U.; Kwok, W.K.; Thompson, J.E.; Williams, J.M.; Ren, J.; Whangbo, M.H. The first ambient pressure organic superconductor containing oxygen in the donor molecule, βm-(BEDO-TTF)3Cu2(NCS)3, Tc = 1.06 K. Inorg. Chem. 1990, 29, 1599–1601. [Google Scholar] [CrossRef]
- Kahlich, S.; Schweitzer, D.; Heinen, I.; Lan, S.E.; Nuber, B.; Keller, H.J.; Winzer, K.; Helberg, H.W. (BEDO-TTF)2ReO4(H2O): A new organic superconductor. Solid State Comm. 1991, 80, 191–195. [Google Scholar] [CrossRef]
- Ishizaki, Y.; Izumi, M.; Ohnuki, H.; Lipinska, K.K.; Imakubo, T.; Kobayashi, K. Formation of two-dimensional weak localization in conducting Langmuir-Blodgett films. Phys. Rev. B 2001, 63, 134201. [Google Scholar] [CrossRef]
- Ishizaki, Y.; Izumi, M.; Ohnuki, H.; Imakubo, T.; Kalita-Lipinska, K. Observation of two-dimensional weak localization as a sign of coherent carrier transport in the conducting Langmuir–Blodgett films of BEDO-TTF and stearic acid. Colloids Surf. A 2002, 198–200, 723–728. [Google Scholar] [CrossRef]
- Ito, H.; Tamura, H.; Kuroda, S.; Yamochi, H. Structural and Transport Studies of BEDO-TTF-Arachidic-Acid Conducting Langmuir-Blodgett Films. Trans. MRS-J 2005, 30, 131–134. [Google Scholar]
- Lee, P.A.; Ramakrishhnan, T.V. Disordered electronic systems. Rev. Mod. Phys. 1985, 57, 287–337. [Google Scholar] [CrossRef]
- Hikami, S.; Larkin, A.I.; Nagaoka, Y. Spin-Orbit Interaction and Magnetoresistance in the Two Dimensional Random System. Prog. Theor. Phys. 1980, 63, 707–710. [Google Scholar] [CrossRef]
- Ulmet, J.P.; Bachere, L.; Askenazy, S.; Ousset, J.C. Negative magnetoresistance in some dimethyltri-methylene-tetraselenafulvalenium salts: A signature of weak-localization effects. Phys. Rev. B 1988, 38, 7782–7788. [Google Scholar] [CrossRef]
- Prokhorova, T.G.; Simonov, S.V.; Khasanov, S.S.; Zorina, L.V.; Buravov, L.I.; Shibaeva, R.P.; Yagubskii, E.B.; Morgunov, R.B.; Foltynowiczc, D.; S’wietlikc, R. Bifunctional molecular metals based on BEDO-TTF radical cation salts with paramagnetic [MIII(CN)6]3− anions, M= Fe, Cr, (Fe0.5Co0.5). Synth. Met. 2008, 158, 749–757. [Google Scholar] [CrossRef]
- Dubrovakii, A.D.; Spitsina, N.G.; Buravov, L.I.; Shilov, G.V.; Dyachenko, O.A.; Yagubskii, E.B.; Laukhin, V.N.; Canadell, E. New molecular metals based on BEDO radical cation salts with the square planar Ni(CN)42− anion. J. Mater. Chem. 2005, 15, 1248–1254. [Google Scholar]
- Shen, Y.; Ito, H.; Zhang, H.; Yamochi, H.; Cosquer, G.; Herrmann, C.; Ina, T.; Yoshina, S.K.; Breedlove, B.K.; Otsuka, A.; et al. Emergence of Metallic Conduction and Cobalt(II)-Based Single-Molecule Magnetism in the Same Temperature Range. J. Am. Chem. Soc. 2021, 143, 4891–4895. [Google Scholar] [CrossRef] [PubMed]
- Fettouhi, M.; Ouahab, L.; Serhani, D.; Fabre, J.-M.; Ducasse, L.; Arniell, J.; Canet, R.; Delhaesd, P. Structural and physical properties of BEDO-TTF charge-transfer salts: κ-phase with CF3SO3−. J. Mater. Chem. 1993, 3, 1101–1107. [Google Scholar] [CrossRef]
- Shen, Y.; Ito, H.; Zhang, H.; Yamochi, H.; Katagiri, S.; Yoshina, S.K.; Otsuka, A.; Ishikawa, M.; Cosquer, G.; Uchida, K.; et al. Simultaneous manifestation of metallic conductivity and single-molecule magnetism in a layered molecule-based compound. Chem. Sci. 2020, 11, 11154–11161. [Google Scholar] [CrossRef] [PubMed]
- Fettouhi, M.; Ouahab, L.; Gomez-Garcia, C.; Ducasse, L.; Delhaes, P. Structural and physical properties of κ-(BEDT-TTF)2(CF3SO3). Synth. Met. 1995, 70, 1131–1132. [Google Scholar] [CrossRef]
- Ito, H.; Asai, T.; Shimizu, Y.; Hayama, H.; Yoshida, Y.; Saito, G. Pressure-induced superconductivity in the antiferromagnet κ-(ET)2CF3SO3 with quasi-one-dimensional triangular spin lattice. Phys. Rev. B 2016, 94, 020503(R). [Google Scholar] [CrossRef]
- Ito, H.; Suzuki, D.; Yokochi, Y.; Kuroda, S.; Umemiya, M.; Miyasaka, H.; Sugiura, K.I.; Yamashita, M.; Tajima, H. Charge Carriers in Divalent BEDT-TTF Conductor (BEDT-TTF)Cu2Br4. Phys. Rev. B. 2005, 71, 085202. [Google Scholar] [CrossRef]
- Altshuler, B.L.; Aronov, A.G.; Khmelnitsky, D.E. Effects of electron-electron collisions with small energy transfers on quantum localization. J. Phys. C Solid State Phys. 1982, 15, 7367–7386. [Google Scholar] [CrossRef]
- Belitz, D.; Das Sarma, S. Inelastic phase-coherence time in thin metal films. Phys. Rev. B 1987, 36, 7701–7704. [Google Scholar] [CrossRef]
- Sergeev, A.; Mitin, V. Electron-phonon interaction in disordered conductors: Static and vibrating scattering potentials. Phys. Rev. B 2000, 61, 6041–6047. [Google Scholar] [CrossRef]
- Homma, Y.; Itoh, K.; Masunaga, H.; Fujiwara, A.; Nishizaki, T.; Iguchi, S.; Sasaki, T. Mesoscopic 2D Charge Transport in Commonplace PEDOT:PSS Films. Adv. Electron. Mater. 2018, 4, 1700490. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).