The Extreme Values of Young’s Modulus and the Negative Poisson’s Ratios of Rhombic Crystals
Abstract
1. Introduction
2. Young’s Modulus
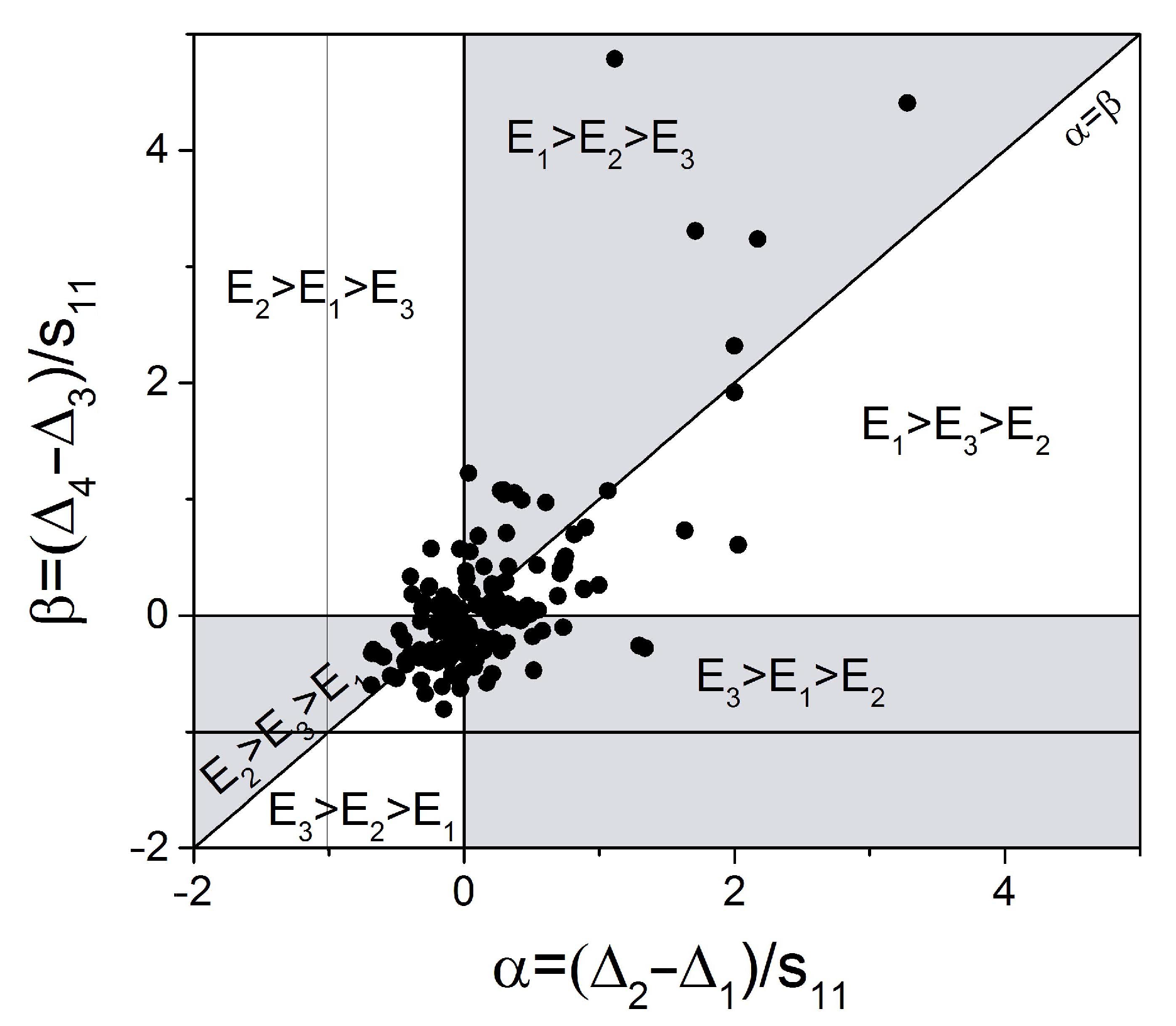
3. Stationary and Extreme Values of Young’s Modulus
4. Young’s Moduli of Tetragonal, Hexagonal and Cubic Crystals
4.1. Tetragonal Crystals
4.2. Hexagonal Crystals
4.3. Cubic Crystals
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ting, T.C.T.; Chen, T. Poisson’s ratio for anisotropic elastic materials can have no bounds. Quart. J. Mech. Appl. Math. 2005, 58, 73–82. [Google Scholar] [CrossRef]
- Lethbridge, Z.A.D.; Walton, R.I.; Marmier, A.S.H.; Smith, C.W.; Evans, K.E. Elastic anisotropy and extreme Poisson’s ratios in single crystals. Acta Mater. 2010, 58, 6444–6451. [Google Scholar] [CrossRef]
- Goldstein, R.V.; Gorodtsov, V.A.; Lisovenko, D.S. Auxetic mechanics of crystalline materials. Mech. Solids 2010, 45, 529–545. [Google Scholar] [CrossRef]
- Nelson, D.F. (Ed.) Second and Higher Order Elastic Constants. In Landolt-Börnstein—Group III Condensed Matter; Springer: Berlin/Heidelberg, Germany, 1992; Volume 29a. [Google Scholar] [CrossRef]
- Ting, T.C.T. The stationary values of Young’s modulus for monoclinic and triclinic materials. J. Mech. 2005, 21, 249–253. [Google Scholar] [CrossRef]
- Ting, T.C.T. Explicit expression of the stationary values of Young’s modulus and the shear modulus for anisotropic elastic materials. J. Mech. 2005, 21, 255–266. [Google Scholar] [CrossRef]
- Norris, A.N. Extreme values of Poisson’s ratio and other engineering moduli in anisotropic materials. J. Mech. Mater. Struc. 2006, 1, 793–812. [Google Scholar] [CrossRef][Green Version]
- Cazzani, A.; Rovati, M. Extrema of Young’s modulus for cubic and transversely isotropic solids. Int. J. Solids Struct. 2003, 40, 1713–1744. [Google Scholar] [CrossRef]
- Cazzani, A.; Rovati, M. Extrema of Young’s modulus for elastic solids with tetragonal symmetry. Int. J. Solids Struct. 2005, 42, 5057–5096. [Google Scholar] [CrossRef]
- Norris, A.N. Poisson’s ratio in cubic materials. Proc. Roy. Soc. A 2006, 462, 3385–3405. [Google Scholar] [CrossRef]
- Epishin, A.I.; Lisovenko, D.S. Extreme values of the Poisson’s ratio of cubic crystals. Tech. Phys. 2016, 61, 1516–1524. [Google Scholar] [CrossRef]
- Gorodtsov, V.A.; Lisovenko, D.S. Extreme values of Young’s modulus and Poisson’s ratio of hexagonal crystals. Mech. Mater. 2019, 134, 1–8. [Google Scholar] [CrossRef]
- Love, A.E.H. A Treatise on the Mathematical Theory of Elasticity; Cambridge University Press: Cambridge, UK, 1892; Volume 1. [Google Scholar]
- Lakes, R.S. Foam structures with a negative Poisson’s ratio. Science 1987, 235, 1038–1040. [Google Scholar] [CrossRef]
- Friis, E.A.; Lakes, R.S.; Park, J.B. Negative Poisson’s ratio polymeric and metallic foams. J. Mater. Sci. 1988, 23, 4406–4414. [Google Scholar] [CrossRef]
- Evans, K.E.; Nkansah, M.A.; Hutchinson, I.J.; Rogers, S.C. Molecular network design. Nature 1991, 353, 124. [Google Scholar] [CrossRef]
- Evans, K.E. Auxetic polymers: A new range of materials. Endeavour 1991, 15, 170–174. [Google Scholar] [CrossRef]
- Wojciechowski, K.W. Constant thermodynamic tension Monte Carlo studies of elastic properties of a two-dimensional system of hard cyclic hexamers. Mol. Phys. 1987, 61, 1247–1258. [Google Scholar] [CrossRef]
- Wojciechowski, K.W. Two-dimensional isotropic system with a negative Poisson ratio. Phys. Lett. A 1989, 137, 60–64. [Google Scholar] [CrossRef]
- Tretiakov, K.V.; Wojciechowski, K.W. Poisson’s ratio of simple planar ‘isotropic’ solids in two dimensions. Phys. Status Solidi B 2007, 244, 1038–1046. [Google Scholar] [CrossRef]
- Tretiakov, K.V.; Wojciechowski, K.W. Auxetic, partially auxetic, and nonauxetic behaviour in 2D crystals of hard cyclic tetramers. Phys. Status Solidi RRL 2020, 14, 2000198. [Google Scholar] [CrossRef]
- Wojciechowski, K.W.; Brańka, A.C. Negative Poisson ratio in a two-dimensional “isotropic” solid. Phys. Rev. A 1989, 40, 7222–7225. [Google Scholar] [CrossRef]
- Wojciechowski, K.W. Non-chiral, molecular model of negative Poisson ratio in two dimensions. J. Phys. A 2003, 36, 11765–11778. [Google Scholar] [CrossRef]
- Narojczyk, J.W.; Kowalik, M.; Wojciechowski, K.W. Influence of nanochannels on Poisson’s ratio of degenerate crystal of hard dimers. Phys. Status Solidi B 2016, 253, 1324–1330. [Google Scholar] [CrossRef]
- Tretiakov, K.V.; Piglowski, P.M.; Hyzorek, K.; Wojciechowski, K.W. Enhanced auxeticity in Yukawa systems due to introduction of nanochannels in [001]-direction. Smart Mater. Struct. 2016, 25, 054007. [Google Scholar] [CrossRef]
- Piglowski, P.M.; Wojciechowski, K.W.; Tretiakov, K.V. Partial auxeticity induced by nanoslits in the Yukawa crystal. Phys. Status Solidi RRL 2016, 10, 566–569. [Google Scholar] [CrossRef]
- Pigłowski, P.; Narojczyk, J.; Poźniak, A.; Wojciechowski, K.; Tretiakov, K. Auxeticity of Yukawa systems with nanolayers in the (111) crystallographic plane. Materials 2017, 10, 1338. [Google Scholar] [CrossRef]
- Tretiakov, K.; Pigłowski, P.; Narojczyk, J.; Bilski, M.; Wojciechowski, K. High partial auxeticity Induced by nanochannels in [111]-direction in a simple model with Yukawa interactions. Materials 2018, 11, 2550. [Google Scholar] [CrossRef]
- Tretiakov, K.V.; Pigłowski, P.M.; Narojczyk, J.W.; Wojciechowski, K.W. Selective enhancement of auxeticity through changing a diameter of nanochannels in Yukawa systems. Smart Mater. Struct. 2018, 27, 115021. [Google Scholar] [CrossRef]
- Narojczyk, J.W.; Wojciechowski, K.W.; Tretiakov, K.V.; Smardzewski, J.; Scarpa, F.; Piglowski, P.M.; Kowalik, M.; Imre, A.R.; Bilski, M. Auxetic properties of a f.c.c. crystal of hard spheres with an array of [001]-nanochannels filled by hard spheres of another diameter. Phys. Status Solidi B 2019, 256, 1800611. [Google Scholar] [CrossRef]
- Narojczyk, J.; Wojciechowski, K. Poisson’s ratio of the f.c.c. hard sphere crystals with periodically stacked (001)-nanolayers of hard spheres of another diameter. Materials 2019, 12, 700. [Google Scholar] [CrossRef]
- Narojczyk, J.W.; Wojciechowski, K.W.; Smardzewski, J.; Imre, A.R.; Grima, J.N.; Bilski, M. Cancellation of auxetic properties in f.c.c. hard sphere crystals by hybrid layer-channel nanoinclusions filled by hard spheres of another diameter. Materials 2021, 14, 3008. [Google Scholar] [CrossRef]
- Grima, J.N.; Evans, K.E. Auxetic behavior from rotating squares. J. Mater. Sci. Lett. 2000, 19, 1563–1565. [Google Scholar] [CrossRef]
- Grima, J.N.; Jackson, R.; Alderson, A.; Evans, K.E. Do zeolites have negative Poisson’s ratios? Adv. Mater. 2000, 12, 1912–1918. [Google Scholar] [CrossRef]
- Grima, J.N.; Evans, K.E. Self expanding molecular networks. Chem. Commun. 2000, 1531–1532. [Google Scholar] [CrossRef]
- Grima, J.N.; Alderson, A.; Evans, K.E. Negative Poisson’s ratios from rotating rectangles. Comput. Methods Sci. Technol. 2004, 10, 137–145. [Google Scholar] [CrossRef]
- Grima, J.N.; Alderson, A.; Evans, K.E. Auxetic behaviour from rotating rigid units. Phys. Status Solidi B 2005, 242, 561–575. [Google Scholar] [CrossRef]
- Grima, J.N.; Gatt, R.; Alderson, A.; Evans, K.E. On the potential of connected stars as auxetic systems. Molec. Simul. 2005, 31, 925–935. [Google Scholar] [CrossRef]
- Grima, J.N.; Gatt, R.; Alderson, A.; Evans, K.E. On the origin of auxetic behaviour in the silicate α-cristobalite. J. Mater. Chem. 2005, 15, 4003–4005. [Google Scholar] [CrossRef]
- Grima, J.N.; Evans, K.E. Auxetic behavior from rotating triangles. J. Mater. Sci. 2006, 41, 3193–3196. [Google Scholar] [CrossRef]
- Grima, J.N.; Gatt, R.; Alderson, A.E.; Evans, K. An alternative explanation for the negative Poisson’s ratios in α-cristobalite. Mater. Sci. Eng. A 2006, 423, 219–224. [Google Scholar] [CrossRef]
- Grima, J.N.; Gatt, R.; Ravirala, N.; Alderson, A.; Evans, K.E. Negative Poisson’s ratios in cellular foam materials. Mater. Sci. Eng. A 2006, 423, 214–218. [Google Scholar] [CrossRef]
- Grima, J.N.; Zammit, V.; Gatt, R.; Alderson, A.; Evans, K.E. Auxetic behaviour from rotating semi-rigid units. Phys. Status Solidi B 2007, 244, 866–882. [Google Scholar] [CrossRef]
- Grima, J.N.; Gatt, R.; Zammit, V.; Williams, J.J.; Evans, K.E.; Alderson, A.; Walton, R.I. Natrolite: A zeolite with negative Poisson’s ratios. J. Appl. Phys. 2007, 101, 086102. [Google Scholar] [CrossRef]
- Grima, J.N.; Farrugia, P.S.; Caruana, C.; Gatt, R.; Attard, D. Auxetic behaviour from stretching connected squares. J. Mater. Sci. 2008, 43, 5962–5971. [Google Scholar] [CrossRef]
- Attard, D.; Grima, J.N. Auxetic behaviour from rotating rhombi. Phys. Status Solidi B 2008, 245, 2395–2404. [Google Scholar] [CrossRef]
- Grima, J.N.; Farrugia, P.S.; Gatt, R.; Attard, D. On the auxetic properties of rotating rhombi and parallelograms: A preliminary investigation. Phys. Status Solidi B 2008, 245, 521–529. [Google Scholar] [CrossRef]
- Attard, D.; Manicaro, E.; Grima, J.N. On rotating rigid parallelograms and their potential for exhibiting auxetic behaviour. Phys. Status Solidi B 2009, 246, 2033–2044. [Google Scholar] [CrossRef]
- Grima, J.N.; Cassar, R.N.; Gatt, R. On the effect of hydrostatic pressure on the auxetic character of NAT-type silicates. J. Non-Cryst. Solids 2009, 355, 1307–1312. [Google Scholar] [CrossRef]
- Attard, D.; Manicaro, E.; Gatt, R.; Grima, J.N. On the properties of auxetic rotating stretching squares. Phys. Status Solidi B 2009, 246, 2045–2054. [Google Scholar] [CrossRef]
- Grima, J.N.; Gatt, R.; Ellul, B.; Chetcuti, E. Auxetic behaviour in non-crystalline materials having star or triangular shaped perforations. J. Non-Cryst. Solids 2010, 356, 1980–1987. [Google Scholar] [CrossRef]
- Grima, J.N.; Gatt, R. Perforated sheets exhibiting negative Poisson’s ratios. Adv. Eng. Mater. 2010, 12, 460–464. [Google Scholar] [CrossRef]
- Grima, J.N.; Manicaro, E.; Attard, D. Auxetic behaviour from connected different-sized squares and rectangles. Proc. Roy. Soc. A 2011, 467, 439–458. [Google Scholar] [CrossRef]
- Grima, J.N.; Chetcuti, E.; Manicaro, E.; Attard, D.; Camilleri, M.; Gatt, R.; Evans, K.E. On the auxetic properties of generic rotating rigid triangles. Proc. Roy. Soc. A 2012, 468, 810–830. [Google Scholar] [CrossRef]
- Gatt, R.; Mizzi, L.; Azzopardi, K.M.; Grima, J.N. A force-field based analysis of the deformation mechanism in α-cristobalite. Phys. Status Solidi B 2015, 252, 1479–1485. [Google Scholar] [CrossRef]
- Gatt, R.; Mizzi, L.; Azzopardi, J.I.; Azzopardi, K.M.; Attard, D.; Casha, A.; Briffa, J.; Grima, J.N. Hierarchical auxetic mechanical metamaterials. Sci. Rep. 2015, 5, 8395. [Google Scholar] [CrossRef] [PubMed]
- Dudek, K.K.; Gatt, R.; Mizzi, L.; Dudek, M.R.; Attard, D.; Evans, K.E.; Grima, J.N. On the dynamics and control of mechanical properties of hierarchical rotating rigid unit auxetics. Sci. Rep. 2017, 7, 46529. [Google Scholar] [CrossRef] [PubMed]
- Attard, D.; Casha, A.; Grima, J. Filtration properties of auxetics with rotating rigid units. Materials 2018, 11, 725. [Google Scholar] [CrossRef] [PubMed]
- Evans, K.E.; Alderson, A. Rotation and dilation deformation mechanisms for auxetic behaviour in the α-cristobalite tetrahedral framework structure. Phys. Chem. Min. 2001, 28, 711–718. [Google Scholar] [CrossRef]
- Alderson, A.; Evans, K.E. Molecular origin of auxetic behavior in tetrahedral framework silicates. Phys. Rev. Lett. 2002, 89, 225503. [Google Scholar] [CrossRef]
- Alderson, A.; Alderson, K.L.; Evans, K.E.; Grima, J.N.; Williams, M.R.; Davies, P.J. Molecular modeling of the deformation mechanisms acting in auxetic silica. Comput. Methods Sci. Technol. 2004, 10, 117–126. [Google Scholar] [CrossRef]
- Alderson, A.; Alderson, K.L.; Evans, K.E.; Grima, J.N.; Williams, M.R.; Davies, P.J. Modelling the deformation mechanisms, structure-property relationships and applications of auxetic nanomaterials. Phys. Status Solidi B 2005, 242, 499–508. [Google Scholar] [CrossRef]
- Alderson, A.; Alderson, K.L.; Evans, K.E.; Grima, J.N.; Williams, M.S. Modelling of negative Poisson’s ratio nanomaterials: Deformation mechanisms, structure-property relationships and applications. J. Metastab. Nanocryst. Mater. 2005, 23, 55–58. [Google Scholar] [CrossRef]
- Alderson, A.; Evans, K.E. Deformation mechanisms leading to auxetic behaviour in the α-cristobalite and α-quartz structures of both silica and germania. J. Phys. Condens. Matter 2008, 21, 025401. [Google Scholar] [CrossRef] [PubMed]
- Grima, J.N.; Zammit, V.; Gatt, R.; Attard, D.; Caruana, C.; Chircop Bray, T.G. On the role of rotating tetrahedra for generating auxetic behavior in NAT and related systems. J. Non-Cryst. Solids 2008, 354, 4214–4220. [Google Scholar] [CrossRef]
- Attard, D.; Grima, J.N. A three-dimensional rotating rigid units network exhibiting negative Poisson’s ratios. Phys. Status Solidi B 2012, 249, 1330–1338. [Google Scholar] [CrossRef]
- Azzopardi, K.M.; Brincat, J.P.; Grima, J.N.; Gatt, R. Anomalous elastic properties in stishovite. RSC Adv. 2015, 5, 8974–8980. [Google Scholar] [CrossRef]
- Nazaré, F.; Alderson, A. Models for the prediction of Poisson’s ratio in the ‘α-cristobalite’ tetrahedral framework. Phys. Status Solidi B 2015, 252, 1465–1478. [Google Scholar] [CrossRef]
- Grima-Cornish, J.N.; Vella-Żarb, L.; Grima, J.N. Negative linear compressibility and auxeticity in boron arsenate. Annal. Physik 2020, 532, 1900550. [Google Scholar] [CrossRef]
- Grima-Cornish, J.N.; Grima, J.N.; Attard, D. A novel mechanical metamaterial exhibiting auxetic behavior and negative compressibility. Materials 2020, 13, 79. [Google Scholar] [CrossRef]
- Dudek, K.K.; Attard, D.; Gatt, R.; Grima-Cornish, J.N.; Grima, J.N. The multidirectional auxeticity and negative linear compressibility of a 3D mechanical metamaterial. Materials 2020, 13, 2193. [Google Scholar] [CrossRef]
- Grima-Cornish, J.N.; Vella-Żarb, L.; Wojciechowski, K.W.; Grima, J.N. Shearing deformations of β-cristobalite-like boron arsenate. Symmetry 2021, 13, 977. [Google Scholar] [CrossRef]
- Milstein, F.; Huang, K. Existence of a negative Poisson ratio in fcc crystals. Phys. Rev. B 1979, 19, 2030–2033. [Google Scholar] [CrossRef]
- Baughman, R.H.; Shacklette, J.M.; Zakhidov, A.A.; Stafström, S. Negative Poisson’s ratios as a common feature of cubic metals. Nature 1998, 392, 362–365. [Google Scholar] [CrossRef]
- Paszkiewicz, T.; Pruchnik, M.; Wolski, S. Slowness surfaces and energy focusing patterns of auxetic cubic media. Comput. Methods Sci. Technol. 2004, 10, 183–195. [Google Scholar] [CrossRef]
- Paszkiewicz, T.; Wolski, S. Anisotropic properties of mechanical characteristics and auxeticity of cubic crystalline media. Phys. Status Solidi B 2007, 244, 966–977. [Google Scholar] [CrossRef]
- Paszkiewicz, T.; Wolski, S. Elastic properties of cubic crystals: Every’s versus Blackman’s diagram. J. Phys. Conf. Ser. 2008, 104, 012038. [Google Scholar] [CrossRef]
- Jasiukiewicz, C.; Paszkiewicz, T.; Wolski, S. Auxetic properties and anisotropy of elastic material constants of 2D crystalline media. Phys. Status Solidi B 2008, 245, 562–569. [Google Scholar] [CrossRef]
- Brańka, A.C.; Wojciechowski, K.W. Auxeticity of cubic materials: The role of repulsive core interaction. J. Non-Cryst. Solids 2008, 354, 4143–4145. [Google Scholar] [CrossRef]
- Branka, A.C.; Heyes, D.M.; Wojciechowski, K.W. Auxeticity of cubic materials. Phys. Status Solidi B 2009, 246, 2063–2071. [Google Scholar] [CrossRef]
- Branka, A.C.; Heyes, D.M.; Wojciechowski, K.W. Auxeticity of cubic materials under pressure. Phys. Status Solidi B 2011, 248, 96–104. [Google Scholar] [CrossRef]
- Branka, A.C.; Heyes, D.M.; Maćkowiak, S.; Pieprzyk, S.; Wojciechowski, K.W. Cubic materials in different auxetic regions: Linking microscopic to macroscopic formulations. Phys. Status Solidi B 2012, 249, 1373–1378. [Google Scholar] [CrossRef]
- Goldstein, R.V.; Gorodtsov, V.A.; Lisovenko, D.S. Cubic auxetics. Dokl. Phys. 2011, 56, 399–402. [Google Scholar] [CrossRef]
- Goldstein, R.V.; Gorodtsov, V.A.; Lisovenko, D.S. Relation of Poisson’s ratio on average with Young’s modulus. Auxetics on average. Dokl. Phys. 2012, 57, 174–178. [Google Scholar] [CrossRef]
- Goldstein, R.V.; Gorodtsov, V.A.; Lisovenko, D.S. Classification of cubic auxetics. Phys. Status Solidi B 2013, 250, 2038–2043. [Google Scholar] [CrossRef]
- Goldstein, R.V.; Gorodtsov, V.A.; Lisovenko, D.S.; Volkov, M.A. Negative Poisson’s ratio for cubic crystals and nano/microtubes. Phys. Mesomech. 2014, 17, 97–115. [Google Scholar] [CrossRef]
- Krasavin, V.V.; Krasavin, A.V. Auxetic properties of cubic metal single crystals. Phys. Status Solidi B 2014, 251, 2314–2320. [Google Scholar] [CrossRef]
- Ho, D.T.; Park, S.D.; Kwon, S.Y.; Park, K.; Kim, S.Y. Negative Poisson’s ratios in metal nanoplates. Nat. Commun. 2014, 5, 3255. [Google Scholar] [CrossRef]
- Ho, D.T.; Kim, H.; Kwon, S.Y.; Kim, S.Y. Auxeticity of face-centered cubic metal (001) nanoplates. Phys. Status Solidi B 2015, 252, 1492–1501. [Google Scholar] [CrossRef]
- Ho, D.T.; Park, S.D.; Kwon, S.Y.; Han, T.S.; Kim, S.Y. Negative Poisson’s ratio in cubic materials along principal directions. Phys. Status Solidi B 2016, 253, 1288–1294. [Google Scholar] [CrossRef]
- Goldstein, R.V.; Gorodtsov, V.A.; Lisovenko, D.S.; Volkov, M.A. Two-layer tubes from cubic crystals. Dokl. Phys. 2016, 61, 604–610. [Google Scholar] [CrossRef]
- Lisovenko, D.S.; Baimova, J.A.; Rysaeva, L.K.; Gorodtsov, V.A.; Rudskoy, A.I.; Dmitriev, S.V. Equilibrium diamond-like carbon nanostructures with cubic anisotropy: Elastic properties. Phys. Status Solidi B 2016, 253, 1295–1302. [Google Scholar] [CrossRef]
- Goldstein, R.V.; Gorodtsov, V.A.; Lisovenko, D.S.; Volkov, M.A. Two-layered tubes from cubic crystals: Auxetic tubes. Phys. Status Solidi B 2017, 254, 1600815. [Google Scholar] [CrossRef]
- Lisovenko, D.S.; Baimova, Y.A.; Rysaeva, L.K.; Gorodtsov, V.A.; Dmitriev, S.V. Equilibrium structures of carbon diamond-like clusters and their elastic properties. Phys. Solid State 2017, 59, 820–828. [Google Scholar] [CrossRef]
- Goldstein, R.V.; Gorodtsov, V.A.; Lisovenko, D.S. Longitudinal elastic tension of two-layered plates from isotropic auxetics-nonauxetics and cubic crystals. Eur. J. Mech. A Solids 2017, 63, 122–127. [Google Scholar] [CrossRef]
- Gorodtsov, V.A.; Lisovenko, D.S.; Lim, T.C. Three-layered plate exhibiting auxeticity based on stretching and bending modes. Compos. Struct. 2018, 194, 643–651. [Google Scholar] [CrossRef]
- Rysaeva, L.K.; Baimova, J.A.; Lisovenko, D.S.; Gorodtsov, V.A.; Dmitriev, S.V. Elastic properties of fullerites and diamond-like phases. Phys. Status Solidi B 2019, 256, 1800049. [Google Scholar] [CrossRef]
- Goldstein, R.V.; Gorodtsov, V.A.; Lisovenko, D.S.; Volkov, M.A. Thin homogeneous two-layered plates of cubic crystals with different layer orientation. Phys. Mesomech. 2019, 22, 261–268. [Google Scholar] [CrossRef]
- Bryukhanov, I.A.; Gorodtsov, V.A.; Lisovenko, D.S. Chiral Fe nanotubes with both negative Poisson’s ratio and Poynting’s effect. Atomistic simulation. J. Phys. Cond. Matt. 2019, 31, 475304. [Google Scholar] [CrossRef] [PubMed]
- Bryukhanov, I.A.; Gorodtsov, V.A.; Lisovenko, D.S. Modeling of the mechanical properties of chiral metallic nanotubes. Phys. Mesomech. 2020, 23, 477–486. [Google Scholar] [CrossRef]
- Bielejewska, N.; Brańka, A.C.; Pieprzyk, S.; Yevchenko, T. Another look at auxeticity of 2D square media. Phys. Status Solidi B 2020, 257, 2000485. [Google Scholar] [CrossRef]
- Gorodtsov, V.A.; Lisovenko, D.S. Auxetics among materials with cubic anisotropy. Mech. Solids 2020, 55, 461–474. [Google Scholar] [CrossRef]
- Volkov, M.A.; Gorodtsov, V.A.; Fadeev, E.P.; Lisovenko, D.S. Stretching of chiral tubes obtained by rolling-up plates of cubic crystals with various orientations. J. Mech. Mater. Struct. 2021, 16, 139–157. [Google Scholar] [CrossRef]
- Sirotin, Y.I.; Shaskolskaya, M.P. Fundamentals of Crystal Physics; Mir: Moscow, Russia, 1982. [Google Scholar]
- Nye, J.F. Physical Properties of Crystals; Clarendon Press: Oxford, UK, 1957; 329p. [Google Scholar]
- Goldstein, R.V.; Gorodtsov, V.A.; Lisovenko, D.S. Young’s modulus of cubic auxetics. Lett. Mater. 2011, 1, 127–132. [Google Scholar] [CrossRef]
- Smirnov, V.I. A Course of Higher Mathematics, Vol. I: Elementary Calculus; Pergamon Press: Oxford, UK, 1964; 546p. [Google Scholar]
- Gorodtsov, V.A.; Tkachenko, V.G.; Lisovenko, D.S. Extreme values of Young’s modulus of tetragonal crystals. Mech. Mater. 2021, 154, 103724. [Google Scholar] [CrossRef]
- Goldstein, R.V.; Gorodtsov, V.A.; Lisovenko, D.S.; Volkov, M.A. Auxetics among 6-constant tetragonal crystals. Lett. Mater. 2015, 5, 409–413. [Google Scholar] [CrossRef][Green Version]
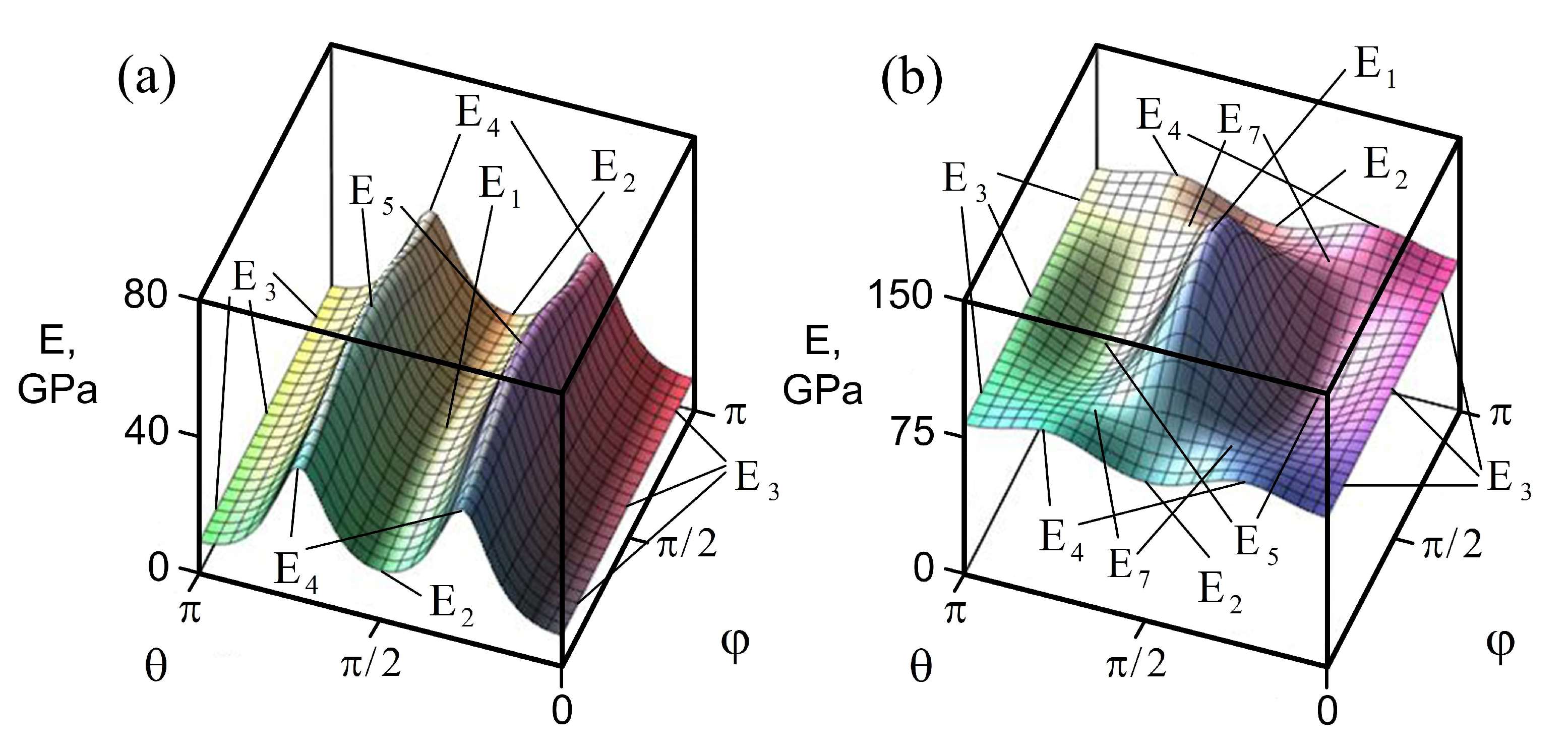
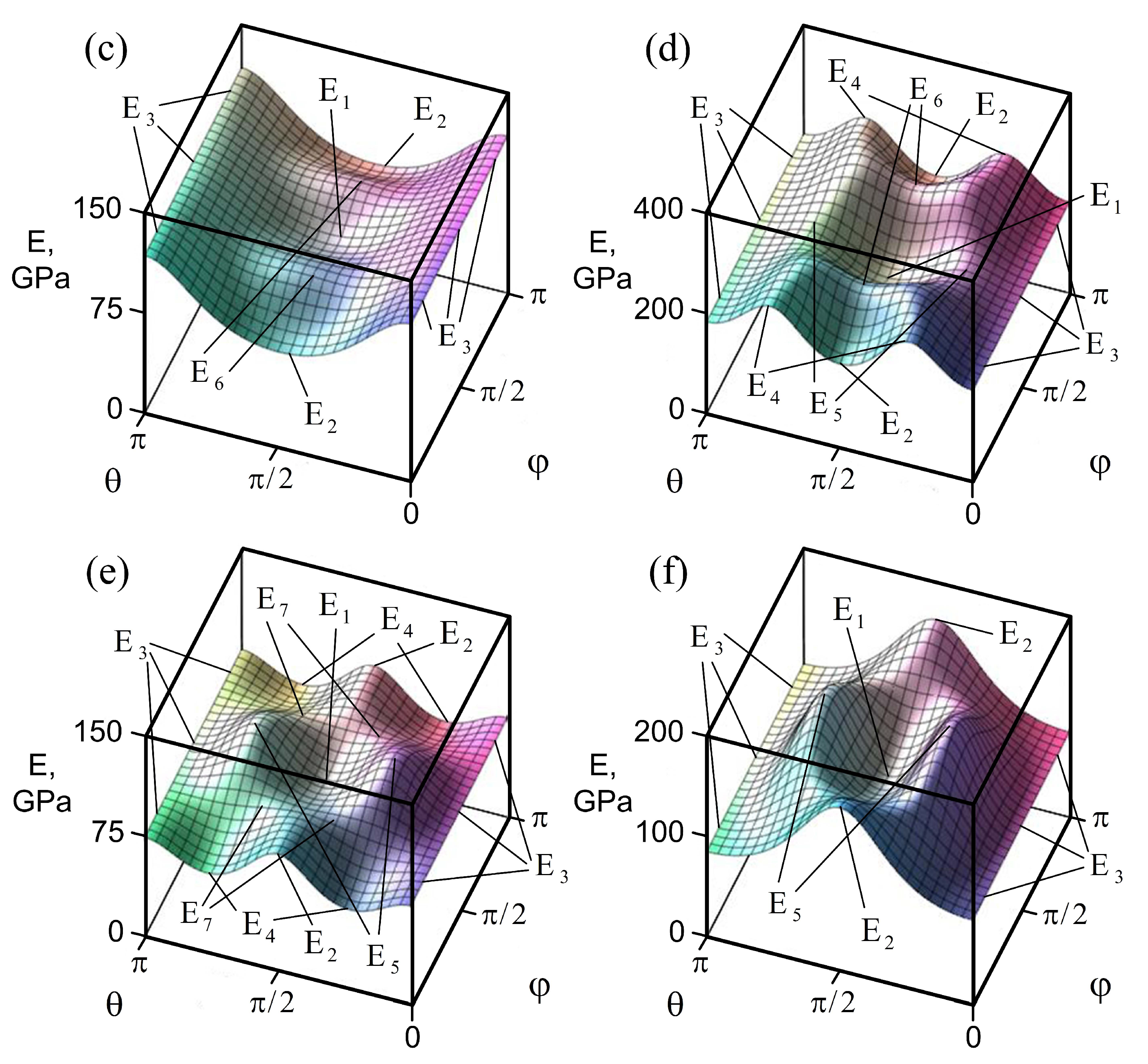
| Crystals | , | , | , | , | , | , |
|---|---|---|---|---|---|---|
| TPa | TPa | TPa | TPa | TPa | TPa | |
| CaSO | ||||||
| CaCO | 4.54 | 3.48 | 2.48 | |||
| BaMnF, s | 1.1 | 17.4 | 33.9 | 12.9 | 19.1 | |
| CsSO | 2.6 | 4.4 | 2.8 | 8.6 | 5.4 | 9.4 |
| Ga | 4.2 | 6.0 | 1.95 | 2.1 | ||
| InSe | 15.8 | 43.0 | 28.0 | 2.76 | ||
| PbBr | 51.6 | 55.9 | 11.1 | 25.6 | ||
| LiGaO, s | 0.55 | 2.35 | 2.35 | 1.25 | ||
| MgBaF | 11.3 | 8.8 | 1.7 | |||
| CoSiO | 1.09 | |||||
| RbSO | 2.35 | 3.95 | 1.65 | 3.95 | ||
| AgTlSe | 11.0 | 87.6 | 143 | 104 | 143 | |
| NaNO | ||||||
| -S | 40.0 | 52.0 | 26.5 | |||
| 9.6 | 96.3 | 60.7 | ||||
| TbF | 1.55 | 8.65 | 10.5 | 1.9 | ||
| NiB | 4.37 | 3.73 | 2.77 | 1.6 | 3.63 | 3.1 |
| -U | 1.22 | 5.32 | 3.38 | |||
| ZnSb | 2.35 | 7.65 | 7.25 |
| Crystals | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| GPa | GPa | GPa | GPa | GPa | GPa | GPa | |||||||
| AlSiO | 188 | Min | 251 | – | 310 | Max | 247 | Min | – | – | 259 | Max | – |
| CaSO | 90.9 | Max | 175 | Max | 105 | – | 90.5 | – | 71.6 | – | 32.4 | Min | – |
| CaCO | 144 | Max | 75.8 | Min | 82.0 | – | 89.5 | Max | 66.3 | Min | – | – | 85.8 |
| BaMnF, s | 58.8 | – | 36.6 | Min | 29.9 | Min | 45.2 | – | 90.1 | Max | – | – | – |
| BaSO | 58.1 | Min | 53.2 | – | 92.6 | Max | 36.5 | Min | – | – | 73.2 | Max | – |
| CsSO | 32.7 | Min | 30.9 | Min | 27.5 | Min | 32.9 | – | 33.4 | – | 33.7 | Max | – |
| BeAlO4 | 478 | Max | 386 | Max | 417 | – | 372 | Min | 374 | – | 379 | – | – |
| MgSiO | 190 | – | 148 | Min | 192 | – | – | – | 182 | Min | 202 | Max | – |
| MgSiO | 297 | Max | 171 | – | 203 | – | 171 | Min | 199 | – | – | – | – |
| Ga | 82.0 | Min | 71.4 | Min | 118 | Max | – | – | – | – | 95.5 | Max | – |
| InSe | 23.8 | Min | 58.8 | Max | 37.0 | – | – | – | 62.7 | Max | – | – | – |
| I | 3.05 | Min | 9.71 | – | 7.58 | – | 6.24 | Min | 30.8 | Max | 13.5 | Max | – |
| LaCuO | 117 | Min | 116 | Min | 159 | – | 161 | – | 161 | – | 202 | Max | – |
| PbBr | 19.7 | – | 24.7 | – | 18.2 | – | 27.0 | Max | 38.7 | Max | 10.1 | Min | – |
| LiGaO, s | 137 | – | 110 | Min | 125 | – | 132 | Max | 118 | Min | 139 | Max | 130 |
| MgBaF | 70.9 | – | 69.4 | – | 86.2 | – | – | – | 129 | Max | 61.9 | Min | 72.8 |
| CNOH | 7.0 | – | 4.91 | Min | 3.51 | Min | 19.6 | Max | – | – | 13.7 | – | – |
| CoSiO | 240 | Max | 138 | – | 170 | – | 133 | Min | 165 | – | – | – | – |
| MgGeO | 282 | Max | 161 | – | 187 | – | 153 | Min | 173 | – | – | – | – |
| NiSiO | 270 | Max | 175 | Min | 189 | – | 192 | – | – | – | – | – | – |
| KNO | 26.4 | Max | 20.1 | – | 15.4 | – | – | – | 14.4 | Min | – | – | 19.2 |
| KSeO | 40.3 | Max | 39.5 | Max | 30.6 | – | 24.7 | Min | – | – | 37.6 | – | – |
| KSO | 42.4 | – | 45.9 | – | 44.2 | – | 47.4 | Max | 46.7 | Max | 38.4 | Min | – |
| KZnCl | 15.6 | Max | 15.7 | Max | 20.8 | Max | 15.2 | – | 14.8 | – | 13.3 | Min | – |
| RbHSO | 22.9 | – | 30.1 | – | 32.6 | Max | 14.3 | Min | 15.7 | Min | 31.5 | Max | – |
| RbSO | 38.8 | – | 39.8 | – | 36.5 | Min | 40.6 | Max | 40.1 | Max | 36.9 | Min | – |
| RbZnBr | 12.2 | – | 12.9 | Max | 16.9 | Max | 12.5 | – | – | – | 10.0 | Min | – |
| AlSiO | 242 | Max | 153 | Min | 279 | – | 325 | Max | 196 | Min | – | – | 225 |
| AgNO | 11.3 | Min | 13.5 | Min | 29.2 | Max | – | – | – | – | 25.6 | Max | – |
| AgTlSe | 18.7 | – | 14.4 | Min | 9.17 | Min | 38.8 | – | 49.6 | Max | – | – | – |
| NaBF | 39.4 | Max | 29.9 | – | 51.7 | Max | – | – | 13.9 | Min | 29.6 | – | – |
| NaGeO, s | 66.0 | – | 83.8 | Max | 71.4 | – | – | – | 94.7 | Max | 54.5 | Min | – |
| NaNO | 25.1 | Max | 49.8 | Max | 54.1 | Max | 33.7 | – | 25.0 | – | 15.9 | Min | – |
| NaSO | 65.4 | Max | 93.5 | Max | 58.8 | – | 42.6 | Min | 51.1 | – | 63.0 | – | – |
| SrSO | 45.5 | Min | 45.9 | – | 87.7 | Max | 39.0 | Min | – | – | 74.6 | Max | – |
| -S | 14.1 | Min | 12.0 | – | 33.3 | Max | 11.5 | Min | – | – | 18.7 | Max | – |
| 13.4 | Max | 9.01 | Min | 13.3 | – | 19.3 | Max | 10.8 | Min | – | – | 11.6 | |
| MnSiO | 198 | Max | 116 | Min | 146 | – | – | – | 143 | – | – | – | – |
| TbF | 101 | Min | 163 | Max | 85.1 | Min | – | – | 166 | Max | – | – | – |
| TlSO | 21.7 | Min | 21.0 | Min | 27.7 | – | 28.2 | Max | 27.9 | – | 22.2 | – | – |
| NiB | 150 | Min | 166 | Min | 182 | – | 246 | Max | 203 | – | 232 | – | – |
| -U | 204 | Max | 149 | Min | 209 | – | 288 | Max | 170 | Min | – | – | 189 |
| ZnSb | 72.5 | Min | 87.7 | Max | 74.6 | – | 59.8 | Min | 101 | Max | – | – | 81.7 |
| Crystals | |||||
|---|---|---|---|---|---|
| (CH)NCHCOO·(CH)(COOH) | 2.92 | 37.0 | 12.7 | 0.91 | |
| I | 3.05 | 30.8 | 10.1 | −0.48 | 1.31 |
| SC(NH) | 2.39 | 23.8 | 9.96 | 1.00 | |
| 2.09 | 24.6 | 11.8 | 1.07 | ||
| (CH)NCHCOO·HBO | 1.85 | 18.3 | 9.89 | 1.22 | |
| Cu-14 wt% Al 3.0 wt% Ni | 22.3 | 167 | 7.49 | 1.43 | |
| NHBO4HO | 6.85 | 50.7 | 7.40 | 0.85 | |
| NHHCO1/2HO | 10.5 | 61.0 | 5.81 | 0.05 | 0.82 |
| CNOH | 3.51 | 19.6 | 5.58 | 1.05 | |
| (Fe,Mg)(Al,Fe)OSiO(O,OH) | 57.8 | 312 | 5.40 | 0.95 | |
| CaSO | 32.4 | 175 | 5.40 | 0.76 | |
| AgTlSe | 9.17 | 49.5 | 5.40 | 1.07 | |
| CHCOOLi·2HO | 11.6 | 53.8 | 4.64 | 0.04 | 0.68 |
| CaPb(CN)5HO | 9.79 | 43.5 | 4.44 | 0.07 | 0.71 |
| (CD)N | 4.46 | 19.2 | 4.30 | 0.00 | 0.71 |
| KBO4HO | 10.2 | 43.1 | 4.22 | 0.06 | 0.82 |
| Cd(COOH) | 8.06 | 33.3 | 4.13 | 0.98 | |
| CH | 3.22 | 13.1 | 4.07 | 0.77 | |
| Ca(COOH) | 11.8 | 47.8 | 4.05 | 0.81 | |
| CHN | 2.84 | 11.0 | 3.87 | 0.76 | |
| PbBr | 10.1 | 38.7 | 3.83 | 0.90 | |
| NaBF | 13.9 | 51.7 | 3.72 | 0.71 | |
| (CHNHCHCOOH)CaCl | 12.6 | 44.9 | 3.56 | 0.76 | |
| NaCHO2HO | 11.0 | 37.9 | 3.45 | −0.05 | 0.88 |
| CH(NO) | 5.68 | 19.4 | 3.42 | 0.60 | |
| NIPC | 2.39 | 8.15 | 3.41 | −0.16 | 0.84 |
| NaNO | 15.9 | 54.1 | 3.40 | 0.09 | 0.64 |
| CsSCN | 6.38 | 21.1 | 3.31 | 0.01 | 0.78 |
| (CH)NCHCOO·CaCl2HO | 7.63 | 23.6 | 3.09 | 0.79 | |
| CHOHO | 8.61 | 26.4 | 3.07 | 0.00 | 0.74 |
| CHClNO | 9.90 | 30.3 | 3.06 | 0.05 | 0.61 |
| ZnSOHO | 16.1 | 48.8 | 3.03 | 0.71 | |
| 15.6 | 30.0 | 1.92 | −0.04 | 0.66 | |
| [CNHCHO | 3.61 | 10.9 | 3.02 | 0.94 | |
| BaMnF, | 29.9 | 90.1 | 3.01 | 0.87 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gorodtsov, V.A.; Lisovenko, D.S. The Extreme Values of Young’s Modulus and the Negative Poisson’s Ratios of Rhombic Crystals. Crystals 2021, 11, 863. https://doi.org/10.3390/cryst11080863
Gorodtsov VA, Lisovenko DS. The Extreme Values of Young’s Modulus and the Negative Poisson’s Ratios of Rhombic Crystals. Crystals. 2021; 11(8):863. https://doi.org/10.3390/cryst11080863
Chicago/Turabian StyleGorodtsov, Valentin A., and Dmitry S. Lisovenko. 2021. "The Extreme Values of Young’s Modulus and the Negative Poisson’s Ratios of Rhombic Crystals" Crystals 11, no. 8: 863. https://doi.org/10.3390/cryst11080863
APA StyleGorodtsov, V. A., & Lisovenko, D. S. (2021). The Extreme Values of Young’s Modulus and the Negative Poisson’s Ratios of Rhombic Crystals. Crystals, 11(8), 863. https://doi.org/10.3390/cryst11080863







