Investigation of Elastic Properties of the Single-Crystal Nickel-Base Superalloy CMSX-4 in the Temperature Interval between Room Temperature and 1300 °C
Abstract
1. Introduction
2. Materials and Methods
2.1. Investigated Specimens
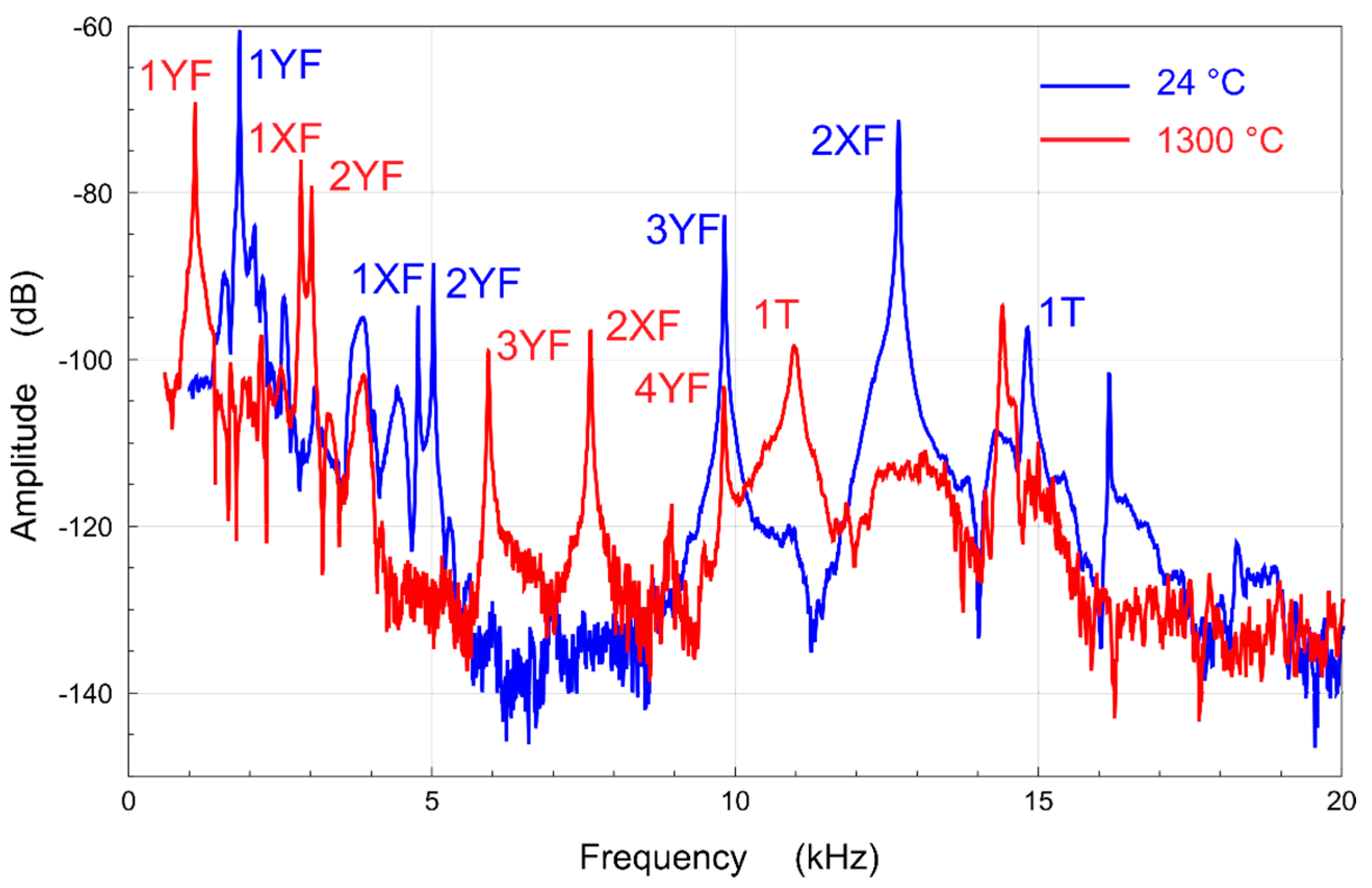
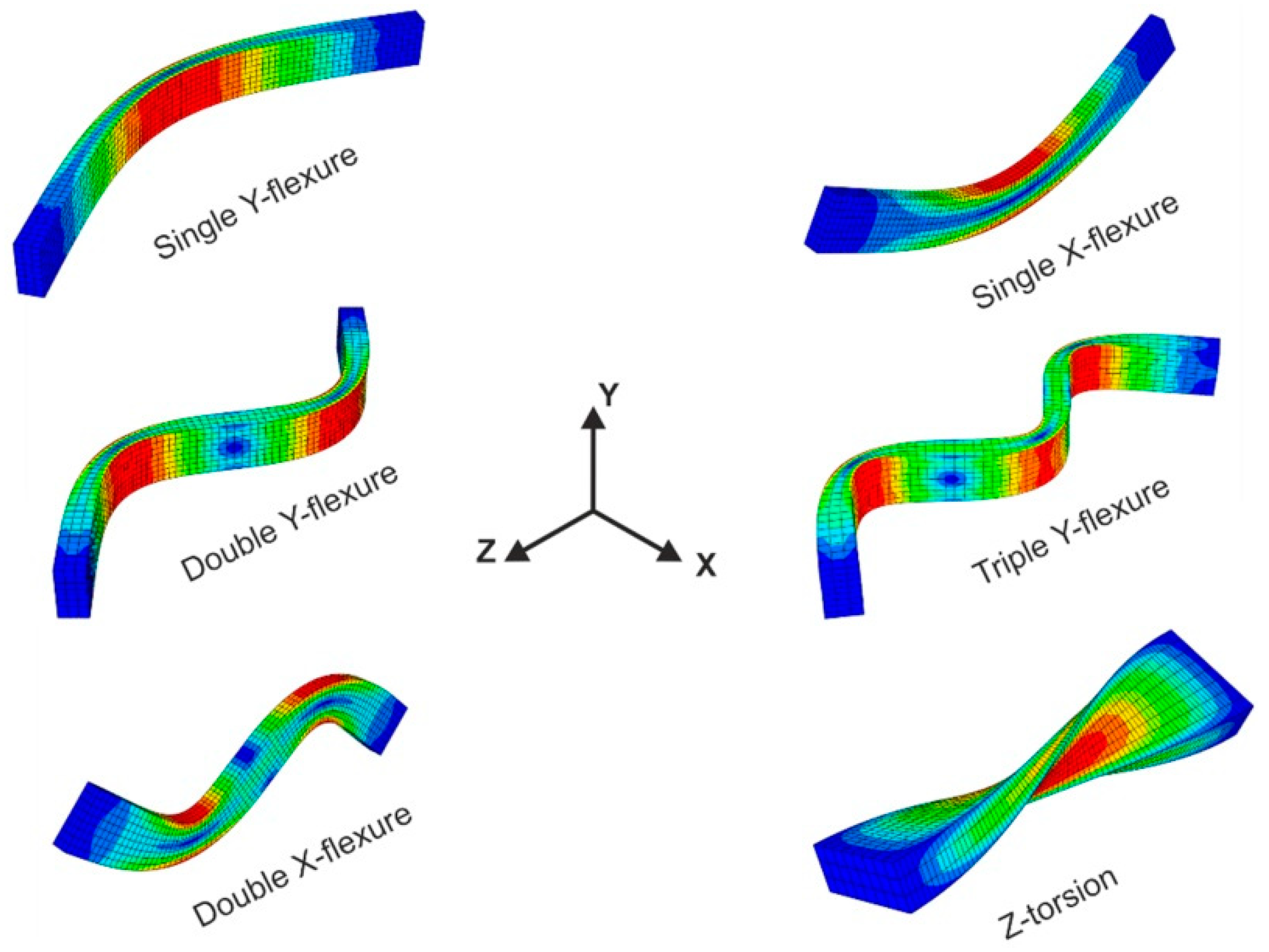
2.2. Measurement of Elastic Constants
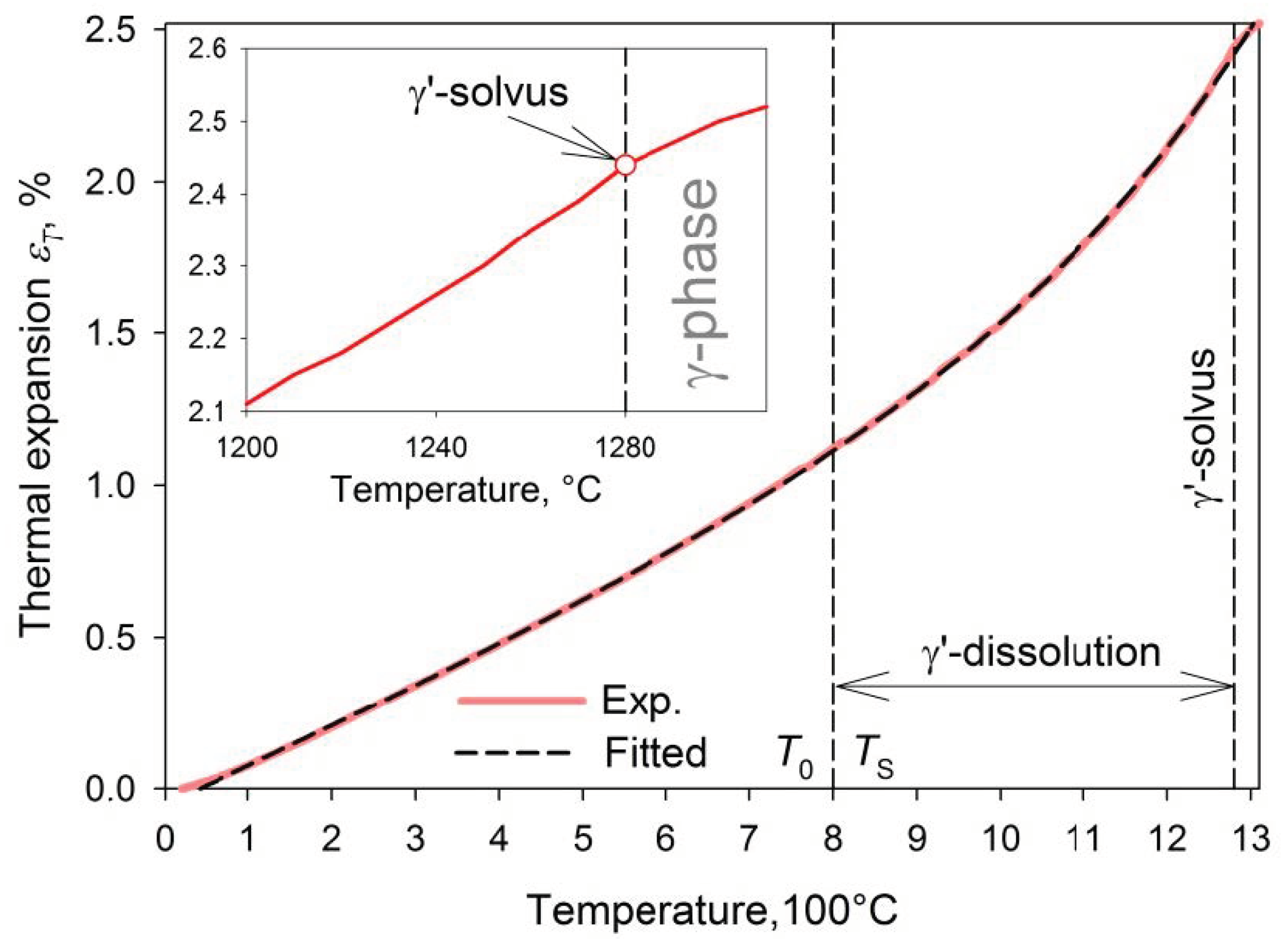
2.3. Measurement of Material Density and Thermal Expansion
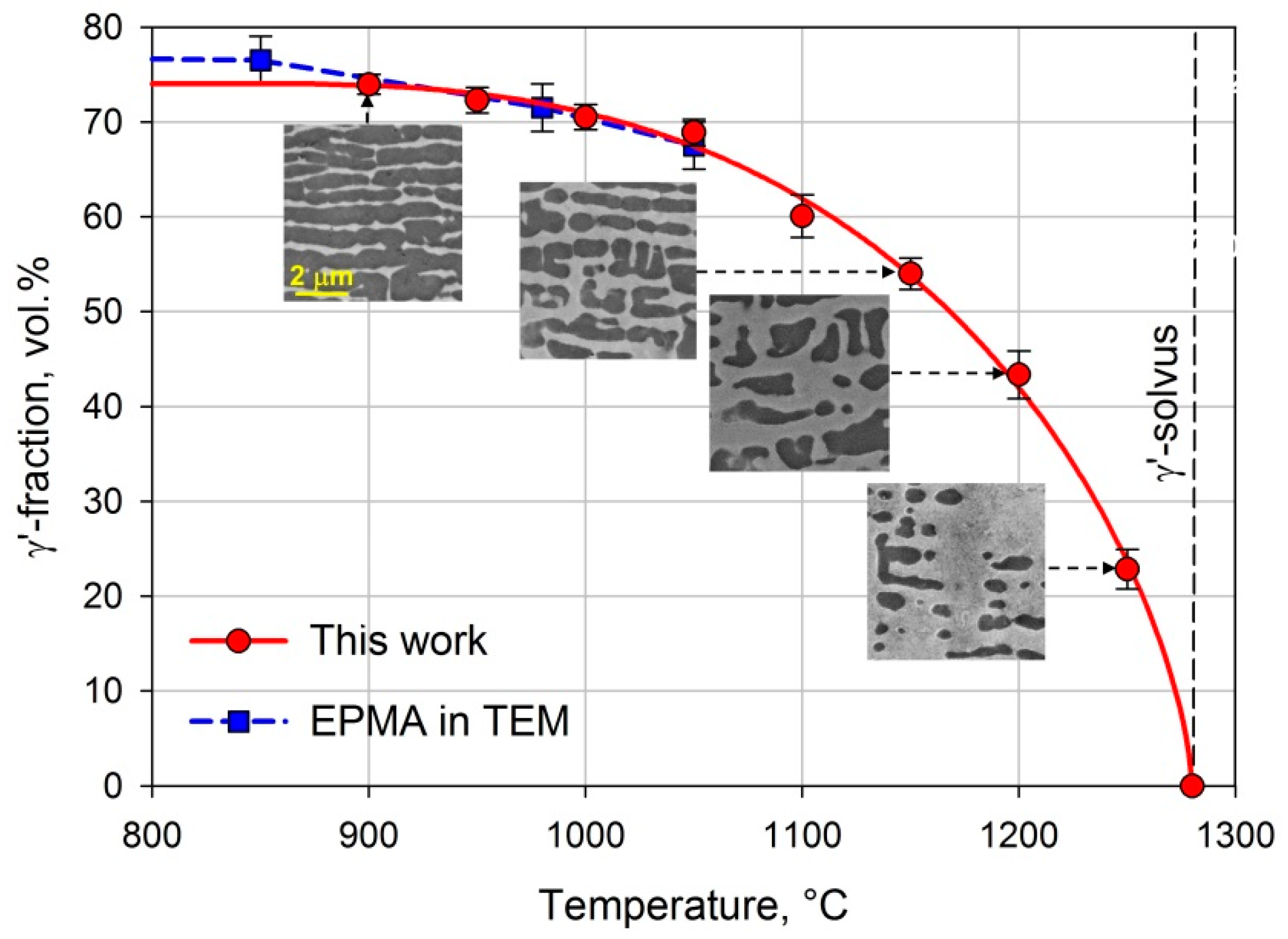
2.4. Measurement of the Temperature Dependence of γ′-Volume Fraction
3. Results
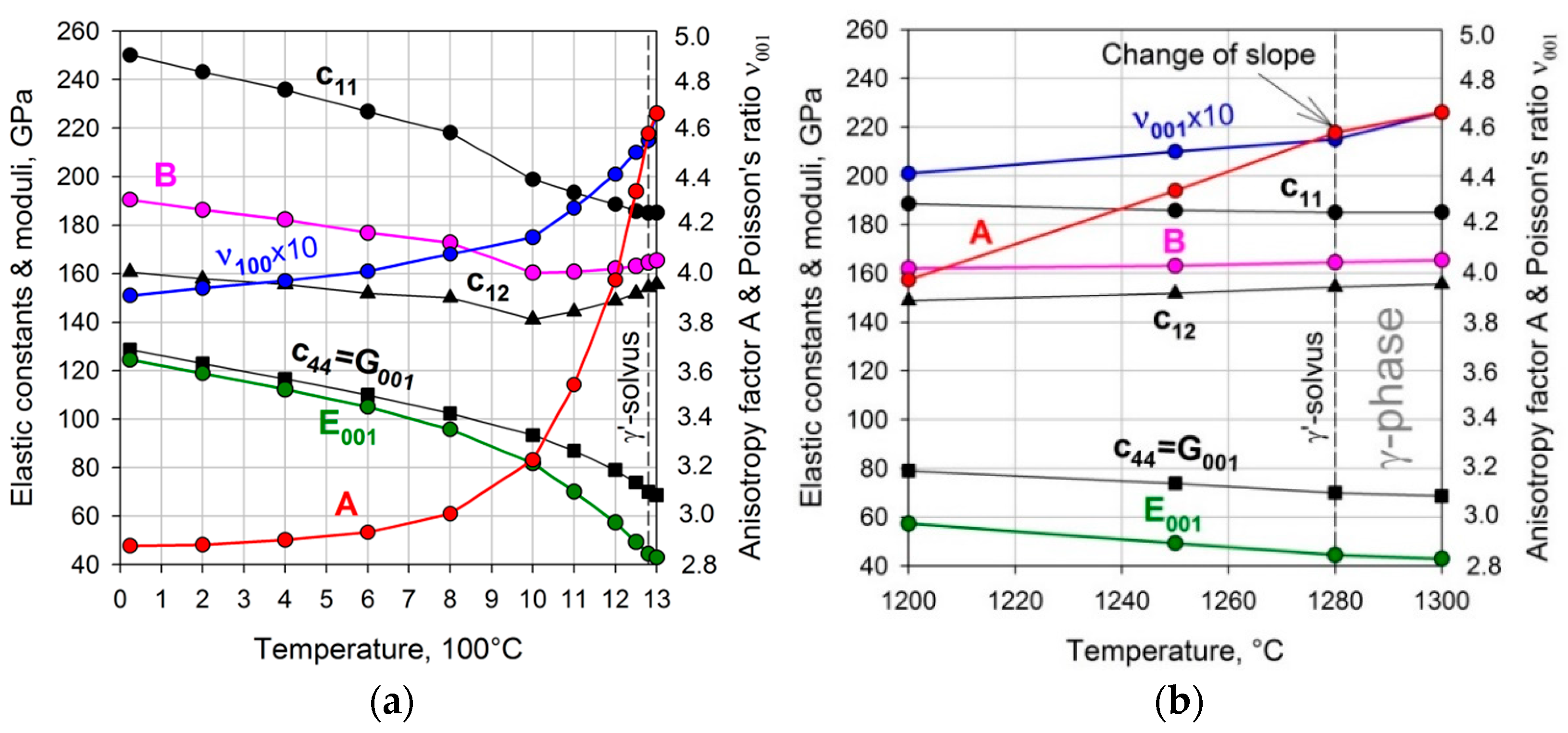
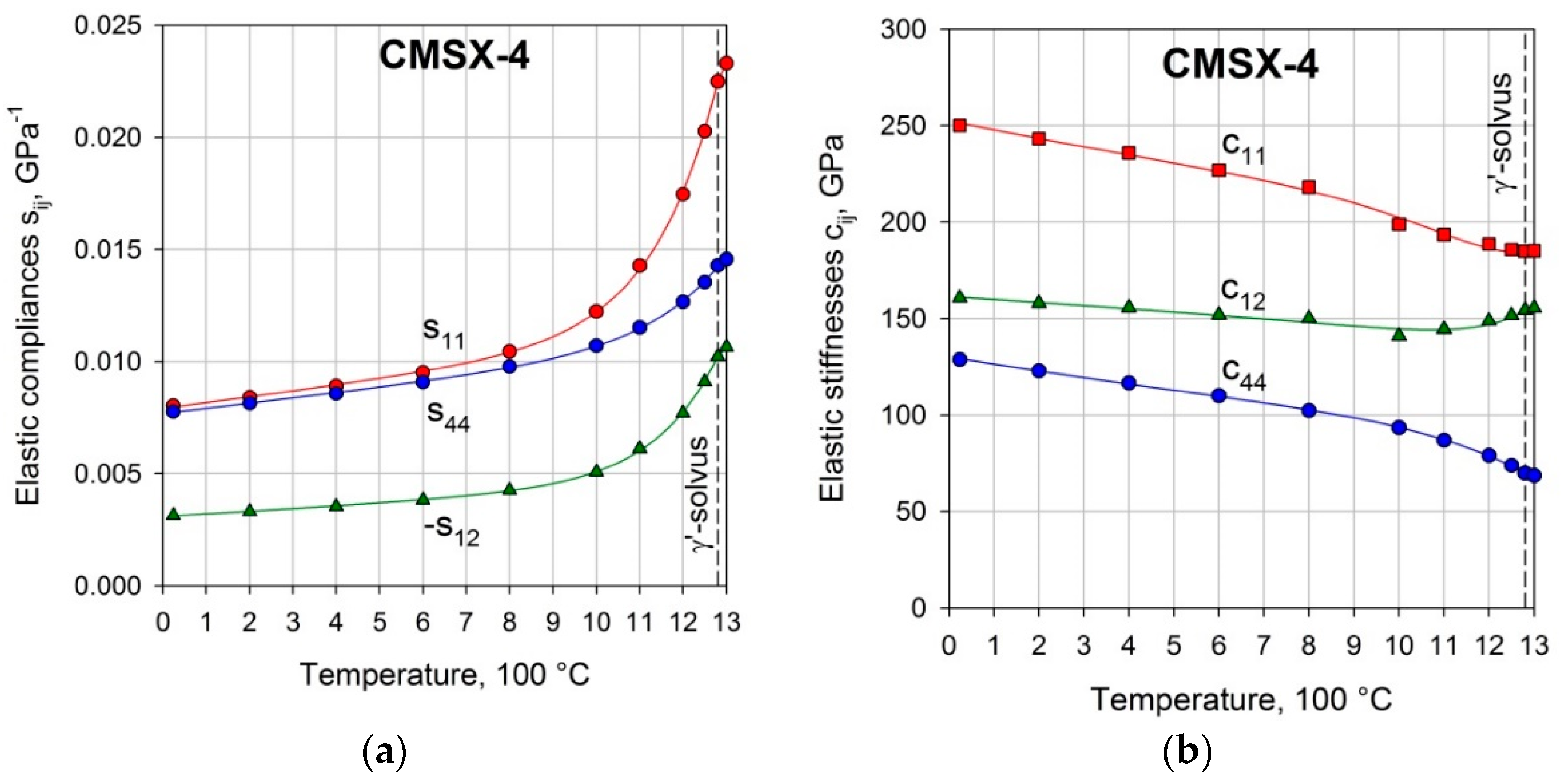
3.1. Temperature Dependence of Elastic Constants of Superalloy CMSX-4
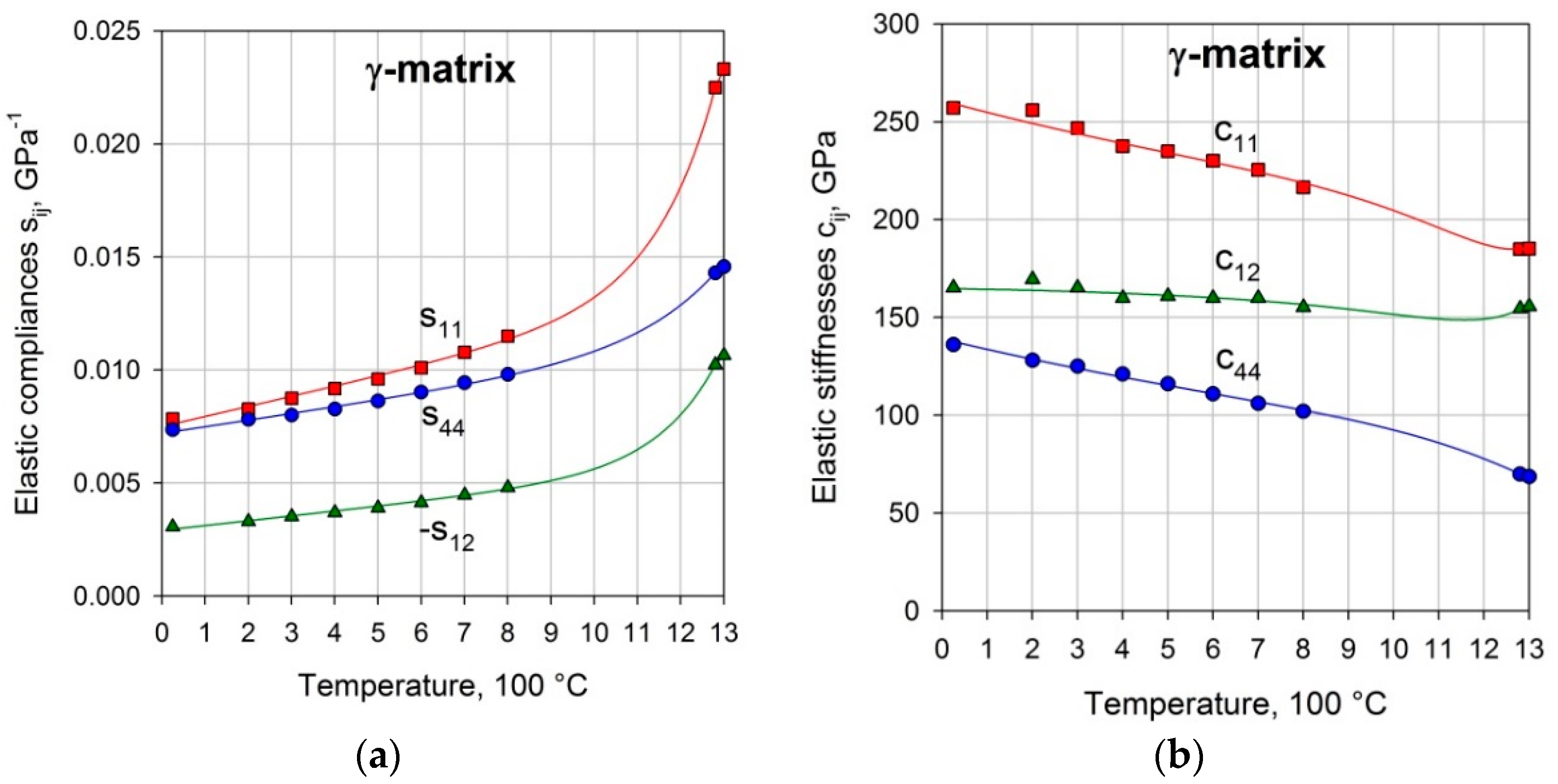
3.2. Temperature Dependence of Elastic Constants of the Matrix Alloy
3.3. Calculation of Elastic Constants for the γ′-Phase
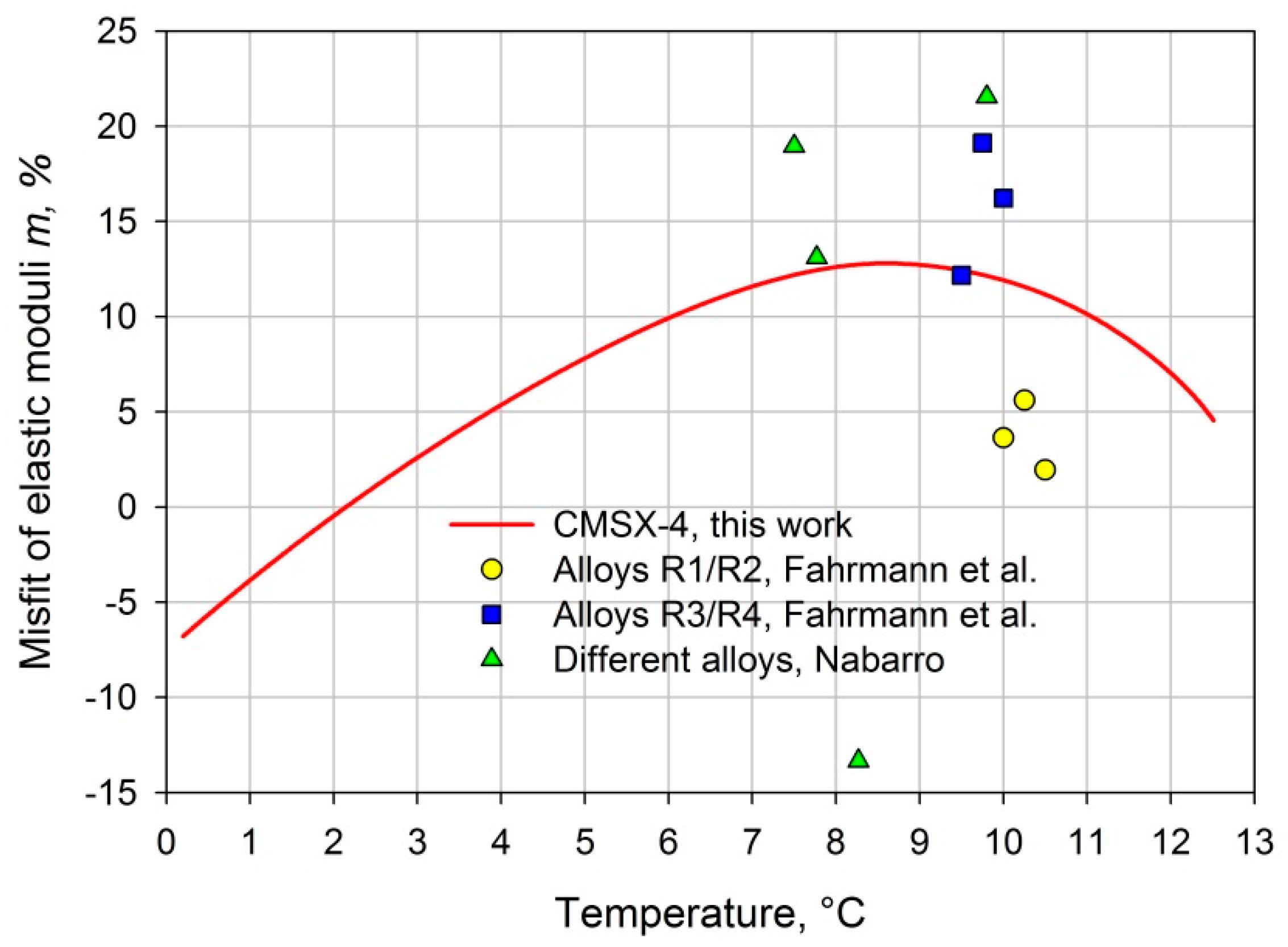
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| T, °C | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | - | - | 0.0238 | 0.0329 | 0.0425 | 0.053 | 0.0641 | ||
| 100 | 0.076 | 0.088 | 0.1 | 0.113 | 0.125 | 0.138 | 0.15 | 0.16 | 0.176 | 0.19 |
| 200 | 0.203 | 0.217 | 0.23 | 0.245 | 0.258 | 0.272 | 0.286 | 0.3 | 0.314 | 0.329 |
| 300 | 0.342 | 0.355 | 0.368 | 0.382 | 0.396 | 0.41 | 0.424 | 0.438 | 0.451 | 0.464 |
| 400 | 0.479 | 0.494 | 0.508 | 0.523 | 0.537 | 0.552 | 0.567 | 0.581 | 0.596 | 0.61 |
| 500 | 0.625 | 0.639 | 0.653 | 0.667 | 0.682 | 0.697 | 0.712 | 0.727 | 0.743 | 0.758 |
| 600 | 0.774 | 0.79 | 0.806 | 0.822 | 0.839 | 0.856 | 0.873 | 0.89 | 0.906 | 0.924 |
| 700 | 0.941 | 0.958 | 0.975 | 0.993 | 1.01 | 1.03 | 1.05 | 1.06 | 1.08 | 1.1 |
| 800 | 1.12 | 1.14 | 1.15 | 1.17 | 1.19 | 1.21 | 1.23 | 1.25 | 1.27 | 1.29 |
| 900 | 1.31 | 1.33 | 1.35 | 1.38 | 1.4 | 1.42 | 1.44 | 1.46 | 1.49 | 1.51 |
| 1000 | 1.53 | 1.56 | 1.58 | 1.61 | 1.63 | 1.66 | 1.68 | 1.71 | 1.74 | 1.76 |
| 1100 | 1.79 | 1.82 | 1.85 | 1.88 | 1.91 | 1.94 | 1.97 | 2.01 | 2.04 | 2.07 |
| 1200 | 2.11 | 2.15 | 2.18 | 2.22 | 2.26 | 2.3 | 2.35 | 2.39 | 2.44 | 2.47 |
| 1300 | 2.5 | 2.52 |
References
- Reed, R.C. The Superalloys: Fundamentals and Applications; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar] [CrossRef]
- Shalin, R.E.; Svetlov, I.L.; Kachanov, E.B.; Toloraya, V.N.; Gavrilin, O.S. Single-Crystals of Nickel-Base Superalloys; Mashinistroeniye: Moscow, Russia, 1997. [Google Scholar]
- Ghosh, R.N.; Curtis, R.V.; McLean, M. Creep deformation of single crystal superalloys—Modelling the crystallographic anisotropy. Acta Metall. Mater. 1990, 38, 1977–1992. [Google Scholar] [CrossRef]
- Méric, L.; Poubanne, P.; Cailletaud, G. Single Crystal Modeling for Structural Calculations: Part 1—Model Presentation. J. Eng. Mater. Technol. 1991, 113, 162–170. [Google Scholar] [CrossRef]
- Meéric, L.; Cailletaud, G. Single Crystal Modeling for Structural Calculations: Part 2—Finite Element Implementation. J. Eng. Mater. Technol. 1991, 113, 171–182. [Google Scholar] [CrossRef]
- Tinga, T. Multiscale Modelling of Single Crystal Superalloys for Gas Turbine Blades. Ph.D. Thesis, Eindhoven University of Technology, Eindhoven, The Netherlands, 7 May 2009. [Google Scholar] [CrossRef]
- Zhou, N.; Shen, C.; Mills, M.; Wang, Y. Contributions from elastic inhomogeneity and from plasticity to γ′ rafting in single-crystal Ni–Al. Acta Mater. 2008, 56, 6156–6173. [Google Scholar] [CrossRef]
- Link, T.; Epishin, A.; Fedelich, B. Inhomogeneity of misfit stresses in nickel-base superalloys: Effect on propagation of matrix dislocation loops. Philos. Mag. 2009, 89, 1141–1159. [Google Scholar] [CrossRef]
- Cottura, M.; Appolaire, B.; Finel, A.; Le Bouar, Y. Coupling the Phase Field Method for diffusive transformations with dislocation density-based crystal plasticity: Application to Ni-based superalloys. J. Mech. Phys. Solids 2016, 94, 473–489. [Google Scholar] [CrossRef]
- Böttger, B.; Apel, M.; Budnitzki, M.; Eiken, J.; Laschet, G.; Zhou, B. Calphad coupled phase-field model with mechano-chemical contributions and its application to rafting of γ′ in CMSX-4. Comput. Mater. Sci. 2020, 184, 109909. [Google Scholar] [CrossRef]
- Krivko, A.I.; Epishin, A.I.; Svetlov, I.L.; Samoilov, A.I. Elastic properties of single crystals of nickel alloys. Strength Mater. 1988, 20, 214–223. [Google Scholar] [CrossRef]
- Svetlov, I.L.; Epishin, A.I.; Krivko, A.I.; Samoilov, A.I.; Odintsev, I.N.; Andreev, A.P. Anisotropy of Poisson ratio of nickel-base alloy single-crystals. Dokl. Akad. Nauk SSSR 1988, 302, 1372–1375. [Google Scholar]
- Epishin, A.I.; Lisovenko, D.S. Extreme values of the Poisson’s ratio of cubic crystals. Tech. Phys. 2016, 61, 1516–1524. [Google Scholar] [CrossRef]
- Schneider, W. Hochtemperaturkriechverhalten und Mikrostruktur der einkristallinen Nickelbasis-Superlegierung CMSX-4 bei Temperaturen von 800 °C bis 1100 °C. Ph.D. Thesis, University of Erlangen-Nuremberg, Erlangen-Nuremberg, Germany, 1993. [Google Scholar]
- Hermann, W.; Sockel, H.; Han, J.; Bertram, A. Elastic properties and determination of elastic constants of nickel-base superalloys by a free-free beam technique. In Proceedings of the Superalloys 1996, Seven Springs Mountain Resort, Champion, PA, USA, 22–26 September 1996; Kissinger, R.D., Deye, D.J., Anton, D.L., Cetel, A.D., Nathal, M.V., Pollock, T.M., Woodford, D.A., Eds.; TMS: Warrendale, PA, USA, 2000; pp. 229–238. [Google Scholar] [CrossRef]
- Siebörger, D.; Knake, H.; Glatzel, U. Temperature dependence of the elastic moduli of the nickel-base superalloy CMSX-4 and its isolated phases. Mater. Sci. Eng. A 2001, 298, 26–33. [Google Scholar] [CrossRef]
- Demtröder, K.; Eggeler, G.; Schreuer, J. Influence of microstructure on macroscopic elastic properties and thermal expansion of nickel-base superalloys ERBO/1 and LEK94. Mater. Werkst. 2015, 46, 563–576. [Google Scholar] [CrossRef]
- Le Graverend, J.-B.; Cormier, J.; Gallerneau, F.; Kruch, S.; A Mendez, J. Highly non-linear creep life induced by a short close γ′-solvus overheating and a prior microstructure degradation on a nickel-based single crystal superalloy. Mater. Des. 2014, 56, 990–997. [Google Scholar] [CrossRef]
- Epishin, A.; Fedelich, B.; Link, T.; Feldmann, T.; Svetlov, I.L. Pore annihilation in a single-crystal nickel-base superalloy during hot isostatic pressing: Experiment and modelling. Mater. Sci. Eng. A 2013, 586, 342–349. [Google Scholar] [CrossRef]
- Epishin, A.; Link, T.; Fedelich, B.; Svetlov, I.L.; Golubovskiy, E.R. Hot isostatic pressing of single-crystal nickel-base superalloys: Mechanism of pore closure and effect on mechanical properties. In Proceedings of the of Eurosuperalloys 2014, Giens, France, 12–16 May 2014; Guedou, J.Y., Ed.; EDP: Les Ulis, France, 2014; Volume 14, p. 8003. [Google Scholar] [CrossRef]
- Epishin, A.; Fedelich, B.; Nolze, G.; Schriever, S.; Feldmann, T.; Ijaz, M.F.; Viguier, B.; Poquillon, D.; Le Bouar, Y.; Ruffini, A.; et al. Creep of Single Crystals of Nickel-Based Superalloys at Ultra-High Homologous Temperature. Met. Mater. Trans. A 2018, 49, 3973–3987. [Google Scholar] [CrossRef]
- Tien, J.K.; Copley, S.M. The effect of uniaxial stress on the periodic morphology of coherent gamma prime precipitates in nickel-base superalloy crystals. Met. Mater. Trans. A 1971, 2, 215–219. [Google Scholar] [CrossRef]
- Pineau, A. Influence of uniaxial stress on the morphology of coherent precipitates during coarsening-elastic energy considerations. Acta Met. 1976, 24, 559–564. [Google Scholar] [CrossRef]
- Svetlov, I.; Golovko, B.; Epishin, A.; Abalakin, N. Diffusional mechanism of γ′-phase particles coalescence in single crystals of nickel-base superalloys. Scr. Met. Mater. 1992, 26, 1353–1358. [Google Scholar] [CrossRef]
- Nabarro, F.R.N. Rafting in Superalloys. Met. Mater. Trans. A 1996, 27, 513–530. [Google Scholar] [CrossRef]
- Nazmy, M.; Epishin, A.; Link, T.; Stäubli, M. A review of degradation in single crystal nickel based superalloys. Energy Mater. 2006, 1, 263–268. [Google Scholar] [CrossRef]
- Fedelich, B.; Epishin, A.; Link, T.; Klingelhöffer, H.; Künecke, G.; Portella, P.D. Rafting during high temperature deformation in a single crystal superalloy: Experiments and modeling. In Proceedings of the Superalloys 2012, Seven Springs Mountain Resort, Champion, PA, USA, 9–13 September 2012; Huron, E.S., Reed, R.C., Hardy, M.C., Mills, M.J., Montero, R.E., Portella, P.D., Telesman, J., Eds.; TMS: Warrendale, PA, USA, 2012; pp. 491–500. Available online: https://www.tms.org/Superalloys/10.7449/2012/Superalloys_2012_491_500.pdf (accessed on 1 October 2020).
- Titus, M.S.; Suzuki, A.; Pollock, T.M. High Temperature creep of new L12 containing cobalt-base superalloys. In Proceedings of the Superalloys 2012, Seven Springs Mountain Resort, Champion, PA, USA, 9–13 September 2012; Huron, E.S., Reed, R.C., Hardy, M.C., Mills, M.J., Montero, R.E., Portella, P.D., Telesman, J., Eds.; TMS: Warrendale, PA, USA, 2012; pp. 823–832. Available online: https://www.tms.org/Superalloys/10.7449/2012/Superalloys_2012_823_832.pdf (accessed on 1 October 2020).
- Epishin, A.; Petrushin, N.; Nolze, G.; Gerstein, G.; Maier, H.J. Investigation of the γ′-Strengthened Quaternary Co-Based Alloys Co-Al-W-Ta. Met. Mater. Trans. A 2018, 49, 4042–4057. [Google Scholar] [CrossRef]
- Fisher, E. On the elastic moduli of nickel rich Ni-Al alloy single crystals. Scr. Met. 1986, 20, 279–284. [Google Scholar] [CrossRef]
- Kuhn, H.-A.; Sockel, H.G. Contributions of the Different Phases of Two Nickel-Base Superalloys to the Elastic Behaviour in a Wide Temperature Range. Phys. Status Solidi 1990, 119, 93–105. [Google Scholar] [CrossRef]
- Fahrmann, M.; Hermann, W.; Boegli, A.; Pollock, T.; Sockel, H. Determination of matrix and precipitate elastic constants in (γ–γ′) Ni-base model alloys, and their relevance to rafting. Mater. Sci. Eng. A 1999, 260, 212–221. [Google Scholar] [CrossRef]
- Ichitsubo, T.; Koumoto, D.; Hirao, M.; Tanaka, K.; Osawa, M.; Yokokawa, T.; Harada, H. Elastic anisotropy of rafted Ni-base superalloy at high temperatures. Acta Mater. 2003, 51, 4863–4869. [Google Scholar] [CrossRef]
- Dye, D.; Coakley, J.; Vorontsov, V.A.; Stone, H.J.; Rogge, R. Elastic moduli and load partitioning in a single-crystal nickel superalloy. Scr. Mater. 2009, 61, 109–112. [Google Scholar] [CrossRef]
- Harris, K.; Erickson, G.L.; Sikkenga, S.L.; Brentnall, W.D.; Aurrecoechea, J.M.; Kubarych, K.G. Development of two rhenium containing superalloys for single crystal blade and directionally solidified vane applications in advanced turbine engines. J. Mater. Eng. Perform. 1993, 2, 481–487. [Google Scholar] [CrossRef]
- Brückner, U.; Epishin, A.; Link, T. Local X-ray diffraction analysis of the structure of dendrites in single-crystal nickel-base superalloys. Acta Mater. 1997, 45, 5223–5231. [Google Scholar] [CrossRef]
- Brückner, U.; Epishin, A.; Link, T.; Dressel, K. The influence of the dendritic structure on the γ/γ′-lattice misfit in the single-crystal nickel-base superalloy CMSX-4. Mater. Sci. Eng. A 1998, 247, 23–31. [Google Scholar] [CrossRef]
- Förster, F. Ein neues Messverfahren zur Bestimmung des Elastizitätsmoduls und der Dämpfung. Z. Metallkunde 1937, 29, 109–115. [Google Scholar]
- ASTM International. Standard Test Method for Dynamic Young’s Modulus, Shear Modulus, and Poisson’s Ratio by Sonic Resonance. Revision 13. ASTM E1875. Available online: https://www.astm.org/Standards/E1875.htm (accessed on 1 December 2020).
- Zienkiewicz, O.C.; Taylor, R.L. The Finite Element Method, 5th ed.; Butterworth & Heinemann: Oxford, UK, 2000; Volume 1. [Google Scholar]
- Abaqus/Standard. 3ds.com. Available online: https://www.3ds.com/products-services/simulia/products/abaqus/abaqusstandard/ (accessed on 1 February 2021).
- Link, T.; Epishin, A.; Gottwald, A.; Wichmann, T. Quantitative analysis of the structure of single crystal superalloys. In Proceedings of the Fortschritte in der Metallographie, 37 Metallographie-Tagung, Berlin, Germany, 17–19 September 2003; Portella, P.D., Ed.; Werkstoff-Informationsges: Frankfurt, Germany, 2004; pp. 257–262. [Google Scholar]
- Cormier, J.; Milhet, X.; Mendez, J. Effect of very high temperature short exposures on the dissolution of the γ′ phase in single crystal MC2 superalloy. J. Mater. Sci. 2007, 42, 7780–7786. [Google Scholar] [CrossRef]
- Tiley, J.; Viswanathan, G.; Hwang, J.; Shiveley, A.; Banerjee, R. Evaluation of gamma prime volume fractions and lattice misfits in a nickel base superalloy using the external standard X-ray diffraction method. Mater. Sci. Eng. A 2010, 528, 32–36. [Google Scholar] [CrossRef]
- Glatzel, U. Microstructure and Internal Strains of Undeformed and Creep Deformed Samples of a Nickel-Base Superalloy; Verlag Dr. Köster: Berlin, Germany, 1994. [Google Scholar]
- Hemmersmeier, U.; Feller-Kniepmeier, M. Element distribution in the macro- and microstructure of nickel base superalloy CMSX-4. Mater. Sci. Eng. A 1998, 248, 87–97. [Google Scholar] [CrossRef]
- Roebuck, B.; Cox, D.; Reed, R. The temperature dependence of γ′ volume fraction in a Ni-based single crystal superalloy from resistivity measurements. Scr. Mater. 2001, 44, 917–921. [Google Scholar] [CrossRef]
- Caron, P. High γ′ Solvus New Generation Nickel-Based Superalloys for Single Crystal Turbine Blade Applications. In Proceedings of the Superalloys 2000, Seven Springs Mountain Resort, Champion, PA, USA, 17–21 September 2000; Pollock, T.M., Kissinger, R.D., Bowman, R.R., Green, K.A., McLean, M., Olson, S., Schirra, J.J., Eds.; TMS: Warrendale, PA, USA, 2000; pp. 737–746. [Google Scholar] [CrossRef]
- Mackay, R.; Gabb, T.P.; Garg, A.; Rogers, R.B.; Nathal, M. Influence of composition on microstructural parameters of single crystal nickel-base superalloys. Mater. Charact. 2012, 70, 83–100. [Google Scholar] [CrossRef]
- Epishin, A.; Link, T.; Klingelhöffer, H.; Fedelich, B.; Brückner, U.; Portella, P. New technique for characterization of microstructural degradation under creep: Application to the nickel-base superalloy CMSX-4. Mater. Sci. Eng. A 2009, 510–511, 262–265. [Google Scholar] [CrossRef]
- IMAGE J. Available online: https://imagej.nih.gov/ij/ (accessed on 5 December 2020).
- Hill, R. The Elastic Behaviour of a Crystalline Aggregate. Proc. Phys. Soc. Sect. A 1952, 65, 349–354. [Google Scholar] [CrossRef]
- Morris, P.R. Elastic constants of polycrystals. Int. J. Eng. Sci. 1970, 8, 49–61. [Google Scholar] [CrossRef]
- Matthies, S.; Humbert, M. On the Principle of a Geometric Mean of Even-Rank Symmetric Tensors for Textured Polycrystals. J. Appl. Crystallogr. 1995, 28, 254–266. [Google Scholar] [CrossRef]
- Mura, T. Micromechanics of Defects in Solids; Springer: Dordrecht, The Netherlands, 1982. [Google Scholar]
- Hill, R. Elastic properties of reinforced solids: Some theoretical principles. J. Mech. Phys. Solids 1963, 11, 357–372. [Google Scholar] [CrossRef]
- Thomson, W. Elements of a mathematical theory of elasticity. Philos. Trans. R. Soc. Lond. 1856, 146, 481–498. [Google Scholar] [CrossRef]
- Sutcliffe, S. Spectral Decomposition of the Elasticity Tensor. J. Appl. Mech. 1992, 59, 762–773. [Google Scholar] [CrossRef]
- Mehrabadi, M.M.; Cowin, S.C. eigentensors of linear anisotropic elastic materials. Q. J. Mech. Appl. Math. 1990, 43, 15–41. [Google Scholar] [CrossRef]
- Walpole, L.J. Fourth-rank tensors of the thirty-two crystal classes: Multiplication tables. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1984, 391, 149–179. [Google Scholar] [CrossRef]
- Matthies, S.; Humbert, M. The Realization of the Concept of a Geometric Mean for Calculating Physical Constants of Polycrystalline Materials. Phys. Status Solidi 1993, 177, K47–K50. [Google Scholar] [CrossRef]
- Brückner, U.; Epishin, A.; Nolze, G. Determination of the sign of the γ/γ′-misfit in nickel-base superalloys by use of spectral impure Cu(Cr) radiation. Scr. Mater. 1997, 36, 1279–1282. [Google Scholar] [CrossRef]

| T, °C | 900 | 950 | 1000 | 1050 | 1100 | 1150 | 1200 | 1250 | 1280 |
|---|---|---|---|---|---|---|---|---|---|
| 74.0 | 72.3 | 70.5 | 68.9 | 60.1 | 54.0 | 43.4 | 22.8 | 0 |
| T, °C | 24 | 200 | 400 | 600 | 800 | 1000 | 1100 | 1200 | 1250 | 1280 | 1300 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 250 | 243 | 236 | 227 | 218 | 199 | 193 | 189 | 186 | 185 | 185 | |
| 161 | 158 | 155 | 152 | 150 | 141 | 144 | 149 | 152 | 154 | 156 | |
| 129 | 123 | 117 | 110 | 102 | 93 | 87 | 79 | 74 | 70 | 69 |
| Elastic Compliances of Superalloy CMSX-4 | ||||
|---|---|---|---|---|
| , GPa−1 | a, 10−3 GPa−1 | b, 10−6 GPa−1 °C−1 | c, 10−6 GPa−1 | d, 10−6 °C−1 |
| 7.90 | 2.58 | 2.10 | 6.71 | |
| 3.08 | 1.17 | 0.886 | 6.84 | |
| 7.68 | 2.30 | 2.11 | 5.82 | |
| Elastic Compliances of Matrix | ||||
|---|---|---|---|---|
| , GPa−1 | a, 10−3 GPa−1 | b, 10−6 GPa−1 °C−1 | c, 10−6 GPa−1 | d, 10−6 °C−1 |
| 7.49 | 4.44 | 1.05 | 7.10 | |
| − | 2.90 | 2.12 | 0.399 | 7.31 |
| 7.19 | 2.89 | 3.26 | 5.43 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Epishin, A.; Fedelich, B.; Finn, M.; Künecke, G.; Rehmer, B.; Nolze, G.; Leistner, C.; Petrushin, N.; Svetlov, I. Investigation of Elastic Properties of the Single-Crystal Nickel-Base Superalloy CMSX-4 in the Temperature Interval between Room Temperature and 1300 °C. Crystals 2021, 11, 152. https://doi.org/10.3390/cryst11020152
Epishin A, Fedelich B, Finn M, Künecke G, Rehmer B, Nolze G, Leistner C, Petrushin N, Svetlov I. Investigation of Elastic Properties of the Single-Crystal Nickel-Base Superalloy CMSX-4 in the Temperature Interval between Room Temperature and 1300 °C. Crystals. 2021; 11(2):152. https://doi.org/10.3390/cryst11020152
Chicago/Turabian StyleEpishin, Alexander, Bernard Fedelich, Monika Finn, Georgia Künecke, Birgit Rehmer, Gert Nolze, Claudia Leistner, Nikolay Petrushin, and Igor Svetlov. 2021. "Investigation of Elastic Properties of the Single-Crystal Nickel-Base Superalloy CMSX-4 in the Temperature Interval between Room Temperature and 1300 °C" Crystals 11, no. 2: 152. https://doi.org/10.3390/cryst11020152
APA StyleEpishin, A., Fedelich, B., Finn, M., Künecke, G., Rehmer, B., Nolze, G., Leistner, C., Petrushin, N., & Svetlov, I. (2021). Investigation of Elastic Properties of the Single-Crystal Nickel-Base Superalloy CMSX-4 in the Temperature Interval between Room Temperature and 1300 °C. Crystals, 11(2), 152. https://doi.org/10.3390/cryst11020152






