Bridgman Growth and Physical Properties Anisotropy of CeF3 Single Crystals
Abstract
1. Introduction
2. Materials and Methods
2.1. Crystal Growth Prosess and Samples Preparation
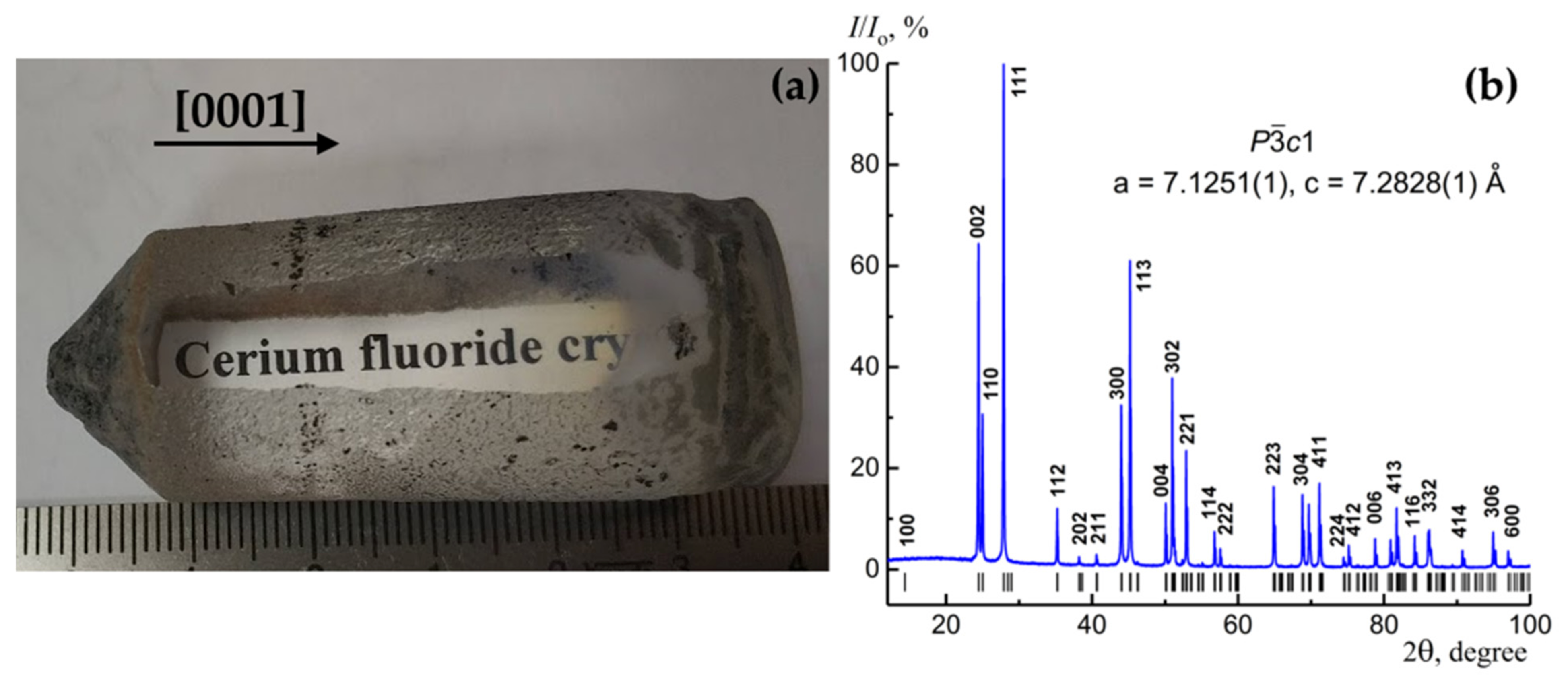
2.2. X-ray Diffraction (XRD) Analysis
2.3. Microhardness of Crystal
2.4. The Thermal Conductivity
2.5. The Electric Conductivity
3. Results and Discussion
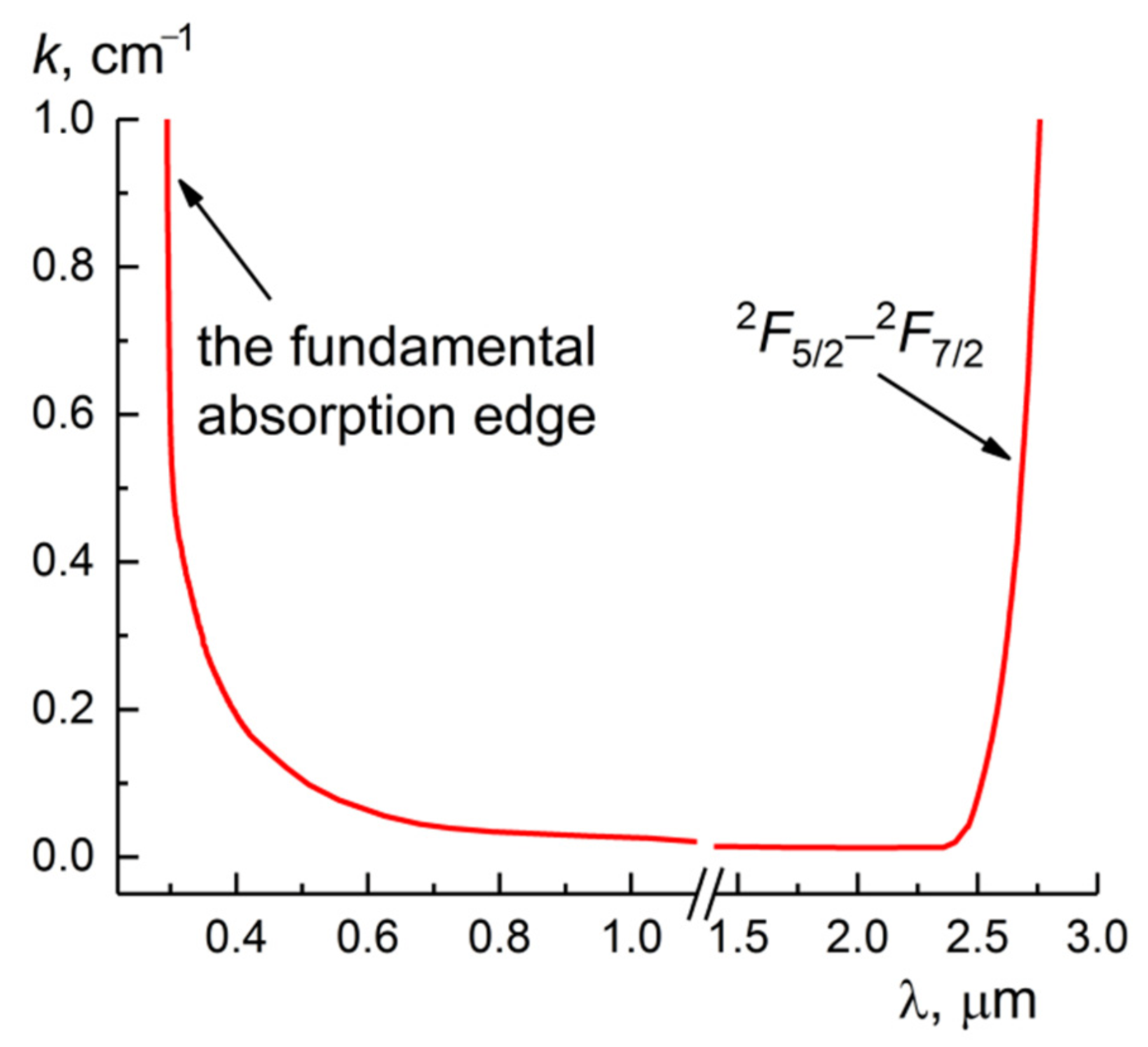
3.1. Crystal Growth and Characterization
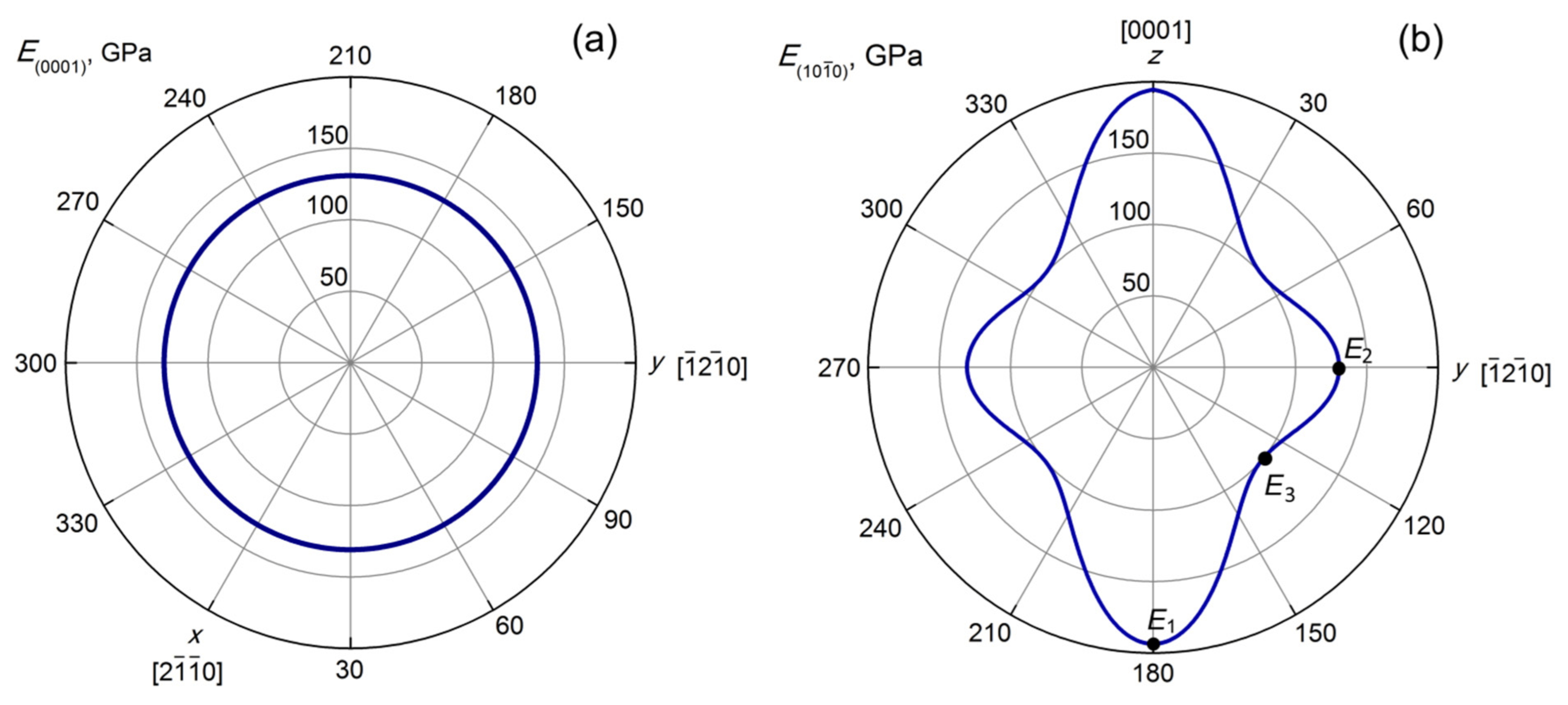
3.2. Elastic Properties of the CeF3 Crystals
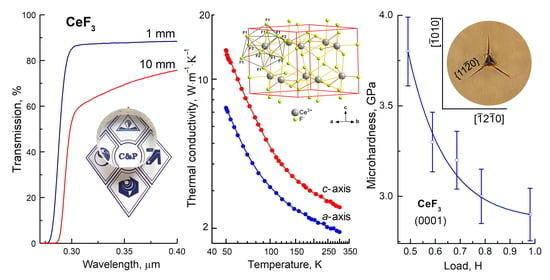
3.3. Microhardness Testing of the CeF3 Crystals
3.3.1. The Vickers Microhardness of the and Planes
3.3.2. The Vickers Microhardness of the (0001) Crystallographic Plane
3.3.3. The Berkovich Microhardness of the (0001) Plane of the CeF3 Crystal
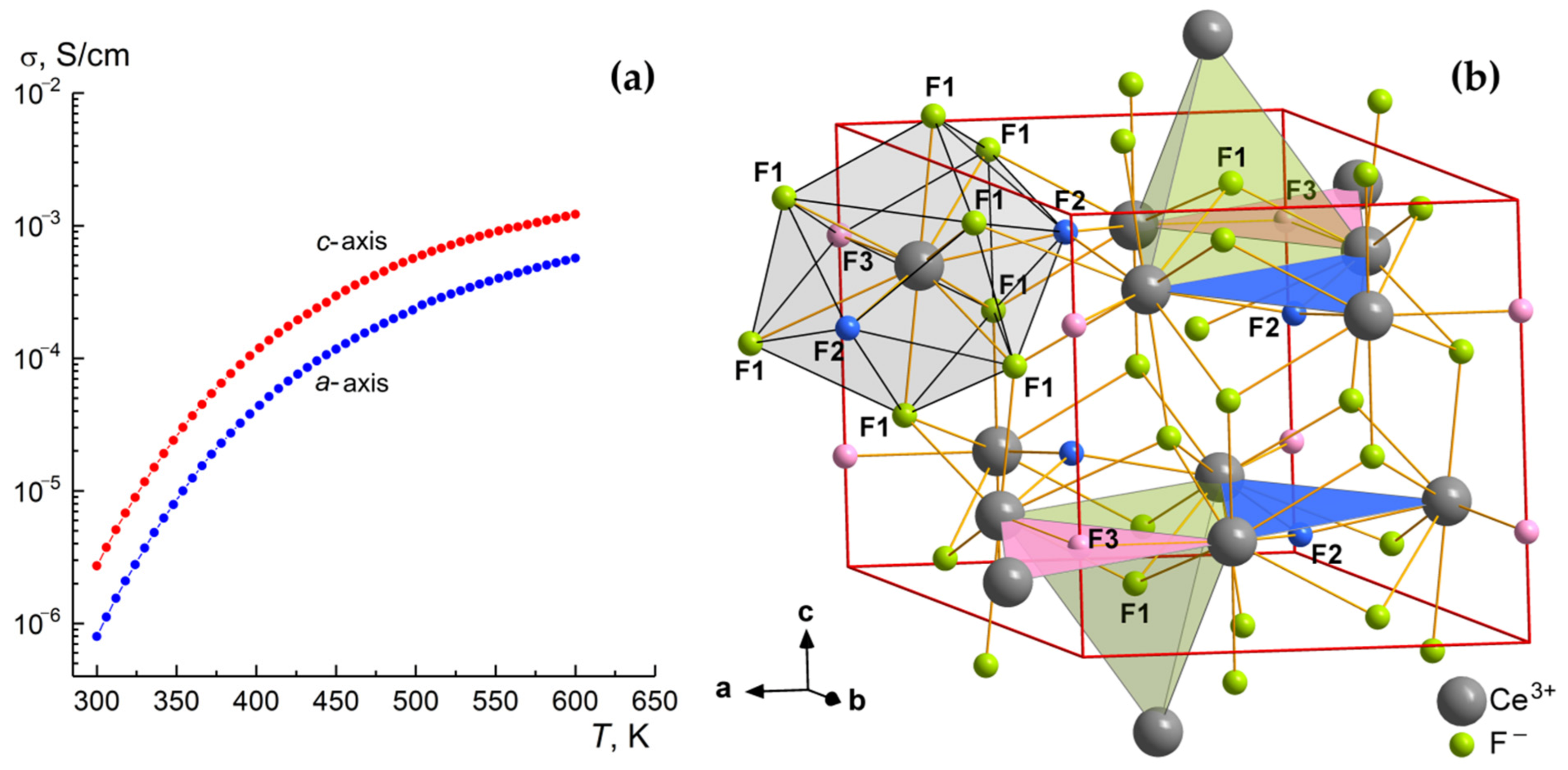
3.4. Ionic Conductivity Measurements
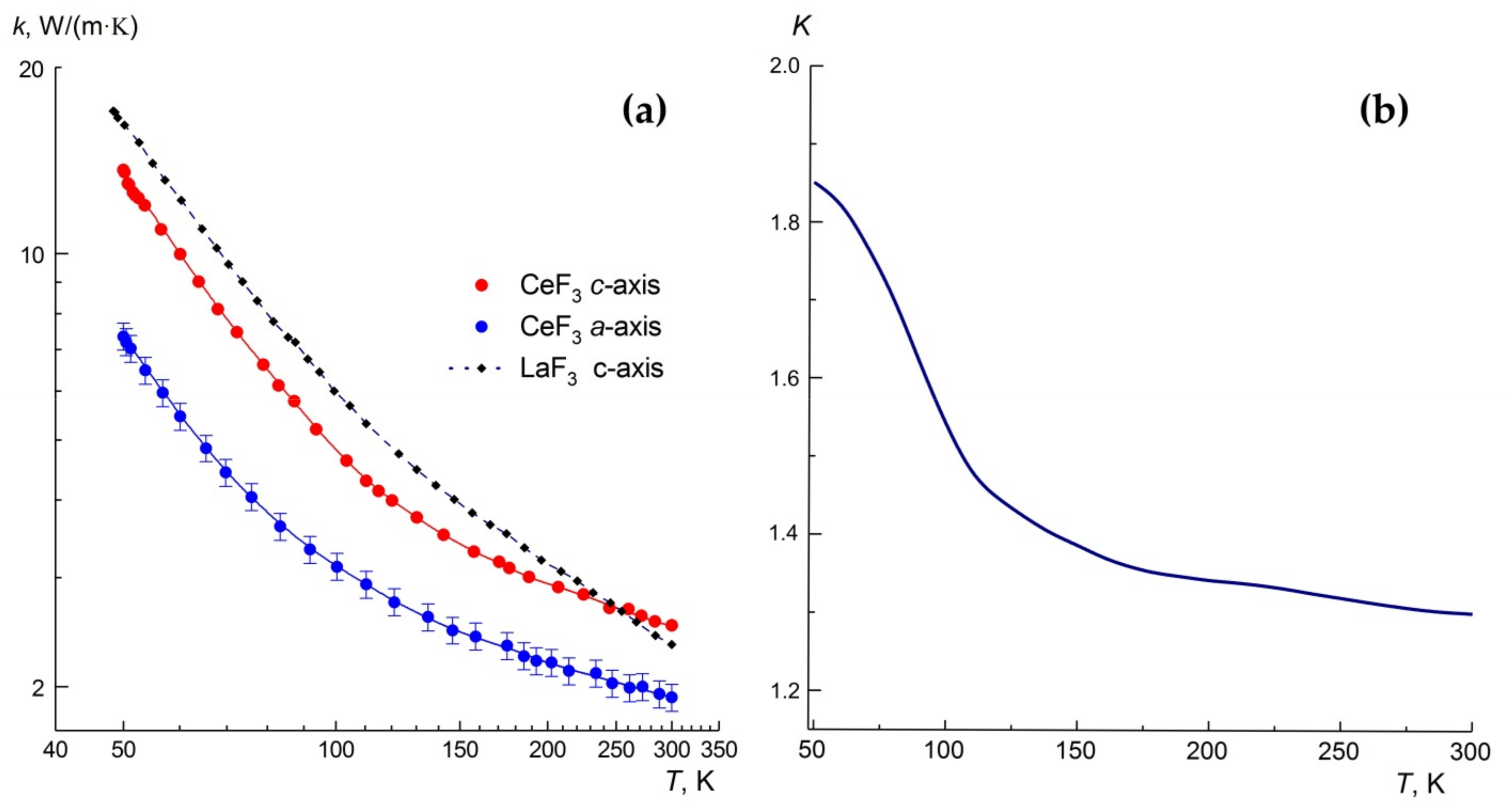
3.5. Anisotropy of the Thermal Conductivity of the CeF3 Crystals
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sobolev, B.P. The Yttrium, Lanthanum, and Lanthanide Trifluorides: Internal Periodicity of Phase Transitions. Crystallogr. Rep. 2019, 64, 713–723. [Google Scholar] [CrossRef]
- Pastor, R.C.; Harrington, J.A.; Gorre, L.E.; Chew, R.K. New coating materials for IR laser optical components. Mater. Res. Bull. 1979, 14, 543–551. [Google Scholar] [CrossRef]
- Elias, L.R.; Flach, R.; Yen, W.M. Variable bandwidth transmission filter for the vacuum ultraviolet: La1−xCexF3. Appl. Opt. 1973, 12, 138–139. [Google Scholar] [CrossRef] [PubMed]
- Krivandina, E.A.; Zhmurova, Z.I.; Sobolev, B.P.; Glushkova, T.M.; Kiselev, D.F.; Firsova, M.M.; Shtyrkova, A.P. Growth of R1−ySryF3−y crystals with rare earth elements of the cerium subgroup (R = La, Ce, Pr, or Nd; 0 ≤ y ≤ 0.16) and the dependence of their density and optical characteristics on composition. Crystallogr. Rep. 2006, 51, 895–901. [Google Scholar] [CrossRef]
- Fedorov, V.A.; Karimov, D.N.; Komar’kova, O.N.; Krivandina, E.A.; Zhmurova, Z.I.; Sobolev, B.P. Nanostructured crystals of fluorite phases Sr1−xRxF2+x (R are rare-earth elements) and their ordering. IV. Study of the optical transmission spectra in the 2-17-μm wavelength range. Crystallogr. Rep. 2010, 55, 122–126. [Google Scholar] [CrossRef]
- Connor, J.O.; Hargreaves, W.A. Lattice energy transfer and stimulated emission from CeF3:Nd3+. Appl. Phys. Lett. 1964, 4, 208–209. [Google Scholar] [CrossRef]
- Dmitruk, M.V.; Kaminskii, A.A.; Shcherbakov, I.A. Spectroscopic investigation of stimulated emission from lasers based on CeF3:Nd3+ crystals. Sov. Phys. JETP 1968, 27, 900–903. Available online: http://jetp.ac.ru/cgi-bin/dn/e_027_06_0900.pdf (accessed on 5 July 2021).
- Wang, Q.; Su, L.; Li, H.; Zheng, L.; Tang, H.; Guo, X.; Xu, J. Growth and spectroscopic characteristics of Er-doped CeF3 crystal. J. Cryst. Growth 2011, 318, 733–736. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, L.; Li, S.; Zhang, S.; Zhang, P.; He, M.; Xu, M.; Hang, Y. Crystal growth and 570 nm emission of Dy3+ doped CeF3 single crystal. J. Lumin. 2019, 215, 116707. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, L.; Quan, C.; Li, S.; Zhang, S.; Zhang, Y.; Fang, Q.; He, M.; Xu, M.; Hang, Y. Growth, thermal, and polarized spectroscopic properties of Nd:CeF3 crystal for dual-wavelength lasers. J. Lumin. 2020, 217, 117558. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, L.; Li, S.; Zhang, S.; Zhang, Y.; Fang, Q.; He, M.; Xu, M.; Hang, Y. Growth and mid-infrared luminescence property of Ho3+ doped CeF3 single crystal. Infrared Phys. Technol. 2020, 105, 103230. [Google Scholar] [CrossRef]
- Nowroozi, M.A.; Mohammad, I.; Molaiyan, P.; Wissel, K.; Munnangi, A.R.; Clemens, O. Fluoride ion batteries—past, present, and future. J. Mater. Chem. A 2021, 9, 5980–6012. [Google Scholar] [CrossRef]
- Sobolev, B.P.; Sorokin, N.I.; Bolotina, N.B. Nonstoichiometric single crystals M1–xRxF2+x and R1–yMyF3–y (M—Ca, Sr, Ba; R—rare earth elements) as fluorine-conducting solid electrolytes. In Progress in Fluorine Science; Tressaud, A., Poeppelmeier, K.V., Eds.; Elsevier: Amsterdam, The Netherlands, 2016; Volume 1, pp. 465–491. [Google Scholar] [CrossRef]
- Sorokin, N.I.; Karimov, D.N.; Sobolev, B.P. Increase in the fluorine-ion conductivity of single crystals of tysonite-type CeF3 superionic conductor by substituting polarized Cd2+ ions for Ce3+ ions. Crystallogr. Rep. 2018, 63, 769–773. [Google Scholar] [CrossRef]
- Sorokin, N.I.; Sobolev, B.P. Nonstoichiometric fluorides—solid electrolytes for electrochemical devices: A review. Crystallogr. Rep. 2007, 52, 842–863. [Google Scholar] [CrossRef]
- Dieudonné, B.; Chable, J.; Body, M.; Legein, C.; Durand, E.; Mauvy, F.; Fourcade, S.; Leblanc, M.; Maisonneuve, V.; Demourgues, A. The key role of the composition and structural features in fluoride ion conductivity in tysonite Ce1−xSrxF3−x solid solutions. Dalton Trans. 2017, 46, 3761–3769. [Google Scholar] [CrossRef]
- Moses, W.W.; Derenzo, S.E. Cerium fluoride, a new fast, heavy scintillator. IEEE Trans. Nucl. Sci. 1989, 36, 173–176. [Google Scholar] [CrossRef][Green Version]
- Kobayashi, M.; Ishii, M.; Krivandina, E.A.; Litvinov, M.M.; Peresypkin, A.I.; Prokoshkin, Y.D.; Rykalin, V.I.; Sobolev, B.P.; Takamatsu, K.; Vasil’chenko, V.G. Cerium fluoride, a highly radiation-resistive scintillator. Nucl. Instrum. Methods Phys. Res. A 1991, 302, 443–446. [Google Scholar] [CrossRef]
- Auffray, E.; Baccaro, S.; Beckers, T.; Benhammou, Y.; Belsky, A.N.; Borgia, B.; Boutet, D.; Chipaux, R.; Dafinei, I.; de Notaristefani, F.; et al. Extensive studies on CeF3 crystals, a good candidate for electromagnetic calorimetry at future accelerators. Nucl. Instrum. Methods Phys. Res. A 1996, 383, 367–390. [Google Scholar] [CrossRef]
- Yoshikawa, A.; Satonaga, T.; Kamada, K.; Sato, H.; Nikl, M.; Solovieva, N.; Fukuda, T. Crystal growth of Ce: PrF3 by micro-pulling-down method. J. Crys. Growth 2004, 270, 427–432. [Google Scholar] [CrossRef]
- Inagaki, T.; Yoshimura, Y.; Kanda, Y.; Matsumoto, Y.; Minami, K. Development of CeF3 crystal for high-energy electromagnetic calorimetry. Nucl. Instrum. Methods Phys. Res. A 2000, 443, 126–135. [Google Scholar] [CrossRef]
- Nikl, M. Wide band gap scintillation materials: Progress in the technology and material understanding. Phys. Stat. Solidi (a) 2000, 178, 595–620. [Google Scholar] [CrossRef]
- Molina, P.; Vasyliev, V.; Víllora, E.G.; Shimamura, K. CeF3 and PrF3 as UV-visible Faraday rotators. Opt. Express 2011, 19, 11786–11791. [Google Scholar] [CrossRef]
- Starobor, A.; Mironov, E.; Palashov, O. High-power Faraday isolator on a uniaxial CeF3 crystal. Opt. Lett. 2019, 44, 1297–1299. [Google Scholar] [CrossRef] [PubMed]
- Vojna, D.; Slezák, O.; Yasuhara, R.; Furuse, H.; Lucianetti, A.; Mocek, T. Faraday rotation of Dy2O3, CeF3 and Y3Fe5O12 at the mid-infrared wavelengths. Materials 2020, 13, 5324. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Wang, J.; Chen, J.; Dai, Y.; Su, L.; Li, X.; Kalashnikova, A.M.; Wu, F. Bridgman growth and magneto-optical properties of CeF3 crystal as Faraday Rotator. Opt. Mater. 2020, 100, 109675. [Google Scholar] [CrossRef]
- Zhao, G.; Zhao, C.; Yang, Y.; Xu, M.; Li, S.; Hang, Y. Magneto-optical performances of novel neodymium-doped CeF3 crystal. Mater. Lett. 2021, 130134. [Google Scholar] [CrossRef]
- Sobolev, B.P. Chemical aspects of crystal growth of multicomponent fluoride materials from the melt. Crystallogr. Rep. 2002, 47, S63–S75. [Google Scholar] [CrossRef]
- Pastor, R.C. Crystal growth of metal fluorides for CO2 laser operation: II. Optimization of the reactive atmosphere process (RAP) choice. J. Cryst. Growth 1999, 203, 421–424. [Google Scholar] [CrossRef]
- Fedorov, P.P.; Osiko, V.V. Crystal Growth of Fluorides. In Bulk Crystal Growth of Electronic, Optical & Optoelectronic Materials; Capper, P., Ed.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2005; pp. 339–355. [Google Scholar] [CrossRef]
- Bolotina, N.B.; Chernaya, T.S.; Verin, I.A.; Khrykina, O.N.; Sobolev, B.P. Dimorphism of RF3 (R = La–Nd) crystals based on the data of X-ray diffraction studies. Crystallogr. Rep. 2016, 61, 29–34. [Google Scholar] [CrossRef]
- Greis, O.; Cader, M.S.R. Polymorphism of high-purity rare earth trifluorides. Thermochim. Acta 1985, 87, 145–150. [Google Scholar] [CrossRef]
- Afanasiev, M.L.; Habuda, S.P.; Lundin, A.G. The symmetry and basic structures of LaF3, CeF3, PrF3 and NdF3. Acta Cryst. B 1972, 28, 2903–2905. [Google Scholar] [CrossRef]
- Zalkin, A.; Templeton, D.H.; Hopkins, T.E. The Atomic Parameters in the Lanthanum Trifluoride Structure. Inorg. Chem. 1966, 5, 1466–1468. [Google Scholar] [CrossRef]
- Smann, M. Über Verbindungen vom Anti-LaF3-Strukturtyp. Z. Kristallogr. 1965, 122, 399–406. [Google Scholar] [CrossRef]
- Laiho, R.; Lakkisto, M. Investigation of the refractive indices of LaF3, CeF3, PrF3 and NdF3. Philos. Mag. B 1983, 48, 203–207. [Google Scholar] [CrossRef]
- Laiho, R.; Lakkisto, M.; Levola, T. Brillouin scattering investigation of the elastic properties of LaF3, CeF3, PrF3 and NdF3. Philos. Mag. A 1983, 47, 235–244. [Google Scholar] [CrossRef]
- Hart, S. The elastic constants of cerium fluoride. Phys. Status Solidi A 1973, 17, K107–K110. [Google Scholar] [CrossRef]
- Savinkov, A.V.; Korableva, S.L.; Tagirov, M.S.; Suzuki, H.; Matsumoto, K.; Abe, S. Revised measurements and interpretation of magnetic properties of oriented CeF3 single crystals. J. Low Temp. Phys. 2016, 185, 603–608. [Google Scholar] [CrossRef]
- Fedorov, P.P.; Alexandrov, A.A. Synthesis of inorganic fluorides in molten salt fluxes and ionic liquid mediums. J. Fluor. Chem. 2019, 227, 109374. [Google Scholar] [CrossRef]
- Krivandina, E.A.; Zhmurova, Z.I.; Berezhkova, G.V.; Sobolev, B.P.; Glushkova, T.M.; Kiselev, D.F.; Firsova, M.M.; Shtyrkova, A.P. Crystal growth, density, and mechanical properties of La1−xSrxF3−x solid solutions (0 ≤ x ≤ 0.15) with the tysonite structure. Crystallogr. Rep. 1995, 40, 686–690. [Google Scholar]
- Popov, P.A.; Sidorov, A.A.; Kul’chenkov, E.A.; Anishchenko, A.M.; Avetisov, I.S.; Sorokin, N.I.; Fedorov, P.P. Thermal conductivity and expansion of PbF2 single crystal. Ionics 2017, 23, 233–239. [Google Scholar] [CrossRef]
- Korczak, W.; Mikołajczak, P. Crystal growth and temperature variation of the lattice parameters in LaF3, CeF3, PrF3 and NdF3. J. Cryst. Growth 1983, 61, 601–605. [Google Scholar] [CrossRef]
- Goldstein, R.V.; Gorodtsov, V.A.; Komarova, M.A.; Lisovenko, D.S. Extreme values of the shear modulus for hexagonal crystals. Scr. Mater. 2017, 140, 55–58. [Google Scholar] [CrossRef]
- Gorodtsov, V.A.; Lisovenko, D.S. Extreme values of Young’s modulus and Poisson’s ratio of hexagonal crystals. Mech. Mater. 2019, 134, 1–8. [Google Scholar] [CrossRef]
- Sizova, N.L.; Karimov, D.N.; Kosova, T.B.; Lisovenko, D.S. Mechanical properties of CeF3 single crystals. Crystallogr. Rep. 2019, 64, 942–946. [Google Scholar] [CrossRef]
- Anthony, J.W.; Bideaux, R.A.; Bladh, K.W.; Nicois, M.C. Handbook of Mineralogy; Mineral Data Publishing: Tucson, Arizona, 1997; 628p. [Google Scholar]
- Paradowski, M.L.; Korczak, W.; Misiak, L.E.; Korczak, Z. Growth and investigation of LaxRE1–xF3 (RE=Ce, Pr, Nd) single crystals. Proc. SPIE 1999, 47–51. [Google Scholar] [CrossRef]
- Shikimaka, O.; Grabko, D. Deformation created by Berkovich and Vickers indenters and its influence on surface morphology of indentations for LiF and CaF2 single crystals. J. Phys. D: Appl. Phys. 2008, 41, 074012. [Google Scholar] [CrossRef]
- Sangwal, K. Review: Indentation size effect, indentation cracks and microhardness measurement of brittle crystalline solids—some basic concepts and trends. Cryst. Res. Technol. 2009, 44, 1019–1037. [Google Scholar] [CrossRef]
- Mott, B.W. Micro-Indentation Hardness Testing; Butterworths: London, UK, 1956. [Google Scholar]
- Boyarskaya, Y.S. Deformation of Crystals in Microhardness Testing; Stiintza: Kishinev, Moldova, 1972. (In Russian) [Google Scholar]
- Lawn, B.R.; Evans, A.G.; Marshall, D.B. Elastic/Plastic indentation damage in ceramics: The median/Radial crack system. J. Am. Ceram. Soc. 1980, 63, 574–581. [Google Scholar] [CrossRef]
- Tanaka, K.; Kitahara, Y.; Ichinose, Y.; Iimura, T. Fracture analysis of single crystal manganese zinc ferrites using indentation flaws. Acta Metall. 1984, 32, 1719–1729. [Google Scholar] [CrossRef]
- Aronova, A.M.; Berezhkova, G.V.; Butashin, A.V.; Kaminskii, A.A. Strength and plasticity of single crystals of La3Ga5SiO14. Sov. Phys. Crystallogr. 1990, 35, 550–552. [Google Scholar]
- Sobolev, B.P. Lanthanum and lanthanide trifluorides: Lanthanide contraction and volume of fluorine ion. Crystallogr. Rep. 2000, 65, 175–181. [Google Scholar] [CrossRef]
- Schoonman, J.; Oversluizen, G.; Wapenaar, K.E.D. Solid electrolyte properties of LaF3. Solid State Ionics 1980, 1, 211–221. [Google Scholar] [CrossRef]
- Sorokin, N.I.; Sobolev, B.P. Anionic high-temperature conduction in single crystals of nonstoichiometric phases R1–yMyF3–y (R = La–Lu, M = Ca, Sr, Ba) with the tysonite (LaF3) structure. Russ. J. Electrochem. 2007, 43, 398–409. [Google Scholar] [CrossRef]
- Sinitsyn, V.V.; Lips, O.; Privalov, A.F.; Fujara, F.; Murin, I.V. Transport properties of LaF3 fast ionic conductor studied by field gradient NMR and impedance spectroscopy. J. Phys. Chem. Solids 2003, 64, 1201–1205. [Google Scholar] [CrossRef]
- Privalov, A.F.; Vieth, H.-M.; Murin, I.V. Nuclear magnetic resonance study of superionic conductors with tysonite structure. J. Phys. Cond. Matter 1994, 6, 8237–8243. [Google Scholar] [CrossRef]
- Lips, O.; Kruk, D.; Privalov, A.; Fujara, F. Simultaneous effects of relaxation and polarization transfer in LaF3-type crystals as sources of dynamic information. Solid State Nucl. Magn. Reson. 2007, 31, 141–152. [Google Scholar] [CrossRef]
- Fujara, F.; Kruk, D.; Lips, O.; Privalov, A.F.; Sinitsyn, V.; Stork, H. Fluorine dynamics in LaF3-type fast ionic conductors—Combined results of NMR and conductivity techniques. Solid State Ionics 2008, 179, 2350–2357. [Google Scholar] [CrossRef]
- Hoff, C.; Wiemhofer, H.-D.; Glumov, O.; Murin, I.V. Orientation dependence of the ionic conductivity in single crystals of lanthanum and cerium trifluoride. Solid State Ionics 1997, 101–103, 445–449. [Google Scholar] [CrossRef]
- Roos, A.; Aalders, A.F.; Schoonman, J.; Arts, A.F.M.; de Wijn, H.W. Electrical conduction and 19F NMR of solid solutions La1−xBaxF3−x. Solid State Ionics 1983, 9–10, 571–574. [Google Scholar] [CrossRef]
- Popov, P.A.; Moiseev, N.V.; Filimonova, A.V.; Fedorov, P.P.; Konyushkin, V.A.; Osiko, V.V.; Papashvili, A.G.; Smirnov, A.N.; Mironov, I.A. Thermal conductivity of LaF3–based single crystals and ceramics. Inorg. Mater. 2012, 48, 304–308. [Google Scholar] [CrossRef]
- Sorokin, N.I.; Karimov, D.N.; Buchinskaya, I.I.; Sobolev, B.P.; Popov, P.A. Electrical and thermal conductivities of congruently melting single crystals of isovalent M1–xM’xF2 solid solutions (M, M’ = Ca, Sr, Cd, Pb) in relation to their defect fluorite structure. Crystallogr. Rep. 2015, 60, 532–536. [Google Scholar] [CrossRef]
- Fedorov, P.P.; Sorokin, N.I.; Popov, P.A. Inverse correlation between the ionic and thermal conductivities of single crystals of M1–xRxF2+x (M = Ca, Ba, R—rare-earth element) fluorite solid solutions. Inorg. Mater. 2017, 53, 626–632. [Google Scholar] [CrossRef]
- Sorokin, N.I.; Sobolev, B.P. The intrinsic fluorine-ion conductivity of crystalline matrices of fluoride superionics: BaF2 (fluorite type) and LaF3 (tysonite type). Phys. Solid State 2018, 60, 2450–2456. [Google Scholar] [CrossRef]
- Aliev, A.E.; Krivorotov, V.F.; Khabibullaev, P.K. Specific heat and thermal conductivity of superionic conductors in the superionic phase. Phys. Solid State 1997, 39, 1378–1382. [Google Scholar] [CrossRef]
- Westrum, E.F., Jr.; Beale, A.F., Jr. Heat capacities and chemical thermodynamics of cerium (III) fluoride and cerium (IV) oxide from 5 to 300° K. J. Phys. Chem. 1961, 65, 353–355. [Google Scholar] [CrossRef]
- Popov, P.A.; Fedorov, P.P.; Osiko, V.V. Thermal conductivity of single crystals with a fluorite structure: Cadmium fluoride. Phys. Solid State 2010, 52, 504–508. [Google Scholar] [CrossRef]
- Spedding, F.H.; Beaudry, B.J.; Henderson, D.C.; Moorman, J. High temperature enthalpies and related thermodynamic functions of the trifluorides of Sc, Ce, Sm, Eu, Gd, Tb, Dy, Er, Tm, and Yb. J. Chem. Phys. 1974, 60, 1578–1588. [Google Scholar] [CrossRef]
- King, E.G.; Christensen, A.U. Low-Temperature Heat Capacity and High-Temperature Heat Content of Cerous Fluoride; Bureau of Mines, Report of Investigations 5510; U.S. Dept. of the Interior: Washington, DC, USA, 1959; 7p. [Google Scholar]
- Spedding, F.H.; Henderson, D.C. High temperature heat contents and related thermodynamic functions of seven trifluorides of the rare earths: Y, La, Pr, Nd, Gd, Ho, and Lu. J. Chem. Phys. 1971, 54, 2476–2483. [Google Scholar] [CrossRef]
- Lyon, W.G.; Osborne, D.W.; Flotov, H.E.; Grandjean, F. Thermodynamics of the lanthanide trifluorides. I. The heat capacity of lanthanum trifluoride, LaF3 from 5 to 350° K and enthalpies from 298 to 1477° K. J. Chem. Phys. 1978, 69, 167–173. [Google Scholar] [CrossRef]




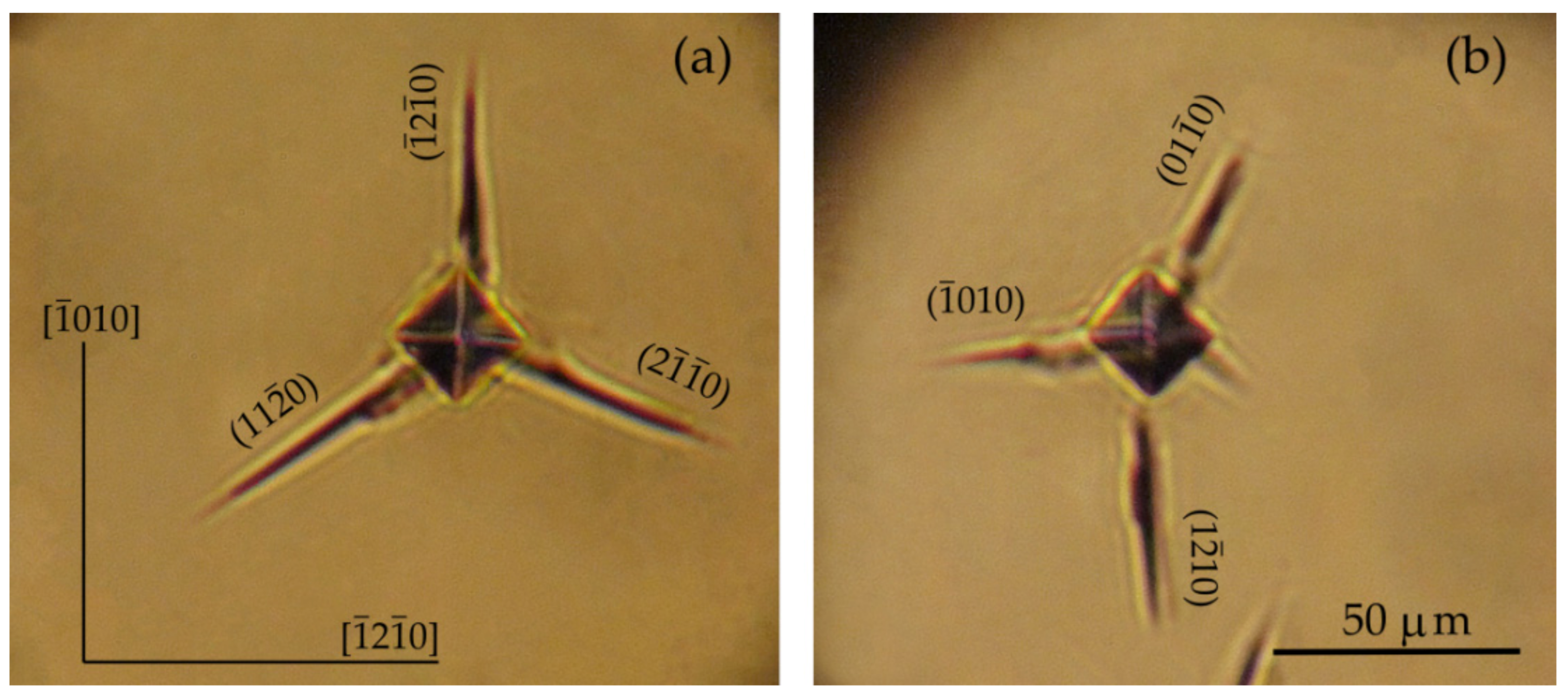


| Plane | Orientation of Indenter Diagonals | HV, GPa | Anisotropy Coefficient KI = HV max/ HV min |
|---|---|---|---|
| , | 2.9 | 1.00 | |
| , | 2.3 2.8 2.1 | 1.33 |
| Parameters | ||||
|---|---|---|---|---|
| LT Region | HT Region | LT Region | HT Region | |
| A, SK/cm | 9.8 × 103 | 56 | 1.5 × 104 | 59 |
| Hσ, eV | 0.45 | 0.26 | 0.44 | 0.22 |
| σdc, S/cm | 8.0 × 10−7 (300 K) | 5.7 × 10−4 (600 K) | 2.7 × 10−6 (300 K) | 1.2 × 10−3 (600 K) |
| Composition | T, K | Anisotropy Coefficient σ||c/σ⊥c | σ||c, S/cm | Reference |
|---|---|---|---|---|
| LaF3 | 300 500 | 2.0 1.6 | 1.0 × 10−6 1.5 × 10−3 | [57] [63] |
| CeF3 | 300 500 | 3.4 2.4 | 2.7 × 10−6 5.6 × 10−4 | Present work |
| La0.896Ba0.104F2.896 | 500 | 1.0 | 1.0 × 10−2 | [64] |
| Ce0.92Sr0.08F2.92 | 320 | 1.0 | 6.0 × 10−4 | [58] |
| Direction | 50 K | 100 K | 300 K |
|---|---|---|---|
| c-axis | 13.60 ± 0.70 | 4.82 ± 0.24 | 2.51 ± 0.12 1.74 [10] |
| a-axis | 7.35 ± 0.37 | 3.13 ± 0.16 | 1.92 ± 0.09 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karimov, D.N.; Lisovenko, D.S.; Ivanova, A.G.; Grebenev, V.V.; Popov, P.A.; Sizova, N.L. Bridgman Growth and Physical Properties Anisotropy of CeF3 Single Crystals. Crystals 2021, 11, 793. https://doi.org/10.3390/cryst11070793
Karimov DN, Lisovenko DS, Ivanova AG, Grebenev VV, Popov PA, Sizova NL. Bridgman Growth and Physical Properties Anisotropy of CeF3 Single Crystals. Crystals. 2021; 11(7):793. https://doi.org/10.3390/cryst11070793
Chicago/Turabian StyleKarimov, Denis N., Dmitry S. Lisovenko, Anna G. Ivanova, Vadim V. Grebenev, Pavel A. Popov, and Natalya L. Sizova. 2021. "Bridgman Growth and Physical Properties Anisotropy of CeF3 Single Crystals" Crystals 11, no. 7: 793. https://doi.org/10.3390/cryst11070793
APA StyleKarimov, D. N., Lisovenko, D. S., Ivanova, A. G., Grebenev, V. V., Popov, P. A., & Sizova, N. L. (2021). Bridgman Growth and Physical Properties Anisotropy of CeF3 Single Crystals. Crystals, 11(7), 793. https://doi.org/10.3390/cryst11070793