Abstract
Recycled aggregate concrete is a solution used to minimize the environmental impact of the concrete industry. Notwithstanding research worldwide validating structural applications of recycled aggregate concrete, specific design guidelines are lacking and are needed to address reservations of construction agents. Design guidelines should be based on reliability concepts, including the stochastic modeling of material properties and the calibration of design clauses through reliability methods. This paper concerns the concrete cover design of recycled aggregate concrete elements exposed to chloride ingress. Only coarse recycled aggregates produced from concrete waste are studied. The paper describes the chloride ingress model of fib Bulletin 34, presents experiments on the chloride ion migration of several analogue natural and recycled aggregate concrete mixes, tackles the stochastic modeling of the chloride migration coefficient, and calibrates concrete cover design for recycled aggregate concrete using reliability methods. The concrete cover design followed the deemed-to-satisfy provisions of Eurocode 2 and EN 206. The case studies used in the reliability analyses covered several design situations. A 5 mm increase of concrete cover is recommended as a simple option that ensures that the probability of depassivation due to chloride ingress on recycled aggregate concrete elements is equivalent to that for analogue natural aggregate concrete elements.
1. Introduction
1.1. General Introduction
The use of reinforced recycled aggregate concrete for structural purposes has been extensively investigated [1,2,3] and is a suitable solution to reduce the environmental impacts associated with landfill disposals and with the extraction of stone, since recycled aggregate concrete is made by replacing a fraction (that may be total) of natural aggregates (NA) with recycled aggregates, which are produced from construction and demolition waste (CDW). Several investigations argue that the best type of recycled aggregate for concrete production is the coarse fraction of recycled aggregate produced from concrete rejects [4]. Herein RA is used to designate coarse recycled concrete aggregates and RAC to designate concrete with replacement of NA with RA.
The main environmental benefit of RAC is recycling CDW and the minimization of the consumption of NA (either produced from stone crushing in quarries or from fluvial dredging). Notwithstanding the demonstration of the technical feasibility of RAC through laboratory experiments [3], full-scale testing [5], and through pilot applications [6], the construction industry avoids RAC and opts for NAC. This is partly due to the lack of specific guidelines for RAC design.
However, most research on RAC has not addressed a key issue: CDW is more heterogeneous than stone [7] and, therefore, the properties of RA are more variable than those of NA (as observed in [8]) and the properties of RAC are presumed to be more variable than those of natural aggregate concrete (NAC), despite reports of contradictory findings in the few investigations on the variability of the (mechanical) properties of RAC [9]. Nevertheless, research on the variability of the properties of RAC is scarce and hinders the evaluation of this hypothesis. If RAC is indeed more variable than NAC, its structural design needs to take into account reliability concepts—this is required because the design clauses of codes have an underlying probabilistic basis founded on reliability concepts [10,11,12].
This paper addresses the consequences of the heterogeneity of RA on the design of concrete cover for chloride ingress-prone environments. An experimental campaign is made to assess the influence of RA on the variability of the chloride diffusion coefficient, stochastic models are developed from the experimental data, and reliability analyses are made to calibrate concrete cover that ensure that its design for NAC and RAC is similarly reliable. To the authors’ best knowledge, this is the first investigation that presents an experimental campaign designed to assess the variability of the chloride ingress on RAC, as well as the first publication on the reliability-based calibration of concrete cover for RAC.
1.2. Properties of Recycled Aggregate Concrete
The effects of RA incorporation on the properties of RAC are caused by the composition of RA, which are produced by crushing concrete rejects and are composed of stone and attached mortar. The attached mortar is more porous, deformable, and weaker than stone [13]. This has direct detrimental consequences on the properties of concrete, as well as an indirect detrimental effect: since the attached mortar is rougher than stone, the mix design of RAC typically requires a larger water/cement ratio (w/c) for the same workability of NAC. This effect is not only caused by the roughness of the mortar, but also because most RA currently produced are either crushed in laboratories or in CDW plants that are not technically-developed. In both cases, crushing is typically made with a single jaw crusher, and the resulting particles are more elongated than those that result from riverbed dredging and conventional quarrying [14] (whose typical process includes a primary impact or jaw crusher and a secondary hammer mill or cone crusher, sometimes followed by tertiary crushing). More elongated particles result in less workable concrete [15] and offsetting this effect with a larger w/c leads to increases of concrete porosity, decreasing mechanical properties [16] and resistance to the ingress of external agents, including chloride ions.
Since RAC mixes are more permeable than equivalent NAC mixes, water absorption by capillarity and by immersion increases [3,17] and resistance to the ingress of carbon dioxide and chloride ions decreases [18,19]. Carbonation depths may increase up to 215% for total incorporation of RA when the mix design of RAC and NAC are similar (that is, only the incorporation of RA and the necessary increase of the w/c ratio differ) [20], but some studies argue that, if mixes with the same compressive strength are compared (this may be achieved if a decrease of workability is accepted or when water-reducing admixtures are used), the carbonation depth of NAC and RAC will be similar [21].
In the case of chloride ingress, the incorporation of RA is not expected to be as detrimental. The attached mortar of RA is partly composed of tricalcium aluminate, which binds chloride ions and reduces the effective chloride ion penetration [22]. This binding produces Friedel’s salt [23] and, for NAC, may only occur in the cement paste. A meta-analysis with data from rapid non-steady-state chloride migration tests [24] argued that when mixes with the same compressive strength are compared, the influence of RA on the ingress of chloride ions is negligible [25]. However, conclusions based on meta-analysis are skewed towards particular aspects of each experiment (lithology of the NA used, concrete mix design, relative porosity of the attached mortar of the RA and of the new mortar of RAC, the type of specimen tested [26], and dependence on a particular publication in which a very large number of compositions is analyzed, amongst other factors), possibly leading to erroneous conclusions when generalizing for recommendations for structural design.
A fair comparison between NAC and RAC should compare mixes developed with a similar mix design, raw materials, and test protocol. This was a major concern of this paper.
2. Chloride Cover Design and Reliability and Modeling of Depassivation by Chloride Ions
2.1. Eurocode 2 Concrete Cover Design
The Eurocode 2 design of concrete cover for chloride environments was made by following the recommendations for limiting values of concrete composition of EN 206 [27] and an environmental exposure class (XS1 to XS3) that represents the conditions for chloride ingress and corrosion of the reinforced concrete member. Then, based on a tabular format that relates the environmental exposure class with particular aspects related to the structural member: strength class, design working life, geometry (slab or otherwise), and special quality control measures, a minimum concrete cover for durability was determined. This concrete cover was then increased to account for deviations during construction.
This approach does not require calculations or traditional limit state design and was designated as a “deemed-to-satisfy” design: as long as the requirements determined by the standard are followed, the design is considered to ensure adequate functionality and safety. This type of design was used since durability modeling is complex and the relevant parameters needed for design (e.g., humidity, temperature, the modeling of the ingress of external agents into concrete) are not easily determined or consensual. Moreover, mechanical strength was indirectly assessed through compressive strength.
Ideally, “deemed-to-satisfy” design should ensure that, for different cases of design, the probability of failure () is similar. is an underlying concept of most design codes, because most parameters involved in design are random phenomena and current codes were developed with probabilistic concepts [28,29]. The is conceptually equivalent to what society accepts as the probability that a design that complies with a given limit state ends up failing according to that limit state during the design working life of the structure. The calculation of is difficult and, in some cases, no analytical expressions to calculate may be determined. Due to this reason, reliability methods are the most common tool used to estimate . A limit state function that determines the conditions for failure was established by comparing resistance (R) with action-effects (S):
and is given by the condition:
is typically quantified through the reliability index () which is given by:
where is the inverse of the standard normal distribution. Limit states with large consequences of failure, such as death or loss of limb (ultimate limit states) are associated with small values of (1 × 10−3 to 8.5 × 10−6)/large values of (3.1 to 4.3), while limit states related to functionality are associated with larger values of (6.7% to 50%)/smaller values of (0 to 1.5) [30].
In a recent publication [31] on the β obtained when the “deemed-to-satisfy” provisions of Eurocode 2 [32] for chloride cover design are used, a very heterogeneous range of β was found. This heterogeneity was observed between different environmental exposure classes and within the same environmental exposure class. Moreover, the “deemed-to-satisfy” provisions of different countries are not necessarily the same (e.g., there are differences in the minimum composition requirements of EN 206 [27], on the environmental conditions that correspond to a given environmental class, and on the concrete cover tolerance) and regional differences in β were also observed. Analogue findings were reported in a similar investigation [33,34,35] on the β that results from the “deemed-to-satisfy” provisions of Eurocode 2 [32] for carbonation cover design. In both investigations, the limit state function concerned the depassivation of reinforcement and either the carbonation model or the chloride ingress model of fib Bulletin 34 [23] were used.
2.2. Fib Bulletin 34 Model for Depassivation Due to Chloride Ingress
The model for depassivation due to chloride ingress presented in fib Bulletin 34 [23] was developed for chloride resistance assessed through the chloride migration coefficient tested under non-steady-state migration [24].
Depassivation occurs as soon as the critical chloride content at the reinforcement surface—which is at a distance from the surface of concrete equal to concrete cover (), reaches a critical value . and the chloride content inside concrete are defined as a percentage of cement by weight (wt. %/cement). The chloride content at depth x and time t was modeled as:
with: and ; erf is the Gauss error function.
Since depassivation is defined by , where is the reference period of the reliability analysis, the limit state equation is:
The meaning of all terms presented in Equations (4) and (5) is shown in Table 1. In this table, the stochastic models used in the reliability analyses of this paper are also presented.

Table 1.
Ratio of the standard deviations of recycled aggregate concrete (RAC) and natural aggregate concrete mixes.
Some of stochastic models shown in Table 1 are not those presented in fib Bulletin 34 [23] because the reliability analyses of this paper used the stochastic models of fib Bulletin 76 [31] since they are more recent. Furthermore, the stochastic models for the chloride migration coefficient () are those determined experimentally for the specific mixes produced in the paper. The first footnote of Table 1 concerns concrete’s mix design, which is presented in Section 3.
Additional information concerning this model can be read in [23,31].
3. Materials and Methods
3.1. Test Protocol
The experimental campaign included tests on the aggregates and on concrete mixes. The fine and coarse aggregates were characterized as follows:
- Shape index [37]—for coarse aggregates only;
- Loose bulk density [38];
- Saturated surface dry (SSD) density [39];
- 24 h water absorption [39];
- 10 min water absorption [40]—for RA only.
Mixing time lasted 10 min, so the 10 min water absorption was needed to determine the w/c of the mixes. The water absorbed by the RA during mixing is relevant and was estimated through the 10 min water absorption and the humidity content of the RA before mixing (tested before each batch). Then, this amount of water was added to that defined during mix design.
The tests made concrete types were:
- Slump [41], measured on a standard Abrams’ cone immediately after mixing;
- Compressive strength [42], tested with a load rate of 0.6 MPa/s;
- Non-steady-state chloride migration [24], in which samples are put into vacuum, submerged in a solution saturated with calcium hydroxide, and subjected to forced chloride ingress (through electrical current, a catholyte solution of sodium chloride, and an anolyte solution of sodium hydroxide) in a migration cell.
The specimens tested for compressive strength (150 mm cubes) were stored in a wet chamber (temperature of 20 ± 2 °C and relative humidity of 95 ± 5%) until the test age (3 specimens at 28 days and 2 at 91 days).
The non-steady-state chloride migration test was performed on cylindrical specimens (diameter of 100 mm, height of 50 mm) at 28 days of age. Curing was on the wet chamber for 14 days, followed by 14 additional days on a dry chamber (temperature of 20 ± 2 °C and relative humidity of 20 ± 5%). 13 to 15 specimens were tested. In the case of mix HSC-NAC (see Section 3.3), 9 specimens were tested at 28 days.
3.2. Raw Materials
The concrete mixes were produced using: siliceous river sand (Lisbon, Portugal) as natural fine aggregates; crushed limestone (Lisbon, Portugal) as NA; water from the public supply; either CEM I 42.5 R or CEM II B\L 32.5 N [43] (both from Lisbon, Portugal) as cement; fly ash (FA, sourced from Abrantes, Portugal) as an addition with: SiO2 content of 52%; Al2O3 of 19%; Fe2O3 of 16%; CaO of 5%; negligible contents of Na2O, MgO, K2O, TiO2, and CuO; and a high-range water-reducing admixture (HRWRA, procured from Lisbon, Portugal) with: pH: 5.0 ± 1.0; density: 1.07 ± 0.02 kg/litre; solid content of 32% ± 2.0%; chloride ions < 0.1%).
The RA were produced from ready-mixed concrete (specification: C30/37, XC3(P), Cl0.4, 14, S3 [27]). The maximum aggregate diameter () of the RA was 20 mm, a much larger value than that of the source concrete. This option was deliberate and is expected to increase any detrimental effect caused by the RA on the properties and heterogeneity of concrete, since it leads to a larger attached mortar content [44].
3.3. Concrete Mix Design
Five compositions with different strength class, compactness and binder were defined. Each composition was batched twice, either with NA only, or with fine sand and total replacement of NA with RA. Table 2 presents the mixes tested. Cement content by volume was 0.115 except in the case of CEM I: 280, whose cement content by volume was 0.092. The cement content by weight was 350 kg/m3 except CEM I: 280 (280 kg/m3) and CEM I—FAC (263 kg/m3 but 287.7 kg/m3 if the k-value concept of EN 206 [27] is used). In this table and elsewhere, references to cement type concern the specification of EN-197 [43] and all references to water content and w/c concern the effective water of mix design. The water absorbed by the RA was estimated as stated in Section 3.1.

Table 2.
Concrete mix design (kg/m3).
The two cements used differ in strength class (either 42.5 or 32.5) and composition: CEM I 42.5R is an ordinary Portland cement composed by at least 95% of clinker, while CEM II/B-L 32.5N replaces part of Portland cement by limestone filler (incorporated in the range of 21% to 35%), therefore having a smaller clinker content than CEM I 42.5R. Hydrated cement pastes made with CEM II/B-L 32.5N have a smaller content of calcium oxides. The same is valid for CEM I: FAC mixes, since these mixes have smaller content of cement due to volume substitution (25%) with FA. The mixes of composition CEM I: 280 were produced with a reduced clinker content to evaluate the properties of a permeable concrete.
The of all mixes was 20 mm. The grading of the aggregates was determined by adjusting a Faury’s curve to the grading of the fine natural aggregates and NA used (tested after [45]). The same grading of NA was imposed to RA by sieving. Figure 1 shows the combined grading of fine and coarse aggregates for all compositions.
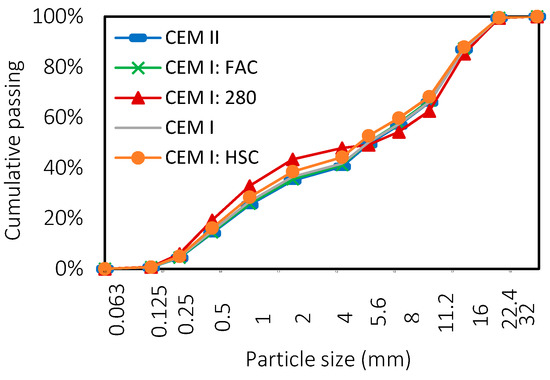
Figure 1.
Grading of the mixes.
The differences between the compositions of the analogue NAC and RAC mixes of the same composition are due to: (i) adjustments to the w/c through preliminary trial batches, made to ensure that all mixes comply with the target slump class (S3 [27]—125 ± 25 mm) and; (ii) the smaller density of RA in comparison to NA, which affects batching since the replacement of NA with RA was made in volume, so that the relative volume of aggregates and paste is not affected by the incorporation of RA.
Mixing took place indoors and lasted 10 min: two thirds of the total mixing water (effective plus water absorbed by the RA) and all aggregates (fine and coarse) were introduced in a tilting drum mixer; after six min, the cement, FA, and remaining water were added and mixing lasted for four additional minutes. In the case of CEM I: HSC-NAC and CEM I: HSC-RAC, after the initial six min of mixing, the cement, HRWRA and remaining water were added, mixing was resumed for two min, stopped for two minutes, and resumed again for another two min. All molds used to cast the specimens were plastic, compaction was made with an electrical shaft vibrator, and the specimens were demolded 16 to 24 h after casting.
4. Results
4.1. Aggregates
As found in several publications [4,13,46], the properties of RA are less suited for concrete production than those of NA:
- The shape index of NA was 15.39, while that of RA was 16.25. Larger shape indices are associated to more elongated particles and to workability losses;
- The 24 h water absorption of NA was small (1.3%), while that of RA was quite large (9.28%) and needs to be accounted for when batching;
- The 10 min water absorption of RA was 6.87% (74% of the 24 h water absorption). This value agrees with what has been reported in other publications [9,18,47] in which the same procedure [40] is used to estimate the water absorption over time;
- The density of RA (2478 kg/m3) is smaller than that of NA (2657 kg/m3). This is due to the smaller density of the attached mortar (a rough estimate is 2000 kg/m3 [47] for conventional concrete mix design) in comparison to the density of limestone (e.g., of the limestone used in this paper has a density of 2657 kg/m3). This was accounted for during mix design, since coarse aggregate replacement is done by volume (see Section 3.3).
4.2. Concrete
Table 3 shows the slump of all mixes after the preliminary trial mixes. The w/c is reproduced in this table as well. All mixes complied with the target slump (125 ± 25 mm). The full incorporation of RA led to increases of w/c between 7% and 9%, except for CEM I: 280, in which the incorporation of RA resulted in an increase of w/c of 13%. The w/c increases when RA were incorporated due to the roughness and elongated shape of RA, which increased both the energy needed for particle movement due to increased friction (roughness) and difficulty in rolling elongated particles (flakiness) [15], and due the quantity of paste needed to lubricate the particles, which resulted in a smaller amount of free water that promotes workability. The composition CEM I: 280 is associated with a larger increase of w/c when RA are used, since this mix has smaller volumes of water and binder; therefore, any increase in the amount of water and paste needed to lubricate the aggregates has a larger relative influence on workability.

Table 3.
Slump and w/c.
Despite the mixes of composition CEM I: HSC having a relative difference in slump similar to the others (7% increase for RAC), Table 3 shows that CEM I: HSC‑NAC could have been batched with a smaller w/c (the difference between the values of slump of this pair of mixes is larger than that of all other pairs). If mix CEM I: HSC-NAC had been produced with a smaller w/c, its durability and mechanical properties would improve.
Figure 2 presents the results of the compressive strength tests. In this figure and elsewhere, the standard deviation is marked as error bars.
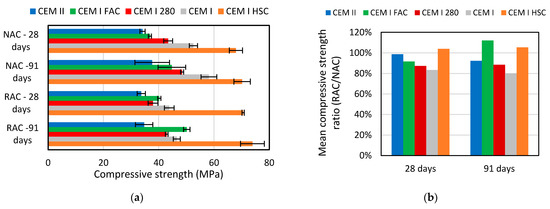
Figure 2.
Compressive strength: (a) Compressive strength of each mix; (b) Ratio of the mean compressive strength (RAC/NAC) of each composition.
Figure 2 shows that: (i) the mix design successfully resulted in pairs of NAC/RAC mixes that cover different strength demands; (ii) strength development over time was as expected: both CEM I: FAC mixes had the largest strength development over time, a well-known phenomenon due to the pozzolanic activities of concrete with FA [48] and both CEM I: HSC mixes had the smallest strength increase over time, due to the strength of limestone aggregates and of RA limiting the strength development of high strength concrete [9], as well as due to these mixes using a hard setting cement (CEM I) and a polycarboxylic HRWRA with long chains, which improves early-strength development [49]; (iii) the incorporation of RA decreased the compressive strength, except in the case of HSC. This was not expected and is understood by the comments concerning the w/c and slump of HSC-NAC.
The smallest detrimental influence of RA on the compressive strength was observed for CEM II and CEM I: FAC. Both were compositions whose strength was below the specified strength of the source concrete used to produce the RA; therefore, strength was less limited by the incorporation of (low) mechanical strength RA. Moreover, in the case of CEM I: FAC, the synergetic effect FA and RA also contributed to this observation, since the pozzolanic activities of FA with hydrated cement occur not only with the new cement paste, but also with the attached mortar of the RA. As time passes, the pozzolanic activities of the FA (thus, the synergy between FA and RA) tend to be more relevant and FAC-RAC becomes less porous. This explanation has been presented in other investigations in which similar results were reported [9,50].
The results of water absorption by capillarity are shown in Figure 3. The water absorption by capillarity of mix CEM II—NAC was not tested. In general, the incorporation of RA increased the water absorption through capillarity. This is due to two reasons: the increase of the w/c when RA are used, which leads to concrete with a more porous hydrated cement paste, and the porosity of these RA, which are composed of a larger-than-usual attached mortar content (see the observations made in Section 3.1 concerning ). The attached mortar will absorb water and contribute to the water absorbed by capillarity.
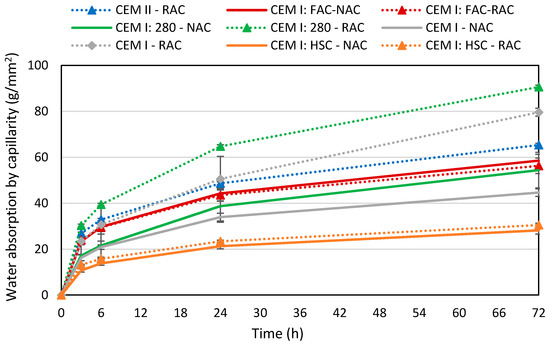
Figure 3.
Water absorption by capillarity.
A more detailed analysis shows that: (i) the incorporation of RA increased the water absorption by capillarity largely in the cases in which neither the HRWRA nor FA were used (78% in the case of CEM I and 66% in the case of CEM I: 280); (ii) when FA were used, the 72 h water absorption by capillarity decreases—this effect is attributed to the densification of the mesostructure due to the synergetic pozzolanic activity of FA and RA; (iii) the water absorption by capillarity increased by only 8% in the case of CEM I: HSC. This was a consequence of two factors: the comments made concerning the slump and w/c of CEM I: HSC—NAC, and the small w/c and dense hydrated cement paste of these mixes—since the cement paste of these mixes is dense, water does not penetrate deeply into concrete and only superficial aggregates are exposed to water ingress; therefore, the porosity of the RA does not have a relevant influence on the water absorption of concrete [3].
Figure 4 shows the chloride migration coefficients of all mixes. Figure 4b) shows that the comparison between compositions is as expected: the larger the compressive strength, the smaller the chloride diffusion coefficient, a finding that is related to less porous concrete being both stronger and less permeable, and thus less prone to the ingress of external agents. Moreover, the NAC mixes with the smallest content of clinker (CEM II: NAC and CEM I: NAC) are also those with the smallest compressive strength. The only exceptions concerning the trend towards compressive strength and chloride migration coefficient being negatively correlated are the pair of mixes of CEM I: 280. The chloride migration coefficient of CEM I: 280—NAC was smaller than that of CEM I—NAC, which goes against expectations but may be justified by experimental scatter (the standard deviations observed on this test were large), while the chloride migration coefficient of CEM I: 280—RAC was the largest observed. Since CEM I: 280 has a larger w/c than that of CEM II—RAC (the mix with the smallest compressive strength, made with a smaller w/c but with a cement of smaller specified compressive strength), this finding was expected.
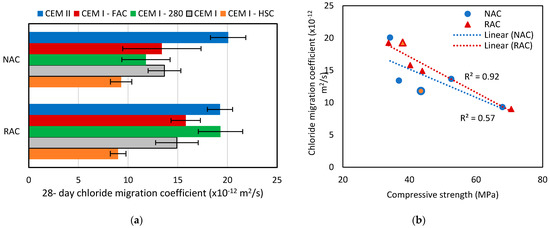
Figure 4.
Chloride migration coefficient: (a) 28-day chloride migration coefficient of all mixes; (b) Correlation between 28-day compressive strength and 28-day chloride migration coefficient. CEM I: 280 mixes represented with a yellow fill.
The next section of the paper concerns reliability analyses and requires the stochastic modelling of the chloride migration coefficient. This was analysed through normal probability paper plots. Two ideas are put forward:
1. Specific sets of data are prone to insufficient data about the tails of the probability distribution due to experimental testing necessarily leading to scarce, if any, data in these regions. This may result in choosing a probability distribution based on the best fit of various probability distributions based on goodness-of-fit testing leading to an arbitrary probability distribution. As argued in [51], tradition should take precedence when a probability distribution is chosen. Both fib Bulletin 34 [23] and fib Bulletin 76 [31] model the chloride migration coefficient as normal-distributed;
2. The option here was to check whether the fit of normal distributions suits the data well. Checking whether a traditionally-used distribution suits data rather than defining a best-fit distribution based on goodness-of-fit testing is the option taken in other documents related to stochastic modelling—e.g., [10,11,52].
Figure 5 presents normal distribution paper plots of the experimental results of the chloride migration coefficient of two mixes (a NAC and a RAC of different compositions). A suitable fit to a normal distribution was confirmed.
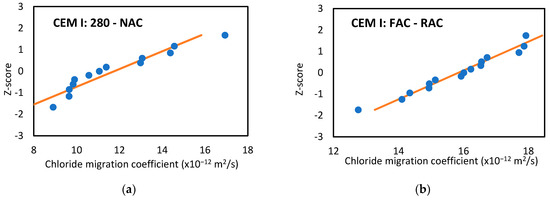
Figure 5.
Normal probability plots of chloride migration coefficient of: (a) CEM I: 280—NAC; (b) CEM I: FAC—RAC.
The stochastic modeling of normal distributions also requires values for mean and standard deviation (the coefficient of variation may also be used for this purpose). These were determined after: (i) analyzing, out of the standard deviation and the coefficient of variation, which is the least dependent on the particular mix tested, and then choosing that parameter as the representative for the second moment descriptor; (ii) analyzing the influence of the incorporation of RA on that second moment descriptor; (iii) determining a practical second moment descriptor for each mix.
Through least squares minimization, it was found that the most suitable statistical descriptor is standard deviation. Table 4 presents the ratio between the standard deviation of the NAC and RAC mixes of each composition. It is found that the ratio varies largely between compositions and that there is an unexpected trend towards the standard deviation of the chloride diffusion coefficient of RAC mixes being smaller than that of NAC mixes.

Table 4.
Ratio of the standard deviations of RAC and NAC mixes.
Publications on the variability of the compressive strength of RAC [9,53,54] reported that the full incorporation of RA does not result in any clear trend towards the variability of this property (this is not a consensual finding [55]). In [9], a hypothesis for this observation has been put forward: internal curing provided by RA [56] may mitigate micro-cracks caused by early drying and mitigate localized damage. Internal curing may also contribute to a homogeneous local w/c around the aggregates. Both effects would contribute to reducing the variability of the durability properties of concrete. However, specific research in this area is needed prior to definite conclusions and these findings may be exclusively due to test scatter. Conservatively assuming that this is the case, the mean value of the standard deviation of chloride migration coefficient of the NAC and RAC mix of each composition was used to define a suitable standard deviation for the stochastic model. The mean values were rounded up and are presented in Table 4.
Only the second moment descriptor is proposed in Table 4 and the reliability analyses will be made with the mean value of the chloride migration coefficient determined for each mix. This option was made based on the reasoning that, in future applications of the methodology used in this paper, experiments with a large sample size will not be made and that this paper’s proposal for the second moment descriptor and probability distribution of the chloride migration coefficient may be used by others for mixes with a similar mix design. However, tests with a small number of samples to determine the mean value of the chloride migration coefficient shall necessarily be available from specific testing of those mixes.
5. Reliability-Based Calibration of Concrete Cover
The reliability analyses were made assuming that failure occurs when the critical chloride content for depassivation is reached at a depth equal to the clear cover of the reinforcement.
Different case studies were analyzed. These concerned different environmental exposure classes, determined based on the concrete mix design requirements of EN 206 [27], as well as different structural members (slabs and beams), due to the different nominal covers prescribed in Eurocode 2 [32]. The nominal covers () were those that result from direct application of the requirements of Eurocode 2 [32] for durability plus the default (non-national) tolerance of 10 mm for execution deviations of Eurocode 2 [32]. The concrete cover and environmental exposure class of all compositions were XS1 and = 40 mm for slabs and a = 45 mm for columns, except in the case of CEM I: HSC, whose exposure class was XS3 and the covers were = 50 mm for slabs and = 55 mm for columns. Only chloride ingress due to seawater was analyzed. Compositions of class XS2 were not produced in the experimental program (Section 4) nor analyzed in this section, since elements subjected to the exposure class XS2 are submerged and have a negligible risk of corrosion [31,57].
The limit state function of the reliability analyses is that presented in Equations (4) and (5) for = 50 years, the design working life of most structures. The stochastic variables used in the limit state function are presented in Table 1. No stochastic variables were correlated.
The code used for the reliability analysis was validated through comparison with examples provided in fib Bulletin 76 [31]. The outputs of the reliability analysis [58] used in the analysis of results were β and the square of the direction cosines () of each stochastic variable. The of a stochastic variable is, for uncorrelated stochastic variables, the percentage of the total uncertainty of the structural design that is caused by uncertainty in that variable when transformed into the standard normal space.
Figure 6 presents the reliability indices of each case of design without specific partial factors for RAC. From this figure, it is understood that the incorporation of RA decreases by β for most compositions tested. Cases in which this did not occur were CEM I: HSC (in which the comparison of NAC and RAC is skewed due to the comments made in the discussion of the slump and w/c presented in Table 3) and CEM II.
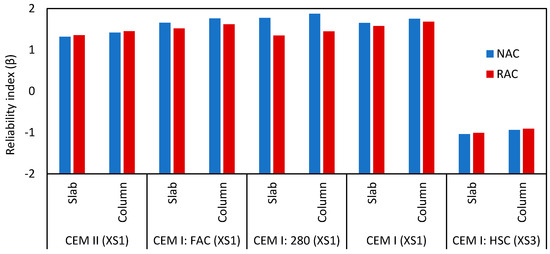
Figure 6.
Reliability indices of all cases studies. No changes to cover design due to RA.
Figure 7 presents the of some cases of design. No noteworthy differences were found between cases of design or due to the incorporation of RA. Parameters that do not depend on the incorporation of RA contribute the most to the uncertainty of the concrete’s cover design. The most relevant parameters (, the ageing exponent, and ) are related to the modeling of chloride ingress and the main reason for their preponderance on variability is their large standard deviation, which is caused by the wide applicability of parameter α (defined as independent of concrete mix design, including blend of binder) and epistemic uncertainty [59], which complicates the quantification of parameter , since this parameter depends on concrete mix design, geometrical properties, and environmental conditions [23]. The large of the two parameters is a compromise between practicability and available information vs. accuracy. The most relevant finding from the information presented in Figure 7 is that the influence of the uncertainty of the chloride migration coefficient on β is small (the of is 1%). This implies that the influence of the incorporation of RA on concrete cover design for depassivation due to chloride ingress may be assessed through experiments with a conventional (small) number of specimens, since the influence of the RA on β will be almost exclusively due to their influence on the mean chloride migration coefficient.
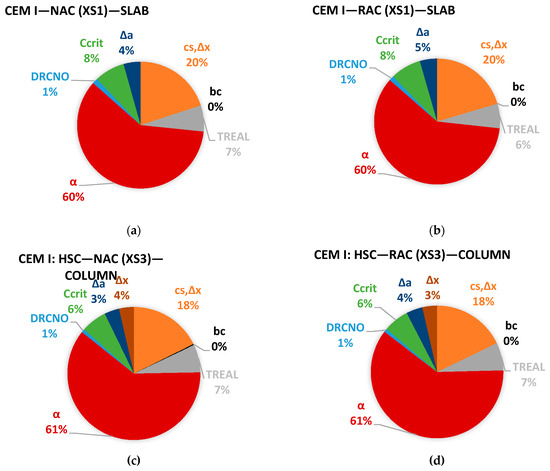
Figure 7.
of four cases of design: (a) CEM I—NAC, XS1, and slab; (b) CEM I: RAC, XS1, and slab; (c) CEM I: HSC—NAC, XS3, and column; (d) CEM I: HSC—RAC, XS3, and column.
Figure 8 shows the β values obtained by increasing concrete cover by 5 mm. This measure more than offsets the detrimental effect caused by RA on β in all cases but CEM I: 280, and is recommended as a measure for Eurocode 2 [32] cover design of structural members made with full incorporation of RA subjected to environmental exposure conditions of the XS class. It may be argued that this increase in cover was not strictly required, since the influence of RA on β was not large and the β of RAC members became larger than that of NAC in four of the five compositions analyzed. However, construction agents are sceptical towards the use of structural RAC and overly-cautious recommendations are advisable.
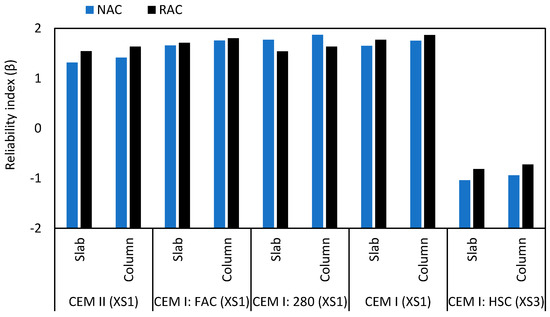
Figure 8.
Reliability indices of all cases studies. Cover increases of 5 mm when RA are used.
6. Conclusions
This paper studied the influence of the incorporation of coarse recycled aggregates produced from concrete waste on the design of reinforced concrete cover for environments prone to seawater chloride ingress. The requirement of research ground on reliability concepts was discussed and an experimental campaign covering a broad range of concrete mix design was conducted. This experimental campaign compared the properties of natural aggregate concrete and analogue recycled aggregate concrete mixes and assessed the chloride migration coefficient through tests with a large number of samples, so that this property could be stochastically modeled. To the authors’ best knowledge, this is the first publication on this topic.
In general, it was found that the incorporation of coarse recycled concrete aggregates:
- Decreased the compressive strength;
- Increased the water absorption by capillarity;
- Increased the chloride migration coefficient.
- These findings agree with the state of the art on the properties of recycled aggregate concrete and are caused by the porosity of recycled aggregates and by the increase in the water/cement ratio required to offset the influence of recycled aggregates on workability.
A stochastic model for the chloride migration coefficient was developed:
- Normal distributions suit the experimental data of chloride migration tests well;
- Recycled aggregates did not increase the variability of this property. Similar findings have been reported in other publications that studied the variability of the mechanical properties of concrete produced with recycled aggregates produced from concrete waste;
- The negligible influence of these recycled aggregates on the variability of the chloride migration coefficient may be due to internal curing mechanisms, though more research should follow to confirm this hypothesis.
Using the stochastic models developed and the chloride ingress model of fib Bulletin 34, the reliability of the cover design of recycled aggregate concrete slabs and columns was compared with that of natural aggregate concrete elements designed for the same situations:
- The use of recycled aggregates somewhat reduces the reliability index;
- This effect is caused by the influence of the incorporation of recycled aggregates on the mean value of the chloride migration coefficient;
- An increase of concrete cover of 5 mm is recommended as a compromise that ensures that the reliability index of recycled aggregate concrete is at least as large as that of natural aggregate concrete;
- The overall uncertainty of concrete cover design is mostly dependent on the uncertainty of parameters of design that do not depend on recycled aggregates (e.g., the ageing exponent of fib Bulletin 34 and the superficial chloride content). Therefore, the practical consequences of recycled aggregate incorporation on concrete cover design for chloride ingress may be assessed through the mean values of experimental data.
As future research, the authors suggest:
- The definition of ageing exponents that depend on the type of binder, in order to reduce the effect of the uncertainty of this parameter in the reliability;
- The experimental testing of the variability of other durability mechanisms, such as carbonation ingress and sulfate attack, and of concrete made with other types of recycled aggregates, such as fine recycled aggregates and recycled aggregates produced from other types of waste;
- The definition of strength classes and environmental exposure conditions that are ideal for applications of recycled aggregate concrete. This task has to be performed while taking into consideration the practical implications of using recycled aggregate concrete for the structural design (the volume of concrete will tend to increase when recycled aggregates are incorporated) and should be assessed through economic and environmental life-cycle assessments.
Author Contributions
Conceptualization, J.N.P. and J.d.B.; methodology, J.N.P.; software, J.N.P.; validation, J.d.B.; formal analysis, A.A. and J.N.P.; investigation, A.A.; resources, J.d.B.; data curation, A.A.; writing—original draft preparation, J.N.P.; writing—review and editing, J.d.B.; visualization, A.A. and J.N.P.; supervision, J.d.B.; project administration, J.d.B.; funding acquisition, J.d.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data are contained within the article.
Acknowledgments
The authors appreciate the support of the CERIS research center, of IST, University of Lisbon, of the Construction Laboratory of ISEL, the Polytechnic Institute of Lisbon, and of FCT (Portuguese Foundation for Science and Technology).
Conflicts of Interest
The authors declare no conflict of interest.
References
- De Brito, J.; Silva, R. Current status on the use of recycled aggregates in concrete: Where do we go from here? RILEM Tech. Lett. 2016, 10, 1–5. [Google Scholar] [CrossRef]
- Xiao, J. Recycled Aggregate Concrete Structures; Tracts in Civil Engineering; Springer: Berlin, Germany, 2018; 668p. [Google Scholar]
- Thomas, C.; Setién, J.; Polanco, J.A.; Alaejos, P.; Sánchez de Juan, M. Durability of recycled aggregate concrete. Constr. Build. Mater. 2013, 40, 1054–1065. [Google Scholar] [CrossRef]
- Silva, R.V.; de Brito, J.; Dhir, R.K. Properties and composition of recycled aggregates from construction and demolition waste suitable for concrete production. Constr. Build. Mater. 2014, 65, 201–217. [Google Scholar] [CrossRef]
- Pacheco, J.; de Brito, J.; Ferreira, J.; Soares, D. Destructive horizontal load tests of full-scale recycled aggregate concrete structures. ACI Struct. J. 2015, 112, 815–826. [Google Scholar] [CrossRef]
- Xiao, J.; Wang, C.; Ding, T.; Akbarnezhad, A. A recycled aggregate concrete high-rise building: Structural performance and embodied carbon footprint. J. Clean. Prod. 2018, 199, 868–881. [Google Scholar] [CrossRef]
- Khoury, E.; Ambrós, W.; Cazacliu, B.; Sampaio, C.H.; Remond, S. Heterogeneity of recycled concrete aggregates, an intrinsic variability. Constr. Build. Mater. 2018, 175, 705–713. [Google Scholar] [CrossRef]
- Pepe, M.; Grabois, T.M.; Silva, M.A.; Tavares, L.M.; Toledo Filho, R.D. Mechanical behaviour of coarse lightweight, recycled and natural aggregates for concrete. Proc. Inst. Civil Eng. Constr. Mater. 2018, 173, 70–78. [Google Scholar] [CrossRef]
- Pacheco, J.; de Brito, J.; Chastre, C.; Evangelista, L. Experimental investigation on the variability of the main mechanical properties of recycled aggregate concrete. Constr. Build. Mater. 2019, 201, 110–120. [Google Scholar] [CrossRef]
- Nowak, A.S.; Szerszen, M. Calibration of Design Code for Buildings (ACI 318): Part 1—Statistical Models for Resistance. ACI Struct. J. 2003, 100, 377–382. [Google Scholar] [CrossRef]
- Foster, S.J.; Stewart, M.G.; Loo, M.; Ahammed, M.; Sirivivatnanon, V. Calibration of Australian Standard AS3600 Concrete structures: Part I statistical analysis of material properties and model error. Aust. J. Struct. Eng. 2016, 17, 242–253. [Google Scholar] [CrossRef]
- Gulvanessian, H.; Holický, M. Reliability based calibration of Eurocodes considering a steel member. In Proceedings of the JCSS Workshop on Reliability Based Code Calibration, Zurich, Switzerland, 21–22 March 2002; 12p. [Google Scholar]
- Tam, V.W.Y.; Tam, C.M.; Le, K.N. Removal of cement mortar remains from recycled aggregate using pre-soaking approaches. Resour. Conserv. Recy. 2007, 50, 82–101. [Google Scholar] [CrossRef]
- De Brito, J.; Ferreira, J.; Pacheco, J.; Soares, D.; Guerreiro, M. Structural, material, mechanical and durability properties and behaviour of recycled aggregates concrete. J. Build. Eng. 2016, 6, 1–16. [Google Scholar] [CrossRef]
- Tattersall, G.H. Workability and Quality Control of Concrete; E&FN Spon: London, UK, 1991; p. 254. [Google Scholar]
- Pacheco, J.; de Brito, J.; Chastre, C.; Evangelista, L. Scatter of constitutive models of the mechanical properties of concrete: Comparison of major international codes. J. Adv. Concr. Technol. 2019, 17, 102–125. [Google Scholar] [CrossRef]
- Zaharieva, R.; Buyle-Bodin, F.; Skoczylas, F.; Wirquin, E. Assessment of the surface permeation properties of recycled aggregate concrete. Cem. Concr. Compos. 2003, 25, 223–232. [Google Scholar] [CrossRef]
- Soares, D.; de Brito, J.; Ferreira, J.; Pacheco, J. Use of coarse recycled aggregates from precast concrete rejects: Mechanical and durability performance. Constr. Build. Mater. 2014, 71, 263–272. [Google Scholar] [CrossRef]
- Zhang, K.; Xiao, J. Prediction model of carbonation depth for recycled aggregate concrete. Cem. Concr. Compos. 2018, 88, 86–99. [Google Scholar] [CrossRef]
- Silva, R.V.; Neves, R.; de Brito, J.; Dhir, R.K. Carbonation behaviour of recycled aggregate concrete. Cem. Concr. Compos. 2015, 62, 22–32. [Google Scholar] [CrossRef]
- Koulouris, A.; Limbachiya, M.C.; Fried, A.N.; Roberts, J.J. Use of recycled aggregate in concrete application: Case studies. In Proceedings of the International Conference on Sustainable Waste Management and Recycling: Challenges and Opportunities; Limbachiya, M.C., Roberts, J.J., Eds.; Thomas Telford: London, UK, 2004; pp. 245–257. [Google Scholar]
- Villagran-Zaccardi, Y.A.; Zega, C.J.; Di Maio, A.A. Chloride penetration and binding in recycled concrete. J. Mater. Civ. Eng. 2008, 20, 449–455. [Google Scholar] [CrossRef]
- fib Bulletin 34: Model Code for Service Life Design; fib: Lausanne, Switzerland, 2006; p. 116.
- NT-Build-492. Concrete, Mortar and Cement-Based Repair Materials: Chloride Migration Coefficient from Non-Steady-State Migration Experiments; Nordtest: Espoo, Finland, 1999; p. 8. [Google Scholar]
- Silva, R.V.; Brito, J.d.; Neves, R.; Dhir, R. Prediction of chloride ion penetration of recycled aggregate concrete. Mater. Res. 2015, 18, 427–440. [Google Scholar] [CrossRef]
- Pacheco, J.; de Brito, J.; Chastre, C.; Evangelista, L. Probabilistic conversion of the compressive strength of cubes to cylinders of natural and recycled aggregate concrete specimens. Materials 2019, 12, 280. [Google Scholar] [CrossRef] [PubMed]
- EN-206. Concrete: Specification, Performance, Production and Conformity. Incorporating Corrigendum May 2014; CEN: Brussels, Belgium, 2013; p. 98. [Google Scholar]
- Vrouwenvelder, T. Eurocode1, basis of design, background information. IABSE Rep. 1996, 74, 25–32. [Google Scholar]
- Gulvanessian, H.; Calgaro, J.A.; Holicky, M. Designers’ guide to EN1990 Eurocode: Basis of structural design. In Designers’ Guide to the Eurocodes; Thomas Telford: London, UK, 2002; p. 197. [Google Scholar]
- ISO-2394:1998. General Principles on Reliability for Structures; ISO: Geneve, Switzerland, 1998; p. 76. [Google Scholar]
- fib Bulletin 76: Benchmarking of Deemed-to-Satisfy Provisions in Standards; fib: Lausanne, Switzerland, 2015; p. 191.
- EN-1992-1-1. Eurocode 2—Design of Concrete Structures: Part 1-1: General Rules and Rules for Buildings; Comité Européen de Normalisation (CEN): Brussels, Belgium, 2008; p. 259. [Google Scholar]
- Von Greve-Dierfeld, S.; Gehlen, C. Performance-based durability design, carbonation, part 3: PSF approach and a proposal for the revision of deemed-to-satisfy rules. Struct. Concr. 2016, 17, 718–728. [Google Scholar] [CrossRef]
- Von Greve-Dierfeld, S.; Gehlen, C. Performance based durability design, carbonation part 1—Benchmarking of European present design rules. Struct. Concr. 2016, 17, 309–328. [Google Scholar] [CrossRef]
- Von Greve-Dierfeld, S.; Gehlen, C. Performance-based durability design, carbonation part 2—Classification of concrete. Struct. Concr. 2016, 17, 523–532. [Google Scholar] [CrossRef]
- JCSS. Probabilistic Model Code. Part 3: Material Properties. 2001. Available online: https://www.jcss-lc.org/publications/jcsspmc/part_iii.pdf (accessed on 11 March 2021).
- EN-933-4. Tests for Geometrical Properties of Aggregates. Determination of Particle Shape. Shape Index; Comité Européen de Normalisation (CEN): Brussels, Belgium, 2008; p. 14. [Google Scholar]
- EN-1097-3. Tests for Mechanical and Physical Properties of Aggregates. Determination of Loose Bulk Density and Voids; Comité Européen de Normalisation (CEN): Brussels, Belgium, 1998; p. 10. [Google Scholar]
- EN-1097-6. Tests for Mechanical and Physical Properties of Aggregates. Determination of Particle Density and Water Absorption; Comité Européen de Normalisation (CEN): Brussels, Belgium, 2013; p. 54. [Google Scholar]
- Rodrigues, F.; Evangelista, L.; de Brito, J. A new method to determine the density and water absorption of fine recycled aggregates. Mater. Res. 2013, 16, 1045–1051. [Google Scholar] [CrossRef]
- EN-12350-2. Testing Fresh Concrete. Slump-Test; Comité Européen de Normalisation (CEN): Brussels, Belgium, 2009; p. 12. [Google Scholar]
- EN-12390-3. Testing Hardened Concrete. Part3: Compressive Strength of Test Specimens; Comité Européen de Normalisation (CEN): Brussels, Belgium, 2009; p. 22. [Google Scholar]
- EN-197. Cement. Composition, Specifications and Conformity Criteria for Common Cements; Comité Européen de Normalisation (CEN): Brussels, Belgium, 2011; p. 50. [Google Scholar]
- Sanchez de Juan, M.; Alaejos Gutierrez, P. Study on the influence of attached mortar content on the properties of recycled concrete aggregate. Constr. Build. Mater. 2009, 23, 872–877. [Google Scholar] [CrossRef]
- EN-933-1. Tests for Geometrical Properties of Aggregates. Determination of Particle Size Distribution. Sieving Method; Comité Européen de Normalisation (CEN): Brussels, Belgium, 2012; p. 22. [Google Scholar]
- Pedro, D.; de Brito, J.; Evangelista, L. Performance of concrete made with aggregates recycled from precasting industry waste: Influence of the crushing process. Mater. Struct. 2015, 48, 3965–3978. [Google Scholar] [CrossRef]
- Lavado, J.; Bogas, J.; de Brito, J.; Hawreen, A. Fresh properties of recycled aggregate concrete. Constr. Build. Mater. 2020, 233, 117322. [Google Scholar] [CrossRef]
- Kurda, R.; de Brito, J.; Silvestre, J.D. A comparative study of the mechanical and life cycle assessment of high-content fly ash and recycled aggregates concrete. J. Build. Eng. 2020, 29, 101173. [Google Scholar] [CrossRef]
- Hirschi, T.; Wombacher, F. Influence of different superplasticizers on UHPC. In Proceedings of the Second International Symposium on Ultra High Performance Concrete; Kassel University Pres: Kassel, Germany, 2008. [Google Scholar]
- Kurad, R.; Silvestre, J.D.; de Brito, J.; Ahmed, H. Effect of incorporation of high volume of recycled concrete aggregates and fly ash on the strength and global warming potential of concrete. J. Clean. Prod. 2017, 166, 485–502. [Google Scholar] [CrossRef]
- Thoft-Christensen, P.; Baker, M.J. Structural Reliability Theory and Its Applications; Springer: Berlin, Germany, 1982. [Google Scholar]
- Pacheco, J.; de Brito, J.; Chastre, C.; Evangelista, L. Statistical analysis of Portuguese ready-mixed concrete production. Constr. Build. Mater. 2019, 209, 283–294. [Google Scholar] [CrossRef]
- Henry, M.; Hagiwara, K.; Nishimura, T.; Kato, Y. Effect of recycled aggregate quality on variation and estimation of concrete strength. Proc. Jpn. Concr. Inst. 2011, 33, 1535–1540. [Google Scholar]
- Ying, J.; Xiao, J.; Meng, Q. On Probability Distribution of Chloride Diffusion Coefficient for Recycled Aggregate Concrete. Int. J. Concr. Struct. Mater. 2016, 10, 61–73. [Google Scholar] [CrossRef]
- Etxeberria, M.; Vazquez, E.; Mari, A.; Barra, M. Influence of amount of recycled coarse aggregates and production process on properties of recycled aggregate concrete. Cem. Concr. Res. 2007, 37, 735–742. [Google Scholar] [CrossRef]
- Yildirim, S.T.; Meyer, C.; Herfellner, S. Effects of internal curing on the strength, drying shrinkage and freeze–thaw resistance of concrete containing recycled concrete aggregates. Constr. Build. Mater. 2015, 91, 288–296. [Google Scholar] [CrossRef]
- LNEC-E465. Methodology for Estimating the Concrete Performance Properties Allowing to Comply with the Design Working Life of the Reinforced or Prestressed Concrete Structures under the Environmental Exposures XC and XS (in Portuguese); National Laboratory of Civil Engineering (Laboratório Nacional de Engenharia Civil—LNEC): Lisboa, Portugal, 2005; p. 25. [Google Scholar]
- Lemaire, M. Structural Reliability; Jone Wiley & Sons: Hoboken, NJ, USA, 2009; p. 504. [Google Scholar]
- Der Kiureghian, A.; Ditlevsen, O. Aleatory or epistemic? Does it matter? Struct. Saf. 2009, 31, 105–112. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).